降水临近预报通常是指未来短时间内的详细降雨预报, 用于预测待定区域的降水强度和位置等, 这种预报以分钟级、千米级或者街道级的频率展现^[1]. 准确的预报可以为公众提供及时的天气通知, 对保护人民的生命财产安全起着重大作用.

在气象雷达中, 雷达回波是指天气雷达通过发射电磁波探测降水粒子返回雷达并形成的回波图像, 气象预报员则可以根据回波图像分析降水的位置、强度和分布. 随着气象观测技术的发展, 多普勒天气雷达以其探测范围广, 时间间隔短等优势逐渐成为测量云、降水和强对流天气主要工具^[2,3]. 雷达回波外推则是利用过去一段时间探测到的雷达回波数据预测未来雷达回波强度变化, 从而直观的呈现未来天气状况, 已经发展为主要的降水临近预报方式.

雷达回波外推方法可分为两类: 传统的雷达回波外推方法、深度学习的雷达回波外推方法. 传统的雷达回波外推方法是比较基础的预报手段, 通常有单质心法^[4,5]、互相关法^[6,7]和光流法^[8,9]等. 单质心法主要使用记忆方式跟踪三维雷达, 适用于强雷暴单体, 当面临局部对流变化快的天气情况时预测效果较差^[10]. 互相关法通过计算相邻时空内降水回波的相关性推断回波运动信息, 在强对流天气下会逐渐失去跟踪有效性. 光流法通过计算相邻帧之间对应像素点的瞬时运动速度生成下一帧的预测, 它依赖于线性外推原理且计算成本较高, 因此难以满足实时预报的需求.

近年来, 深度学习技术在时间序列预测方面做出了巨大的贡献, 它把短程降水预报视为时间序列预测问题, 利用历史时间序列样本预测未来时空变量^[11]. 基于卷积的递归神经网络(convolutional recurrent network, ConvRNN)和卷积神经网络(convolutional neural network, CNN)在降水临近预报领域应用的最多. Shi等人^[12]提出ConvLSTM模型, 使用卷积结构捕获时间和空间信息. 之后, Shi等人^[13]又改进了ConvLSTM模型中的卷积递归结构, 提出了具有可学习卷积的TrajGRU模型. Wang等人^[14]基于ConvLSTM模型提出了PredRNN模型, 使用之字形的信息流传结构扩展了神经网络的感受野. Wang等人^[15]又提出MIM模型, 使用两个对称的MIM-N和MIM-S替换了遗忘门, 并将两者的差分信息作为输入以便学习时空运动的非平稳状态. 以上模型均建立在ConvRNN上, 这种模型都存在两个明显的问题. 首先是回波特征衰减, 这类模型使用固定的尺度提取时空特征只能实现单次的数据预测, 不能以并行的方式实现训练和预测, 从而忽略了时空运动的复杂性^[16]. 随着预测提前期的增加, 不同时刻固定尺度的存储单元之间的误差逐渐累积, 使得最终外推结果慢慢低于真实值. 其次是预测模糊问题, 由于卷积算子对平移不变性的归纳偏倚使得模型难以捕捉降水场的时空特征而逐渐产生了偏差^[17,18]. 这种空间变异性表示的缺失不仅使得预测图像变得模糊, 还会导致下游应用的误差扩大.

许多研究者试图使用基于端到端的CNN网络解决ConvRNN中的信息丢失问题. Trebing等人^[19]提出了SmaAt-UNet模型, 利用可分离卷积释放算力, 并在U-Net模型中增加了注意力机制. Gao等人^[20]提出SimVP模型, 使用Inception模块和群卷积捕获时空信息. 与使用堆叠方式的ConvRNN相比, 端到端的卷积时空预测模型能够更好地预防信息流传过程中的回波衰减, 并且实现了多步预测. 然而, 基于CNN的模型更偏向于空间维度的建模, 无法对时间特征精准建模, 会丢失不同尺度的时间特征信息.

面对预测模糊, 目前常用GAN^[21]网络来缓解. Jing等人^[22]提出一种AENN模型, 该模型是基于ConvLSTM和卷积神经网络的生成对抗性外推模型. Tian等人^[17]提出了GA-ConvGRU模型, 该模型将ConvGRU作为生成器进行优化, 但容易受到训练不稳定的影响. Gong等人^[23]提出AGAN网络, 试图增添雷达回波局部空间的变异性表示能力, 但该模型没有考虑到预测结果会在训练过程中产生动态变化, 只使用固定的权重让模型变得难以收敛. 与基于ConvRNN方法的模型相比, 使用ConvRNN作为生成器CNN作为判别器的模型经过训练, 可以生成更好的预测图像. 然而, GAN网络采用对抗性损失进行训练, 无法衡量真实图像和生成图像之间的差距.

综上, 现有的使用深度学习方式计算的时空相关性只能从固定的局部空间中学习相邻帧中有限的回波特征, 从而导致预测图像失去时空可变性. 而GAN网络存在严重的梯度消失问题, 模型训练困难. 因此, 本文基于CNN和GAN提出了一种多尺度生成对抗模型(MCGAN). 本文的主要工作如下.

(1)提出了一种基于编码器-解码器架构的多尺度卷积时空预测模型来构建生成器, 并利用设计的多尺度卷积块完成了对多个时间和空间尺度的统一建模. 另外, 本文设计了一个下采样门控单元以避免在下采样过程中产生的上下文信息丢失和重影问题.

(2)本文提出了一种动态时空变异性损失函数. 首先分析每个回波帧的数据分布, 为每个回波区间分配权重, 然后将权重赋予沿时空维度计算的变异系数, 并将其作为正则化项. 动态时空变异性损失在训练过程中实现了正则化, 具有表示时空变异性的特征.

(3)利用上海市公共雷达数据集验证了本文所提模型的有效性. 实验结果表明, 与ConvLSTM模型、TrajGRU模型、PredRNN模型和MIM模型相比, MCGAN模型有用更准确、更清晰的预测效果.

1 数据来源

本文使用的数据集是来自Chen等人^[24]提供的上海市公共雷达回波数据集. 该数据集由双偏振天气监视雷达——1988多普勒雷达(WSR-88D)收集的复合反射率数据组成, 覆盖了上海浦东地区. 该数据集的时间范围是2015年10月–2018年7月, 时间间隔是6 min, 使用体积扫描的方式生成了170000张经过线性转换的雷达回波灰度图像, 存储为PNG格式, 图像大小为501×501. 为方便训练, 首先要过滤掉非连续的帧, 接着使用滑动窗口生成了76779个长度为20的雷达回波图像样本, 训练集包含53745个序列样本, 测试集包含23034个序列样本. 每组样本的前10帧作为输入帧, 时间间隔为6 min, 后10帧作为预测帧, 时间间隔为12 min, 即使用前1 h的历史回波图预测未来2 h的预测回波图. 另外, 本文将数据集中每帧的基本反射率阈值都控制在了0–70 dBZ之间.

2 分析方法 2.1 生成对抗网络(GAN)

GAN^[21]由Goodfellow等人提出, 其目的是使生成目标尽可能地近似于真实目标的分布. 它由生成器和判别器组成, 两者皆是深度神经网络. 生成器学习输入变量的潜在信息而努力生成真实的数据分布, 判别器则是努力判断生成目标的真实性, 因此两者是互相对抗的关系. GAN通过玩最大最小值游戏实现目标的优化, 表示为:

$ \begin{split} \mathop {\min }\limits_G \mathop {\max }\limits_D V\left(D, G\right)=&{E}_{X\sim{p}_{{\mathrm{data}}}\left(X\right)}\left[\mathrm{log}\left(D\left(X\right)\right)\right]\\ &+{E}_{Z\sim{p}_{{\textit{z}}}\left({\textit{z}}\right)}\left[\mathrm{log}\left(1-D\left(G\left({\textit{z}}\right)\right)\right)\right]\end{split} $

(1)

其中, $G$表示生成器, $D$表示判别器. ${p_{{\mathrm{data}}}}\left( X \right)$是真实目标$X$的分布, ${p_{\textit{z}}}\left( {\textit{z}} \right)$是输入噪声的先验分布. 当在输入数据充分的情况下, 生成器和判别器以实现纳什均衡未目的不断交替训练. 在降水临近预报领域, 生成器输入的不是随机噪声, 而是时间序列雷达图像.

2.2 MCGAN模型

本文提出的MCGAN模型架构如图1所示. 历史雷达回波图像序列进入生成器生成预测图像, 再与对应时间点的地面观测图像组成样本对, 输入判别器进行判断. 生成器和判别器协同工作, 最终通过对抗性损失来优化整个网络.

2.2.1 多尺度卷积生成器

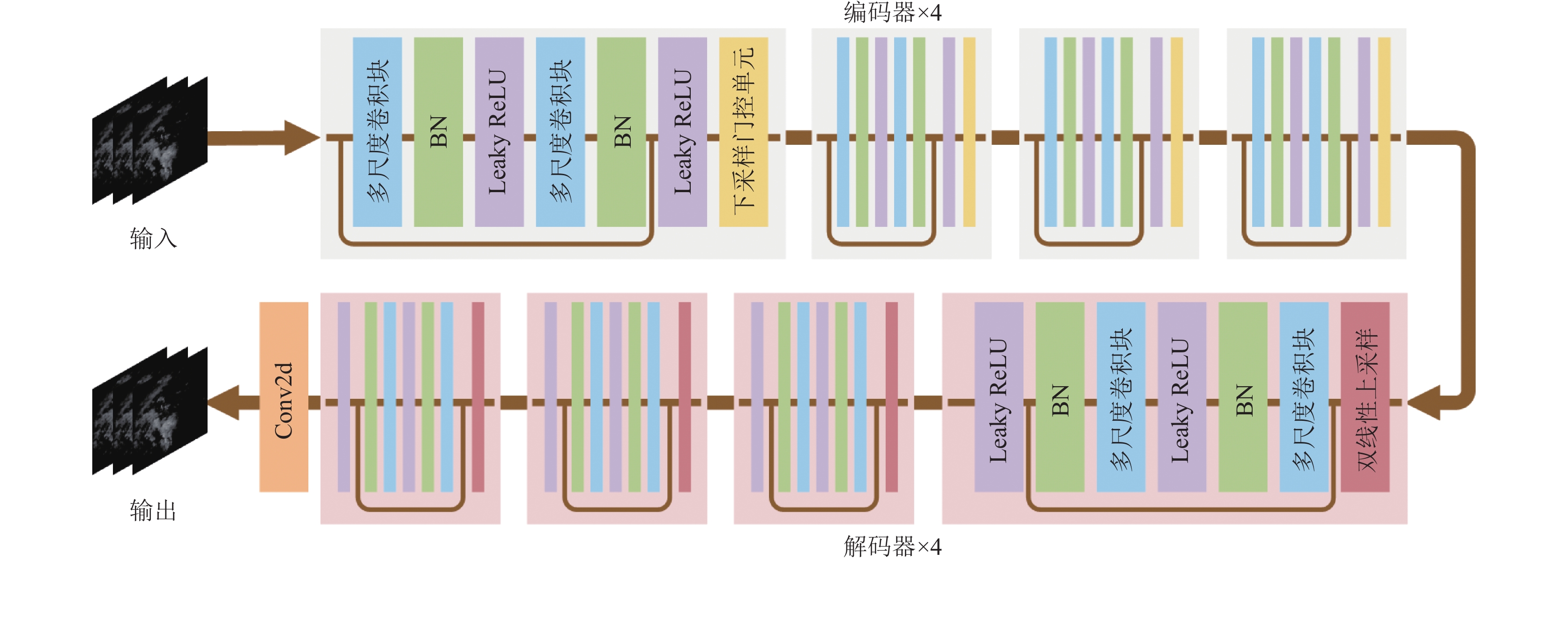
本文的生成器结构如图2所示, 采用了对称式的编码器-解码器架构, 搭建成端到端的时空与预测模型, 利用多尺度卷积块增加模型的感受野, 提取不同时间尺度和空间尺度下的时空运动特征, 实现多尺度的时空信息建模.

编码器由4个编码块组成, 各编码块都有两个多尺度卷积块和一个下采样门控单元. 当输入特征经过每个编码块时, 其时空分辨率会缩小至原来的一半, 通道数增加到原来的2倍. 解码器由4个解码块组成, 各解码块有两个多尺度卷积块和一个双线性上采样层. 输入数据经过每个解码块时, 其时空分辨率会以2倍的方式恢复. 另外, 编码器和解码器部分还使用了残差的方式来提高模型性能, 每个卷积核都使用了批量归一化和斜率为0.2的泄露整流线性单元. 生成器的最后一层只使用了普通的二维卷积转换通道数.

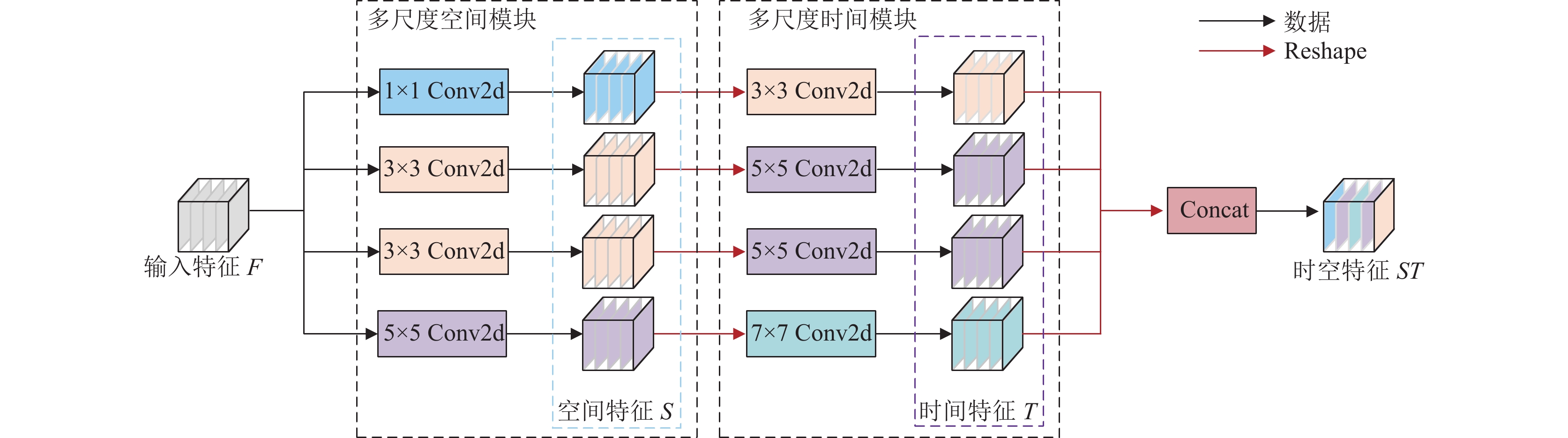
多尺度卷积块: 多尺度卷积块用于捕捉输入特征中的多尺度时空运动变化, 其结构如图3所示. 本文构建了拥有3个尺度的空间单元和时间单元, 使用不同大小的卷积核和不同的位置分布来捕捉输入特征的时空依赖性. 在多尺度空间特征提取单元中, 卷积核的大小为(1×1)、(3×3)、(5×5), 在多尺度时间特征提取单元中, 卷积核的大小为(3×3)、(5×5)、(7×7). 由于二维卷积最多能处理四维数据, 因此需要将拥有5个维度的输入数据([ 批量大小, 序列长度, 通道数, 高, 宽])转换成4个维度([ 批量大小×序列长度, 通道数, 高, 宽]), 第1维度是[ 批量大小×序列长度]. 在经过多尺度空间特征提取单元获取空间特征$ S $后, 将$ S $转换成[ 批量大小, 序列长度×通道数, 高, 宽]以便在多尺度时间特征提取单元中捕获时间特征$ T $, 然后再转换回[ 批量大小×序列长度, 通道数, 高, 宽], 并沿通道维度拼接获得时空特征$ ST $.

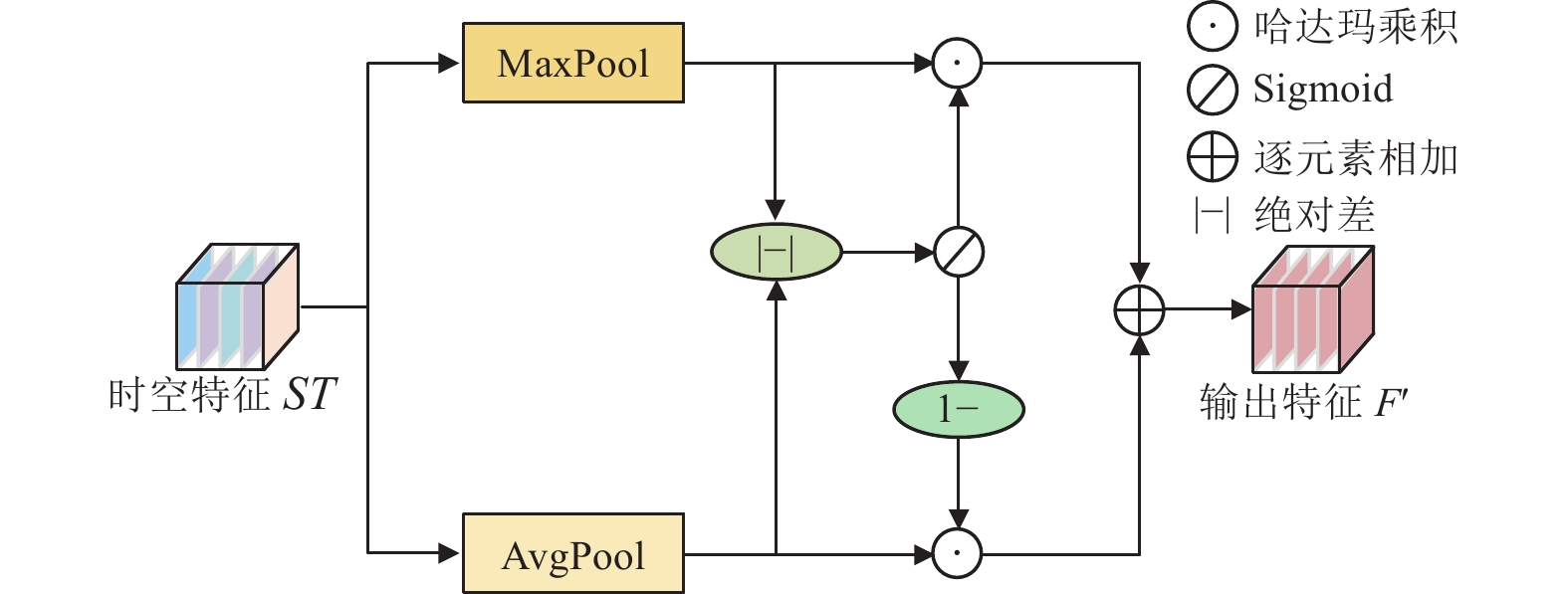
下采样门控单元: 为了获取更多的特征信息以及降低计算复杂度, 许多采用编码器-解码器架构的模型使用下采样的方式处理高维信息, 又为补充下采样造成的信息丢失引入了跳跃链接, 而解码器重建的是未来时刻的图像, 因此采用跳跃连接这种简单的映射会因时空位置的偏移而产生重影效应. 为了解决在下采样过程中造成的上下文信息丢失和重影问题, 本文设计了一个下采样门控单元, 其结构如图4所示. 使用门控机制让最大值下采样和平均值下采样进行信息交互, 省略了跳跃链接从而避免引入冗余信息. 其计算过程如下.

$ {\textit{ST}}' = \sigma \left( {\left| {{M_{ST}} - {A_{ST}}} \right|} \right) $

(2)

$ F' = {\textit{ST}}' \odot {M_{ST}} + \left( {1 - {\textit{ST}}'} \right) \odot {A_{ST}} $

(3)

其中, ${M_{ST}}$和${A_{ST}}$分别表示经过最大池化和平均池化后的特征, ${\textit{ST}}'$表示${M_{ST}}$和${A_{ST}}$之差的绝对值经过Sigmoid函数, ${\textit{ST}}'$中所有之的范围被控制在[0.5, 1]之间, $F'$表示自适应学习的特征.

2.2.2 判别器

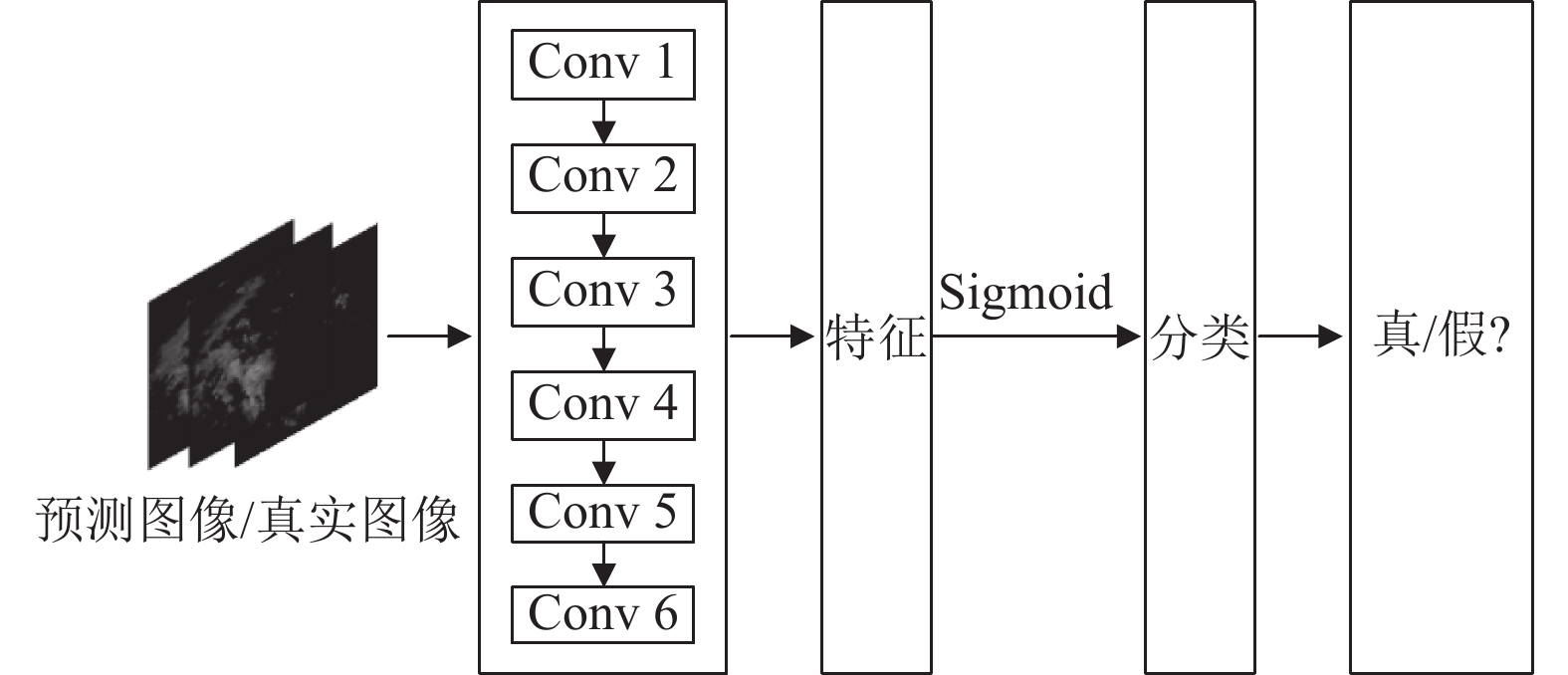
判别器的结构如图5所示. 本文的判别器是一个全卷积的网络, 可以减少模型参数量, 降低过拟合的风险. 输入图像依次经过6层卷积层, 然后使用Sigmoid函数生成最终表示来自真实图像的概率, 因此, 判别器可以看作一个二元分类器. 判别器中各层的参数设置如表1所示.

2.3 动态时空变异性损失函数

GAN使用二元交叉熵函数作为损失函数, 如式(1)所示, 但该函数存在梯度消失问题. 当预测值趋近于1时, $\log \left( {D\left( X \right)} \right)$会趋近于1, 而当预测值趋近于0时, $\log \left( {1 - D\left( {G\left( {\textit{z}} \right)} \right)} \right)$则会趋近于0, 那么损失函数的梯度就接近于0. 这种情况尤其在使用Sigmoid激活函数后更为严重. 为解决上述问题, 本文使用动态时空变异性损失函数来训练模型, 该函数引入了一个额外的正则化项, 即变异系数. 变异系数在应用统计学中的定义是观测样本的标准差除以平均值. 该指标多应用于气候科学和水文领域中来表述不同地区和降水场的降雨量变化^[25], Gong等人^[23]首次将其作为正则化项应用于短临预报领域.

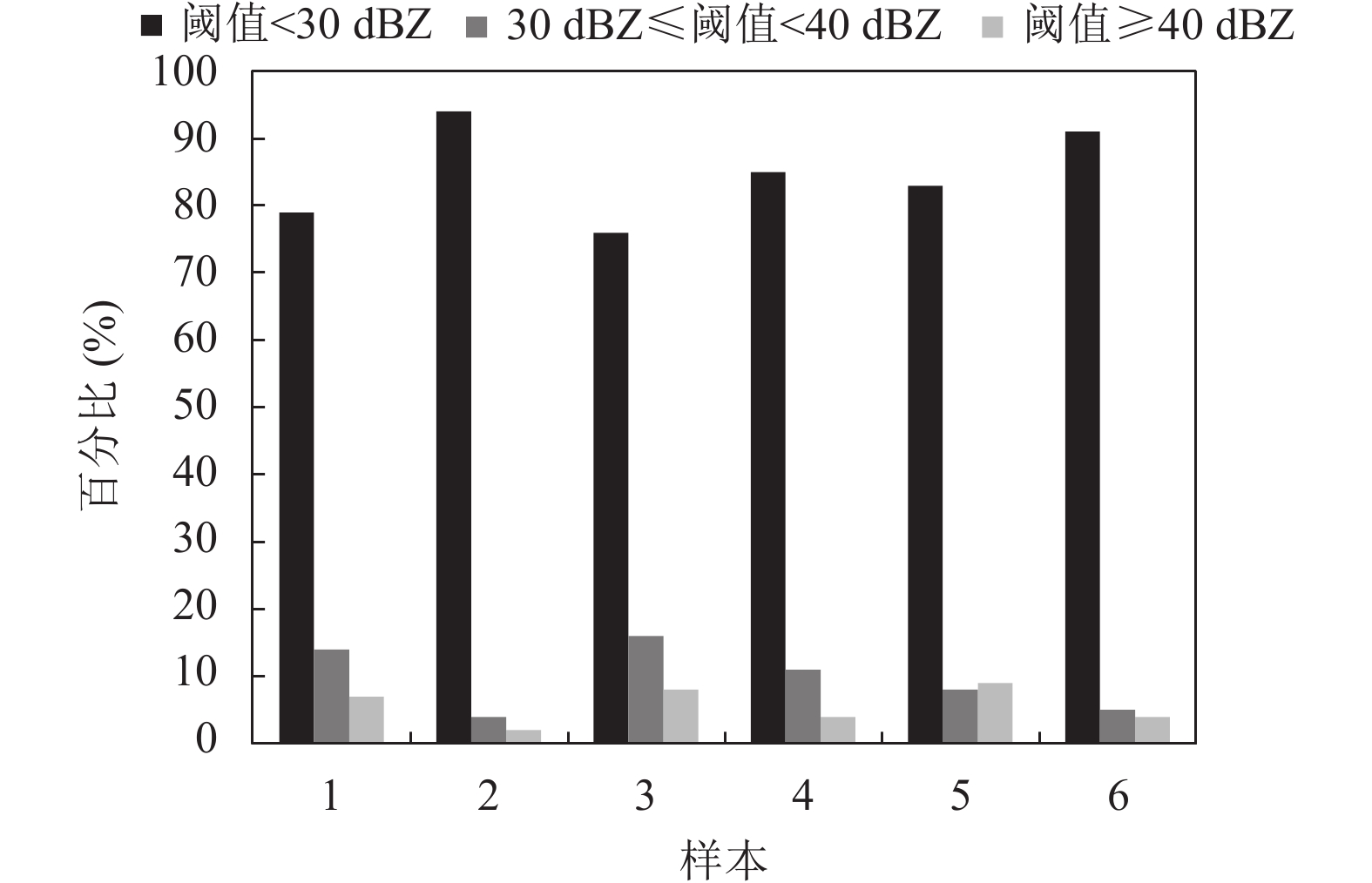
本文利用上海市雷达回波数据集, 分析了雷达回波反射率值的分布情况. 从具有强回波值的输入样本中随机选取6组样本作为数值统计, 每组样本含有20帧连续的雷达回波图像. 将划分阈值设置为30 dBZ和40 dBZ, 每个范围的阈值占比如图6所示.

由于较大比重的低回波样本对模型预测强回波样本会产生很大干扰, 使得模型的模糊问题越来越严重, 因此, 需要一个合理的动态分配权重的方案. 本文使用具有动态权重的变异系数来表示不同强度的回波值的时空变异性. 动态权重按照式(4)计算, 如式(5)所示, 标准差和平均值沿时间维度和空间维度计算. 判别器和生成器的损失函数分别如式(6)和式(7)所示.

$ {W_{t, h, w}} = \left\{ {\begin{array}{*{20}{l}} 1,& 0 \leqslant {R_{t, h, w}} \lt 15\;{\mathrm{dBZ}} \\ 2,& 15\;{\mathrm{dBZ}} \leqslant {R_{t, h, w}} \lt 25\;{\mathrm{dBZ}} \\ 5,& 25\;{\mathrm{dBZ}} \leqslant {R_{t, h, w}} \lt 35\;{\mathrm{dBZ}} \\ 10,& 35\;{\mathrm{dBZ}} \leqslant {R_{t, h, w}} \lt 45\;{\mathrm{dBZ}} \\ 20,& 45\;{\mathrm{dBZ}} \leqslant {R_{t, h, w}} \lt 55\;{\mathrm{dBZ}} \\ 30,& 55\;{\mathrm{dBZ}} \leqslant {R_{t, h, w}} \leqslant 70\;{\mathrm{dBZ}} \end{array}} \right. $

(4)

$ DyS{C}_{v}\left({X}_{t}\right)= \frac{{\sigma }_{t, h, w}\left({X}_{t}\right)}{mea{n}_{t, h, w}\left({X}_{t}\right)}\times{W}_{t, h, w} $

(5)

$ \mathcal{L}_{D}= -\frac{1}{N}{\displaystyle \sum }_{t=1}^{N}\left[\mathrm{log}\left(D\left({X}_{t}\right)\right)+\mathrm{log}\left(1-D\left({\hat{X}}_{t}\right)\right)\right] $

(6)

$ \begin{split} {\mathcal{L}_G} = & - \frac{1}{N}\mathop \sum \limits_{t = 1}^N \log \left( {1 - D\left( {{{\hat X}_t}} \right)} \right) + \lambda \left[ {DyS{C_v}\left( {{X_t}} \right)} \right. \\ &\left. {{\text{ }} - DyS{C_v}\left( {{{\hat X}_t}} \right)} \right] \end{split} $

(7)

其中, ${R_{t, h, w}}$表示坐标$ \left( {t, {\text{ }}h, {\text{ }}w} \right) $处的雷达回波反射率值, ${W_{t, h, w}}$表示坐标处的权重. ${X_t}$和${\hat X_t}$分别为第t时刻观测雷达回波图像和预测雷达图像, $ mean $表示在坐标轴$ \left( {t, {\text{ }}h, {\text{ }}w} \right) $处图像的平均值, $\sigma $是其标准差.

3 实验和结果 3.1 实验细节

在MCGAN网络的训练中, 批量大小设置为10, 总迭代数为500轮, 生成器的学习率设置为1×10⁻⁴, 判别器的学习率设置为$ 5 \times {10^{ - 5}} $, 采用多步方案设置, 将学习率在第50轮、100轮、200轮和300轮迭代时减半. 使用式(7)中的损失函数训练生成器. 其中${{\lambda }} = 5 \times {10^{ - 3}}$. 生成器和判别器使用Adam优化器进行训练, 其中${\beta _1} = 0.9$, ${\beta _2} = 0.99$. 本文所做实验均在PyTorch框架下实现, 并使用NVIDIA GeForce RTX 3090 Ti运行训练.

3.2 评估指标

从两个方面来评估所提模型的性能, 分别是图像质量评估和预测精度评估. 首先, 在图像质量评估中采用了3种指标: 均方误差(mean squared error, MSE)、结构相似性 (structural similarity index, SSIM)和峰值信噪比(peak signal-to-noise ratio, PSNR).

MSE衡量了预测结果与其真实结果的平均平方差. MSE的值越小, 表示模型的预测效果越好. 计算方式如式(8), $X$表示观测雷达回波图像, $\hat X$表示预测雷达回波图像, $H$是图像的高度, $W$是图像的宽度.

$ {\textit{MSE}}\left( {X, \hat X} \right) = \frac{{\displaystyle\mathop \sum \nolimits_i^H \displaystyle\mathop \sum \nolimits_j^W {{\left( {{X_{i, j}} - {{\hat X}_{i, j}}} \right)}^2}}}{{HW}} $

(8)

SSIM通过比较两个图像的亮度、对比度和结构来计算两幅图像的相似性, 取值范围是[−1, 1], SSIM越接近1, 表示两幅图像越相似, 那么图像质量就越高. 计算方法如式(9), 其中$\mu $代表平均值, $\sigma $表示协方差, ${c_1}$和${c_2}$是两个常量.

$ {\textit{SSIM}}\left( {X, \hat X} \right) = \frac{{\left( {2{\mu _X}{\mu _{\hat X}} + {c_1}} \right)\left( {2{\sigma _{X\hat X}} + {c_1}} \right)}}{{\left( {\mu _X^2 + \mu _{\hat X}^2 + {c_1}} \right)\left( {\sigma _X^2 + \sigma _{\hat X}^2 + {c_2}} \right)}} $

(9)

PSNR比较了原始图像和经过处理的图像之间的信噪比, 以分贝 (dB) 为单位, 其值越大表示图像质量越高. 计算方法如式(10), $MAX_X^{{\text{ }}2}$表示图像中最大的像素值.

$ {\textit{PSNR}} = 10\log{_{10}}\left( {\frac{{MAX_X^{{\text{ }}2}}}{\textit{MSE}}} \right) $

(10)

另外, 在预测精度评估中, 本文采用了4种在气象领域常用的降水临近预报指标: 检测概率(probability of detection, POD)、误报率(false alarm rate, FAR)、关键成功指数(critical success index, CSI)和海德克技能得分(Heidke skill score, HSS). 为了更全面地评估模型性能, 本文设置了多个不同的评估阈值, 分别为25 dBZ、35 dBZ和45 dBZ. 用于计算评估指标的混淆矩阵如表2所示.

根据表2, 可以使用式(11)–式(14)得到POD、FAR、CSI和HSS:

$ POD= \frac{TP}{TP+FN} $

(11)

$ {\textit{FAR}}= \frac{FP}{FP+TP} $

(12)

$ {\textit{CSI}}= \frac{TP}{TP+FP+FN} $

(13)

$ {\textit{HSS}} = \frac{{2 \times \left( {TP \times TN - FN \times FP} \right)}}{{\left( {TP + FN} \right)\left( {FN + TN} \right) + \left( {TP + FP} \right)\left( {FP + TN} \right)}} $

(14)

3.3 实验结果

为了分析MCGAN在雷达回波外推中的优势, 本文衡量了25 dBZ、35 dBZ、45 dBZ阈值下的预测效果, 并且选取了4个主流模型作为比较模型, 分别是ConvLSTM、PredRNN、TrajGRU和MIM. 在实验中, 利用前10帧时间间隔为6 min的历史雷达回波图像预测后10帧时间间隔为12 min的未来雷达回波图像, 即预测提前期为2 h.

首先, 在图像质量评价指标上进行了评估, 结果如表3所示, 使用粗体显示最佳结果.

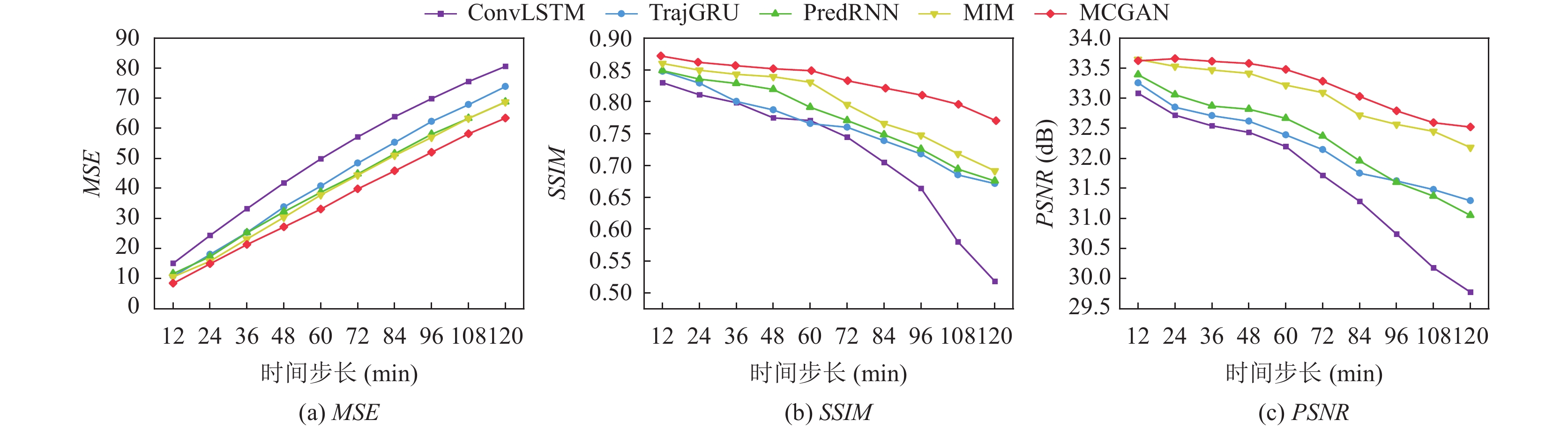
从表3中可以看出, MCGAN模型在所有指标中都取得了最好的结果. 在图像质量方面, MCGAN模型相比排名第2的MIM模型在MSE指标上下降了11.15%, 在SSIM指标上增加了8.99%, 在PSNR指标上增加了2.95%. 很显然, 这代表MCGAN模型能够生成更加清晰的图像. 此外, 为了更清楚地观察MCGAN模型在每个时间节点的性能, 本文绘制了MSE、SSIM和PSNR指标的折线图, 如图7所示, 展示了测试集上5种模型每帧平均评估值. 可以得出, MCGAN模型在不同时间步下, 预测图像的清晰度明显优于其他模型.

为了对算法的预测精度性能进行全面评估, 本文还给出了不同降雨量对应的多个阈值的预测精度评估分数. 测试结果如表4所示, 使用粗体显示最佳结果. 从重要的CSI和HSS得分来看, MCGAN与其他模型相比拥有更加准确的预测性能. MCGAN模型在所有预测精度指标上都取得了最好的临近预报分数, 尤其在强回波阈值上有明显改善. 比如, 在45 dBZ阈值下, MCGAN模型的CSI值比MIM模型增加25.42%, 比PredRNN模型增加34.55%, HSS值也分别增加了12.59%、22.58%. 很明显, MCGAN模型即使在强降雨中也具有更好的预测精度.

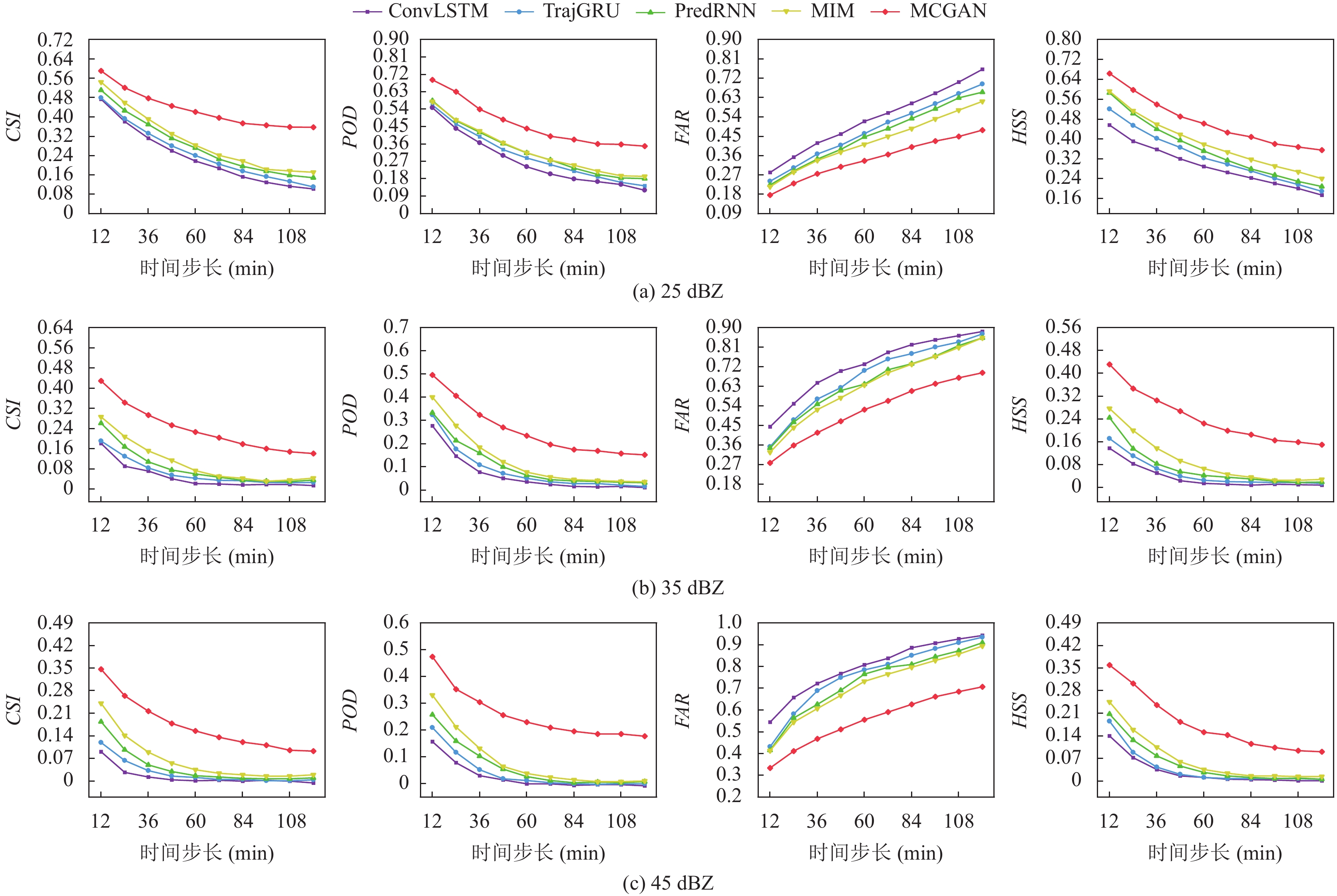
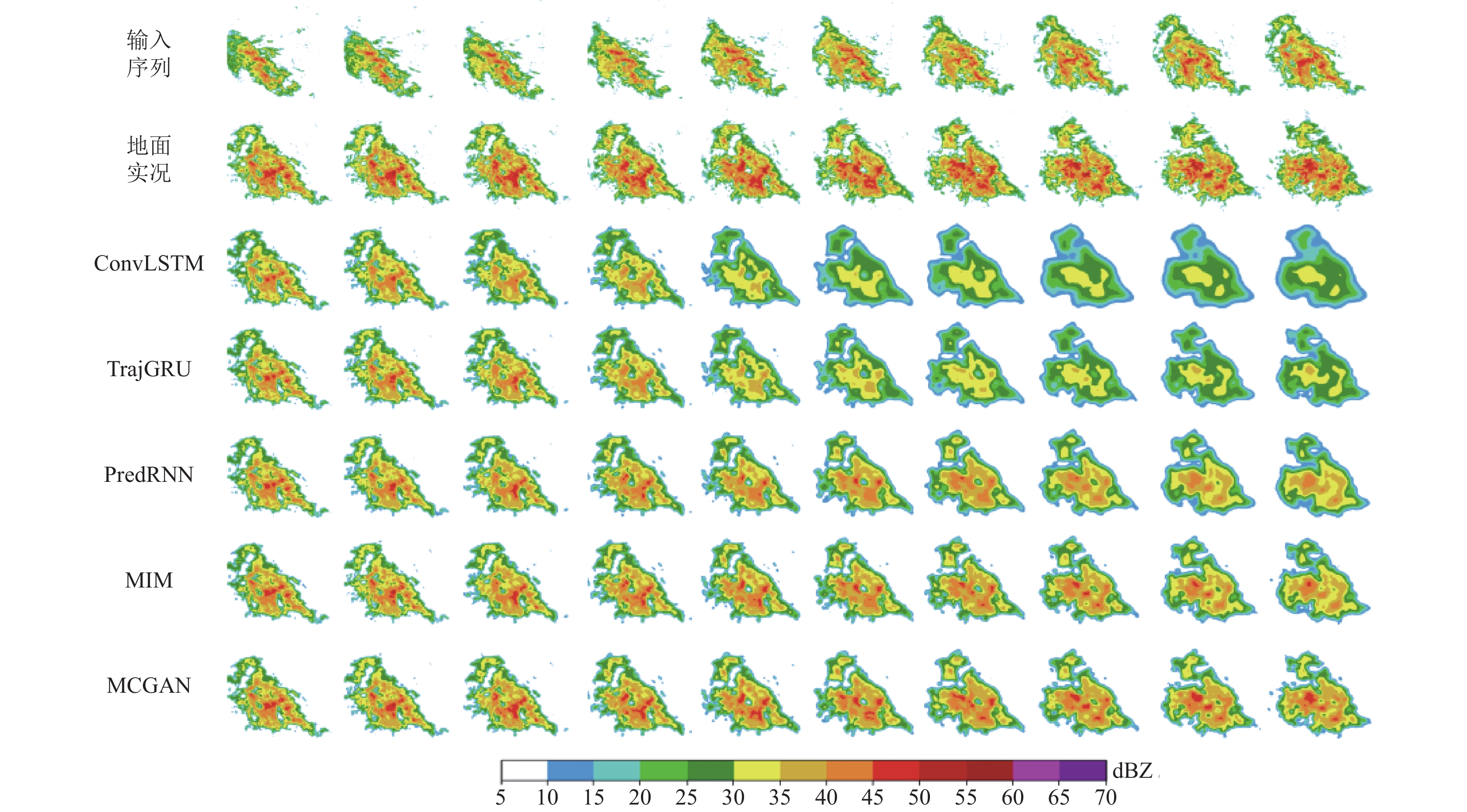
图8进一步显示了2 h提前期下测试数据集在不同指标下的平均评估分数. 可以看出CSI和HSS得分具有相似的趋势, 并且都随着预测提前期的增加而下降. 从评估指标来看, 不管是不同的提前期还是不同的降雨强度, MCGAN模型总能优于基线模型, 而基线模型的临近预报性能随着提前期的增加而下降得更快. 为了方便观察MCGAN模型与其他模型对雷达回波强度和分布的预测效果, 本文选择了两组降雨示例作为展示. 图9是一次对流降雨的生消过程, 对流降雨具有局部性, 降雨强度高, 分布不均匀的特性, 使得预测任务非常艰巨. 图9通过对比5种模型未来2 h的对流降雨结果, 展现了MCGAN模型优越的性能, 该模型预测效果最接近原始的雷达回波图像. ConvLSTM模型和TrajGRU模型在超过1 h提前期的情况下, 预测效果衰减剧烈, 并且在总体回波区域上出现严重的预测模糊问题, 无法对强回波做到准确预测. PredRNN模型和MIM模型虽然在预测提前期上优于以上两个模型, 但是对强回波的预测能力也比较弱, 只能预测回波的整体轮廓, 对局部的回波细节预测仍然不够准确. 然而, MCGAN却能达到更高的预测效果, 随着时间的增加, 比较模型都逐渐失去了正确的预测轨迹, 而MCGAN却保留了较多的回波信息.

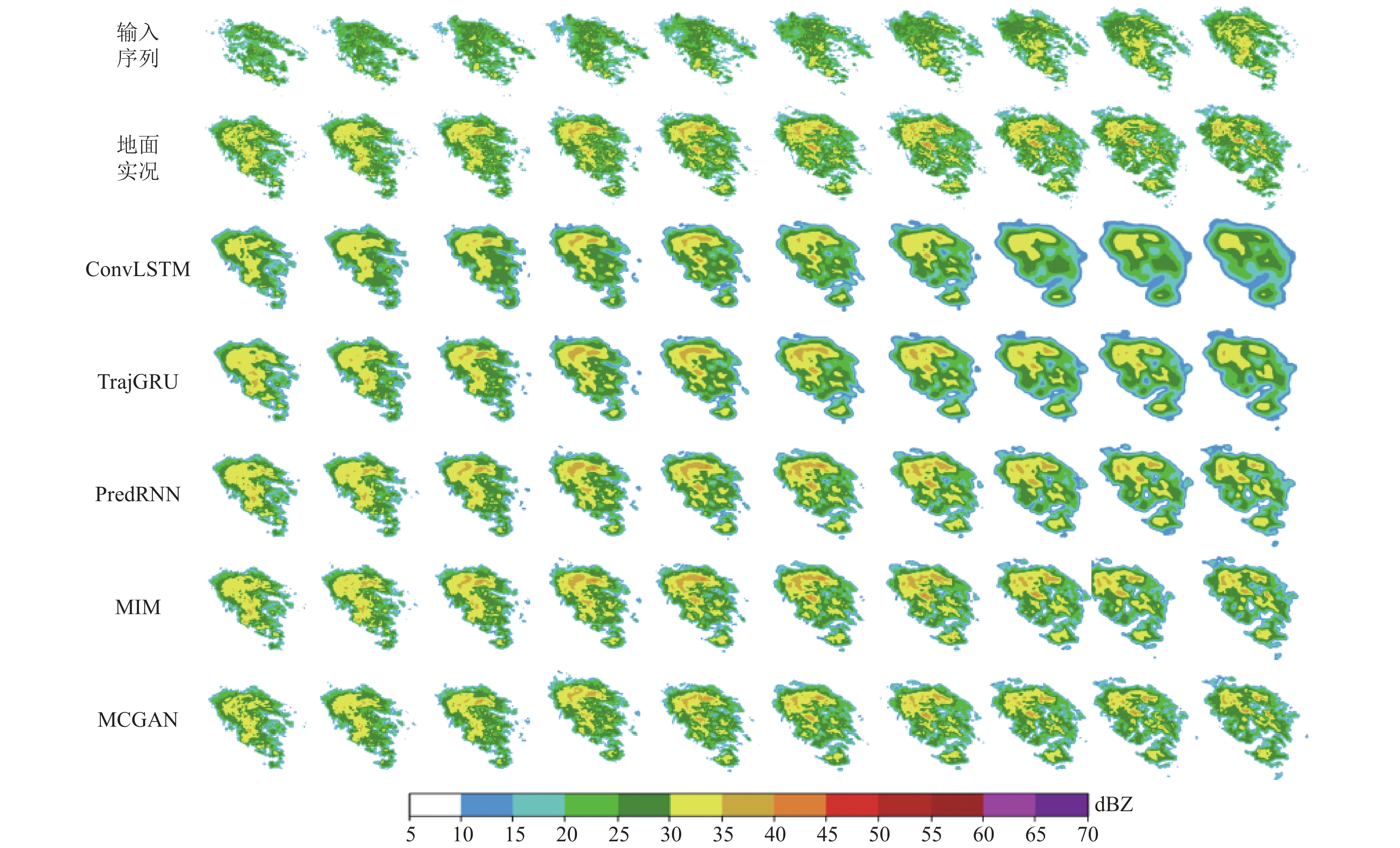
与变化迅速的对流降水相比, 稳定的降水结构通常是连续的, 降水强度较小, 但覆盖范围相对广阔. 图10显示了在稳定降水结构中MCGAN模型与其他模型之间的比较. ConvLSTM模型和TrajGRU模型只能做到粗略预测降水范围. 在视觉上产生模糊的效果. PredRNN模型和MIM模型在预测局部雷达回波强度方面不太敏感. 总体来说, MCGAN在稳定降水场中拥有更加准确、全面、清楚的整体和局部回波状态.

3.4 消融实验

为了验证MCGAN模型各个模块对最终预测效果的作用, 进行了消融实验, 表5显示了模型的定量分析结果. 从表5中可以看出, 完整的MCGAN模型拥有最强的拟合雷达回波运动变化的能力. 在图像质量评估指标上, MSE的得分低于其余3种情况下的模型, 这表明MCGAN模型的预测图像更接近真实图像, 相应的像素差异较小. 基于SSIM和PSNR的指标得分更高, 那么预测图像在亮度、对比度和结构上也趋于接近真实图像. 当模型中去掉多尺度卷积块使用单一的结构时, 会造成模型无法获得多个时间尺度和空间尺度的运动状态, 只能传递固定尺度的时空特征, 从而增加了模型陷入梯度消失和错误累加的风险. 当模型中去掉下采样门控单元采用传统的跳跃连接的方式时, 这种直接映射的方式使得模型丢失了一些上下文特征, 从而产生重影问题, 使得预测图像的清晰度和精确度下降. 当模型在训练过程中不使用动态时空变异性损失函数时, MCGAN模型得到更低的CSI值和HSS值, 以及更高的MSE值; SSIM值和PSNR值也有所下降, 并且比缺失其他模块的模型得到预测效果更差. 这表明本文使用的损失函数可以通过拟合预测图像和观测图像之间时空变异性差距来增强预测效果.

4 结论与展望

本文基于对雷达回波外推算法的研究提出了一个MCGAN模型. 由于主流的深度学习模型只能提取和传输固定尺度的时空特征, 使得模型对资料的利用率不足, 因此 MCGAN模型根据时空运动的复杂性特征构建了多个尺度的空间卷积块和时间卷积块来增强时空预测模型的建模能力. 另外, 针对许多采用编码器-解码器架构的模型使用跳跃连接而造成的重影问题, MCGAN模型设计了一种下采样门控机制, 从而减少信息丢失. 最后, 为了解决深度学习模型在预测过程中因丢失空间变异性而产生的模糊问题, 本文将MCGAN模型在GAN网络框架下进行训练, 并使用动态时空变异系数作为正则化项设计了一个新的损失函数.

以上方法均在实验中进行了证明, MCGAN模型无论是在图像质量评估(MSE 、SSIM、PSNR)方面还是在预测精度评估(CSI、POD、FAR、HSS)方面都优于主流的深度学习方法. 消融实验同时也证明了各个模块对总体模型的影响. 虽然本文提出的模型拥有更高的预测精度和更多的回波细节, 但是仅使用雷达回波图像数据作为外推的主要目标具有一定的局限性. 未来, 可以通过引入环境场信息和卫星产品来增强外推模型的可靠性, 并进一步增加外推的提前期.