多策略大规模多目标优化算法

引用本文

裴倩如, 邹锋, 陈得宝. 多策略大规模多目标优化算法. 计算机系统应用, 2024, 33(11): 142-156.http://www.c-s-a.org.cn/1003-3254/9672.html

Pei QR, Zou F, Chen DB. Large-scale Multi-objective Optimization Algorithm with Multiple Strategies. Computer Systems and Applications, 2024, 33(11): 142-156(in Chinese).http://www.c-s-a.org.cn/1003-3254/9672.html

多策略大规模多目标优化算法

裴倩如^1,2, 邹锋^1,2,3, 陈得宝^1,2

1. 淮北师范大学物理与电子信息学院, 淮北 235099;
2. 淮北师范大学智能计算及应用安徽省重点实验室, 淮北 235099;
3. 合肥工业大学工业安全与应急技术安徽省重点实验室, 合肥 230601

收稿日期：2024-04-19; 修改日期：2024-05-14; 采用时间：2024-05-29; csa 在线出版时间：2024-09-29

基金项目：安徽省高校自然科学基金 (2022AH040064); 安徽省高校学科(专业)拔尖人才学术资助项目 (gxbjZD2022021); 安徽省智能计算理论及应用优秀科研创新团队 (2023AH010044); 中央高校基本科研业务费专项资金 (PA2023GDSK0049)

通讯作者：邹锋, E-mail: zoufeng@chnu.edu.cn.

摘要：在解决大规模多目标优化问题(LSMOP)时, 随着决策变量维数的增加会使得MOEA/D算法在决策空间扩展性差且容易收敛于局部最优. 针对这一问题, 提出了一种大规模多策略MOEA/D算法 (MSMOEA/D). MSMOEA/D算法在优化过程中引入了一种基于自动编码器的混合初始化策略, 以改善初始种群的覆盖程度, 从而促进全局搜索. 然后, 提出一种基于聚合函数值的邻域调整策略, 通过调整邻域大小, 能够在搜索过程中更精确地控制搜索范围, 避免因邻域过大或过小而导致的搜索效率低下. 此外, 在优化过程中采用了基于非支配排序的变异选择策略. 不同的子问题根据位于非支配排序第1层的个体数量选择变异策略, 避免种群陷入局部最优, 提高算法的整体性能. 最后, 使用LSMOP和DTLZ测试问题对MSMOEA/D算法和其他已有算法进行了评估. 实验结果证实了MSMOEA/D算法解决大规模多目标优化问题的有效性.

关键词: 大规模多目标优化 MOEA/D 自动编码器邻域大小变异策略

Large-scale Multi-objective Optimization Algorithm with Multiple Strategies

PEI Qian-Ru^1,2, ZOU Feng^1,2,3, CHEN De-Bao^1,2

1. School of Physics and Electronic Information, Huaibei Normal University, Huaibei 235099, China;
2. Anhui Province Key Laboratory of Intelligent Computing and Applications, Huaibei Normal University, Huaibei 235099, China;
3. Anhui Province Key Laboratory of Industry Safety and Emergency Technology, Hefei University of Technology, Hefei 230601, China

Abstract: When dealing with large-scale multi-objective optimization problem (LSMOP), the MOEA/D algorithm shows poor scalability in the decision space and a tendency to converge to local optima as the dimensionality of decision variables increases. To address this issue, this study proposes a large-scale MOEA/D algorithm with multiple strategies (MSMOEA/D). The MSMOEA/D algorithm introduces a hybrid initialization strategy based on autoencoders in the optimization process to expand the coverage of the initial population, thus promoting global search. Moreover, a neighborhood adjustment strategy based on aggregation functions is proposed, which can more accurately control the search range during the search process by adjusting neighborhood sizes, thereby avoiding low search efficiency caused by excessively large or small neighborhoods. Furthermore, a mutation-selection strategy based on non-dominated sorting is adopted during the optimization process. Different subproblems select their mutation strategies according to the number of individuals in the first level of non-dominated sorting to avoid the population falling into local optima and enhance the overall performance of the algorithm. Finally, the MSMOEA/D algorithm and other existing algorithms are evaluated using LSMOP and DTLZ test problems. Experimental results verify the effectiveness of the proposed algorithm for solving LSMOPs.

Key words: large-scale multi-objective optimization (LSMOP) MOEA/D autoencoder neighborhood size mutation strategy

优化问题广泛存在现实生活中, 比如投资者试图获得最大化收益和承担最小风险; 工厂期望投入最少的人工成本获得较高的生产效率等. 这些问题都需要考虑多个目标^[1–4], 这些目标之间通常存在争议, 不可能同时达到最优结果. 因此, 为了使总体目标尽可能优化, 需要各目标之间的协调与妥协^[5]. 近几十年来, 多目标进化算法蓬勃发展^[5–8]. 自VEGA算法提出以来^[9], 对多目标进化算法(MOEA)的研究一直在稳步增长. 大多数MOEA可以分为3类: 第1类是基于帕累托支配的MOEA, 代表算法有: NSGA^[10]和NSGA-II^[11]. 第2类基于分解的MOEA, 代表算法有: MOEA/D^[12]、RVEA^[13]和MMOPSO^[14]. 第3类MOEA侧重于基于性能指标的MOEA, 代表算法有: IBEA^[15]、HypE^[16]和GrEA^[17,18]. 随着科学技术的进步, 实际生产生活中的多目标优化问题日趋复杂, 问题决策变量的数量大幅增加. 例如, 神经网络的训练问题, 车辆的路径规划问题等. 虽然大规模单目标优化领域发展非常成熟^[19], 但在处理大规模多目标优化问题(LSMOP)时, 大规模单目标优化和大规模多目标优化仍然存在一定的差异^[20], 因此解决LSMOP成为研究热点. 大规模多目标优化算法主要分为以下3类: 第1类使用的是分而治之的思想^[21]. Potter等人是CC框架的最初支持者^[22]. 协同进化的分组方法包括固定分组^[23]、随机分组^[24]、Delta分组^[25]、动态分组^[26]和差分分组^[27]. 这类算法的性能依赖于正确的分组, 且有较大的局限性. 第2类是基于决策变量分析的求解方法, 主要是挖掘决策变量与优化问题之间的相关性, 典型的例子是MOEA/DVA^[28], LMEA^[29]. 这类算法由于变量之间存在相关性, 难以划分, 因此会导致变量的分类不正确, 并且会因为分组而增加计算量. 第3类是问题转换的方法, 问题转换策略是将LSMOP转化为小规模MOP, 然后使用传统的进化算法进行优化. 代表算法有: WOF^[30]和LSMOF^[31]. 这类算法由于问题的重构, 没有考虑到一些决策变量的信息, 使得算法的多样性不好. 除此之外, 学者们还提出了其他一些解决LSMOP的方法. 例如, DGEA算法^[32]和SparseEA算法^[33]. 该类算法计算量大, 收敛速度慢.

MOEA/D算法能够有效解决多目标问题, 但是在处理大规模优化问题时存在以下不足: 当初始种群质量较差时, 可能会限制算法对搜索空间的覆盖范围, 导致算法难以找到更优解. 此外, 固定的邻域结构并不适用于所有测试问题. 同时, 单一的突变策略可能会导致算法收敛速度较慢, 并需要大量函数求值才能跳出局部最优解. 为了解决这些问题, 本文提出了一种基于多策略的大规模多目标优化算法(MSMOEA/D). 该算法采用混合初始化策略来增加种群的多样性, 通过优化邻域调整来提高算法的全局搜索能力, 并采用多种突变策略来弥补单一突变策略的不足. 这些改进措施旨在帮助算法更有效地探索搜索空间, 避免局部收敛, 并最终找到更优解.

1 相关背景知识 1.1 大规模多目标优化问题

多目标优化问题(MOP)可表述为:

$\left\{ \begin{gathered} \min {\text{ }}F(x) = {({f_1}(x), {f_2}(x), \cdots, {f_M}(x))^{\mathrm{T}}} \\ {\text{s.t. }}x = ({x_1}, {x_2}, \cdots, {x_D}) \in {R^D} \\ \end{gathered}\right. $

(1)

其中, $ {f_M}(x) $为第$ M $个个体的目标值, 当$ D \geqslant 100, M \geqslant 2 $, 将其命名为LSMOP. 最优解集在决策空间中称为帕累托集(PS), 在目标空间中称为帕累托前沿(PF)^[11].

1.2 自动编码器

自动编码器(AE)是一种用于半监督学习和无监督学习的人工神经网络, 它能够学习数据的有效特征, 广泛应用于机器学习的多个任务中, 如数据压缩^[34]、特征提取^[35]、数据重构^[36]和生成模型^[37]. 它由两部分组成: 编码器和解码器. 编码器包含输入层和隐藏层, 将高维输入转换为低维潜在变量, 以便神经网络捕获最具信息量的特征. 解码器包含隐藏层和输出层, 将低维变量恢复到原始维度. 在训练过程中, 通过最小化输入数据与解码器输出之间的重构误差, 自动编码器获得数据的压缩表示, 这种表示捕获了输入数据的基本特征, 允许自编码器保留关键特征信息^[38]. 3层自动编码器模型如图1所示.

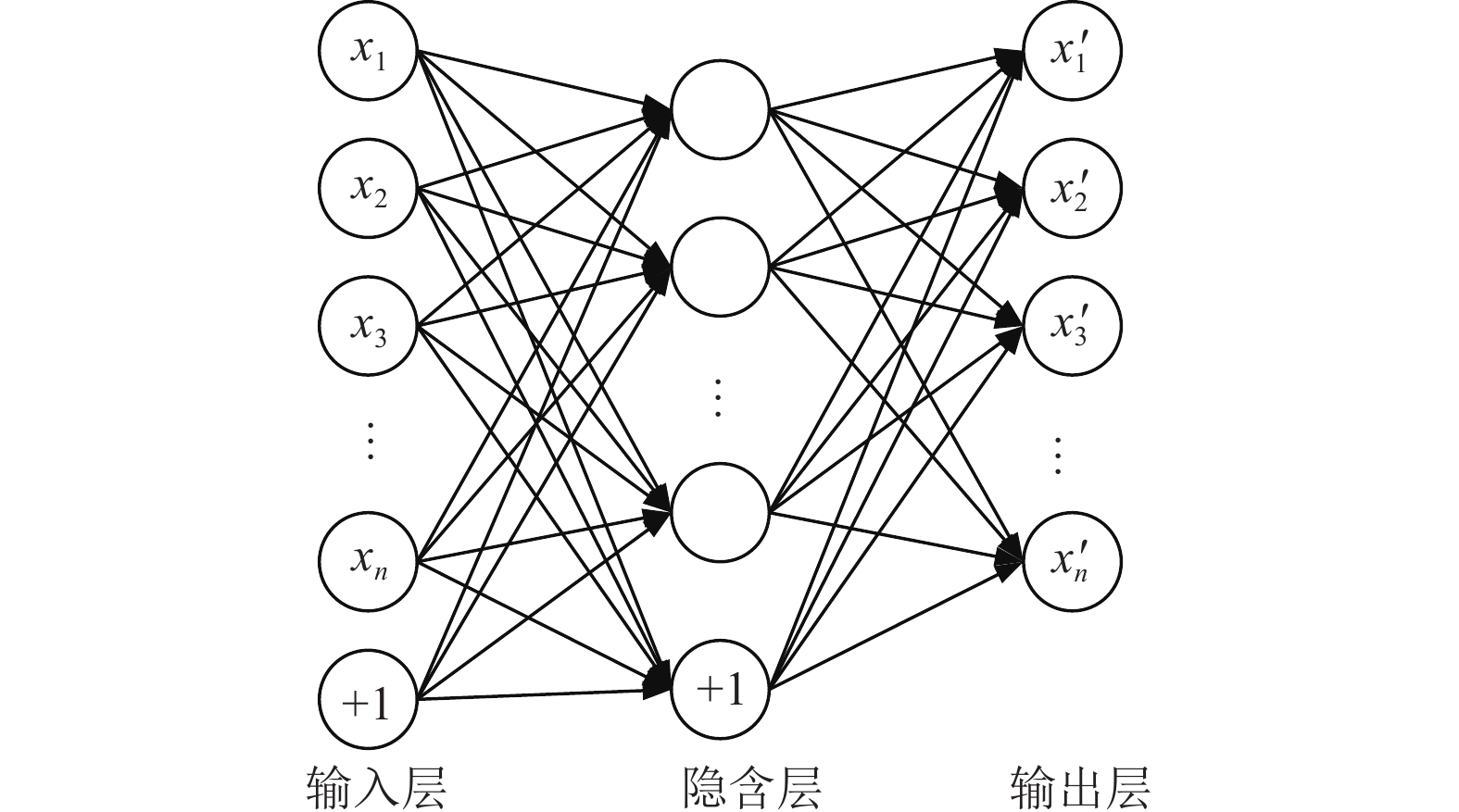
图 1 一个3层自动编码器模型

2 多策略大规模多目标优化算法

本文将从混合初始化策略、邻域调整策略和突变选择策略3个方面介绍多策略的大规模多目标优化算法. 图2是算法的主要流程图.

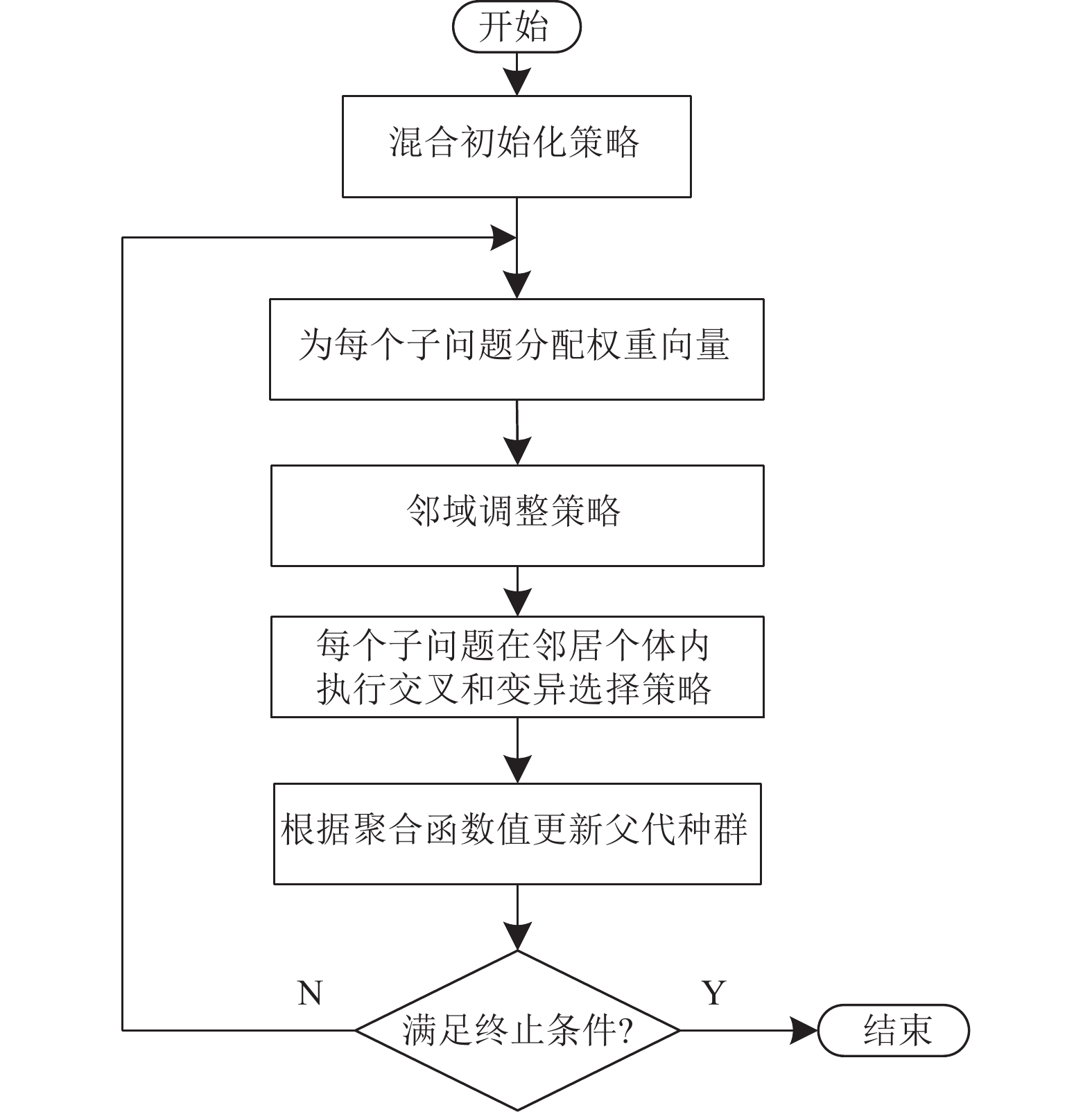
图 2 算法的主要流程图

2.1 基于自动编码器的混合初始化策略

种群初始化在优化算法中非常重要, 它直接影响了算法的搜索效率和最终的优化结果. 在高维空间中, 种群初始化容易受到维度诅咒的影响, 导致种群分布不均匀, 从而阻碍了对搜索空间中有价值信息的有效探索和利用. 自动编码器可以学习数据的特征表示, 有助于捕获数据中的重要特征. 这些学习到的特征可以用于初始化种群, 从而提高算法对问题的理解和搜索效率. 因此, 本文在种群初始化阶段使用了基于自动编码器的混合初始化策略. 通过自动编码器的数据不是直接从输入映射到输出. 自动编码器的编码过程能够从输入数据中学习到隐藏的特征, 而解码则使用新获取的特征重建输入数据. 通过利用神经网络的非线性特征提取能力, 自动编码器可以实现有效的数据表示.

由于这一特点, 本文使用自动编码器从随机初始化的种群中提取特征. 首先使用随机生成的种群对自动编码器进行训练, 然后利用训练好的自动编码器对输入数据进行重构, 以更清晰地表示决策变量的特征, 并降低计算成本, 获得更好的结果. 然而, 自动编码器重构的种群可能过于集中, 导致算法的多样性下降. 因此, 本文将自动编码器重构的种群与随机生成的种群合并, 并进行环境选择. 这一步骤利用非支配排序和拥挤距离来选择最终的初始种群, 从而为后续优化过程提供更好的初始种群, 加快收敛速度并找到更优的解决方案. 本文将隐藏层的大小设置为10, 输入和输出层的数量对应于决策变量的维度.

混合初始化策略的伪代码如算法1.

算法1. 混合初始化策略

输入: 当前优化问题(MOP), 种群数(N).

输出: 最终种群(Pop).

1. 随机生成种群population

2. autoencoder=训练自动编码器(population)

3. reconstructed_population=重构(autoencoder, population)

4. merged_population=合并种群(population, reconstructed_population)

5. Pop=环境选择(merged_population)

2.2 基于聚合函数值的邻域调整策略

邻域大小对进化算法的效果有显著影响. 较大的邻域可以加速算法的收敛速度, 但可能会牺牲种群的多样性, 从而限制了局部搜索能力. 相反, 较小的邻域可以保持种群的多样性, 增强局部搜索的效果, 但可能会导致算法陷入局部最优解^[39]. 在算法的早期阶段, 种群的进化速度较快, 收敛性较强, 因此需要适当减小邻域的大小, 以保留种群的多样性. 在中间阶段, 种群的进化速度减慢, 此时可以适当增加邻域的大小, 以避免种群进入进化停滞状态. 在算法发展的后期, 需要特别关注种群的多样性, 因此应适当减小邻域的大小, 以确保种群在Pareto前沿的分布更加均匀.

不同的进化过程对邻域大小有不同的要求. 为了提高种群进化效率, 本文提出了基于聚合函数值的邻域自适应调整策略, 该策略根据当前种群的进化进程和聚合函数值的变化程度动态调整邻域. 具体措施如下: 如果当前进化代数超过10并且评价次数小于最大评价次数的0.8倍时, 根据聚合函数的改进程度值(improve)每隔10代调整邻域大小, 具体邻域调整过程如下: 如果聚合函数的改进程度大于0.01, 则表明种群处于快速进化状态, 需要减小邻域大小, 因此邻域等于最小邻域值, 以防止陷入局部最优, 否则邻域等于最大邻域值, 以防止陷入进化停滞, 增加产生更好后代的概率. 如果当前进化代数小于10, 或者评价次数大于等于最大评价次数的0.8倍, 采用包含评价次数的公式来调整邻域大小. 这种邻域调整方法可以有效地在算法的收敛性和多样性之间取得平衡. 聚合函数改进程度值“improve”公式如下:

$ improve = \frac{{\dfrac{{\displaystyle\sum\limits_{i = 1}^N {(g_{gen}^{te}({x^i})) - (g_{{gen-}10}^{te}({x^i}))} }}{N}}}{{\dfrac{{\displaystyle\sum\limits_{i = 1}^N {(g_{{gen-}10}^{te}({x^i}))} }}{N}}} $

(2)

其中, $ gen $是进化代数, $ {x^i} $是第i个个体, $ {g}^{te}(\cdot) $ 是切比雪夫聚合函数值, $ N $ 种群数目.

对于双目标优化问题, 当邻域大小超过70时, 算法的有效性不受邻域大小选择的实质性影响. 对于三目标优化问题, 当邻域大小超过40时, 邻域大小的设置对算法的有效性影响不太显著. 然而, 当邻域大小小于10时, 算法的有效性显著下降. 因此, 本文将最大邻域指定为40, 最小邻域指定为10.

基于聚合函数值的邻域调整策略的伪代码如算法2所示.

算法 2. 邻域调整策略

输入: 当前代数(gen), 评价次数(FES), 最大评价次数(MAXFES), 聚合函数值改进程度(improve), 最大邻域值(n_max), 最小邻域值(n_min).

输出: 邻域大小(niche).

1. if gen>10&&FES<0.8×MAXFES

2.　 if improve>0.01

3.　　 niche=n_min;

4.　 else

5.　　 niche=n_max;

6.　 end

7. else

8.　 D = FES/MAXFES;

9.　 niche=ceil(n_min+(n_max–n_min)×sin(π×D));

10. end

2.3 基于非支配排序的突变选择策略

突变因子($ F $)决定了种群中个体差异的程度, 进而影响算法对最优解的搜索效果. 增加$ F $可以扩大搜索空间, 促进种群的多样性, 有利于识别最优解, 但会导致收敛速度变慢. 相反, 减小$ F $可以加速收敛速度, 但也增加了过早收敛至局部最优解的风险. 因此, 突变算子在算法中起着至关重要的作用. 本文采用了SaDE算法中的变异算子, 设置方法参考文献[40]. 突变算子采用高斯随机数, 均值和标准差均设为0.5. 突变算子的值应保证在0–1之间.

不同的变异策略具有各自独特的特点, 即使是相同算法在不同阶段采用相同的变异策略, 也会呈现不同的效果. 在算法进化的早期阶段, 全局搜索能力较强的突变策略更有优势, 而在算法的后期阶段, 局部搜索能力较强的突变策略更有优势. 因此, 在算法进化的各个阶段采用合适的突变策略可以提高算法的有效性. 其中, DE/rand/1突变方法具有较强的全局搜索能力, DE/current-to-rand/2突变方法具有较强的局部搜索能力.

本文选择的突变方法操作如下.

(1) DE/rand/1

$ newPop = x_{r_1}^G + F\times(x_{r_2}^G - x_{r_3}^G) $

(3)

其中, $ x_{r_1}^G $, $ x_{r_2}^G $ 和$ x_{r_3}^G $ 是随机挑选的邻居, $ F $是高斯随机数.

(2) DE/current-to-rand/2

$ newPop = x_i^G + K \times (x_i^G - x_{r_1}^G) + F \times (x_{r_2}^G - x_{r_3}^G) + F \times (x_{r_4}^G - x_{r_5}^G) $

(4)

其中, $ K $被设置为0.5, $ x_i^G $ 是当前个体, $ x_{r_1}^G $, $ x_{r_2}^G $, $ x_{r_3}^G $, $ x_{r_4}^G $和 $ x_{r_5}^G $ 是在邻域中随机选择的个体, $ F $是一个高斯随机数.

对种群进行非支配排序, 当处在第1级的种群数较多时, 可以说明种群的收敛性较好, 反之, 种群的多样性较好. 本文使用非支配排序来进行突变策略的选择. 在基因重组过程中, 首先选择高斯随机数作为变异算子, 然后, 对邻域种群进行非支配排序, 使用NUM来评价种群的收敛性. 具体操作如下: 首先, 对邻域种群进行非支配排序, 如果NUM大于等于$ b $, 则表明整体收敛性可能较好. 然后在邻域内执行DE/rand/1变异方法; 否则, 执行DE/current-to-rand/2变异方法, 这种突变选择方法提高了算法的收敛速度和整体有效性.

以LSMOP1为例, 该问题具有两个目标和100个决策变量维度. 在参数选择过程中, 需要考虑算法的性能指标, 其中包括generation distance (GD)和spacing (SP).

由表1可知, 当NUM大于或等于邻域种群数量的一半时, GD和SP值最小, 因此我们选择NUM大于或等于niche/2.

表 1 由LSMOP1上的GD和SP决定b的值

基于非支配排序的突变策略选择伪代码如算法3.

算法 3. 突变选择策略

输入: 邻域大小(niche), 非支配排序等级 (FrontNo).

输出: 新的后代.

1. 从邻居中随机选择5个个体

2. 基于高斯分布生成变异因子F

3. if length (find (FrontNo==1))>=niche/2

4. 　执行DE/rand/1变异策略生成新的后代

5. else

6. 　执行DE/current-to-rand/2变异策略生成新的后代

7. end if

8. 对新的后代执行高斯变异, 并防止超过上限和下限的值

9. 计算新后代的适应度值

10. 返回新的后代

3 实验结果分析 3.1 实验设置和比较算法

为了评估MSMOEA/D算法的有效性, 选择了二目标和三目标LSMOP测试问题^[41], 以及三目标DTLZ1-4和DTLZ6^[42]测试问题进行性能评估. 本文的比较算法在PLATEMO^[43]平台上运行, 改进后的算法在Matlab 2020b上运行. 为了确保公平性, 所有算法在64位Windows 10系统上独立运行了20次, 使用的处理器为Intel (R) Core (TM) i5-4460 CPU@3.20 GHz, 内存大小为4.00 GB.

本文的比较算法有: MOEA/D^[12]、CCGDE3^[23]、RVEA^[13]、MMOPSO^[14]、LMEA^[29]、DGEA^[32].

3.2 参数设置和评价指标

(1)参数设置: 当目标数为3时, 种群大小设置为300. 当目标数为2时, 种群大小设置为100. 由于DTLZ和LSMOP属于不同类型的多目标优化问题, 它们具有不同的问题特征和搜索空间结构. 所以参数设置不同. LSMOP测试问题中决策变量的维数设置为100、200和500维. 最多可进行D×10000次评估. 对于DTLZ测试问题, 将决策变量的维数设置为500和1000维, 最大评估次数分别为500000、700000. 邻域大小为0.1×N. 交叉算子为1, 突变概率配置为1/D, 其中D表示决策变量的维数, 多项式突变的分布指数设为20. 比较算法的其他参数设置: LMEA算法中Type=2. MOEA/D算法中Type=2. 对比算法的其他详细参数均为文献中所推荐的数值.

(2)评价指标: 采用收敛性指标GD^[44]和多样性指标SP^[45].

3.3 实验结果 3.3.1 DTLZ上各种算法的实验结果及分析

表2和表3分别给出了MOEA/D、CCGDE3、RVEA、MMOPSO、LMEA、DGEA和改进算法在500维和1000维DTLZ测试问题上的GD和SP结果. 记录实验中GD和SP指标的平均值, 方差值在括号中表示. 根据结果的平均值, 用粗体强调比较算法中较优的结果.

统计结果表明, 改进算法在DTLZ1、DTLZ3、DTLZ6问题上表现出较好的收敛性, MOEA/D算法在DTLZ2、DTLZ4问题上表现出较好的收敛性. 共有10个问题, 改进后的算法在平均值方面有6个优势. 综上所述, 改进后的算法在大多数测试问题上表现出比对比算法更好的性能, 可以推断出在上面的DTLZ测试问题时, 该算法的收敛性优于其他算法.

改进算法在DTLZ1、DTLZ3和DTLZ6问题上的收敛性优于MOEA/D算法. 与CCGDE3、MMOPSO、LMEA和DGEA算法相比, 改进算法在DTLZ1–DTLZ4和DTLZ6问题上具有更好的收敛性. 在DTLZ1、DTLZ3、DTLZ6问题上, 改进算法的收敛性优于RVEA算法.

统计结果表明, 改进算法在DTLZ3、DTLZ4、DTLZ6测试问题上具有较好的多样性, 而DGEA算法在DTLZ1测试问题上表现最好. RVEA算法在DTLZ2测试问题上表现最佳. 总共有10个问题, 改进后的算法在平均值方面有6个优势. 可以得出结论, 该算法在上面的DTLZ测试问题上比其他比较算法具有更好的多样性.

与MOEA/D算法相比, 改进算法在DTLZ3、DTLZ4、DTLZ6测试问题上具有更好的多样性. 改进算法在DTLZ1–DTLZ4和DTLZ6测试问题上的多样性优于CCGDE3和LMEA算法, 在DTLZ1、DTLZ3、DTLZ4和DTLZ6测试问题上的多样性优于RVEA和MMOPSO算法. 在DTLZ2、DTLZ3、DTLZ4、DTLZ6测试问题上的多样性优于DGEA算法的多样性.

表 2 500维和1000维DTLZ问题的GD结果

表 3 500维和1000维DTLZ问题的SP结果

图 3 7种算法在三目标500维DTLZ6测试问题上找到的非支配解

由图3可以看出, 改进算法在三目标500维DTLZ6测试问题上取得了比其他算法更好的PF. 改进后的算法相比对比算法在收敛性和多样性上都有显著提高.

3.3.2 LSMOP上各种算法的实验结果及分析

表4和表5分别给出了MOEA/D、CCGDE3、RVEA、MMOPSO、LMEA、DGEA和改进算法在100维、200维和500维二目标LSMOP测试问题上的GD和SP结果. 记录实验中GD和SP指标的平均值, 方差值在括号中. 根据结果的平均值, 用粗体形式强调了比较算法中较优的结果.

统计结果表明, 改进算法在LSMOP1、100维LSMOP2、LSMOP4、LSMOP5、LSMOP8、LSMOP9测试问题上均有较好的收敛性. RVEA算法在LSMOP3测试问题上表现最优. MMOPSO算法在500维LSMOP7测试问题上表现最优. 在200维和500维LSMOP2、LSMOP6, 100维和200维LSMOP7测试问题上, DGEA算法表现最优. 测试问题共27道, 改进后的算法在平均值上有16个优势. 可以推断该算法在二目标LSMOP测试问题上比其他对比算法具有更好的收敛性.

统计结果表明, 改进算法在LSMOP1、100维LSMOP2、LSMOP4、LSMOP5、100维和200维LSMOP8测试问题上具有良好的多样性, 其中RVEA算法在LSMOP3测试问题上表现最好. MMOPSO算法在200维、500维LSMOP6、500维LSMOP7、LSMOP9测试问题上表现最好. DGEA算法在200维和500维LSMOP2、100维LSMOP6、100维和200维LSMOP7、500维LSMOP8测试问题上具有良好的多样性. 共有27个测试问题, 改进后的算法在平均值方面有12个优势. 可以推断该算法在双目标LSMOP测试问题上比其他比较算法表现出更好的多样性.

表 4 在二目标LSMOP上的GD值

问题	维度	MOEA/D	CCGDE3	RVEA	MMOPSO	LMEA	DGEA	MSMOEA/D
LSMOP1	100	1.3474E–3 (4.93E–4)	1.8994E+0 (3.85E–1)	2.9838E–2 (1.17E–2)	2.0073E–3 (1.04E–3)	2.5623E–2 (7.55E–2)	2.8226E–4 (2.49E–5)	2.7000E–5 (3.00E–6)
	200	2.0162E–3 (1.07E–3)	1.8761E+0 (4.42E–1)	4.2738E–2 (1.26E–2)	2.2098E–3 (1.30E–3)	9.5077E–2 (1.55E–1)	5.2846E–4 (6.56E–5)	3.7000E–5 (5.00E–6)
	500	2.5346E–3 (1.68E–3)	1.8756E+0 (1.41E–1)	4.1496E–2 (1.31E–2)	1.1907E–2 (3.32E–3)	8.2316E–2 (1.57E–1)	1.5665E–3 (2.26E–4)	6.7000E–5 (8.00E–6)
LSMOP2	100	3.4295E–3 (2.73E–4)	3.7624E–2 (2.39E–3)	1.2854E–2 (7.78E–4)	3.8220E–3 (1.68E–3)	1.1845E–2 (1.06E–2)	1.8391E–3 (4.86E–4)	6.6100E–4 (4.30E–4)
	200	2.9517E–3 (2.99E–4)	2.0063E–2 (1.30E–3)	7.7078E–3 (4.76E–4)	7.6660E–3 (1.18E–3)	1.1086E–2 (5.18E–3)	1.6695E–3 (8.52E–5)	3.9300E–3 (2.23E–3)
	500	2.9064E–3 (2.33E–4)	9.2410E–3 (2.31E–4)	4.5868E–3 (1.06E–4)	5.2550E–3 (1.45E–4)	7.5591E–3 (1.07E–3)	9.0679E–4 (4.86E–5)	3.8590E–3 (9.00E–5)
LSMOP3	100	3.5740E+3 (7.11E+3)	1.3448E+4 (4.93E+3)	5.7064E–6 (1.55E–6)	3.5480E–1 (2.50E–1)	1.6881E+1 (5.36E+1)	1.9041E–1 (1.11E–1)	1.0829E–1 (3.96E–2)
	200	5.8365E–3 (8.56E–3)	1.6651E+4 (4.66E+3)	6.2497E–6 (1.63E–6)	5.5025E–1 (5.24E–1)	5.5004E+0 (1.31E+1)	1.7808E–1 (7.69E–2)	1.1416E–1 (3.14E–2)
	500	1.5970E+3 (7.14E+3)	2.1778E+4 (2.58E+3)	7.6470E–6 (1.19E–6)	2.9252E–1 (2.87E–1)	3.0354E+0 (7.45E+0)	1.4580E–1 (1.60E–1)	3.2533E+2 (3.52E+2)
LSMOP4	100	4.0187E–3 (1.25E–3)	6.3156E–2 (1.15E–2)	3.7481E–2 (2.94E–3)	5.4718E–3 (3.03E–3)	1.1399E–2 (1.91E–2)	1.6538E–3 (2.18E–4)	1.6350E–3 (1.84E–4)
	200	2.5791E–3 (3.18E–4)	3.7771E–2 (3.63E–3)	2.0815E–2 (1.68E–3)	6.6703E–3 (2.84E–3)	5.8560E–3 (9.06E–3)	1.1768E–3 (1.29E–4)	1.1440E–3 (1.52E–4)
	500	1.4011E–3 (5.37E–5)	1.5606E–2 (8.18E–4)	8.4442E–3 (3.60E–4)	8.8599E–3 (1.67E–3)	1.8612E–3 (2.95E–3)	6.8546E–4 (2.74E–5)	6.4900E–4 (1.40E–5)
LSMOP5	100	1.8835E+0 (4.74E+0)	5.1287E+0 (1.31E+0)	3.3466E–2 (9.93E–3)	2.7572E–4 (2.06E–4)	2.4426E+0 (2.88E+0)	4.1833E–4 (1.58E–4)	4.7000E–5 (4.00E–6)
	200	1.0735E+0 (1.09E+0)	5.7061E+0 (1.09E+0)	2.8355E–2 (1.13E–2)	1.4604E–4 (6.16E–5)	4.5647E+0 (2.44E+0)	9.2346E–4 (1.50E–4)	7.0000E–5 (5.00E–6)
	500	1.2004E+0 (1.29E+0)	5.6938E+0 (5.87E–1)	1.3996E–2 (4.43E–3)	3.9467E–4 (1.59E–4)	5.8576E+0 (2.16E+0)	2.1789E–3 (1.31E–4)	1.2200E–4 (8.00E–6)
LSMOP6	100	8.8158E+2 (8.85E+2)	5.0656E+3 (2.94E+3)	1.6210E+3 (7.25E+3)	1.4513E–1 (2.37E–2)	1.5815E+2 (2.59E+2)	2.3246E–2 (3.69E–2)	4.8162E–1 (1.13E+0)
	200	6.1653E+4 (3.80E+4)	1.6500E+4 (6.92E+3)	4.7718E+2 (2.12E+3)	1.1019E–1 (8.87E–2)	7.7663E+2 (1.98E+3)	6.7537E–2 (8.96E–2)	5.1290E+3 (6.33E+2)
	500	9.7100E+4 (4.93E+4)	3.3683E+4 (8.70E+3)	6.2241E+2 (2.69E+3)	5.6220E–2 (2.03E–2)	1.4996E+4 (1.47E+4)	1.6886E–2 (1.07E–2)	5.7897E+3 (7.22E+2)
LSMOP7	100	2.3159E+3 (5.53E+3)	3.9999E+4 (2.95E+4)	2.5628E+0 (3.27E+0)	1.3769E+1 (6.05E+1)	8.9039E–1 (5.50E–1)	3.1797E–1 (4.29E–1)	1.2603E+3 (1.17E+3)
	200	3.4929E+3 (5.62E+3)	4.1153E+4 (2.32E+4)	1.3365E+0 (2.34E+0)	1.0284E+2 (3.92E+2)	6.2875E–1 (2.67E–1)	2.8827E–1 (2.72E–1)	1.4060E+3 (7.44E+2)
	500	3.0166E+3 (3.82E+3)	3.7616E+4 (1.29E+4)	4.1456E–1 (5.14E–1)	1.5574E–1 (1.24E–1)	6.0022E–1 (2.85E–1)	2.6501E–1 (1.50E–1)	1.5622E+3 (1.02E+2)
LSMOP8	100	3.3365E–3 (9.12E–4)	2.6125E+0 (8.39E–1)	4.4616E–2 (1.40E–2)	5.8692E–3 (9.35E–4)	9.0759E–3 (3.21E–3)	4.8974E–3 (1.43E–3)	9.8900E–4 (5.83E–4)
	200	2.8092E–3 (7.38E–4)	3.4620E+0 (1.01E+0)	5.0404E–2 (1.08E–2)	5.5889E–3 (3.55E–4)	4.6059E–3 (1.17E–3)	2.5369E–3 (1.05E–3)	1.3050E–3 (4.73E–4)
	500	1.7095E–3 (3.19E–4)	2.8864E+0 (8.48E–1)	3.9691E–2 (4.90E–3)	3.5134E–3 (4.37E–4)	6.5058E–3 (1.63E–2)	1.6342E–3 (1.63E–4)	1.0900E–3 (1.91E–4)
LSMOP9	100	4.9560E–3 (3.35E–3)	6.2648E+0 (2.19E+0)	1.8781E–1 (4.96E–2)	1.7158E–2 (1.20E–2)	7.2449E–2 (1.30E–1)	1.3635E–3 (2.78E–4)	2.0500E–4 (2.00E–5)
	200	1.0266E–2 (4.75E–3)	7.5598E+0 (2.36E+0)	1.0911E–1 (1.02E–2)	6.1749E–2 (9.10E–3)	2.2793E–2 (6.83E–2)	2.1184E–3 (3.71E–4)	2.1200E–4 (1.90E–5)
	500	1.1618E–2 (1.04E–3)	7.4252E+0 (2.06E+0)	5.3798E–2 (7.17E–3)	2.2886E–2 (1.22E–3)	4.3667E–3 (1.49E–2)	1.2620E–2 (6.01E–3)	1.7200E–4 (1.90E–5)

表 4 在二目标LSMOP上的GD值

表 5 在二目标LSMOP上的SP值

Problem	Dimension	MOEA/D	CCGDE3	RVEA	MMOPSO	LMEA	DGEA	MSMOEA/D
LSMOP1	100	7.3620E–3 (2.88E–3)	4.7049E–1 (2.64E–1)	2.8221E–2 (1.90E–2)	6.7153E–3 (6.12E–4)	1.6303E–2 (1.14E–2)	3.6876E–4 (6.19E–5)	3.2000E–5 (1.80E–5)
	200	1.1445E–2 (1.53E–2)	3.6987E–1 (1.69E–1)	2.6056E–2 (1.10E–2)	7.1743E–3 (5.31E–4)	2.3783E–2 (2.44E–2)	4.0572E–4 (1.18E–4)	3.2000E–5 (3.00E–5)
	500	9.0710E–3 (2.48E–3)	2.9043E–1 (9.00E–2)	2.3719E–2 (1.86E–2)	6.2851E–3 (6.02E–4)	1.0847E–1 (3.84E–1)	1.4132E–3 (3.68E–4)	4.9000E–5 (6.70E–5)
LSMOP2	100	2.3764E–3 (1.39E–4)	1.0424E–2 (1.69E–3)	6.3173E–3 (1.72E–3)	7.1415E–3 (7.27E–4)	1.4264E–2 (3.47E–3)	1.0267E–3 (2.36E–4)	4.0800E–4 (2.79E–4)
	200	1.6461E–3 (1.57E–4)	1.1856E–2 (1.00E–3)	1.7495E–3 (2.68E–4)	7.9120E–3 (1.06E–3)	1.0996E–2 (2.07E–3)	6.8134E–4 (6.63E–5)	1.6610E–3 (1.02E–3)
	500	1.2453E–3 (7.96E–5)	1.0017E–2 (1.33E–3)	6.1398E–4 (1.68E–4)	8.0124E–3 (7.82E–4)	7.2862E–3 (8.51E–4)	3.2672E–4 (2.65E–5)	1.4380E–3 (6.60E–5)
LSMOP3	100	1.4660E+4 (2.85E+4)	3.7449E+3 (2.03E+3)	9.9515E–7 (4.88E–7)	9.4738E–1 (9.21E–1)	4.7855E+0 (1.58E+1)	3.2312E–1 (2.85E–1)	2.8036E–2 (1.16E–2)
	200	3.0182E–3 (6.25E–3)	4.4478E+3 (2.29E+3)	1.1413E–6 (4.56E–7)	8.0254E–1 (8.29E–1)	1.2130E+0 (2.49E+0)	3.7162E–1 (1.78E–1)	2.2977E–2 (8.12E–3)
	500	7.6587E+3 (3.43E+4)	4.8316E+3 (2.27E+3)	1.6563E–6 (4.48E–7)	6.8022E–1 (6.16E–1)	1.2579E+0 (2.34E+0)	5.6510E–1 (6.92E–1)	9.0258E+2 (2.05E+2)
LSMOP4	100	1.6473E–2 (4.29E–3)	1.4629E–2 (3.20E–3)	2.5220E–2 (6.49E–3)	7.1197E–3 (7.51E–4)	1.8102E–2 (4.87E–3)	8.6689E–4 (1.56E–4)	5.6200E–4 (2.25E–4)
	200	1.2841E–2 (1.28E–3)	1.1571E–2 (1.51E–3)	8.7935E–3 (1.72E–3)	6.7299E–3 (6.54E–4)	1.3405E–2 (1.91E–3)	5.4778E–4 (1.72E–4)	3.9000E–4 (1.40E–4)
	500	8.4101E–3 (5.74E–4)	1.1116E–2 (7.70E–4)	2.9483E–3 (4.71E–4)	6.9557E–3 (7.49E–4)	1.1395E–2 (2.04E–3)	2.3744E–4 (2.67E–5)	1.7700E–4 (1.20E–5)
LSMOP5	100	5.5188E+0 (1.25E+1)	1.2333E+0 (9.46E–1)	1.6071E–1 (1.44E–1)	7.1077E–3 (4.94E–4)	1.1013E+0 (1.28E+0)	7.0619E–3 (2.01E–3)	6.1550E–3 (2.00E–5)
	200	3.4088E+0 (6.92E+0)	7.8265E–1 (3.82E–1)	5.3971E–2 (3.58E–2)	7.2666E–3 (7.00E–4)	1.7173E+0 (1.14E+0)	7.5601E–3 (2.26E–3)	6.1490E–3 (9.00E–6)
	500	2.2955E+0 (6.54E+0)	5.4830E–1 (3.03E–1)	2.4506E–2 (1.23E–2)	6.8390E–3 (7.51E–4)	1.8257E+0 (7.91E–1)	6.8982E–3 (1.33E–3)	6.1550E–3 (1.00E–5)
LSMOP6	100	1.6863E+3 (1.64E+3)	3.9010E+3 (5.09E+3)	1.5641E+3 (6.99E+3)	2.9262E–2 (5.46E–2)	5.9384E+1 (1.08E+2)	1.9171E–2 (4.10E–2)	4.1932E+0 (1.08E+1)
	200	7.3307E+4 (5.13E+4)	4.7957E+3 (3.49E+3)	4.5462E+2 (1.91E+3)	2.7968E–2 (2.72E–2)	2.6851E+2 (6.86E+2)	1.9797E–1 (3.53E–1)	1.0000E+3 (0.00E+0)
	500	1.8735E+5 (6.81E+4)	5.4084E+3 (2.08E+3)	5.7219E+2 (2.54E+3)	2.3844E–2 (2.89E–2)	7.2806E+3 (8.57E+3)	1.2415E–1 (2.56E–1)	1.0000E+3 (1.00E–6)
LSMOP7	100	1.1252E+4 (2.09E+4)	4.3404E+4 (1.00E+5)	2.0647E+0 (2.87E+0)	1.2131E+2 (5.42E+2)	1.8361E+0 (1.36E+0)	3.6321E–2 (3.50E–2)	7.2349E+2 (4.56E+2)
	200	1.8091E+4 (2.41E+4)	3.0364E+4 (7.10E+4)	1.6169E+0 (3.94E+0)	6.1589E+2 (2.14E+3)	9.3504E–1 (1.11E+0)	2.1829E–1 (2.85E–1)	9.2459E+2 (2.46E+2)
	500	1.8509E+4 (2.33E+4)	7.5602E+3 (8.77E+3)	2.2832E–1 (4.63E–1)	6.2575E–2 (7.44E–2)	1.7080E+0 (1.13E+0)	3.9942E–1 (3.65E–1)	8.0191E+2 (4.19E+2)
LSMOP8	100	9.9808E–3 (6.95E–4)	4.3776E–1 (2.86E–1)	6.4822E–2 (9.03E–2)	1.4750E–2 (8.64E–3)	2.5976E–2 (9.99E–3)	2.1189E–2 (1.11E–2)	6.2440E–3 (4.80E–5)
	200	1.0211E–2 (1.72E–3)	6.3206E–1 (4.26E–1)	4.3143E–2 (7.76E–2)	1.1042E–2 (5.98E–3)	2.3499E–2 (1.05E–2)	1.0800E–2 (5.74E–3)	6.2780E–3 (4.40E–5)
	500	1.1753E–2 (5.76E–4)	3.9281E–1 (2.60E–1)	3.0964E–2 (3.11E–2)	7.6569E–3 (1.47E–3)	5.7746E–2 (1.60E–1)	6.3577E–3 (7.62E–4)	1.2186E–2 (1.45E–2)
LSMOP9	100	2.4685E–2 (1.01E–2)	8.8835E–1 (6.05E–1)	4.9579E–2 (2.35E–2)	7.0039E–3 (1.05E–3)	2.0381E–2 (1.25E–2)	1.1651E–2 (1.12E–3)	1.4712E–2 (7.50E–5)
	200	2.8853E–2 (7.23E–3)	1.0119E+0 (7.30E–1)	3.5784E–2 (1.45E–2)	9.8181E–3 (1.29E–3)	1.9774E–2 (8.39E–3)	1.0992E–2 (1.22E–3)	1.4712E–2 (2.10E–5)
	500	2.1112E–2 (1.85E–3)	7.0207E–1 (6.66E–1)	1.9048E–2 (7.10E–3)	8.3371E–3 (9.21E–4)	2.4597E–2 (1.35E–2)	1.2694E–2 (4.78E–3)	1.4741E–2 (1.90E–5)

表 5 在二目标LSMOP上的SP值

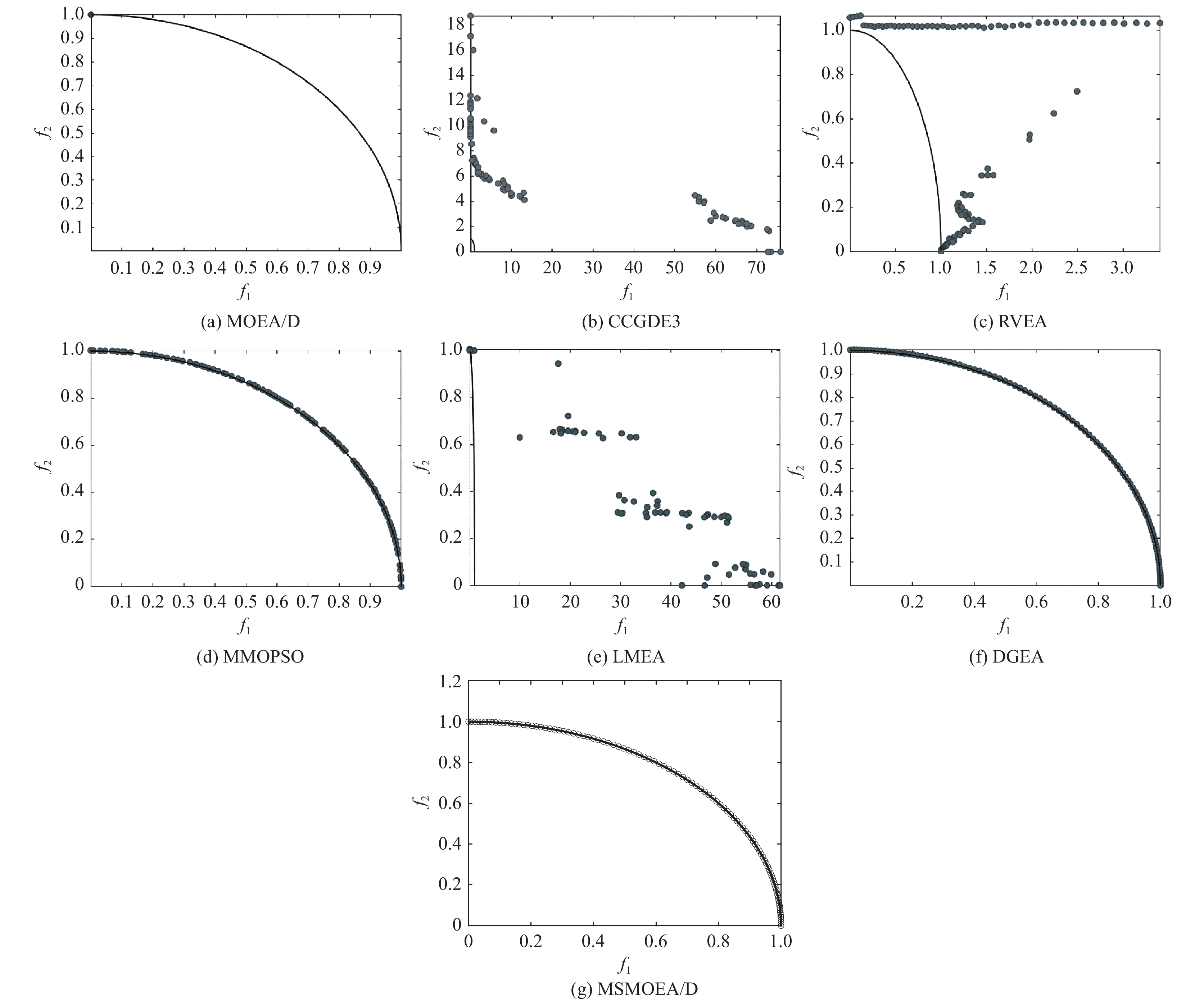
图 4 7种算法在二目标100维LSMOP5测试问题上找到的非支配解

从图4可以明显看出, 改进算法在二目标100维LSMOP5测试问题上取得了比其他算法更好的效果. 与比较算法相比, 改进算法在收敛性和多样性方面都有了明显的改进.

表6和表7分别给出了MOEA/D、CCGDE3、RVEA、MMOPSO、LMEA、DGEA和改进算法在100、200和500维三目标 LSMOP测试问题上的GD和SP结果. 记录实验中GD和SP指标的平均值, 方差值在括号中. 根据结果的平均值, 用粗体形式强调了比较算法中较优的结果.

统计结果表明, 改进算法对500维LSMOP3、LSMOP5、LSMOP6、LSMOP7、500维LSMOP8、LSMOP9测试问题具有较好的收敛性. MOEA/D在LSMOP1、100维LSMOP2、LSMOP4、100维和200维LSMOP8测试问题上具有良好的收敛性. MMOPSO在100维和200维LSMOP3测试问题上表现最好. DGEA在200维和500维LSMOP2测试问题上表现最好. 共有27个测试问题, 改进后的算法在平均值方面有14个优势. 可以得出结论, 在三目标LSMOP测试问题上, 改进算法在收敛性上相较于比较算法有了明显的提高.

统计结果表明, 改进算法在100维、200维LSMOP5、LSMOP6、LSMOP7测试问题上具有较好的多样性. MOEA/D算法在200维LSMOP1、500维LSMOP3、100维LSMOP8、LSMOP9测试问题上具有较好的多样性. RVEA算法在500维LSMOP1、200和500维LSMOP2、200和500维LSMOP4、500维LSMOP5测试问题上表现最优. MMOPSO算法在100维和200维LSMOP3测试问题上表现最优. 在100维LSMOP1、100维LSMOP2、100维LSMOP4、200维和500维LSMOP8测试问题上, DGEA算法表现最优. 总共有27个测试问题, 改进后的算法在平均值上有8个优势. 在三目标LSMOP测试问题上, 该算法在多样性方面表现较差.

表 6 在三目标LSMOP上的GD值

问题	维度	MOEA/D	CCGDE3	RVEA	MMOPSO	LMEA	DGEA	MSMOEA/D
LSMOP1	100	5.4749E–3 (1.21E–3)	6.1240E–1 (1.76E–1)	3.7444E–2 (4.52E–2)	1.2674E–2 (3.07E–3)	2.9850E–2 (4.98E–2)	1.6249E–2 (2.16E–3)	6.5810E–3 (5.16E–4)
	200	6.7891E–3 (8.36E–4)	9.3467E–1 (1.49E–1)	1.8380E–2 (2.46E–3)	1.5278E–2 (1.99E–3)	4.7054E–2 (9.85E–2)	2.5771E–2 (1.91E–3)	9.8270E–3 (8.04E–4)
	500	8.2013E–3 (1.21E–3)	1.1686E+0 (1.13E–1)	1.7779E–2 (2.37E–3)	2.1679E–2 (3.92E–3)	6.9201E–2 (1.06E–1)	3.2138E–2 (2.40E–3)	1.2316E–2 (3.17E–4)
LSMOP2	100	3.3504E–3 (1.92E–4)	1.6106E–2 (8.99E–4)	8.0211E–3 (4.81E–4)	1.0868E–2 (3.88E–4)	6.3243E–3 (3.54E–3)	5.6522E–3 (1.61E–3)	5.5320E–3 (3.24E–4)
	200	2.7883E–3 (1.29E–4)	8.9212E–3 (3.45E–4)	3.8946E–3 (1.17E–4)	7.0129E–3 (3.35E–4)	5.9420E–3 (1.15E–3)	2.4764E–3 (2.07E–4)	4.5060E–3 (2.34E–4)
	500	1.7725E–3 (1.11E–4)	3.6070E–3 (1.18E–4)	1.7908E–3 (3.10E–5)	3.2888E–3 (1.51E–4)	2.6348E–3 (5.71E–4)	1.1273E–3 (6.24E–5)	2.4710E–3 (9.20E–5)
LSMOP3	100	1.1112E–1 (5.98E–2)	5.4356E+2 (3.50E+2)	3.0070E+2 (4.41E+2)	5.0055E–2 (2.43E–2)	4.3094E–1 (7.40E–1)	1.1019E+0 (7.89E–1)	8.4824E–2 (5.29E–2)
	200	9.7383E–2 (4.91E–2)	8.5099E+2 (2.80E+2)	4.7658E+2 (1.98E+2)	2.6412E–2 (6.84E–3)	7.8878E+1 (3.23E+2)	5.6659E–1 (3.80E–1)	7.1212E–2 (3.52E–2)
	500	1.3885E–1 (3.27E–2)	1.4522E+3 (2.96E+2)	6.3195E+2 (2.09E+2)	1.1697E–1 (6.22E–2)	1.0631E+2 (3.39E+2)	4.8672E–1 (3.12E–1)	9.3460E–2 (1.87E–2)
LSMOP4	100	4.0144E–3 (7.72E–4)	7.3157E–2 (6.34E–3)	3.4896E–2 (7.28E–3)	1.2253E–2 (2.08E–3)	9.4470E–3 (9.64E–3)	1.4171E–2 (9.35E–4)	7.0260E–3 (2.29E–4)
	200	4.8818E–3 (5.21E–4)	4.2139E–2 (1.99E–3)	1.4970E–2 (1.17E–3)	1.9034E–2 (3.66E–3)	9.4585E–3 (7.60E–3)	1.0623E–2 (7.62E–4)	7.4840E–3 (1.86E–3)
	500	3.3715E–3 (1.18E–4)	1.7391E–2 (6.47E–4)	6.2467E–3 (1.74E–4)	1.4052E–2 (7.73E–4)	3.6306E–3 (1.78E–3)	4.8318E–3 (1.55E–4)	8.8950E–3 (9.20E–3)
LSMOP5	100	1.4115E–1 (4.58E–1)	2.6443E+0 (4.88E–1)	3.4564E–2 (1.01E–2)	1.1439E–2 (1.59E–2)	1.9932E+0 (1.22E+0)	1.9714E–2 (3.27E–3)	2.2760E–3 (4.58E–4)
	200	3.5162E–2 (7.05E–2)	3.0576E+0 (2.75E–1)	4.9666E–2 (4.80E–2)	1.7146E–2 (2.01E–2)	2.3074E+0 (1.30E+0)	2.0466E–2 (1.71E–3)	2.3690E–3 (3.02E–4)
	500	8.2566E–2 (2.34E–1)	3.5001E+0 (3.15E–1)	1.9831E–2 (6.75E–2)	4.5937E–3 (1.01E–3)	2.8391E+0 (6.54E–1)	2.2149E–2 (2.65E–3)	4.5840E–3 (2.97E–4)
LSMOP6	100	3.6377E+2 (1.24E+3)	9.6964E+3 (7.86E+3)	1.5452E+1 (2.09E+1)	8.1444E+1 (2.45E+2)	1.6545E+4 (2.41E+4)	1.2246E+2 (3.86E+2)	9.3212E–2 (8.95E–2)
	200	7.9896E+2 (3.05E+3)	1.0321E+4 (6.68E+3)	2.0800E+1 (1.70E+1)	7.8935E–1 (1.94E+0)	1.9763E+4 (1.52E+4)	4.0039E–1 (2.76E–1)	8.9423E–2 (5.89E–2)
	500	2.2567E+3 (5.58E+3)	1.5871E+4 (5.92E+3)	2.2154E+3 (5.05E+3)	1.4299E+0 (3.93E+0)	2.4395E+4 (2.71E+4)	1.8172E+2 (5.73E+2)	1.0345E–1 (7.71E–2)
LSMOP7	100	7.7776E+2 (3.47E+3)	5.6661E+3 (2.27E+3)	4.8262E+2 (1.41E+3)	1.2784E–1 (9.38E–2)	4.7916E–1 (1.70E–1)	1.5453E–1 (9.49E–3)	1.0295E–1 (6.89E–2)
	200	2.0203E+0 (4.49E+0)	1.2230E+4 (2.17E+3)	2.7286E+2 (1.00E+3)	1.2872E–1 (5.39E–2)	6.7264E+2 (3.01E+3)	1.7603E–1 (6.69E–3)	9.0734E–2 (4.29E–2)
	500	1.2017E+3 (3.89E+3)	2.1939E+4 (5.34E+3)	4.2692E+3 (5.26E+3)	7.2338E+1 (3.23E+2)	3.3328E–1 (4.18E–1)	1.7473E–1 (1.00E–2)	7.3398E–2 (1.23E–2)
LSMOP8	100	2.2639E–3 (5.08E–4)	9.7400E–1 (1.87E–1)	1.5810E–1 (6.50E–1)	1.0530E–2 (9.99E–4)	7.1768E–1 (3.16E+0)	1.3971E–2 (3.23E–3)	4.2170E–3 (1.41E–3)
	200	3.3360E–3 (4.66E–4)	1.2346E+0 (2.07E–1)	6.7149E–2 (1.06E–1)	7.3594E–3 (2.19E–4)	4.8419E–2 (1.14E–1)	5.2768E–3 (7.03E–4)	4.5680E–3 (3.50E–4)
	500	4.0599E–3 (8.79E–4)	1.6253E+0 (3.02E–1)	1.5392E–2 (2.60E–3)	5.8964E–3 (4.14E–3)	8.9759E–2 (1.37E–1)	3.5690E–3 (2.38E–4)	2.8820E–3 (1.42E–4)
LSMOP9	100	3.1331E–2 (1.77E–2)	8.1903E+0 (3.34E+0)	3.8066E–1 (7.26E–2)	1.9325E–1 (1.85E–2)	3.2805E–1 (7.75E+0)	4.4544E–1 (3.17E–1)	7.5000E–4 (1.14E–4)
	200	9.7769E–3 (9.58E–3)	7.7564E+0 (2.24E+0)	2.5153E–1 (6.47E–2)	8.9050E–2 (2.95E–3)	1.6801E–2 (1.15E–2)	2.8251E–1 (1.84E–1)	7.7900E–4 (1.54E–4)
	500	5.4415E–3 (3.11E–3)	1.0202E+1 (3.18E+0)	2.0762E–1 (1.68E–1)	3.0390E–2 (2.40E–3)	1.4334E–2 (1.33E–2)	1.8229E–1 (1.63E–1)	3.6630E–3 (2.63E–3)

表 6 在三目标LSMOP上的GD值

表 7 在三目标LSMOP上的SP值

问题	维度	MOEA/D	CCGDE3	RVEA	MMOPSO	LMEA	DGEA	MSMOEA/D
LSMOP1	100	3.1850E–2 (2.41E–3)	3.5228E–1 (6.71E–2)	5.9037E–2 (4.45E–2)	3.5112E–2 (4.36E–3)	3.2514E–1 (6.25E–1)	2.7978E–2 (2.95E–3)	4.2361E–2 (2.92E–3)
	200	3.2478E–2 (3.19E–3)	4.6754E–1 (4.44E–2)	3.6771E–2 (6.50E–3)	3.7606E–2 (2.98E–3)	3.0260E–1 (5.45E–1)	3.7475E–2 (2.98E–3)	4.3883E–2 (1.25E–3)
	500	3.6010E–2 (4.90E–3)	5.8764E–1 (3.35E–2)	3.4145E–2 (6.31E–3)	4.3068E–2 (4.33E–3)	5.8488E–1 (8.55E–1)	4.1213E–2 (2.62E–3)	4.4720E–2 (9.43E–4)
LSMOP2	100	3.5476E–2 (7.85E–4)	3.4457E–2 (2.98E–3)	1.1909E–2 (7.75E–4)	3.2881E–2 (1.93E–3)	3.0271E–2 (7.52E–3)	9.0429E–3 (1.41E–3)	3.8353E–2 (5.83E–4)
	200	3.2995E–2 (1.06E–3)	3.0513E–2 (2.21E–3)	4.3013E–3 (3.68E–4)	3.1271E–2 (1.54E–3)	2.2563E–2 (2.30E–3)	4.4231E–3 (6.58E–4)	3.5830E–2 (3.00E–4)
	500	3.1548E–2 (7.58E–4)	2.9538E–2 (2.53E–3)	1.2712E–3 (8.89E–5)	2.8377E–2 (1.19E–3)	2.0715E–2 (1.91E–3)	2.0629E–3 (4.10E–4)	3.3401E–2 (1.13E–4)
LSMOP3	100	7.8893E–2 (2.80E–2)	1.0957E+2 (1.13E+2)	2.4409E+2 (6.56E+2)	5.2754E–2 (4.75E–2)	2.6078E–1 (1.73E–1)	3.9897E+0 (3.36E+0)	7.7444E–2 (3.87E–2)
	200	5.8215E–2 (3.04E–2)	1.1590E+2 (6.42E+1)	1.9465E+2 (1.44E+2)	1.1944E–2 (1.34E–2)	8.0068E+2 (3.33E+3)	2.8810E+0 (2.51E+0)	7.8231E–2 (4.15E–2)
	500	7.3075E–2 (2.93E–2)	1.9079E+2 (6.29E+1)	1.6812E+2 (4.77E+1)	3.5161E–1 (5.45E–1)	8.6661E+2 (2.81E+3)	2.1737E+0 (1.83E+0)	8.9564E–2 (2.87E–2)
LSMOP4	100	3.0085E–2 (3.22E–3)	6.6648E–2 (3.82E–3)	3.6030E–2 (8.13E–3)	3.4078E–2 (2.16E–3)	5.5567E–2 (4.29E–2)	2.6106E–2 (6.09E–3)	3.9222E–2 (5.27E–4)
	200	3.7475E–2 (2.06E–3)	4.8408E–2 (2.44E–3)	1.4305E–2 (2.52E–3)	3.7138E–2 (2.99E–3)	3.8552E–2 (1.06E–2)	1.5958E–2 (6.96E–4)	4.0443E–2 (2.82E–3)
	500	3.2464E–2 (9.21E–4)	3.6231E–2 (2.21E–3)	5.5609E–3 (3.42E–4)	3.4359E–2 (1.43E–3)	3.1215E–2 (6.69E–3)	8.2798E–3 (2.40E–4)	3.9264E–2 (8.89E–4)
LSMOP5	100	5.3462E–2 (9.85E–2)	1.7246E+0 (3.59E–1)	8.6566E–2 (2.65E–2)	8.2411E–2 (1.91E–1)	2.9459E+0 (1.61E+0)	5.8917E–2 (1.19E–2)	4.5928E–2 (7.60E–3)
	200	5.8860E–2 (8.32E–2)	1.7900E+0 (1.81E–1)	6.3518E–2 (5.18E–2)	8.7392E–2 (9.27E–2)	2.5897E+0 (1.14E+0)	7.3402E–2 (2.88E–2)	4.5540E–2 (5.97E–3)
	500	2.4304E–2 (2.11E–2)	2.1275E+0 (3.07E–1)	1.7393E–2 (5.72E–2)	2.0105E–2 (1.02E–2)	2.2835E+0 (6.94E–1)	6.4413E–2 (1.40E–2)	3.6209E–2 (6.57E–3)
LSMOP6	100	1.8685E+2 (7.84E+2)	3.3054E+4 (4.49E+4)	4.4403E+1 (7.43E+1)	1.3465E+2 (5.36E+2)	4.6636E+4 (6.30E+4)	1.0662E+3 (3.36E+3)	6.4095E–2 (3.56E–2)
	200	3.7172E+2 (1.11E+3)	1.2633E+4 (2.19E+4)	6.5659E+1 (7.94E+1)	3.4522E+0 (7.68E+0)	5.8400E+4 (4.69E+4)	1.4644E+0 (1.16E+0)	6.1937E–2 (4.19E–2)
	500	1.6802E+3 (4.21E+3)	9.8686E+3 (2.85E+3)	9.8160E+3 (2.44E+4)	1.0574E+0 (2.41E+0)	3.7140E+4 (4.43E+4)	9.8400E+1 (3.02E+2)	9.1198E–2 (9.63E–2)
LSMOP7	100	4.1053E+3 (1.83E+4)	5.3302E+3 (1.68E+3)	6.7193E+2 (2.02E+3)	3.3926E–1 (1.16E+0)	5.6323E–1 (2.62E–1)	6.1298E–1 (1.54E–1)	5.0322E–2 (3.92E–2)
	200	3.1311E–1 (7.56E–1)	9.7391E+3 (2.10E+3)	3.5298E+2 (1.29E+3)	6.1041E–2 (4.58E–2)	7.6976E+1 (3.42E+2)	6.0630E–1 (8.71E–2)	5.3814E–2 (2.16E–2)
	500	4.5096E+2 (1.38E+3)	1.5299E+4 (4.80E+3)	4.7005E+3 (5.50E+3)	1.2514E+3 (5.60E+3)	5.4936E–1 (7.97E–1)	2.5503E–1 (2.35E–1)	3.3680E–2 (1.09E–2)
LSMOP8	100	3.1874E–2 (6.17E–3)	6.4405E–1 (1.59E–1)	1.6917E–1 (7.04E–1)	3.5934E–2 (3.80E–3)	5.7642E–1 (2.22E+0)	4.4998E–2 (2.68E–2)	4.2017E–2 (1.84E–2)
	200	3.7792E–2 (6.11E–3)	7.8048E–1 (1.15E–1)	9.2451E–2 (4.89E–2)	3.5667E–2 (2.90E–3)	3.9082E–1 (8.79E–1)	3.3444E–2 (9.03E–4)	5.5830E–2 (1.22E–3)
	500	3.9386E–2 (3.45E–3)	9.7433E–1 (1.67E–1)	7.0163E–2 (3.69E–2)	5.4272E–2 (7.63E–2)	1.3554E+0 (2.13E+0)	3.3056E–2 (2.82E–4)	5.2222E–2 (6.67E–4)
LSMOP9	100	3.8950E–2 (1.82E–2)	8.1178E–1 (5.40E–1)	1.5857E–1 (4.02E–2)	5.7085E–2 (8.46E–3)	6.6989E–1 (1.77E+0)	1.1297E+0 (1.43E+0)	5.5791E–2 (1.13E–2)
	200	3.3328E–2 (1.38E–2)	4.9922E–1 (2.39E–1)	1.3585E–1 (4.31E–2)	4.8438E–2 (5.24E–3)	5.8093E–2 (3.80E–2)	6.8061E–1 (7.11E–1)	5.7035E–2 (1.10E–2)
	500	2.7731E–2 (1.21E–2)	6.2792E–1 (3.03E–1)	1.4952E–1 (7.92E–2)	3.7025E–2 (8.49E–3)	5.5287E–2 (2.79E–2)	4.8692E–1 (5.99E–1)	3.8752E–2 (1.16E–2)

表 7 在三目标LSMOP上的SP值

图 5 7种算法在三目标100维LSMOP9测试问题上找到的非支配解

从图5可以看出, 在三目标 100维LSMOP9测试问题上, 改进算法与其他算法相比收敛性更优.

4 结论和展望

MSMOEA/D算法首先引入了基于自动编码器的混合初始策略, 以获得更优质的初始种群, 为后续的优化过程提供良好的起点, 从而使算法能够更充分地探索解空间. 接着, 根据当前种群和聚合函数值的变化程度动态调整邻域, 以在不同的进化阶段更好的交换信息. 最后, 采用基于非支配排序的变异选择策略, 以实现算法全局和局部搜索能力的平衡. 在LSMOP和DTLZ测试问题上的实验结果表明, 与其他算法相比, 改进的MSMOEA/D算法在解决LSMOP问题上是有效的.

解决大规模优化问题是进化算法领域的一个重要挑战, 得到了众多学者的关注. 虽然提出的改进算法具有更强的收敛能力, 但在三目标LSMOP测试问题上的实验结果表明, 种群在Pareto前沿分布不均匀. 因此, LSMOP的解决方案还需要进一步研究. 未来, 我们可以考虑使用决策空间中的方向向量来指导有前途后代的生成, 并扩展算法在高维目标优化问题和实际问题中的应用.

参考文献

[1]	黄杰, 武瑞梓, 李均利. 进化算法在复杂网络中的应用综述. 计算机系统应用, 2023, 32(4): 16-41. DOI:10.15888/j.cnki.csa.009037
[2]	Zhang L, Pan HB, Su YS, et al. A mixed representation-based multiobjective evolutionary algorithm for overlapping community detection. IEEE Transactions on Cybernetics, 2017, 47(9): 2703-2716. DOI:10.1109/TCYB.2017.2711038
[3]	常大亮, 史海波, 刘昶. 具有紧时高能耗工序特征的多目标调度优化问题求解. 中国机械工程, 1–12. http://kns.cnki.net/kcms/detail/42.1294.th.20240308.1647.008.html. (2024-03-10)[2024-04-19].
[4]	姜涛, 梁振宇, 程然, 等. GPU加速的演化算法求解多目标流水车间调度问题. 计算机应用, 2024, 44(5): 1364-1371. DOI:10.11772/j.issn.1001-9081.2024010028
[5]	Zhou AM, Qu BY, Li H, et al. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm and Evolutionary Computation, 2011, 1(1): 32-49. DOI:10.1016/j.swevo.2011.03.001
[6]	谢承旺, 余伟伟, 郭华, 等. DAV-MOEA: 一种采用动态角度向量支配关系的高维多目标进化算法. 计算机学报, 2022, 45(2): 317-333. DOI:10.11897/SP.J.1016.2022.00317
[7]	顾清华, 骆家乐, 李学现. 基于小生境的多目标进化算法. 计算机工程与应用, 2023, 59(1): 126-139. DOI:10.3778/j.issn.1002-8331.2207-0006
[8]	Huband S, Barone L, While L, et al. A scalable multi-objective test problem toolkit. Proceedings of the 3rd International Conference on Evolutionary Multi-criterion Optimization. Guanajuato: Springer, 2005. 280–295.
[9]	Schaffer JD. Some experiments in machine learning using vector evaluated genetic algorithms (artificial intelligence, optimization, adaptation, pattern recognition) [Ph.D. thesis]. Nashville: Vanderbilt University, 1985.
[10]	Srinivas N, Deb K. Multiobjective optimization using nondominated sorting in genetic algorithms. Evolutionary Computation, 1994, 2(3): 221-248. DOI:10.1162/evco.1994.2.3.221
[11]	Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017
[12]	Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759
[13]	Cheng R, Jin YC, Olhofer M, et al. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. DOI:10.1109/TEVC.2016.2519378
[14]	Lin QZ, Li JQ, Du ZH, et al. A novel multi-objective particle swarm optimization with multiple search strategies. European Journal of Operational Research, 2015, 247(3): 732-744. DOI:10.1016/j.ejor.2015.06.071
[15]	Zitzler E, Künzli S. Indicator-based selection in multiobjective search. Proceedings of the 8th International Conference on Parallel Problem Solving from Nature. Birmingham: Springer, 2004. 832–842.
[16]	Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76. DOI:10.1162/EVCO_a_00009
[17]	Yang SX, Li MQ, Liu XH, et al. A grid-based evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721-736. DOI:10.1109/TEVC.2012.2227145
[18]	Tian Y, Zhang XY, Cheng R, et al. Guiding evolutionary multiobjective optimization with generic front modeling. IEEE Transactions on Cybernetics, 2020, 50(3): 1106-1119. DOI:10.1109/TCYB.2018.2883914
[19]	Li MQ, Yang SX, Liu XH. Diversity comparison of Pareto front approximations in many-objective optimization. IEEE Transactions on Cybernetics, 2014, 44(12): 2568-2584. DOI:10.1109/TCYB.2014.2310651
[20]	Tian Y, Si LC, Zhang XY, et al. Evolutionary large-scale multi-objective optimization: A survey. ACM Computing Surveys, 2022, 54(8): 174.
[21]	Jian JR, Zhan ZH, Zhang J. Large-scale evolutionary optimization: A survey and experimental comparative study. International Journal of Machine Learning and Cybernetics, 2020, 11(3): 729-745. DOI:10.1007/s13042-019-01030-4
[22]	Potter MA, De Jong KA. A cooperative coevolutionary approach to function optimization. Proceedings of the 3rd Conference on Parallel Problem Solving from Nature. Jerusalem: Springer, 1994. 249–257. [doi: 10.1007/3-540-58484-6_269]
[23]	Antonio LM, Coello CAC. Use of cooperative coevolution for solving large scale multiobjective optimization problems. Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Cancun: IEEE, 2013. 2758–2765. [doi: 10.1109/CEC.2013.6557903]
[24]	Omidvar MN, Li XD, Yang ZY, et al. Cooperative co-evolution for large scale optimization through more frequent random grouping. Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Barcelona: IEEE, 2010. 1–8. [doi: 10.1109/CEC.2010.5586127]
[25]	Omidvar MN, Li XD, Yao X. Cooperative co-evolution with delta grouping for large scale non-separable function optimization. Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Barcelona: IEEE, 2010. 1–8.
[26]	Li XD, Yao X. Cooperatively coevolving particle swarms for large scale optimization. IEEE Transactions on Evolutionary Computation, 2012, 16(2): 210-224. DOI:10.1109/TEVC.2011.2112662
[27]	Omidvar MN, Li XD, Mei Y, et al. Cooperative co-evolution with differential grouping for large scale optimization. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 378-393. DOI:10.1109/TEVC.2013.2281543
[28]	Ma XL, Liu F, Qi YT, et al. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables. IEEE Transactions on Evolutionary Computation, 2016, 20(2): 275-298. DOI:10.1109/TEVC.2015.2455812
[29]	Zhang XY, Tian Y, Cheng R, et al. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 97-112. DOI:10.1109/TEVC.2016.2600642
[30]	Zille H, Ishibuchi H, Mostaghim S, et al. A framework for large-scale multiobjective optimization based on problem transformation. IEEE Transactions on Evolutionary Computation, 2018, 22(2): 260-275. DOI:10.1109/TEVC.2017.2704782
[31]	He C, Li LH, Tian Y, et al. Accelerating large-scale multiobjective optimization via problem reformulation. IEEE Transactions on Evolutionary Computation, 2019, 23(6): 949-961. DOI:10.1109/TEVC.2019.2896002
[32]	He C, Cheng R, Yazdani D. Adaptive offspring generation for evolutionary large-scale multiobjective optimization. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 786-798. DOI:10.1109/TSMC.2020.3003926
[33]	Tian Y, Zhang XY, Wang C, et al. An evolutionary algorithm for large-scale sparse multiobjective optimization problems. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 380-393. DOI:10.1109/TEVC.2019.2918140
[34]	Yildirim O, Baloglu UB, Tan RS, et al. A new approach for arrhythmia classification using deep coded features and LSTM networks. Computer Methods and Programs in Biomedicine, 2019, 176: 121-133. DOI:10.1016/j.cmpb.2019.05.004
[35]	宁安安, 张俊, 年梅. 基于自编码器的网络游戏流量分类. 计算机系统应用, 2023, 32(7): 113-120. DOI:10.15888/j.cnki.csa.009158
[36]	Rui T, Zhang S, Ren TW, et al. Data Reconstruction based on supervised deep auto-encoder. Proceedings of the 18th Pacific-Rim Conference on Multimedia Information Processing. Harbin: Springer, 2018. 869–879.
[37]	卢学明, 于在川, 许升起. 基于深度生成模型的煤矿运输皮带异物检测. 计算机系统应用, 2022, 31(5): 358-363. DOI:10.15888/j.cnki.csa.008468
[38]	贾文娟, 张煜东. 自编码器理论与方法综述. 计算机系统应用, 2018, 27(5): 1-9. DOI:10.15888/j.cnki.csa.006336
[39]	李二超, 陈瑞婷. 基于变异算子和邻域值自适应的MOEA/D算法. 计算机工程与应用, 2019, 55(9): 49-55. DOI:10.3778/j.issn.1002-8331.1808-0028
[40]	Qin AK, Suganthan PN. Self-adaptive differential evolution algorithm for numerical optimization. Proceedings of the 2005 IEEE Congress on Evolutionary Computation. Edinburgh: IEEE, 2005. 1785–1791. [doi: 10.1109/CEC.2005.1554904]
[41]	Cheng R, Jin YC, Olhofer M, et al. Test problems for large-scale multiobjective and many-objective optimization. IEEE Transactions on Cybernetics, 2017, 47(12): 4108-4121. DOI:10.1109/TCYB.2016.2600577
[42]	Deb K, Thiele L, Laumanns M, et al. Scalable multi-objective optimization test problems. Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu: IEEE, 2002. 825–830. [doi: 10.1109/CEC.2002.1007032]
[43]	Tian Y, Cheng R, Zhang XY, et al. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [Educational Forum]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. DOI:10.1109/MCI.2017.2742868
[44]	van Veldhuizen DA. Multiobjective evolutionary algorithms: Classifications, analyses, and new innovations [Ph.D. thesis]. Dayton: Air Force Institute of Technology, 1999.
[45]	Schott JR. Fault tolerant design using single and multicriteria genetic algorithm optimization [Master’s thesis]. Cambridge: Massachusetts Institute of Technology, 1995.