1 引言

时间序列数据是按照时间顺序排列的数据序列, 具有较强的时间相关性和连续性, 是工程、医疗、气象等众多领域中常见的数据类型, 因此时序数据对于人们理解系统的演变过程具有重要的研究意义^[1]. 然而在实际应用场景中, 时序数据常会因为传感器故障、数据采集错误或通信中断等原因而出现部分数据缺失的情况, 这将会对时序数据的分析、预测和分类等下游任务产生不利的影响.

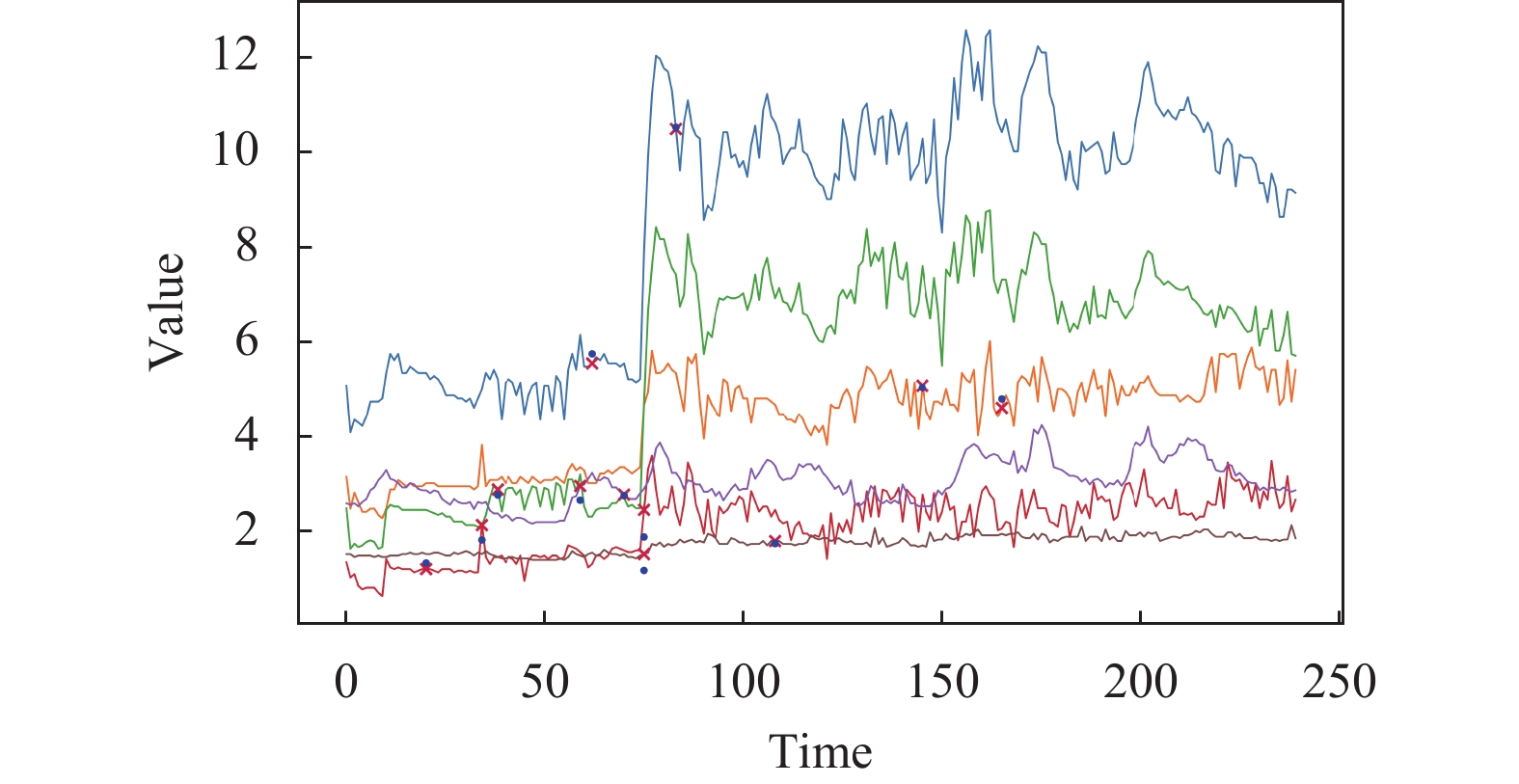
时序数据插补是解决数据缺失问题的重要手段之一. 其核心目标是通过捕获现有数据中潜在的信息以 推断出缺失位置的数据, 实现对残缺时序样本的修复, 从而为后续的分析和预测任务提供可靠的数据基础. 因此研究有效的时序数据插补方法对于众多领域的发展具有广泛的意义, 并且在理论方面和实际应用中具有重要的价值^[2]. 多元时序数据插补的示例如图1所示, “×”标记的位置表示发生数据缺失, 而“·”标记的位置表示模型根据现有数据估计的插补数据, 两者的距离越近表明模型的插补准确率越高.

早期研究中的传统统计方法如均值插补、中值插补和多项式插值等, 对数据分布的假设较为严格, 难以适应不同类型的时序数据. 而K近邻、回归模型和随机森林等机器学习方法虽然简单高效, 但随着大数据时代的到来, 这些方法难以捕捉高维数据中复杂的非线性关系^[3]. 此外, 在大部分应用场景下略长插补的时间几乎不会对下游任务造成负面影响, 因此人们对于时序插补的实时性需求较少, 而时序插补的准确率才是首要的考量因素.

近年来, 基于深度学习的时序数据插补方法受到了广泛关注, 循环神经网络(recurrent neural network, RNN)展示了深度学习模型处理高维时序数据的强大能力. Che等人^[4]通过改进门控循环单元(gated recurrent unit, GRU)设计了一种插补模型GRU-D, 利用时间间隔矩阵记录最后一次观测缺失数据的时间, 并根据权重衰减机制反应时序数据的长短期依赖关系. Yoon等人^[5]将RNN改进为一种双向的时序插补模型M-RNN (multi-directional recurrent neural network), 通过结合前向和后向的信息, 实现对多元时间序列动态变化的全面捕获. Cao等人^[6]提出的模型BRITS (bidirectional recurrent imputation for time series)无需对数据的生成过程强加假设, 即可通过Bi-RNN实现有效的缺失插补. 然而, 基于RNN的插补方法仍然存在较大的误差, 难以满足大部分场景的插补需求, 并且随着网络层数的增加容易引发梯度爆炸和消失等问题.

Luo等人^[7]提出了一种基于生成对抗网络(generative adversarial network, GAN)的时序插补模型, 并设计了GRUI以及E²GAN^[8]. 然而, 基于GAN的模型训练方式通常比较复杂, 生成器与鉴别器之间的博弈过程容易引发训练不稳定等问题. Fortuin等人^[9]提出一种基于变分自编码器(variational autoencoder, VAE)的时序插补模型GP-VAE. 然而基于VAE的插补模型输出的样本质量容易受到潜在空间结构的限制. 因此, 相比于之前的研究工作, 基于GAN和VAE架构的模型虽然成功地将时序插补的准确率提升至一个全新的高度, 但是两者在训练阶段中仍可能遭遇模式崩溃等问题^[10]. Vaswani等人^[11]于2017年提出的Transformer在各种自然语言处理任务中证明了其出色的性能, 并被广泛应用于其他研究领域^[12], 包括时间序列插补. 例如, Shan等人^[13]提出的NRTSI模型直接利用Transformer编码器部分对不规则采样的时间序列进行建模. 另一方面, 随着人们对概率建模的研究逐渐深入, 扩散模型在生成任务中取得了一系列卓越的成就. 例如Tashiro等人^[14]提出的一种基于扩散的时序插补模型CSDI可以实现更精准的时序插补, 并且与其他确定性插补方法不同, CSDI还支持概率性插补. 然而, 上述的时序插补方法仅支持学习时域特征中的潜在信息, 这将导致模型学习的能力无法得到充分的发挥.

为了进一步提升时序插补的准确率, 同时尽可能避免梯度爆炸和模式崩溃等问题, 本文提出了一种基于扩散与时频注意力的时序插补模型DTFA. 受扩散模型的启发, 本研究在训练过程中通过随机掩码策略移除部分观测值, 并使用前向扩散得到的高斯噪声填补缺失部分. 接着DTFA中的噪声估计网络将学习根据现有数据来估计缺失部分的高斯噪声, 在此过程中实现对时序数据的建模. 在真实插补场景中, DTFA将使用高斯噪声$ \varepsilon $填补时序数据的缺失片段, 预训练的噪声估计网络则根据现有数据推测出一个估计噪声${\varepsilon _\theta }$, 最后通过逆向扩散对高斯噪声$ \varepsilon $进行去噪, 逐渐将其转换为插补数据, 实现从噪声$ \varepsilon $中重建数据.

为使DTFA兼顾学习时域和频域信息, 本研究在噪声估计网络中分别引入了时域注意力模块和频域注意力模块, 以便DTFA更全面地学习多维特征在时域和频域中的时间依赖性与特征相关性, 以及更好地识别和理解复杂的数据模式. 除此之外, 为了给噪声估计网络提供更好的全局背景, DTFA还采用了一种增强控制条件的方法. 该方法通过线性插补模块对残缺的时序样本计算出一个粗略但有效的线性插补结果, 并将其作为噪声估计网络的控制条件之一.

本文的贡献主要有如下几点.

(1)本文提出了一种基于扩散与时频注意力时序插补模型DTFA. 该模型通过时域注意力模块和频域注意力模块捕获时序数据在时域和频域中的时间依赖性与特征相关性, 并进行了有效的特征融合.

(2)本文设计了一种增强控制条件的方法, 通过对样本中缺失的部分进行初步的线性插补, 以提高数据的完整性, 并为噪声估计网络提供了更强的全局信息.

(3)本文在ETTm1^[15]、Electricity^[16]和Wind Power^[17]这3个公开的数据集上对DTFA进行验证, 并使用9种不同缺失程度的EETm1数据集进行更细粒度的对比, 误差指标均低于一系列的基线模型, 证明了DTFA的通用性和可靠性.

2 相关工作 2.1 时间序列插补

多元时间序列是一种具有时间依赖性的数据, 被广泛应用于现实世界中的电力系统监测、交通状态监测和生态系统监测^[18–20]等场景中. 然而, 传感器故障引起时序数据丢失是一个常见问题, 这将导致下游任务难以开展和推进. 时序插补的主要目标是捕获现有数据的时空依赖性并推理缺失位置的数据. 在此, 本文总结了几类先前的时序插补相关工作.

起初, 由于RNN的结构特性比较适用于序列数据, 因此被研究人员广泛应用于时序插补任务中. Che等人^[4]提出一种基于RNN的插补方法GRU-D, 它属于GRU的一种变体. 同时, 作者还提出了时间衰减机制的概念, 即利用最后一次观测值与整体平均值作为插补的依据. Yoon等人^[5]提出了M-RNN, 尝试通过从双向RNN的隐藏状态中捕获缺失特征之间的相关性来插补缺失值. 但是由于M-RNN将缺失值视为常量, 意味着它忽略了缺失变量之间的联系. 与M-RNN类似, Cao等人^[6]提出的BRITS也同样利用了双向 RNN来对时间序列进行建模, 然而BRITS将缺失值视为RNN图的变量, 并且还特别关注了特征之间的相关性. 另外, M-RNN和BRITS同样采用了GRU-D的时间衰减机制以提高插补性能.

随着数据和计算需求的指数级增长, 神经网络也在深度和广度上稳步增长. 以RNN为主要架构的模型因其顺序处理特性或内存限制, 在处理较长序列数据时可能面临可扩展性问题, 甚至引起梯度消失或爆炸. 因此, 研究者们尝试将其他研究领域的优秀研究方法迁移到时序插补领域之中, 如基于GAN的方法和基于VAE的方法.

Yoon等人^[21]提出一种基于GAN的插补方法GAIN (generative adversarial imputation net), 利用提示向量进行数据生成, 但是在时序数据上的适用性欠佳. Luo等人^[7]提出了一种RNN单元, 名为GRUI (gated recurrent unit for data imputation), 并利用GRUI层和全连接层构建生成器与鉴别器, 以共同组成GRUI-GAN模型整体结构. 然而该方法需要分为两个阶段来训练, 并且第2阶段需要投入大量时间寻找最佳匹配的输入向量. 因此, Luo等人^[8]又提出了一种端到端的模型E²GAN (end-to-end GAN-based imputation model), 其生成器由基于GRUI的自动编码器构成, 以避免GRUI-GAN中的“噪声”优化阶段. 另外, 作者采用了压缩和重构策略, 以减少训练的时间并降低训练的难度. Fortuin等人^[9]受GPPVAE和HI-VAE的启发, 提出了第1个基于VAE的时序插补方法GP-VAE. 它使用高斯过程先验来捕捉时间动态, 并且可以实现概率性插补. 然而, 基于GAN的模型可能会遇到难以收敛和模式崩溃的问题^[22], 基于VAE的模型也可能因隐变量与数据分布不匹配而导致难以学习复杂数据的情况, 从而使模型的插补误差较大.

2.2 基于注意力的时间序列插补

以注意力结构为基础的Transformer结构在许多任务中都表现出了卓越的性能. 目前, 越来越多研究者致力于利用自注意力机制来设计时序插补模型, 如GLIMA、CDSA、DeepMVI和MTSIT等^[23]. 最近, Shan等人^[13]提出了一种更加新颖的时序插补模型NRTSI (non-recurrent time series imputation), 将时间序列表示为一个集合, 直接利用Transformer编码器进行建模, 并通过一种分层插补的策略来进行缺失插补. Du等人^[24]提出了一种基于联合优化训练的方法SAITS (self-attention-based imputation for time series), 通过两个对角掩码自注意力块来进行插补. 然而SAITS对于非线性关系的建模能力较弱, 且对超参数的选择较为敏感.

2.3 基于扩散的时间序列插补

扩散概率模型作为新兴的深度生成模型之一, 在图像生成和音频生成等多个领域均证明了其优秀的性能. 目前扩散模型在时间序列领域的预测任务中已有一些应用先例^[17,25], 然而在时序插补任务中的应用仍然较少. Kong等人^[26]提出一种用于音频生成的模型DiffWave, 由于音频属于一种特殊的时间序列, 因此将其进行适当的修改, 即可应用于时序插补领域. 例如, Tashiro等人^[14]提出了一个多元时间序列的概率插补模型CSDI (conditional score-based diffusion models for imputation), 初步展示了扩散模型在时序插补领域中的性能优势. 该模型将现有数据作为观测条件来插补缺失数据, 并结合注意力模块捕获数据之间的关联性. Liu等人^[27]提出了PriSTI (spatiotemporal imputation with enhanced prior modeling)模型, 通过条件特征提取模块将提取的时空依赖性作为全局上下文先验.

然而, 所有上述包含RNN的插补模型都容易受到误差累积的影响^[28], 即当前的插补结果可能是由一系列错误的历史插补结果依次推理的, 而基于GAN与VAE的模型也容易引发模式崩溃和难以收敛的问题. 除此之外, 上述所有模型仅考虑从时域中获取信息, 并没有挖掘频域中的隐含信息, 这将不利于模型学习深层的数据关系. 受上述相关工作的启发, 本论文提出一种基于扩散与时频注意力的时间序列插补模型DTFA. 该模型在已捕获时域特征的基础之上, 充分挖掘了频域特征, 通过从更丰富的角度学习时序数据的时间依赖性和特征相关性, 从而提高插补的准确率. 此外, 本文还提出了一种增强控制条件的方法, 通过线性插补模块对现有数据进行初步插补, 从而为噪声估计网络提供更完整的控制条件以及更有效的全局信息.

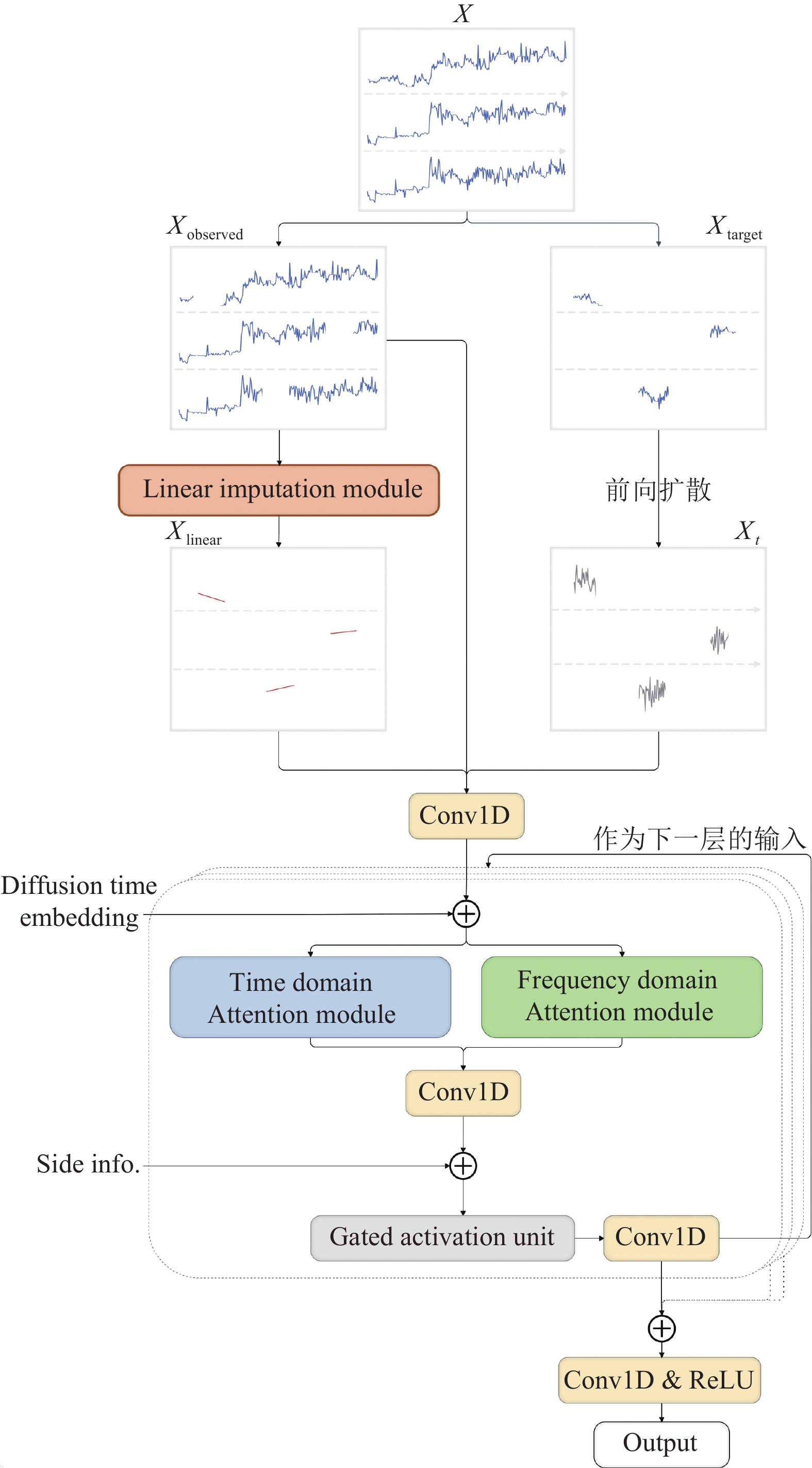
3 方法

本文提出的基于扩散与时频注意力的时间序列插补模型DTFA整体结构如图2所示. 本节将首先介绍时序插补任务中的一些关键定义, 然后简要介绍DTFA中使用扩散思想插补时序数据的原理和设计思路, 最后将介绍DTFA中核心组成部分的结构, 如线性插补模块、噪声估计网络及其内部的时域注意力模块和频域注意力模块.

3.1 任务定义

本文将每个多元时序样本表示为$ X \in {\mathbb{R}^{L \times D}} $, 其中$L$表示样本的采样点数, $D$表示样本的特征维数, 则${X^{l, d}}$表示在第$l$时刻所观测到第$d$维特征的原始数据.

MLM (masked language modeling)在自然语言处理领域中是一种常见的自监督学习方法^[29], 在本研究的时序插补任务中依然可以发挥作用. 其基本思想是在时间序列样本中随机选择一部分数据进行掩码标记, 并利用模型预测掩码位置的数据. 本研究将通过该自监督训练的方式, 迫使DTFA学习时间序列中的模式以及上下文信息. 具体而言, 本研究对每个样本$X$都利用与之对应的掩码矩阵$M \in {\mathbb{R}^{L \times D}}$进行随机掩码标记, 其中$ M $的每个元素定义如下:

$ {M}^{l, d}=\left\{\begin{array}{l}1, \;\;若{X}^{l, d}可以观测\\ 0, \;\;若{X}^{l, d}视为缺失\end{array}\right. $

(1)

因此, $X$可由$M$划分为两个部分:

$ X = {X_{\rm observed}} + {X_{{\text{target}}}} $

(2)

$ {X_{\rm observed}} = M \odot X $

(3)

$ {X_{{\text{target}}}} = (1 - M) \odot X $

(4)

其中, $ \odot $表示矩阵点乘. ${X_{{\text{observed}}}}$将作为模型的观测条件, 而$ {X_{{\text{target}}}} $在训练阶段将通过$t$步前向扩散计算带噪数据${X_t}$, 在测试阶段则用于评估模型插补结果${X_{\rm impute}} = {\mathrm{DTFA}}({X_{\rm observed}})$的误差.

最后, 可以将插补后的样本表示为:

$ \hat X = M \odot {X_{\rm observed}} + (1 - M) \odot {X_{\rm impute}} $

(5)

3.2 线性插补模块

线性插补模块将对残缺的样本进行初步的插补, 以保证观测条件的完整性和连续性. 具体而言, 在给定的${X_{{\text{observed}}}}$中, 对于任意缺失片段左右两个已知数据点$ ({l_1}, X_{\rm observed}^{^{{l_1}, {d_n}}}) $和$ ({l_2}, X_{\rm observed}^{^{{l_2}, {d_n}}}) $, 线性插补模块将通过两者之间的直线以粗略地估计中间缺失区域每个点的数值$ (l, X_{\rm linear}^{l, {d_n}}) $, 其中${l_1} \lt l \lt {l_2}$, $ 1 \leqslant n \leqslant D $, 公式如下:

$ X_{\rm linear}^{l, {d_n}} = X_{\rm observed}^{{l_1}, {d_n}} + \frac{{(l - {l_1})(X_{\rm observed}^{{l_2}, {d_n}} - X_{\rm observed}^{{l_1}, {d_n}})}}{{{l_2} - {l_1}}} $

(6)

这种基于线性插补的观测条件增强方法具有计算高效、保留数据趋势和时空一致性的优点, 特别是在缺失片段中数据变化平缓或者缺失值较少的情况下, 它能够简单高效地解决了观测信息完整性的问题, 并为下游的噪声估计网络提供可靠的全局先验信息. 另外, ${X_{\rm linear}}$与${X_{{\text{observed}}}}$在DTFA训练和测试的全过程中都是可见的.

3.3 DTFA模型

基于物理热力学扩散思想的扩散模型, 类似一个更深层次的变分自编码器, 包括了前向扩散和反向扩散两个过程^[30].

在DTFA的训练阶段, 本研究首先对数据集执行滑动窗口取样, 将原始样本记为$X$, 并根据随机掩码将$X$分解为互补的${X_{{\text{observed}}}}$和${X_{{\text{target}}}}$两部分. 接着使用$ \varepsilon \sim N(0, {\text{{\rm I}}}) $对${X_{{\text{target}}}}$执行前向扩散过程得到带噪数据${X_t}$. 由于扩散模型是基于马尔可夫过程的数学假设的, 因此根据马尔可夫链的性质可知, 只要向样本中加入足够多次的噪声, 最终将得到纯随机噪声分布的数据${X_t}$, 概率分布$q({X_t}\mid{X_{{\text{target}}}})$也将趋于稳定的标准高斯分布. 本文将$ {q_{\rm data}}({X_0}) $定义为原始数据的分布, $X_t^{}$则表示原始数据$X_0^{}$经过了t次前向扩散后的带噪数据, 其中$ t \in [1, T] $, $ T $是人为设定的超参数. 则前向扩散过程可以表示为:

$ q({X_{1:T}}\mid{X_0}) = \prod\limits_{t = 1}^T {q({X_t}\mid{X_{t - 1}})} $

(7)

$ q({X_t}\mid{X_{t - 1}}) = N({X_t};\sqrt {1 - {\beta _t}} {X_{t - 1}}, {\beta _t}I) $

(8)

其中, ${\beta _t}$表示所添加噪声的方差, 是可以自行调整的超参数. 为了方便表示, 本文将${{1 - }}{\beta _t}$记为$ {\hat \alpha _t} $, 将$ \prod\nolimits_{i = 1}^t {{{\hat \alpha }_i}} $记为$ {\alpha _t} $, 标准高斯噪声记为$ \varepsilon \sim N(0, {\rm I}) $.则采样$X_t^{}$具有以下闭合解:

$ q({X_t}\mid{X_0}) = N({X_t};\sqrt {{\alpha _t}} {X_0}, (1 - {\alpha _t}){I}) $

(9)

$ {X_t} = \sqrt {{\alpha _t}} {X_0} + (1 - {\alpha _t})\varepsilon $

(10)

接着, 线性插补模块将根据残缺的${X_{{\text{observed}}}}$计算出线性插补条件${X_{\rm linear}}$. 最后将采用一维卷积模块对${X_{\rm linear}}$、${X_{{\text{observed}}}}$与${X_t}$进行特征融合后输入到噪声估计网络之中, 以估计${X_t}$在各个时间步中的噪声$ \varepsilon $.

训练扩散模型的本质是训练其中的噪声估计网络${\varepsilon _\theta }$. 本研究设计的噪声估计网络由3个残差层组成, 并在每层都引入了时域注意力模块与频域注意力模块, 便于更细粒度地提取数据中的深层时频特征, 以实现更准确的噪声估计. 本文将在第3.4节与第3.5节对时域注意力模块与频域注意力模块的内部结构进行详细介绍. DTFA的训练目标$ \mathop {\min }\limits_\theta {{\mathcal{L}}}(\theta ) $可表示为:

$ \mathop {\min }\limits_\theta {E_{{X_0}\sim {q_{\rm data}}({X_0}), \varepsilon \sim N(0, I)}}{\left\| {\varepsilon - {\varepsilon _\theta }({X_t}, {X_{\rm observed}}, {X_{\rm linear}}, t)} \right\|^2} $

(11)

DTFA的测试阶段与训练阶段不同之处在于, 带噪数据${X_t}$不再通过对${X_{{\text{target}}}}$执行前向扩散获取, 取而代之的是随机采样的高斯噪声$ \varepsilon \sim N(0, {{I}}) $, 并且${X_{{\text{target}}}}$将作为ground truth以评估DTFA的插补误差. 另外, 噪声估计网络根据输入的带噪数据${X_t}$、${X_{{\text{observed}}}}$和${X_{\rm linear}}$得到估计噪声${\varepsilon _\theta }$, 将用于对${X_t}$执行反向扩散过程进行去噪, 以实现对掩码数据的重建.

DTFA的反向扩散过程是一种对高斯噪声样本$ \varepsilon \sim N(0, {{{I}}}) $逐步去噪的生成过程. 与前向扩散的不同之处在于, 反向扩散过程是由一系列神经网络参数化的高斯分布所组成的马尔可夫链实现的, 即本研究的噪声估计网络${\varepsilon _\theta }$.

预训练的噪声估计网络${\varepsilon _\theta }$在${X_{{\text{observed}}}}$和${X_{\rm linear}}$引导下, 将反向扩散过程直接应用于标准高斯噪声$\varepsilon = {X_t}\sim N(0, {I})$, 使${X_t}$转变为略微去噪后的带噪数据${X_{t - 1}}$, 该反向扩散过程可以表示为:

$ \begin{split} & {p_\theta }({X_{0:T}}\mid{X_{\rm observed}}, X_{\rm linear}) \\ & = p({X_T})\prod\limits_{t = 1}^T {{p_\theta }({X_{t - 1}}|{X_t}, {X_{\rm observed}}, X_{\rm linear})} \end{split} $

(12)

$ \begin{split} & {p_\theta }({X_{t - 1}}\mid{X_t}, {X_{{\text{observed}}}}, X_{\rm linear}) \\ & = N({X_{t - 1}};{\mu _\theta }({X_t}, {X_{{\text{observed}}}}, X_{\rm linear}, t), \sigma _t^2I) \end{split} $

(13)

根据Ho等人^[31]提出的一种参数化${\mu _\theta }$和$\sigma _t^2$的方法, 本研究将其表示为:

$ \begin{split} & {\mu _\theta }({X_t}, {X_{\rm observed}}, X_{\rm linear}, t) \\ & = \frac{1}{{\sqrt {{\alpha _t}} }}\left( {{X_t} - \frac{{{\beta _t}}}{{\sqrt {1 - {\alpha _t}} }}{\varepsilon _\theta }({X_t}, {X_{\rm observed}}, X_{\rm linear}, t)} \right) \end{split} $

(14)

$ \sigma _t^2 = \frac{{1 - {\alpha _{t - 1}}}}{{1 - {\alpha _t}}}{\beta _t} $

(15)

同理, DTFA将${X_{t - 1}}$再按照上述的反向扩散过程迭代去噪$t - 1$次, 最终得到一个高度符合数据集分布的时序样本${X_0}$, 将其记为${X_{\rm impute}}$以作为模型的插补结果. 本文将在第4.2节中介绍根据插补结果${X_{\rm impute}}$与ground truth ${X_{{\text{target}}}}$评估模型插补性能的方法.

3.4 时域注意力模块

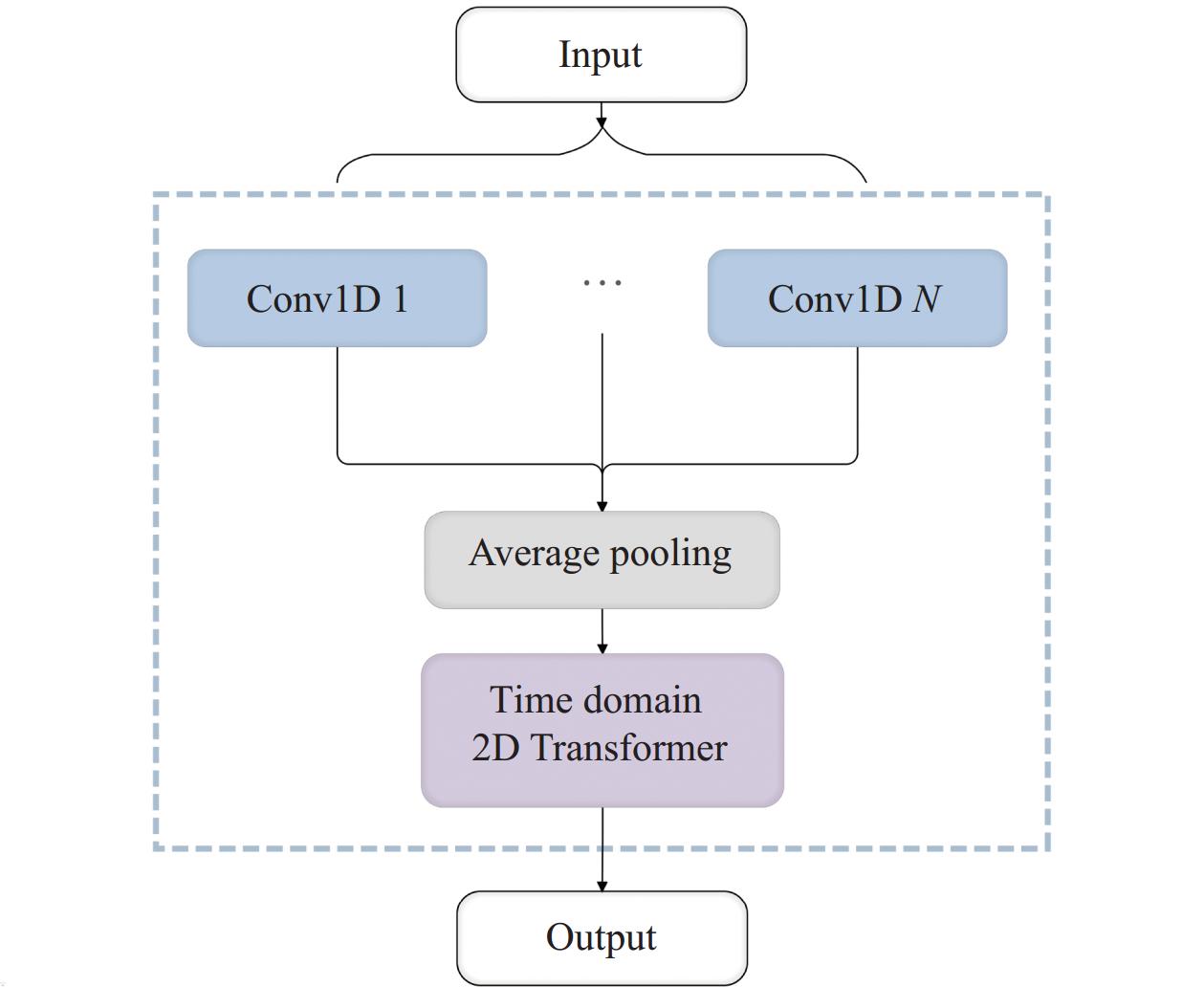
本文提出了一种采用多尺度卷积核结构的时域注意力模块, 其主要目标是捕捉时序数据在时域中的重要特征与时空关系, 具体结构如图3所示.

本研究设置了8个不同大小的卷积核, 分别为1、2、4、8、16、32、64和128. 得益于每个卷积核具有不同大小的感受野, DTFA可以通过多个卷积核的组合识别时序数据中多种尺度的特征, 从而可以更准确地捕获不同时间跨度的依赖性. 其中, 较小的卷积核专注于捕获局部模式与短期依赖关系, 而较大的卷积核则负责捕获全局模式与长期依赖关系. 此外, 该设计在特定情况下有助于模型更好地适应不同尺度的数据变化, 可减少DTFA对单一尺度特征的过度依赖, 从而提高模型的鲁棒性并降低过拟合的风险. 因此, 该特性对于处理具有不同周期性与时序特性的时序数据尤为重要.

提取到的多尺度特征将通过平均池化层合并为一个统一的表示, 接着输入到时域二维Transformer层中. 时域二维Transformer层由时间Transformer层和特征Transformer层组成, 每层都使用Transformer编码器学习整个序列的上下文信息. 时间Transformer层将沿着时间轴的方向学习各个特征的时间依赖性, 而特征Transformer层则沿着特征轴的方向学习各个时刻的特征相关性.

3.5 频域注意力模块

由于时域特征仅能表示数据中局部的趋势和模式, 而频域特征通常还包含关于数据周期性和波动性等更丰富的信息, 所以仅依靠时域特征进行学习的模型无法充分发挥其学习能力. 因此, 学习时序数据的频域表示将更有利于提取深层特征并提高插补模型的准确率, 特别是对于具有复杂频率特征的时序数据效果更加显著.

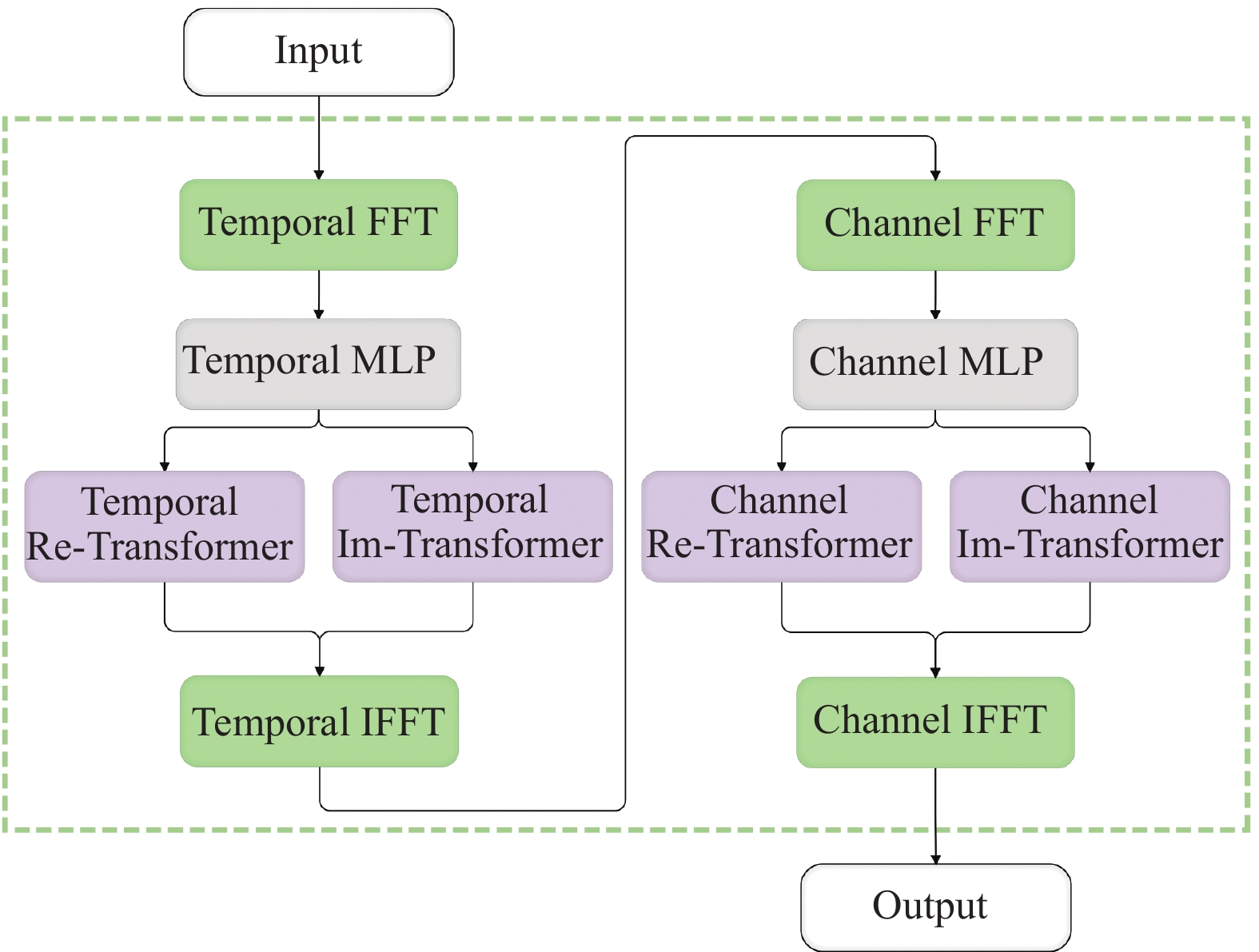
本文提出了一种频域注意力模块, 主要包括快速傅里叶变换层(FFT)、多层感知机(MLP)、Transformer层和快速傅里叶逆变换层(IFFT), 如图4所示.

在该模块中, Temporal FFT层与Channel FFT层将时序数据分别在时间维度和通道维度上进行时频域之间的转换. 转换后的频域数据$Y$将分别输入Temporal MLP与Channel MLP进行学习, 实现数据中周期性和频率成分特征的提取, 以及捕捉不同通道之间的潜在关系和共变模式. 该MLP的输出可以统一表示为:

$ {Y_{\rm MLP}} = \sigma (YW + B) $

(16)

其中, $\sigma $表示激活函数, ${Y_{\rm MLP}} \in {{{\mathbb{C}}}^{n \times m}}$, $Y \in {{{\mathbb{C}}}^{n \times m}}$, $W \in {{{\mathbb{C}}}^{m \times m}}$, $B \in {{{\mathbb{C}}}^m}$. 由于$Y$与$W$均为复数矩阵, 根据复数乘法法则, 可以将式(16)表示为:

$ \begin{split} {Y_{\rm MLP}}& = \sigma (YW + B) \\ & = \sigma (({Y_r} + j{Y_i})({W_r} + j{W_i}) + ({B_r} + j{B_i})) \\ & = \sigma ({Y_r}{W_r} + j{Y_r}{W_i} + j{Y_i}{W_r} - {Y_i}{W_i} + {B_r} + j{B_i}) \\ & = \sigma ({Y_r}{W_r} - {Y_i}{W_i} + {B_r}) + j\sigma ({Y_r}{W_i} + {Y_i}{W_r} + {B_i}) \end{split} $

(17)

因此, 本研究将单独计算${Y_{\rm MLP}}$的实部与虚部部分. 对于计算得到的实数矩阵与虚数矩阵通过Re-Transformer层与Im-Transformer层学习关键的频率分量特征与模式, 以及抑制噪声频率的影响. 最后将整合后的复数矩阵通过Temporal IFFT层或Channel IFFT层转换为时域表示.

4 实验 4.1 数据集

本研究使用3个公开的多元时间序列数据集EETm1、Electricity和Wind Power对DTFA进行插补准确率的评估.

ETTm1^[15]: 电力变压器温度数据集中的每个采样点都包含了关于油温以及6种不同类型的外部电源负载特征的信息, 时间戳范围为2016年7月1日–2018年6月26日. ETTm1数据集为ETT数据集预处理之后的一种版本, 数据以15 min为间隔均匀采样, 共计69680个采样点. 本研究将ETTm1的前4个月数据作为测试集, 接下来的4个月数据作为验证集, 剩余的16个月数据作为训练集. 并且本研究通过滑动窗口来进行多元时序样本的取样, 其中窗口大小设置为24, 滑动步长设置为12.

Wind Power^[16]: 该风力发电数据集的时间戳范围为2020年1月1日–2021年5月22日, 共计7个特征, 数据以15 min为间隔均匀采样, 共计48673个样本点. 数据集的划分比例和取样方法与ETTm1数据集的相同, 即窗口大小设置为24, 滑动步长设置为12.

Electricity^[17]: 源自UCI存储库中的Electricity电力数据集包含从370个客户端收集的用电量数据, 单位为千瓦时. 该数据集以15 min为间隔均匀采样, 共计140256个采样点, 每个采样点具有370个特征. 在本研究对该数据集通过大小为100和步长为100的窗口进行取样.

4.2 评价指标与实验细节

本研究使用3个时序插补领域中常用的评价指标来衡量DTFA的性能: 均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和连续分级概率评分(continuous ranked probability score, CRPS), 三者的数值越小表明模型的插补性能越好.

RMSE与MAE量化了真实值与预测值之间的差异, 主要用于评估模型在回归任务中的性能. RMSE偏向关注异常离群值, 而MAE可以更好地体现误差的实际情况. 本研究中的RMSE和MAE计算方式可以表示为:

$ {\mathit{RMSE}} = \sqrt {\frac{{{{\displaystyle\sum\nolimits_{l = 1}^L {\displaystyle\sum\nolimits_{d = 1}^D {\left[ {{{\left( {({X_{{\text{target}}}} - (1 - M) \odot {X_{\rm impute}})} \right)}^2}} \right]} } }^{l, d}}}}{{\displaystyle\sum\nolimits_{l = 1}^L {\displaystyle\sum\nolimits_{d = 1}^D {{{(1 - M)}^{l, d}}} } }}} $

(18)

$ MAE = \frac{{{{\displaystyle\sum\nolimits_{l = 1}^L {\displaystyle\sum\nolimits_{d = 1}^D {\left| {({X_{{\text{target}}}} - (1 - M) \odot {X_{\rm impute}})} \right|} } }^{l, d}}}}{{\displaystyle\sum\nolimits_{l = 1}^L {\displaystyle\sum\nolimits_{d = 1}^D {{{(1 - M)}^{l, d}}} } }} $

(19)

CRPS是一种评估数据与概率分布差异的指标, 因此特别适用于评估DTFA的插补准确性. 本文参考了Tashiro等人^[14]的计算方法, 将其定义为分位数损失$ {\Lambda }_{\alpha }({D}^{-1}(\alpha ), X)=(\alpha -{\text{}}_{X \lt {D}^{-1}(\alpha )})(X-{D}^{-1}(\alpha )) $的积分, 其中分位数水平$\alpha \in [0, 1]$, ${D^{ - 1}}(\alpha )$是分布$D$的分位数, ${{\mathbb{I}}}$为指示函数.

由于本研究设置生成100个样本以近似缺失值的分布, 因此将计算0.05刻度的离散分位数水平的分位数损失. 最后, 本研究对所有插补结果的CRPS计算平均值作为评估指标. 具体计算方式如下:

$ \begin{split} {\mathit{CRPS}}({D^{ - 1}}, x) & = \int_0^1 {2{\Lambda _\alpha }({D^{ - 1}}(\alpha ), x)} {\mathrm{d}}\alpha \\ & \simeq \sum\limits_{i = 1}^{19} {2{\Lambda _{i \times 0.05}}({D^{ - 1}}(i \times 0.05), x)/19} \end{split} $

(20)

$ {\mathit{CRPS}}(D, \tilde X) = \frac{{\displaystyle\sum\nolimits_{\tilde x \in \tilde X} {{\mathit{CRPS}}({D^{ - 1}}, \tilde x)} }}{{\left| {\tilde X} \right|}} $

(21)

本研究中的DTFA是基于PyTorch框架搭建的, 并在16 GB显存的NVIDIA GeForce RTX 4070 Ti SUPER GPU计算资源上进行训练、验证以及测试. 实验的参数设置如表1所示.

4.3 基线方法

为了验证DTFA的性能优越性, 本研究选取了一系列基于深度学习的基线方法与之对比.

M-RNN^[5]: 该模型使用双向RNN络进行插值, 并采用了GRU-D的时间衰减函数来捕获信息缺失.

BRITS^[6]: 该模型同样使用了双向RNN以及GRU-D的时间衰减函数来对时间序列进行建模, 不同之处在于它将缺失值作为RNN图的变量, 接着使用RNN的隐藏状态进行插补.

Transformer^[11]: 在本研究中仅使用了Transformer的编码器部分, 去除了Transformer的解码器部分.

SAITS^[24]: 该模型采用了一种掩码插补和观测值重建的联合优化训练方法, 并使用两个对角屏蔽自注意力块和一个加权组合块以对时间序列建模.

GP-VAE^[9]: 该模型在潜在空间中利用高斯先验过程捕获时间动态, 其ELBO仅依赖现有数据的特征.

CSDI^[14]: 该模型是一种基于分数的条件扩散模型, 通过使用二维注意力机制以进一步捕获时间和特征的相关性.

4.4 对比实验

本研究在ETTm1、Wind Power和Electricity数据集上进行了插补效果的对比实验, 如表2所示. 其中测试集的缺失率设置为10%, 最优的指标通过加粗来表示. 该对比实验表明, DTFA在ETTm1、Wind Power和Electricity数据集上插补误差均都低于其他基线模型, 充分证明了DTFA通用性和泛化能力. 具体而言, DTFA在ETTm1数据集上的RMSE与MAE分别为0.103和0.065, 比最优基线模型的误差分别降低了7.21%和4.41%; 在Wind Power数据集上的RMSE与MAE分别为0.127和0.022, 比最优基线模型的误差分别降低了3.05% 和15.38%; 在Electricity数据集上的RMSE与MAE分别为0.122和0.053, 比最优基线模型的误差分别降低了6.87%和5.36%.

M-RNN因其无法考虑缺失变量之间的关系, 导致插补误差较大, 尽管BRITS通过将缺失值视为RNN图的变量以捕获特征的相关性, 两者的插补性能也无法摆脱RNN结构特性的限制, 从而难以大幅降低插补误差. GP-VAE可能因隐变量与数据分布匹配困难而导致误差较大. Transformer与SAITS受益于注意力机制, 在3个数据集上的插补性能上实现新的突破. CSDI与DTFA是基于扩散架构的插补模型, 两者相较于其他基线模型在RMSE和MAE指标上具有明显优势, 在特征维度较高的Electricity数据集上效果更为显著. 综上所述, DTFA实现了扩散架构与时频注意力的有效结合, 并对于多种数据场景具有较好的泛化性.

为了进一步比较DTFA与基线模型在不同缺失率数据集上的插补性能, 本研究向ETTm1测试集分别引入10%–90%数据缺失以进行验证, 表3–表5分别详细展示了RMSE、MAE和CRPS的评估结果. 该实验结果表明, 尽管面对不同程度缺失的数据集, DTFA的插补效果依然优于其他基线方法, 且完整度较高的数据集可以更充分地发挥DTFA的学习能力. 具体而言, DTFA的RMSE相较于最优的基线模型降低了0.58%–8.53%, MAE相较于最优的基线模型降低了0.98%–7.79%, CRPS相较于最优的基线模型降低了1.08%–7.35%.

4.5 消融实验

为了深入研究DTFA中不同组件对整体性能的增益, 本研究设计了3组消融实验, 并在缺失率为10%的ETTm1数据集上进行验证, 实验结果如表6所示.

该消融实验表明, 当去除线性插补模块后, DTFA仅以现有数据作为辅助条件进行训练, 导致模型的插补误差增大. 该现象可以印证线性插补模块在一定程度上为DTFA提供有效的全局信息和缺失数据的潜在变化趋势. 而当去除时域注意力或频域注意力模块后, 模型的准确率大幅下降, 该现象可以印证结合时频特征进行学习有助于更好地挖掘数据的时间依赖性和特征相关性. 综上所述, 线性插补模块、时域注意力模块和频域注意力模块均对DTFA的插补性能有着不同程度的性能增益.

4.6 残差层数的对比

为了进一步探索DTFA的最优性能与残差层数之间的关系, 本研究将残差层从1层逐渐增加至6层分别进行验证, 在缺失率为10%的ETTm1数据集上的实验结果如表7所示.

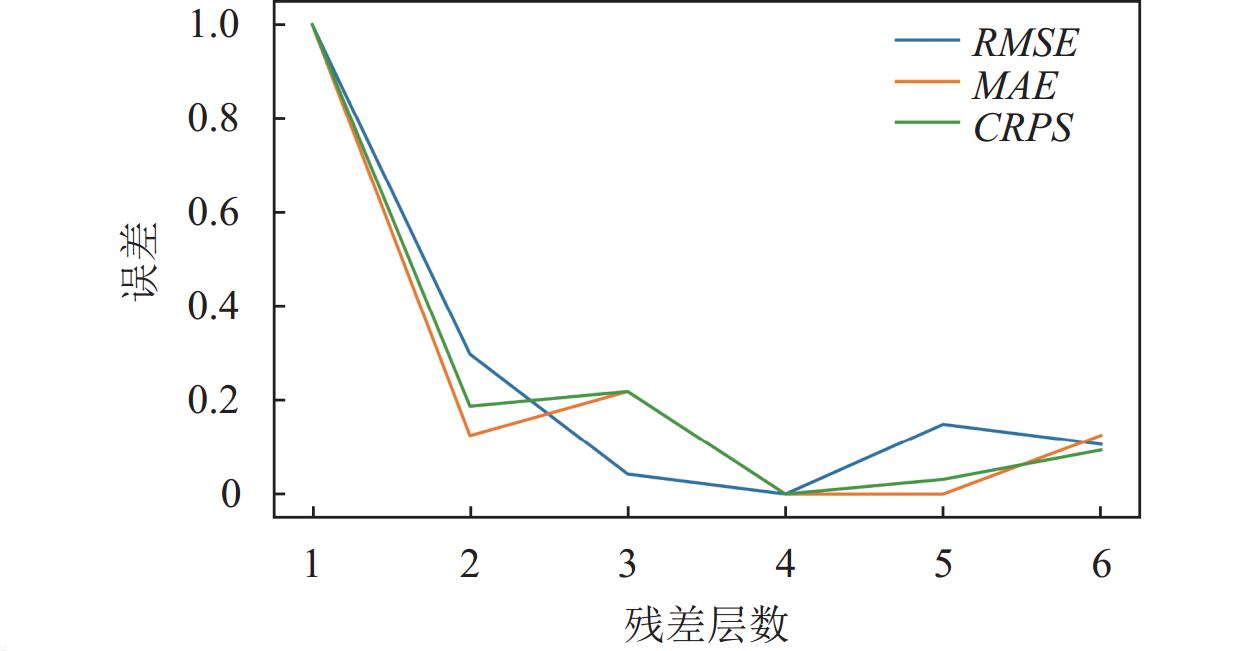
为了突出3种评价指标的变化趋势, 本研究对表7数据可视化之前对数据进行了最小-最大归一化处理, 如图5所示, 其中蓝色线表示RMSE, 橙色线表示MAE, 绿色线表示CRPS. 根据图5中各曲线整体趋势可知, 当残差层数仅为1时, DTFA无法充分捕获时间序列中的动态规律, 从而无法充分发挥其插补性能. 随着残差层数的增加, 3种误差指标在整体上具有下降的趋势. 当残差层数为4时, 模型表现出最佳的性能, 而当残差层数为5或更多时, 模型的误差呈上升趋势, 出现了过拟合的现象, 不仅浪费计算资源, 而且对模型的性能产生了负面的影响. 因此, 选择合适的残差层数, 可在一定程度上降低模型的插补误差.

5 结论与展望

本文提出一种基于扩散与时频注意力的时间序列插补模型DTFA, 通过线性插补模块进行初步的缺失插补以保证数据的完整性和连续性. 为捕捉时序数据在时域和频域中的重要特征和时空关系, 本研究将分别通过时域注意力模块与频域注意力模块提取特征信息以学习更高质量的表示. 其中DTFA的时域注意力模块利用多尺度卷积核的结构识别时间序列中多种尺度的特征, 并利用Transformer编码器捕获不同时间跨度的时间相关性. 而DTFA的频域注意力模块则使用FFT获取时序数据的频域表示, 并利用MLP与Transformer编码器学习频域特征中潜在的相关性以及依赖性. 最后, 本研究通过对比实验证明DTFA在ETTm1、WindPower和Electricity数据集上的插补性能均优于其他基线模型, 同时通过消融实验证明了DTFA核心模块的有效性.

在数字经济蓬勃发展与物联网设备不断进步的推动下, 人们迫切需要更高准确率的插补方法. 由于目前主流的基线模型暂时无法通过简单地加深网络层数实现更准确的插补, 因此DTFA成功地解决了时序插补领域中最具有挑战性的难题. 在今后的研究中将考虑提高DTFA针对更大规模数据集的扩展性, 以及提高DTFA的训练和推理的速度.