在过去的10年中, 多智能体强化学习(MARL)问题引起了显著的关注. 在MARL中, 系统内的智能体学习如何协调以获得最大化累积的全局奖励[1]. 许多复杂的现实问题, 如控制机器人群体[2]和自动驾驶[3], 可以被建模为合作型MARL问题, 并在商业应用中具有巨大潜力. 然而, 合作型MARL受到可扩展性和部分可观察性问题的阻碍. 随着代理数量的不断增加, 联合状态-动作空间呈指数级增长, 导致了网络训练的维度灾难. 此外, 智能体必须根据局部的动作-观察历史做出个体决策, 然而这并不能准确反映整体系统的真实状态.
为了解决上述问题, 一种称为“中心化训练分布式执行(CTDE)”的流行范式被提出. CTDE范式在训练期间通过汇总系统中的所有信息来优化个体的分散策略, 从而提供了完全集中的值函数. 一旦训练完成, 执行时智能体只需要考虑自己的局部动作-观察历史进行决策. 最近, 诸如VDN[4]和QMIX[5]等方法均采用了CTDE范式. 然而, 由于值函数分解具有单调约束性, 这两种方法在联合状态-动作空间评估全局Q值时可能面临困难. 因此, QTRAN[6]提出了一种更一般的分解形式, 即采用软正则化进行约束以保证分解的准确性与通用性. 由于优化问题的约束在计算上是难以处理的, 因此, QTRAN必须使用两个惩罚项来放宽这些约束, 结果产生了次优解. 为了解决QTRAN在理论和实际应用中的局限性, QTRAN++被提出, 其采用了非固定估计量、更精细的损失函数和用于联合动作-价值估计量的混合网络架构. 这些变化显著提升了网络的收敛性能. 然而, 由于QTRAN和QTRAN++过于依赖单一的联合动作-价值估计量, 它们在复杂环境中的效果受到限制, 这可能导致收敛速度缓慢与估计不准确, 且QTRAN++的半单调混合网络进一步加剧了这一问题. 此外, QTRAN和QTRAN++忽略了对各智能体观察信息的预处理, 而是直接将它们输入神经网络, 使得整个网络需要大量的反向传播来学习到最优解.
本文提出一种新的基于值的算法, 称为OPTQTRAN, 它缓解了上述提到的种种限制. 该算法在StarCraft multi-agent challenge (SMAC)[7], 一个复杂的MARL环境中取得了最先进的结果. OPTQTRAN对智能体的训练过程进行了关键性修改, 首先, 本文提出了一种新颖的双联合动作-价值估计量的结构, 与QTRAN和QTRAN++明显不同. 具体来说, 该结构引入了一个分解网络模块来计算额外的联合动作-价值并优化整体损失函数. 此外, 本文引入了一个自适应网络来计算联合动作-价值, 解决了QTRAN++的半单调混合网络中估计偏差的问题. 最后, 本文引入了一个多单元网络模块, 将智能体的观察分组到不同的单元中, 以使效用函数估计量携带更多基本信息. 本文在SMAC环境中进行了对OPTQTRAN方法的广泛评估, 将其与6个MARL基准算法在6个不同场景中进行比较. 值得注意的是, OPTQTRAN在所有实验中都取得了最先进的性能. 此外, 本文进行了消融实验以展示OPTQTRAN算法中每个模块的有效性. 实验结果表明, 每个模块在实现OPTQTRAN的卓越性能方面都发挥了关键作用. 根据本文的实验, 我们相信OPTQTRAN方法可以成为未来研究MARL任务的强大基准.
2 相关工作CTDE范式在多智能体强化学习领域取得了显著的流行, 其假设在训练期间可以获得完整的全局状态信息, 而训练完成后智能体可以仅根据局部观测信息来执行策略. 目前许多种类的方法都采用了CTDE范式来训练智能体, 包括基于策略和基于值的方法. 基于策略的方法通常采用演员-评论家(actor-critic algorithm)框架, 其中独立的演员用于实现分布式执行. 反事实的多智能体策略梯度(COMA)[8]通过估算反事实基线来解决信用分配问题, 并使用联合评论家网络训练个体策略. MADDPG[9]扩展了DDPG[10]算法, 以一种集中的方式学习合作和竞争性游戏的个体策略. 另一个例子是MAAC[11], 它在评论家网络中引入了注意力机制以增强可扩展性. 最近, ROMA[12]提出了一个以角色为导向的框架, 利用带有正则化项的深度强化学习和角色条件策略来学习角色. FOP[13]将最大熵多智能体强化学习分解为局部策略, 并证明了其收敛性. 此外, IRAT[14]构建了个体策略和团队策略, 并应用差分约束以缓解稀疏奖励.
在基于值的方法中, VDN将联合动作-价值估计量表示为各个智能体的效用函数之和. QMIX通过引入混合网络来捕捉联合动作-价值估计量中各智能体效用函数之间的非线性单调关系, 以此对VDN进行了扩展, 但也保留着和VDN一样的问题, 即没有摆脱单调性假设关系. Qatten引入了多头注意力机制, 在理论研究发现的基础上对联合动作-价值估计量进行了近似分解. QPLEX[15]则采用了双工对抗网络架构来分解联合价值函数. RODE[16]提出了一种基于角色的多智能体强化学习方法, 利用角色选择器将联合动作空间分解为与不同角色对应的有限动作空间. PAC[17]提出了一种使用最优联合动作生成反事实预测的方法, 涉及编码局部观察、优化交互信息以及使用变分推断生成辅助信息. 最近, QTRAN被提出以消除QMIX中的联合动作-价值估计量中的单调性假设问题. QTRAN通过神经网络的训练目标强制将联合动作-价值估计量分解为各智能体效用函数之和, 而不是直接将其分解. 然而, QTRAN在理论基础和实际应用之间仍存在差距, 为了解决这个问题提出了QTRAN++. 首先, 通过修改优化损失函数, QTRAN++稳定了训练过程. 其次, 通过利用一个非固定的真实动作-价值估计量, 使得在训练中其和转化的联合动作-价值函数间进行模仿学习, 大幅提升训练效率.
另外, 最近已经提出了几种方法来解决QMIX局限性的问题. Mahajan等人[18]提出了一种专门的探索算法MAVEN来解决智能体的探索问题. Yang等人[19]提出了Q-DPP算法来激励智能体获得多样化的行为模型并协调它们之间的探索行为. Rashid等人[20]则提出了CW-QMIX和OW-QMIX算法, 通过使用加权投影让智能体能学习到更多更好的联合动作. 最后, Pan等人[21]提出了RES算法, 通过向基准Q值添加一个正则项来惩罚偏离以此改善QMIX的过度估计问题.
3 准备工作 3.1 分散部分可观察马尔可夫决策过程(DEC-POMDP)本文将一个完全合作的多智能体任务建模为一个由元组
IGM原则[5]已经成为实现基于值的 CTDE 的一种流行的方法. 其具体表现为以中心化的方式训练智能体, 使智能体能够访问其他智能体或全局状态的信息, 并且在分布式执行阶段, 每个智能体能够基于其局部的动作-观察历史做出自己的决策. 通过使用IGM 原则, 智能体做出的决策可以在个体性能与全局最优性间做出平衡, 从而提高系统的整体性能. 本文使用
| ∀τ∈T,argmaxQjt(τ,a)=(argmaxa1∈AQ1(τ1,a1),⋯,argmaxan∈AQn(τn,an)) | (1) |
在本节中, 本文将展示OPTQTRAN的算法框架. 首先, 在第4.1节中对算法的网络结构进行概述, 然后在第4.2节中介绍分解网络模块, 即实现了双联合动作-价值估计量结构并为此设计一个新的损失函数, 最后, 在第4.3节中, 将呈现两个模块: 一个用于联合动作-价值估计量的自适应网络模块, 以及另一个用于效用函数的多单元网络模块.
4.1 网络结构概述如图1所示, 本文采用了超网络(hypernetwork)[22]为3个混合网络生成权重参数. 超网络是采用一个神经网络来为另一个神经网络生成权重参数的网络结构. 需要注意的是为普通混合网络(common mixing network)生成的权重参数是任意值, 而为单调混合网络(monotonic mixing network)生成的权重参数是大于0的, 即QMIX中所使用的网络结构. 本文将普通混合网络和单调混合网络分别定义为
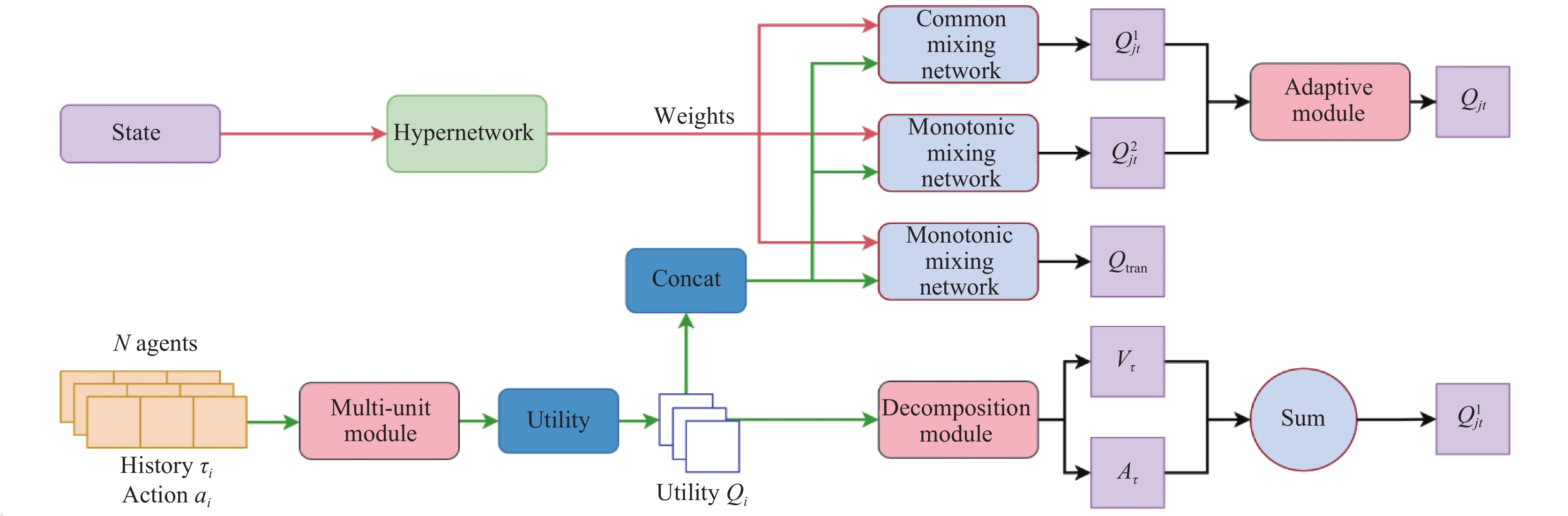
|
图 1 整体算法结构 |
4.2 分解网络模块
如图2所示, 本文将效用函数的输出值
| Ai(τi,ai)=Qi(τi,ai)−Vi(τi) | (2) |
| Vi(τi)=maxaiQi(τi,ai) | (3) |
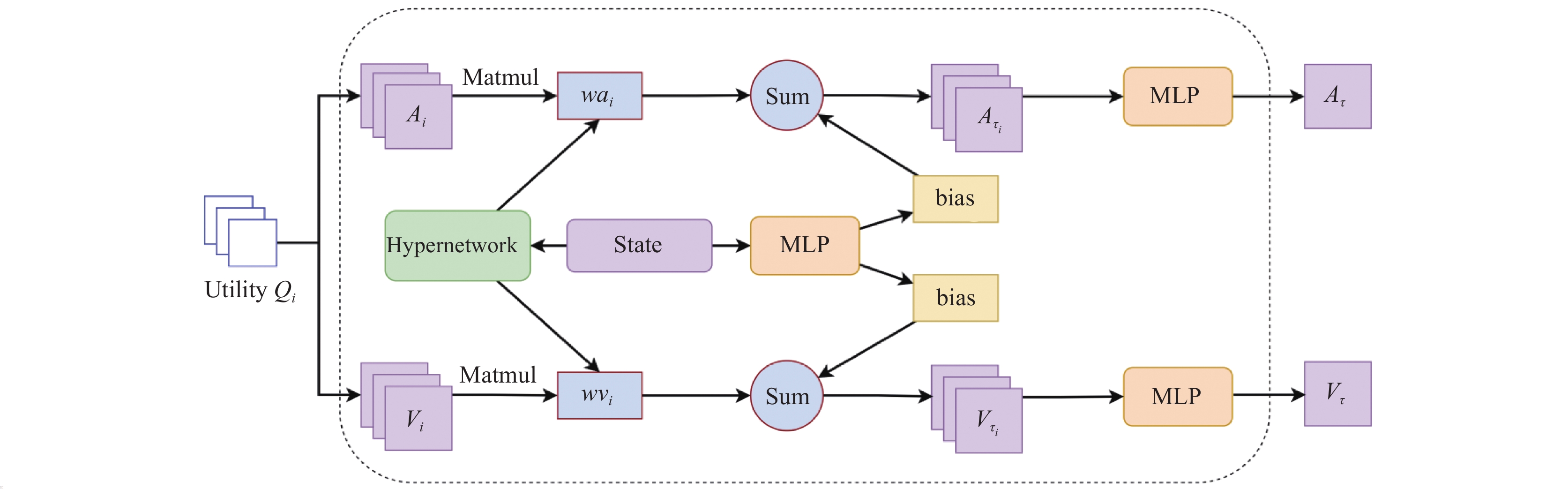
|
图 2 分解网络模块结构 |
然后为了将每个智能体的动作-观测历史
| Ai(s,τ,ai)=wai(s)Ai(τi,ai)+bi(s) | (4) |
| Vi(s,τ)=wvi(s)Vi(τi)+bi(s) | (5) |
之后本文采用两个多层网络感知机(MLP)将
| Q′jt=Vtot(s,τ)+Atot(s,τ,a) | (6) |
其中, 本文对联合动作-价值函数做了符号简化, 即将
| {Ladv1=(Qjt(s,τ,a)−Q′jt(s,τ,a))2Ladv2=(Vtot(s,τ)−(Qjt(s,τ,ˉa)+Qjt(s,τ,˜a))×0.5)2Ladv3=(Q′jt(s,τ,a)−(r+γQtargetjt′(s′,τ′,ˉa′)))2Ladv=λadv1Ladv1+λadv2Ladv2+λadv3Ladv3 | (7) |
其中,
为了加快训练初期的速度, 本文采用损失函数
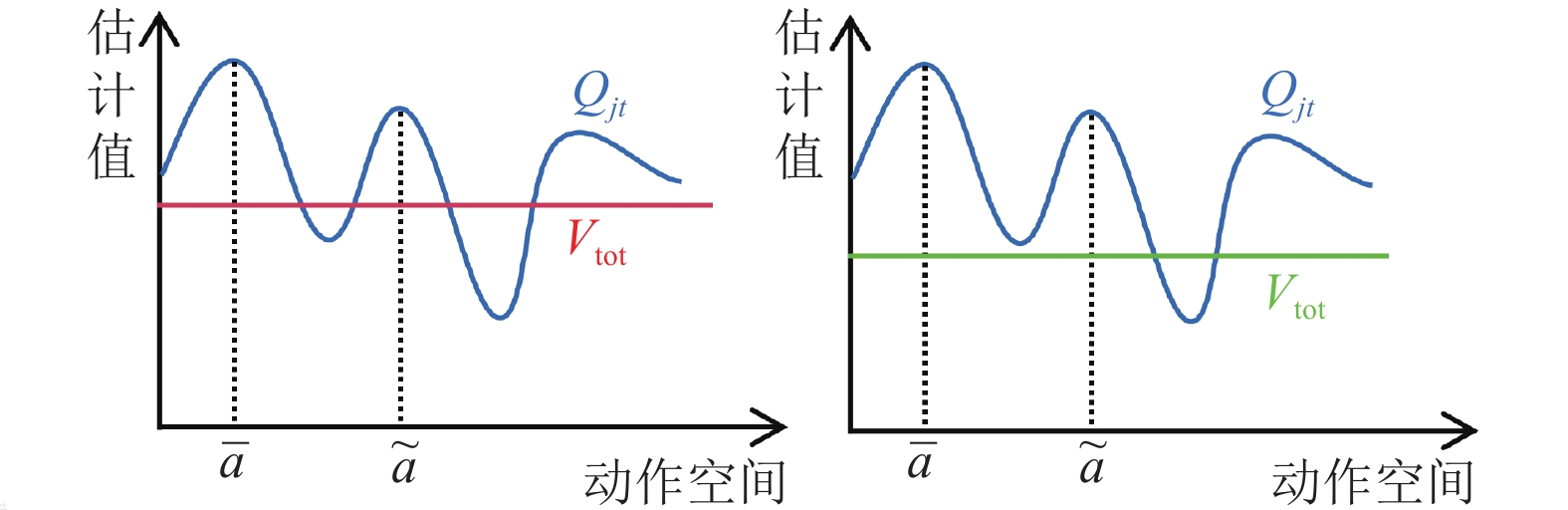
|
图 3 |
此处, 本文采用红色的线来给
| Lnewadv2=(Qjt(s,τ,ˉa)−max{Qjt(s,τ,ˉa),Qjt(s,τ,˜a)})2+Ladv2 | (8) |
其中, 在训练时本文将
| LQTRAN++=Ltd+λoptLopt+λnoptLnopt | (9) |
| Lopt=(Qjt(s,τ,ˉa)−Qtran(s,τ,ˉa))2 | (10) |
| {Lnopt={(Qjt(s,τ,a)−Qtran(s,τ,a))2,ifQjt(s,τ,a)⩾ | (11) |
| {L_{\rm td}} = {({Q_{jt}}(s, {\boldsymbol{\tau}} , {\boldsymbol{a}}) - (r + \gamma Q_{jt}^{\rm target}(s', {\boldsymbol{\tau}} ', \bar {\boldsymbol{a}}')))^2} | (12) |
其中,
| L = {L_{\text{QTRAN++}}} + {\lambda _{\rm adv1}}{L_{\rm adv1}} + {\lambda _{\rm adv2}}{L_{\rm adv2}} + {\lambda _{\rm adv3}}{L_{\rm adv3}} | (13) |
在本节中将具体介绍自适应网络模块与多元网络模块的架构, 以及它们对网络结构优化所起的重要作用. 首先, 自适应网络模块为
● 自适应网络模块. 在QTRAN++中, 其只是将
本文对自适应网络模块的详细阐述如图5. 上方的超网络将
| {Q_{jt}} = {w_1}({Q_{jt}^2}){Q_{jt}^1} + {w_2}({Q_{jt}^1}){Q_{jt}^2} + b(s) | (14) |
其中,
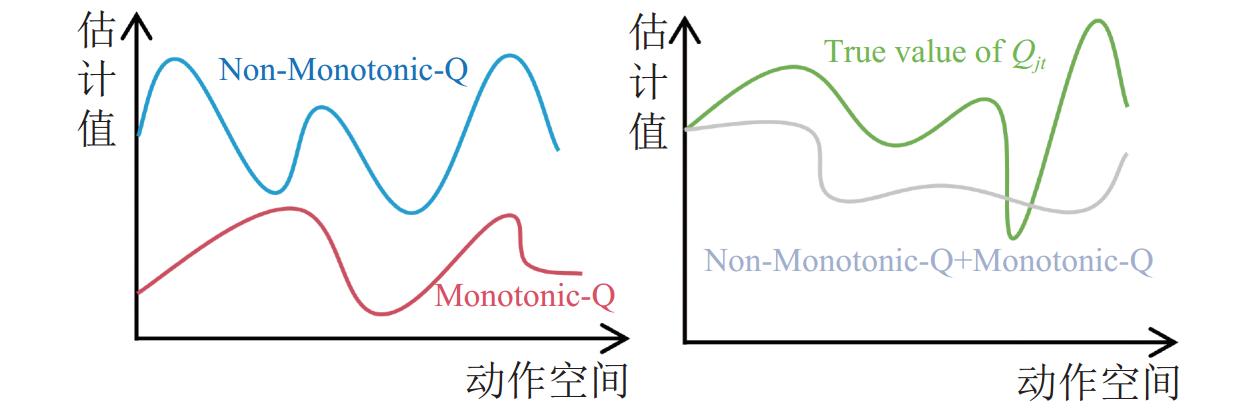
|
图 4 QTRAN++的局限性 |

|
图 5 自适应网络模块结构 |
● 多元网络模块. 在许多MARL任务中, 如SMAC基准环境, 效用函数通常采用DRQN网络为每个智能体生成
模块的具体细节如图6所示. 这一方法的主要思路是为DRQN网络[23]的输入增加一个可训练的参数, 以此来缓解学习压力. 首先, 智能体的观测

|
图 6 多元网络模块结构 |
5 实验 5.1 矩阵游戏
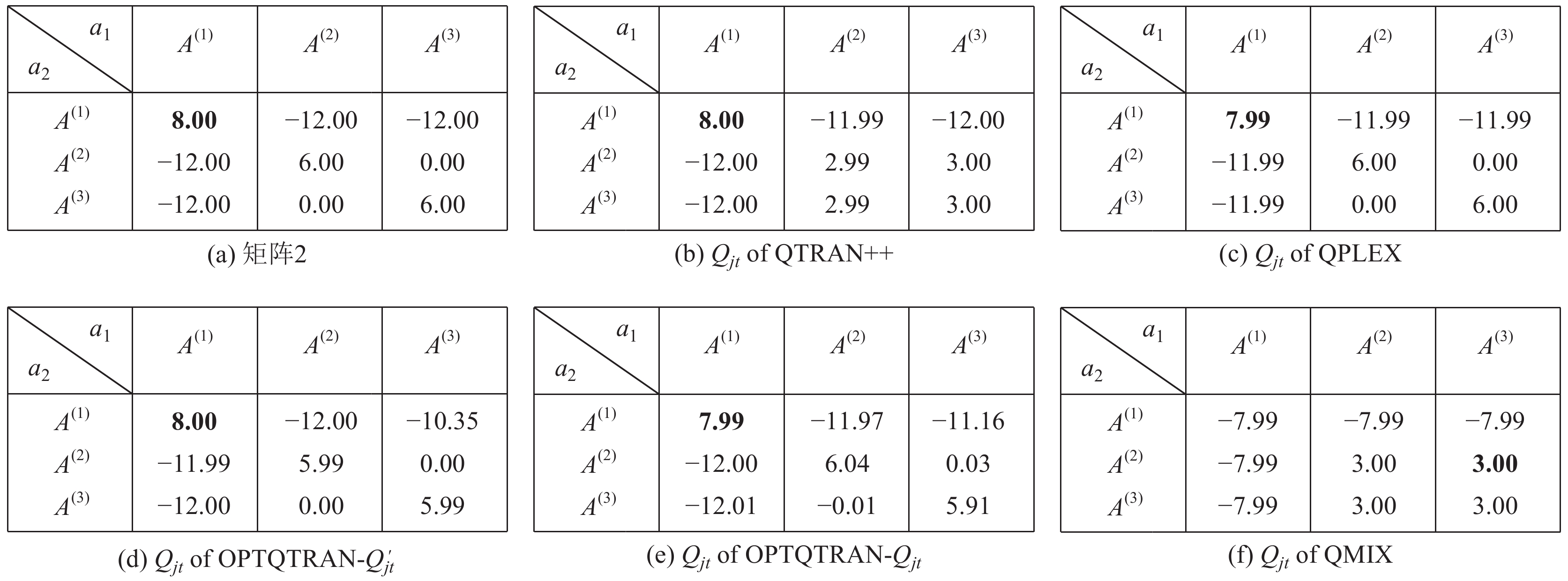
在本节中将研究图7与图8中两个具有挑战性的矩阵游戏, 它们描绘了基本的合作型多智能体任务, 在这两个游戏中想要跳出局部最优的情况是十分困难的. 整体实验设置包括了两个智能体且每个智能体可以选择3个动作, 其中最优的联合动作为
在SMAC环境中对不同的算法进行评估, 这是一个在线训练平台, SMAC模拟了由不同策略控制的智能体之间的战斗场景, 并且将所有训练需要的信息实时返回. 每一个智能体接收一个本地观测, 其中包括了自身和附近所有可视单位的信息, 如彼此间的距离、位置、生命值、护盾等. 此外, 在智能体训练期间还会提供一个包含了所有智能体信息的全局状态. 本文将OPTQTRAN与6个主流的基准算法(QMIX、QTRAN、VDN、Qatten、QPLEX和QTRAN++)在6个不同难度级别的地图场景进行了比较. 所有智能体的策略网络都采用DRQN结构, 包含了两个64维的全连接层和一个64维的GRU. 混合网络是一个32维度的隐藏层, 且使用ELU激活函数. 超网络采用两个64维的全连接层, 激活函数使用ReLU. 同时使用学习率为

|
图 7 矩阵游戏1 |
|
图 8 矩阵游戏2 |
每经过
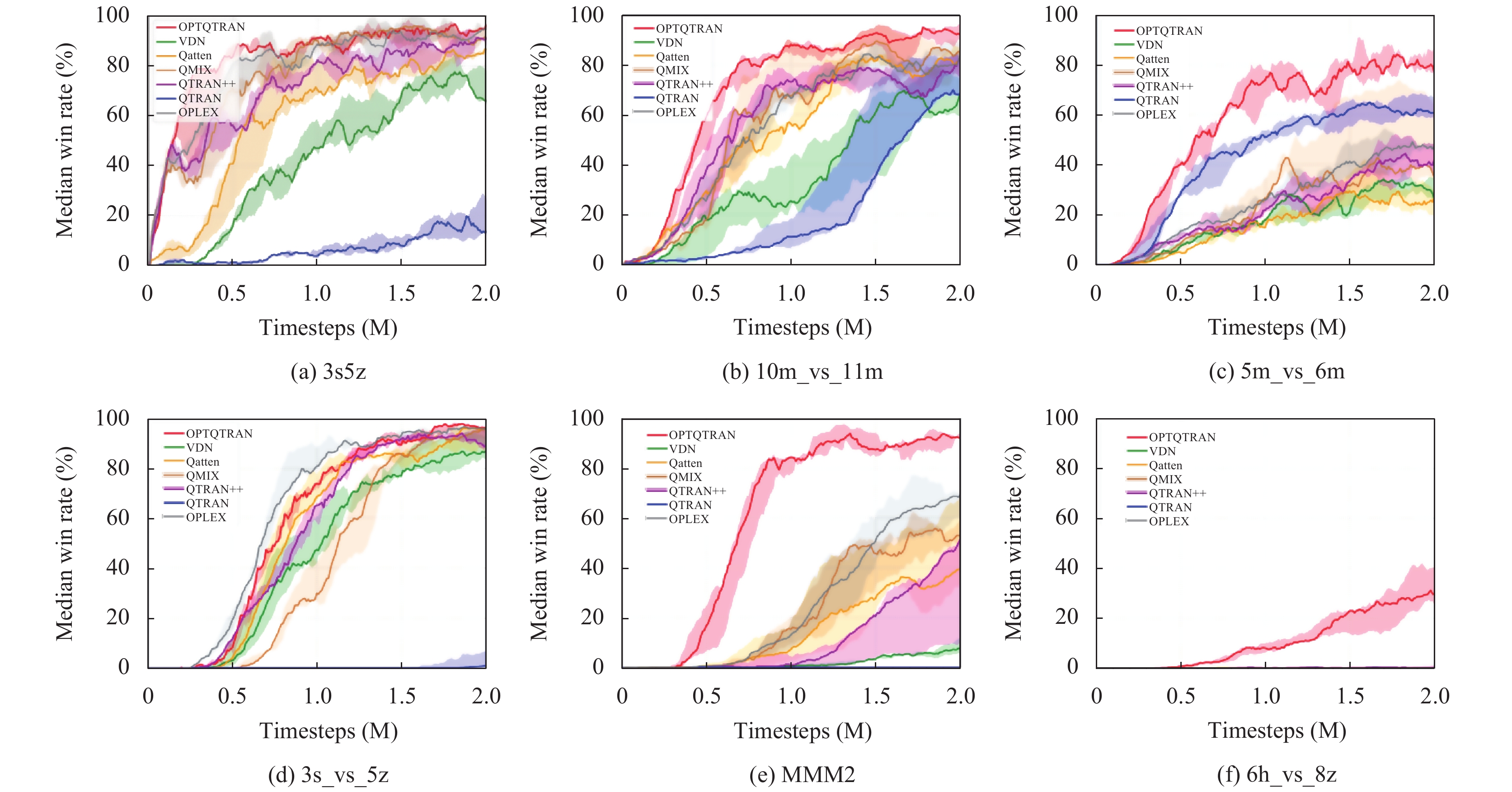
实验结果对比如图9所示. 本文的评估涵盖了一系列具有挑战性的任务场景, 现有的方法难以在不同的场景中保持一致的性能, 而OPTQTRAN始终能够达到几近最优的结果. 例如, 在图9(a)中, QTRAN++、Qatten和QMIX存在局部最优问题, 表现为胜率一开始增加, 然后突然急剧下降. 相反, OPTQTRAN学习到了一种有效的策略, 并避免了这个问题. 在图9(b)和图9(c)中, 两支队伍拥有相同类型的智能体, 但对手数量比我方多出一个, 在这种情况下, 即使是策略选择中的微小偏差也可能导致失败, 需要智能体在进攻和生存间做出平衡. 值得注意的是, 虽然QTRAN获得了很高的胜率, 但仍然不及OPTQTRAN的表现. 在图9(d)中呈现了这样一个场景, 其中3个我方追随者必须在大部分回合中引诱敌对狂热者, 导致延迟奖励问题. OPTQTRAN比除了QPLEX之外的所有其他基准算法都表现优异. 在图9(e)和图9(f)的高度具有挑战性的场景中, 这些场景要求智能体之间进行有效的协作决策, 本文的算法相对于基准算法表现出优越的性能. 特别是图9(f)对其他算法而言, 这是一个相当困难的情况, 而本文的算法仍旧可以取得一定的胜率.
可视化分析如图10. 在图10(a)和10(b)中, 双方各剩下4个智能体, 以人的角度分析, 此时最优的策略应该是集中火力攻击敌对单位, 然而, QTRAN++倾向于学习一个“局部最优”策略, 即智能体远离敌对单位以避免受伤. 相反, OPTQTRAN学到了“最佳”策略, 即所有智能体都攻击敌人.
|
图 9 实验结果对比 |

|
图 10 可视化策略分析 |
此外, 在图10(c)和图10(d)中, 想要获胜必须在摧毁敌方治疗单位的同时保护我方的治疗单位. 在这种情况下, 生命值并不是关键因素, 保护重要的友方单位和摧毁重要的敌方单位才至关重要. QTRAN++显然未能学到该获胜的策略, 反而在对局开始时选择快速歼灭敌方普通单位, 陷入局部最优导致了最终的失败. 相反, OPTQTRAN成功地避免了这一情况, 选择在保护治疗单位的同时攻击敌方治疗单位. 综上实验结果表明, 在这些具有挑战性的情景中, OPTQTRAN显著优于QTRAN++.
5.2.3 消融实验消融实验旨在评估OPTQTRAN方法中每个组件的影响. 首先我们移除了分解网络模块, 引入了只使用一个联合动作-价值估计量的OPTQTRAN-NO-DEC变体. 接下来, 我们将OPTQTRAN与ADD-OPTQTRAN进行比较, 后者采用了一个加法形式计算
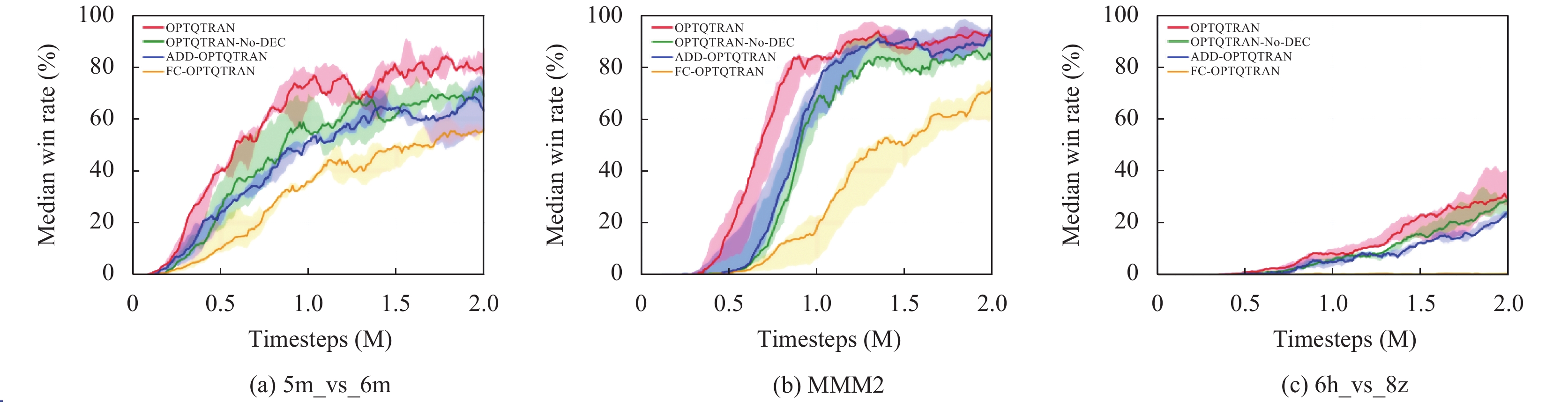
在图11中展示了消融实验的结果, 即OPTQTRAN的每个模块在改进其性能方面的有效性, 实验共涵盖了3种不同的任务场景. 从结果中, 我们观察到分解和自适应网络模块在一定程度上提高了整体模型的性能, 而多元网络模块在实现卓越性能方面发挥了至关重要的作用. 我们认为多单元网络模块之所以能够显著加速训练, 是由于超网络所带来的额外有效信息. 在图11(a)、(b)中可以明显看出在去除了分解网络模块和替换了自适应网络模块后, 模型整体的性能出现了一定程度的下滑, 而在图11(c)中, 用 MLP 网络替换超网络导致性能显著下降, 更突显了超网络在为每个单元高效生成适当权重中所发挥的关键作用.
|
图 11 消融实验 |
6 总结
本文提出了一种基于CTDE执行范式的协作多智能体强化学习方法并命名为OPTQTRAN. 该方法具有许多突出优势, 包括通过对损失函数和网络结构的优化来加速训练, 通过先进的联合动作-价值估计量的计算来提高网络泛化性能, 以及将多元网络模块用于更具信息性的效用函数估计量. 为了评估OPTQTRAN的有效性, 本文在具有挑战性的SMAC环境中进行了实验. 实证结果表明, 该方法建立了一个新的卓越性能基准, 这些发现为开发更高效的MARL算法提供了宝贵的见解, 期待本文的工作能够继续激发该领域更多的研究.
| [1] |
Busoniu L, Babuska R, De Schutter B. A comprehensive survey of multiagent reinforcement learning. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2008, 38(2): 156-172. DOI:10.1109/TSMCC.2007.913919 |
| [2] |
Yogeswaran M, Ponnambalam SG, Kanagaraj G. Reinforcement learning in swarm-robotics for multi-agent foraging-task domain. Proceedings of the 2013 IEEE Symposium on Swarm Intelligence. Singapore: IEEE, 2013. 15–21.
|
| [3] |
Cao YC, Yu WW, Ren W, et al. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Transactions on Industrial Informatics, 2013, 9(1): 427-438. DOI:10.1109/TII.2012.2219061 |
| [4] |
Sunehag P, Lever G, Gruslys A, et al. Value-decomposition networks for cooperative multi-agent learning based on team reward. Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems. Stockholm, 2018. 2085–2087.
|
| [5] |
Rashid T, Samvelyan M, De Witt CS, et al. Monotonic value function factorisation for deep multi-agent reinforcement learning. Journal of Machine Learning Research, 2020, 21(178): 1-51. |
| [6] |
Son K, Kim D, Kang WJ, et al. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 5887–5896.
|
| [7] |
Samvelyan M, Rashid T, de Witt CS, et al. The StarCraft multi-agent challenge. Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems. Montreal, 2019. 2186–2188.
|
| [8] |
Foerster J, Farquhar G, Afouras T, et al. Counterfactual multi-agent policy gradients. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI, 2018. 2974–2982.
|
| [9] |
Lowe R, Wu Y, Tamar A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6382–6393.
|
| [10] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2016.
|
| [11] |
Iqbal S, Sha F. Actor-attention-critic for multi-agent reinforcement learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 2961–2970.
|
| [12] |
Wang TH, Dong H, Lesser V, et al. ROMA: Multi-agent reinforcement learning with emergent roles. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 9876–9886.
|
| [13] |
Zhang TH, Li YH, Wang C, et al. FOP: Factorizing optimal joint policy of maximum-entropy multi-agent reinforcement learning. Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 12491–12500.
|
| [14] |
Wang L, Zhang YP, Hu YJ, et al. Individual reward assisted multi-agent reinforcement learning. Proceedings of the 39th International Conference on Machine Learning. Baltimore: PMLR, 2022. 23417–23432.
|
| [15] |
Wang JH, Ren ZZ, Liu T, et al. QPLEX: Duplex dueling multi-agent Q-learning. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [16] |
Wang TH, Gupta T, Mahajan A, et al. RODE: Learning roles to decompose multi-agent tasks. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [17] |
Zhou HH, Lan T, Aggarwal V. PAC: Assisted value factorisation with counterfactual predictions in multi-agent reinforcement learning. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2022. 1146.
|
| [18] |
Mahajan A, Rashid T, Samvelyan M, et al. MAVEN: Multi-agent variational exploration. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 684.
|
| [19] |
Yang YD, Wen Y, Wang J, et al. Multi-agent determinantal Q-learning. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 10757–10766.
|
| [20] |
Rashid T, Farquhar G, Peng B, et al. Weighted QMIX: Expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 855.
|
| [21] |
Pan L, Rashid T, Peng B, et al. Regularized Softmax deep multi-agent Q-learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2021. 1365–1377.
|
| [22] |
Ha D, Dai AM, Le QV. Hypernetworks. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2017.
|
| [23] |
Hausknecht M, Stone P. Deep recurrent Q-learning for partially observable MDPs. Proceedings of the 2015 AAAI Fall Symposia. Arlington: AAAI, 2015. 29–37.
|
 2024, Vol. 33
2024, Vol. 33



