2. 武汉科技大学 智能信息处理与实时工业系统湖北省重点实验室, 武汉 430081
2. Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System, Wuhan University of Science and Technology, Wuhan 430081, China
在遥感影像处理领域, 多模态协同观测已是大势所趋. 由于平台飞行高度不同、传感器成像模式不同、成像视角显著差异等因素, 导致获取的影像间存在很大的透视几何畸变和非线性辐射差异等现象, 传统的特征匹配方法在多源遥感影像匹配方面已不再适用[1]. 因此, 深入研究多源遥感影像的稳健可靠匹配方法, 对推动多源遥感影像高精度自动化空中三角测量, 提高地形地物三维重建效率及贴近摄影测量变形监测等均有重要意义[2].
1 相关研究根据多源遥感影像特征匹配所用到的技术, 本文将多源遥感影像的匹配方法分为3种: 基于影像中轮廓结构的方法、基于深度学习的匹配方法和基于频域信息的方法. 由于经典特征匹配方法对非线性辐射畸变较为敏感, 对于多模态影像无法获取稳定可靠的同名特征, 因此需要研究具有多重不变特征的多模态影像高可靠性特征匹配方法, 构建非线性辐射差异不变的稳健特征描述符[3]. 针对多模态遥感影像, 抗辐射畸变描述符的设计思路可总结为以下几个方面: (1)利用多模态影像的轮廓信息; (2)采用深度学习算法进行多模态影像匹配; (3)利用频域信息构造特征描述符.
在第1类思路中, 尽管多模态遥感影像中存在着非线性辐射差异, 但同名地物仍具有相似的结构, 可由其共同的轮廓形成特征. 国内研究者已在这一领域进行了广泛的研究, 樊仲黎等人[4]通过梯度幅值和梯度方向构造出能有效表达地物几何结构的特征描述符, 在光学与合成孔径雷达(synthetic aperture radar, SAR)影像配准方面取得了较好的结果. 将几何图层结构用于图像匹配也是近年的一个热点, 众多研究者由此来生成描述符. 而几何图层则利用影像的局部自相似性[5]来表示边缘轮廓特征, 其本质是量化局部窗口中灰度像素的统计同现特性, 降低了非线性辐射畸变带来的影响. Chen等人[6]在自相似性的基础上引入局部三值模式, 在相关性曲面上逐窗口计算中心对称的局部三值模式并将其编码, 在模拟数据集和少量的真实数据上取得了较好效果. Sedagha等人[7]深入研究自相似性的几何意义, 用相关性曲面代替梯度幅值为特征点分配方向, 计算自相似性描述子来进行特征编码, 但显式的分配方向依然不够准确. Xiong 等人[8]将自相似性和统计学中的斯皮尔曼等级相关系数结合起来生成描述符, 在光学和SAR影像匹配上获得了辐射畸变抗性. 轮廓特征是近年来用于多源遥感影像匹配的常见思路, 在特定的场景下取得了理想的结果, 但算法效果受到轮廓的显著性以及对应轮廓提取算法的性能制约, 其中轮廓的显著性也没有显式的定义.
第2类, 采用深度学习算法进行多源遥感影像匹配. 南轲等人[9]提出基于孪生网络(siamese network)特征表达的多模态影像匹配方法, 利用Harris算法检测特征点, 随后利用孪生网络提取影像中的特征, 最后用模板匹配策略搜索对应同名点, 效果优于传统的模板匹配方法. 蓝朝桢等人[10]提出基于深度学习特征的匹配方法(cross modality matching net, CMM-Net), 利用卷积神经网络学习异源遥感影像的高维特征, 然后采用传统特征匹配思路进行特征匹配与粗差剔除, 取得了稳健的匹配结果. Quan等人[11]提出了生成匹配网络算法, 该生成网络采用生成对抗网络的架构为光学影像生成伪SAR影像, 作为后续深层卷积神经网络的输入, 用以训练多模态影像块的匹配标签, 该方法与经典模板匹配方法相比有所提升. Zeng等人[12]利用深度卷积神经网络进行影像的语义分割, 在此基础上提取影像的区块特征, 最后采用互信息作为测度优化影像间的转换关系, 该方法在SAR、光学影像匹配上取得了较好的结果. 相较于深度学习技术在多模态医学影像匹配领域的广泛应用, 深度学习在多模态遥感影像匹配领域的研究并不活跃, 其主要原因在于难以获取大量的多模态遥感影像数据用于训练与测试, 同时遥感影像的高分辨率、较大的几何畸变都为深度学习在该领域的应用带来困难.
第3类, 利用频域信息构造特征描述符. 在空间域, 图像经傅里叶变换, 可用幅度和相位表示, 但包含局部特征信息的局部相位、幅值还需通过其他方式获取. 由于Log-Gabor滤波器对影像进行卷积得到的结果对光照强度和对比度变化具有较强抗性, 众多研究者采用多样化的编码策略, 直接使用卷积所得结果对特征进行描述[13]. Aguilera等人[14]使用多尺度、多方向的Log-Gabor对影像进行滤波以此表示特征, 一定程度上增强了匹配性能. 然而, 该方法未顾及描述符的旋转与尺度不变性. Kovesi提出了相位一致性度量(phase congruency, PC)[15], 该度量不受信号幅度的影响, 且不受图像的对比度和强度变化影响. 近年来, 基于相位一致性的研究不断深入, 众多研究者提出了许多基于此原理的算法. 文献[16–18]在这方面进行了深入研究, 利用共生滤波器构造尺度空间, 在此基础上提出了多模态遥感影像的共生滤波空间匹配方法, 或利用各向异性扩散滤波构造尺度空间, 提出了顾及绝对相位方向的异源遥感影像匹配算法, 此外还提出了加权相位方向直方图的思路, 在多模态遥感影像匹配方面均取得了较好的结果. Ye等人[19,20]提出了有向相位一致性算法, 该算法将PC和方向直方图策略相结合, 根据图像的结构属性描述提取的特征, 从而提升了匹配的准确性. Li等人[21]基于相位一致性提出了辐射不变特征变换算法, 该方法首先用相位一致性进行边缘检测和角点检测, 随后根据最大索引图构建描述子, 在各类多源遥感影像上均取得了较好的匹配结果. 基于相位一致性的多模态遥感影像匹配方法因其具有抵抗灰度变化的能力, 一直是该领域的研究热点. 但是这类方法仅给出了解决非线性辐射差异的思路, 并未顾及到尺度以及旋转不变性, 没有在理论上构造满足实际需求的具有多重不变性的描述符, 有的方法提供了解决尺度不变性的方案, 但实际上还是采用传统的构造尺度空间思路, 进行尺度空间采样, 且采样间隔的相关参数需人工干涉.
针对多模态遥感影像存在非线性辐射畸变的问题, 本文提出了一种结合相位对称特征与基于排序局部自相似性的多模态遥感影像匹配方法. 本文的基本思路是利用相位对称性提取影像间共存的结构特征, 在此基础上使用加速分段测试算法(features from accelerated segment test, FAST)[22]进行特征提取, 随后在相位一致性的基础上计算基于排序的自相似性测度, 构造特征描述子. 最后使用快速抽样一致性算法(fast sample consensus, FSC)[23]进行粗差剔除. 实验结果显示, 与现有的几种先进多模态影像匹配方法相比, 本文方法在正确匹配点数量, 匹配精度和匹配正确率方面, 能够取得更优结果. 证明本文方法能够实现多模态遥感影像的鲁棒匹配.
1.1 Log-Gabor滤波器计算相位对称性和相位一致性需先获得信号在频域的局域信息, 再由滤波器将其卷积后得到相位分量. 而Log-Gabor滤波器可构造任意长度的带宽, 适用于计算相位信息. Log-Gabor滤波器的计算公式如式(1):
| LG(ω)=exp(−log(ω/ωω0ω0)22(log(κ/κω0ω0))2) | (1) |
其中,
为了计算相位对称性和相位一致性, 需将一维Log-Gabor滤波器扩展到二维. 二维Log-Gabor滤波器计算公式如式(2):
| LGs,o(ω,θ)=exp(−log(ω/ωωsωs)22(log(κ/κωsωs))2)exp−(θ−θs,o)2σ2θ | (2) |
其中,
Shechtman等人[5]提出了局部自相似性描述符(local self-similarity, LSS), LSS描述符捕获图像中的几何图层结构, 并且对图像中的辐射变化具有鲁棒性. 描述符根据中心图像块的LSS计算相关面, 然后在对数极坐标网格中得到描述符值.
在以q为中心的局部区域, 计算中心图像块与周围邻域中所有图像块之间的平方误差和(sum of square differences, SSD), 得到距离表面
| Sq(x,y)=exp(−SSDq(x,y)max(varnoise,varauto(q))) | (3) |
其中, q为中心像素;

|
图 1 对数极坐标中的LSS描述符 |
2 本文算法 2.1 本文算法流程图
本文提出的多模态遥感影像匹配方法主要包括以下几个步骤.
(1)构造相位对称图: 根据相位对称计算模型生成参考影像和待匹配影像的相位对称图. (2) FAST特征提取: 分别在参考影像和待匹配影像的相位对称图上进行FAST特征点提取, 得到初始匹配点对. (3)生成RPCLSS特征描述子: 计算相位一致性的值, 在此基础上将斯皮尔曼等级相关系数与局部自相似性相结合生成RPCLSS特征描述子. (4)匹配与粗差剔除: 采用归一化互相关作为相似性度量获得影像初始匹配. 最后采用FSC算法来进行错误匹配的剔除. 本文方法流程图如图2所示.

|
图 2 本文方法流程图 |
2.2 多模态特征提取
在影像的局部频域表达中, 对称点和反对称点会产生易于识别的局部相位模式, 而这种相位信息可以用于构建一种对比度不变的对称性测量方法, 且不需要事先识别或分割对象[24]. 利用该测度可提取多模态影像间共存的结构特征, 进而把多模态转换为单模态.
信号的分析是通过将信号与每对正交小波进行卷积来表示的, 每个正交滤波器对的响应形成了一个响应向量, 其计算方式为:
| [en(x),on(x)]=[I(x)∗Men,I(x)∗Mon] | (4) |
其中,
| An(x)=√en(x)2+on(x)2 | (5) |
| Φn(x)=atan2(en(x),on(x)) | (6) |
最后, 相位对称的计算公式如式(7):
| Sym(x)=∑n⌊An(x)[|cos(ϕn(x))|−|sin(ϕn(x))|]−T⌋∑nAn(x)+ε=∑n⌊[|en(x)|−|on(x)|]−T⌋∑nAn(x)+ε | (7) |
其中,
由于遥感影像普遍存在着非线性辐射畸变, 且FAST算法的尺度不变性和灰度不变性较差, 直接对图像进行FAST特征提取, 往往检测到的特征点较少, 无法取得较好效果. Kovesi等人[24]提出的相位对称测度会在对称点和反对称点产生易于识别的局部相位模式, 且这种相位信息不需要事先识别或分割对象, 通过对影像的相位对称图进行FAST特征提取, 有效降低影像非线性灰度变化对特征点检测的影响, 提高稳定特征点的数量. 用两种方法进行FAST特征提取结果如图3所示. 由图3可知构建相位对称图进而进行FAST特征提取可提取不同模态影像间共存的结构特征, 能够显著提升所得特征点数量.

|
图 3 两种方法对比结果展示 |
2.3 RPCLSS描述符的构造
将LSS描述符应用于多模态图像配准时, 可以发现在实验中存在一些问题, 导致配准失败. 原因可归结为: 虽然LSS描述符可以捕获图像中的形状结构, 但简单地计算周围邻域图像块之间强度的平方误差和并不能充分考虑多模态图像中的非线性辐射畸变. 此外, 将相关曲面转换为对数极坐标会引起特征的局部仿射畸变. 针对LSS描述符在多模态遥感影像中的判别能力相对较低的缺点, 本文提出了一种结合相位一致性与基于排序的局部自相似性的特征描述符RPCLSS.
在构造RPCLSS描述符阶段, 本文采用相位一致性值取代图像的强度值进行计算, 二维相位一致性计算公式如式(8):
| PC(x,y)=∑S∑OωO(x,y)⌊ASO(x,y)ΔΦSO(x,y)−T⌋∑S∑OASO(x,y)+ξ | (8) |
其中,
随后, 本文采用统计学中的斯皮尔曼等级相关系数 (
引入相位一致性和斯皮尔曼等级相关系数来对LSS进行改进, 使用PC值代替图像强度值来计算相关性, 得到的相关表面计算公式如式(9):
| RSqPC(x,y)=exp(−SADqPC(x,y)max(varnoise,varauto(q))) | (9) |
其中, R表示通过排序来获得
与式(3)相比, 式(9)使用PC值取代图像强度值进行计算, 既保留了图像的主要结构特征, 又在一定程度上降低了图像的噪声带来的影响, 使描述符更具判别性; 其次, 虽然式(9)要进行排序操作, 但省去了单调函数的计算, 并使用绝对误差和操作代替耗时的平方误差和操作; 同时式(9)使用每个扇面内相关值的平均值而不是最大值作为描述符值来提高描述符的辨识能力, 因为平均值是统计学中的中心倾向度量, 而使用最大值度量会丢失匹配细节使得描述符辨识能力较差[8], 在每个扇面中求平均值的计算公式如式(10):
| I(x,y)=1n∑r1⩽x⩽r2θ1⩽y⩽θ2SADqPC(x,y) | (10) |
其中,
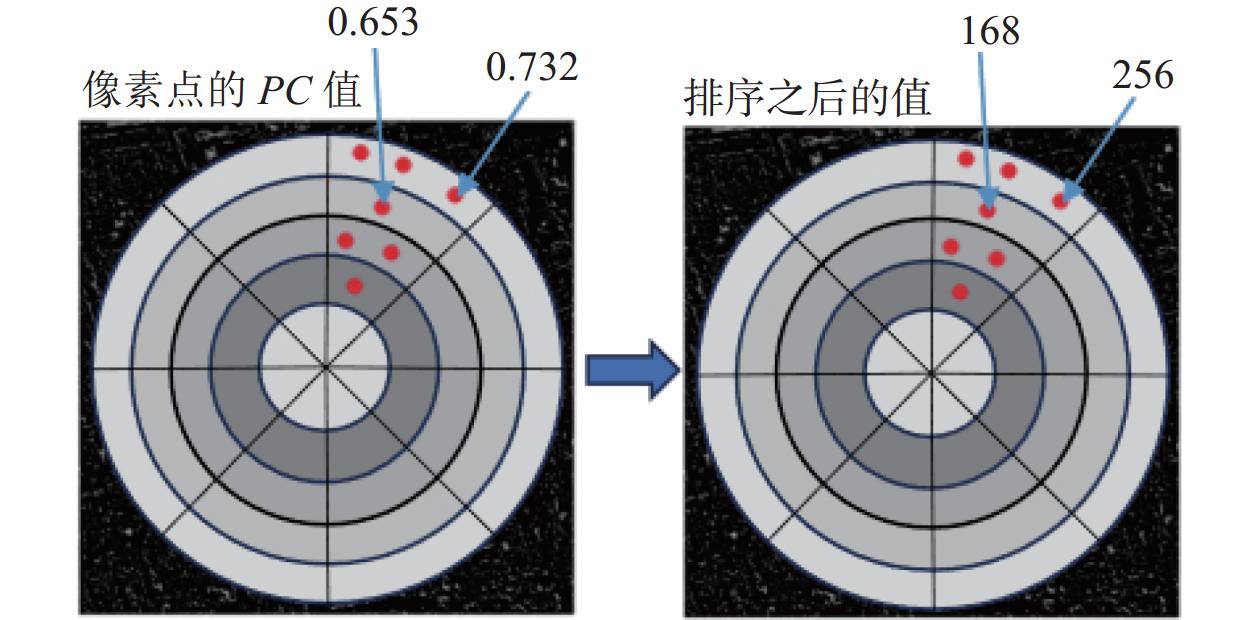
|
图 4 排序操作示意图 |
RPCLSS描述符和LSS描述符在对数极坐标中的对比结果如图5所示. 由图5(b)和图5(c)可知, 对于存在模态差异的红外和光学影像对, LSS描述符的辨识能力较差, 有明显的不相似情况. 而本文所提出的RPCLSS描述符在红外和光学影像对上生成的描述符明显更加相似, 证明RPCLSS可在一定程度上消除模态差异, 且拥有良好的辨识能力.

|
图 5 RPCLSS和LSS在对数极坐标中的对比结果图 |
2.4 RPCLSS匹配和粗差剔除
在匹配和粗差剔除阶段, 采用归一化互相关(normalized cross correlation, NCC)作为相似性度量进行匹配来获取影像的初始匹配. 随后采用FSC算法对初始匹配中的错误匹配进行剔除[23], 最后对获取的匹配点进行精度评估.
3 实验结果与分析 3.1 实验影像数据本文实验选用Skyearth团队公开的多模态遥感影像的数据集作为实验集, 该数据集包含光学-光学、红外-光学、深度图-光学、MAP-光学、SAR-光学、昼-夜6种数据类型, 几乎涵盖了多源数据解译、多结构数据配准和多光谱数据融合等多模态影像匹配的所有应用场景. 每个类型包含10幅影像对, 共60对影像. 获取地址为https://skyearth.org/public-ation/project/CoFS-M/. 所用影像对的非线性辐射差异非常显著, 易于验证各种多模态遥感影像匹配算法的性能差异. 部分实验数据如图6所示.
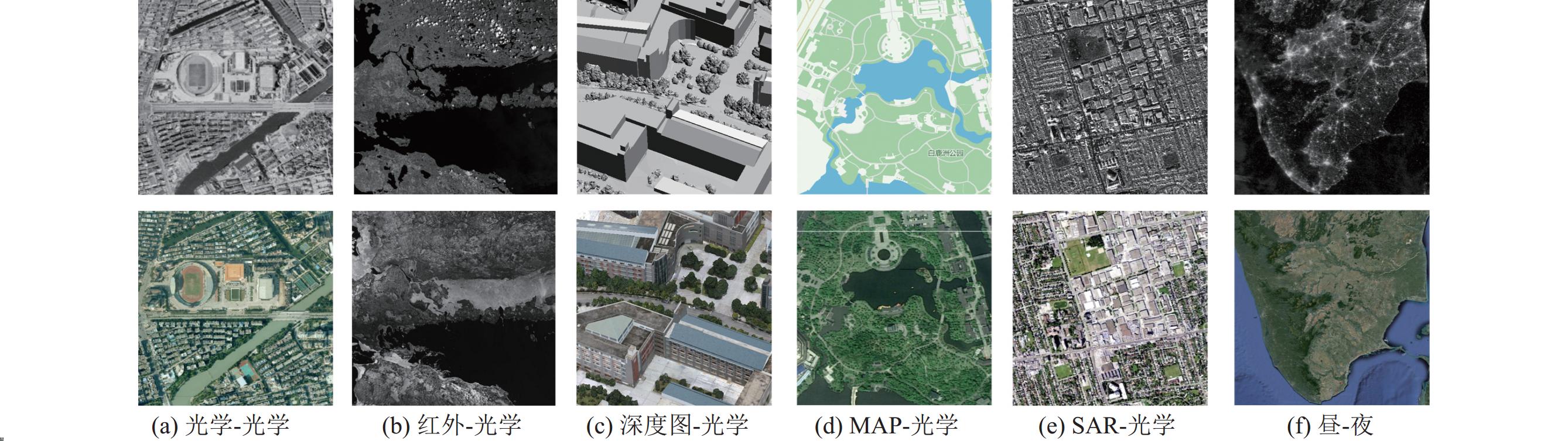
|
图 6 部分实验数据展示 |
3.2 评价指标与参数设置
为了验证本文算法的效果, 将其与传统遥感影像匹配方法SURF[26]以及当前4种先进的多模态遥感影像特征匹配方法LGHD[14]、PSO-SIFT[27]、RIFT[21]、POSS[28]进行对比分析. 采用平均正确匹配点数量(average number of correct matches, NCM)、平均均方根误差(average root mean square error, RMSE)和正确匹配率(correct matches ratio, CMR)这几个指标作为评价标准. 其中正确匹配点数量根据数据集中的Ground truth计算得来: 将待匹配影像特征点坐标经过仿射变换后与参考影像中对应特征点求欧氏距离, 误差在3像素内的匹配点对认定为正确匹配. 匹配的精度用RMSE的均值来进行度量, RMSE均值越小, 表示匹配的精度越高. 正确匹配率的计算公式如式(11)所示, RMSE的计算公式如式(12):
| precision=CMCM+FM | (11) |
| RMSE=√1MM∑i=1[(xi−x″i)2+(yi−y″i)2] | (12) |
其中, CM为正确匹配点数; FM为错误匹配点数; M表示所有的匹配个数;
在本文中, RPCLSS在生成描述子阶段将图像块大小设置为17, 相关局部窗口大小设置为100, 半径间隔数设置为4, 角度数设置为20. 其他几种方法的参数采用其各自文献中推荐的参数, 在匹配过程中使用描述符的NCC作为相似性度量. 本文中全部结果都是在PC上得到的, 运行系统为Windows 10, 代码均由Matlab实现, 平台处理器是Intel(R) Core(TM) i5-8300H CPU 2.30 GHz.
3.3 定性分析为了定性说明几种方法的匹配效果, 将这6种匹配方法在光学-光学、昼-夜、SAR-光学、红外-光学、MAP-光学和深度-光学6种不同类型的遥感影像对上进行匹配, 并对其结果进行可视化展示, 结果如图7所示.

|
图 7 各方法在6种模态下的匹配结果 |
从正确匹配点分布的整体情况来看, RPCLSS、POSS和RIFT展现出的效果最佳, PSO-SIFT与LGHD方法次之, 而SURF方法的效果最差. 在(b)组红外-光学类型上, POSS的效果最佳, 其次为RPCLSS和RIFT方法, PSO-SIFT和LGHD方法稍逊一筹, 而SURF方法效果最差, 仅有3对正确匹配. 在(d)组MAP-光学类型上, POSS的效果最好, RPCLSS和RIFT的效果次之, PSO-SIFT和LGHD虽然存在正确匹配点, 但数量较少, 匹配效果较差, SURF方法效果最差, 甚至没有正确匹配点. 对于其他分组, RPCLSS都表现出了最好的效果, 识别到的正确匹配点最多, POSS方法和RIFT方法次之, PSO-SIFT和LGHD方法紧随其后, SURF方法最差且在某些类型的影像上没有正确匹配点. 直观上, 从定性的整体匹配性能来看, RPCLSS
图8展示了RPCLSS匹配的棋盘融合效果图, 图8(a)、(c)、(e)原始影像对; 图8(b)为图8(a)的棋盘融合图; 图8(d)为图8(c)的棋盘融合图; 图8(f)为图8(e)的棋盘融合图. 从展示的棋盘融合图可以看出, 两幅图像的边缘和区域能够对应, 进一步证明了RPCLSS拥有良好的匹配性能.

|
图 8 RPCLSS匹配的棋盘融合图结果 |
3.4 定量分析
除了直观的定性分析外, 本文还给出了各个方法的定量分析. 匹配方法的优劣可以通过正确匹配点数NCM和匹配点的均方根误差RMSE来表示, 为了进一步说明RPCLSS的匹配效果, 将6种方法在6种不同类型多模态影像上进行实验, 并统计每种方法的平均NCM和平均RMSE进行定量分析, 其中平均NCM的单位为点个数, 平均RMSE的单位为像素.
各个方法在数据集上的平均正确匹配点数量和平均均方根误差如表1所示. 最佳性能结果已在表中用黑色粗体标注.
| 表 1 6种方法的定量比较结果 |
总体而言, 本文方法在6类影像上的效果优于其他5种方法. 在实验的6种数据类型中, 平均正确匹配点数量方面, RPCLSS明显多于SURF、LGHD和PSO-SIFT方法, SURF方法效果最差, 在大部分类型影像上的平均NCM很少且大多数都低于10, 其原因为SURF在特征描述求主方向阶段过于依赖局部区域像素的梯度方向. 而梯度信息对几何畸变和辐射畸变敏感, 容易造成大量的错误匹配. LGHD方法优于SURF, 但在MAP-光学、SAR-光学和昼-夜类型影像上匹配效果较差, 且平均NCM不超过20, 其原因为LGHD使用多尺度、多方向的Log-Gabor滤波器描述特征点的邻域, 在某些具有少量非线性强度变化的图像上效果较好, 但对于存在显著对比度和强度差异的场景适应性很差. 在各个类型中, LGHD的平均NCM和平均RMSE均低于RPCLSS. PSO-SIFT方法在总体上优于LGHD, 但在MAP-光学类型上匹配效果不佳, 平均NCM小于30, 且在红外-光学类型上平均NCM略少于LGHD, 平均RMSE略高于LGHD, 这是因为PSO-SIF结合匹配点的位置、尺度和方向信息减小了图像之间的图像强度差异, 提高了正确匹配点的数量, 但在非线性辐射畸变差异较大的MAP影像上效果不佳. 在6个类型中, PSO-SIFT方法的平均NCM和平均RMSE均低于RPCLSS. RIFT方法在光学-光学、红外-光学、深度图-光学和SAR-光学类型上效果良好, 平均NCM均达到了200以上, 在MAP-光学类型效果略差, 平均NCM低于100, 其原因为RIFT虽然生成最大值索引图增加了匹配点数量, 但使用相位一致性信息进行匹配, 图像从空间域转换到了频率域, 使得匹配精度降低. 在所有类型中, RIFT的效果优于PSO-SIFT, 但在平均NCM和平均RMSE方面低于RPCLSS. POSS方法在6类数据上有着不错的表现, 但它的平均NCM和平均RMSE略低于RPCLSS. 在平均NCM方面, RPCLSS的平均NCM数量约为LGHD方法的5倍, PSO-SIFT的3倍, RIFT的1.25倍. POSS方法的1.1倍. 在平均RMSE方面, RPCLSS的整体RMSE精度要优于其他几种方法. 为了进一步评估RPCLSS的性能, 通过计算正确匹配率来进行分析. 分别统计了6种方法在6类数据集上的正确匹配率情况, 结果如图9所示.
由图9可知, 在光学-光学、红外-光学、SAR-光学、昼-夜类型上, RPCLSS、POSS和RIFT方法表现出较高的正确匹配率, 约在0.5左右波动. 其中, RPCLSS方法的波动幅度较小且相对稳定, 略优于RIFT和POSS方法. PSO-SIFT方法在正确匹配率方面表现不佳, 大约在0.2–0.4之间. LGHD方法的正确匹配率在0.2–0.35之间. 而SURF方法的效果最差, 其正确匹配率最低, 在0.1–0.2之间, 甚至在某些影像上无法正确匹配. 在深度图-光学类型上, RPCLSS、POSS和RIFT性能优于其他3种方法, 平均正确匹配率约为0.4. PSO-SIFT的平均正确匹配率约为0.28, 高于LGHD和SURF方法. 在MAP-光学类型上, RPCLSS方法的平均正确匹配率约为0.29高于其他方法. 总体而言, 在这6种数据类型上, RPCLSS方法都展现出不弱于其他几种方法的效果, 能够取得较好的匹配性能.
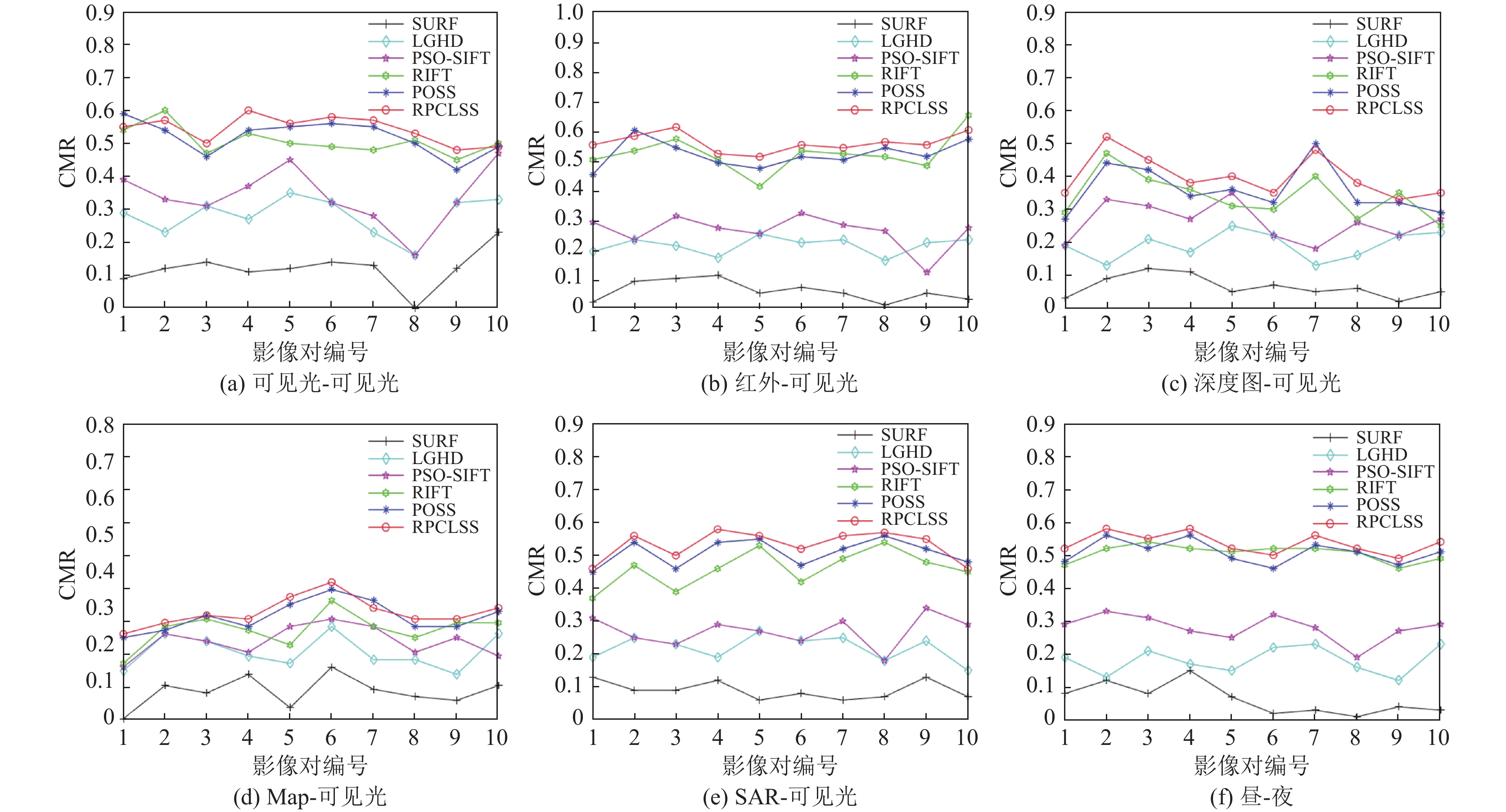
|
图 9 6种方法的正确匹配率展示 |
4 结论与展望
针对多模态遥感影像存在非线性辐射畸变的问题, 本文提出了一种结合相位对称特征与基于排序的局部自相似性的多模态遥感影像匹配方法. 通过对影像的相位对称图进行特征点提取, 有效降低图像非线性灰度变化对特征点检测的影响, 提高稳定特征点的数量. 将基于排序的局部自相似性与相位一致性相结合生成抗辐射畸变的特征描述符RPCLSS来对特征进行区分描述. 将提出的方法在公开的多源遥感影像数据集上与现有的5种先进匹配方法进行对比实验, 实验结果表明, 本文方法在正确匹配点数量, 匹配精度和匹配正确率方面, 要优于现有的几种先进多模态遥感影像匹配方法. 但本文方法也存在局限性, 如本文方法暂无法适应复杂纹理结构、计算描述子之间的归一化互相关时速度较慢, 影响算法效率. 后续工作将进一步改善算法效率, 进行深入研究来提升算法性能.
| [1] |
Xie XW, Zhang YJ, Ling X, et al. A novel extended phase correlation algorithm based on Log-Gabor filtering for multimodal remote sensing image registration. International Journal of Remote Sensing, 2019, 40(14): 5429-5453. DOI:10.1080/01431161.2019.1579941 |
| [2] |
张永军, 张祖勋, 龚健雅. 天空地多源遥感数据的广义摄影测量学. 测绘学报, 2021, 50(1): 1-11. DOI:10.11947/j.AGCS.2021.20200245 |
| [3] |
Yan XH, Zhang YJ, Zhang DJ, et al. Multimodal image registration using histogram of oriented gradient distance and data-driven grey wolf optimizer. Neurocomputing, 2020, 392: 108-120. DOI:10.1016/j.neucom.2020.01.107 |
| [4] |
樊仲藜, 张力, 王庆栋, 等. SAR影像和光学影像梯度方向加权的快速匹配方法. 测绘学报, 2021, 50(10): 1390-1403. DOI:10.11947/j.AGCS.2021.20200587 |
| [5] |
Shechtman E, Irani M. Matching local self-similarities across images and videos. Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE, 2007. 1–8.
|
| [6] |
Chen SH, Li XR, Yang H, et al. Robust local feature descriptor for multisource remote sensing image registration. Journal of Applied Remote Sensing, 2018, 12(1): 015005. |
| [7] |
Sedaghat A, Ebadi H. Distinctive order based self-similarity descriptor for multi-sensor remote sensing image matching. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 108: 62-71. DOI:10.1016/j.isprsjprs.2015.06.003 |
| [8] |
Xiong X, Xu Q, Jin GW, et al. Rank-based local self-similarity descriptor for optical-to-SAR image matching. IEEE Geoscience and Remote Sensing Letters, 2020, 17(10): 1742-1746. DOI:10.1109/LGRS.2019.2955153 |
| [9] |
南轲, 齐华, 叶沅鑫. 深度卷积特征表达的多模态遥感影像模板匹配方法. 测绘学报, 2019, 48(6): 727-736. DOI:10.11947/j.AGCS.2019.20180432 |
| [10] |
蓝朝桢, 卢万杰, 于君明, 等. 异源遥感影像特征匹配的深度学习算法. 测绘学报, 2021, 50(2): 189-202. |
| [11] |
Quan D, Wang S, Liang XF, et al. Deep generative matching network for optical and SAR image registration. Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium. Valencia: IEEE, 2018. 6215–6218.
|
| [12] |
Zeng L, Du YL, Lin HP, et al. A novel region-based image registration method for multisource remote sensing images via CNN. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 1821-1831. DOI:10.1109/JSTARS.2020.3047656 |
| [13] |
Nunes CFG, Padua FLC. A local feature descriptor based on Log-Gabor filters for keypoint matching in multispectral images. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1850-1854. DOI:10.1109/LGRS.2017.2738632 |
| [14] |
Aguilera CA, Sappa AD, Toledo R. LGHD: A feature descriptor for matching across non-linear intensity variations. Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP). Quebec City: IEEE, 2015. 178–181.
|
| [15] |
Kovesi P. Image features from phase congruency. Videre: Journal of Computer Vision Research, 1999, 1(3): 1-26. |
| [16] |
姚永祥, 张永军, 万一, 等. 顾及各向异性加权力矩与绝对相位方向的异源影像匹配. 武汉大学学报(信息科学版), 2021, 46(11): 1727-1736. |
| [17] |
Zhang YJ, Yao YX, Wan Y, et al. Histogram of the orientation of the weighted phase descriptor for multi-modal remote sensing image matching. ISPRS Journal of Photogrammetry and Remote Sensing, 2023, 196: 1-15. DOI:10.1016/j.isprsjprs.2022.12.018 |
| [18] |
Yao YX, Zhang YJ, Wan Y, et al. Multi-modal remote sensing image matching considering co-occurrence filter. IEEE Transactions on Image Processing, 2022, 31: 2584-2597. DOI:10.1109/TIP.2022.3157450 |
| [19] |
Ye YX, Shan J, Bruzzone L, et al. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(5): 2941-2958. DOI:10.1109/TGRS.2017.2656380 |
| [20] |
Ye YX, Shen L. HOPC: A novel similarity metric based on geometric structural properties for multi-modal remote sensing image matching. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, III-1: 9-16. |
| [21] |
Li JY, Hu QW, Ai MY. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Transactions on Image Processing, 2020, 29: 3296-3310. DOI:10.1109/TIP.2019.2959244 |
| [22] |
Rosten E, Drummond T. Machine learning for high-speed corner detection. Proceedings of the 9th European Conference on Computer Vision. Graz: Springer, 2006. 430–443.
|
| [23] |
Wu Y, Ma WP, Gong MG, et al. A novel point-matching algorithm based on fast sample consensus for image registration. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 43-47. DOI:10.1109/LGRS.2014.2325970 |
| [24] |
Kovesi P. Symmetry and asymmetry from local phase. Proceedings of the 10th Australian Joint Conference on Artificial Intelligence. Perth: Australian Computer Society, 1997. 2–4.
|
| [25] |
Goshtasby AA. Image registration: Principles, tools and methods. London: Springer, 2012.
|
| [26] |
Bay H, Ess A, Tuytelaars T, et al. Speeded-up robust features (SURF). Computer Vision and Image Understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 |
| [27] |
Ma WP, Wen ZL, Wu Y, et al. Remote sensing image registration with modified SIFT and enhanced feature matching. IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 3-7. DOI:10.1109/LGRS.2016.2600858 |
| [28] |
Fan JW, Xiong Q, Ye YX, et al. Combining phase congruency and self-similarity features for multimodal remote sensing image matching. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 1-5. |
 2024, Vol. 33
2024, Vol. 33



