随着三维数据采集技术的快速发展, 获取点云数据变得更加简单和便捷. 与二维光学图像信息相比, 三维点云数据不仅包含地理空间位置和表面强度信息, 而且具有更强的抗干扰能力, 能够在光照变化和图像失真等情况下保持稳定^[1]. 因此, 三维点云在无序分拣、工业测量、汽车无人驾驶、医疗健康等领域广泛应用.

点云分割是点云处理和分析的基本步骤, 通过将无序三维点划分为具有类似语义信息或功能意义的局部区域, 实现更加精确高效的数据处理与应用. 此过程为后续三维重建及场景理解等任务提供了必要且有价值的信息. 随着技术的不断发展, 点云分割方法也不断涌现. 这些方法包括2D和3D相结合的点云分割^[2]、传统的区域生长^[3]、聚类^[4]和模型拟合^[5]等方法以及基于深度学习^[6–9]的方法. 然而, 在应对复杂场景时, 诸如点云密度不均、噪声或异常值以及遮挡物等因素会影响这些方法的效果, 导致过度分割或分割不足, 从而影响工业生产环境中的实际应用. 因此, 在保证实时性前提下进一步提高精度已成为国内外学者研究重点.

超体素这一术语早期主要应用于医学体积图像和视频处理. 它被定义为二维图像区域的堆叠, 后来逐渐扩展到三维点云数据处理中. 与直接基于点的分割相比, 作为后续处理的基本单元, 超体素能够有效抑制噪声和异常值对结果产生的影响, 并且大幅降低时间消耗. 经典的体素云连通算法(VCCS)^[10]采用了这种体素的结构, 该算法使用聚类方法把具有相似属性的体素聚类为超体素, 并同时获得它们之间相邻关系. 然而, 在处理密集粘连点云时, 生成的超体素数据容易产生边界越界问题. Lin等人^[11]提出将超体素分割视为子集选择问题, 并利用各点的局部信息, 采用一种有效的启发式方法来优化该问题. 这种方法可以更有效地保留物体的边界和小结构, 但整个过程耗时严重不具有实时性. Luo等人^[12]采用了Canny边缘检测算法, 并结合深度图像, 以确定实体物体的边界. 这种方法有效地解决了组织点云中体素边界越界的问题. 然而, 实际应用中往往无法获得深度图像的数据. Saglam等人^[13]使用局部几何差异方法可以在较短时间内处理超体素的边界结构, 但这种方法并不总能保证边界结构的稳定性. 因此, 针对上述文章中处理超体素越界存在的问题, 本文提出了边界点提取和边界细化的方法, 使得细化后的超体素数据能够更好地依附于边界, 并在较少时间消耗的情况下完成.

生成超体素数据仅是点云分割的初步步骤, 仍需进一步处理以生成具有语义意义的点云块. Xu等人^[14]将体素聚类问题转化为图分割问题, 利用感知组合规律构建完全连接的局部图. 该算法强调分割精确性而非自动化, 但构建图或能量函数时算法复杂度较高, 处理难度大. Stein等人^[15]提出了局部凸邻接生长算法(LCCP), 该方法利用体素点云数据构建邻接表, 并根据定义的凹凸性准则采用区域增长方式对局部凸性进行物体分割. 然而, 随着超像素分辨率的变化, 该方法对噪声和异常值更加敏感. 文献[16]通过八叉树结构将点云划分为多个子块, 再基于平滑度约束对子块进行区域生长分割, 以应对平面空间特征差异较大的情况, 从而实现了复杂管道的点云分割. 在基于超体素数据区域生长的过程中, Luo等人^[17]将点特征直方图和超体素法线相结合, 分别表示局部面片的几何约束项和平滑约束项, 以使得生长过程更加合理. 韩英等人^[18]提出了一种加入颜色信息的方法, 并通过色差阈值作为聚类标准. 这些方法在存在噪声或相邻区域之间过渡平滑的情况下容易出现错误. 基于前述研究, 我们提出了一种优化的区域生长方法, 旨在实现超体素的合并. 该方法融合了点特征直方图和超体素法线, 以定义超体素的空间连通性约束和平滑约束, 并用于确定是否合并相邻的超体素. 此外, 根据场景中的对象都具有凸性结构, 本文采用了凹凸性准则来优化区域生长方法, 并将候选面片合并为更大的超体素, 提高了分割的鲁棒性和准确性, 同时减少了对原始三维点云数据噪声的影响.

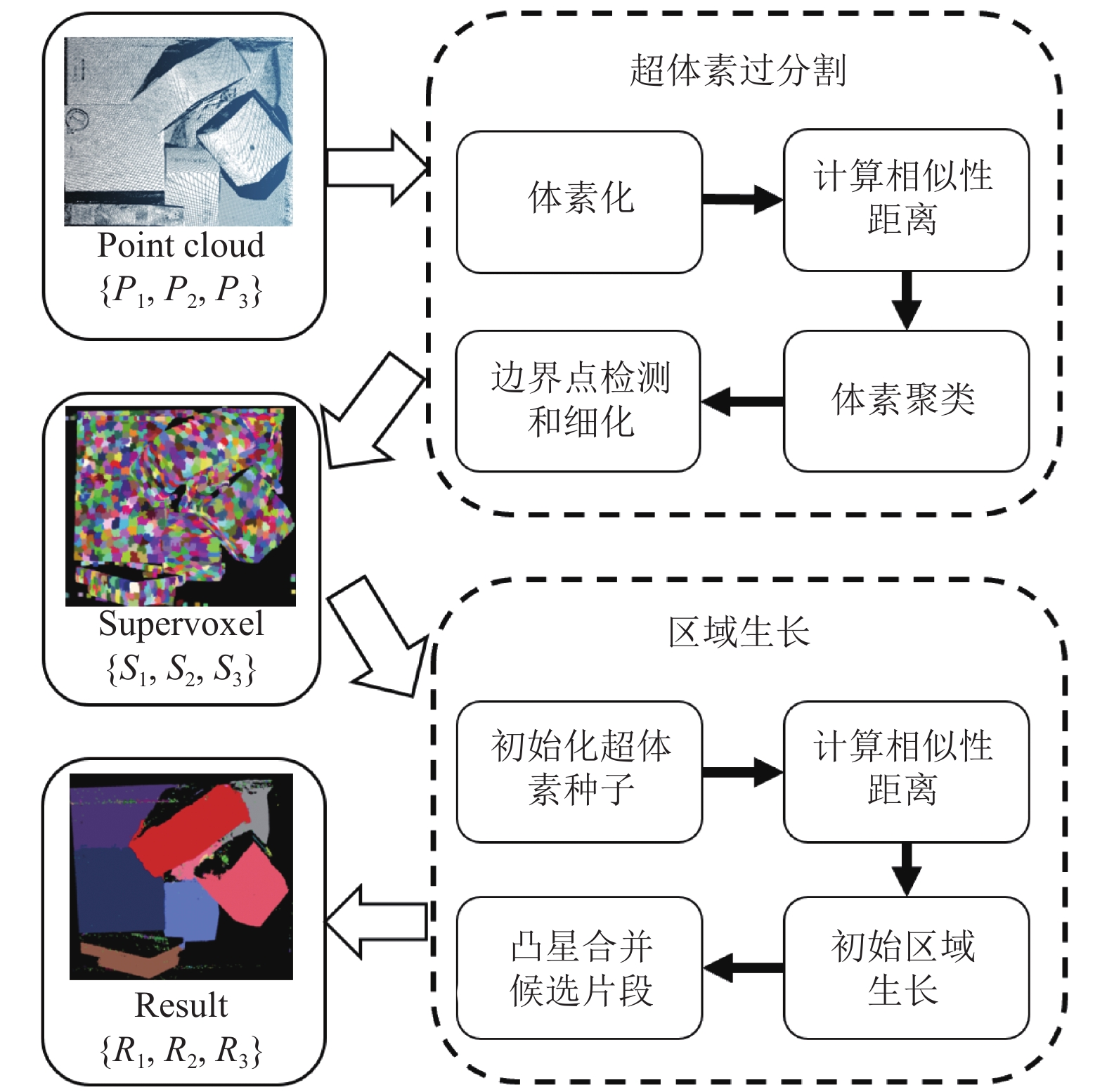
1 研究方法

本文提出的算法主要分为3个阶段. 第1阶段, 参考体素云连通性分割方法的相似性度量, 定义使用曲率特征代替颜色特征进行相似性度量. 由于曲率特征对点云边界处更加敏感, 因此得到过分割的超体素数据更加规整. 第2阶段, 在得到的超体素数据中根据距离约束查找边界点并进行细化处理, 以使细化后的超体素数据更好地拟合边界. 第3阶段选用超体素中心代替超体素进行区域生长以获得候选片段, 并基于相邻面凸凹性合并这些候选片段, 最终实现完整且精确的对象级分割结果. 算法整体框架如图1所示.

1.1 生成超体素

超体素是一种用于处理三维点云数据的特殊数据结构. 它通过将密集点云数据聚类成稀疏的三维面片来实现, 这些面片通常附着于点云对象的边界. 同一面片内的点应具有相似的外观或特征, 且很可能位于同一局部区域. 这一直观的概念有助于我们理解物体的空间结构并进行更有效的分割.

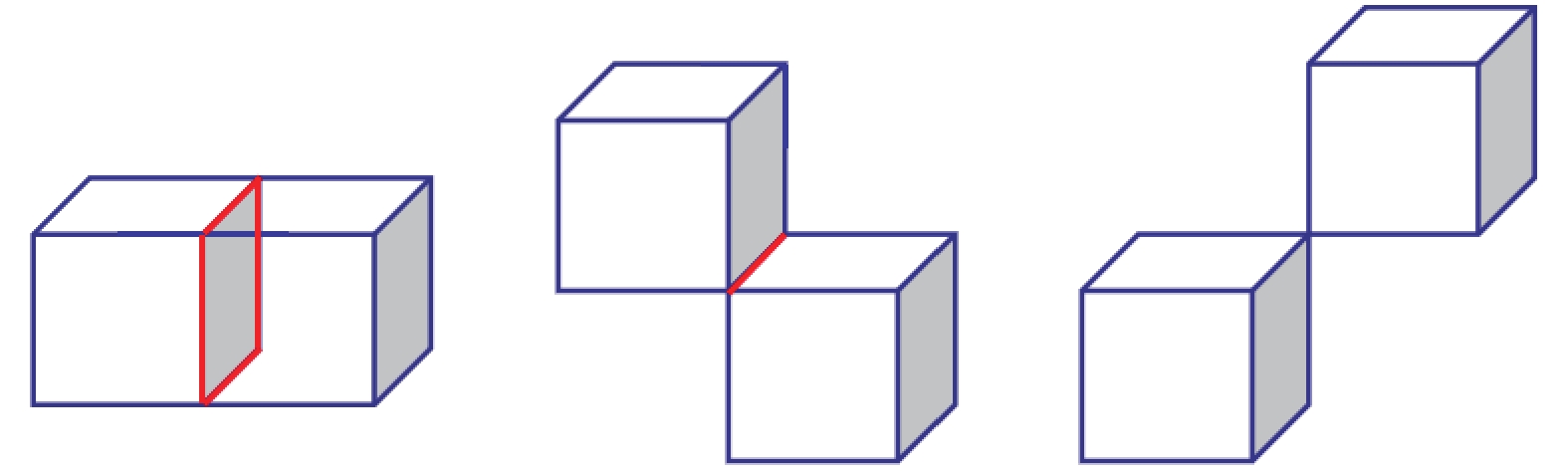
在本研究中, 本文借鉴了体素云连通性分割算法, 结合了相邻体素的空间连通性和几何特征来构建超体素. 超体素在体素化的三维空间中保持邻接关系, 即共享一个面、边或顶点, 如图2所示. 通过对输入点云进行体素化并考虑其26个邻居来构造邻接图, 在此基础上生成初始超体素.

通过相似性距离标准计算邻接体素与聚类中心所有体素的距离均值, 对距离最近的体素进行标记, 并逐层向外搜索至下一个体素, 直至所有体素均得到遍历. 当所有体素的邻接图搜索结束后, 更新已经聚类的超体素, 当聚类中心稳定或达到最大的迭代次数时完成体素云连通性分割. 本文提出使用曲率特征替代颜色特征作为相似性度量标准, 即利用式(1)计算超体素中心体素与相邻体素之间的相似性距离.

$ D = \sqrt {\begin{array}{*{20}{c}} {\dfrac{{\alpha D_c^2}}{{{m^{\text{2}}}}}} + {\dfrac{{\beta D_v^2}}{{3{R^2}}}} + {\varepsilon D_f^2} \end{array}} $

(1)

其中, $ D $表示超体素的中心和相邻体素之间的相似性距离; D_c表示归一化的曲率变化值; D_v表示用于聚类的归一化空间距离; R表示种子分辨率; D_f表示使用快速点特征直方图(FPFH)对几何特征描述^[19]. 此外, α、β和ε分别表示体素之间曲率、空间和几何关系的影响程度.

1.2 边界细化

使用第1.1节中的方法生成了超体素数据, 但该数据可能会出现部分超体素越过边界的问题. 为了解决这个问题, 本文提出了边界点检测和细化方法.

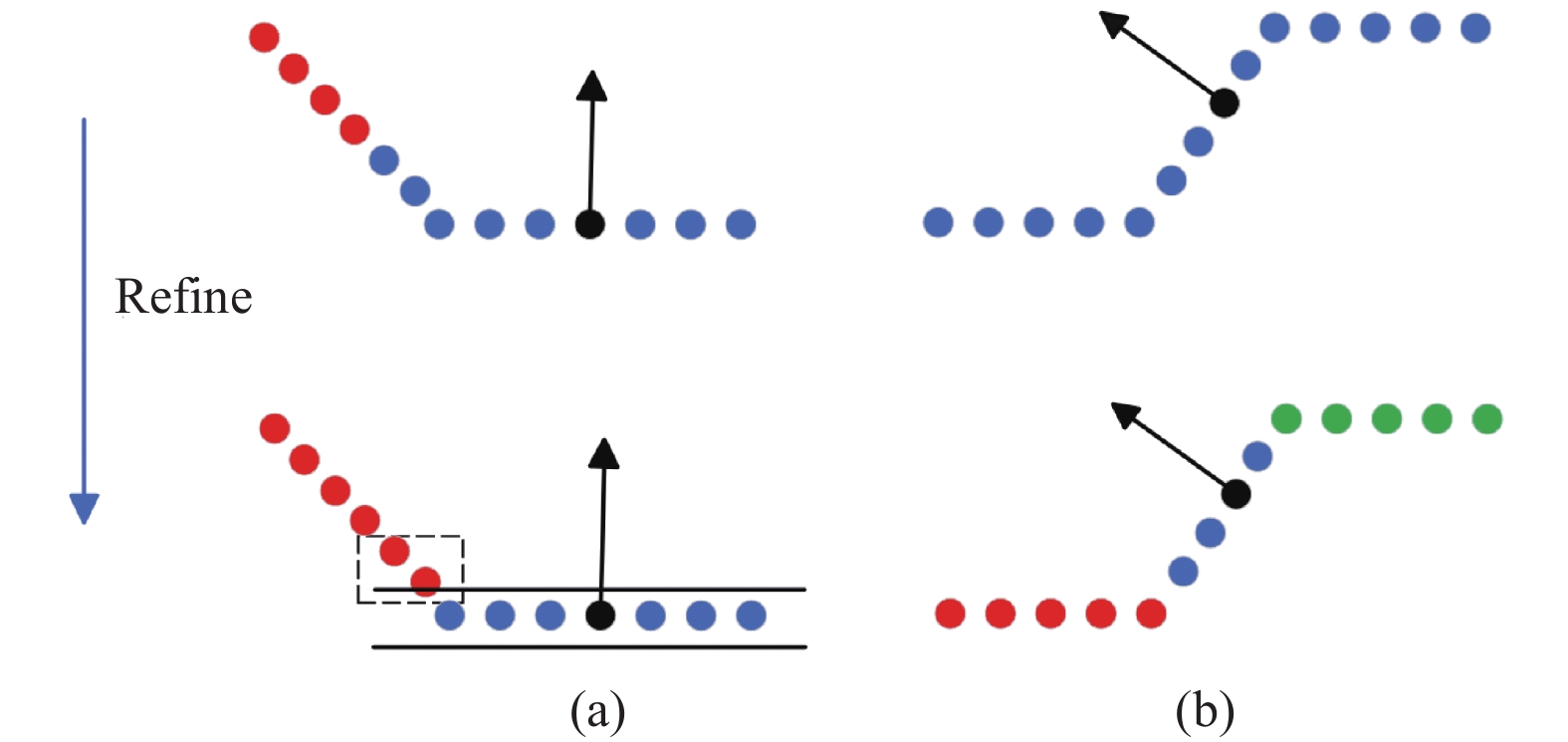
1.2.1 边界点检测

超体素过分割后容易产生图3中的两种分割错误. 第1种情况, 如图3(a), 是由于相似性距离判断的局限性而导致的边界点误差, 其忽略了点与超体素平面之间的连接. 当两个非共面超体素的平面法向量相差较小时, 这个问题变得更加严重. 第2种情况是超体素的欠分割, 如图3(b)所示, 其中超体素内的几个小平面由于超体素分辨率设置而耦合. 这两种情况都限制了超体素的分割有效性.

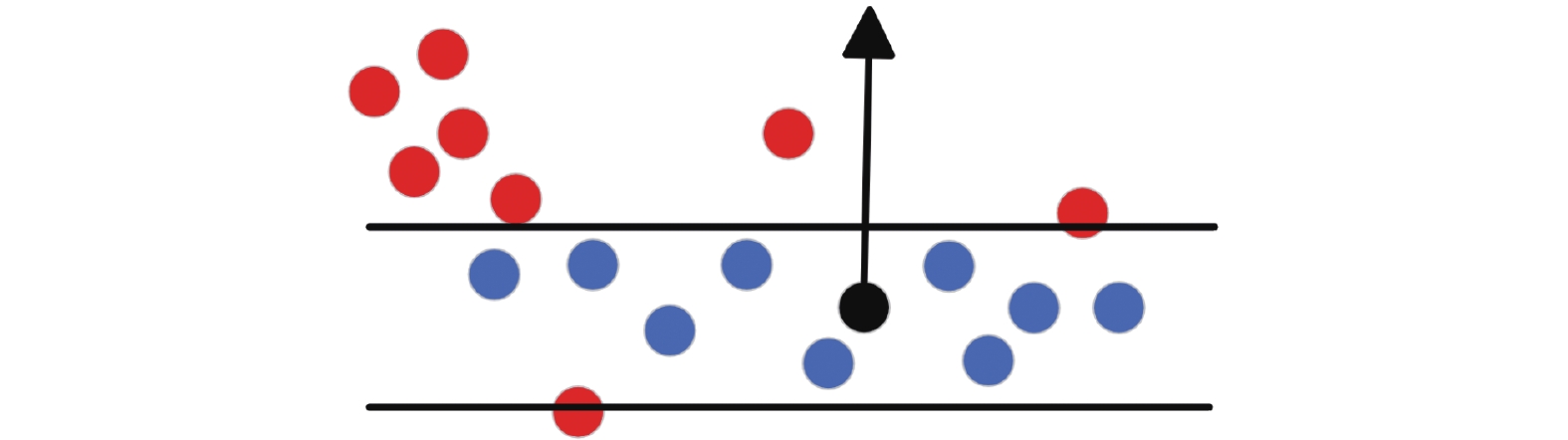
超体素块由多个大小一致和形状规则的体素组成. 在图4所示的超体素块中, 黑色点表示超体素的中心, 箭头方形表示超体素的法向方向. 根据法向量, 上下平移设定两个平面, 两个平面中间的点为该超体素的内点(即蓝色点保留), 两个平面外的体素(即红色点)为边界体素. 重新分配边界体素可以使得超体素块更加合理, 以提高超体素块的质量和准确性, 使其更符合实际物体的形状和结构特征.

1.2.2 边界点细化

在边界点细化阶段, 首先记录每个边界点所属的超体素, 然后通过超体素邻接表查找相邻超体素, 计算边界点和相邻超体素中心点之间的相似性度量$ D' $ (如式(2)), 并记录计算出最小的$ D' $的超体素, 最后将边界点重新分配到该超体素中. 该相似性度量由法向量和空间距离构成, 以突出点云的边界信息. 进行迭代聚类, 直至所有被定义的边界点都得到正确的分类.

$ D' = \sqrt {\begin{array}{*{20}{c}} {{\varphi _1}\left\| {{N_i} - {{\left. {{N_b}} \right\|}_{\text{2}}}} \right.} + {{\varphi _2}} \end{array}{{\left\| {\left. {{P_i} - {P_b}} \right\|} \right.}_{\text{2}}}} $

(2)

其中, $ D^{\prime} $是边界点和相邻超体素中心之间的相似性距离; $ N_{i} $是边界点相邻超体素的中心的法向量; $ N_{b} $是边界点的法向量; $ P_{i} $和$ P_{b} $是它们在由法向量N_i定义的切平面上的位置. 此外$ \varphi_{1} $和$ \varphi_{2} $表示两者的权重因子.

1.3 超体素区域生长

经过第1.2节边界点细化后的超体素数据, 我们采用区域生长方法以获得候选片段, 每个候选片段通常代表实体的一个面. 首先输入超体素数据, 并选择超体素中心体素替代超体素, 使用KD树搜索算法得到一个初始化的种子超体素集合. 然后进行区域生长计算, 以平滑度作为约束条件, 其中平滑度是通过计算法向量之间的角度确定的. 对于一个种子超体素, 如果相邻的超体素中心和种子超体素之间的法向量角度小于阈值, 则将相邻超体素加入当前生长面中. 两块超体素法向量方向基本相同, 仅基于平滑度的生长会导致错误结果. 因此需要同时满足平滑度和空间连通性约束式(3).

$ \left\{ \begin{gathered} \theta = {\cos ^{ - 1}}({{\vec n}_s} \cdot {{\vec n}_e}) < {\theta _{\rm th}} \\ d = {{\vec n}_s} \cdot \frac{{{p_s} - {p_{\text{e}}}}}{{{{\left\| {{p_s} - {p_{\text{e}}}} \right\|}_{\text{2}}}}} < {d_{\rm th}} \\ \end{gathered} \right. $

(3)

其中, $ \theta $表示为平滑度; $ \vec{n}_{s} $, $ \vec{n}_{e} $分别表示种子点超体素和相邻超体素中心的法向量; $ d $表示本文定义的空间距离; $ p_{s}, p_{e} $分别表示种子点超体素和相邻超体素的质心.

1.4 相邻面片融合

生长的过程通常应用于场景中的单个面, 并没有将整个对象分割出来. 为了实现对象级的分割, 因此需要进一步合并未增长的面片. 观察室内场景的常见物体, 如包装盒、杯子等, 几乎所有的对象都是由凸性结构组成的, 并且不同对象之间存在凹性连接. 因此这里使用不同物体间的凹凸性原则, 物体间为凸性连接则进行合并, 凹性连接定义为物体的边界.

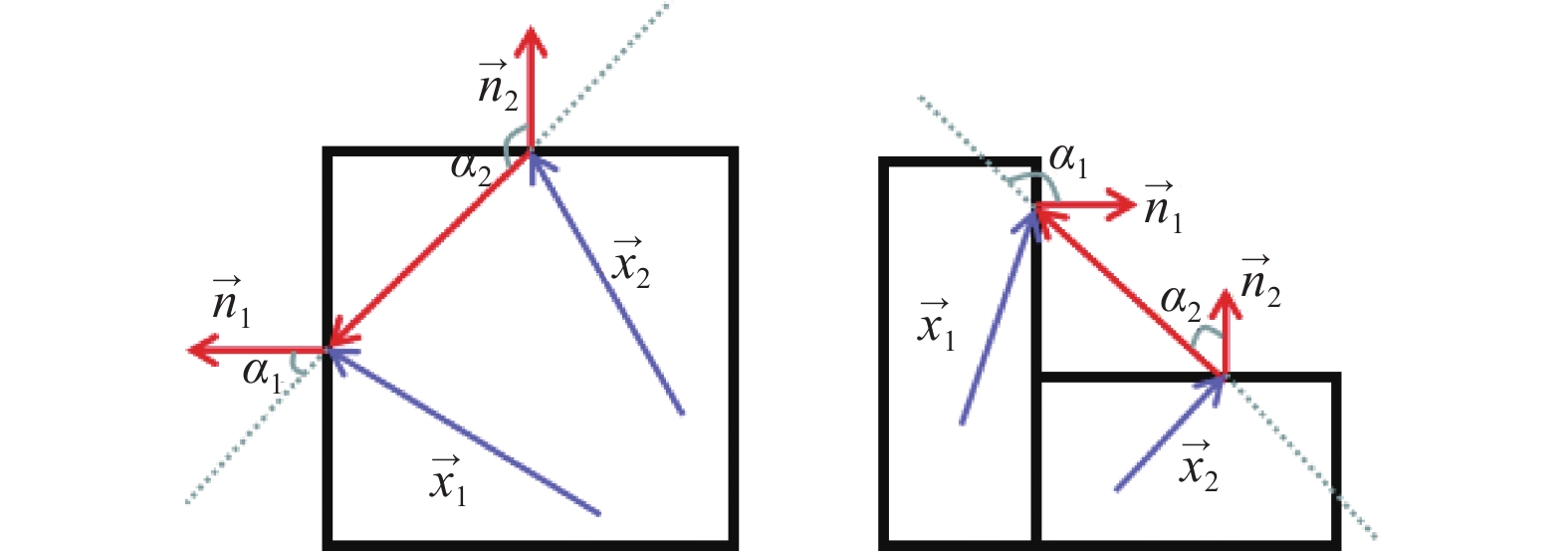
1.4.1 凹凸性定义

如图5所示, 仅利用空间信息和法线信息来定义物体表面上点云数据中的凹性与凸性. 两个相邻的超体素, $ \vec{x}_{1} $和$ \vec{x}_{2} $是两个超体素的质心向量, $ \vec{n}_{1} $和$ \vec{n}_{2} $是两个超体素的法向量, 进而得到向量($ \vec{x}_{1}-\vec{x}_{2} $)和法向量的夹角α₁和α₂. 如果α₁大于α₂则两个体素之间为凹性, 反之为凸性. 除此之外, 如果两个超体素被标记为凸性且有公共的邻居, 这个邻居也会被标记为与这两个体素凸性连接. 在实际应用中, 由于数据噪声的影响, 来自同一面的两个相邻的超体素可能会因为它们相似的法线表现出一定的凹度而被误判为凹性. 为了避免这种情况, 引入了一个阈值$ \beta $来增强鲁棒性: 如果两个法线之间的角度小于$ \beta $, 则超体素将具有凸性关系.

$ C = \left\{ {\begin{array}{*{20}{l}} {convex, }&{(\mathop \alpha \nolimits_{\text{1}} < \mathop \alpha \nolimits_2 ) \vee (\angle ({{\vec n}_1}, {{\vec n}_2}) < \beta )} \\ {concave, }&{\text{otherwise} } \end{array}} \right. $

(4)

对于两个相邻的面片, 首先遍历其中一个面片内的超体素, 判断每个超体素与它的相邻超体素标签是否一致, 如果不一致则被认定为边界受监督超体素. 然后通过使用本文对凹凸性的定义, 计算边界受监督超体素的凹凸性. 如约束条件(5)所示, 当超体素认定为凸性关系的数量大于边界受监督超体素总数的一半时, 就认为这两个面是凸性连接. 然而, 当只有一个监督超体素时, 会被误判为凸性连接, 因此受监督超体素总数应大于1.

$ c\left( {{f_a}, {f_b}} \right) = \left\{ \begin{gathered} \begin{array}{*{20}{l}} {convex, }&{\text{if}}\;{\left(\dfrac{{{N_c}}}{{{N_t}}} \geqslant 0.5\right)} \& \& ({N_t} > 1) \\ {concave, }&{\text{else}} \end{array} \\ \end{gathered} \right. $

(5)

1.4.2 凹凸性合并

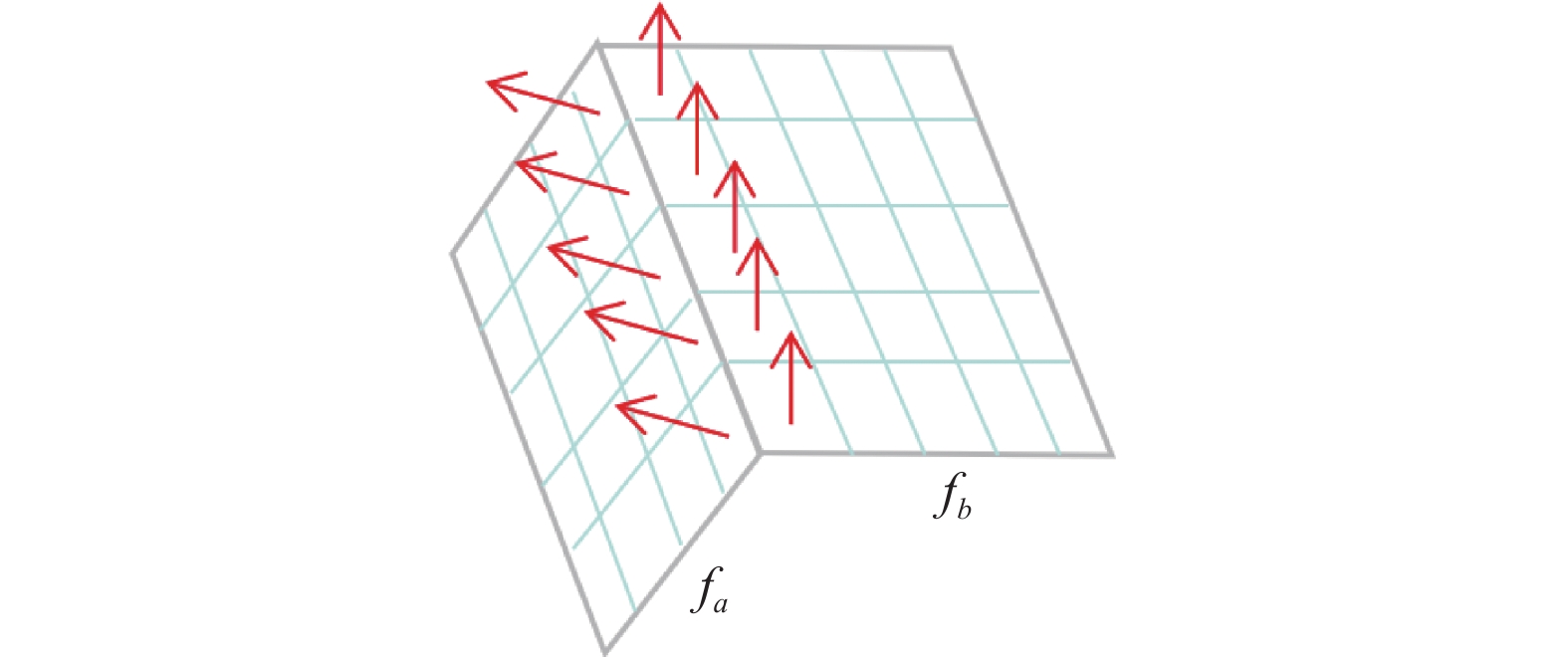
在合并过程开始之前, 根据面片内超体素的数量使用升序对面片集合进行排序. 首先处理超体素数量较少的面片, 合并其相邻的面片, 从而加速执行合并过程. 如图6中$ f_{a} $表示含有超体素数量较少的面片, 通过遍历$ f_{a} $内部超体素找到相邻的面片$ f_{b} $, 然后通过式(7)判断边界受监督超体素的凹凸性, 进一步确定是否可以合并. 满足凸性连接关系时, 即更改$ f_{{b}} $里面所有超体素的标签为a. 如果不满足凸性连接关系, 就不做改变.

2 实验

本文算法计算机运行配置为Intel(R) Core(TM) i5-12500H CPU和16 GB运行内存, 实验软件平台为基于Visual Studio 2019, 调用库为点云库PCL 1.11.1^[20], 编程语言C++.

实验数据1: 对象分割数据集(OSD-v0.2^[21]), 该数据集是由Richtsfeld等人于2012年提出. 它包含了111个场景, 这些场景是在近距离下拍摄的桌子上放置了杂乱的物体. 这一设计旨在模仿真实世界中的物体排列情况, 其中大部分物体呈盒子状或圆柱形. 每个场景的点云数量达到了23万, 其中包含了各种遮挡, 从部分到完全遮挡, 这增加了对象分割任务的难度. 这些特性使得该数据集成为了评估对象分割算法在复杂场景中性能的理想选择.

实验数据2: 利用图7中的双目结构光相机生成了自制的点云数据. 这些数据由各种形状的零食盒子杂乱摆放而成, 每个单独的点云数据包含大约80万个点, 远超过了OSD-v0.2中单个场景的点数. 这样庞大的数据量能够更准确地反映物体的真实信息, 尤其适用于工业领域中的分拣等需求. 另外, 为了应对特殊情况, 我们在考虑到复杂的摆放情况时人为地减小了物品之间的间隔, 从而增加了分割任务的难度. 这一实验数据的设计和特点使可作为一个有价值的资源.

实验数据3: Semantic3D^[22], 大型标记的3D点云数据集, 专为室外自然场景的语义分割而设计. 这个数据集包含了超过40亿个点, 覆盖了多种城市场景, 如教堂、街道、铁轨、广场、村庄、足球场、城堡等. 数据集的采集采用了最先进的设备进行静态扫描, 以确保高质量的数据获取. 这些数据非常细致, 能够准确地反映真实世界的场景细节, 包括建筑物、道路、植被等.

通过对以上3种不同类型的点云数据进行测试和比较, 可以更加全面、准确地评估本文提出算法在实际应用中表现如何.

2.1 室内物品点云分割实验结果

实验数据1和实验数据2均为室内桌面物体的点云数据集. 本节使用这些数据进行实验时, 采用了与VCCS算法相同的种子分辨率和体素分辨率. 经过多次实验, 在OSD-v0.2数据集下确定了最佳的参数配置, 其中种子分辨率为0.06 m, 体素分辨率为0.007 m, 即种子分辨率是体素分辨率的8倍左右. 实验结果如图8所示, 展示了在不同复杂程度的点云上的效果, 包括leran26、test45、test51和test64. 图8中第1行为真实场景图, 第2行为VCCS方法生成的超体素效果图, 第3行则是本文算法所产生的超体素效果图. 从图8中可以观察到, 我们提出的算法生成的超体素数据更加规整, 相比之下, VCCS方法生成的超体素数据存在超体素越过边界的情况. 这种规整的超体素数据有助于后续的聚类生长过程, 提高了聚类的效果和准确性.

此外, 我们还使用自制点云数据进行了实验, 如图9所示, 从左往右依次为真实场景图、VCCS算法效果图、本文算法效果图. 考虑到点云数据的庞大性, 我们对其进行了降采样处理, 以提高算法的性能. 实验结果表明, 本文算法在处理大规模点云数据时表现出色, 能够有效地生成规整且准确的超体素, 为后续的点云分割和处理提供了良好的基础.

为了验证算法改进的有效性, 本文对优化步骤前后的误分割点云数量进行了统计. 表1中展示了在增加曲率特征和边界细化算法前后, 超体素误分割的点数对比结果. 实验结果表明, 经过改进的算法大幅度减少了误分割的点数.

本文通过与区域生长点云分割算法(RG^[23])和基于VCCS生成的超体素做局部凸邻接生长算法(简称为V-L)进行对比实验, 展示了提出的算法在分割精度上的显著优势. 实验结果如图10中所示, 本文算法在处理复杂情况时表现更为出色, 并具有更高的分割精度. 具体来说, 在处理粘连情况时, RG算法往往存在着欠分割的问题, 即未能准确地将两个物体分开. 而对于中间的粘连情况, LCCP算法的表现也不尽如人意, 这可能是由于VCCS算法生成的超体素越过边界而导致的. 与之相比, 我们的算法更加注重边界处的分割, 因此在处理这种情况时效果更佳.

此外, 对于一些特殊情况如图10中的第3行案例, VCCS算法会错误地将圆柱体和长方体当作一个物体进行分割, 而我们提出的算法则能更好地保持边界的准确性. 在自行制作的点云数据上进行的实验结果也证实了我们算法的优越性. 即便在点云质量较差的情况下, 3种方法都不能很好地分割圆柱形物体, 但我们的算法在分割两个长方体物体时的效果优于其他两种方法. 综合对比分析显示, 本文提出的算法在分割精度上更贴近真实效果, 这表明其具有更高的准确性和鲁棒性, 可在实际应用中发挥更大的作用.

2.2 室外自然场景点云分割实验结果

为了体现本文模型对复杂场景的泛化性和鲁棒性, 我们选择了更具挑战性的Semantic3D数据集进行实验, 并选取了stgallencathedral1和stgallencathedral3作为具体测试对象. 这两个场景具有复杂的结构和丰富的细节, 能够有效测试模型在处理复杂环境时的性能. 本文对比了我们提出的算法与Poux F提出的自动区域生长分割系统(RGS)^[24], 以评估我们算法在这些复杂情况下的表现.

图11展示了两个场景的点云分割结果(左图为stgallencathedral1, 右图为stgallencathedral3), 并分别对比了RGS算法和本文算法的表现 (从上往下分别为原始点云数据、RGS算法分割结果、本文算法分割结果). 实验结果表明, 在处理这些复杂场景时, RGS算法存在一些局限性, 例如在分割物体或保持边界准确性方面表现不佳. 以及在stgallencathedral1场景实验中, RGS算法未能将阁楼和屋顶区分开, 而是将它们分割成同一物体. 在stgallencathedral3场景实验中, RGS算法错误地将红色汽车旁边的墙面分割成两个物体, 并且左边的钟楼出现了过分割的情况. 相比之下, 本文算法在这些方面表现更为出色, 展现了更高的分割精度和鲁棒性. 特别是在处理stgallencathedral3场景中的细节丰富的建筑区域时, 本文算法能够更准确地分割出不同的建筑部分, 并保持其边界的清晰.

这些实验结果充分证明了本文算法在处理复杂场景时的优越性, 表现出更强的泛化能力和鲁棒性, 能够为实际应用中需要处理复杂环境的场景提供更可靠的解决方案.

2.3 评价

为了更加客观地评价本文提出的算法, 使用准确率(P)、召回率(R)及综合P和R的综合评估的得分(F)对于参考方法和本文改进分割方法进行评估, 如式(6)所示:

$ \left\{ \begin{gathered} P = \mathit{TP/(TP + FP)} \\ R = \mathit{TP/(TP + FN)} \\ F = 2PR/(P + R) \\ \end{gathered} \right. $

(6)

其中, TP表示样本中准确分割的点云; FP表示样本中其他物体被误判到该物体的点云; FN表示样本中被误判为其他物体的点云. FP的大小为实际分割点云大小减去准确分割点云大小, FN的大小为分割块的真实点云大小减去准确分割点云大小. 评估数据使用OSD-v0.2数据集中的点云实例.

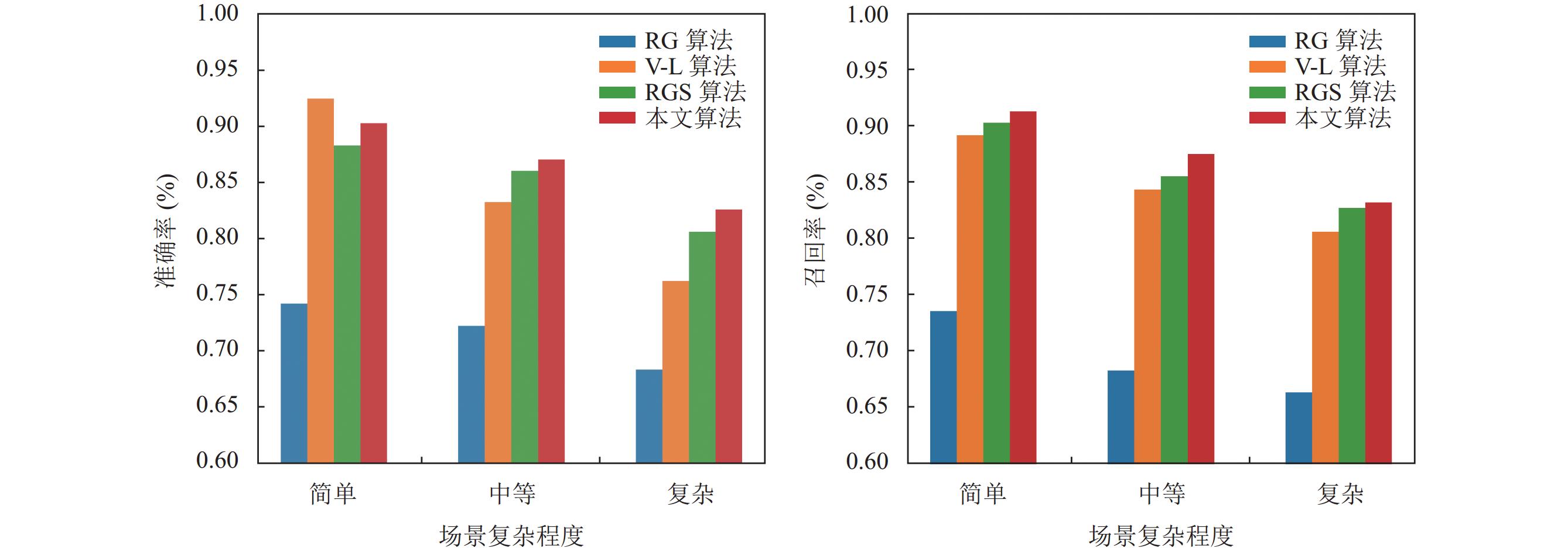
经过对柱形图(图12)和表2的详细分析, 本文算法在处理不同复杂程度场景时相较于RGS、V-L算法、RG算法表现更为出色, 尤其是在保持边界结构方面表现突出. 虽然算法的处理时间在不影响实时性的前提下略有增加, 但准确性和召回率却大幅提升. 这意味着我们可以更快速、更精准地获取所需信息. 此外, 在实际应用中, 本文算法还具备良好的可扩展性和稳定性, 能够适应各种数据规模和类型的处理需求.

3 结论

本文提出了一种面向3D视觉引导的点云分割算法, 包括超体素点云的细化、基于超体素的区域生长和基于凹凸性相邻面的合并. 该算法的优点在于以超体素为基础做边界细化, 有效解决了部分超体素边界越界问题, 根据物体结构之间凹凸性关系融合区域生长的相邻面, 最终得到更加完整和精确的对象分割结果. 本文方法在OSD-v0.2数据集、Semantic3D数据集和自制数据集上进行实验, 并使用准确率和召回率作为评价标准. 与VCCS算法结果对比, 本文生成的超体素更好地与边界拟合; 与RG算法、LCCP算法、RGS算法结果对比, 本文得到了更好的对象分割结果, 并具有一定的实时性. 特别是在处理堆叠和遮挡对象时表现出明显效果提升.