阿尔茨海默病(Alzheimer’s disease, AD)是一种不可逆的神经退行性疾病^[1], 其临床表征包括认知功能下降、记忆力受损、语言障碍等, 具有病因未明、无法治愈、高遗传性等特点. 该病症状逐渐恶化, 对患者的健康和生命质量构成威胁, 并给家庭和社会带来负担. 根据《2023中国阿尔茨海默病数据与防控策略》公布的数据, 我国目前约有983万阿尔茨海默病患者; 预计到2030年, 我国60岁以上阿尔茨海默病患病人数将增至1911万人, 造成的直接经济负担将达到9738亿元^[2]. 在阿尔茨海默病的临床表征中, 认知功能下降是最严重的症状, 伴随着脑部结构的变化, 例如海马体萎缩^[3]、丘脑局部体积缩小^[4]及下侧脑室体积扩大^[5]等. 因此, 寻找与认知能力改变相关的脑部结构对阿尔茨海默病的早期诊断至关重要. 然而, 评估认知功能的量表数据在实际收集中可能会受到外界干扰或个体差异的影响而产生异常值, 同时影像数据具有高维度、异常值及大多服从重尾分布的特点. 因此, 开发一种能全面探究认知功能与脑部结构之间关系的统计学方法就显得尤为重要.

许多科研工作者已对常见的认知得分与神经影像学生物标志物之间的关系进行了研究. 其中, Wan等人^[6]建立了一个稀疏多元回归模型, 并基于机器学习中的稀疏贝叶斯学习推导出一个有效算法. 针对反映患者整体认知障碍情况的认知得分, 该模型筛选出了AD相关的生物标志物, 如海马体积、杏仁核体积和内嗅皮层厚度. 当存在多个认知得分预测任务时, 可以采用多任务学习(multi-task learning, MTL)^[7]方法, 充分利用相关任务中的共享信息. 为此, Liang等人^[8]提出了双图引导的自定进度多任务特征学习(bi-graph guided self-paced multi-task feature learning)框架, 用于探索多个任务之间的关系, 以提高认知得分的预测性能, 并识别出与认知相关的生物标志物, 如海马、中颞叶和内嗅. 此外, Zhang等人^[9]提出一种通用的多模态多任务学习(multi-modal multi-task learning)方法, 采用$ {L}_{2, 1} $范数正则化回归模型进行特征选择, 联合执行AD分类与认知得分预测的任务, 并在特征选择中筛选出与疾病高度相关的海马区域. 为了充分挖掘预测任务之间的内在关联性, Cao等人^[10]提出了一种基于共享子空间和稀疏组套索的多任务学习模型, 用于建立认知得分和磁共振成像(magnetic resonance imaging, MRI)特征之间的关系. 该模型在整个特征空间中采用稀疏组套索惩罚方法, 选择一组共同的生物标志物, 并通过探索共享特征子空间来考虑多个任务的相关性. 该方法在认知得分的预测任务中表现良好, 并成功选择出与认知障碍高度相关的重要特征, 如海马体、内嗅、中颞回等. 但是由于各种原因, 一些受试者可能无法按计划参与实验, 导致认知得分数据的不完整. 为此, Chen等人^[11]提出一种带有不完整标签的低秩稀疏特征选择模型(low-rank sparse feature selection with incomplete labels)用于预测认知表现, 并识别出与AD认知障碍高度相关的神经影像标志物, 如海马体、中颞区、内嗅和胼胝体. 研究发现, 阿尔茨海默病患者在早期认知表现为正常, 随后发展为轻度认知障碍, 最终为痴呆^[12]. 由此可知, 在疾病的发展过程中, 患者的认知能力水平逐渐由高到低变化. 然而, 上述的机器学习方法的研究主要基于条件均值, 从而忽略了认知能力在不同水平下提供的信息, 无法根据认知能力的水平高低进行更加细致的分析. 此外, 在处理脑部影像数据时, 这些方法还面临一些挑战, 主要包括影像数据大多为高维的, 且服从重尾分布和存在较多的异常值. 这些问题将对系数估计产生较大的影响, 使模型的准确性和稳定性难以保证.

为了解决这些问题, 可采用分位数回归方法^[13]. 分位数回归方法旨在对响应变量在不同分位点上的条件分布进行统计建模, 考虑了数据在不同分位点下的变化, 而非仅关注其条件均值. 常见的分位点包括四分位数、中位数等. 通过对响应变量的不同分位点进行建模, 可以全面获得关于响应变量在不同条件下的全面信息. 此外, 分位数回归使用加权最小绝对离差和法进行估计, 通常不受离群点的影响, 从而缓解了异常值带来的影响, 提高了模型的稳健性和可靠性. 为了进一步解决影像学数据中的高维问题, 可以在分位数回归模型中添加稀疏性要求. 由此获得的稀疏分位数回归方法可在模型的拟合效果和泛化能力之间取得平衡, 有效解决过拟合问题, 适用于解决高维数据的特征选择问题. 该方法在统计学领域的回归分析中发挥着重要作用, 作为一个极其灵活而有效的工具, 可帮助研究者更全面地理解和解释复杂数据之间的关系. 因此, 本文采用稀疏分位数回归方法对影像学数据进行分析, 旨在研究认知得分在不同分位点下与神经影像学数据之间的关系, 从而更全面地揭示阿尔茨海默病患者的认知情况与脑部影像数据之间潜在关联, 为深入理解该疾病的发展提供更为可靠的统计分析框架.

本文其余内容的结构如下: 第1节分为3个部分: (1)给出了数据来源及预处理; (2)对数据进行描述; (3)详细介绍了稀疏分位数回归方法以及迭代重加权${L_1}$惩罚平滑分位数回归算法. 第2节展示使用稀疏分位数回归方法进行数据分析得到的结果. 最后, 在第3节对全文进行总结.

1 方法 1.1 数据来源及预处理

阿尔茨海默病神经影像学计划(ADNI)为由美国国立卫生研究院(NIH)资助的多中心开源数据库, 旨在探索阿尔茨海默病谱系中临床、认知、影像、遗传和生化生物标志物之间的关联, 并推动阿尔茨海默病的预测、诊断和治疗研究. ADNI包括多种数据类型, 如磁共振成像 (MRI)、正电子发射断层扫描(PET)、基因组学数据、认知功能评估数据以及临床神经心理评估量表等. 该计划在美国和加拿大设置50多个研究站点, 对象年龄跨度为55–90岁之间, 更多详细的信息请参阅www.adni-info.org.

我们从ADNI数据库中获取一组数据, 包含了静息态功能磁共振成像(rs-fMRI)数据、认知功能评估数据和临床数据. 静息态功能磁共振成像是一种用于研究大脑自发活动和功能连接的功能磁共振成像技术, 在神经科学领域中得到广泛应用. 认知功能评估数据包括简易精神状态检查量表(minimum mental state examination, MMSE)和阿尔茨海默病评定量表延迟词语回忆量表(score from task 4 (word recognition) of the Alzheimer’s disease assessment scale, ADASQ4). MMSE是一种综合性认知量表, 用于评估老年人认知和智能功能, 包括定向力、记忆力、注意计算力、回忆能力和语言能力. 评定总分为30分, 得分越高表示被测试者的认知功能越好. ADASQ4是ADAS-Cog中的延迟回忆测试项目, 是一种针对记忆的评估量表, 得分越高说明被测试者的记忆能力越差. 临床变量包括年龄(AGE)、性别(PTGENDER)、是否为主观记忆抱怨患者(DX)、受教育年限(PTEDUCAT)、族群(PTETHCAT)、种族(PTRACCAT)、婚姻状况(PTMARRY)和载脂蛋白E量化值(APOE4).

静息态功能磁共振成像数据的预处理包括一系列标准化步骤, 均通过DPABI软件实现^[14]. 首先, 将原始DICOM格式数据转换为NII格式, 并从T1加权结构影像中去除颅骨和颈部. 随后, 对rs-fMRI数据进行严格的校正, 以纠正由头部运动引起的低频漂移和运动伪影, 并进行时间错位切片的时间校正. 为了减轻空间不一致性, 采用全宽度为4 mm的高斯核进行空间平滑. 为了提高整体数据质量, 消除数据中低水平的噪音. 处理后的图像按照MINI152标准空间进行对齐, 完成预处理过程. 最后, 基于预处理后的rs-fMRI时间序列数据, 采用解剖学标记图谱(AAL)^[15]来勾画特定感兴趣区域(region of interest, ROI)的时间序列, 最终获得大脑中134个ROI的体积数据.

考虑DPABI软件处理得到的ROI体积数据、认知功能评估数据和临床数据, 我们提取其中的基线数据 (baseline data)用于研究. 此外, 对其中的ROI体积数据进行主成分分析, 提取前5个主成分变量. 为了便于分析, 将临床数据中的分类变量转换成相应的哑变量.

1.2 数据描述

经过预处理后, 数据中样本总数为278, 其中包括134个ROI体积数据、5个主成分变量、8个临床变量以及2个不同的认知得分. 样本分组情况包括249个认知正常对照组(cognitive normal, CN)和29个主观记忆抱怨患者(subjective memory complaints, SMC). SMC指个体主观上感觉自我认知能力下降, 但客观认知能力方面无障碍, 主要发生在老年时期 ^[16]. 研究指出, SMC可作为认知下降的早期临床指标, 并与轻度认知障碍(mild cognitive impairment, MCI)和痴呆风险增加相关联, 可能是由CN向MCI过渡的阶段^[17].

根据疾病分组信息, 对样本的年龄、性别、受教育年限等临床数据及认知得分进行描述性统计分析和统计检验. 其中, 数值变量将展示其均值(方差)和Wilcox秩和检验结果, 分类变量将展示其在对应类别中的数量(占比)和卡方检验结果. 为了进一步观察影像数据的分布特征, 我们对ROI体积数据进行峰度分析, 并采用箱线图进行展示.

1.3 稀疏分位数回归模型及算法 1.3.1 稀疏分位数回归模型

考虑响应变量$y \in \mathbb{R}$和$ p $维预测向量${\boldsymbol{x}} \in {\mathbb{R}^p}$. 在给定${\boldsymbol{x}}$的条件下, $y$的条件分布累积函数表示为$F(y\mid {\boldsymbol{x}})$, $y$的第$\tau $条件分位点表示为$ {Q}_{y}\left(\tau \mid {\boldsymbol{x}}\right)= \mathrm{inf}\{y:F \left(y\mid {\boldsymbol{x}}\right) \geqslant\tau \} $, 其中$\tau \in (0, 1)$. 由此可知, $y$以第$\tau $条件分位点${Q_y}\left( {\tau \mid {\boldsymbol{x}}} \right)$为界, 有$\tau $的概率$y$的取值会小于或等于${Q_y}\left( {\tau \mid {\boldsymbol{x}}} \right)$, 有$1 - \tau $的概率$y$的取值会大于${Q_y}\left( {\tau \mid {\boldsymbol{x}}} \right)$. 其中, 中位数是常见的分位点, 对应$\tau $为0.5. 针对$y$的第$\tau $条件分位点${Q_y}\left( {\tau \mid {\boldsymbol{x}}} \right)$, 我们考虑如下线性分位数回归模型:

$ {Q_y}\left( {\tau \mid {\boldsymbol{x}}} \right) = {{\boldsymbol{x}}^{\text{T}}}{\boldsymbol{\beta}} \left( \tau \right) $

其中, ${\boldsymbol{\beta}} \left( \tau \right) = \left( {{\beta _1}\left( \tau \right), {\beta _2}\left( \tau \right), \cdots , {\beta _p}\left( \tau \right)} \right) \in {\mathbb{R}^p}$是依赖于$\tau $的系数向量. 因此, 通过设定不同的分位点, 可以获得更多关于响应变量$y$的信息. 为方便起见, 在本文的其余部分使用${\boldsymbol{ \beta}} $替代${\boldsymbol{\beta}} \left( \tau \right)$. 给定$n$个响应变量y和预测向量x的独立观测数据$ \left\{ {({y_i}, {{\boldsymbol{x}}_i})} ,{i = 1, \cdots , n} \right\} $, 稀疏分位数回归估计量通常被定义为以下优化问题的全局最优解或局部最优解:

$ \underset{{\boldsymbol{\beta}} \in {\mathbb{R}}^{p}}{\mathrm{min}}\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}{\rho }_{\tau }\left({y}_{i}-{{\boldsymbol{x}}}_{i}^{\text{T}}{\boldsymbol{\beta}} \right)+{\displaystyle \sum }_{j=1}^{p}{q}_{\mu }\left(\left|{\beta }_{j}\right|\right) $

(1)

其中, ${\rho _\tau }\left( u \right) = u\left\{ {\tau - I\left( {u < 0} \right)} \right\}$是分位数损失函数, ${q_\mu }\left( \cdot \right)$是控制模型复杂度的惩罚函数, 定义$\hat{Q}({\boldsymbol{\beta}}) = \dfrac{1}{n}{\displaystyle\sum}_{i=1}^{n}\rho_{\tau}(y_i- {\boldsymbol x}_i^{\rm T}\boldsymbol{\beta})$. 对系数的大小进行惩罚可以有效减少模型的复杂度, 防止模型在训练数据上过拟合, 从而提高模型在未知数据上的泛化能力.

1.3.2 迭代重加权${L_1}$惩罚平滑分位数回归算法

一方面, 分位数损失函数的分段线性导致了非光滑性, 给分位数回归问题的计算方面带来了巨大的挑战. 因此, 许多学者提出了有关平滑分位数回归方法. 在线性分位数回归的背景下, Fernande等人^[18]提出对目标函数进行平滑, 不限于损失函数中的指示函数. 他们证明了由此产生的平滑分位数回归估计量具有更小的均方误差, 并且是渐近可微的. 另一方面, 一些非凸正则化方法被引入分位数回归的研究中. 因此, 针对分位数损失的不可微性和目标函数的非凸性, Tan等人^[19]采用了卷积型平滑方法以提高其光滑度和局部强凸性, 并提出了迭代重加权${L_1}$惩罚平滑分位数回归算法. 该算法通过解决一系列凸问题, 从而避免了直接解决非凸优化问题所带来的计算复杂性. 接下来将详细介绍该算法.

优化问题(1)分为两个部分进行处理: 对于不光滑的分位数损失函数部分$\hat Q\left( {\boldsymbol{\beta}} \right)$, 使用核函数进行平滑; 对于惩罚函数部分$ {\displaystyle \sum }_{j=1}^{p}{q}_{\mu }\left(\left|{\beta }_{j}\right|\right) $, 使用局部线性近似的方法进行近似. 具体步骤如下.

首先, 给定${\boldsymbol{\beta}} \in {\mathbb{R}^p}$, 设$\hat F\left( { \cdot ;{\boldsymbol{\beta}} } \right)$为残差$\{ {r_i}\left( {\boldsymbol{\beta}} \right) = {y_i} - {\boldsymbol{x}}_i^{\text{T}}{\boldsymbol{\beta}} $, $\left. {i = 1, \cdots , n} \right\}$的经验累积分布函数, 即$ \hat{F}\left(u;{\boldsymbol{\beta}} \right)= \left(1/n\right){\displaystyle\sum }_{i=1}^{n}I\left\{{r}_{i}\left({\boldsymbol{\beta}} \right)\leqslant u\right\} $, 其中$u \in \mathbb{R}$. 因此, 方程(1)中的经验分位数损失可表示为:

$ \hat Q\left( {\boldsymbol{\beta}} \right) = \int_{ - \infty }^\infty {{\rho _\tau }(u)} {\text{d}}\hat F\left( {u;{\boldsymbol{\beta}} } \right) $

使用核累积分布函数估计量替代不连续的$ \hat F\left( {u;{\boldsymbol{\beta}} } \right) $, 可得平滑分位数损失函数:

$ \begin{split} {{\hat Q}_h}\left( {\boldsymbol{\beta}} \right) = & \mathop \int \nolimits_{ - \infty }^\infty {\rho _\tau }\left( u \right){\text{d}}{{\hat F}_h}\left( {u;{\boldsymbol{\beta}} } \right) \\ =& \frac{1}{{nh}}\mathop \sum \limits_{i = 1}^n \mathop \int \nolimits_{ - \infty }^\infty {\rho _\tau }\left( u \right)K\left( {\frac{{u + {\boldsymbol{x}}_i^{\text{T}}{\boldsymbol{\beta}} - {y_i}}}{h}} \right){\text{d}}u \end{split} $

其中, $K$是一个对称非负且积分为1的核函数. 由此得到的平滑经验分位数损失函数$ {\hat Q_h}\left( {\boldsymbol{\beta}} \right) $具有二阶连续可导性, 并且在真实系数向量的锥形局部邻域内高概率下具有强凸性.

然后, 基于一步局部线性逼近算法 (local linear approximation, LLA)^[20], 提出下面的多步迭代正则化方法. 首先初始化${\hat {\boldsymbol{\beta}} ^{(0)}}$, 然后通过求解式(2)可以依次得到迭代值${\hat {\boldsymbol{\beta}} ^{(l)}} = {\left( {\hat {{\beta}} _1^{(l)}, \cdots , \hat {{\beta}} _p^{(l)}} \right)^{\text{T}}}, l = 1, 2, \cdots $

$ \min _{\boldsymbol{\beta} \in \mathbb{R}^p}\left\{\hat{Q}_h(\boldsymbol{\beta})+\sum_{j=1}^p q'_\mu\left(\left|\hat{\beta}_j^{(l-1)}\right|\right)\left|\beta_j\right|\right\} $

(2)

其中, $q'_\mu( \cdot )$是${q_\mu }( \cdot )$的一阶导数. 惩罚函数${q_\mu }( \cdot )$若有精确的导数表达式, 将对产生稀疏解起到重要作用. 因此, 需要对惩罚函数的性能提出一些特定要求. 其中满足需求的惩罚函数包括: Lasso 惩罚, SCAD 惩罚, MCP惩罚等. 如果使用这些惩罚函数, 并初始化${\hat {\boldsymbol{\beta}} ^{(0)}} = 0$, 则有$q'_\mu\left( {\left| {\hat \beta _j^{(0)}} \right|} \right) = q'_\mu(0) = \mu $, $j = 1, \cdots , p$. 因此, 第1步迭代实际为计算一个${L_1}$惩罚平滑分位数回归估计量. 注意到, 在后续迭代中, 问题(2)均可表示为加权${L_1}$惩罚平滑分位数回归:

$ \min _{{\boldsymbol{\beta}} \in \mathbb{R}^p}\left\{\hat{Q}_h(\boldsymbol{\beta})+\|{\boldsymbol{\lambda}} \circ \boldsymbol{\beta}\|_1\right\} $

(3)

其中, ${\boldsymbol{\lambda}} = {\left( {{\lambda _1}, \cdots , {\lambda _p}} \right)^{\text{T}}} \in {\mathbb{R}^p}$, ${\lambda _j} \geqslant 0, j = 1, \cdots , p$, $ \circ $表示 Hadamard 内积. 在算法1中总结了上述迭代重加权的${L_1}$惩罚算法.

算法1. 迭代重加权$\scriptstyle {L_1}$惩罚平滑分位数回归算法

1) 输入: 数据$\scriptstyle \left\{ {({y_i}, {{\boldsymbol{x}}_i})} \right\}_{i = 1}^n$ , 分位数$\scriptstyle \tau \in (0, 1)$, 平滑参数$\scriptstyle h > 0$;

2) 初始化$\scriptstyle {\hat {\boldsymbol{\beta}} ^{(0)}} \in {\mathbb{R}^p}$;

3) For $\scriptstyle l = 1, 2, \cdots $:

4) 　令$\scriptstyle \lambda _j^{(l - 1)} = q'_\lambda\left( {\left| {\hat \beta _j^{(l - 1)}} \right|} \right), j = 1, \cdots , p$.

5) 　计算

$\scriptsize \hat{\boldsymbol{\beta}}^{(l)} \in \underset{\boldsymbol{\beta} \in \mathbb{R}^p}{\operatorname{argmin}}\left\{\hat{Q}_h(\boldsymbol{\beta})+\left\|{\boldsymbol{\lambda}}^{(l-1)}\circ \boldsymbol{\beta}\right\|_1\right\} $

(4)

6) 直到收敛;

7) 输出: $\scriptstyle {\hat {\boldsymbol{\beta}} ^{(l)}}$.

注意到, 算法1的关键是解决凸问题(4). 具体地, 对于使用高斯核平滑得到平滑分位数回归问题, 在算法1的框架下结合交替方向乘子法算法进行求解. 引入残差向量${\boldsymbol{r}} = {\boldsymbol{Y}} - {\boldsymbol{X}}{\boldsymbol{\beta}} $, 其中${\boldsymbol{r}} = {\left( {{r_1}, \cdots , {r_n}} \right)^{\text{T}}}$, ${\boldsymbol{Y}} = (y_1, \cdots , y_n) $, ${\boldsymbol{X}}=({\boldsymbol{x}}_1,\cdots,{\boldsymbol{x}}_n) $. 因此, 算法1中的问题(4)等价于以下形式:

$\left\{\begin{split} & \mathop {{\text{min}}}\limits_{{\boldsymbol{\beta}} \in {\mathbb{R}^p}, {\boldsymbol{r}} \in {\mathbb{R}^n}} \left\{ {{{\hat Q}_h}\left( {\boldsymbol{r}} \right) + {{\left\| {{{\boldsymbol{\lambda}} ^{\left( {l - 1} \right)}} \circ {\boldsymbol{\beta}} } \right\|}_1}} \right\} \\ & {\text{s.t. }}\;{\boldsymbol{r}} = {\boldsymbol{Y}} - {\boldsymbol{X}}{\boldsymbol{\beta}} \end{split} \right.$

(5)

给定$\rho > 0$, 方程(5)的增广拉格朗日形式为:

$ \begin{split} {L_\rho }\left( {{\boldsymbol{\beta}} , {\boldsymbol{r}}, {\boldsymbol{\eta}} } \right) = &{{\hat Q}_h}\left( {\boldsymbol{r}} \right) + {\left\| {{{\boldsymbol{\lambda}} ^{\left( {l - 1} \right)}} \circ {\boldsymbol{\beta}} } \right\|_1} + \left\langle {{\boldsymbol{\eta}} , {\boldsymbol{r}} - {\boldsymbol{Y}} + {\boldsymbol{X}}{\boldsymbol{\beta}} } \right\rangle \\ & + \frac{\rho }{2}\left\| {{\boldsymbol{r}} - {\boldsymbol{Y}} + {\boldsymbol{X}}{\boldsymbol{\beta}} } \right\|_2^2 \end{split} $

其中, ${\boldsymbol{\eta}} $是拉格朗日乘子. 每一步只更新一个变量并固定另外两个变量, 如此交替重复更新, 即可得到ADMM算法的迭代过程. 具体步骤如算法2所示.

算法2. 用于求解高斯核平滑问题(4)的ADMM算法

1) 输入: 分位点$\scriptstyle \tau $, 平滑参数$\scriptstyle h$, 正则化参数$\scriptstyle {{\boldsymbol{\lambda}} ^{\left( {l - 1} \right)}}$, 以及收敛标准$\scriptstyle \varepsilon $;

2) 初始化变量$\scriptstyle {\hat {\boldsymbol{\beta}} ^{(0)}} = 0, {\hat {\boldsymbol{r}}^{(0)}} = 0, {\hat {\boldsymbol{\eta}} ^{(0)}} = 0 $;

3) while $\scriptstyle {\left\| {{{\hat {\boldsymbol{\beta}} }^{(t)}} - {{\hat {\boldsymbol{\beta}} }^{(t - 1)}}} \right\|_2} > \varepsilon $ do:

4) 　更新$\scriptstyle {\boldsymbol{\beta}} $为:

$ \scriptsize\begin{array}{l}{\hat{{\boldsymbol{\beta}} }}^{(t)}=\underset{{\boldsymbol{\beta}} \in {\mathbb{R}}^{p}}{\text{argmin}}\left\{\dfrac{\rho }{2}{\Vert {\boldsymbol{Y}}-{\hat{{\boldsymbol{r}}}}^{(t-1)}-\dfrac{1}{\sqrt{\rho }}{\hat{{\boldsymbol{\eta}} }}^{(t-1)}-{\boldsymbol{X\beta}} \Vert }_{2}^{2} +{\Vert {\lambda }^{(l-1)}\circ {\boldsymbol{\beta}} \Vert }_{1}\right\};\end{array} $

5) 　迭代以下步骤, 直到收敛: 对于每个$\scriptstyle i = 1, \cdots , n$, 通过求解以下方程更新$\scriptstyle {r_i}$:

$ \scriptsize　\begin{split} \tau - {{\Phi }}\left( {\frac{{ - {r_i}}}{h}} \right) + \hat \eta _i^{\left( {t - 1} \right)} + \rho \left( {{r_i} - {y_i} + \left\langle {{{\boldsymbol{x}}_i}, {{\hat {\boldsymbol{\beta}} }^{\left( t \right)}}} \right\rangle } \right) = 0 \end{split} $

其中, $\scriptstyle {{\Phi }}\left( \cdot \right)$为标准正态分布的累积分布函数;

6) 　更新$\scriptstyle {\boldsymbol{\eta}} $为:

$\scriptsize\begin{split} {\hat {\boldsymbol{\eta}} ^{\left( t \right)}} = {\hat {\boldsymbol{\eta}} ^{\left( {t - 1} \right)}} + \rho \left( {{{\hat {\boldsymbol{r}}}^{\left( t \right)}} - {\boldsymbol{Y}} + {\boldsymbol{X}}{{\hat {\boldsymbol{\beta}}}^{\left( t \right)}}} \right) ; \end{split} $

7) end while;

8) 输出: 估计参数$ \scriptstyle {\hat {\boldsymbol{\beta}} ^{(t)}} $.

1.4 统计方法

对于认知得分MMSE和ADAQS4, 我们依次使用Lasso正则化分位数回归方法, 建立以认知得分为响应变量, 以其余ADNI数据为解释变量的稀疏分位数回归模型. 使用迭代重加权${L_1}$惩罚平滑分位数回归算法进行求解, 以寻找在不同分位点下与该认知得分有关的ROI, 其中$\tau $有{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9}. 我们将在表格中总结在不同分位点下与认知得分显著相关($p < 0.05$)的ROI. 为了更加清晰地展现在不同分位点下与认知能力相关的ROI的显著性情况, 我们将使用具体的ROI热图进行展示. ROI热图通过R包ggseg实现, 由于现有的地图集不能完全匹配本文研究数据的ROI划分结构, 因此结合两个地图集来展示ROI显著性热图情况, 包括aseg地图集^[21]和aicha地图集^[22].

2 实验结果 2.1 数据描述 2.1.1 ADNI数据的人口统计学数据描述

对ADNI数据库中下载的数据进行如第1.1节所述的数据预处理步骤, 得到249名CN患者和29名SMC患者的数据, 该数据的变量包括134个ROI体积数据、5个主成分变量、8个临床变量以及2个不同的认知得分. 描述性统计见表1, 可以看出CN和SMC两组整体上没有显著差异.

2.1.2 ROI体积数据描述

为了进一步了解ROI体积数据的分布特征, 我们对其进行峰度分析. 峰度是衡量数据分布形态的统计指标, 反映数据分布相对于正态分布是重尾还是轻尾, 峰度较高的数据集往往具有重尾或异常值.

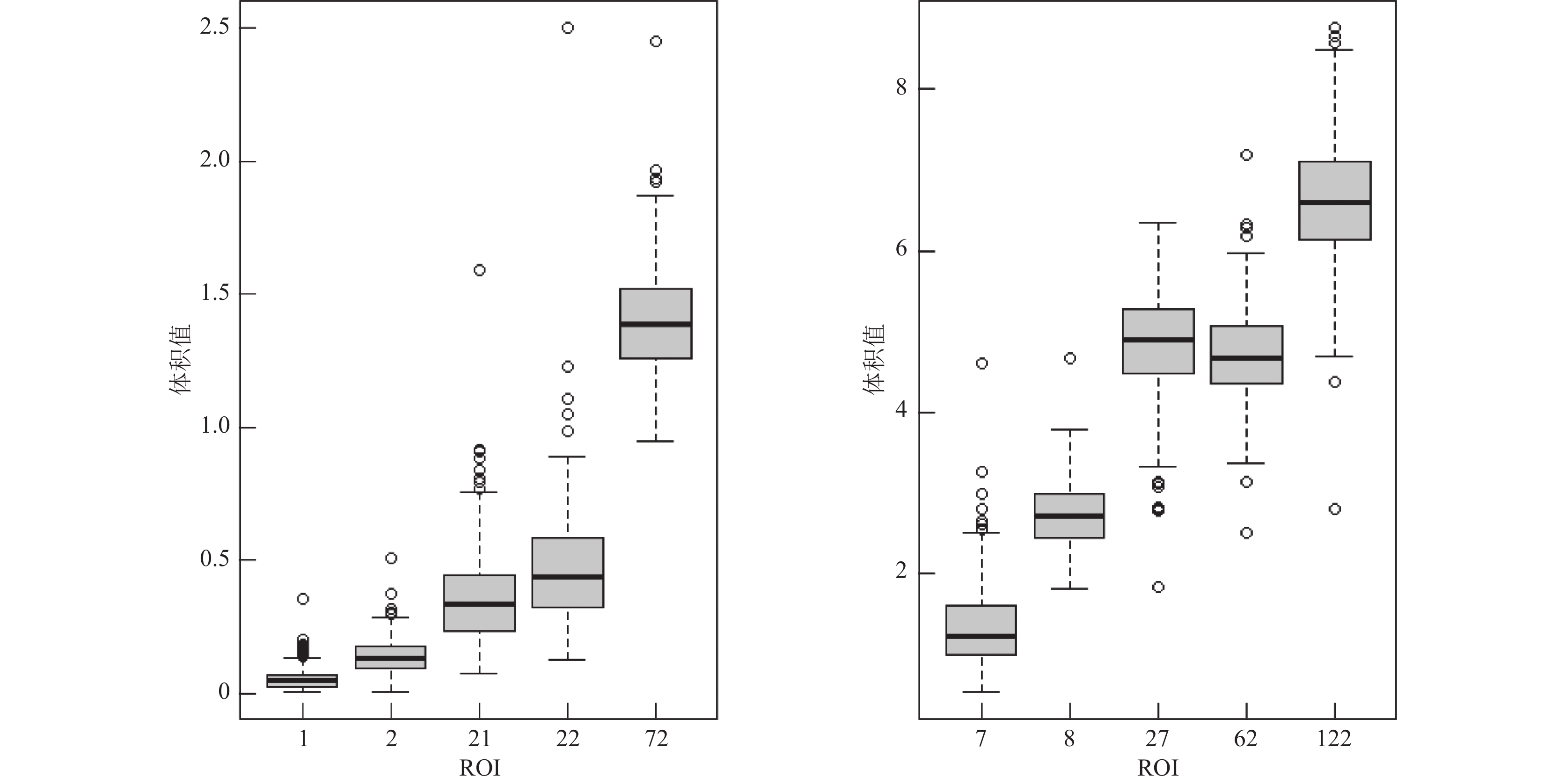
依次计算134个ROI体积数据的峰度, 观察到有70个ROI体积数据的峰度值超过0, 由此推断数据存在一定程度的重尾情况. 对峰度前10的ROI体积数据使用箱线图进行展示, 根据ROI体积数据的值域分为两个坐标系进行画图, 如图1所示. 其中峰度前10的ROI对应的脑部区域 (序号)为: 第三脑室(X3rd ventricle) (1)、第四脑室 (X4th ventricle) (2)、脑干 (brain stem) (7)、右尾状核 (right caudate) (8)、右脑室 (right lateral ventricle) (21)、左脑室 (left lateral ventricle) (22)、右丘脑 (right thalamus proper) (27)、左枕下回 (left inferior occipital gyrus) (62)、左内侧额叶皮层 (left medial frontal cortex) (72)、左边缘上回 (left supramarginal gyrus) (122). 通过图1可知, 这些具有重尾现象的数据也伴随着较多的异常值.

因此, 结合数据的高维性以及具有重尾和异常值的特点, 我们选择稀疏分位数回归方法进行数据分析.

2.2 实验结果 2.2.1 认知得分一: MMSE

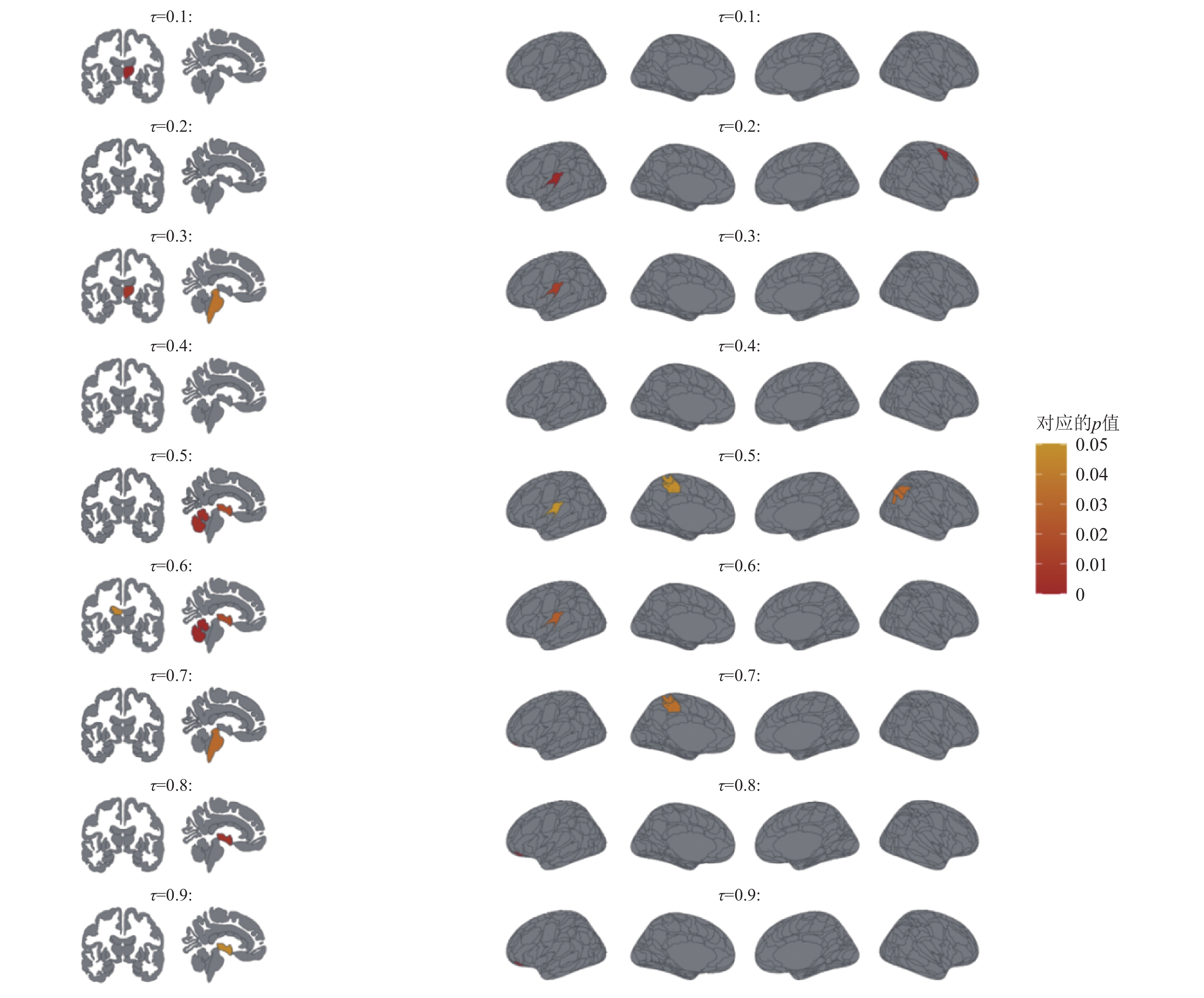
我们在表2中展示在不同分位点下与认知得分MMSE显著相关的ROI; 并且在图2中以热图的形式进一步展示在不同分位点下与认知得分MMSE相关的ROI的显著性情况.

通过表2, 我们观察到在临床变量中, 年龄(AGE)和受教育年限(PTEDUCAT)与老年人的认知情况密切相关. 针对认知得分MMSE的整体条件分布情况, 稀疏分位数回归方法共挑选出了如下显著的ROI: 第三脑室 (X3rd ventricle)、脑干 (brain stem)、左下侧脑室 (left inf lat vent)、右丘脑 (right thalamus proper)、小脑蚓部第六和第七小叶 (cerebellar vermal lobules VI VII)、右角回 (right angular gyrus)、右额极 (right frontal pole)、右内侧眶回 (right medial orbital gyrus)、中央前回中部 (right percentral gyrus medial segment)、左后扣带回 (left posterior cingulate gyrus)、左后脑岛 (left posterior insula)和左后眶回 (left posterior orbital gyrus). 其中脑干、右丘脑、右额极、中央前回中部、左后脑岛与较低的认知得分相关, 因此可视为与认知能力下降症状有关的生物标志物. 着重关注这些ROI的变化, 有助于阿尔茨海默病的早期诊断工作. 如图2所示, 左半图为aseg地图集, 右半图为aicha地图集. 我们发现在低分位点区, 右丘脑、中央前回中部和左后脑岛显著性较强; 在高分位点区, 小脑蚓部第六和第七小叶、右内侧眶回及左后眶回显著性较强.

对于上述所选的大多数ROI, 已有文献证实其与认知能力或AD的相关性. 其中, 第三脑室是一个狭窄的漏斗状脑腔, 位于前脑间脑两个半球之间的中线^[23]. 有研究表明, 第三脑室的宽度可作为脑萎缩的标志, 用于判断认知能力是否正常^[24], 并且第三脑室被发现是与AD有关的区域^[25]. 脑干是连接大脑与脊髓和小脑的结构, 负责生命的许多重要功能, 如呼吸、意识、血压、心率和睡眠^[26]. 在与AD相关的研究中发现, 脑干上的蓝斑完整性与记忆力和思维能力的衰退有关, 可作为AD潜在的早期指标^[27]. 下侧脑室的扩大与AD的进展密切相关^[28]; 相比于AD中最萎缩的结构都是海马体, AD患者最扩大的结构是下侧脑室^[5], 是用于分类NC、MCI和AD的主要预测因子之一^[28]. 丘脑是感觉的高级中枢, 是最重要的感觉传导接替站. 研究表明, 丘脑与轻度行为障碍相关^[29]; 并且丘脑的局部体积萎缩可以作为转化为痴呆的重要预测指标^[4]. 小脑蚓部第六和第七小叶与社会功能^[30]、注意力导向缺陷^[31]及自闭症谱系障碍(autism spectrum disorder)^[32]有关. 角回位于下顶叶后部, 与语言^[33]、数字处理^[34]、空间认知^[35]、记忆检索^[36]、注意力^[37]和心理理论^[38]有关, 并且研究表明角回与AD患者的精神神经症状密切相关^[39]. 额极是前额叶皮层的额叶部分, 是一个高度分化的皮质区域^[40], 在许多认知任务中起着关键作用, 包括情感处理、社会认知、情景记忆和工作记忆等^[41], 此外, 有研究发现额极与AD的无抑制行为有关^[42]. 眶回是大脑额叶底部的脑回, 被H型的眶沟分隔为4个部分, 按照位置分别为前眶回、后眶回、内侧眶回和外侧眶回, 其中的内侧眶回参与社会理解和情景记忆功能^[43], 并与智力和注意力密切相关^[44]. 扣带回位于大脑半球内侧面的扣带沟与胼胝体沟之间的脑回^[45], 由前扣带回、中扣带回和后扣带回3个部分组成. 其中的后扣带回是AD发病早期受累的皮质回^[46], 其皮质厚度减少是AD病理学的特征^[47], 与患者的时间和地点定向障碍症状有关^[48]. 脑岛位于西尔维亚裂缝的深处, 在支持人类认知和行为的多个关键功能方面发挥着作用^[49]; 脑岛分为前脑岛和后脑岛. 前脑岛与参与认知控制和情感过程的额叶、前扣带回和顶叶区域相连, 而后脑岛与参与感觉运动过程的颞带和后扣带回区域相连^[50]. 有研究发现, 轻度认知障碍前期的患者显示出右侧后岛脑体积显著减小^[51].

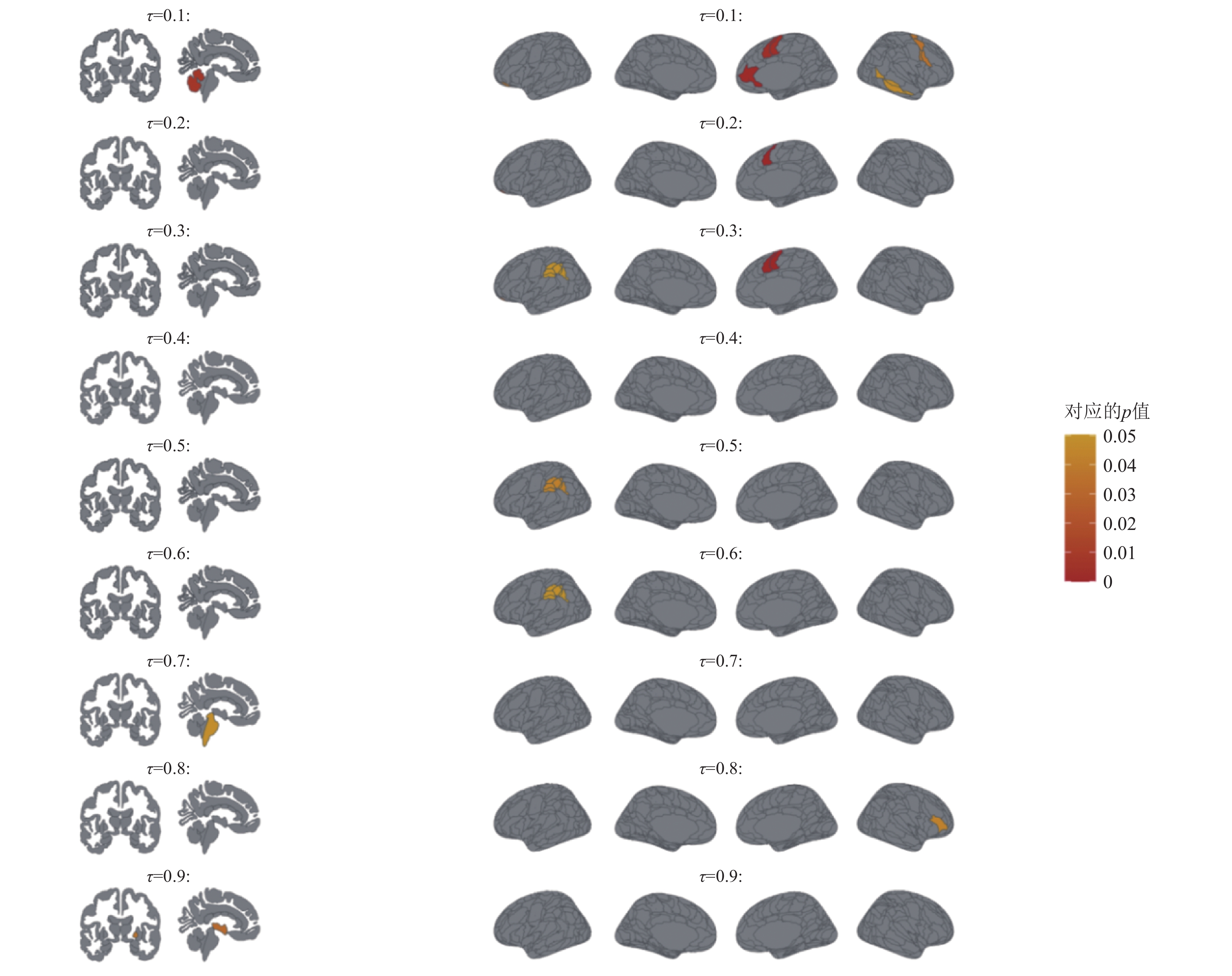
2.2.2 认知得分二: ADASQ4

我们在表3中展示在不同分位点下与认知得分ADASQ4显著相关的ROI; 并且在图3中以热图的形式(左半图为aseg地图集, 右半图为aicha地图集), 进一步展示在不同分位点下与记忆得分ADASQ4相关的ROI的显著性情况.

通过表3, 我们观察到在临床变量中, 年龄(AGE)与记忆能力密切相关. 针对记忆力认知得分ADASQ4的整个条件分布情况, 稀疏分位数回归方法共选出了如下显著相关的ROI: 第三脑室、脑干、左小脑外部 (left cerebellum exterior)、苍白球 (pallidum)、右基底前脑 (right basal forebrain)、右前眶回 (right anterior orbital gyrus)、右中扣带回 (right middle cingulate gyrus)、左内侧眶回(left medial orbital gyrus)、右颞中回 (right medial temporal gyrus)、左顶叶顶盖 (left parietal operculum)、右中央前回 (right percentral gyrus)、左上缘回 (left supramarginal gyrus)和右额下回三角区 (right triangular part of the inferior frontal gyrus). 其中第三脑室、脑干、苍白球、左上缘回和右额下回三角区与较差的记忆力相关. 因此, 在针对记忆力下降的相关研究中, 可以关注这些ROI的变化. 通过图3, 我们发现相比于高分位点区的ROI, 低分位点区的ROI的显著性更强, 其中右颞中回显著性最强.

上述所选与记忆力相关的ROI, 其中第三脑室、脑干和内侧眶回, 已通过第2.2.1节了解其与认知能力的关联, 由此可进一步说明它们在认知能力中的重要性. 除了上述的3个ROI, 其余多数ROI已有文献证实与记忆能力或AD相关. 其中, 基底前脑是指一系列延生的亚皮层核团, 其投射到对认知相关的脑区^[52], 对学习和记忆^[53,54]至关重要, 参与注意力处理过程^[52]. 研究表明, 基底前脑的病理学可能发生在AD的早期阶段^[55], 可以作为记忆力下降的早期指标^[53]. 前眶回是位于大脑额叶底部的眶回的组成部分之一. 在与AD的相关研究中发现, 前眶回与AD的发病年龄呈显著相关^[56], 也是用于预测二型糖尿病患者是否有潜在MCI的脑区之一^[57]. 中扣带回是扣带回的组成部分之一, 在认知能力和决策上起到关键作用^[58], 是AD焦虑的脑部病变区域之一^[59], 并且与AD患者的冷漠症状有关^[60]. 颞中回是大脑颞叶上的一个回, 涉及观察运动^[61]、识别面部表情^[62]、语言语义处理等功能. 其中语言处理方面包括语义记忆^[63]、词汇理解和语言认知^[64]等不同过程. 顶叶顶盖包含次级躯体感觉皮层, 与物体几何形状的触觉记忆有关^[65], 也是用于预测MCI到AD转化的重要脑区之一^[66]. 上缘回是短时记忆网络的关键节点之一^[67], 并且在语言网络中参与词语工作记忆任务^[68]. 上缘回与AD患者的记忆表现相关^[69], 并对MCI具有鉴别诊断价值^[70]. 额下回三角区与语言的语义处理有关^[71], 并被证实在记忆的认知控制中发挥作用^[72]. 研究发现该区域是健康者与MCI患者最显著的差异位置之一^[73], 其激活水平与AD患者在执行语言任务时沉默持续时间有关^[74].

2.2.3 小结

上述结果表明, 稀疏分位数回归方法所识别的ROI大多与先前发现的大脑认知功能一致, 显示了该方法在寻找相关ROI方面的有效性. 除此之外, 我们还观察到一些新的与认知情况相关的ROI, 如与认知能力相关的后眶回以及与记忆力相关的小脑外部、苍白球、中央前回区域. 这些是新发现的相关ROI, 目前尚无文献显示它们与认知情况之间的具体关联. 这进一步表明该方法有助于揭示以往尚未被发现的ROI与认知表现之间的关系, 为阿尔茨海默病的研究领域提供了新的信息和方向.

3 结论与展望

在全球老龄化的背景下, 阿尔茨海默病已成为重要的公共卫生挑战之一. 然而, 目前的治疗方案无法彻底治愈该病, 只能部分缓解症状和延缓疾病进展. 因此, 早期诊断和干预被视为是降低阿尔茨海默病危害的关键措施. 对于提高患者治疗效果、减轻家庭负担、合理利用医疗资源以及推进科学研究具有重要意义. 鉴于阿尔茨海默病最主要的病症为认知能力的下降, 本文通过稀疏分位数方法寻找与认知能力相关的ROI, 为该病的早期诊断提供了重要的“先验”信息.

稀疏分位数回归方法在不同分位点下建立模型并实现特征选择, 可以更全面地提供认知能力与神经影像数据之间的信息, 筛选出更多相关ROI. 这些筛选出的ROI大部分已在文献中得到证实与认知能力或阿尔茨海默病关系密切, 显示了该方法在发现相关ROI方面的有效性. 此外, 我们还发现了一些新的与认知能力相关的ROI, 丰富了对这些ROI已有的功能的了解, 填补了当前文献中的知识空白. 这些新发现可能意味着在阿尔茨海默病领域内还有尚未被深入研究的ROI, 为进一步探索这些区域提供了可行性, 也为未来的疾病诊断、预防和治疗提供了新的方向.

然而, 本文的研究仍存在一些不足. 例如, 由于技术水平有限, 无法对这些新发现的与认知能力相关的ROI进行深入研究, 以进一步证实它们与认知能力的相关性. 此外, 本研究仅使用了基线数据进行分析. 若能充分利用纵向数据, 可以获得更多信息, 进而深化对阿尔茨海默病认知功能变化的理解. 这些不足可能导致模型遗漏或错误地理解重要信息. 因此, 在未来的研究中, 可以扩展稀疏分位数回归在纵向数据中的应用, 提高模型的变量选择能力, 并深入探索认知功能与ROI之间的动态关系.