近年来, 鉴于保障电力系统的可靠性、电网的安全运行以及降低运营成本等多重需求^[1], 电力系统运营商对短期负荷预测的稳定性、准确性和效率提出了更为严格的标准. 在这一背景下, 短期电力负荷预测显得尤为关键. 电力负荷预测按照时间跨度的不同, 可以细分为超短期、短期、中期以及长期负荷预测. 其中, 短期负荷预测专注于对接下来几小时至数天内的电力需求进行预测, 以便电力系统运营商能够有效地规划发电资源、调度能源分配和管理负荷需求.

随着计算机技术的广泛应用, 智能电网迅速发展, 在电网规划和运行中, 准确的负荷预测变得至关重要. 因此, 理解数据的内在特征和提高预测精度成为一项重要且有意义的任务. 多年来, 国内外学者们提出了不同的方法进行预测, 它们大致可以分为3类: (1)传统预测方法; (2)机器学习方法; (3)深度学习方法. 传统的预测方法有回归分析^[2]、ARIMA^[3,4]、季节指数平滑^[5]、卡尔曼滤波^[6]等, 上面提出的传统方法都是基于统计学实现的, 在简单的预测模型、数据样本和高计算效率方面具有一定的优势^[7,8]. 然而, 这些方法对非线性、复杂的数据样本并不有效. 随着人工智能网络模型在许多领域取得的重大进展, 出现了机器学习算法, 如循环神经网络(recurrent neural network, RNN)^[9], 长短期记忆(long short term memory, LSTM)^[10]和门控循环单元(gated recurrent unit, GRU)^[11]等, 这些技术已经在短期负荷预测中取得了良好的效果. 然而, 当单一预测模型遇到长序列、多维输入的电力负荷预测问题时, 会出现序列记忆丢失、数据结构混乱和无法深入挖掘序列潜在特征等问题, 从而影响负荷预测的准确性. 朱江行等人^[12]将Prophet和XGBoost结合的一种对电力负荷预测的模型. Khan等人^[13]和孟磊等人^[14]使用CNN提取特征向量, 把处理之后的特征向量一同送入LSTM中进行预测. Li等人^[15]将CNN提取构造的特征向量送入门控递归单元(GRU)进行预测, 两种模型都获得了高精度的预测值. Javed等人^[16]提出了一种基于特征提取的CNN-BiLSTM组合预测模型, 充分利用电力负荷数据的时间特性, 解决了梯度消失问题, 加快了训练速度, 有效地分析和处理了电力负荷数据的潜在信息. Mounir等人^[17]使用EMD算法分解原始电力负荷数据, 为了预测每个本征模态函数, 采用了混合模型BiLSTM, 最终叠加各子序列的预测结果来进行电力负荷预测. Sideratos等人^[18]采用EEMD分解的方法对负荷数据进行分解, 对每一个时间序列的分量建立起各种Elman递归神经网络模型, 然而在实际的预测过程中, 调整模型参数的过程比较复杂. 因此, 为了提高短期电力负荷预测的精度, 本文提出了一种自适应噪声完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)、堆叠双向门控循环单元(stacked bidirectional gated recurrent unit, SBiGRU)和优化的多头注意力机制(optimized multi-head attention, OMHA)的组合模型. 该预测模型是在EEMD分解的过程中, 通过加入自适应白噪声得到CEEMDAN算法, 使其作为误差序列的分解算法, 获得内在模态函数(IMF)分量和唯一的残差信号, 它可以在少量的实验中重构错误序列, 从而提高了序列分解的效率. 使用降噪自编码器DAE (denoising autoencoder)有效地学习潜在特征序列, 将获取的影响特征因子与IMF分量合成一个新的矩阵, 从而整合了CEEMDAN和DAE的信息. 新的矩阵将作为SBiGRU的输入, 使SBiGRU同时考虑来自前向和后向序列的信息, 以学习时间序列中的复杂关系, 可以有效地处理时间序列数据, 提高了模型的综合性能. 引入多头注意力机制模块, 可以为SBiGRU的隐藏状态分配不同的权重, 从而增强了不同信息对负荷需求的影响. 根据实验的结果数据可以进一步得出: CEEMDAN-SBiGRU-OMHA的组合模型在预测精度方面表现更出色.

1 模型概述 1.1 完备集合经验模态分解

Huang等人^[19]在1998年提出经验模态分解(EMD). 该方法更适用于增强复杂波动信号的平滑性, 将非平滑信号根据波动划分为IMF. 每个IMF都遵循以下模式.

1) 极值点个数i和零点个数v必须满足i=v或i–v=|1|;

2) 极大值的上包络线和极小值的下包络线序列均值之和为0.

为了解决EMD模态混叠的发生, EEMD主要在原始序列中多次添加不同的高斯白噪声, 进行对信号极值点分布的改变, 然而, EEMD方法增加的白噪音会产生冗余, 会对后面工作出现一些误差. 为了解决EMD和EEMD的问题, 完备集合经验模态分解算法在每个分解阶段添加自适应白噪声, 得到IMF分量以及唯一的残差信号, 可以克服EMD中存在的模态混叠现象, 解决了计算效率低和因增加平均次数, 减少重构误差而导致EEMD分解不完全的问题.

记$ s\left( n \right) $为原始电力负荷数据时间序列, $ {v^i}(n) $为第i次实验中添加的高斯白噪声序列, 第i次分解负荷数据时间序列可表示为$ {s^i}(n) = s(n) + {v^i}(n) $. 假设EMD和CEEMDAN产生的第$ k $个模态分量分别表示为$ {E_k}\left( \cdot \right) $和$ {\mathit{IMF}_k} $. CEEMDAN算法实现的具体步骤如下.

步骤1: 通过EMD分解得到第1个IMF分量, 计算CEEMDAN分解得到唯一的残差信号$ {r_1}\left( n \right) $, 如式(1)、式(2)所示:

$ {\mathit{IMF}_1}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {\mathit{IMF}_1^i} \left( n \right) $

(1)

$ {r_1}\left( n \right) = s(n) - {\mathit{IMF}_1}(n) $

(2)

步骤2: 继续获取第2个IMF分量, 如式(3)所示:

$ {\mathit{IMF}_2}(n) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}({r_1}(n))} + {\varepsilon _1}{E_1}({v^i}(n)) $

(3)

步骤3: 重复上述步骤, 计算第$ n $个残差信号, 如式(4)所示:

$ {r_k}(n) = {r_{k - 1}}(n) - {\mathit{IMF}_k}(n) $

(4)

则$ n + 1 $个IMF分量如式(5)所示:

$ {\mathit{IMF}_{k + 1}}(n) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}({r_k}(n)) + {\varepsilon _k}} {E_k}({v^i}(n)) $

(5)

重复上述步骤, 等余量信号呈单调的趋势之后, 就停止分解原始信号$ s\left( n \right) $, 如式(6)所示:

$ s(n) = R(n) + \sum\limits_{k = 1}^K {{\mathit{IMF}_k}} $

(6)

其中, $ K $为最终模态分量的数目, $ R\left( n \right) $为最终单调残差信号.

1.2 降噪自编码器DAE

DAE是一种基于自动编码器(autoencoder, AE)优化的模型, 在逼近多变量非线性和防止过拟合问题方面具有良好的性能. 自动编码器如图1所示.

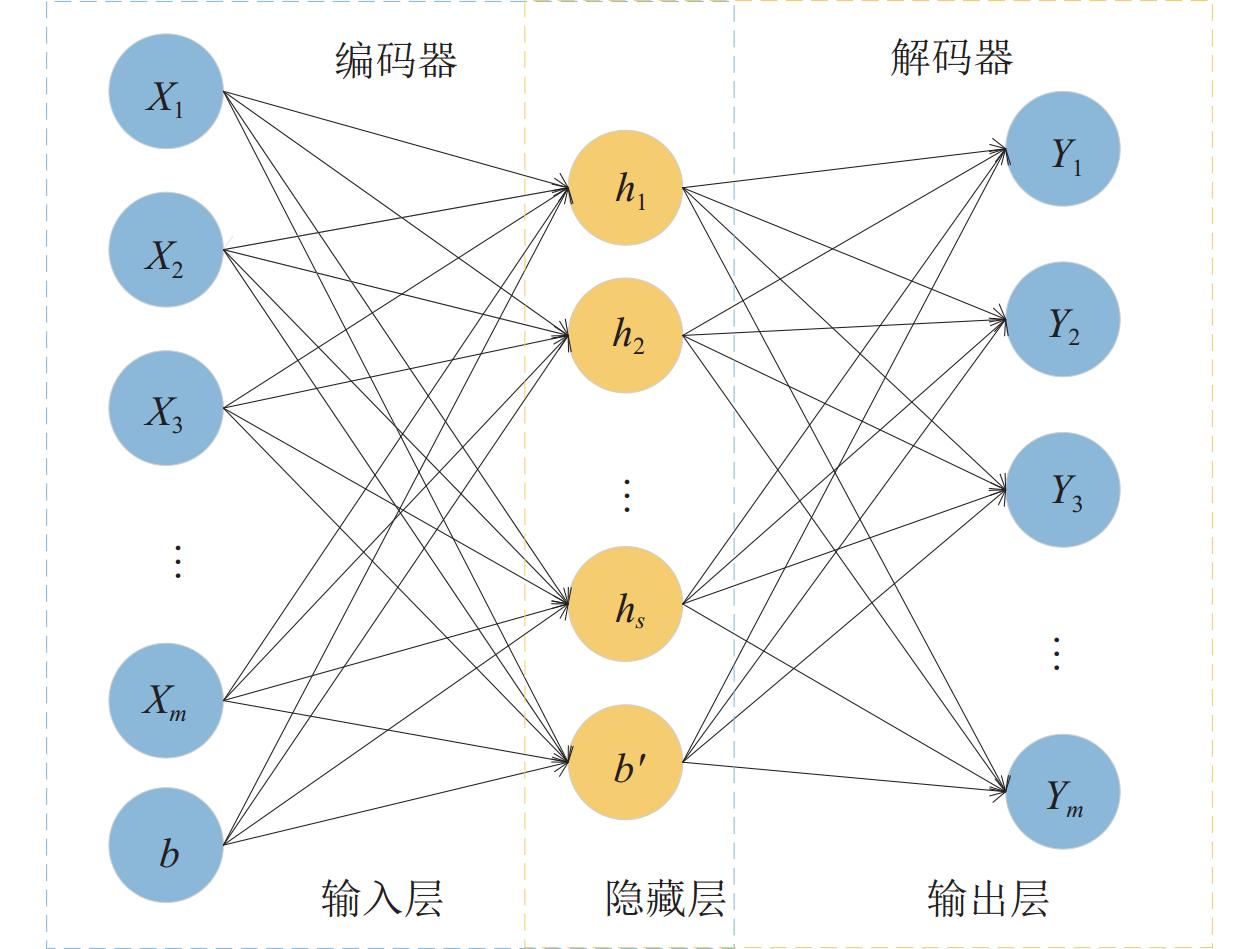
AE是一种无监督学习算法, 也是对传统神经网络算法的改进, 能够自动提取小样本和未标记的特征, 因此该网络可以更好地提高特征提取的运行速度. 它在结构上由3层定义: 输入层、隐藏层和输出层. 虽然输入层和输出层中的节点数保持恒定, 但构成隐藏层、输入层和输出层的节点数可以根据需要而改变.

将原始数据作为输入$ X $, 经过编码器之后, 将输入$ X $映射到隐藏层输出$ Y $, 如式(7)所示:

$ y = {f_\theta }(X) = S(wX + b) $

(7)

其中, $ S $是$ \mathit{Sigmoid} $函数, $ w $是编码器权值矩阵, $ b $是隐藏层的输入偏置向量.

经过编码得到的输出$ Y $, 再输入解码器后得到重构后的数据, 如式(8)所示:

$ Z = {g_\theta }(Y) = S(w'Y + b') $

(8)

其中, $ w' $是解码器权值矩阵, $ b' $是输出层的输入偏置向量.

为了最优化提取数据的有效特征序列, 则重建的损失函数如式(9)所示:

$ L(X, Z) = {\left\| {X - Z} \right\|^2} $

(9)

将通过最小化平均重建误差以获得稳定的, 最优的参数, 如式(10)所示:

$ {\min _\theta }{J_{\rm DAE}}\left( \theta \right) = {\min _\theta }\sum\limits_{i = 1}^n {L\left( {{X_i}, {Z_i}} \right)} = {\min _\theta }\sum\limits_{i = 1}^n {L\left( {{X_i}, {g_\theta }\left( {{f_\theta }\left( {{X_i}} \right)} \right)} \right)} $

(10)

其中, $ \theta $为调节参数, $ {X_i} $和$ {Z_i} $分别是第i次输入样本和输出样本数据, $ n $为输入样本的数量.

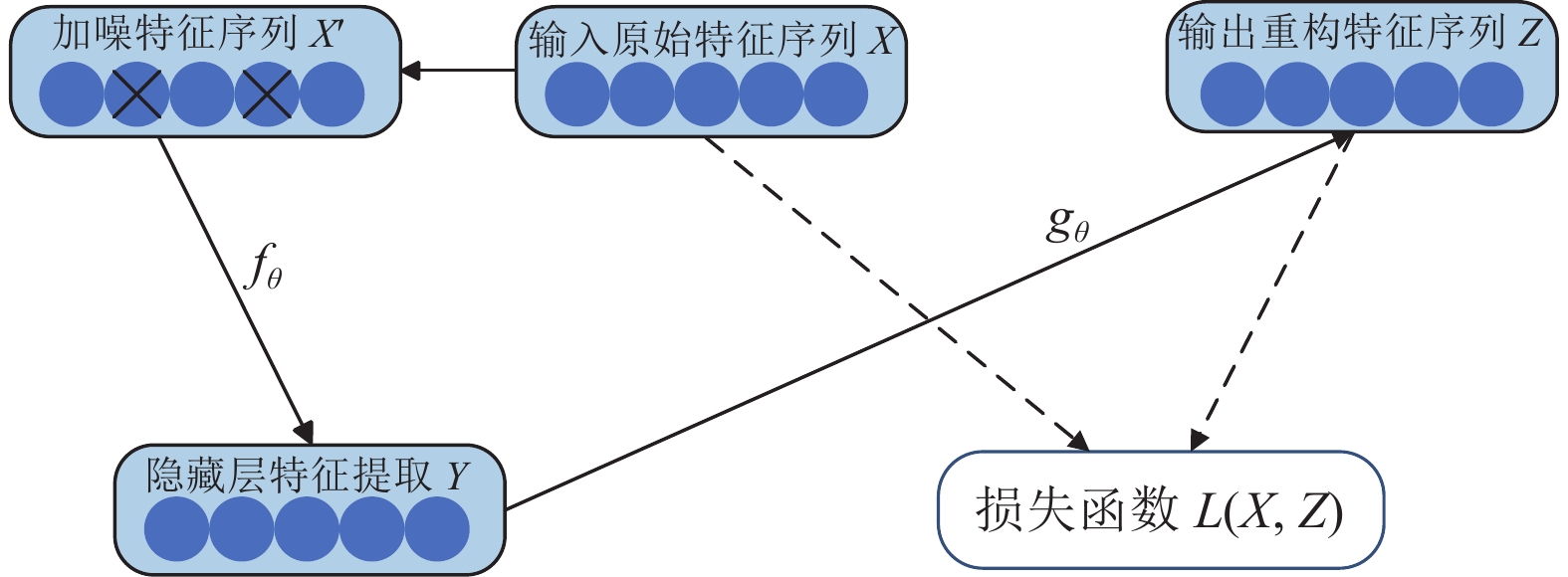
DAE是在自编码器AE的基础上引入了一个加噪操作, 迫使编码器去学习输入信号, 使之更加具有鲁棒性. 这个加噪操作在输入层和隐藏层之间发挥作用, 它的引入使得编码器在训练过程中更好地捕捉了稳定的负荷变化特征因子表达, 同时确保了输出不会完全等于输入. DAE结构图如图2所示.

DAE由输入特征序列$ X $、加噪特征序列$ X' $、中间特征$ Y $和重构特征序列$ Z $组成. DAE的结构为编码器$ {f_\theta } $和解码器$ {g_\theta } $.

1.3 堆叠式双向门控循环单元

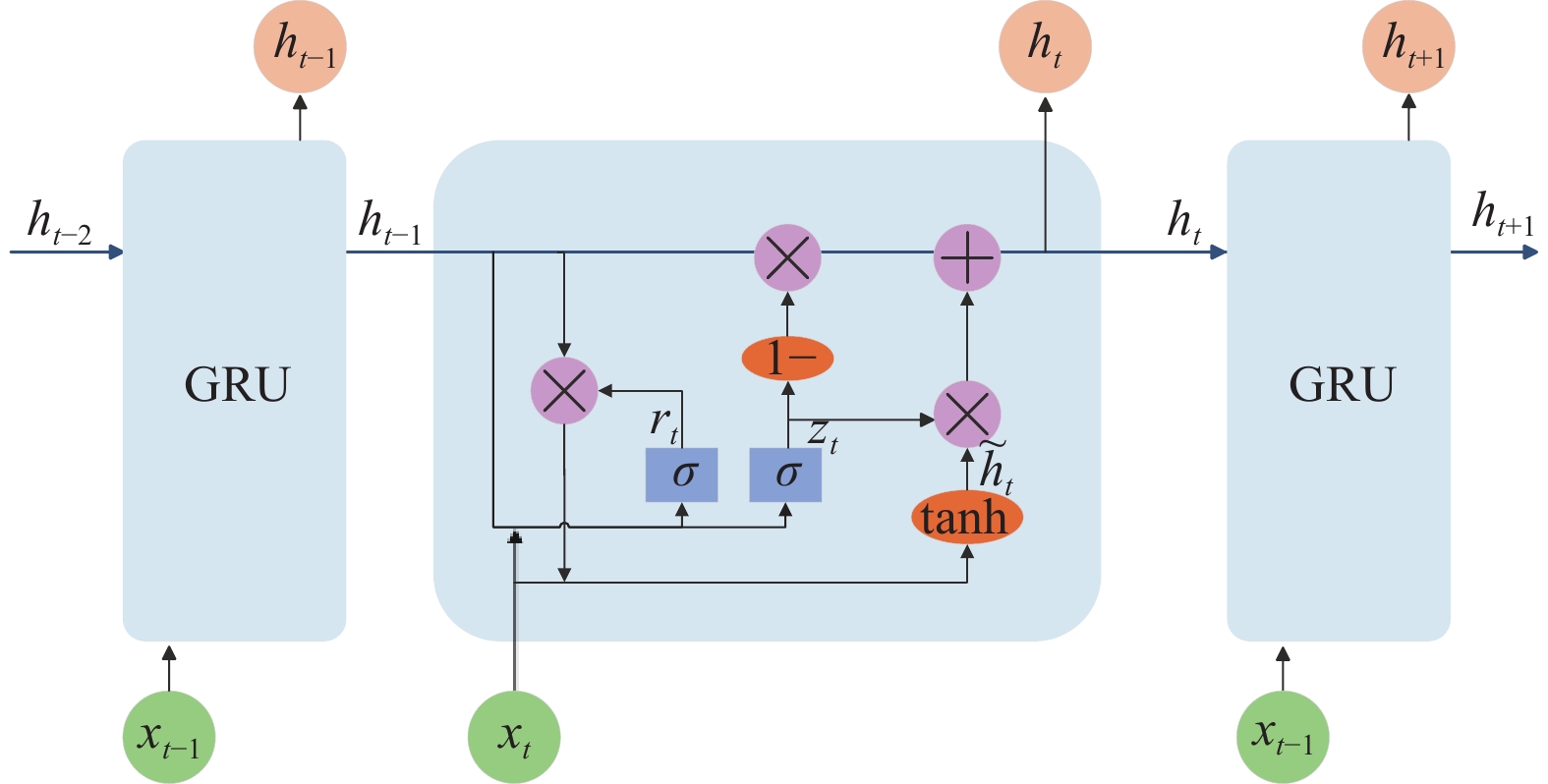
GRU简化了LSTM的内部结构, 将LSTM里的遗忘门和输入门合并为更新门, 其主要是在前一时刻的数据上执行一定程度的记忆和有选择性的遗忘, 而重置门负责处理当前的信息并将其传递给神经网络单元, 有助于捕获时序信息中的短期依赖关系. GRU简化了模型, 使模型参数更少, 可以解决长时间序列有效连接问题, 解决梯度爆炸或者梯度消失的问题, 对短期电力负荷预测具有一定的实用性. GRU如图3所示.

具体计算过程如式(11)–式(14)所示:

$ {{\textit{z}}_t} = \sigma ({W_{\textit{z}}} \cdot \left[ {{h_{t - 1}}, {x_t}} \right]) $

(11)

$ {r_t} = \sigma ({W_r} \cdot \left[ {{h_{t - 1}}, {x_t}} \right]) $

(12)

$ {\tilde h_t} = \tanh (W \cdot \left[ {{r_t} \times {h_{t - 1}}, {x_t}} \right]) $

(13)

$ {h_t} = (1 - {{\textit{z}}_t}) \times {h_{t - 1}} + {{\textit{z}}_t} \times {\tilde h_t} $

(14)

其中, $ {x_t} $是当前输入信息, $ {h_{t - 1}} $是最后保存的隐藏状态, $ W $是权重, $ \sigma $是$ \mathit{Sigmoid} $激活函数, 将值压缩到0–1之间. 通过$ \rm tanh $激活函数将输出值缩小到[−1, 1], 得到隐藏状态$ {\tilde h_t} $. $ {r_t} $用于调整输入信息$ {x_t} $的比例. $ {r_t} $的取值范围为0到1, 该值越小, 保留的输入信息越多. $ {W_r} $和$ {W_Z} $是可训练参数矩阵. $ {{\textit{z}}_t} $用于调整历史信息保存的程度. $ {{\textit{z}}_t} $取值从0–1, 值越小, 保留的历史信息就越多. $ {h_t} $用于保留需要向后传递的信息.

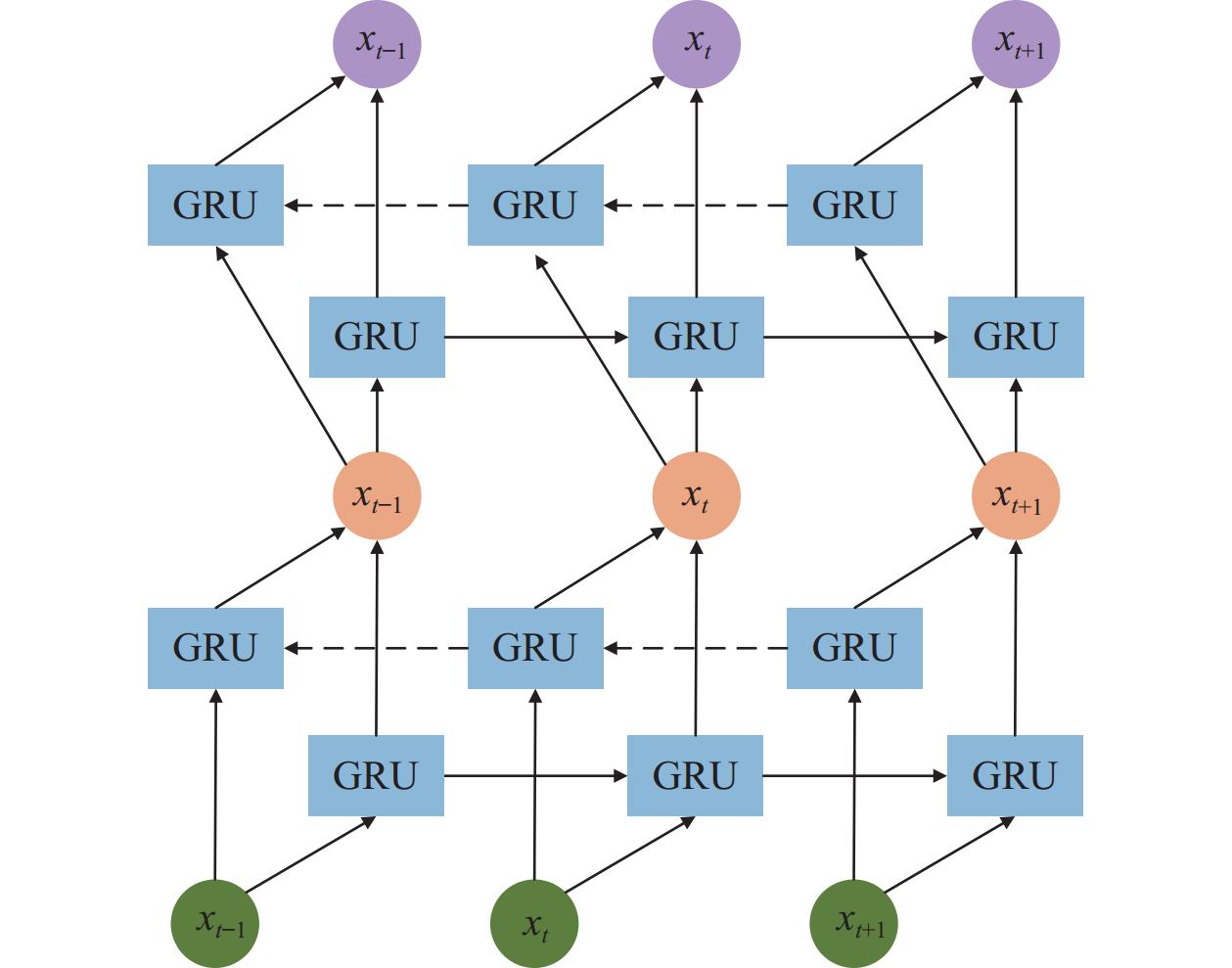
GRU只能获取历史时间信息而无法获取未来时间的信息特征. 因为双向门控循环单元是由前向GRU和反向GRU组成的, 它能将隐藏层分为向前和向后两个相对的部分, 所以其可以分别读取过去和未来时间的信息. 计算公式如式(15)–式(17)所示:

$ {\overrightarrow h _t} = GRU({x_t}, {\overrightarrow h _{t + 1}}) $

(15)

$ {\overleftarrow h _t} = GRU({x_t}, {\overleftarrow h _{t - 1}}) $

(16)

$ {h_t} = {W_t}{\overrightarrow h _t} + {V_t}{\overleftarrow h _t} + {b_t} $

(17)

其中, $ {\overrightarrow h_t} $表示$ t $时刻的前向隐藏层状态, $ \overleftarrow h _t $表示$ t $时刻的后向隐藏层状态, $ {W_t} $和$ {V_t} $表示$ {\overrightarrow h_t} $和$ \overleftarrow{h} _t $对应的权重, $ {b_t} $表示$ t $时刻隐藏层的偏移量. SBiGRU由两个BiGRU堆叠组成, SBiGRU的网络结构如图4所示.

1.4 优化多头注意力机制

注意力机制是受人脑思考问题时资源分配机制的启示而提出的一种深度学习方法. 在处理数据信息时, 它使用权重大小来测量不同的特征信息, 为重要特征提供较大的权重, 为相对不重要的特征提供较小的权重. 它提高了特征学习的效率, 可以从海量数据中挖掘出更有价值的隐含信息. 然而, 普通注意力机制只能从一个维度提取传感器数据特征依赖关系, 只能学习具有局限性的特征信息. 因此, 引入多头注意力机制来解决这个问题.

多头注意力机制首先通过全连接层(FC)将输入映射到$ b $个不同的子空间. 每个子空间包含一个查询矩阵Q, 关键矩阵K和值矩阵V. 然后, 使用缩放的点积注意力函数在$ b $个子空间中并行执行注意力计算. 计算公式如式(18)所示:

$ {\mathit{Attention}}\left( {Q, K, V} \right) = {\mathit{Softmax}} \left( {\frac{{Q \cdot {K^{\mathrm{T}}}}}{{\sqrt {{d_k}} }}} \right) \cdot V $

(18)

其中, Q、K、V分别表示查询、键、值, $ {d_k} $表示k对应的维数, 计算Q与K的每个值的相似性以获得权重后, 必须将得到的权重除以$ {d_k} $, 以防止Q和K的内积过大; $ {\mathit{Softmax}}\left( \cdot \right) $表示对得分归一化.

在多个末端并行生成多头注意力, 并将注意力的结果组合起来以获得最终输出, 计算公式如式(19)、式(20)所示:

$ Multihead\left( {Q, K, V} \right) = Concat\left( {hea{d_1}, \cdots , hea{d_h}} \right){W^O} $

(19)

$ hea{d_i} = Attention\left( {QW_i^Q, KW_i^K, VW_i^V} \right) $

(20)

其中, $ i = 1, 2, \cdots , h $; $ W_i^Q, W_i^K, W_i^V $为预测矩阵, $ Multihead\left( \cdot \right) $表示$ h $个头的注意力输出相加.

为了解决SBiGRU学习序列数据时, 会出现效率低、时间长和局部信息丢失等问题, 本文引入了残差机制和层归一化优化的多头注意力机制, 模型结构的简化提高了训练速度, 可以帮助模型有效地学习强相关因素的影响, 还去除了掩码矩阵操作和前馈层的计算过程. 优化后的多头注意力机制提高了预测精度, 计算公式如式(21)、式(22)所示:

$ {y_t} = Multihead\left( {Q, K, V} \right) + {h_t} $

(21)

$ E = Normali{\textit{z}}ation\left( {{y_t}} \right) $

(22)

其中, $ {h_t} $为多头注意力机制的输入; $ {y_t} $是经过优化后的多头注意力机制的输出; $ E $为$ {y_t} $归一化之后的输出.

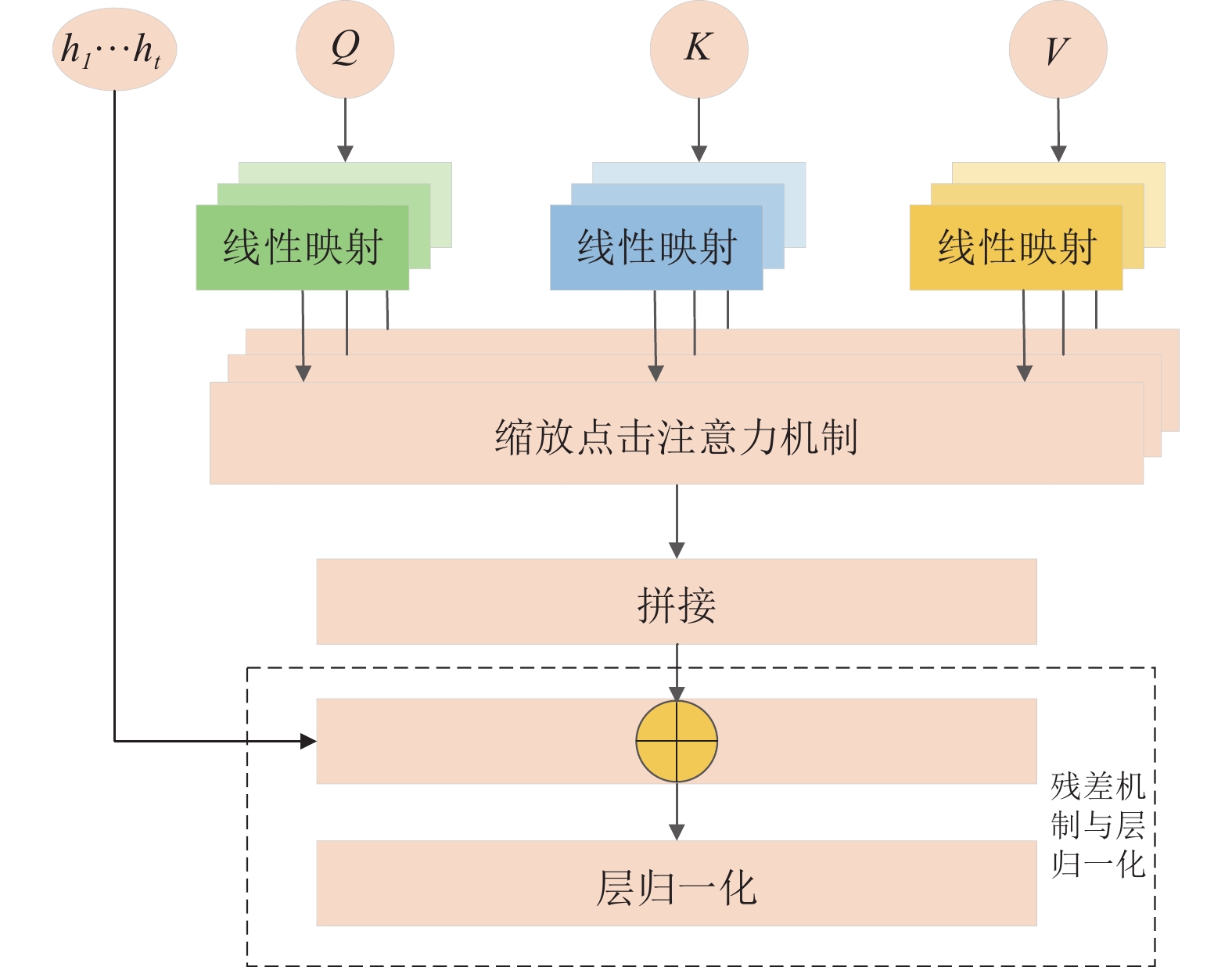
优化后的多头注意力机制的结构如图5所示.

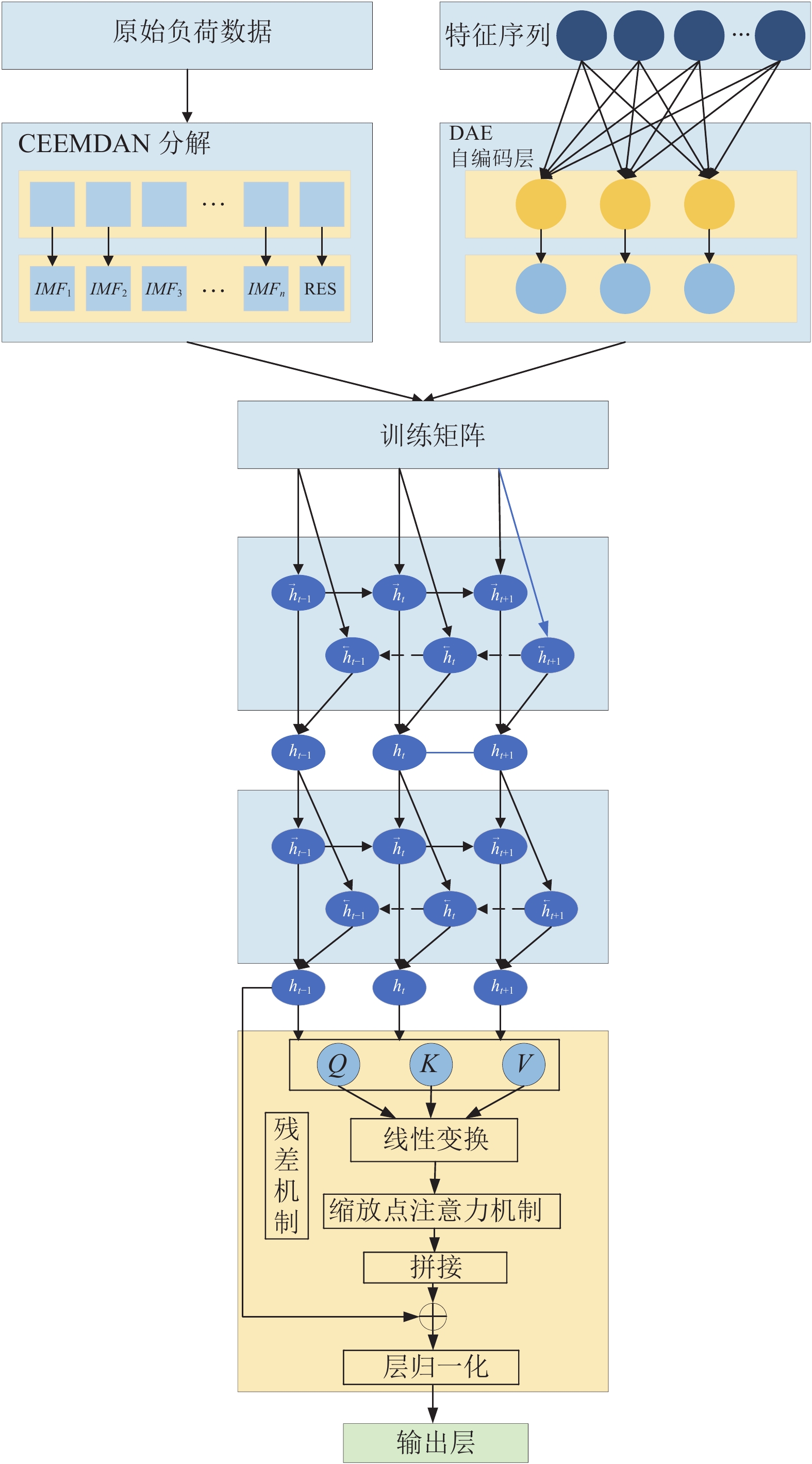
1.5 CEEMDAN-SBiGRU-OMHA模型总框架

本文提出一种CEEMDAN-SBiGRU-OMHA短期电力负荷预测模型. 模型总框架如图6所示.

1) 使用CEEMDAN算法将负荷数据分解为多个IMF分量和唯一残差RES.

2) 由于IMF数量较多, 引入降噪自编码器DAE让其有效地学习更多的潜在特征序列, 可以帮助模型识别和提取潜在的、对负荷需求具有影响的特征, 从而优化数据的质量.

3) 将提取相应的特征矩阵输入到SBiGRU层进行训练, 这种两层BiGRU不仅可以为每个时间点的负荷预测提供过去和未来的负荷信息, 而且通过其多层网络设计结构提高了模型的泛化能力.

4) SBiGRU网络层提取的特征用于优化多头注意力机制层的查询(Q)、键(K)、值(V). 优化后的多头注意力机制层对这些查询、键、值进行线性变换、缩放点积注意力机制和拼接处理. 根据权重的分配原理计算不同特征向量对应的概率, 随后迭代更新权重参数矩阵以提升模型的效果. 为了应对数据的残缺问题, 将SBiGRU层的输出与经优化后的多头注意力机制层的输出相加并进行层归一化.

5) 将优化多头注意力机制训练好的矩阵输入到输出层, 通过全连接层输出最终的电力负荷预测值.

2 算例分析 2.1 实验数据集

本文的实验研究是选取澳大利亚某地区的电力负荷数据, 数据集包含历史负荷、日平均气温和节假日数据, 负荷数据采样周期为3 h, 样本数为19808个, 其中前19500个负荷数据作为验证集, 后308个负荷数据作为测试集.

2.2 数据预处理

在实验之前, 我们使用归一化对样本数据进行预处理, 将其限制在[0, 1]的范围内, 以消除奇异样本数据对预测精度的负面影响. 归一化如式(23)所示:

$ {x_c} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $

(23)

其中, $ {x_c} $为归一化的负荷数据, $ {x_i} $为原始负荷数据, $ {x_{\max }} $和$ {x_{\min }} $分别为数据的最大值和最小值.

2.3 评价指标

本研究采用均方根误差(RMSE)、平均绝对百分比误差(MAPE)和相关系数(R²)作为预测的误差评价指标. 评价指标计算如式(24)–式(26)所示:

$ \mathit{RMSE} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - {{\hat x}_i})}^2}} } $

(24)

$ \mathit{MAPE} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{x_i} - {{\hat x}_i}}}{{{x_i}}}} \right|} \times 100{\text{%}}$

(25)

$ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - {{\hat x}_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x )}^2}} }} $

(26)

其中, $ {x_i} $为第$ i $个预测样本的实际值, $ {\hat x_i} $为预测值, $ \bar x $为预测样本均值, $ n $为样本总数. RMSE和MAPE值越小, 预测效果越好, $ {R^2} $值越趋向于1, 拟合程度越好.

3 实验研究 3.1 实验设置

实验代码基于PyTorch深度学习框架编写, 并在PyCharm代码编辑器上运行. 训练过程使用显存为24 GB的GPU (NVIDIA GeForce RTX 3090). 具体实验参数设置如表1所示.

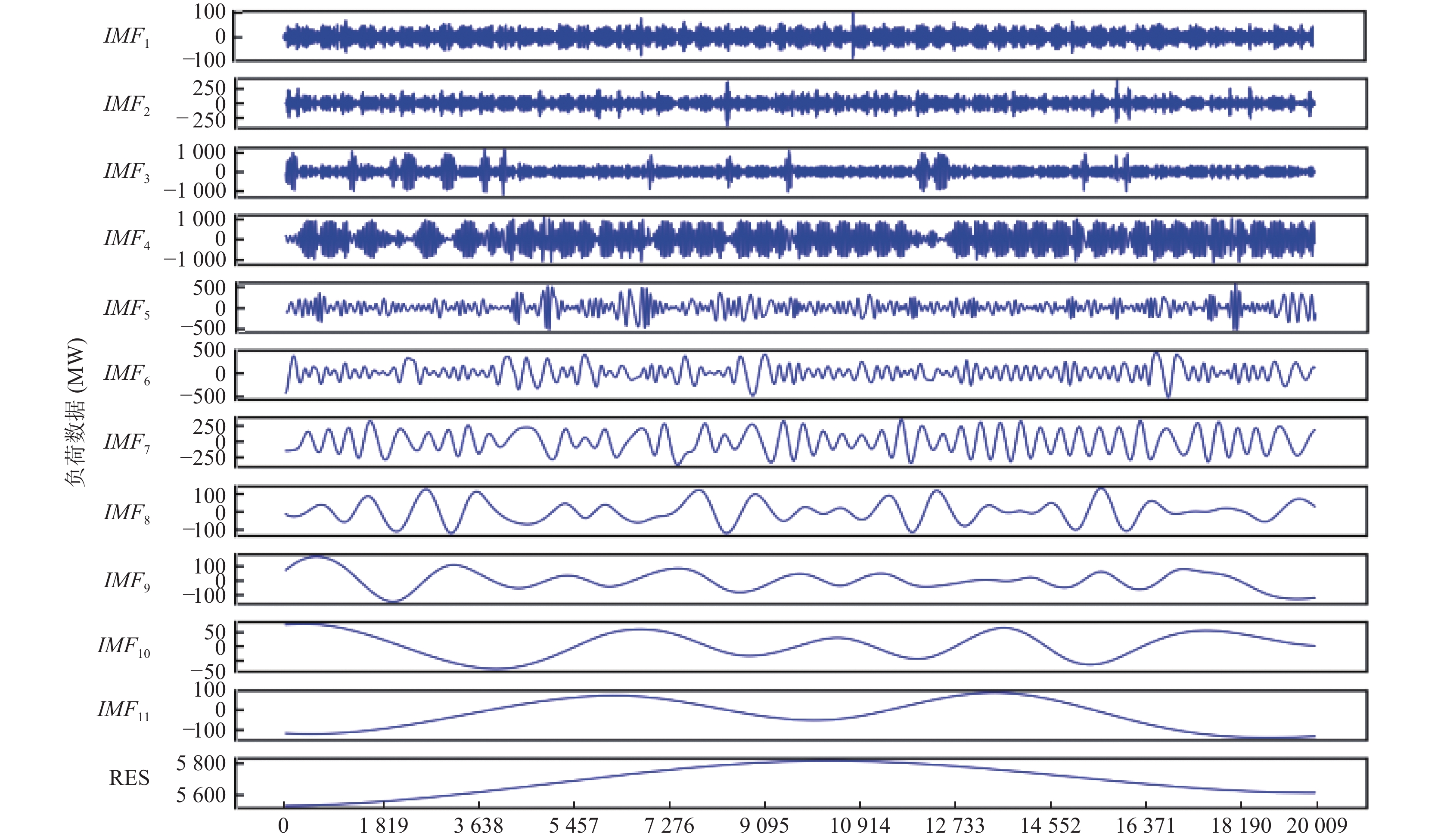
3.2 CEEMDAN的分解

当余量信号$ R(n) $变为常数或单调函数时, 经验模态分解(EMD)过程终止, 从而确定最终的本征模态函数(IMF)分量个数. 在对负荷数据进行分解后, 得到11个IMF分量和1个RES趋势项. 结果如图7所示, 各个分量的频率从高到低依次分布, 低频分量的波动更加规律和平缓. 每个IMF分量代表了不同时间尺度上的特征, 使模型能够充分挖掘数据特征, 同时避免了各个局部特征之间的相互干扰, 最终的残差分量反映了负荷的总体趋势.

3.3 实验结果分析 3.3.1 对比实验

为了验证本文模型的有效性, 将其与以下5个模型进行比较, 结果如表2所示.

相比于以上5种深度学习模型, 本文所提出的CEEMDAN-SBiGRU-OMHA组合模型在短期电力负荷预测方面具有优势. 从表2中可以看出, 单一模型的预测精度无明显区别, 本文提出的模型相比其他模型: RMSE值分别优化了41.72%、39.66%、38.24%、30.94%、29.96%; MAPE值分别优化了73.89%、71.49%、61.28%、38.96%、31.33%; R²值分别优化了4.20%、2.60%、1.96%、1.23%、0.51%. CEEMDAN-SBiGRU-OMHA能够提高预测结果的主要原因在于: SBiGRU的高效序列处理能力更全面地捕捉序列中的依赖关系. 同时, 引入优化后的多头注意力机制有效提高了对关键信息的捕捉能力, 从而在电力负荷预测任务中表现更为卓越.

3.3.2 消融实验

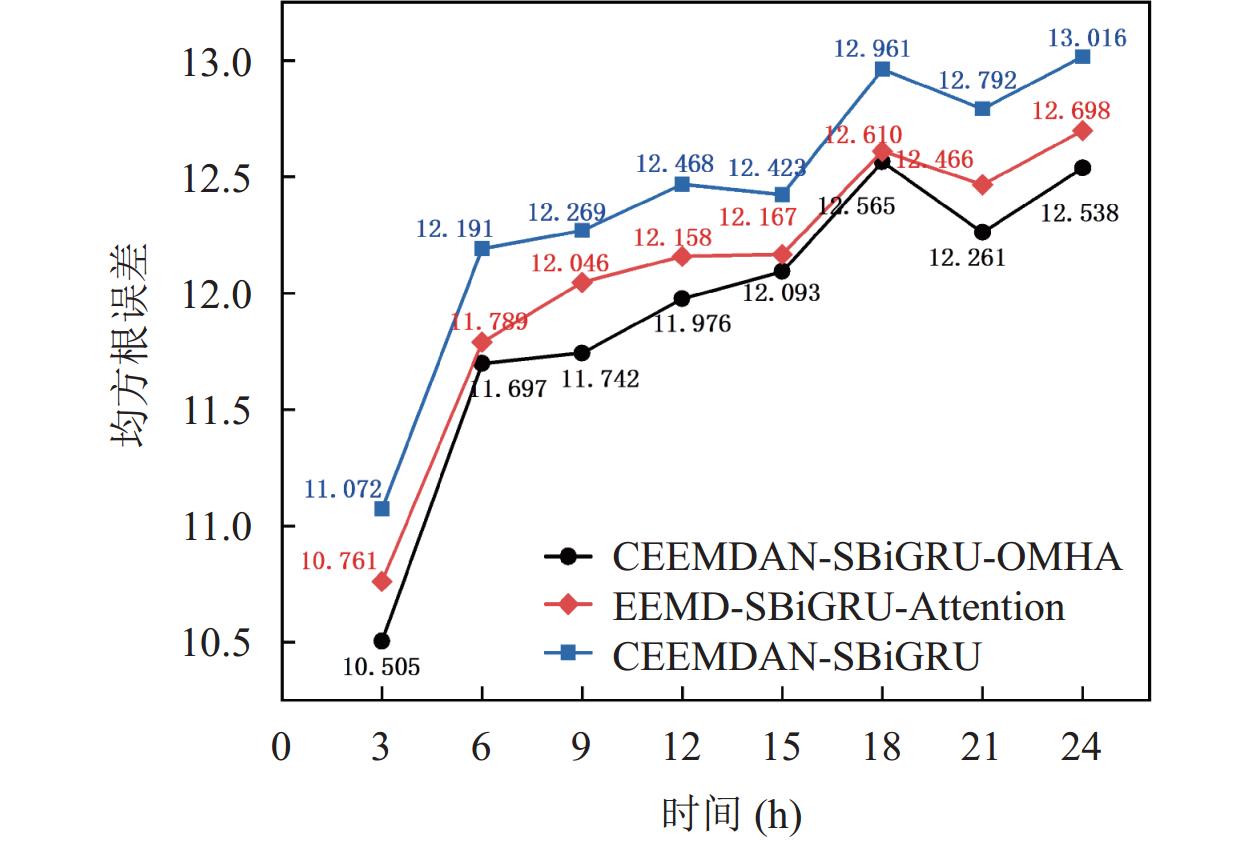
为了进一步说明本文提出模型的有效性, 还与CEEMDAN-SBiGRU和EEMD-SBiGRU-Attention模型进行了比较, 结果如图8–图10所示.

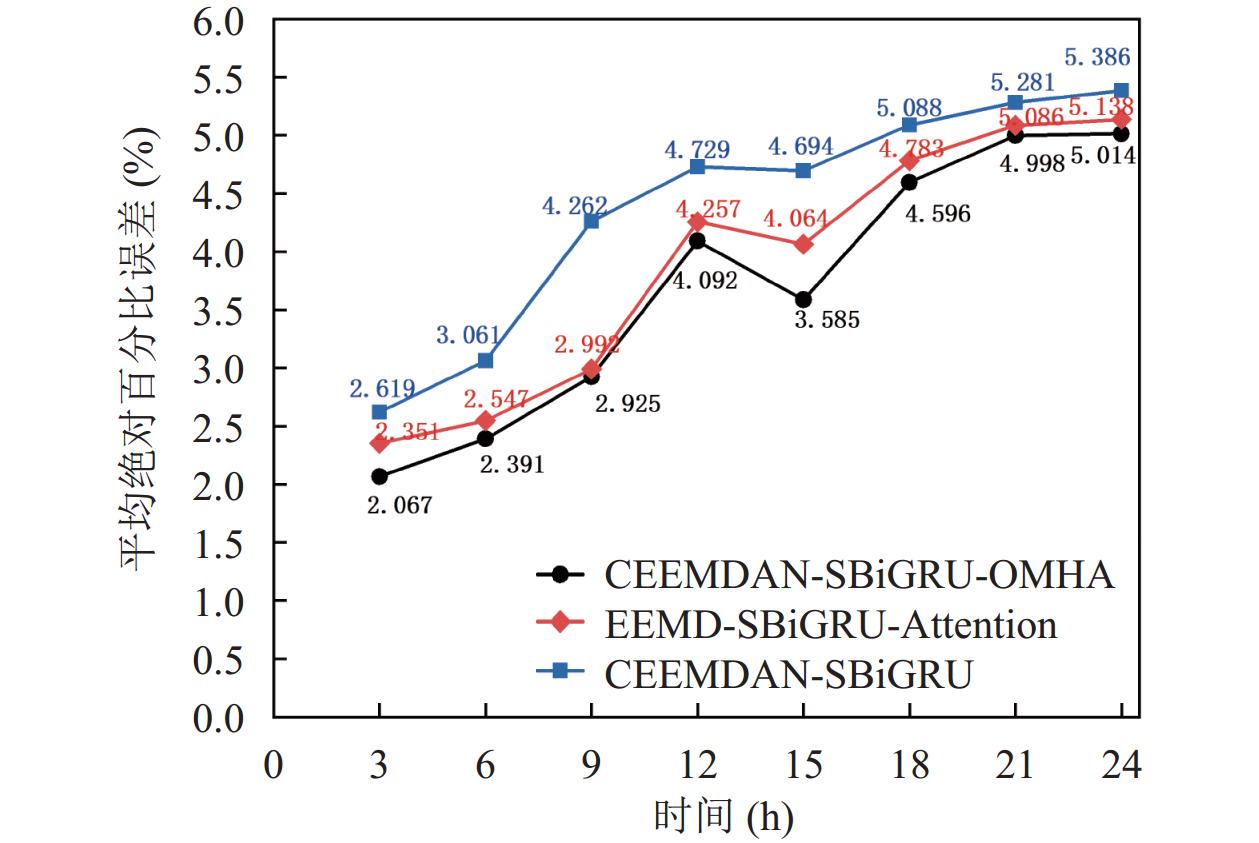
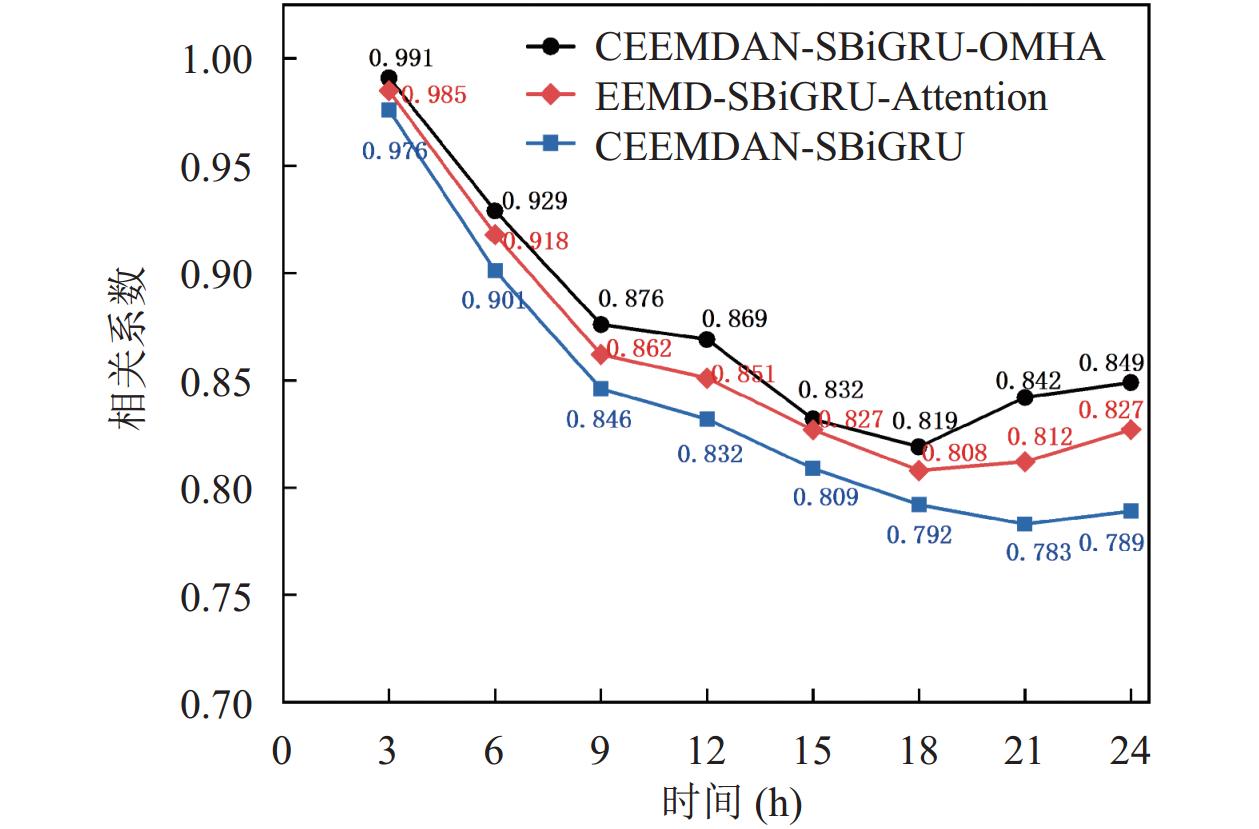
图8–图10表明, 在24 h时间间隔内, 基于CEEMDAN-SBiGRU-OMHA组合模型在3种评价指标上均优于EEMD-SBiGRU-Attention, CEEMDAN-SBiGRU模型. 其中图8和图9表明, CEEMDAN-SBiGRU-OMHA模型在 RMSE与MAPE上相比EEMD-SBiGRU-Attention模型分别平均降低了1.5%与0.2%, 相比CEEMDAN-SBiGRU模型分别平均降低了4%与0.7%, 可见, 通过添加优化后的多头注意力机制, 可以更好地提高捕捉关键信息的能力; 利用CEEMDAN方法对非光滑、非线性的原始数据进行分解, 可以有效地提取光滑信息; 此外, 通过在预测过程中利用这种平滑信息的叠加增强预测结果, 提高预测的准确性. 图10表明, CEEMDAN-SBiGRU-OMHA预测模型的R²值整体优于其他两个模型的值, 分别提高了12%与28%, 这说明本文提出的组合模型对于预测精度有明显的提升.

4 结论

实验结果表明, CEEMDAN-SBiGRU-OMHA在预测短期电力负荷方面表现出色, 其预测误差最小, 预测精度最高. 并与LSTM、GRU、LSTM-AE-CNN、SRDCC-BiLSTM和EMD-BI-LSTM模型进行了比较, 基于实验结果, 可以得出以下结论: 1) CEEMDAN-SBiGRU-OMHA的3个评估指标均优于其他预测模型, 表明本文提出的预测模型具有更好的性能; 2)通过使用CEEMDAN方法, 将误差序列分解为多个更稳定的分量, 以更精确地捕捉电力负荷的复杂性和波动性; 3)利用降噪自编码器DAE能够学习更多的潜在特征序列, 将这些特征因子加入分解得到的IMF分量中. 这有助于更全面地考虑不同的因素对电力负荷的影响, 有效地去除数据中的干扰噪声, 从而提高预测的综合性能; 4)通过引入SBiGRU模型, 为每个分量建立SBiGRU预测模型, 以提高更稳定分量的误差预测精度. 这有助于减少误差并提高模型的稳定性; 5)引入了残差机制和层归一化改进的多头注意力机制, 以提升对负荷数据的处理效率. 这一改进有效解决了重要信息丢失的问题, 保障了关键特征的完整传递, 从而提高了预测准确度.