1 引言

动作识别技术是计算机视觉领域的一个重要研究方向, 已经广泛应用于视频监控、体育、游戏等行业中. 一般来说, 动作识别的目的是从包含完整动作执行的视频中识别人的动作^[1], 然而人体动作识别领域有着不同的研究方向, 早期的人体动作识别方法大部分使用RGB视频作为数据源, 然而RGB视频存在光照、背景、遮挡等噪声干扰. 随着传感器成本下降, 数据源增多, 基于三维骨架的人体动作识别方法的研究得到重视. 三维骨架信息只包含几个人体运动关节节点的三维坐标信息, 保留了动作的空间结构, 解耦了动作提取和动作识别的过程. 本文研究的动作识别, 是直接从已经获得到的三维骨架运动来进行的动作识别. 基于三维骨架的识别方法数据维度低, 处理效率高, 可以通过人工植入约束规则的方式改善模型的识别率.

基于三维骨架的识别方法主要包含端到端的黑盒识别方法和基于模式识别的白盒识别方法. 端到端的方法主要依赖深度学习技术, 其提取的特征难以解释, 并且分类过程不明确. 白盒方法虽然相比黑盒方法, 分类过程可解释, 但是有的白盒方法不能体现动作之间的区别和联系, 并为整个动作过程提取特征. 为了解决白盒方法存在的一些问题, 本文设计了一个基于层次结构的白盒识别方法, 层次结构将动作数据组织起来. 之后, 将动作的关键姿态作为模板, 这样可以减少相似帧的重复计算. 最后, 为了防止分类时某个动作因为无关关节的影响而被分到另外一类动作中, 将身体动作按照5个部位进行分解, 从不同的部位动作中推断整个身体的动作.

2 研究现状

三维骨架数据指的是描述人体运动的三维空间坐标数据, 通常通过传感器或摄像机捕捉到的人体关键点的位置信息来表示. 这种数据记录了身体不同部位(如头部、肩膀、手肘、膝盖等)在三维空间中的运动轨迹, 形成一个关节之间连接的骨架结构. 基于三维骨架的动作识别方法主要包含端到端的黑盒识别方法和基于模式识别的白盒识别方法.

2.1 基于模式识别的白盒识别方法

白盒方法的识别过程可以划分为动作表示和动作分类两个过程, 动作表示是将动作数据转化成一系列特征, 动作分类是使用动作特征进行分类.

Wang等人^[2]提出一种关节的特征, 其中利用每个关节与其他关节之间的相对位置作为特征的一部分, 他们也从关节中选择对动作影响大的关节赋予高权重. Lv等人^[3]基于对动作和能够区分动作的特征的分析, 设计了几种类型的特征, 如下所示: 关节的坐标分量, 例如髋关节的垂直位置、每个非根关节的坐标、相连关节的坐标、对称关节点的坐标、所有腿部和躯干相关关节的坐标、所有手臂相关关节的坐标, 不同类型代表动作不同的动态级别. 例如, 类型2, 3和4分别对应于关节位置和关节角度. 类型5特征用于检测周期性运动, 类型6和类型7特征为识别提供了总体指导. Ofli等人^[4]通过计算两个连接肢体之间的关节角度, 将关节角度的时间序列作为骨架运动数据, 在对骨架运动数据进行时间分段, 计算每个时间段内关节的信息量并排序, 然后将信息量最大的前N个关节序列作为人类关节动作识别的新特征, 其中包含: 每个时间段中最有信息的关节集合, 以及在所有时间段中最有信息的关节集合的时间顺序. 并且, Ofli等人还在文章中证明了选择最具有时间信息的关节的原因. Yang等人^[5]通过计算帧内节点间的成对距离、当前帧和前一帧之间的关节差, 然后将运动特征合并作为动作的每一帧特征, 可以表示动作的空间与时间特征.

得到动作表示后, 可以通过一些分类方法将其分类到合适的动作类, 常见的分类方法有聚类、支持向量机、神经网络.

2.2 端到端的黑盒识别方法

端到端的黑盒方法主要使用深度学习技术, 大致可以分为基于循环神经网络(recurrent neural network, RNN)、卷积神经网络(convolutional neural network, CNN)、图卷积网络(graph convolutional network, GCN)的方法.

在RNN方法中, 骨架序列是关节坐标位置的自然时间序列. Du等人^[6]提出一种分层RNN, 没有将整个骨架作为输入, 分为了5个部分(两只手臂、两条腿和一个躯干), 分别送到5个子网. 随着层数增加, 子网提取的表示被分层融合为更高层的输入. 骨架序列的最终表示被送入单层感知器, 感知器的最终输出是最后的结果. Wang等人^[7]提出了双流RNN, 时间流的RNN模拟了关节的时间动态, 将每个时间步不同关节的三维坐标连接起来, 使用RNN处理生成的序列. 空间流的RNN建模关节的空间依赖性, 将关节的图结构转换为关节序列, RNN架构的每一步输入对应特定关节的坐标向量, 由于关节只有3个坐标, 选择一个时间步长为中心的时间窗口, 并将该窗口内的坐标连接起来以表示该关节. 并使用旋转、缩放和剪切作为数据增强技术. 基于RNN的方法更多的关注的是时间序列的变化, 对骨架的空间结构关注不多, 而CNN在这方面要强一些.

CNN一般专注于图像的任务, 为了使用CNN对三维骨架动作进行分类, 可以将三维骨架序列数据转换为伪图像, 然后投入网络中进行学习. Du等人^[8]将每个骨架序列表示为一个特殊图像, 其中序列的时间动态编码为行中的变化, 每个关节的3个分量$(x, y, {\textit{z}})$表示为每个像素对应的3个分量$(R, G, B)$, 然后输入CNN中. Wang等人^[9]提出了关节轨迹图, 通过将关节轨迹及其动态学编码为图像中的颜色分布, 使三维骨架序列中携带的时空信息表示为3幅2D图像, 称为关节轨迹图. 3个关节轨迹图在3个正交平面中生成, 并相互提供补充信息. 通过3个关节轨迹图的乘法分数融合, 进一步提高了最终识别率. 基于CNN的方法通过编码时间动态将骨架序列表示为图像, 然而在卷积过程中, 只有卷积核内相邻的关节才被考虑, 一些与所有关节相关的潜在相关信息可能会被忽略.

将骨架序列转化为序列向量或二维图像并不能完全表达相关关节之间的相关性, 图卷积把人的3D骨架数据看作一个拓扑图. 图卷积网络作为卷积网络的一种扩展, 其技术中的重要问题是骨架数据的表示, 将原始数据组织成特定的图. 对于一个图结构而言, 可以把图卷积理解为把一个节点邻居节点的特征加权并相加到该节点, 当然, 一个节点可能有许多的特征向量. Yan等人^[10]提出了一种基于骨架的动作识别模型, 时空图卷积网络(spatial temporal graph convolutional network, ST-GCN), 将关节作为图节点, 人体结构和时间过程中的自然连接作为图边缘, 由于不能把所有节点的特征直接相加, 因此ST-GCN对节点的每个邻居节点编号, 相同序号的邻居节点构成邻居子集, 形成节点的邻接矩阵, 并提出了3种人体结构的分区策略, 然后再进行卷积, 为了平衡每一个节点的贡献, ST-GCN提出一个正则化邻接矩阵, 将其与之前的邻接矩阵相乘, 以此平衡节点之间的权重.

2.3 小结

黑盒的深度学习方法是一个端到端的方法, 能够从大量的数据中训练参数, 使模型更好的拟合数据, 同时可移植性也使得模型能在不同的训练集上进行迁移. 但是深度学习的一个缺点是模型中间过程提取的特征我们可能无法理解其含义, 并且分类过程不明确.

深度学习的另一个缺点是, 因为深度学习是一个端到端的训练参数的模型, 给定一个动作输入, 就会输出一个动作类别或不同类别所属的概率, 并且因为数据量大、模型参数多, 所以其准确率高, 所以当出现错误分类时, 我们可能无法知道是在哪个节点出现错误, 只能调节参数或调整训练集来重新训练模型.

白盒方法, 人们能够理解其含义, 其提取的手工特征的可解释性是其最有竞争力的优点. 但是现在的一些白盒方法没有组织结构, 并且为动作数据的所有帧提取特征进行比较.

为了解决白盒方法存在的一些问题, 本文通过树结构将动作数据有结构有层次的组织起来, 然后向层次结构中植入人体结构知识以及动作关键姿态知识.

3 基础知识 3.1 人体三维骨架数据获取

人体三维骨架数据可以通过使用Kinect传感器捕捉身体各个部位的空间坐标信息, 然后存储下来. Kinect传感器可以同时记录动作的RGB视频和深度映射图像, 以及传感器与人体之间的距离. 使用深度图像中像素点所包含的三维深度信息可以得到关节点的空间坐标.

获取人体三维骨架关节坐标可以分为3个步骤: 人体轮廓分割、人体部位识别、关节点定位^[11].

人体轮廓分割: Kinect传感器通过RGB视频和深度图像, 对深度不同的平面逐一分析, 以此提取图像的边缘信息, 以此得到深度图像中的人体轮廓.

人体部位识别: 使用背景去除方法获得人体目标, 对人体目标中的每个像素进行分析, 判断其是否属于人体像素点, 然后使用特征值分类匹配, 确定其所属的人体部位, 最后使用人体骨架模型拟合所有部位.

关节点定位: 识别出人体部位后, 将这些相对位置拟合到人体三维骨架中, 然后根据每个像素点的位置来确定骨架的关节位置, 最后将关节点的三维坐标存储下来.

随着深度学习的发展, 人们可以从二维图像中识别出人体三维骨架数据, 像OpenPose、DensePose. 但是这种方法提取的三维骨架的准确性不能得到保证.

3.2 数据集介绍

目前常见的人体三维骨架数据集包括: UTKinect-Action3D、NTU RGB+D、UTD-MHAD等.

UTKinect-Action3D由单个Kinect捕获的, 有10种类型的动作: 走路、坐下、站起、捡起、携带、投掷、推、拉、挥手、拍手. 有10个受试者, 每个受试者执行每个动作两次. 记录了3个通道: RGB、深度和骨架关节位置, 该数据集总共包含199个动作序列.

NTU RGB+D 包含 60 个动作类别和56880 个视频样本, 由3台 Kinect V2 摄像机同时捕获. 包含了足够多的动作种类, 并同时提供了二维视频和三维骨架, 其中三维骨架数据包含每帧 25 个人体关节的三维坐标. 在2019年, 他们又发布了扩展版本, 将动作种类扩展到120种, 动作样本扩展到1144880个.

CZU-MHAD数据集是一个用于多模态人体动作识别的数据集, 由浙江大学的研究人员开发, 通过同步采集RGB视频、深度视频、骨架数据以及惯性传感器数据等多种模态的信息, 来捕捉人体动作的多方面特征. CZU-MHAD 数据集包含5名受试者(5名男性)执行的22个动作, 比如常见的手势(如画圈)、日常活动(如拍手、弯腰)和训练动作(如左转身运动、左侧运动), 每个受试者重复每个动作大于8次, 共包含大于880个样本.

3.3 最近邻算法

最近邻算法利用训练数据对特征向量空间进行划分, 并将划分结果作为最终算法模型. 存在一个样本数据集合, 也称作训练样本集, 并且样本集中的每个数据都存在标签, 即我们知道样本集中每一数据与所属分类的对应关系. 输入没有标签的数据后, 将这个没有标签的数据的每个特征与样本集中的数据对应的特征进行比较, 然后提取样本中特征最相近的数据(最近邻)的分类标签, 在进行距离计算时, 通常选择欧氏距离.

假设任意实例$x$表示为下面的特征向量: $[{a_1}(x), {a_2}(x), \cdots, {a_n}(x)]$, 其中${a_r}(x)$表示实例$x$的第$r$个属性值, 那么那么两个实例${x_i}$和${x_j}$间的距离定义为$d({x_i}, {x_j})$, 其中:

$ \begin{array}{*{20}{c}} {d\left( {{x_i}, {x_j}} \right) = \sqrt {\displaystyle\mathop \sum \nolimits_{r = 1}^n {{\left[ {{a_r}\left( {{x_i}} \right) - {a_r}\left( {{x_j}} \right)} \right]}^2}} } \end{array} $

(1)

3.4 动态时间规整算法

动态时间规整(dynamic time warping, DTW), 最初是用在语音识别中, 使用动态规划的思想来寻找两条不同长度语音序列的最小距离的匹配路径. 设有两个时间长不不同的序列为$Q$和$C$, 且长度分别为$n$和$m$, 即:

$ Q = \{ {q_1}, {q_2}, \cdots, {q_n}\} $

(2)

$ C = \{ {c_1}, {c_2}, \cdots, {c_m}\} $

(3)

为了对齐两个序列, 需要创建一个$n \times m$的矩阵网格, 矩阵中的格点$(i, j)$是${q_i}$和${c_j}$的距离$d({q_i}, {c_j})$, 通常选择欧氏距离. 将两个序列对齐可以理解为寻找一条通过此网格中若干格点的路径, 路径通过的格点即为两个序列对齐的点. 为了选择合适的路径, 需要满足以下约束.

1) 边界约束: 任何动作做的快慢可能不一致, 但其各部分的先后次序不变, 因此所选的路径是从左下角出发, 在右上角结束.

2) 连续性约束: 不能跨过某个点去匹配, 只能和自己相邻的点对齐, 包括对角线上的点.

3) 单调性约束: 选择的路径上的点随着时间是单调进行的.

结合连续性和单调性, 每一个格点就只能来自3条路径, 格点$(i, j)$可以来自$(i - 1, j)$或$(i, j - 1)$或$(i - 1, j - 1)$, 设$g(i, j)$为累计相似距离, 即表示从$d(1, 1)$到$d(i, j)$的所有路径中的相似距离之和最小值, 那么可以按照以下约束条件计算累计相似距离:

$ g(i, j) = \left\{ {\begin{array}{*{20}{l}} {g(i - 1, j) + d(i, j)} \\ {g(i - 1, j - 1) + d(i, j)} \\ {g(i, j - 1) + d(i, j)} \end{array}} \right. $

(4)

计算得到$g(n, m)$的值即为两个序列对齐时最小的累计相似距离, 为了消除时间序列长度带来的影响, 最终得到的距离要除以两个序列的长度和, 即:

$ {D_{{\mathrm{avg}}}} = g(n, m)/(n + m) $

(5)

4 基于层次结构的动作识别方法

本节根据动作之间以及动作和个体之间的关系, 提出具有结构的动作识别模型, 通过树结构将动作数据组织起来. 为动作提取动作模板, 减少输入动作与动作样本之间的比较次数. 之后将动作的关键姿态知识以及人体结构知识植入系统中, 从不同的角度对动作进行分类.

提取动作的关键姿态作为动作模板, 并将动作的关键姿态与输入动作的所有姿态在时间上进行对应, 减少动作序列中相似帧的冗余计算. 但是, 将所有关节对动作的影响都累计在一起, 会出现错误分类的情况, 所以, 将身体分成5个部位. 对动作分类时, 通过对5个部位的分析得到最终结果, 而对个体分类时, 重点关注执行该动作的重点部位即可.

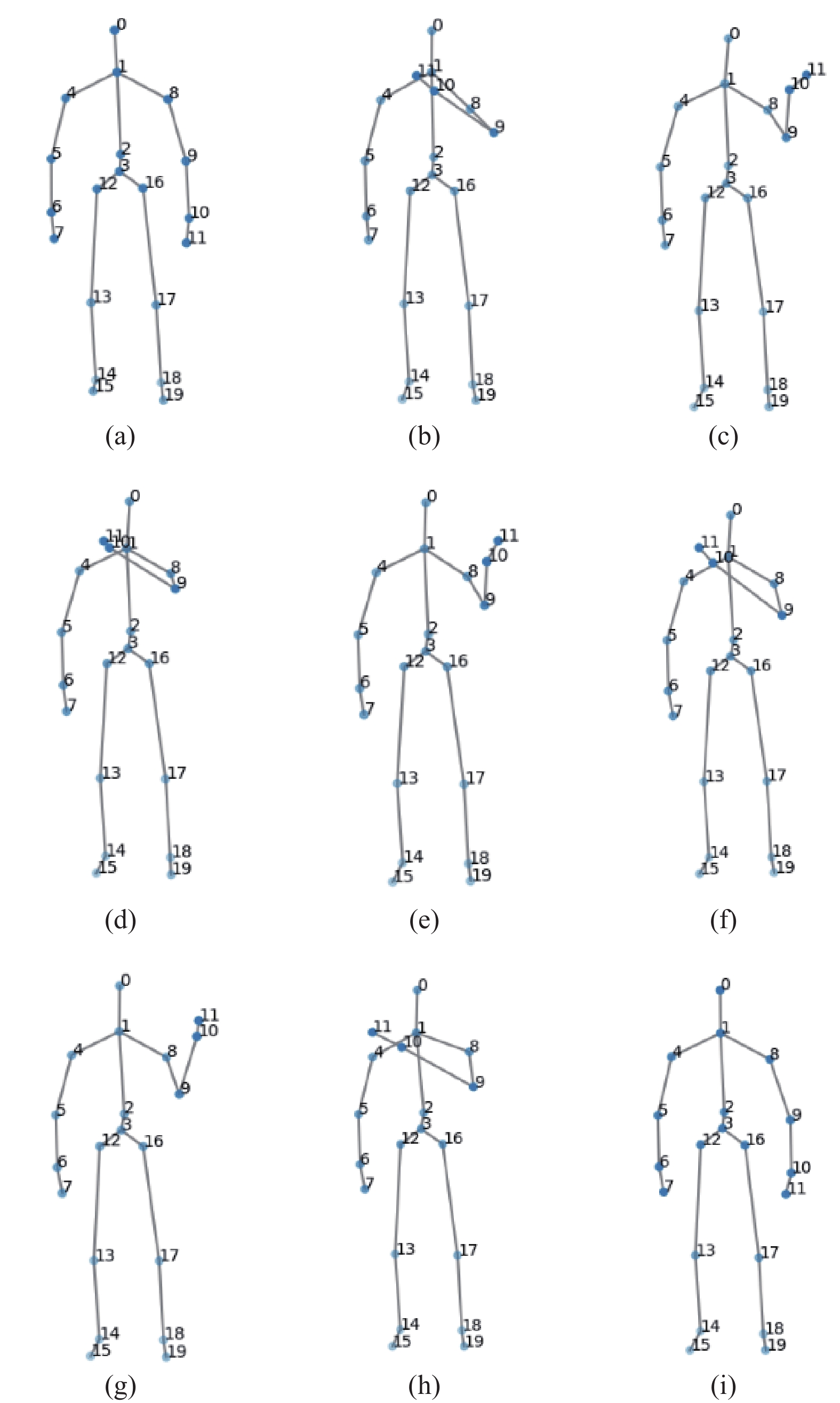
4.1 数据集选择

在本文中使用NTU RGB-D^[12]和CZU-MHAD^[13]数据集作为实验数据集. 由于数据集在采集过程中, 末端关节的采集效果并不好, 存在大量的波动, 所以在实验过程中选择20个关节, 其骨架结构如图1所示, 序号对应的关节名称如表1所示.

从NTU RGB-D中选取2组动作数据, 第1组是坐下、起立、拍手、挥手、鞠躬、双手交叉, 第2组是捡起、踢、插口袋、指、敬礼、双手合十. 每组6个动作, 每个动作选择8个受试者, 每个受试者选择18个数据样本, 其中12个作为训练样本, 6个作为测试样本, 因此每组都有576个训练样本和288个测试样本.

从CZU-MHAD数据集中选取一组动作数据作为第3组数据, 分别是右手画圆、右脚前踢、拍手、弯腰、原地踏步、挥手. 每个动作有5个受试者, 每个受试者执行动作13次, 其中8个作为训练样本, 5个作为测试样本, 因此有240个训练样本和150个测试样本.

4.2 模型构建

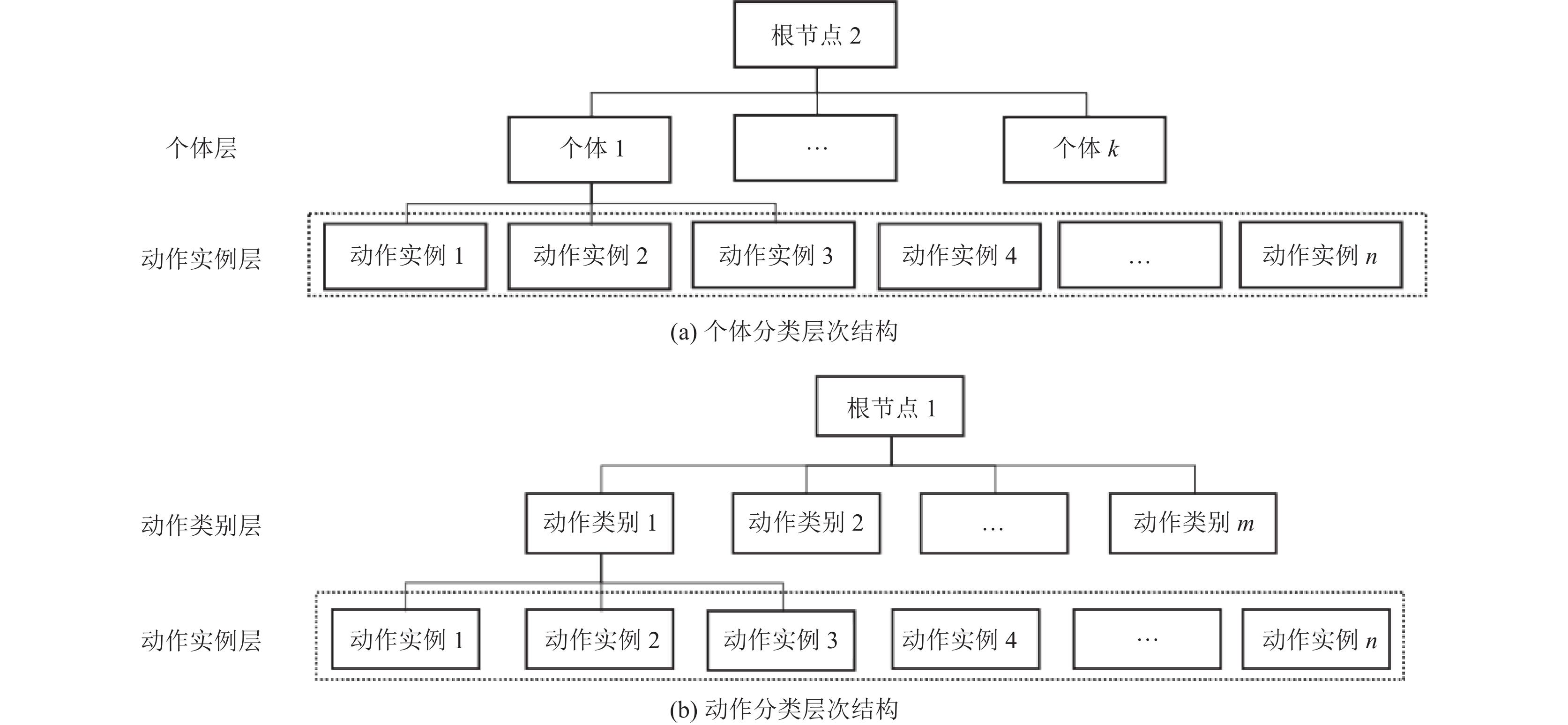
为了体现动作之间的区别与联系以及减少不对应动作类的重复比较, 使用树结构将动作数据按照层次结构组织起来, 这样对于不对应的动作类别, 可以减少冗余的比较, 加快了搜索效率. 因此, 在基于层次结构的识别模型的树结构中, 越接近根节点的一层, 越能表示不同动作的大致模板, 而越远离根节点的层, 越能表示同一动作的细致区别.

为了能让计算机理解一个动作是什么样的, 需要为系统植入动作的知识, 即需要选择标准的动作样本作为模板, 但是由于不同人做的同一动作存在差异, 即使是同一人做的同一动作也会存在区别, 为了将这些动作能够分到同一个正确的区域内, 需要尽可能地选择合适的动作模板将这些动作包括在范围之内. 对于模板动作的选择, 如果数据量不大, 可以通过人工筛选的方法选择, 如果数据量过大, 可以通过数据统计得到. 以此方法去构造基于层次结构的动作识别模型, 其结构如图2所示.

本文的层次结构包含个体分类层次结构和动作分类层次结构. 动作分类层次结构是对不同的动作进行分类, 个体分类层次结构是在动作分类完成后, 对执行动作的个体的身份进行分类, 这也意味着, 每一个动作都有一个个体分类层次结构.

4.3 动作模板获取

个体分类层次结构包括动作实例层和个体层, 动作实例层是所有的动作数据, 个体层是不同个体做同一动作的模板, 所以应为每类动作都构造一个个体分类层次结构.

为了使个体层中的节点能够尽可能的概括其对应个体做同一动作的范围, 需要为个体层的节点选取合适的动作模板. 对某一个体而言, 首先通过动态时间规整将其做的同一动作的动作数据进行对齐, 这样该个体的所有该动作样本都有相同的帧, 然后计算每一帧中所有动作样本对应关节的平均位置得到平均动作作为模板加入个体层对应的个体节点中.

假设有2个动作样本, 是同一个体做的同一动作. 两个动作样本在对齐后有$m$帧, 且骨架有$N$个关节, 即$ A = {A_1}, {A_2}, \cdots, {A_m} $, $ B = {B_1}, {B_2}, \cdots, {B_m} $, 通过式(6)计算平均动作$ {A_{{\mathrm{avg}}}} $的第1帧$ {A_{{\mathrm{avg}}1}} $:

$ {A_{{\mathrm{avg}}1}} = (A_1^i + B_1^i)/2, \;i = 1, 2, \cdots, N $

(6)

然后每一帧按照该方法计算, 即可得到$m$帧的平均动作${A_{{\mathrm{avg}}}} = {A_{{\mathrm{avg}}1}}, {A_{{\mathrm{avg}}2}}, \cdots, {A_{{\mathrm{avg}}m}}$.

之后计算动作中每一帧的关节三维坐标的标准差绝对值, 以第1帧的第1个关节$A_1^1$为例, 通过之前的计算可以得到该关节的三维坐标平均值, 即${x_{{\mathrm{avg1}}}}$、${y_{{\mathrm{avg}}1}}$、${{\textit{z}}_{{\mathrm{avg}}1}}$, 通过式(7)–式(9)计算该关节的三维坐标的标准差绝对值:

$ {s_x} = \left| {\sqrt {\frac{{({{(A_1^1)}_x} - {x_{{\mathrm{avg}}1}})_{}^2 + ({{(B_1^1)}_x} - {x_{{\mathrm{avg}}1}})_{}^2}}{{2 - 1}}} } \right| $

(7)

$ {s_y} = \left| {\sqrt {\frac{{({{(A_1^1)}_y} - {y_{{\mathrm{avg}}1}})_{}^2 + ({{(B_1^1)}_y} - {y_{{\mathrm{avg}}1}})_{}^2}}{{2 - 1}}} } \right| $

(8)

$ {s_{\textit{z}}} = \left| {\sqrt {\frac{{({{(A_1^1)}_{\textit{z}}} - {{\textit{z}}_{{\mathrm{avg}}1}})_{}^2 + ({{(B_1^1)}_{\textit{z}}} - {{\textit{z}}_{{\mathrm{avg}}1}})_{}^2}}{{2 - 1}}} } \right| $

(9)

然后通过$ {x_{{\mathrm{avg}}1}} \pm {s_x} $、$ {y_{{\mathrm{avg}}1}} \pm {s_y} $、$ {{\textit{z}}_{{\mathrm{avg}}1}} \pm {s_{\textit{z}}} $可以得到该关节在该动作的第1帧可能会存在的范围, 通过对所有关节进行计算可以得到该动作第1帧的姿态范围, 进而得到动作范围, 将动作范围的两个边界动作作为模板加入个体层对应的个体节点中.

动作分类层次结构包括动作实例层和动作类别层, 动作实例层是所有动作数据, 动作类别层是不同动作类别的模板. 为了使动作类别层的动作模板能够表示不同人做的同一动作, 选择个体分类层次结构中的平均动作作为模板加入动作类别层.

4.4 特征提取

在提取特征前, 需要对动作数据进行处理, 将动作的三维关节坐标处理成以髋关节为中心的坐标系.

动作是时间上的运动序列, 所以提取动作的空间距离特征和时间序列特征. 典型方案如Yang等人^[5]和Ellis等人^[14]的, 计算每一帧内所有关节对之间的坐标差、后一帧与前一帧对应关节之间的坐标差作为动作的特征. 基于该思路, 提出骨架特征的提取方案.

由于识别模型中有两种类型的层次结构, 所以对于不同的层次结构, 需要考虑不同的影响因素. 对于动作分类层次结构而言, 需要将不同的动作类别区分开来, 因此, 为了减少因身高等因素导致的不同人的同一动作之间的差异过大, 提取特征时, 对数据进行归一化处理. 本文使用的公开数据集中, 每个动作序列中都有人的站姿, 而竖直方向坐标轴为$ {\textit{z}} $坐标轴, 因此取每个动作序列中所有头部关节的${\textit{z}}$值最大值$ {{\textit{z}}_{\max }} $和两个足关节${\textit{z}}$值的最小值$ {{\textit{z}}_{\min }} $的差作为人的高度, 并把所有人体高度归一化为高度$ {L_0} $ (本文设定为1.8 m)^[15] , 即关节坐标除以$ {{\textit{z}}_{\max }} - {{\textit{z}}_{\min }} $后再乘以$ {L_0} $. 而对于个体分类层次结构而言, 需要从同一动作中区分出不同个体, 那么就需要考虑个体之间的差异, 在进行特征提取时, 使用原始三维坐标数据.

设骨架有$ N $个关节, 那么每一帧$ X $可以表示为$ X = \{ {x_1}, {x_2}, \cdots, {x_N}\} ,\; X \in {R^{3 \times N}} $, $ {x_1}, {x_2}, \cdots, {x_N} $是每个关节点的三维坐标. 若一个动作有$ F $帧, 那么可按以下方式提取特征.

首先, 以髋关节为中心, 计算每一帧内其余关节与髋关节的坐标差, 表示运动过程中姿态的空间结构特征, 记为$ fcc \in {R^{F \times 3 \times N}} $:

$ fcc = \{ {x_i} - {x_k}\mid {j, k = 1, 2, \cdots, N;j \ne k} \} $

(10)

然后计算后一帧与前一帧对应关节的坐标差, 表示动作的时间序列特征, 记为$ fcp \in {R^{(F - 1) \times 3 \times N}} $:

$ fcp = \{ x_j^c - x_k^p\mid {x_j^c \in {X_c};x_k^p \in {X_p}} \} $

(11)

为了表示动作的整体运动, 计算每一帧与初始帧之间对应关节的坐标差, 记为$ fci \in {R^{F \times 3 \times N}} $:

$ fci = \{ x_j^c - x_k^i\mid {x_j^c \in {X_c};x_k^i \in {X_i}} \} $

(12)

最后将3种特征组合起来作为每一帧的特征.

4.5 分类过程

构建完识别模型后, 先对动作类别进行分类, 然后去对应的个体层次结构中对个体类别进行分类. 动作分类和个体分类的过程是一样的.

从根节点向下层分类时, 先尝试使用最近邻算法. 假设有两个骨架动作${A_1}$和${A_2}$, 它们的帧数分别是${F_1}$和${F_2}$, 且骨架有$N$个关节, 为两个动作提取3种特征, 然后分别为3种特征计算距离. 计算距离时, 计算${A_1}$中每一帧的特征与${A_2}$中所有帧的特征之间的欧氏距离之和, 而两帧特征之间的距离是所有对应关节的欧氏距离. 为了消除因动作帧数不同而产生的影响, 计算完距离后, 要除以两个动作帧数的乘积. 由于提取3种不同类型的特征, 所以在进行分类时, 每种特征分别使用最近邻算法进行计算, 然后再计算3种特征的距离和. 计算距离公式如下:

$ Dcc = \frac{{\displaystyle\sum\limits_{i = 1}^{F_1} {\displaystyle\sum\limits_{j = 1}^{F_2} {\sqrt {\displaystyle\sum\limits_{s = 1}^N {{{(fcc_i^s - fcc_j^s)}^2}} } } } }}{{F_1 \times F_2}} $

(13)

$ Dcp = \frac{{\displaystyle\sum\limits_{i = 1}^{F_1 - 1} {\displaystyle\sum\limits_{j = 1}^{F_2 - 1} {\sqrt {\displaystyle\sum\limits_{s = 1}^N {{{(fcp_i^s - fcp_j^s)}^2}} } } } }}{{(F_1 - 1) \times (F_2 - 1)}} $

(14)

$ Dci = \frac{{\displaystyle\sum\limits_{i = 1}^{F_1} {\displaystyle\sum\limits_{j = 1}^{F_2} {\sqrt {\displaystyle\sum\limits_{s = 1}^N {{{(fci_i^s - fci_j^s)}^2}} } } } }}{{F_1 \times F_2}} $

(15)

最后将3种特征之间的距离加在一起作为最终距离:

$ D = Dcc + Dcp + Dci $

(16)

得到距离后, 可以选择层次结构中最有可能的节点继续向下搜索, 直到到达最后一层.

但是使用最近邻算法来计算动作之间的距离时, 它会将不同时间区域的帧之间的距离也纳入计算当中, 这是不符合比较思想的. 不同的个体在做同一动作时, 会有差异性, 他们的动作幅度、帧数等都不相同, 甚至同一人做同一动作的不同次数也会有差距, 但是同一个体做的动作在时间序列上存在整体相似性, 因此在进行分类时, 需要考虑时间序列上的整体相似性. 所以使用动态时间规整将输入动作与模板动作在时间上进行对应, 输入动作的每一帧都会与模板动作距离较近某一帧进行对应, 并且在时间上也会进行对应, 然后再计算得到距离.

4.6 关键姿态提取

动作是时间上的姿态序列, 但姿态序列中所有的姿态并非同样重要, 人类的动作有时可以从几个姿态识别出来, 这些特定的姿态被称为关键姿态. 动作中每一帧相当于一个静态姿态, 关键姿态在动作的时间序列中不一定相邻.

通过帧消减法^[16]提取动作模板的关键姿态候选序列, 首先将第一帧作为候选关键姿态, 然后计算后续的帧与第1帧的距离, 如果小于阈值, 则舍弃, 如果大于阈值, 则该帧加入候选关键姿态, 然后再计算后面的帧与该帧之间的距离, 以此类推, 同时保留最后一帧作为候选关键姿态. 得到候选关键姿态后, 再进行人工筛选, 选择最具有代表性的姿态作为关键姿态.

4.7 姿态对应

使用动态时间规整可以将输入动作的姿态与模板的姿态进行对应. 由于动作的帧序列太长, 因此选择同一人做的两次挥手动作的关键姿态为例. 设两次挥手动作的关键姿态序列为$Q$和$C$, 且长度分别为$n$和$m$, 即:

$ Q = \{ {q_1}, {q_2}, \cdots, {q_n}\} $

(17)

$ C = \{ {c_1}, {c_2}, \cdots, {c_m}\} $

(18)

然后创建一个$n \times m$的矩阵网格, 矩阵中的格点中的距离$ d({q_i}, {c_j}) $使用选择欧氏距离进行计算, 即:

$ d({q_i}, {c_j}) = \sqrt {\sum\limits_{s = 1}^N {{{(q_i^s, c_j^s)}^2}} } $

(19)

其中, $ N $是骨架关节数.

挥手动作$Q$和$C$都有6帧关键姿态, 姿态之间的距离如表2所示, 由于得到的距离小数位数过多, 所以只保留6位小数. 然后通过计算可以得到累计距离矩阵, 结果如表3所示. 通过反推可以得到匹配路径, 在表3中通过加粗区域标记出路径.

然后选择$g(6, 6)$作为姿态对应的累计路径, 由于动作的帧数以及关键姿态帧数不同, 所以累计距离要除以姿态数量之和, 以消除影响, 得到最终结果${D_{{\mathrm{avg}}}}$:

$ {D_{{\mathrm{avg}}}} = \frac{{g(6, 6)}}{{6 + 6}} $

(20)

4.8 基于关键姿态的识别模型

根据关键姿态序列, 人们可以分辨出是什么动作. 本节的研究目的在于使用动作的关键姿态进行动作和个体的识别, 以探索动作和姿态之间的关系.

例如, 为某个体的挥手动作选择的关键姿态如图3所示. 从关键姿态图中可以看到, 只看关键姿态之间的变化过程, 也能够区分出个体做的是什么动作, 所以关键姿态能够表示动作信息.

为模板动作提取关键姿态, 然后将动作分类层次结构和个体分类层次结构动作模板使用关键姿态序列模板进行替换, 之后的分类过程不变.

4.9 基于动作分解的识别模型

在之前的实验中计算距离时, 将所有身体部位的关节之间的距离累加在一起作为判断, 但是不同动作有着不同的运动部位, 如果使用累加和进行度量, 会出现某个动作因为无关部位的影响而被分到另外一类动作中, 亦或者某个手脚运动幅度小的动作被错分到某个手部运动剧烈的动作中等情况.

为了尽可能地消除这种影响, 对人体进行部位分解: 左手、右手、左腿、右腿、躯干, 然后根据所有样本给不同的部位划分出不同的动作. 对第1组动作数据的部位动作划分如表4所示, 可以看到挥手动作会存在着左手挥手、右手挥手、坐着挥手等状态, 对同一动作的不同表现形式要全部记录下来.

然后为不同的部位创建不同的分类层次结构, 构造方法与第4.1节中所述的方法相似, 但是只关注不同部位对应的关节, 即在提取模板时, 以部位的方式提取模板. 以左腿为例, 为左腿创建伸直、弯曲、静止、弯曲静止4个个体部位分类层次结构, 如图4所示. 然后选择部位动作的平均动作模板去构建左腿动作分类层次结构, 如图5所示.

对于挥手动作的左腿而言, 会存在静止和弯曲静止两种状态, 虽然都是静止, 但是为了分类的准确性, 最好将这两种状态区分开来, 其余部位的层次结构也类似.

对动作进行分类时, 先使用动态时间规整算法对不同的部位进行分类, 可以知道不同部位做的是什么动作, 得到5个部位的结果. 然后根据整体动作的关键部位进行选择, 即选择满足这些整体动作关键部位最多的动作类别作为最终结果, 不同动作的关键部位如表, 不同动作的关键部位如表5所示. 假设有双臂摆动动作类别和步行动作类别, 将一个步行动作数据输入到系统中, 它可能会满足两个动作类别的关键部位要求, 但是这时候选择步行动作类别作为最终的分类结果, 因为它有更多的部位满足步行动作. 如果存在满足多个动作类别的情况, 那么使用全部关节进行判断, 将动作数据输入到前面提出的动作分类层次结构中.

得到动作类别后, 将其输入到对应动作的个体分类层次结构中. 对个体进行分类时也需要分部位进行分析, 但是只需要对动作对应的关键部位进行分析即可. 在动作分类时已经可以得到左手或右手处于什么状态, 将其输入到对应的分类层次结构中.

对个体进行分类时, 使用动态时间规整算法对动作对应的关键部位分别进行个体分类. 例如为一个拍手动作样本进行个体分类, 可以分别对左手和右手进行个体分类, 得到两个部位的结果, 然后选择满足个体条件最多的个体类别作为分类结果, 如果出现满足多个个体类别的情况, 例如挥手动作的左手被分到个体${P_1}$, 而右手被分到个体${P_2}$, 那么将该数据输入到全部关节的个体分类层次结构中进行二次判断得到结果.

5 实验分析 5.1 基于层次结构的动作识别方法实验结果

实验结果主要对动作分类准确率以及在动作准确的情况下个体分类准确率进行分析, 首先是使用最近邻进行分类, 第1组数据的结果如表6所示. 从结果中可以看到, 对动作类别的识别有着较高的准确率, 但是对个体的分类效果并不好, 这是因为将所有时间区域内的帧都纳入计算中导致的. 然后使用DTW方法进行分类, 结果如表6所示, 通过结果可以发现, 使用时间动态规整后, 拍手与双手交叉的动作识别准确率有所提升, 并且所有动作的个体识别准确率也都有提升. 从两种方法的结果可以得知, 姿态之间的时间关系是非常重要. 因此之后的第2组与第3组实验都使用动态时间规整算法, 结果如表7所示.

5.2 基于关键姿态的识别模型实验结果

得到动作模板的关键姿态后, 由于动作模板的关键姿态之间的时间跨度较大, 所以从中提取时间特征后进行比较是不合理的, 所以直接使用动作的空间特征进行计算.

该部分实验在第1组和第3组数据上进行实验, 首先对第1组数据使用最近邻算法, 对动作分类的混淆矩阵结果如表8所示. 从混淆矩阵中发现效果并不好, 尤其是对起立和坐下两个动作. 使用最近邻算法时, 这两个动作会互相错分到对方的类别当中, 这是因为起立和坐下都只有两个关键姿态, 并且两个关键姿态在时间上的顺序刚好相反, 在使用最近邻时, 没有考虑两个动作的关键姿态之间的时间关系, 因此对于这两个动作的计算结果非常接近, 所以导致了错误分类. 所以, 姿态之间的时间关系是非常重要的, 下面对第1组和第3组数据使用动态时间规整的方法进行实验.

使用动态时间规整的结果如表9所示. 通过对结果的数据分析发现, 模型的效果还可以, 动作的分类准确率和个体的分类准确率都大幅度提升, 坐下和起立两个动作也能正确分类, 说明关键姿态序列能够表示整个动作, 同时也再次说明了姿态之间时间关系的重要性.

5.3 基于动作分解的识别模型实验结果

当有输入动作时, 将不同的部位分别输入到对应的分类层次结构中, 得到每个部位的动作类别后, 选择最大程度满足条件的整体动作作为最后的分类结果. 得到动作类别后, 将其输入到动作对应的个体分类层次结构中, 在个体分类层次结构中, 只需要使用关键部位即可. 将关键部位输入到对应的部位层次结构中, 最后选择满足条件的个体.

首先使用所有帧进行分类, 然后使用关键姿态进行分类, 两种方法在第1组和第3组数据的分类结果如表10和表11所示. 从两个结果中可以看到, 无论是动作的识别准确率还是个体的识别准确率都很高, 这说明人的整体动作可以根据部位进行分解. 通过对不同部位做的动作进行分析, 可以反推得到整体动作. 但是使用关键姿态会降低个体的分类准确率.

6 总结

本文对基于三维骨架的人体动作识别技术进行探讨, 提出了一个基于知识的、白盒的、可解释的识别系统. 首先植入了动作层级之间的关系, 建立了一颗利用层级关系的搜索树, 利用搜索树能够减少冗余比较, 加快搜索速度. 从结果中看到对动作的分类准确率高, 但是对个体的分类准确率却并不理想. 之后使用动态时间规划将输入动作与模板动作在时间关系上进行对应, 提高了对个体识别的准确率. 然后探索姿态与动作之间的关系, 为模板动作提取关键姿态, 将关键姿态知识植入系统. 使用动态时间规整, 将关键姿态之间的时间关系、关键姿态与输入动作的姿态之间的时间关系一一对应, 从结果可以看到, 动作与个体的识别效果都不错, 说明动作可以看作是一系列关键姿态在时间上的序列. 最后, 为了减少在判断动作时所有关节的累加和对最终分类结果的影响, 将人体划分5个部位, 通过分别对5个部位所作的动作进行分析, 综合考虑后反推身体的整体动作, 并且取得了较高的识别准确率.