部分线性模型兼具参数模型和非参数模型之长, 以其灵活性著称. 自从Engle等^[1]首次提出该模型用于描述城市气候对电力消耗的影响以来, 已获得众多学者关注, 涌现出大量相关研究^[2–4]. 样条方法^[5]、分段多项式近似方法^[6], 以及缺失数据的情况^[7–9]等, 都已被纳入这一模型的讨论中. 这些工作极大丰富了部分线性模型的理论和实践应用. 然而, 它们并未考虑大数据应用的两个重大挑战: 计算时间和数据存储. 尤其在数据流场景下, 随着数据的不断积累, 存储需求激增, 每次新数据收集之后都需要对整个数据集重复进行统计分析. 冗杂的计算过程和过高的计算成本, 使得部分线性模型的传统估计计算方法变得不切实际.

近年来, 大数据模型的分析主要遵循3种方法. 第1种是子采样方法(subsampling-based)^[10–14], 该方法在回归模型中得到有效应用, 能有效处理大多数大数据场景. 然而, 经过子抽样获得的有限样本可能会遗漏关键信息, 导致估计不准确; 第2种方法是分治集成法^[15–18](divide-and-conquer), 其主要思路是将大数据集划分为若干子集从而把问题化繁为简. 例如, 在部分线性模型研究中, Zhao等^[19]提出的集成核岭回归方法、Lian等^[20]基于分治集成的投影样条方法. 然而分治集成法和子采样法均依赖于完整数据集, 在现实问题中, 大数据的完整收集通常需要漫长的等待时间. 如果是数据流形式的大数据, 数据更是持续生成而不会停止.

除了前面提到的两种方法, 第3种用于处理大数据模型的方法就是顺序更新法 (sequential-updating). 该方法特别适用于数据流, 因为它能够实时分析, 无需大量存储. 本文后面内容将这种方法称作在线估计方法, 英文写作“ONLINE”, 以区别于每次需要使用所有原始数据重新运行分析的传统方法, 把传统方法写作“OFFLINE”. 近年来关于在线估计方法的研究多见于线性回归模型^[21–24], 对于非参数回归模型, Kong等^[25]提出了一种基于核回归的在线估计方法, 并将其扩展到变系数模型. 由于部分线性模型是一种特殊的变系数模型, 所以也能勉强算作一种部分线性模型的在线估计方法. 然而该方法是根据每一个新到数据点更新估计, 并且基于协变量固定在某点处进行在线计算. 如果使用这种方法处理部分线性模型, 需要假设变系数模型的某些函数项为常数以作为部分线性模型的参数$ \beta $, 这就会使得当固定点选择不当时, 核估计的边界效应将会使得这些函数项的估计效果大打折扣, 参数$ \beta $的估计随着固定点的不同而有较大波动, 可能导致较大的偏差. 因此, 当前亟需一种能够有效处理数据流场景下部分线性模型的分析方法.

本文旨在解决将部分线性模型应用于大数据流时遇到的分析挑战. 为此提出了一种基于部分线性模型两步估计方法的在线更新估计方法. 与以往的研究不同, 本文方法在更新估计参数时不需要考虑选取协变量为合适的给定值. 对于非线性部分, 本文基于Nadaraya-Watson回归和局部线性核回归给出两个在线更新估计量. 通过对线性部分和非线性部分的分开估计从而完成了整个部分线性模型的在线估计. 本文的方法以数据块为单位进行处理, 仅利用当前数据和每次更新的一些汇总统计量, 从而确保了每次更新计算时间的基本一致. 与OFFLINE方法相比, 该方法不会因总样本量的增加而导致计算时间和存储需求的不断增加, 因此在计算效率和成本控制方面具有明显优势.

1 部分线性模型与其大数据估计计算问题

本节首先给出本文研究的对象, 即部分线性模型, 然后再阐述传统方法在数据流场景下所面临的计算难题.

1.1 部分线性模型

假设有n个i.i.d.随机样本$\left\{ {\left( {{y_i}, {{{{x}}}_i}, {{\textit{z}}_i}} \right), i = 1, 2, \cdots , n} \right\}$, 部分线性模型通常表示为:

$ {y_i} = {{\boldsymbol{x}}}_i^ \top {{\beta}} + g\left( {{{\textit{z}}_i}} \right) + {{\varepsilon }_i}, \;\;\;i = 1, \cdots , n $

(1)

其中, 协变量${{{{x}}}_i} \in {\mathbb{R}^p}$、${{\textit{z}}_i} \in {\mathbb{R}^{{q}}}$, 响应变量${y_i} \in \mathbb{R}$. ${{\beta}} $为有限维的参数向量, $g( \cdot )$是一个未知的光滑函数, ${{\varepsilon }_i}$是随机误差项.

1.2 数据流下传统估计方法的计算问题

考虑样本以数据流的形式依次独立被收集, 根据Li^[26]的参数估计方法, 有:

$ \hat {{\beta}} = {\left[ {\sum\limits_{i = 1}^n {{{{\tilde {{x}}}}_i}} {\tilde {{x}}}_i^ \top \hat f_i^2} \right]^{ - 1}}\sum\limits_{i = 1}^n {{{{\tilde {{x}}}}_i}} {\tilde y_i}\hat f_i^2 $

(2)

其中, ${{\tilde {{x}}}_i} = {{{{x}}}_i} - {{\hat {{x}}}_i}$, ${\tilde y_i} = {y_i} - {\hat y_i}$, ${\hat f_i}$是$ {{\textit{z}}_i} $处的核密度估计; ${{\hat {{x}}}_i}$和${\hat y_i}$分别是条件期望$ \mathbb{E}\left( {{{{{x}}}_i}|{{\textit{z}}_i}} \right) $和$\mathbb{E}\left( {{y_i}|{{\textit{z}}_i}} \right)$的NW估计, 即${{\hat {\textit{x}}}_i} = \displaystyle\sum\nolimits_{j = 1}^n {{{\omega }_j}} ({{\textit{z}}_i}){{{\textit{x}}}_j}$, ${\hat y_i}$的计算同理, 这里${{\omega }_j}( \cdot )$是NW估计中所使用的权函数.

式(2)的传统方法在数据流场景下的计算问题在于, 每次新数据的到来, 使用式(2)进行更新计算$\hat {{\beta}} $, 都需要访问所有历史数据重新计算估计量集合$\left\{ \left( {{{{\hat {{x}}}}_i}, {{\hat y}_i}, {{\hat f}_i}} \right),\right. \left. i = 1, 2, \cdots , n \right\}$. 因此, 在计算时间方面, 随总样本量$n$的不断增加, 每次更新所耗时间将不断增加, 且没有上限. 在存储方面, 由于原始数据需要完整保留, 存储消耗也将持续增加. 此外, 非参数部分$\mathbb{E}\left( {{y_i} - {x}_i^ \top \hat {{\beta}} |{{\textit{z}}_i}} \right) = g\left( {{{\textit{z}}_i}} \right)$的估计, 以及所用到核估计中带宽h的重新计算也涉及对所有历史数据的访问, 意味着同样的问题. 上述要求使得传统方法对数据流下部分线性模型的计算难以在单台计算机上实现.

2 部分线性模型的在线更新估计方法

考虑流数据以数据块的形式依次独立被收集, 则式(1)的模型改写为:

$ {{y}_l} = {{{X}}_l}{{\beta}} + g\left( {{{{Z}}_l}} \right) + {\varepsilon _l}, \quad l = 1, 2, \cdots $

(3)

其中, 样本矩阵${{{X}}_l} \in {\mathbb{R}^{{n_l} \times p}}$、${{{Z}}_l} \in {\mathbb{R}^{{n_l} \times q}}$, 向量${{y}_l} \in {\mathbb{R}^{{n_l}}}$. 第l个数据块$\left\{ {\left( {{y_{l, m}}, {{x}_{l, m}}, {{\textit{z}}_{l, m}}} \right), m = 1, 2, \cdots , {n_l}} \right\}$是样本量为${n_l}$的数据子集. 记在终点$K$处的总样本量表示为${N_K} = \displaystyle\sum\nolimits_{k = 1}^K {{n_k}} $, 总样本矩阵表示为${{X}} = {({{X}}_1^ \top , \cdots , {{X}}_K^ \top )^ \top }$, ${{Z}} = {({{Z}}_1^ \top , \cdots , {{Z}}_K^ \top )^ \top }$, 响应变量${y} = {({y}_1^ \top , \cdots , {y}_K^ \top )^ \top }$.

本节将详细介绍针对式(3)的模型而设计的在线估计方法, 以解决第1节中传统方法带来的问题. 该方法基于两步估计过程, 首先是对模型参数部分的在线估计, 这一步骤涉及对模型中的参数进行动态更新. 然后是非参数部分的在线估计, 给出基于局部核回归的具体计算过程以及带宽的选取方式.

2.1 参数部分的在线更新估计

当第k个数据块到达时, 单独使用该样本子集对参数获得一个估计${\hat {{\beta}} _{k, {n_k}}}$, 由式(2)有:

$ {\hat {{\beta}} _{k, {n_k}}} = {\left( {\tilde {{X}}_k^ \top {{{W}}_k}{{\tilde {{X}}}_k}} \right)^{ - 1}}\left( {\tilde {{X}}_k^ \top {{{W}}_k}{{{{\tilde y}}}_k}} \right) $

(4)

其中, ${{{W}}_k} = {{\mathrm{diag}}} \{ \hat f_{k, 1}^2, \cdots , \hat f_{k, {n_k}}^2\} $, ${\tilde {{X}}_k}$和$ {{{\tilde y}}_k} $的计算类似于第1节中的${{\tilde x}_i}$和${\tilde y_i}$. 然而式(4)单独使用当前数据子集并不能概括完整信息, 因此需要合并历史分析再次计算. 设${\tilde {{\beta}} _{k - 1}}$是在时间点$k - 1$得到的在线更新估计, 则在时间点k对参数${{\beta}} $的在线更新估计可以通过${\tilde {{\beta}} _{k - 1}}$和新的数据子集来计算得到:

$ {\tilde {{\beta}} _k} = {\left( {{{{V}}_{k - 1}} + \tilde {{X}}_k^ \top {{{W}}_k}{{\tilde {{X}}}_k}} \right)^{ - 1}}\left( {{{{V}}_{k - 1}}{{\tilde {{\beta}} }_{k - 1}} + \tilde {{X}}_k^ \top {{{W}}_k}{{\tilde {{X}}}_k}{{\hat {{\beta}} }_{k, {n_k}}}} \right) $

(5)

其中, ${{{V}}_k} = \displaystyle\sum\nolimits_{l = 1}^k {\tilde {{X}}_l^ \top } {W_l}{\tilde {{X}}_l}$, $k = 1, 2, \cdots $, 初始值$ {{{V}}_0} $和${\tilde {{\beta}} _0}$设置为$ {{{V}}_0} = {0} $, ${\tilde {{\beta}} _0} = {0}$.

式(5)的在线估计量${\tilde{{ \beta}} _k}$借鉴了Schifano等^[21]针对数据流下线性模型的在线估计方法, 目的是在部分线性模型中, 随着每次新数据块的加入, 参数估计值从${\tilde {{\beta}} _{k - 1}}$到${\tilde {{\beta}} _k}$的持续更新优化. 在计算过程中, 每次只需保留上一个时刻更新计算所得统计量 (${{{V}}_{k - 1}}$, ${\tilde {{\beta}} _{k - 1}}$), 并在当前更新步骤中根据最新观测数据子集计算新的统计量 ($ \tilde {{X}}_k^ \top {{{W}}_k}{\tilde {{X}}_k} $, ${\hat {{\beta}} _{k, {n_k}}}$). 式(5)更新估计的计算复杂度约为$ {\mathrm{O}}(n_k^2p{\text{+}}{{{p}}^3}) $, 空间复杂度${\mathrm{O}}(n_k^{}p + {n_{{k}}}q + {p^2})$. 而传统方法的计算复杂度约为${\mathrm{O}}(N_k^2p{\text{+}}{{{p}}^3})$, 空间复杂度${\mathrm{O}}(N_kp +N_kq + {p^2})$. 因此在线估计方法不仅操作简便, 而且在处理数据流的分析中计算成本更低, 能快速对参数估计持续更新.

值得注意的是, 在普通最小二乘(OLS)估计中, 通常假设设计矩阵是列满秩的. 同样, 在式(4)和式(5)中也需要确保可逆性假设. 然而式(4)可以给出另一种表达形式$\tilde {{X}}_k^ \top {{{W}}_k}{\tilde {{X}}_k}{\hat {{\beta }}_{k, {n_k}}} = \tilde {{X}}_k^ \top {{{W}}_k}{{{\tilde y}}_k}$, 这意味着在式(5)中可以不直接使用${\hat \beta _{k, {n_k}}}$, 因此并不要求矩阵$\tilde {{X}}_1^ \top {{{W}}_1}{\tilde {{X}}_1}$, $ \tilde {{X}}_2^ \top {{{W}}_2}{\tilde {{X}}_2} $, …, $\tilde {{X}}_k^ \top {{{W}}_k}{\tilde {{X}}_k}$均可逆. 如果初始权重矩阵$\tilde {{X}}_1^ \top {{{W}}_1}{\tilde {{X}}_1}$是奇异的, 按照 Schifano等^[21]提供的方法, 可以采用类似于岭回归的策略. 具体来说, 更改初始设置为${{{V}}_0} = \lambda {{{I}}_p}\;(\lambda > 0)$开始进行更新估计, 而不是从${{{V}}_0} = {0}$开始. 直到进行足够多次数的更新, 在不影响式(5)中正常求逆计算的情况下, 可以去除$\lambda {{{I}}_p}$项.

2.2 非参数部分的在线更新估计

两步估计法通过用估计结果替换部分线性模型的参数部分, 从而将模型简化成非参数回归估计. 因此, 本文方法第2步的目标是对非参数部分进行在线更新估计, 即估计$g({\textit{z}}|\hat {{\beta}} )$. 在本节中, 首先将介绍使用局部常数核估计的在线更新估计量, 这是一种比较简单的方法. 然后, 为了提高估计过程的精确度和适应性, 本文将此方法扩展到基于局部线性核估计的在线估计.

2.2.1 基于局部常数核估计的在线更新估计

为简化处理, 这里首先定义几个重要的汇总统计量, 旨在有效压缩并准确概括截止至时间点k的累积数据集信息. 具体定义如下所示:

$ {{{G}}_k}({\textit{z}}, {{{y}}}) = \sum\limits_{l = 1}^k {\sum\limits_{m = 1}^{{n_l}} {{K_{{h_l}}}} } \left( {{{\textit{z}}_{l, m}} - {\textit{z}}} \right){y_{l, m}} $

(6)

$ {{{G}}_k}({\textit{z}}, {{X}}) = \sum\limits_{l = 1}^k {\sum\limits_{m = 1}^{{n_l}} {{K_{{h_l}}}} } \left( {{{\textit{z}}_{l, m}} - {\textit{z}}} \right){{{{x}}}_{l, m}} $

(7)

以及

$ {{{G}}_k}({\textit{z}}) = \sum\limits_{l = 1}^k {\sum\limits_{m = 1}^{{n_l}} {{K_{{h_l}}}} } \left( {{{\textit{z}}_{l, m}} - {\textit{z}}} \right) $

(8)

其中, 符号${K_{{h_l}}}( \cdot )$表示具有带宽${h_l}\;( > 0)$的核函数, 即${K_{{h_l}}}( \cdot ) = K( \cdot /{h_l})/h_l^q$.

通过这些汇总统计量, 结合第2.1节得到的参数估计${\tilde {{\beta}} _k}$, 非参数部分的局部常数核估计的在线计算形式可表示为:

$ {\hat g_k}({\textit{z}}|{\tilde {{\beta}} _k}) = \frac{{{{{G}}_k}({\textit{z}}, {y}) - {{G}}_k^ \top ({\textit{z}}, {{X}}){{\tilde {{\beta}} }_k}}}{{{{{G}}_k}({\textit{z}})}} $

(9)

式(9)所采用的在线估计方法与第2.1节式(5)的参数估计更新方法存在细微差别. 具体地, 式(5)通过保留前一时刻的估计值${\tilde {{\beta}} _{k - 1}}$来更新估计${\tilde {{\beta }}_k}$, 但在式(9)中, 计算${\hat g_k}({\textit{z}}|{\tilde {{\beta}} _k})$不需要保留${\hat g_{k - 1}}({\textit{z}}|{\tilde {{\beta}} _{k - 1}})$, 而是直接使用最新的汇总统计量及参数估计值${\tilde {{\beta}} _k}$进行计算. 此外, 更新汇总统计量的过程仅涉及将先前的汇总统计量$\left\{ {{{{G}}_{k - 1}}({\textit{z}}), {{{G}}_{k - 1}}({\textit{z}}, {y}), {{{G}}_{k - 1}}({\textit{z}}, {{X}})} \right\}$与新数据块中的统计量进行简单的加法处理. 因此, 相较于OFFLINE方法使用所有原始数据的重新计算, 式(9)的计算和存储开销均能显著降低.

2.2.2 基于局部线性核估计的在线更新估计

为了下文清晰地阐述, 记${{\textit{z}}_{l, m}}({\textit{z}}) = {\left[ {1, {{({{{\textit{z}}}_{l, m}} - {\textit{z}})}^ \top }} \right]^ \top }$. 在此基础上, 引入与前文类似的汇总统计量, 具体如下:

$ {{{S}}_k}({\textit{z}}, {{{y}}}) = \frac{1}{{{N_k}}}\sum\limits_{l = 1}^k {{{Z}}_l^ \top } ({\textit{z}}){{{\varOmega }}_l}({\textit{z}}){{{{y}}}_l} $

(10)

$ {{{S}}_k}({\textit{z}}, {{X}}) = \frac{1}{{{N_k}}}\sum\limits_{l = 1}^k {{{Z}}_l^ \top } ({\textit{z}}){{{\varOmega }}_l}({\textit{z}}){{{X}}_l} $

(11)

以及

$ {{{S}}_k}({\textit{z}}) = \frac{1}{{{N_k}}}\sum\limits_{l = 1}^k {{{Z}}_l^ \top } ({\textit{z}}){{{\varOmega }}_l}({{\textit{z}}}){{{Z}}_l}({{z}}) $

(12)

其中, ${{{Z}}_l}({\textit{z}}) = {[{{\textit{z}}_{l, 1}}({\textit{z}}), \cdots , {{\textit{z}}_{l, {n_l}}}({\textit{z}})]^ \top }$, ${{{\varOmega }}_l}({\textit{z}})$表示对角矩阵${{\mathrm{diag}}} \{ {K_{{h_l}}}({{\textit{z}}_{l, 1}} - {\textit{z}}), \cdots , {K_{{h_l}}}({{\textit{z}}_{l, {n_l}}} - {\textit{z}})\} $. 据此, 基于局部线性核估计的在线更新可构建为:

$ {\tilde g_k}({\textit{z}}|{\tilde {{\beta}} _k}) = {{{e}}^ \top }{\left[ {{{{S}}_k}({\textit{z}})} \right]^{ - 1}}\left[ {{{{S}}_k}({\textit{z}}, {{{y}}}) - {{{S}}_k}({\textit{z}}, {{X}}){{\tilde {{\beta}} }_k}} \right] $

(13)

其中, ${{e}} = {(1, 0, \cdots , 0)^ \top } \in {\mathbb{R}^{q + 1}}$. 如同式(9)一样, 式(13)在线估计的计算量大约只是单个子数据集的计算, 但由于基于局部线性核估计的OFFLINE方法的计算复杂度非线性增长, 所以式(13)的计算效率提升更明显.

在核密度估计和核回归中, 带宽的选择显著影响估计的效果. 因此, 在处理部分线性模型中的X对Z的回归, y对Z的回归, 以及非参数成分对Z的回归时, 选择合适的带宽参数尤为关键. 为了提高估计精度, 本文的方法为每个数据子集中的参数和非参数部分各自使用不同的带宽. 具体地, 在子数据集不大的情况下采用CV (cross-validation)方法^[27], 而对规模较大的子数据集采用DPI (direct plug-in)方法^[28].

3 数值模拟

本节是数值模拟实验部分, 目的是验证本文提出的在线估计方法的有效性, 并与OFFLINE方法的估计结果进行数值对比分析.

3.1 随机数生成

实验所用随机数据根据式(1)的部分线性模型生成. 协变量z为一维情况下, 设真实函数$g({\textit{z}}) = 2\sin ({\text π} {\textit{z}})$, 真实参数$\beta = {(2, 1, 2)^ \top }$, 误差项服从标准正态分布. 在此设定中, 实验分别考虑Case 1和Case 2两种情形; 而对于协变量z为二维的情况, 实验则采用Case 3的假设. 3种情形的协变量分布详述如下.

Case 1: ${x}\sim N(0, {{\Sigma }})$, 其协方差矩阵${{\Sigma }} = {({\sigma _{ij}})_{3 \times 3}}$, ${\sigma _{ii}} = 1$, ${\sigma _{ij}} = 0.5\;(i \ne j)$; ${\textit{z}}\sim N(0, 1)$. 这里的x与z相互独立.

Case 2: ${x^{(j)}} = ({\textit{z}} + {U^{(j)}})/2$, 其中${x^{(j)}}$表示的是协变量x的第$j$个分量; ${\textit{z}}\sim U( - 1, 1)$; ${U^{(j)}}\sim U( - 1, 1)$, $j = 1, 2, 3$. 这里的x与${\textit{z}}$具有相互依赖关系.

Case 3: 设定函数$g({{\textit{z}}_1}, {{\textit{z}}_2}) = 2\sin ({\text π} {{\textit{z}}_1}) + 3\cos ({\text π} {{\textit{z}}_2})$, 真实参数${{\beta}} = {(1, 1, 2)^ \top }$; 这里的随机变量${{{x}}}\sim N(0, {{\Sigma }})$, ${\textit{z}}\sim N(0, {{\mathrm{diag}}} (1, 1))$; 误差项服从标准正态分布.

3.2 实验环境

每种情形都重复实验$s $=100次. 为了符合本文考虑的按块到达的数据流场景, 在每次重复实验中, 假设在数据流截止观测点$K$, 总共收集到$K$个数据块子样本, 并且其中每个子样本的样本量${n_k}$均有${n_k} = n$ $(k = 1, 2, \cdots , K)$. 为比较不同条件下的影响, 进行了两组模拟实验: 第1组实验固定总样本量${N_K}$不变, 通过改变子样本量的大小以观察其对在线估计效果的影响; 与之相反, 第2组实验则固定子样本量$n = 1000$, 通过改变总样本量${N_K}$的大小来分析更新次数与估计结果的关系.

在所有模拟计算中, 本文使用高斯核函数进行核估计. 由于涉及的部分子数据集样本量较大, 计算全程采用DPI法选取带宽. 所有实验均在配备16 GB RAM的Intel Core i5-8265U CPU上完成.

3.3 评估指标

为了评估在线估计方法和传统方法在参数${{\beta}} $上的估计表现, 本文将经验均方误差 (MSE) 用作评估指标, 其计算方式为:

$ {\textit{MSE}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{{\beta}} } ) = {s^{ - 1}}\sum\nolimits_{i = 1}^{{s}} {{{({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{{\beta}} } }_i} - {{\beta}} )^2}}} $

(14)

其中, $ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{{\beta }}} _i} $表示的是参数${{\beta}} $的任意估计量$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{{\beta}} } $在第i次重复实验中的结果. 此外, 本文还使用相对效率 (RE) 进行直观比较, 即传统方法与在线方法估计结果的MSE之比.

对于非参数部分, 本文在100个评估点上进行计算, 所以其评估指标MSE计算为:

$ {\textit{MSE}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} ) = \sum\nolimits_{i = 1}^{100} {{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} ({t_i}) - g({t_i})} \right)}^2}} \big/100 $

(15)

其中, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} ( \cdot )$是对未知函数$g( \cdot )$的任意估计. 3种情形中函数$g(t)$的评估点分别设置如下: 在Case 1中, 评估点${t_i} = - 2 + 4(i - 1)/99$, $i = 1, 2, \cdots , 100$; Case 2中, 评估点为${t_i} = - 1 + 2(i - 1)/99$, $i = 1, 2, \cdots , 100$; Case 3中, 评估点集合为$\left\{ {\left( {{t^{(1)}}, {t^{(2)}}} \right)\mid {t^{(1)}}, {t^{(2)}} \in \left\{ { - 1, - 7/9, \cdots , 1} \right\}} \right\}$, 这里的t⁽¹⁾和t⁽²⁾是函数自变量t的分量.

3.4 实验结果

(1) 计算时间对比

表1和表2分别列出了在线估计方法和传统方法的平均计算时间, 其中ONLINE列的时间表示的是在线方法单次更新估计的计算耗时, OFFLINE列代表传统方法更新估计的计算耗时, “LCR”和“LLR”分别代表基于局部常数核回归和局部线性核回归的在线估计方法. 表1和表2的结果表明本文的方法比起OFFLINE方法显著减少单次更新耗时: ONLINE方法更新参数$\beta $估计的计算耗时约是OFFLINE方法的 ${\left( {{n_k}/{N_k}} \right)^2}$倍, 基于LCR在线方法更新非参数部分估计的耗时约是OFFLINE方法的${n_k}/{N_k}$倍, 基于LLR在线方法更新非参数部分的耗时约是OFFLINE方法的 ${\left( {{n_k}/{N_k}} \right)^2}$倍. 由于子样本集的规模n_k基本不变, 耗时上的表现说明随着流数据的总样本量${N_K}$越大, 本文的在线估计方法计算效率上的优势也就越大.

(2) $\beta $估计的对比

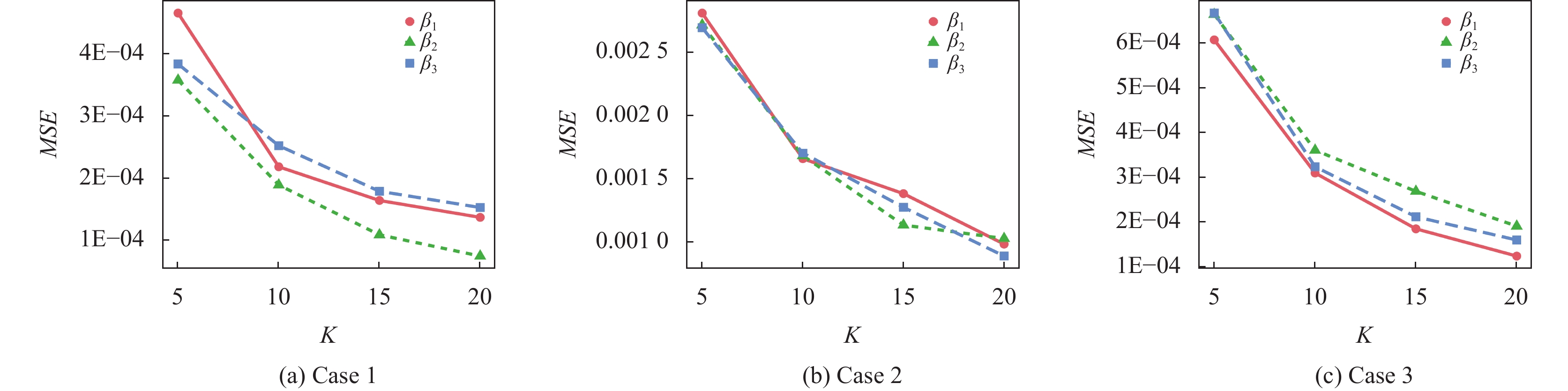
表3和表4和分别展示了使用ONLINE方法和OFFLINE方法估计${{\beta}} $的经验偏差 (Bias)、经验标准误差 (SE)、经验均方误差 (MSE) 以及相对效率 (RE). 可以看到在估计的偏差上, 在线估计量${\tilde {{\beta}} _K}$与OFFLINE估计量$\hat{{ \beta}} $的偏差很接近. 在估计的标准误差方面, 在线估计一致表现出比OFFLINE方法更低的标准误差, 这可能是因为本文的在线估计方法分块进行更新估计, 因此结果具有更好的稳定性. 此外, 固定总样本量${N_K}$, 随着单位子样本量大小的增加; 或者固定单位子样本量, 随着总更新次数K的增加 (如图1), 这两种情况下${\tilde {{\beta}} _K}$的MSE都有着稳步下降的趋势, 直到接近OFFLINE方法的基准, 相对效率接近1. 表明对于参数${{\beta}} $的估计, 本文的在线方法在均方误差上的表现接近传统方法.

(3) 函数$g( \cdot )$估计的对比

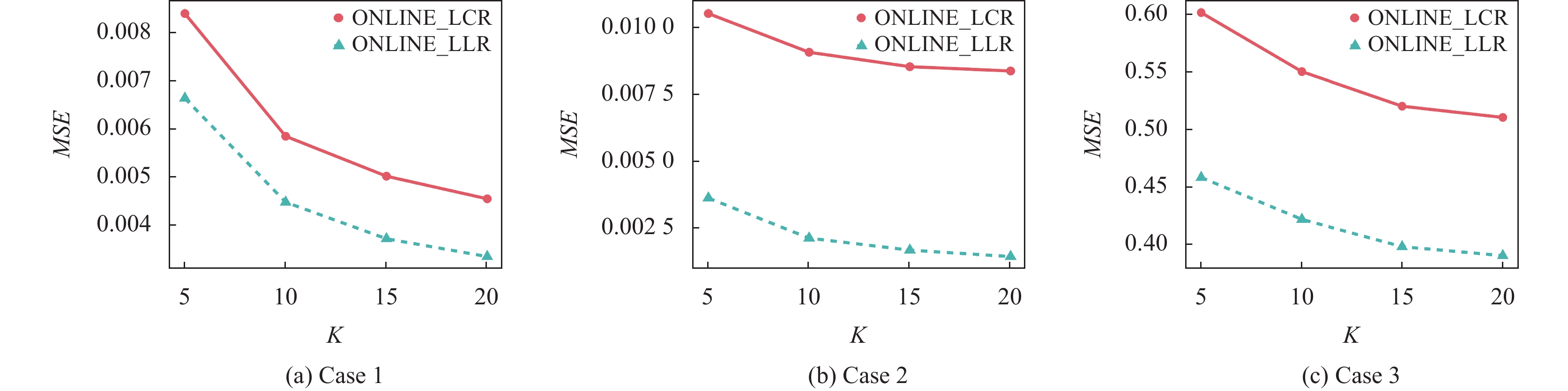
表5和表6给出了两种方法对非参数部分估计的实验结果. 表中列出100次重复实验的偏差平方、方差以及经验均方误差的平均值. 尽管在线估计量的偏差平方大多略高于OFFLINE方法, 但其值仍然较低. 此外, 估计结果的方差均低于OFFLINE方法. 结果表明, 更大的单位子样本量虽然有助于减少偏差, 但是会导致方差的增大. 而在相同的单位子样本量下, 随着更新次数的增加, 偏差平方和方差都有所降低. 总体而言, 本文的在线方法通过多次更新, 能够逐渐降低估计非参数部分的MSE, 如图2所示. 值得注意的是, 在实验的所有情形中, 基于LLR的在线估计方法相较于基于LCR的在线估计方法具有更低的MSE, 其在经验均方误差上的表现更接近于OFFLINE方法, 表明在偏差和方差之间的平衡上, 该方法具有更好的控制性能.

图3进一步展示Case 1 和Case 2中非参数部分估计的图形. 其中, 黑色实线表示真正的函数形式, ONLINE方法和OFFLINE方法的估计以不同颜色的圆点代表. 基于LCR的在线估计方法主要劣势在于拟合边界处表现出更多的边缘效应, 但其在内部点上的估计基本上接近OFFLINE方法的估计. 相比之下, 基于LLR的在线估计在边界和内部点上均表现优异, 几乎与传统方法的估计完全重叠. 图4展示了在Case 3中, 当z为二维时的估计图形, 其中, 蓝色“+”表示OFFLINE方法的估计, 红色圆点表示ONLINE方法的估计. 基于LCR和LLR的在线方法仍然表现出与OFFLINE方法几乎一致的估计结果.

综上所述, 通过考虑协变量之间的不同关系以及z为一维和二维情况下的模拟实验, 本文的方法不仅表现出估计准确性和稳定性, 同时相较于传统方法具有显著的计算效率优势.

4 实际数据分析

本节应用本文的在线估计方法对我国劳动年龄人口的生活质量进行实际数据分析, 研究相关因素对生活质量的影响, 以及提高生活品质的可行途径.

4.1 数据预处理

基于CGSS数据集, 本文采用2017年、2018年、2021年最近3次的调查数据以及时反映当下的社会情况, 聚焦于处于社会中流砥柱的劳动年龄人口, 根据国际标准将18–65岁年龄段的样本筛选出来. 进一步地, 将其中仍在上学阶段和已经离/退休的人群排除, 数据清洗后总共获得17495个有效样本.

(1) 因变量

由于本文关注的对象是现今劳动年龄群体的生活质量, 旨在真实反映人们的获得感、幸福感、安全感. 因此, 这里将主观生活质量综合指标设定为因变量. 该指标基于个体对身体健康、心理健康、幸福程度、社会地位和经济水平5个方面的自我评价构建而成, 分别对应于问卷中的A15、A17、A36、A43a和A43e项. 在此基础上, 将这些指标视为同等重要的变量. 鉴于A43a的原始数据采用十分制, 而其他变量采用的是五分制, 所以在计算中A43a项的权重调整为其他变量的一半. 特别地, 由于原始数据中A43e项将经济地位阶层由高到低标记为1–5, 所以本文将其重新赋值, 以1–5表示从低到高的经济地位. 通过采用min-max标准归一化处理5项变量加权求和的结果, 并将其转换为百分制以直观展示生活质量的综合得分, 使用记号“score”来表示该因变量.

相关变量的描述统计见表7, 频数分布见图5, 图示生活质量综合得分(score)的频数分布图总体呈现钟形分布, 生活质量极高与极低的频率均较低, 样本中大多数劳动年龄群体的生活质量集中在中等水平, 反映出样本总体的生活质量分布较为均衡.

(2) 解释变量

选择合适的解释变量, 对于分析影响生活质量的相关可能尤为重要, 所幸CGSS提供了全面广泛的社会信息. 本文通过对问卷回答的分析, 从人口属性、家庭环境、生活方式、工作环境、社会保障、经济收入6大因素来选择解释变量. 具体变量描述统计见表8, 并在图6展示变量之间的相关系数矩阵图.

(3) 基本分析

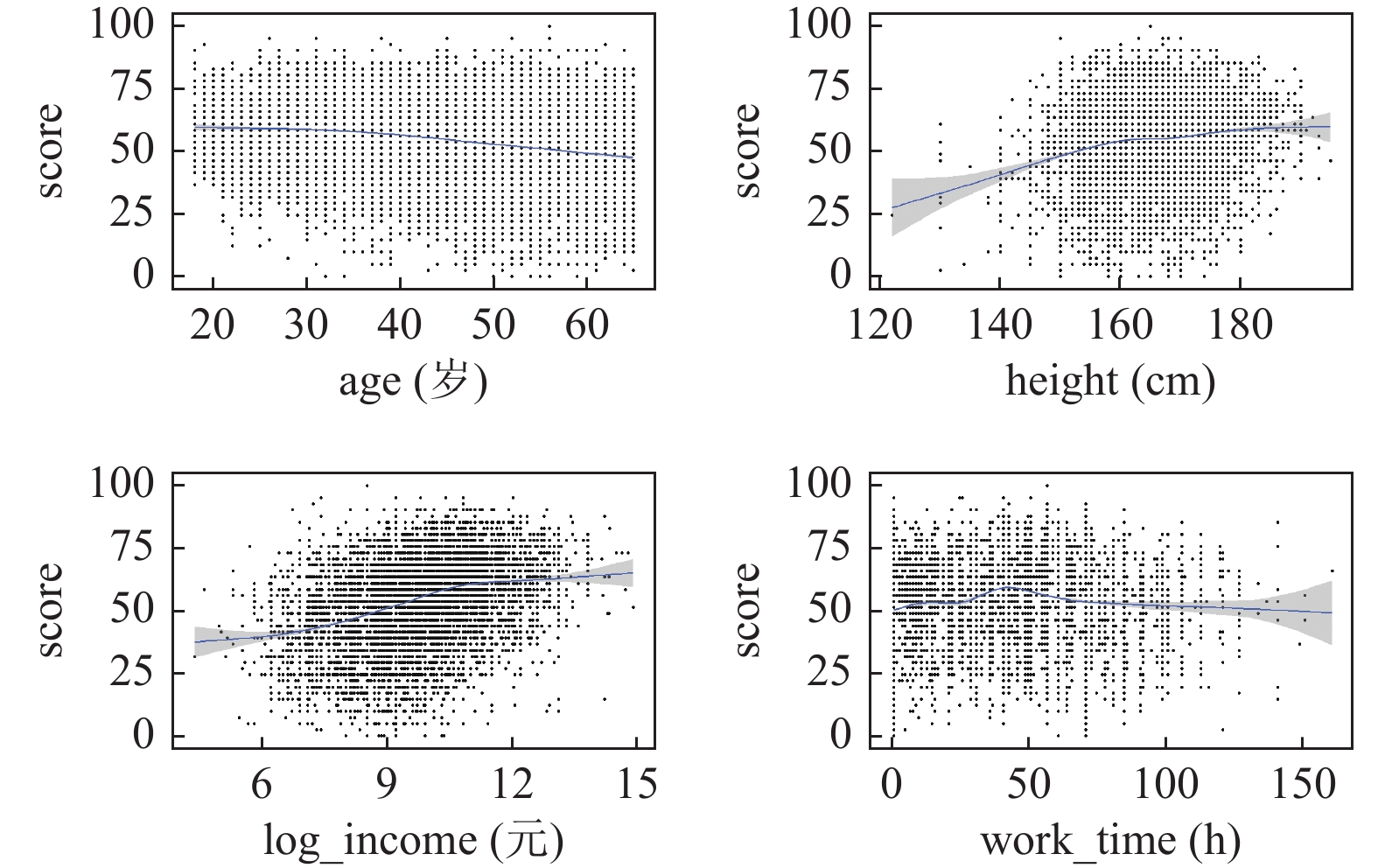
首先, 本文通过图7的散点图辅助分析上述若干解释变量中的连续变量与因变量之间的关系: 其中, 变量age、height、log_income与score之间的散点图呈现出大体上的线性关系, 但在周工作时间与score的散点图上, 拟合曲线显示出不规则的波动, 表明工作时间与生活质量之间存在可能的非线性关系. 结合图6显示各变量之间的线性相关性较弱, 因此, 本文决定采用部分线性模型进行建模, 并将周工作时间作为模型中的非线性因素, 其余变量则纳入模型的线性部分进行分析.

其次, 考虑到部分变量是定序变量, 本文进一步对包括定序变量在内的相关变量与因变量之间的线性关系进行了逐一检验 (见表9). 结果表明, 除了bmi变量的线性影响不显著外, 其余变量的线性回归估计均通过了检验. 据此, 在后续的回归分析中, 本文将bmi变量通过哑变量处理后纳入模型, 而将其他的定序变量按原有的序列性质直接纳入模型的线性部分, 避免不必要的数据转换.

4.2 模型构建

基于第4.1节的数据预处理, 本节将构建部分线性模型, 以准确反映各因素对生活质量的影响, 并应用先前提出的大数据在线估计方法进行分析. 模型以主观生活质量综合得分 (score) 作为响应变量, 选取周工作时间作为非线性部分的协变量. 对于模型的线性部分, 协变量X₁表示年龄; X₂表示为学历水平; X₃表示为身高; 并将bmi变量转换为哑变量, 以身体质量正常组为对照组, X₄、X₅、X₆和X₇分别代表消瘦、过重、肥胖和过度肥胖组. 其他线性协变量包括: X₈户口类别, X₉婚姻状态, X₁₀运动频率, X₁₁社交频率, X₁₂参与医保状态, 以及X₁₃人均年家庭收入的对数.

视2017–2021年间3次问卷调查数据为流数据, 假设数据分批次到达, 单位子数据集样本量$n = 500$. 则总样本量${N_K} = 17495$的样本需要使用本文的方法在线更新估计$K = 35$次. 鉴于子样本量$n = 500$规模相对适中, 带宽选择采用CV方法.

4.3 估计结果及解释

(1) 参数部分估计结果

本文的在线估计方法进行更新计算35次后, 得到参数估计结果如表10所示.

表10的估计结果表明, 健康因素对生活质量的影响尤为显著. 与健康直接相关的变量, 如参与医保、适中的bmi指数、规律运动和社交活动均与生活质量显示出正相关性, 这些因素共同凸显了保持良好健康状况对于提高生活质量的重要性. 此外, 随着年龄的增长, 生活质量可能面临下降的风险, 社会支持和职场环境需更加关注中老年人群的特定需求, 如健康维护、职业培训及心理健康服务.

教育程度和婚姻状况对劳动年龄人口的生活质量呈正相关. 这在一定程度上说明, 提升教育水平和支持家庭稳定性不仅有助于促进个人职业发展和生活满意度的提高, 也有助于构建更和谐文明的社会环境.

而在经济因素上, 结果表现出与劳动年龄人口的生活质量密切相关. 家庭年收入的增加和城市户口直接关联到生活质量的提升. 推动经济发展是改善生活质量的有效途径, 但同时也需要重视资源公平分配, 确保所有群体尤其是低收入和边缘群体能够获得提升生活质量的机会.

(2) 非参数部分估计结果

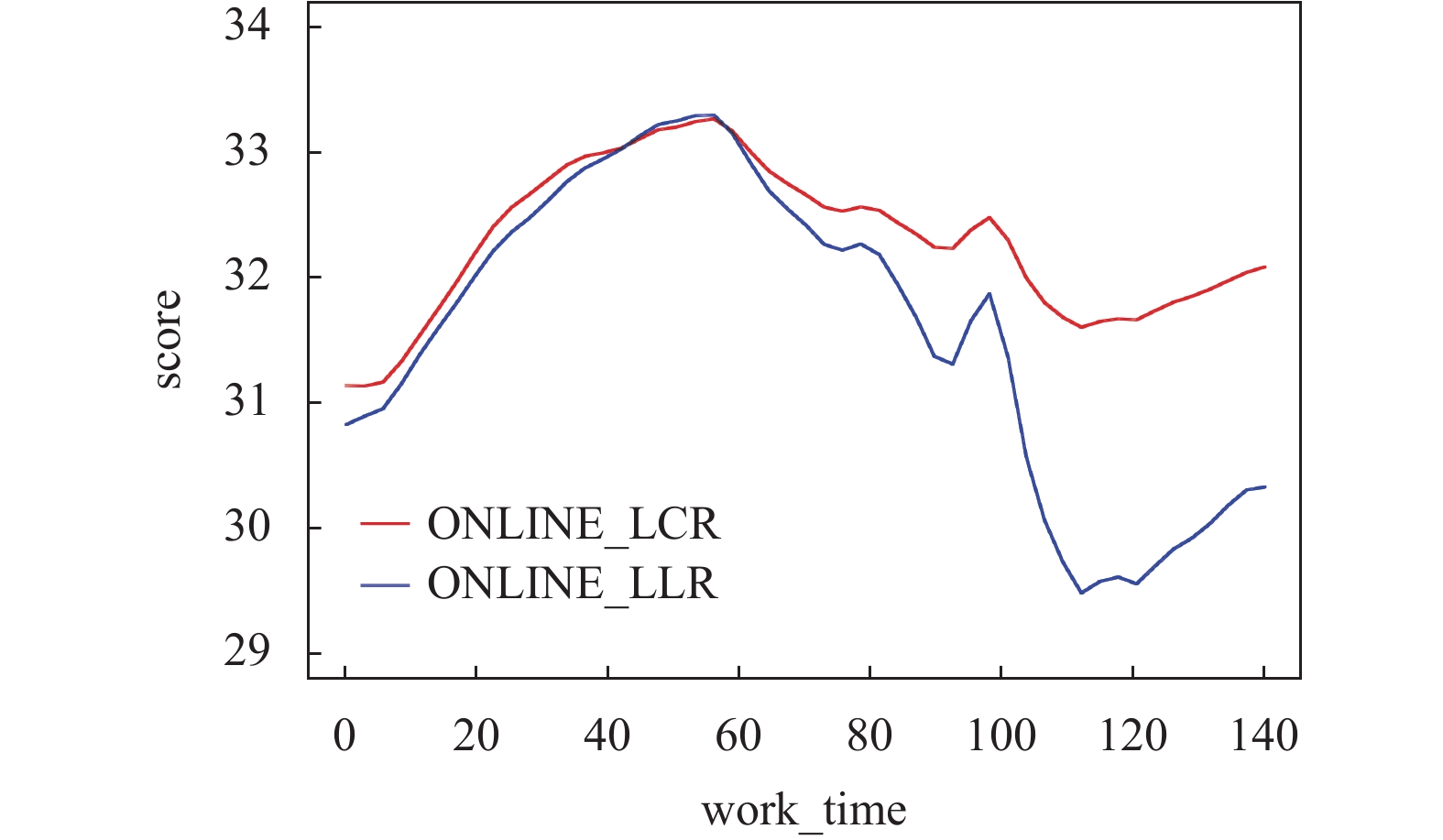
在非参数部分的估计结果如图8所示. 曲线趋势表明, 当周工作时间超过60 h, 生活质量开始显著下降, 而超过100 h后, 生活质量的下降幅度加剧, 呈现出明显的断崖式下跌. 这种趋势暗示长时间工作可能引发健康或家庭等方面的问题, 从而对生活质量产生负面影响. 另一方面, 当周工作时间少于30 h, 生活质量亦呈现下滑趋势, 这可能与经济收入减少、职业发展受限等因素有关.

而生活质量最高的群体是周工作时间在30–60 h之间的全职工作者. 一份稳定的全职工作不仅提供了必要的经济支持, 也带来了个人生活满意度的提升. 基于这一发现, 建议社会政策制定应关注失业和不完全就业的问题, 推广灵活且科学的工作时间配置, 以确保劳动者能够在保持生产力的同时, 享有足够的休息和个人时间, 创造一个健康、高效的工作环境.

5 总结

本文提出了一种在线估计方法, 专为数据流场景下的部分线性模型而设计. 这一方法的核心优势在于其快速的计算能力和对数据存储需求的大幅降低, 有效地解决了部分线性模型大数据分析的重点难题. 经过数值模拟验证, 本文的方法展现了高效的计算能力, 并在均方误差方面的表现与传统方法相当, 是一种快速且有效的数据流计算方法, 为大数据时代下的部分线性模型分析提供了新的视角和工具.