1 引言

随着多媒体技术的快速发展, 人们现在可以轻松地获取、传输、编辑和管理数字多媒体内容. 为了避免这些数据遭受破坏和攻击, 常见的措施包括使用加密和信息隐藏技术. 具体的加密技术^[1]涉及通过一系列特定密钥的加密和解密操作, 在明文和密文之间转换多媒体内容. 此外, 信息隐藏方法^[2,3]可以将多媒体内容无缝嵌入到其他数字媒体中. 压缩感知^[4,5]在图像处理和通信领域也有着广泛的应用. 然而, 在某些情况下, 这些载体可能会意外损坏或丢失, 导致无法恢复原始数据. 为了解决这些挑战, 专家们开发了秘密数据共享技术. 鉴于其出色的安全属性, 秘密共享在诸多领域具有应用, 如区块链^[6]、密钥管理^[7]、数字水印^[8]、认证过程^[9]和分布式存储策略^[10].

在数字时代, 图像携带着丰富的信息并发挥着至关重要的作用. 因此, 秘密图像分享(secret image sharing, SIS)^[11]引起了更多的关注. 从算法角度出发, 秘密图像分享主要由阴影生成算法与秘密重建算法构成; 从主体上分析, 秘密图像分享主要包含两种不同的角色: 分发者(Dealer)和参与者(Participants), 前者负责阴影图像的生成和分发, 后者共同参与管理图像并决定是否通过秘密重建算法恢复原始秘密信息. 根据SIS的(k, n)规则, 即使丢失了多达n–k个阴影, 仍然可以解密并检索原始图像. 传统的SIS所依赖的核心加密方法, 包括视觉密码学方案(visual cryptography scheme, VCS)^[12–15]和基于多项式的SIS^[16–21].

传统的SIS是以k个份额的形式公开秘密图像的全部信息. 而任何信息都不能从少于k个份额中重建. 这就是所谓的“全有或全无”. 因此, 这些方案的实用性受到了限制. 近年来, 渐进式秘密图像共享(progressive secret image sharing, PSIS)方案被提出, 并受到了广泛关注. 在PSIS中, 参与重建的份额越多, 揭露的信息就越多. 当涉及n个份额时, 重建的秘密图像的视觉质量最高. 因此, PSIS提供了多样化的重建模式. Sridhar等人^[22]使用简单的模块化算术运算实现了二合一的渐进式秘密图像分享方案. Lin等人^[23]提出了一种基于XOR的PSIS方案, 该方案在m个参与者之间共享m张秘密图像, 并在t阈值下逐步恢复m张共享图像. Yan等人^[24]提出了一种PSIS方案, 将经典的SIS方案扩展为3种具有选择阈值的算法. 每个秘密像素都被分配一个指定的阈值, 其中预先存在的阈值由用户确定. 每个像素对应不同阈值, 因此在最终重建阶段只有达到阈值的像素才能够被重建, 最终实现图像的渐进式重建. 最近, Xiong等人^[25]提出一种基于中国余数定理和多项式的渐进秘密图像共享方案(CP-PSIS), 以及一个改进的CP-PSIS方案. 该方案首次在拉格朗日插值运算中利用了CRT的同态性, 通过CRT实现了方案的渐进式特征.

然而, 上述的PSIS方案并没有考虑交互过程中的阴影图像的验证问题. 确保共享信息的真实性, 即身份验证, 在实际操作中至关重要. 阴影图像在参与重建前需要通过Dealer对其进行验证, 以防止后续虚假阴影图像导致的重建失败. 除此之外, 当前关于可认证的秘密图像分享方案也存在着一系列问题. 例如, Jiang等人^[26]通过利用了(2, n+1)RG-VCS, 调整每个阴影像素的最低有效位(LSB)使其包含认证信息来实现阴影的认证. 然而, Jiang等人^[26]的方法的一个关键缺点是前7位可能会被不诚实的参与者篡改. 这种方法会导致验证成功但重建失败, 这种现象称为无效验证. 随后, Yan等人^[27]开发了一种具有独立阴影验证的SIS方案. 在这种方案中, 阴影图像是通过将每个阴影像素的4个LSB的XOR值与RG-VCS中的阴影像素位相匹配而生成. 然而, Yan等人的方案中也存在无效验证的风险. 为了解决不诚实参与者导致的验证失败问题, Yan等人^[28]集成了基于多项式的SIS、RG-VCS和哈希函数的特性. 通过采用SHA-256算法来检测阴影图像中的任何变化. 然而, 这种方法也存在一些问题. 哈希函数增加了识别阴影像素的复杂性, 从而增加了算法的复杂度. 此外, 不诚实的参与者可能会修改阴影图像中的最后n行像素, 这表明无效验证的问题仍然存在.

综上所述, 当前PSIS方案中所存在的问题如下.

(1)当前方案缺乏对阴影图像的认证能力, 不诚实参与者会篡改阴影图像导致后续无法解密.

(2)当前方案缺乏灵活性. 在某些场景, 当环境的安全等级发生变化时, 无法改变渐进式重建效果以适应不同的环境.

(3)当前大部分方案的渐进式特征依赖于秘密图像的预处理, 这种预处理会增加算法成本.

针对PSIS所存在的问题, 本文提出了一种(k, n)阈值的可认证渐进式秘密图像分享方案, 以抵御不诚实参与者的欺骗攻击. 在所提出的方案中, 选择257作为素数, 并输入灰度秘密图像${S_1}$和二进制认证图像${S_2}$, 随后生成了n个阴影图像$S{C_i}$. 所提出的方法改进了PSIS技术和VCS技术, 并保证了两种技术的优点. 通过将位平面划分为两部分, 实现了灵活的渐进式重构效果. 通过伪随机数生成器, 实现了对阴影图像的认证能力.

2 相关知识

本节将介绍所提出方案中使用到的已存在的基础研究, 包括基于多项式的秘密图像分享方案、基于随机网格的视觉密码学方案和伪随机数生成算法.

2.1 基于多项式的秘密图像分享

Shamir^[6]提出了一种使用拉格朗日插值多项式将秘密信息分享给n个参与者. 在共享阶段, 选择一个(k–1)度的多项式来生成n个阴影图像.

$ f(x) = ({a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{k - 1}}{x^{k - 1}})({\mathrm{mod}}{\text{ }}P) $

(1)

其中, 秘密值将替换系数$ {a}_{0} $、P是一个素数、${a_1}$,…, ${a_{k - 1}}$是区间 [0, P] 中的随机数. 利用n个不同的值${x_1}$,…, ${x_n}$, 通过式 (1) 生成n个份额$f({x_1})$,…, $ f({x_n}) $. 最终产生n个阴影图像. 在重建阶段, 对于任意的$t\;(t > k)$个阴影图像, 使用式(2)构造原始多项式$f(x)$.

$ \begin{split} f(x) = & \left(f(x_1)\frac{{(x - {x_2})(x - {x_3})\cdots(x - {x_k})}}{{({x_1} - {x_2})({x_1} - {x_3})\cdots({x_1} - {x_k})}} \right. \\ & + f({x_2})\frac{{({x} - {x_1})({x} - {x_3})\cdots({x} - {x_k})}}{{({x_2} - {x_1})({x_2} - {x_3})\cdots({x_2} - {x_k})}} \\ & + \cdots \\ &\left. + f(x_k)\frac{{(x - {x_1})(x - {x_2})\cdots(x - {x_{k - 1}})}}{{{({x_k} - {x_1})({x_k} - {x_2})\cdots({x_k} - {x_{k - 1}})}}}\right)({\mathrm{mod}}\;P) \end{split} $

(2)

通常, 大多数基于多项式的SIS方案中使用P=251. 因此, 8位秘密像素通常被限制在[0, 250]范围内, 范围在[251, 255]的像素被限制在250内, 这将导致图像失真. 不过, 这种失真问题可以通过使用两个像素来表示范围[251, 255]的像素值. 然而, 这种方法会导致阴影图像的尺寸增加. 将P设置为257是目前常用的解决方法, 但是由于多项式生成的像素是随机值, 因此可能会产生一个值为256的无效秘密像素值, 需要一个素数将随机值映射(取模)到一个合适的范围(灰度像素的范围为0–255). 由于大于255的最小素数是257, 因此当选择257作为素数时, 一些像素可能会被映射到256. 对于无效像素, 需要选择系数${a_1}$,…, ${a_{k - 1}}$进行重计算.

2.2 基于随机网格的视觉密码学方案

在介绍基于随机网格的视觉密码学算法(RG-VCS)之前, 首先了解RG-VCS的一些基本概念. 在这个算法中“1”表示黑色像素, “0”表示白色像素. 此外, 符号“$\otimes $” 表示“或操作”. 设$ {S}_{1} $是要处理的秘密图像, 一个(2, 2)门限的RG-VCS算法的共享步骤和重建步骤如下.

共享步骤1: 随机生成第1个阴影图像$ {S}_{1}{C}_{1} $. 这一步意味着不会根据秘密图像$ {S}_{1} $生成第1个阴影图像. 相反, 它是随机生成的.

共享步骤2: 根据式(3)计算并生成$ {S}_{1}{C}_{2} $.

重建阶段: 堆叠两个阴影图像可以得到重建图像$ S'_1 = {S_1}{C_1} \otimes {S_1}{C_2} $, 如式(4)所述. 例如, 当秘密像素${s_1} = {S_1}(h, w) = 1$, 恢复的像素$ {S_1}{C_1} \otimes {S_1}{C_2} = 1 $总是黑色. 当秘密像素的值为${s_1}$=0时, 解码后的像素$ {S_1}{C_1} \otimes {S_1}{C_2} $是白色或黑色的概率各为50%, 因为$ {S_1}{C_1} $是随机生成的. $\overline {{S_1}{C_1}(h, w)}$是$ {{S_1}{C_1}(h, w)}$的取反操作.

$ {S_1}{C_2}(h, w) = \left\{ {\begin{array}{*{20}{c}} {{S_1}{C_1}(h, w)}, \\ {\overline {{S_1}{C_1}(h, w)} }, \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {{\mathrm{if}}{\text{ }}{S_1}(h, w) = 0} \\ {{\mathrm{if}}{\text{ }}{S_1}(h, w) = 1} \end{array} $

(3)

$ \begin{split} & S'_1(h, w) = {S_1}{C_1}(h, w) \otimes {S_1}{C_2}(h, w) \\ & {\text{ = }}\left\{ {\begin{array}{*{20}{c}} {{S_1}{C_1}(h, w) \otimes {S_1}{C_1}(h, w)}, \\ {{S_1}{C_1}(h, w) \otimes \overline {{S_1}{C_1}(h, w)} }, \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {{\mathrm{if}}{\text{ }}{S_1}(h, w) = 0} \\ {{\mathrm{if}}{\text{ }}{S_1}(h, w) = 1} \end{array} \end{split} $

(4)

$ \alpha = \frac{{{P_0} - {P_1}}}{{1 + {P_1}}} = \frac{{P(S'_1[AS0] = 0) - P(S'_1[AS1] = 0)}}{{1 + P(S'_1[AS1] = 0)}} $

(5)

在视觉密码学方案中, 对比度α通常用来描述重建图像的视觉质量. 如式(5)所示, AS0 (AS1)表示${S_1}$的白色(黑色)区域, AS0 (AS1)=$\{ (h, w)|{S_1}(h, w) =0(1) $, $ 0 \leqslant h \leqslant H, 0 \leqslant w \leqslant W\} $, 其中 $ {S}_{1} $表示原始图像, $ S'_1 $表示重建图像, H和W表示图像大小. $S'_1$[AS1]代表$S'_1$的黑色区域. 因此, ${P_1}$表示${S_1}$中黑色区域错误重建的概率, ${P_0}$表示${S_1}$中白色区域的正确重建概率.

2.3 伪随机数生成算法

伪随机数生成器通常需要一个初始种子输入, 也可以使用先前生成的输出序列. Blum-blum-shub (BBS)^[29]算法是一种广泛使用的伪随机数生成技术. 具体步骤如算法1所示. BBS生成器的安全性取决于大整数因式分解的困难性, 因此可将其归为密码学安全的伪随机位生成. 请注意, 并不是每个伪随机数生成器都符合密码学安全的伪随机位生成. 密码学安全的伪随机位生成被区分为能够通过下一个比特测试的伪随机比特生成器. 这个测试表明, 多项式时间算法不可能预测伪随机数序列的下一个比特. 换句话说, 给定输出序列的前k比特, 准确预测第k+1个比特的可能性是1/2.

算法1. BBS

输入: 素数p和q满足 p$\scriptstyle \equiv $q$\scriptstyle \equiv $3 (mod 4); n = p$ \scriptstyle \times $q; Seed (与n互质).

输出: 伪随机数序列R={$\scriptstyle {r}_{1} $, $\scriptstyle {r}_{2} $, $ \scriptstyle {r}_{3} $, …}.

步骤1. 计算$ \scriptstyle {x}_{0} $= (seed²) mod n作为初始值.

步骤2. 生成伪随机序列:

对于 i = 1, 2, 3, …

(1) 计算$\scriptstyle {x_i} = (x_{i - 1}^2)$ mod n.

(2) 从$\scriptstyle {x_i}$中提取随机比特$\scriptstyle {r_i}$, 并将其附加到序列R.

3 本文方案

本节将详细介绍所提出的(k, n)阈值的可认证渐进式秘密图像分享方案的流程, 并在随后对该方案进行理论分析.

3.1 方案流程

所提出的方案如图1所示. 同样的, 本算法主要由阴影图像生成算法与秘密重建算法构成. 主要包含两种不同的角色: 分发者(Dealer)和参与者(Participants), 前者负责阴影图像的生成和分发以及认证, 后者负责图像的管理. 共享过程的详细描述见算法2, 认证及重建过程详见算法3. 关于所提出方案算法的理论分析和实验证明将分别在第3.2节和第4.2节进行说明.

算法2. 所设计的具有认证能力的渐进式秘密图像分享

输入: 灰度秘密图像$\scriptstyle {S_1}$和二进制认证图像$\scriptstyle {S_2}$, 大小均为H×W; 阈值参数为(k, n).

输出: n个阴影图像$\scriptstyle S{C_i}$, i=1, 2,···, n; 以及二进制认证份额D.

步骤 1. 选择质数P=257, 对于所有像素, 重复步骤3–5.

步骤2. 使用(2, 2)RG-VCS将二进制验证图像$ \scriptstyle {S}_{2} $加密为两个阴影图像$\scriptstyle {S_2}{C_1}$和$\scriptstyle {S_2}{C_2}$.

步骤3. 对于当前待处理像$\scriptstyle {S_1}(h, w) $, 通过划分策略BP(a, b)将$\scriptstyle {S_1}(h, w) $分位平面集合“a”以及“b”.

步骤4. 位平面“b”, 构造一个k−1次多项式:

$\scriptstyle f(x) = ({a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{k - 1}}{x^{k - 1}})({\mathrm{mod}}{\text{ }}P) $

其中, $\scriptstyle {a_0} = B$ (B为b的十进制形式), $\scriptstyle {a_i}$使用随机值(i=1, 2,…, k–1), 随后生成n个份额$\scriptstyle f(i)$ (i=1, 2,…, n), 随后将每个份额都转换成二进制$\scriptstyle b(i)$.

步骤5. 通过伪随机数生成器生成一个0–7之间的随机数, 记为Random_Number. 每个Random_Number可以确定一个像素的其中4个位平面.

步骤6. 通过滑动窗口计算当前$\scriptstyle b(i)$某4个位平面的XOR值, 记为$\scriptstyle {\mathrm{XOR4Bits}}(b(i))$ (i=1, 2…, n). 如果$\scriptstyle {\mathrm{XOR4Bits}}(b(i))$=$\scriptstyle {S_2}{C_2}(h, w)$且$\scriptstyle f(i)$< P−1, 则当前生成的份额符合要求. 否则, 返回步骤3.

步骤7. 位平面集合“a”, 通过布尔操作将“a”加密成n个子份额$\scriptstyle a(i)$.

步骤8. 将$\scriptstyle a(i)$随机分配给$\scriptstyle b(i)$, 构造成8个位平面$\scriptstyle a(i)b(i)$, 并转换成十进制$\scriptstyle f(a(i)b(i))$.

步骤9. 将$\scriptstyle f(a(i)b(i))$分配到$\scriptstyle S{C_i}(h, w)$ (i=1, 2,…, n).

步骤10. 输出n幅灰度阴影图像$\scriptstyle S{C_1}$, $\scriptstyle S{C_2}$,···,$\scriptstyle S{C_n}$和一个二进制认证份额D.

算法3. 具有认证能力的渐进式秘密图像分享中的认证与解密

输入: 任意k个阴影图像$\scriptstyle S{C_1}$,···,$\scriptstyle S{C_k}$; 二进制认证份额D和二进制认证图像$\scriptstyle {S_2}$.

输出: 大小为H×W的重建图像SR, k个阴影图像的认证结果$\scriptstyle S{A_i}$ (i=1, 2, …, k).

步骤1. 通过划分策略BP(a, b)将每个像素划分为两个部分, 分别为“a”“b”.

步骤2. Dealer通过伪随机数生成器确定每个子像素的滑动窗口范围. 计算$\scriptstyle {\mathrm{XOR4Bits}}(b)$, 将$\scriptstyle {\mathrm{XOR4Bits}}(b)$与D叠加, 得到解密后的二值认证结果$\scriptstyle {\textit{SA}}{_i}$. 如果$\scriptstyle {\textit{SA}}{_i}$能被人类视觉系统(human visual system, HVS)识别, 且与$\scriptstyle {S_2}$的内容相同, 则认证通过, 执行步骤2.

否则, 识别出伪造的阴影图像, 立即将其(记为$\scriptstyle Fake\_{\textit{SA}}{_i}$)广播给其他参与者.

步骤3. 对于所有的像素位置, 重复步骤3.

步骤4. 通过拉格朗日插值求解以下等式进行原始多项式的重建. 原始位平面“b”即为多项式的系数$\scriptstyle {a_0}$.

$\scriptstyle\left\{\begin{array}{l}\scriptstyle f({i_1}) = {a_0} + {a_{{i_1}}} + \cdots + {a_{k - 1}}i_1^{k - 1}\\\scriptstyle f({i_2}) = {a_0} + {a_{{i_2}}} + \cdots + {a_{k - 1}}i_2^{k - 1}\\\scriptstyle \cdots\\\scriptstyle f({i_k}) = {a_0} + {a_{{i_k}}} + \cdots + {a_{k - 1}}i_k^{k - 1} \end{array}\right.$

步骤5. 通过布尔操作堆叠重构出位平面集合“a”.

步骤6. 合并两类位平面生成最终的秘密像素.

步骤7. 重复以上步骤, 直到处理所有像素. 最终输出大小为H×W的重构图像SR, k个认证结果$\scriptstyle {\textit{SA}}{_i}$.

对于算法2, 以下几点值得强调.

(1) Dealer输入二进制认证图像${S_1}$或者可以通过设置认证密码, 然后将其转换为二进制图像来替代此步骤, 从而消除存储图像的必要性.

(2) 在步骤2中, ${S_2}{C_1}$在共享阶段用于指导创建满足特定条件的阴影图像: ${S_2}{C_2}$为Dealer所持有, 用于后期阴影图像的认证.

(3) 本方案将位平面的划分策略定义为BP(a, b), 其中位平面集合“a”用于布尔操作, “b”用于多项式操作.

(4) 步骤5中伪随机数生成算法生成的随机数范围为0–7. 这里规定每个生成的数字对应于一个滑动窗口. 图2展示了当Random_Number=0时$b(i)$所对应的滑动窗口的范围. 本方案中随机数每增加1则滑动窗口就向右滑动1位. 例如, Random_Number=4时所对应的滑动窗口为${b_2}{b_1}{b_0}{b_6}$.

(5)步骤6是为了利用步骤5生成的Random_Number筛选出满足条件的份额. 通过滑动窗口, 确定$b(i)$ ($b(i)$为$f(i)$二进制形式)的4个位平面是否等于${S_2}{C_2}(i, j)$, 其中i, j= 1, 2, …, n. 例如, 当Random_Number=4时, 通过筛选操作判断${\mathrm{XOR4Bits}}(b(i)) = {\mathrm{XOR}}({b_6}{b_5}{b_4}{b_3}) = {S_2}{C_2}(i, j)$是否成立. 通过该筛选操作, 将生成包含认证信息的阴影图像, 后续Dealer可以直接使用堆叠操作进行后续的认证.

(6) 因为多项式系数${a_i}$是随机的, 当条件不满足时, 需要回到步骤3, 重新生成${a_i}$, 直到所生成的所有份额都满足条件.

(7) 步骤7中位平面集合“a”采用的布尔操作方法. 例如, 通过布尔操作生成n个子份额. 其中, 前k个子份额$(BS_i^1, BS_i^2, \cdots, BS_i^k)$满足$a = (BS_i^1 \oplus BS_i^2 \oplus \cdots \oplus BS_i^k)$, 剩余n–k子份额$BS_i^{k + 1}, BS_i^{k + 2}, \cdots, BS_i^n$位平面都为0.

对于算法3, 需要注意以下几点.

(1) Dealer收集阴影图像并通过堆叠操作检查是否存在不诚实参与者, 从而完成认证. 请注意, 在执行身份验证之前, Dealer仍然使用一个伪随机数来确定滑动窗口的范围, 再对滑动窗口范围的位平面进行堆叠认证.

(2) 步骤5中通过直接堆叠实现位平面集合“a”的重构, 最终合并两类位平面进而重构出秘密图像.

3.2 理论分析与证明

在本节将提供方案理论分析与证明, 并说明了所提出方案的有效性. 假设灰度秘密图像${S_1}$和二进制认证图像${S_2}$是独立的自然图像. 重建阶段收集到的k个灰度像素表示为$s{c_{p1}}, s{c_{p2}}, \cdots, s{c_{pk}}$, 对应于阴影图像$S{C_{p1}}, S{C_{p2}}, \cdots, S{C_{pk}}$.

引理1. 少于k个参与者无法重建秘密图像${S_1}$.

证明: 考虑到式(2), 当存在少于k个参与者, 将只会建立 k–1个等式, 则有m个可能的解, 无法唯一确定秘密像素. 因此, 当阴影图像的数量小于或等于 k–1 时, 秘密图像${S_1}$将无法被重构.

定理1. Dealer可以实现阴影图像的验证.

证明: 根据(2, 2)RG-VCS生成两个阴影图像$ {S_2}{C_1} $和$ {S_2}{C_2} $, 通过堆叠$ {S_2}{C_1} $和$ {S_2}{C_2} $, 可以解密二进制验证图像. 在随后的共享算法中, 通过${\mathrm{XOR4Bits}}(b(i))$ = ${S_2}{C_1}(h, w)$来筛选出符合条件的阴影图像, 并将$ {S_2}{C_2} $作为认证份额分配给Dealer. 因此, Dealer可以通过堆叠D和${\mathrm{XOR4Bits}}(b(i))$来验证阴影图像的$S{C_i}$. 如果验证结果可以通过HVS, 则表明是合法参与者; 否则, 表明是虚假或者不诚实参与者.

最近, Liu等人^[30]提出了一种基于布尔运算和覆盖函数的PSIS. 该方案用于解决以往方案中基于多项式方案的计算复杂度高和基于视觉密码学的像素扩展问题. Liu等人在文中一共提出了3种算法, 算法1使用像素间的布尔运算(像素之间进行布尔运算), 算法2和算法3为位平面间的布尔运算(像素的部分位平面之间进行布尔运算). 对于算法1中的每个像素${B_i}$, 生成n个份额, 其中前k个份额满足${B_i} = S_i^1 \oplus S_i^2 \oplus \cdots \oplus S_i^k$, 剩余n–k份额$S_i^{k + 1}, S_i^{k + 2}, \cdots, S_i^n$都设置为0. 最后再将方案中产生的份额随机划分给n个参与者. Liu等人将前k个子份额称为主份额.

在Liu等人的方案中, 像素$ {B}_{i} $可以用任意t $(k \leqslant t \leqslant n)$个份额精确的解密, 但是需要它们包含所有的k个主份额$S_i^1, S_i^2, \cdots, S_i^k$. 相反, 如果份额集合缺少必要的k个主份额, 则无法正确解密${B_i}$.

通过证明, 可以确定少于k个参与者不能揭示秘密信息, 而k个或更多的参与者可以重建图像. 接下来将对所提方案的渐进重构特性进行了理论分析. 该方案的阈值为(k, n), 划分策略为BP(a, b). 首先, 拉格朗日插值算法实现了“全有或全无”的效果. 因此, 在分析该方案的渐进重构性质时, 只需讨论位平面“a”的恢复. 定理2中证明了所提方案渐进重构的性质. 这里采用$Pro_{(k, n)}^t$表示由$t\;(k \leqslant t)$个参与者参与重建时位平面“a”被正确恢复的概率. 在此, 可以将位平面“a”产生的子份额分为两类, k个主要子份额$(BS_i^1, BS_i^2, \cdots, BS_i^k)$和n–k次子份额$(BS_i^{k + 1}, BS_i^{k + 2}, \cdots, BS_i^n)$.

引理2. 所提出方案的渐进式重构特性由布尔运算决定.

证明: 对于划分策略为BP(a, b)的一个(k, n)门限的可认证的渐进式秘密图像分享(VPSIS)方案. 多项式共享具有“全有或全无”的特点. 具体而言, 当参与者数为k或更多时, 位平面“b”可通过拉格朗日插值算法无损恢复. 重要的是, 任何k个或更多参与者的集合都将使用此算法获得相同的重建图像. 因此, 位平面“b”在渐进重建过程中是固定的. 因此, 该方案的渐进重构由布尔运算决定.

定理2. 所提出方案满足渐进式重建原则.

证明: 引理1证明了该方案的渐进式重构性质是由布尔运算决定的. 因此, 只需要分析位平面“a”的重构. 在Liu等人的方案中, 任意像素都可以被恢复, 但需包含k个主份额. 因此, 任意t个参与者具有$({\mathrm{C}}_{n - k}^{t - k}/{\mathrm{C}}_n^k)$概率恢复像素${B_i}$, 该特性也存在于所提出方案中. 但是, 少于8位平面上的布尔运算不能完全满足该恢复概率. 例如, 在(2, 3)门限的VPSIS中, 最高有效位(b₇=“1”)产生的子份额是(“1”, “0”, “0”), 其中主份额是(“1”, “0”), 次份额是(“0”). 原始位平面b₇不仅可以由两个主要子平面(“1”, “0”)重构, 还可由一个主子份额(“1”)和一个次要子份额(“0”)重构. 因此, $({\mathrm{C}}_{n - k}^{t - k}/{\mathrm{C}}_n^k)$<$Pro_{(k, n)}^t$<1, 当t=k. 当在重建阶段使用更多的参与者时, 拥有更多的主份额的可能性将会增加, 则正确解密的概率将增加. 因此, 当k<t₁<t₂<n, 0<$Pro_{(k, n)}^{{t_1}}$<$Pro_{(k, n)}^{{t_2}}$<1. 当所有子份额都参与重构时, 则有$Pro_{(k, n)}^n$. 基于上述分析, 所提方案满足渐进重构特性.

定理3. 所提出方案渐进式重构效果为$a \times P + b$. 注意, “a”和“b”是划分策略BP(a, b)的两类位平面, P是位平面“a”正确重构的概率.

证明: 通过布尔运算得到的份额最终具有恢复原始秘密值的概率为P. Liu等人^[30]的方案是通过布尔运算实现的, 因此图像的重构层次为$a \times P + b \times P$. 与Liu等人方案相比, 该方案将每个位平面分成两个部分, 分别用于多项式运算和布尔运算. 引理1表明, 达到阈值后多项式运算可以重构位平面“b”, 重构层次为b×1. 因此, 该方案的重构层次为$a \times P + b$. Liu等人的方案只需要布尔运算, 所以$a \times P + b \times P$是一个固定值. 而$a \times P + b$是一个变量, 它依赖于划分策略BP(a, b). 在不同的划分策略下, $a \times P + b$是不同的, 因此可以实现不同的渐进式重建效果.

4 实验与比较

本节将通过实验进一步验证所提出方案的有效性, 讨论不同阈值下的实验结果. 然后将与相关方法进行比较, 以强调所提出方案的优势. 本节实验使用常用的4幅灰度图像和两幅二值图像为实验对象进行测试, 如图3所示. 除了二值图像外, 剩余图像均来自USC-SIPI数据库^[31].

4.1 实验结果

对手模型是信息安全领域的重要组成部分, 它描述了潜在的攻击者、他们的能力以及可能威胁系统的行为. 因此, 在进行实验之前, 必须对这一部分进行描述. 潜在攻击者是指不诚实或假冒的参与者, 也称为内部恶意用户. 这些对手可能拥有强大的计算能力, 能够进行加密分析或解密加密算法. 此外, 威胁分析表明, 攻击者可能会窃取身份验证信息或阴影图像, 导致敏感信息泄露. 他们还可能通过网络攻击破坏系统的正常运行, 导致服务中断. 此外, 攻击者还可能伪造身份验证信息, 冒充合法用户从事未经授权的操作或访问系统. 针对这些威胁, 防御措施包括对内部恶意用户进行身份验证. 在本实验中, 通过改变每个像素的4个最高有效位来模拟不诚实参与者对阴影图像的修改.

图4展示了划分策略为BP(b₇, b₆b₅b₄b₃b₂b₁b₀)的(2, 3)VPSIS实验结果. 图4(a), (b)分别为秘密图像和二进制认证图像. 通过所提出的方案生成3幅阴影图像, 如图4(c)–(e)所示. 图4(f)为二进制认证份额, 用于对阴影图像进行认证. 图4(g)展示了任意两个参与者的重建结果. 图4(f)展示了3个参与者的重建结果. 由图4(g)–(f)可得所提出的方案满足渐进式重建特征. 图4(i)–(k)展示了对3幅阴影图像的认证结果, 可以得出参与者为诚实参与者. 图4(l)显示不诚实参与者提供的虚假阴影图像. 图4(m)显示了对于虚假阴影图像的认证结果, 认证结果表明该参与者为不诚实参与者, 随后将对不诚实参与者进行广播. 为了展示虚假阴影图像的影响, 图4(n)展示了虚假阴影图像和正常阴影图像的重建结果, 结果表明不诚实参与者提供的阴影图像将不能用于重建秘密图像. 图5展示了划分策略为BP(b₇, b₆b₅b₄b₃b₂b₁b₀)的(2, 2)VPSIS的实验结果. 实验结果仍然表明了方案的可认证能力.

为了验证所提出方案在渐进式重构方面也有不错的效果, 在图6和图7分别展示了相同阈值参数下不同划分策略的实验结果. 通过实验结果可以表明, 所提出方案的划分策划可以实验在同一阈值参数下不同的渐进式重建水平. 这一优势大大提高了所提出方案的应用场景.

从实验中可以得出以下结论.

(1)该方案能有效检测和定位不诚实参与者欺骗攻击.

(2)同一阈值参数下可以实现不同的渐进式重建效果.

4.2 阴影图像安全性分析

本节将分析阴影图像的直方图和香农熵, 进一步证明所提出方案的安全性.

4.2.1 直方图

直方图表示图像中每个灰度级的频率分布, 让人方便了解图像的灰度分布. 图8展示了使用阈值(2, 2)和(2, 3)生成的阴影图像的直方图. 其中, 图8(a)–(c)表示一个(2, 3)门限的 VPSIS的3个阴影图像(SC₁, SC₂, SC₃)的直方图. 图8(d)、(e)表示一个(2, 2)门限的 VPSIS的2个阴影图像(SC₄, SC₅)的直方图. 实验结果表明, 各灰度级的频率分布基本一致, 没有明显的峰值或不连续. 除此之外, 通过 HVS 观察, 可以明显看出所生成的阴影图像具有很高的随机性.

4.2.2 香农熵

为了进一步说明生成的阴影图像的安全性和可靠性, 本节采用香农熵进行分析. 香农熵是信息论中的一个重要概念, 用于量化随机变量的不确定性或信息含量. 当随机变量的所有可能值的概率分布相等时, 香农熵达到最大值, 表明不确定性最大. 相反, 如果随机变量的某些值的概率高于其他值, 香农熵就会降低, 表示不确定性降低. 香农熵的计算公式如下所示:

$ H(x) = - \sum\limits_{i = 1}^n {p({x_i})\log{_2}(p({x_i}))} $

(6)

其中, $H(x)$表示图像的香农熵, $p({x_i})$表示灰度值${x_i}$在图像中出现的概率. 通过直方图计算每个灰度值出现的频率, 然后计算概率, 就可以很容易地确定图像的香农熵.

表1和表2分别说明了在不同阈值下生成阴影图像的香农熵值. 在灰度图像中, 香农熵越接近8, 图像的复杂性和随机性就越高. 因此, 本实验部分进一步证实了建议方案的安全性. 根据HVS观察到的直方图结果和相应的香农熵, 可以推断图像具有高度的随机性和复杂性. 所提出的使用伪随机数生成阴影图像的方法是可靠的, 所生成的类似噪声的阴影图像不会泄露任何机密信息.

4.3 相关方法比较

本节将所提出方案与相关方案进行比较, 以突出所提出在此类方案中的优势. 随后, 将从3个方面进行评估: 渐进式重建水平、认证结果的视觉质量、相关方案的特征比较.

4.3.1 渐进式重建效果

本节将与其他方案进行比较, 并使用峰值信噪比(PSNR)来评估重建图像的视觉质量. 目前, 大多数方案的渐进式重构效果不够灵活. 例如, 当参与者数量有限(阈值参数固定)且环境安全级别发生变化时, 传统方案无法改变渐进式重构效果以适应不同的环境. 表3展示了本方案在不同划分策略下与文献[22–24]进行比较的实验结果. 当参与者人数t=3且秘密图像不同时, 文献[22–24]重构图像的PSNR在固定范围内. 相反, 在相同的阈值参数下, 基于不同的划分策略, 所提出的方案可以获得不同的重构效果. 此外, 表4给出了不同方案在阈值参数(3, 5)下的比较. 因此, 与相关方案相比, 本方案具有较高的灵活性. 所提出方案可以根据不同的划分策略适应不同的安全级别, 进一步扩大了所提出方案适用场景.

4.3.2 认证结果视觉质量

本节将讨论阴影图像认证结果的对比度. 低质量的认证结果会妨碍HVS的直接验证. 这一点在视觉秘密共享等系统中至关重要, 因为这些系统将易用性和直观反馈放在首位. 本节分别比较了文献[27,28]的方案和文献[26]的方案.

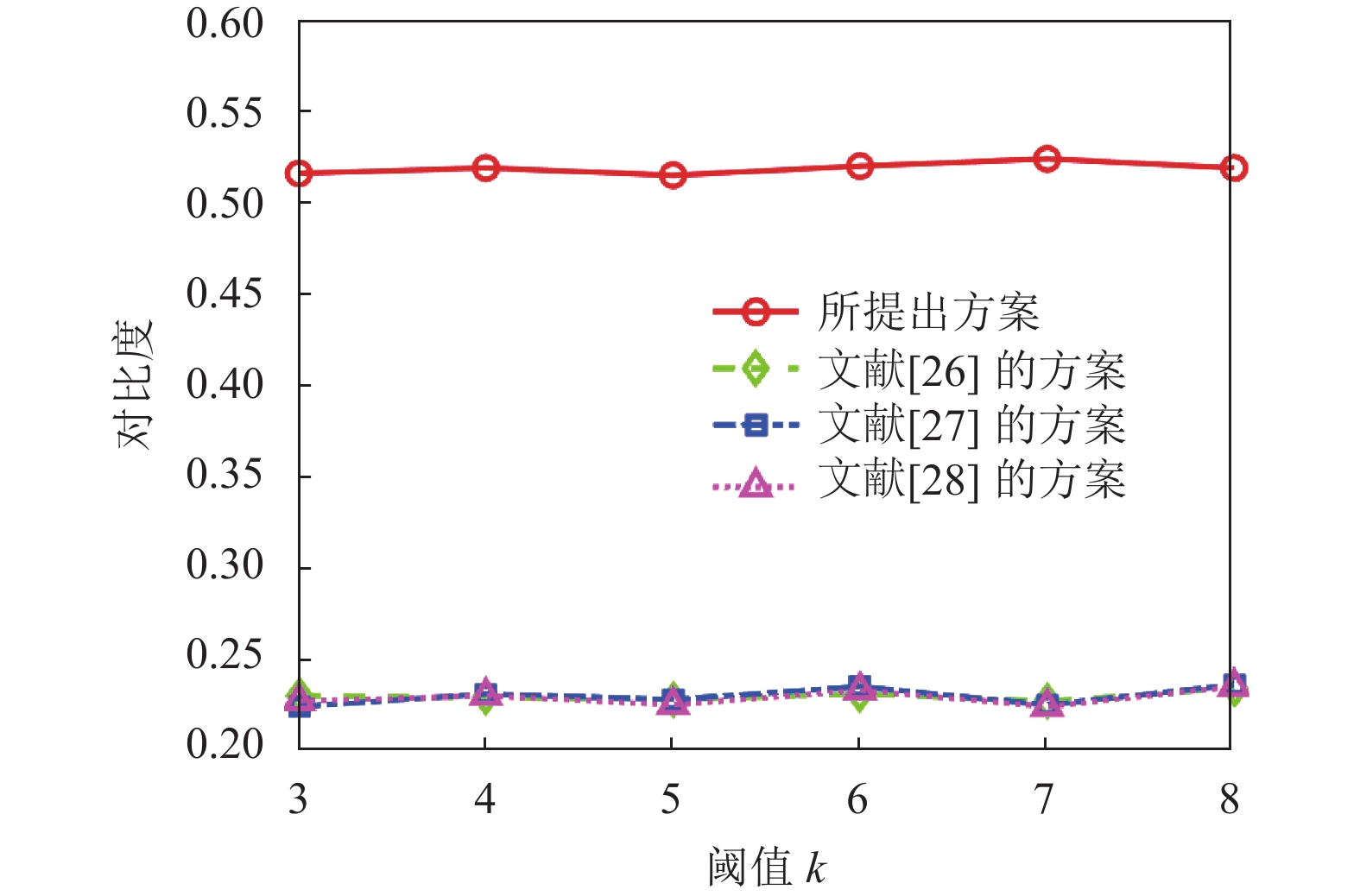
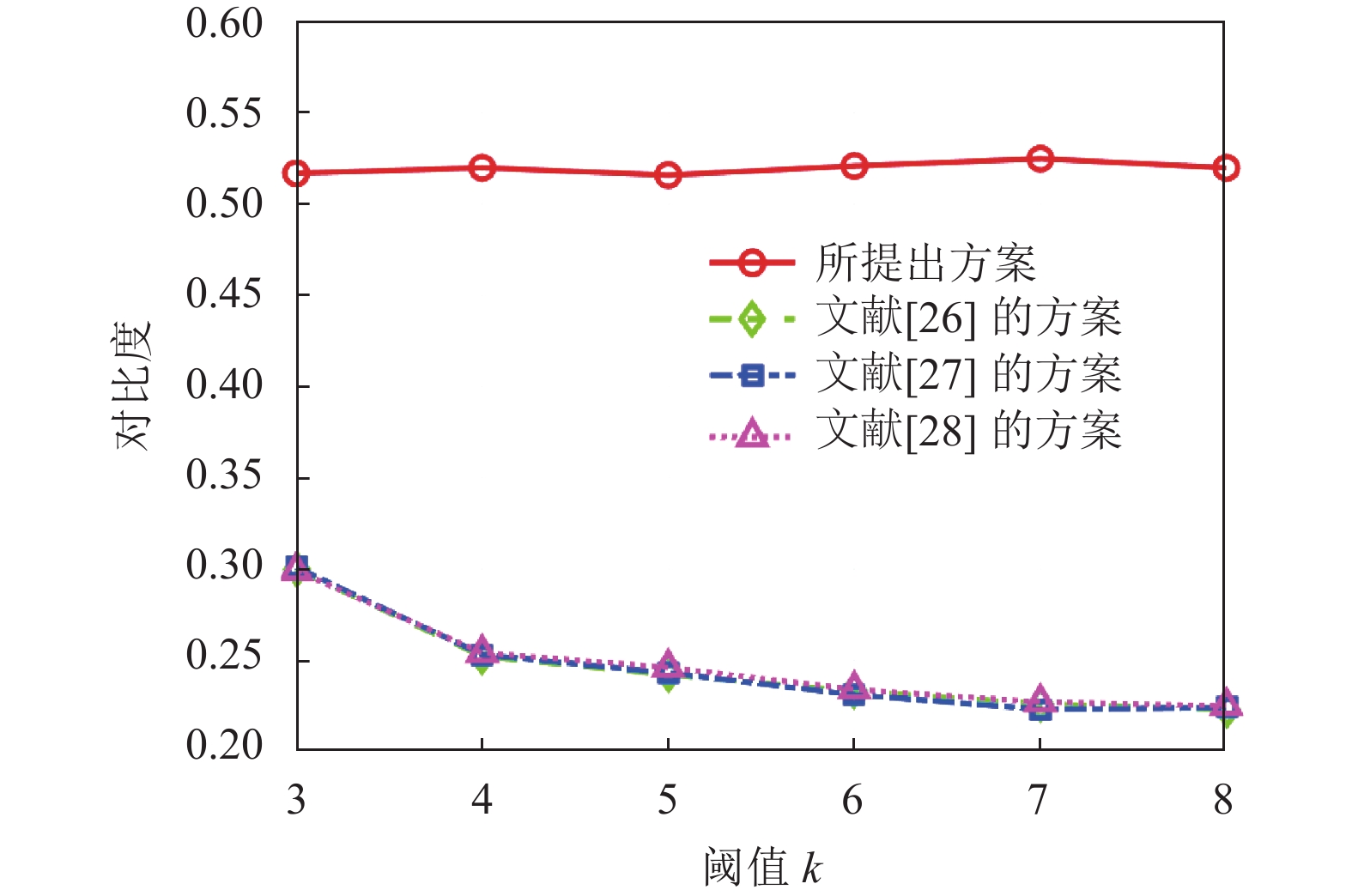
本方案采用(2, 2)RG-VCS, 根据第2.2节所介绍, (2, 2)RG-VCS为全黑视觉密码学方案(黑色区域可以完全恢复), 因此本方案保持着较高对比度的认证结果. 相反, 文献[27,28]和文献[26]的方案采取(2, n+1)RG-VCS, 为实现n+1个二进制份额, 通常采取复制份额的操作. 大量相同的份额将使认证结果的黑色区域无法完全重构. 例如: 当前二进制像素B_i=1 (黑色像素), 通过(2, 2)RG-VCS生成两个份额分别为b₁=0和b₂=1, 最终堆叠两个份额即可重构黑色像素. 若采用阈值参数为(2, n+1)RG-VCS, 则需要对份额进行复制: b₃=b₁、b₄=b₂, … (若 (n+1 mod 2)=0则 b_n+1=b₂; 否则 b_n+1=b₁), 即n+1个份额分别为: b₁=0, b₂=1, b₃=0, b₄=1, b₅=0, … 因此, (2, n+1) RG-VCS的方案在堆叠任意两个份额时, 原始黑色二进制像素将有概率不会被恢复. 图9显示了阈值k=3时不同n值下认证图像的对比度, 突出表明所提出方案保持了较高的对比度性能. 图10显示了n=8时不同阈值k下认证结果的对比度.

4.3.3 特征比较

表5详细比较了所提方案与相关方法的特征比较. 从表5中的数据可以看出, 与传统技术相比, 所提出方案实现了认证能力, 并且保留了渐进式重建效果. 除此之外, 所提出方案的阴影图像不存在无像素扩展, 秘密图像也可以无损重建.

5 结论与展望

本节引入了一种可认证的渐进式图像分享(VPSIS)方案, 旨在有效抵御虚假或者不诚实参与者的欺骗攻击. 该方案巧妙地融合了基于多项式的操作和视觉密码学的优势. 通过使用不同的位平面划分策略, 实现了在同一阈值参数下不同的渐进式重构水平. 同时, 利用堆叠操作实现轻量级的身份认证. 为了增强对阴影图像的认证能力, 采用了伪随机数生成器和(2, 2)RG-VCS来指导阴影图像的生成. 同时该方法仍然具有无损解密和无像素扩展等特点.

出于安全考虑, 本文并未涉及Dealer不参与验证的情况. 当Dealer不参与时, 需要参与者之间进行相互验证, 并通过投票机制找出虚假或者不诚实参与者. 但是, 这将带来安全隐患, 虚假或者不诚实参与者在交互过程中可以获取其他参与者的阴影图像, 这将造成信息泄露的后果. 因此, 今后的研究需要将优先解决参与者互动时的安全问题. 同时, 实现Dealer不参与验证下的可验证的秘密图像分享方案.