2. 北京理工大学 网络空间安全学院, 北京 100081
2. School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing 100081, China
随着全球数字经济的蓬勃发展和大数据时代的来临, 数据成为重要的战略资源, 但随之而来的是数据安全与隐私问题越来越受重视, 如欧盟于2018年开始实施《通用数据保护条例》, 我国也于2021年正式实施《个人信息保护法》. 在隐私保护、数据合规等监管要求下, 数据拥有方陷入“不愿共享、不敢共享、不能共享”的困境, 海量数据散落在众多机构和信息系统中, 形成“数据孤岛”现象, 各数据拥有方无法充分发挥数据的价值. 在此背景下, 文献[1]提出了纵向联邦学习(vertical federated learning, VFL)的概念, 目标是在不泄漏数据隐私的前提下, 具有重合数据样本但特征重叠较少的两方或多方企业进行协作, 构建效果更优的机器学习模型. 近年来, 业界公司和机构对纵向联邦学习的需求愈发凸显, 两方或多方企业可能拥有同一用户群体的不同数据特征, 倾向于联合己方所没有的特征部分, 提高目标模型的准确率, 提高数据的利用价值. 例如, 某电信公司希望借助机器学习模型挖掘潜在客户, 提高移动终端设备的销量. 但自身仅拥有用户的通话和套餐等信息, 数据特征有限, 模型效果不佳, 如果联合电商企业提供用户的购物消费信息、联合银行机构提供用户的存款借贷信息等, 便能丰富用户的数据特征维度, 从而提高目标模型的训练效果. 纵向联邦学习在诸如此类场景中的应用前景十分广阔.
在纵向联邦学习架构中, 通常各参与方拥有自己的本地训练数据特征集以及本地模型, 通过本地模型输出本地数据的中间嵌入表示(embedding), 各方输出的嵌入表示将被一并作为服务器顶层模型的输入, 最终的预测阶段也需要参与方协作推理、共同输出结果. 在此过程中, 中间嵌入以及服务器返回的梯度信息需要巨大的通信量. 传统的纵向联邦学习在通信效率方面仍然存在一定挑战, 特别是在大规模数据场景下, 通信成本往往会成为限制算法性能的瓶颈. 在企业场景实际应用中, 不同数据中心之间的带宽通常小于300 Mb/s[2], 受限于网络带宽等有限的通信资源, 通信开销成本高昂, 往往超过90%的总训练时间都消耗在通信上[3], 导致整体训练十分低效, 通信成为阻碍其实际应用的一大关键瓶颈. 因此, 如何通过有效的算法设计减少通信量、提高通信效率, 成为当前研究的热点之一.
现有针对纵向联邦学习通信效率的研究, 多采用减少通信次数或降低通信量等方法, 仍然存在一些问题: 对训练架构有一定要求, 适用场景受限; 压缩方法造成的信息量损失会对模型的性能造成损害, 难以在不牺牲模型精度的前提下实现高效压缩; 缺乏对于上行嵌入和下行梯度的针对性压缩算法. 这些因素导致现有方法在实际应用中的效果不甚理想.
本文对纵向联邦学习通信效率问题展开研究, 针对上述困点难点, 提出基于嵌入和梯度双向压缩的高效压缩算法, 该算法由嵌入稀疏化、梯度量化以及编码等部分组成. 具体来说, 对于客户端上传的嵌入表示, 采用改进的top-k稀疏化方法并结合缓存重用机制, 对于服务器分发的梯度信息, 采用离散量化与哈夫曼编码相结合的机制. 通过实验结果的对比分析, 证明新算法在纵向联邦学习场景下的可行性和优越性, 能够在保持最终模型准确率的同时减少通信量、提高通信效率, 从而实现模型的高效训练.
2 相关工作提高纵向联邦学习的通信效率通常可以从两种方式考虑, 即减少总的通信轮次或减少每次通信传输的数据量. 减少通信轮次可以通过允许参与方在每次迭代中进行多次本地更新实现, 如Liu等[4]提出了FedBCD算法, 重复利用上一轮次的统计数据进行多次迭代, 以减少通信次数. Castiglia等[5]提出了Flex-VFL算法, 对通信轮次之间的间隔设置阈值, 允许各方执行不同次数的本地迭代. 但这些算法通常对整体训练架构有一定要求, 训练场景不具有普适性; 并且纵向联邦学习的每轮迭代训练需要各方的共同参与来获取己方的梯度信息, 因此这类方法通常需要利用陈旧的他方信息对本地梯度进行估计, 从而可能带来较大的方差和估计误差, 影响整体的收敛效果[3].
减少传输的数据量可以通过压缩传输的数据来实现. 压缩算法作为解决通信效率问题的有效途径被广泛关注, 常见的压缩方法包括模型压缩[6,7]、梯度稀疏化[8,9]和梯度量化[10,11]等, 但是, 如何在不牺牲模型精度的前提下实现高效的压缩仍然是一个具有挑战性的问题. 在纵向联邦学习的训练过程中, 客户端上传本地输出的嵌入表示, 服务器分发与之对应的梯度信息. 于是压缩方法可以从嵌入和梯度两个角度出发. 对于梯度而言, 常用的压缩方法包括稀疏化和量化, 而嵌入表示则通常从稀疏化角度考虑.
对于客户端上传的嵌入表示的压缩, Castiglia等[12]提出了C-VFL算法, 利用top-k[8]方法结合本地多轮更新机制对嵌入表示稀疏化, 并给出了如何选择稀疏化参数来确保收敛的理论证明, 但该方法放松了隐私假设, 将各嵌入共享给所有参与方, 存在一定隐私风险. Inoue等[13]提出了SparseVFL算法, 利用ReLU激活函数将嵌入向量中的负值替换为零, 并结合L1正则化方法来产生稀疏化的嵌入表示, 但该方法简单舍弃嵌入向量的负元素, 稀疏效果依赖于数据分布情况. Cai等[14]提出了AVFL算法, 利用主成分分析(principle component analysis, PCA)进行降维处理, 减少上传的特征数量. Khan等[15]提出了CE-VFL算法, 同时利用PCA和自动编码器(autoencoder)来从原始数据中学习潜在表示. 但此类降维方法仅发送一次嵌入信息, 客户端本地模型无法得到优化, 模型准确性较差. 文家宝等[16]提出了单模型主导联邦学习方法, 在单轮通信中选出主导模型, 调整其他模型参与权重来泛化模型, 但该方法无法直接扩展至纵向场景中, 同样受制于单次通信的弊端.
对于服务器分发的梯度的压缩, Li等[17]提出了GP-AVFL算法, 根据梯度绝对值的大小, 只分发其中最大的若干元素, 同时将其余部分在本地累积到下一轮, 以减少误差, 但该方法仅支持在服务端使用聚合函数, 无法支持可训练的顶层模型, 应用常用场景受限. Inoue等[13]提出梯度掩码策略, 将嵌入中零元素位置对应的梯度元素也设置为0, 从而减少梯度大小, 但该策略忽略了梯度数值本身的分布信息, 压缩效率不理想. Bernstein等[18]提出signSGD方法对梯度进行量化, 仅保留梯度元素的符号而舍弃具体数值, 但此类方法直接应用在纵向联邦学习中会带来收敛问题. 田金箫[19]提出了基于投影的稀疏三元压缩算法, 在服务端采用梯度投影的聚合策略以缓解客户端数据非独立同分布导致的不利影响. 陈律君等[20]使用稀疏化及压缩感知技术减少梯度传输造成的通信开销, 并利用安全多方计算中的加法秘密共享对重要的梯度值加密, 以实现在减少通信开销的同时进一步增强其安全性, 但该方法计算较为耗时、效率不佳.
3 算法设计依据文献[21], 根据服务器模型是否可训练以及服务器是否拥有本地数据和模型, 可以将纵向联邦学习的训练架构分为4类: splitVFL、splitVFLc、aggVFL以及aggVFLc. 本文采用splitVFLc架构, 如图1所示, 即有若干个客户端作为被动方, 提取本地数据特征, 输出嵌入表示, 有一个服务器作为主动方, 拥有这部分数据的标签信息和一个可训练的顶层模型, 但没有自己的本地数据, 仅作为中心服务器聚合各方数据并输出最终结果. 假设所有参与方的样本已经预先对齐. 本节将分别从客户端上传嵌入表示的压缩和服务器分发梯度的压缩两个角度提出具体压缩算法.
|
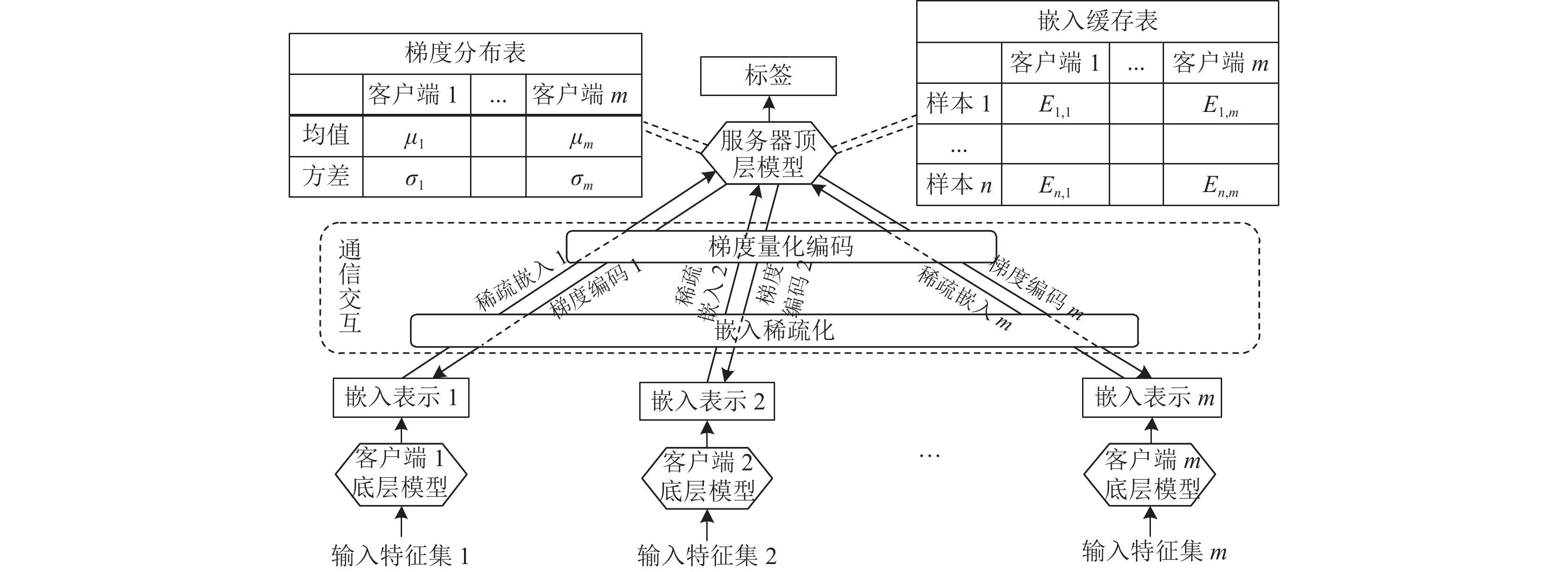
图 1 本文采用的架构及压缩过程示意图 |
图1中通信交互部分体现了训练过程中, 客户端和服务器之间的通信交互过程. 本节所设计的算法为其中的嵌入稀疏化和梯度量化编码两个模块, 同时在服务器增加嵌入缓存表和梯度分布表, 以辅助两个算法模块的具体工作. 对于客户端上传的嵌入表示, 应用嵌入稀疏化算法模块对其进行压缩; 对于服务器分发的梯度, 应用梯度量化编码算法模块对其进行压缩. 通过上下行流量的压缩处理, 降低训练过程中客户端和服务器之间的通信量, 从而降低通信开销. 接下来具体介绍两个算法的具体设计细节.
3.1 嵌入稀疏化算法对于客户端上传的嵌入表示的压缩, 文献[12]采用top-k方法对其进行压缩, 该方法将稀疏算子topk:
| (topk(E))i:={(E)i,i∈{π(1),π(2),⋯,π(k)}0,i∉{π(1),π(2),⋯,π(k)} | (1) |
其中, 嵌入向量
这种策略依据嵌入表示中元素的绝对值大小, 保留前k大的元素进行传输, 其余元素置为0. 但不同于梯度用来更新模型参数, 嵌入表示直接作为服务器模型的输入, 嵌入中绝对值大小不同的元素可能对顶层模型的贡献是一样的. 因此本节采用改进的top-k算法, 根据服务器传回的偏导数
然而稀疏化会引入误差, 造成最终全局模型的准确率下降, 如何平衡好压缩率与准确率之间的关系成为一个关键问题. 为了保持一定压缩效果的同时, 提高模型效果, 受文献[22]启发, 本节在上述改进top-k算法的基础上, 引入嵌入缓存复用机制, 如图1中的嵌入缓存表所示. 具体流程为: 借鉴时间局部性原理, 服务器在每轮迭代中, 将各客户端上传的嵌入表示在本地缓存一份, 服务器对第i个客户端的缓存
| Ht+1ij:={Etij,Etij≠0Htij,Etij=0 | (2) |
其中, j表示第j个元素, t表示第t轮迭代. 在次轮迭代时, 对于客户端上传的稀疏化后的嵌入表示
| Eij:={Eij,Eij≠0Hij,Eij=0 | (3) |
由于各客户端无法获知数据的标签信息, 无法单独完成梯度的反向传播过程, 现有的纵向联邦学习框架通常采用两阶段策略: 即服务器计算损失函数值, 并将其相对于客户端输出嵌入的偏导数
| ∇θclient=∂L∂E⋅∂E∂θclient=∇E⋅∂E∂θclient | (4) |
计算全局模型相对于本地模型
在本文架构中, 服务器分发的梯度数据量与客户端上传的嵌入表示大小相当, 为了减小通信量, 同样需要对梯度进行压缩处理. signSGD[18]等算法常被用于横向联邦学习等分布式机器学习中的梯度压缩, 但由于纵向联邦学习中客户端需要基于服务器分发的梯度信息进一步计算本地梯度从而更新模型, 因此纵向联邦学习的训练过程对于服务器分发梯度的修改更加敏感, 简单地将signSGD等方法应用于纵向联邦学习很可能导致其无法收敛[23].
因此, 受文献[23]启发, 本节采用一种离散量化与编码结合的方法对服务器分发的梯度进行压缩. 具体流程为: 服务器对于每个客户端都在本地缓存一份相应的梯度信息, 如图1中梯度分布表所示. 在将梯度分发给客户端之前, 首先根据本地缓存的对应客户端上轮次的梯度信息, 统计其分布情况, 计算均值μ和方差σ. 随后, 为了约束梯度值的边界方便量化处理, 依据3σ规则[24], 将本轮将要分发的梯度信息的阈值区间设为[μ–3σ, μ+3σ], 梯度中位于此区间外的元素置为零. 最后, 对该区间量化处理, 将其平均划分为P个子区间, 形成P+1个端点值, 将梯度中的每个元素近似到最临近的端点上. 服务器在每轮迭代后, 将重新记录并统计各客户端的原始未经压缩的梯度分布情况, 以实现实时动态更新量化区间, 优化压缩效果.
经过上述离散量化处理后, 所有处于阈值区间中的梯度值均可用这P+1个区间端点值来表示, 处于区间外的值则为0. 为进一步压缩信息量, 这里利用哈夫曼编码(Huffman coding)[25]对处理后可能出现的共P+2个值依据其出现的频率进行最优不定长编码. 以阈值区间[1.0, 2.0]、量化间隔数P取2为例, 梯度映射码表如表1所示.
| 表 1 梯度映射码表示意 |
经过离散量化和编码处理后, 服务器在分发梯度值时, 只需将梯度中所有元素的编码值按位拼接, 形成一个比特串, 传输该串及梯度映射码表即可, 从而实现梯度的高效压缩, 降低服务器分发的数据量.
第3.1节和第3.2节共同构成本文的压缩算法, 整体流程如算法1所示. 在每轮训练中, 各客户端并行执行前向传播, 输出本地数据特征的嵌入表示
算法1. 嵌入和梯度双向压缩算法
输入: 预先对齐的数据集, 客户端数量m, 训练轮次T, 稀疏化k值, 量化间隔数P.
1. for t=1, …, T do
2. for i=1, 2, …, m in parallel do
3. 客户端 Ci:
4. 本地模型输出嵌入表示
5. 稀疏化嵌入:
6. 上传
7. 从服务器下载梯度
8. 更新本地模型
9. end for
10. 服务器:
11. 接收客户端Ci上传的稀疏化嵌入
12. 根据本地缓存填充
13. 将所有客户端的嵌入输入到顶层模型执行前向传播
14. 更新顶层模型, 并计算客户端Ci的梯度
15. 依据本地缓存的上一轮次
16. 对量化后的梯度值进行哈夫曼编码
17. 将编码后的梯度值
18. end for
在算法1的稀疏化嵌入过程中, 首先要依据top-k算法对嵌入元素进行排序, 采用部分快排算法, 则此过程平均复杂度为
本节使用MNIST和CIFAR10数据集进行实验, 其中MNIST数据集为手写数字图像识别任务, 含10类标签, 训练集和测试集分别包含
实验设置4个客户端和1个服务器, 数据特征纵向切分均匀分布于各客户端. 对于MNIST数据集, 客户端和服务器均使用MLP多层感知机模型, 客户端输出嵌入的维度设为128, 批次大小为100, 学习率为0.01; 对于CIFAR10数据集, 客户端使用ResNet18模型, 输出嵌入维度为16, 服务器为1个全链接层, 批次大小为100, 学习率为0.001. 训练中采用的优化方法均为SGD. 稀疏化top-k方法的稀疏率设为0.125, 即只保留12.5%的嵌入元素; 离散量化的量化区间数P设为24. 训练所使用的硬件平台为4核Intel Xeon CPU @ 2.00 GHz, 一个Tesla P100 GPU、显存16 GB. 本节实验的目的在于验证所提算法的有效性和相比现有算法的改进效果, 因此只需保证不同算法在同一数据集上测试时, 其他超参数一致即可, 即控制压缩算法为唯一变量, 而不必选择最优参数组合使模型的准确率最高.
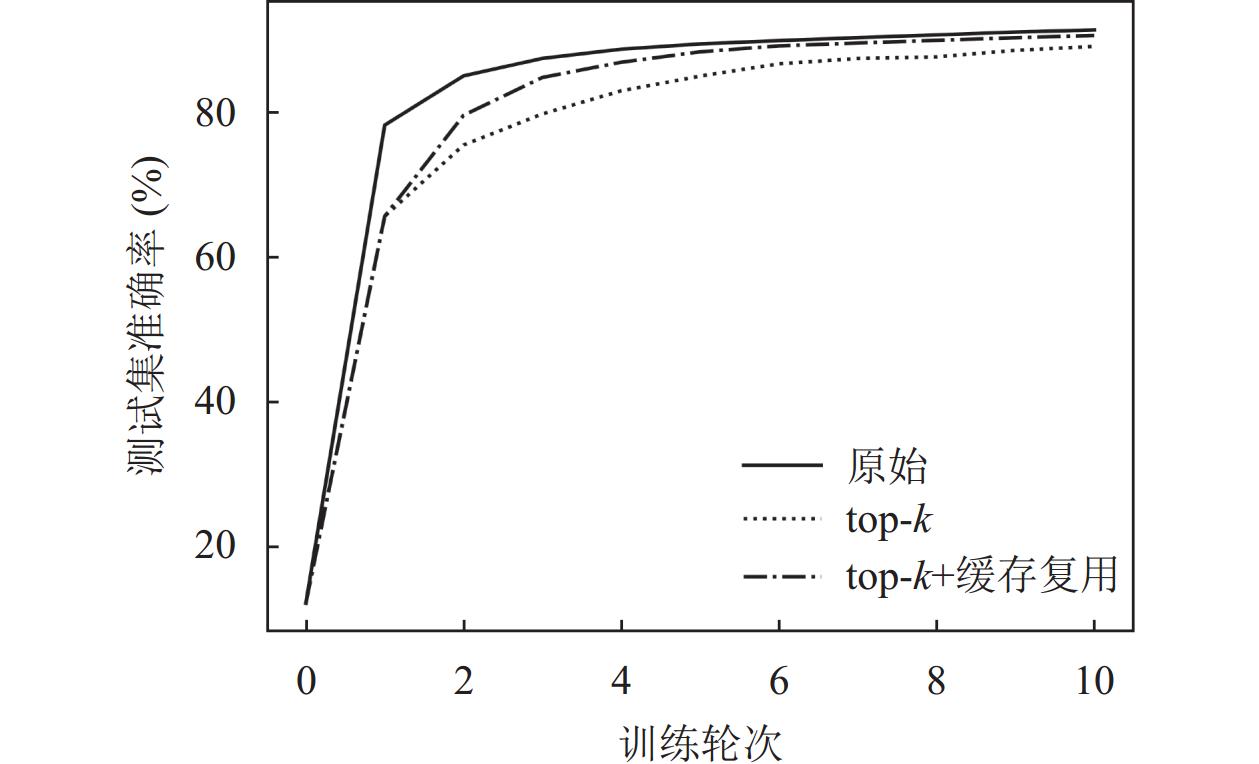
4.2 结果分析首先对本文的嵌入稀疏化算法进行测试, 对比原始未压缩算法、top-k算法以及本文增加缓存复用机制的改进top-k算法, 在MNIST和CIFAR10数据集上的实验结果分别如图2和图3所示.
|
图 2 MNIST数据集嵌入稀疏化测试结果 |
|
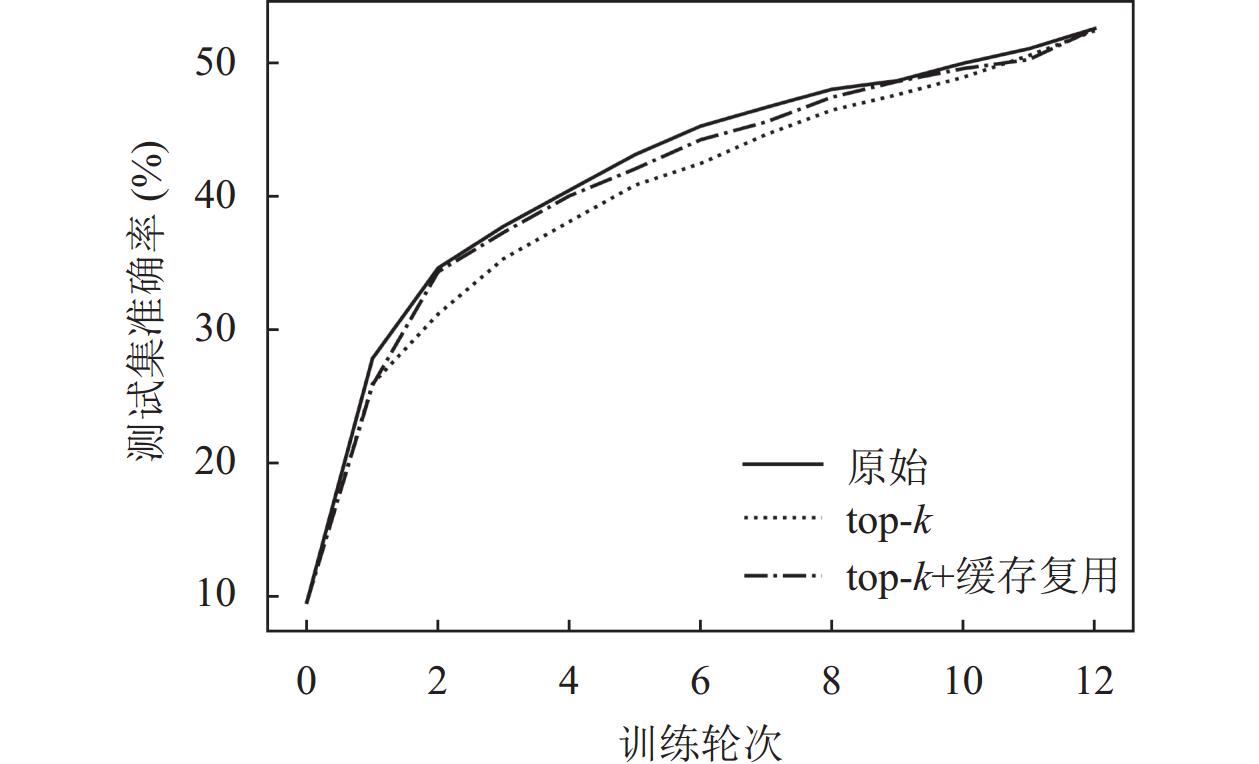
图 3 CIFAR10数据集嵌入稀疏化测试结果 |
从图2和图3中可以看出, 本文提出的增加缓存复用机制的改进top-k方法相比普通top-k方法, 在收敛速度及目标准确率方面都有一定程度的提升, 意味着达到相同准确率本文算法上传的数据量更少, 能够减少客户端上传的开销.
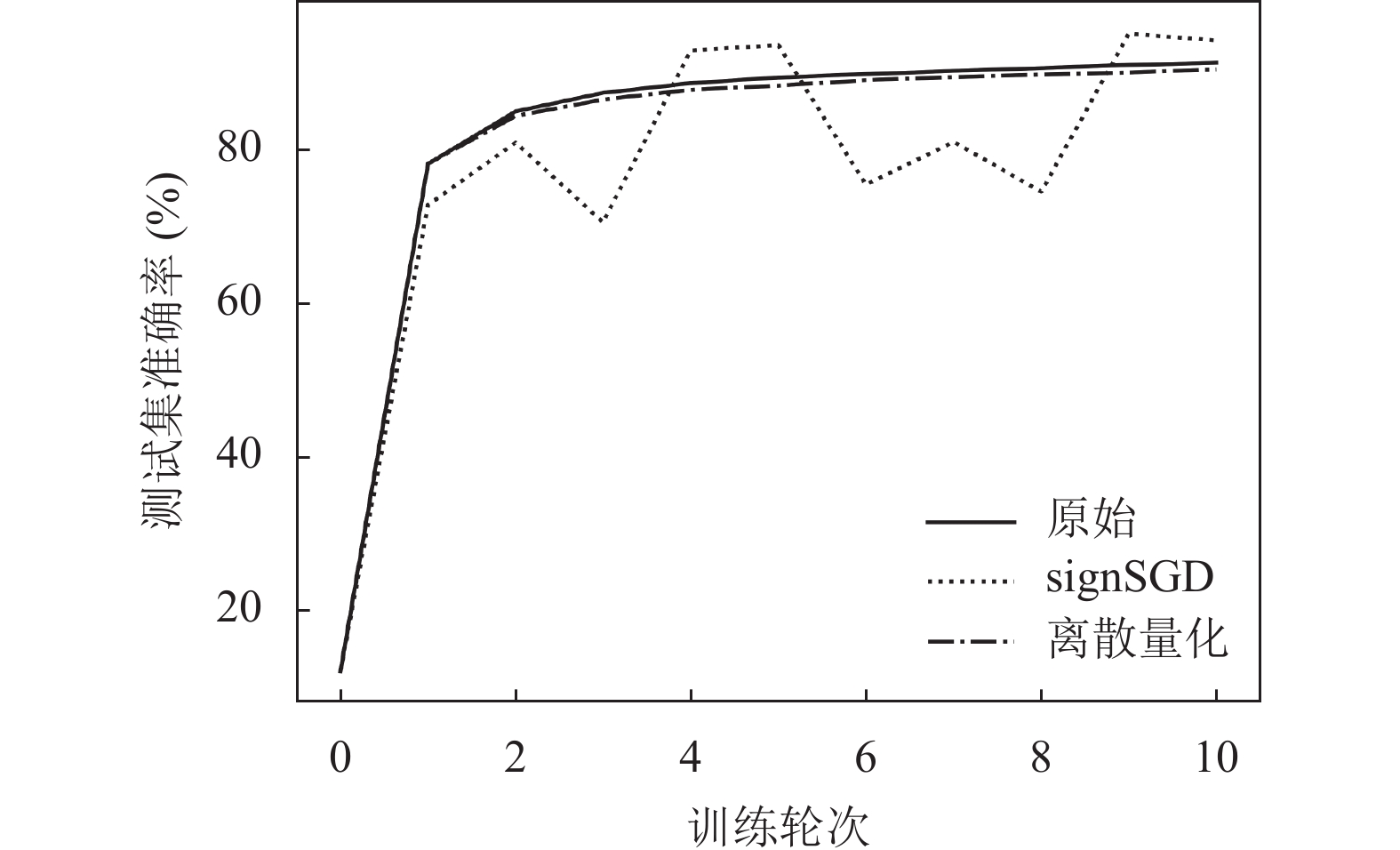
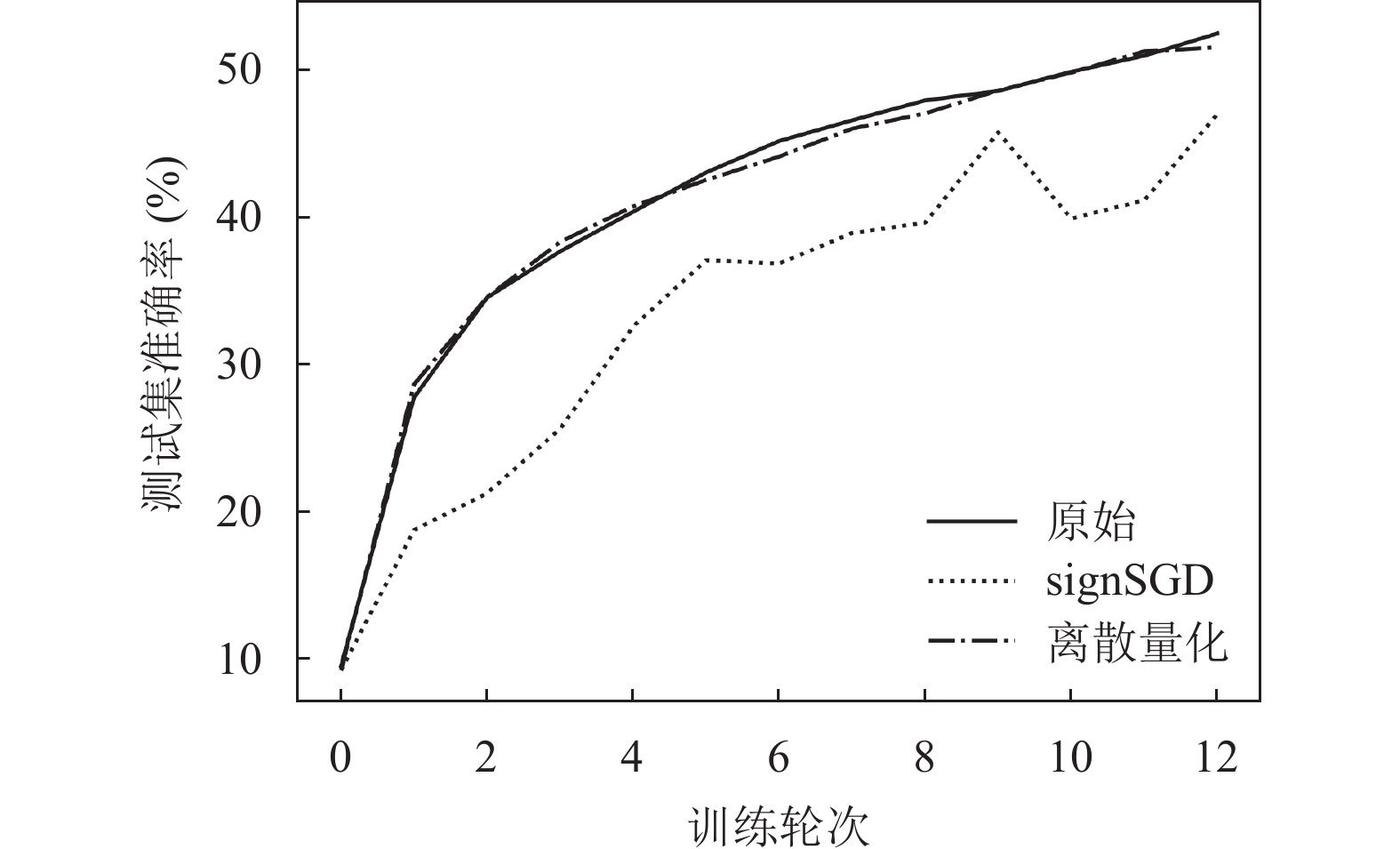
随后对本文的梯度量化算法进行测试, 对比原始未压缩算法、signSGD算法以及本文的离散量化编码算法, 在MNIST和CIFAR10数据集上的实验结果分别如图4和图5所示.
|
图 4 MNIST数据集梯度量化测试结果 |
|
图 5 CIFAR10数据集梯度量化测试结果 |
从图4和图5中可以看出, 本文提出的离散量化方法对于模型的准确率几乎没有影响, 但能显著降低服务器分发的数据量. 而如上文所述, signSGD方法应用于纵向联邦学习中时, 训练过程十分震荡, 会导致模型无法收敛.
表2给出了综合使用本文的嵌入稀疏化和梯度量化算法对客户端和服务器之间的数据传输进行双向压缩的综合效果, 并与top-k和signSGD进行对比.
| 表 2 嵌入和梯度双向压缩综合效果 |
表2中的准确率为相同通信轮次下在测试集上达到的目标准确率, 通信量为服务器与单个客户端之间上传嵌入和分发梯度的数据量之和. 从中可以看出, 综合利用本文的双向压缩算法, 可以在准确率与无压缩场景保持相当的同时, 降低约85%的通信量, 从而提高整体的通信效率, 压缩率和准确率均优于普通top-k方法和signSGD方法.
5 结论与展望本文提出了基于嵌入和梯度双向压缩的纵向联邦学习算法, 该算法对于客户端上传的嵌入表示采用改进的top-k方法进行压缩, 同时采用缓存复用机制提高收敛速率及目标准确率; 对于服务器分发的梯度, 采用离散量化与编码机制相结合的方法进行压缩. 通过上述方法, 减少训练过程中客户端和服务器之间交互的通信量, 提高通信效率. 实验结果表明, 本文算法能够在准确率与无压缩场景保持相当的前提下, 降低约85%的通信量, 提高通信效率, 减少整体训练时间.
本文研究为纵向联邦学习在实际应用中如何解决通信瓶颈问题提供了新的参考. 未来将进一步研究压缩算法中的相关参数对最终效果的影响, 探讨如何在压缩率、收敛速率以及目标准确率之间达到更好的动态平衡.
| [1] |
Yang Q, Liu Y, Chen TJ, et al. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology, 2019, 10(2): 12. DOI:10.1145/3298981 |
| [2] |
Qian ZP, Min CQ, Lai LB, et al. GAIA: A system for interactive analysis on distributed graphs using a high-level language. Proceedings of the 18th USENIX Symposium on Networked Systems Design and Implementation (NSDI 21). 2021. 321–335.
|
| [3] |
Fu FC, Miao XP, Jiang JW, et al. Towards communication-efficient vertical federated learning training via cache-enabled local updates. Proceedings of the VLDB Endowment, 2022, 15(10): 2111-2120. DOI:10.14778/3547305.3547316 |
| [4] |
Liu Y, Zhang XW, Kang Y, et al. FedBCD: A communication-efficient collaborative learning framework for distributed features. IEEE Transactions on Signal Processing, 2022, 70: 4277-4290. DOI:10.1109/TSP.2022.3198176 |
| [5] |
Castiglia T, Wang SQ, Patterson S. Flexible vertical federated learning with heterogeneous parties. IEEE Transactions on Neural Networks and Learning Systems. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=10258117. (published online). [doi: 10.1109/TNNLS.2023.3309701]
|
| [6] |
Shah SM, Lau VKN. Model compression for communication efficient federated learning. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(9): 5937-5951. DOI:10.1109/TNNLS.2021.3131614 |
| [7] |
Xu Y, Liao YM, Xu HL, et al. Adaptive control of local updating and model compression for efficient federated learning. IEEE Transactions on Mobile Computing, 2023, 22(10): 5675-5689. DOI:10.1109/TMC.2022.3186936 |
| [8] |
Lin YJ, Han S, Mao HZ, et al. Deep gradient compression: Reducing the communication bandwidth for distributed training. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018.
|
| [9] |
Wangni J, Wang JL, Liu J, et al. Gradient sparsification for communication-efficient distributed optimization. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 1306–1316.
|
| [10] |
Chen X, Li JT, Chakrabarti C. Communication and computation reduction for split learning using asynchronous training. Proceedings of the 2021 IEEE Workshop on Signal Processing Systems (SiPS). Coimbra: IEEE, 2021. 76–81. [doi: 10.1109/SiPS52927.2021.00022]
|
| [11] |
Mao YZ, Zhao ZH, Yan GF, et al. Communication-efficient federated learning with adaptive quantization. ACM Transactions on Intelligent Systems and Technology, 2022, 13(4): 67. DOI:10.1145/3510587 |
| [12] |
Castiglia TJ, Das A, Wang SQ, et al. Compressed-VFL: Communication-efficient learning with vertically partitioned data. Proceedings of the 39th International Conference on Machine Learning. Baltimore: PMLR. 2022. 2738–2766.
|
| [13] |
Inoue Y, Moriya H, Zhang Q, et al. SparseVFL: Communication-efficient vertical federated learning based on sparsification of embeddings and gradients. Proceedings of the 2023 International Workshop on Federated Learning for Distributed Data Mining. OpenReview.net, 2023.
|
| [14] |
Cai DQ, Fan T, Kang Y, et al. Accelerating vertical federated learning. arXiv:2207.11456, 2022.
|
| [15] |
Khan A, Thij MT, Wilbik A. Communication-efficient vertical federated learning. Algorithms, 2022, 15(8): 273. DOI:10.3390/a15080273 |
| [16] |
文家宝, 陈泯融. 基于宽度网络架构的单模型主导联邦学习. 计算机系统应用, 2024, 33(1): 1-10. DOI:10.15888/j.cnki.csa.009346 |
| [17] |
Li M, Chen YW, Wang YQ, et al. Efficient asynchronous vertical federated learning via gradient prediction and double-end sparse compression. Proceedings of the 16th International Conference on Control, Automation, Robotics and Vision (ICARCV). Shenzhen: IEEE, 2020. 291–296. [doi: 10.1109/ICARCV50220.2020.9305383]
|
| [18] |
Bernstein J, Wang YX, Azizzadenesheli K, et al. signSGD: Compressed optimisation for non-convex problems. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 559–568.
|
| [19] |
田金箫. 提升联邦学习通信效率的梯度压缩算法. 计算机系统应用, 2022, 31(10): 199-205. DOI:10.15888/j.cnki.csa.008748 |
| [20] |
陈律君, 肖迪, 余柱阳, 等. 基于秘密共享和压缩感知的通信高效联邦学习. 计算机研究与发展, 2022, 59(11): 2395-2407. DOI:10.7544/issn1000-1239.20220526 |
| [21] |
Liu Y, Kang Y, Zou TY, et al. Vertical federated learning: Concepts, advances, and challenges. IEEE Transactions on Knowledge and Data Engineering, 2024, 36(7): 3615-3634. DOI:10.1109/TKDE.2024.3352628 |
| [22] |
Jhunjhunwala D, Mallick A, Gadhikar A, et al. Leveraging spatial and temporal correlations in sparsified mean estimation. Proceedings of the 34th Advances in Neural Information Processing Systems. Curran Associates, Inc., 2021. 14280–14292.
|
| [23] |
Fu C, Zhang XH, Ji SL, et al. Label inference attacks against vertical federated learning. Proceedings of the 31st USENIX Security Symposium (USENIX Security 22). Boston: USENIX Association, 2022. 1397–1414.
|
| [24] |
Pukelsheim F. The three sigma rule. The American Statistician, 1994, 48(2): 88-91. DOI:10.2307/2684253 |
| [25] |
Huffman DA. A method for the construction of minimum-redundancy codes. Proceedings of the IRE, 1952, 40(9): 1098-1101. DOI:10.1109/JRPROC.1952.273898 |
 2024, Vol. 33
2024, Vol. 33



