异常检测旨在从数据中寻找不符合预期正常行为的模式和对象[1]. 异常检测是一个被广泛研究的问题, 并在各领域中得到了广泛应用, 例如检测信用卡诈骗[2,3]、保险诈骗[4]、欺诈检测[5]、网络安全入侵检测[6]等. 然而, 目前关于异常检测的研究工作大多强调准确性和效率, 却忽视了异常检测结果的可解释性以及解释的合理性[7]. 未解释的异常对象会导致系统中的潜在问题长期存在而未被发现, 进而影响系统的表现和效率. 因此, 对异常对象进行解释具有重要的研究意义.
模型的可解释性是指能够解释机器学习模型的预测和决策过程的能力[7]. 如图1所示[8], 一个复杂的黑盒模型根据某人的特征将其判断为患有流感. 然而, 该模型仅是给出了预测结果, 而一个好的解释器能够对其做出解释. 解释器给出的解释是由于该实体有流鼻涕特征和头痛特征, 这些特征是患有流感的表征, 对预测结果具有正作用. 同时, 该解释器还给出了无疲劳感特征不是患流感的表征, 对预测结果具有负作用. 最终这些解释将会被发送给人类医生, 帮助医生做最终的决策. 解释模型的预测结果和决策过程对于用户和利益相关者理解模型行为至关重要. 可解释性有助于增强模型的透明度, 提高用户对模型的信任度, 并帮助发现模型中的潜在偏见或错误. 目前存在的解释方法主要通过计算模型中的特征的重要性以及解释特征值对预测的影响从而提供模型的可解释性[9].

|
图 1 模型的解释过程示意图 |
反事实解释方法[10–12]是可解释机器学习的研究热点之一, 旨在生成不同于观察数据的替代情景以解释模型的决策. 在机器学习和人工智能领域, 模型通常通过输入目前对象的特征信息来做出预测或决策. 然而, 由于众多模型的黑盒特性, 使得预测结果难以理解或解释. 反事实解释的目标是通过对输入特征进行扰动, 生成一个新的实例或情景, 使得模型的预测结果与原始预测结果相反. 这个新的实例或情景被称为反事实示例. 通过比较原始实例和反事实示例之间的差异, 可以了解模型在做出预测时考虑了哪些特征、因素或规律.
举个例子, 假设一个已经训练好的模型对个人贷款申请进行预测. 当某人的贷款申请被拒绝时, 可以使用反事实解释来生成一个反事实示例, 即假设此人的某些特征或属性发生变化, 可使得贷款申请被接受. 例如, 如果此人的工资增加了2 000元, 那么他的贷款申请可能会被接受. 这个反事实解释提供了一种解释模型决策的方式, 帮助我们理解模型对不同特征的敏感性和影响. 反事实解释方法可以应用于各种领域, 包括金融、医疗、社交网络等, 以增加模型的可解释性、可信度和可靠性. 该方法提供了一种探索模型内部运作方式的方法, 并有助于发现模型的局限性、偏见或错误.
然而, 直接使用现有反事实方法所产生的反事实示例解释可能并不总是与现实相一致. 例如, 在修改特征的过程中, 一个人的教育水平通常与较高的工资相关, 那么一个建议降低工资同时提高教育水平的反事实解释将不是一个合理的反事实解释. 已有工作提出了在生成反事实解释的过程中添加特征因果约束来限制反事实解释的合理性[12]. 然而, 该方法是针对分类问题设计, 在解释异常检测模型时并不适用. 异常对象的特征值可能完全脱离正常范围, 导致特征之间不存在因果关系. 例如一个异常对象的年龄为一岁, 而其学历为博士, 则原本具有因果关系的两个特征变得不再具有因果关系.
为了解决上述问题, 本文在反事实理论基础上对经典算法进行了改进, 在目标函数中新增了一个特征因果项, 以约束生成的反事实解释特征之间的因果性. 该约束通过量化相关特征之间的改动幅度来衡量因果性. 同时, 本文提出了范围性因果关系的概念, 即在特征扰动没有到达一定程度的情况下不会考虑或者稍微考虑特征间的因果关系, 等相关特征处于一定范围以后再考虑特征间的因果关系. 随后, 基于改进后的遗传算法来对新提出的目标函数进行求解. 此外, 本文还提出了一个用于评价反事实解释合理性的度量指标, 用以评价对比算法反事实解释的合理程度. 本文在真实数据集上与其他先进的方法比较了反事实解释特征之间的合理性, 并在真实数据集上进行具体的案例分析. 实验结果表明, 相比其他对比算法而言, 本文所提出的方法生成的反事实解释有着更高的合理性.
本文的贡献如下.
■ 本文提出了一种新的基于因果约束的异常对象反事实解释方法IARC, 可以生成具有强合理性的反事实解释.
■ 本文提出了一种基于结果因果模型的反事实解释合理性度量指标, 可以衡量反事实解释的矛盾程度.
■ 本文在多个真实数据集下与其他先进的算法进行实验对比和真实案例分析, 实验结果表明IARC算法能为异常对象生成具有更强合理性的反事实解释.
本文接下来的内容安排如下: 第1节介绍了本研究的相关工作. 第2节介绍了算法的实现过程. 第3节将IARC与其他先进算法作比较, 验证了算法的有效性.
1 相关工作可解释的机器学习[13]是指将解释性引入到机器学习模型中, 使其能够解释和理解其预测和决策过程. 可解释的机器学习旨在使复杂的机器学习模型变得透明, 能够解释预测是如何进行及其基础原理[14]. 近年来, 在可解释的机器学习领域取得了重要进展, 涵盖了各种方法和应用[15]. 实现可解释性的主要方法根据分类方式的不同不尽相同, 本文将反事实解释方法列出来单独作为一类, 因此主要包括基于特征重要性的方法、基于特征值的方法和基于反事实的解释方法.
基于特征重要性的方法[16]评估特征对模型决策的贡献, 使人们更好地了解哪些特征对模型的预测有影响. SHAP[17]是一种与模型无关的方法, 该方法通过博弈论计算每个特征对一个实例预测的贡献来解释预测, 最终获得各个特征的重要性.
基于特征值的解释方法[18]通常涉及确定模型需要哪些特征进行预测, 并将这些特征用作解释. 这些方法通常用于解释基于决策树的模型, 因为决策树根据特征值对数据进行分割, 该类方法主要应用于医学诊断和金融风险评估[19].
反事实解释方法[20]生成不同于观察数据的替代情景以解释模型的决策. 它们探讨如果改变特定特征, 模型的输出将如何变化, 大多应用于图像分类和推荐系统等领域[21].
Wachter等人[22]首次将反事实解释用于解释模型预测, Wachter等人提出了一个目标函数, 通过最小化该目标函数, 模型的预测将被反转, 并观察反转后变化的特征以提供解释. Mothilal等人[23]认为反事实解释还应具有多样性, 一个高度多样化的反事实解释可以从多个角度向用户提供解释. Poyiadzi等人[24]认为反事实生成过程中的路径应该对应现有数据点, 因此他们提出了一种名为Face的算法来约束反事实的生成路径. Kanamori等人[25]认为现有的反事实解释没有解决必须同时为多个实例分配解释的情况, 因此他们提出了用决策树为有效行动分配的反事实解释树来解决这个问题. Slack等人[26]认为对原始点进行小干扰会生成更好的反事实解释. Carreira-Perpiñán等人[27]发现当前反事实解释方法存在局限性, 使其无法应用于解释不可微分模型. 因此, 作者提出了一种近似技术来解决解释不可微分模型的挑战. Parmentier等人[28]对树集成的反事实解释采取了一种通用的方法, 他们主张通过基于模型的搜索寻找“最佳”解释. 朱霄等人[29]将反事实方法应用到数据库的参数配置上以实现数据库参数的配置. 刘珈麟等人[30]提出了反事实增强的对抗学习序列推荐. Blanc等人[31]提出一种基于查找优化地反事实解释算法, 该算法可以适用于任何单调模型, 并有着很低的时间复杂度. Tolkachev等人[32]提出一种为自然语言接口生成反事实解释的算法, 该算法基于语义解析的自然语言接口生成解释, 并能够产生更接近用户意图的反事实解释. Guidotti等人[33]调查了最新的解释器生成的反事实解释, 并认为目前的技术水平并没有提供足够完美的反事实解释器. Tešić等人[34]对反事实解释是否会扭曲人们的直觉进行了探究, 并实验得出反事实解释会对人们认知中的因果关系产生影响. Moreira等人[35]多个模型上实验论证生成反事实的有效性, 并认为目前主流的反事实解释方法不受模型类型制约, 但同时生成的解释也不具有实际意义, 因此该作者强烈建议进行定性分析, 以确保对反事实解释的可靠分析.
2 考虑因果约束的反事实解释方法本文提出了一个新的考虑因果约束的反事实解释方法——IARC (interpret anomaly via reasonable counter-factual), 来对异常检测模型的结果进行解释. 该算法核心是在经典反事实解释方法的基础上, 将特征间的因果约束添加到损失函数中, 再通过改进后的遗传算法优化新的目标函数, 最终生成具有强合理性的反事实解释. 为适应异常检测结果的可解释性, 对于正常的特征, 直接考虑特征间的因果关系, 而对于异常特征, 则采取异常特征约束的手段将其限制在正常范围内以后再考虑因果关系.
2.1 经典反事实解释方法反事实解释是用来回答以下问题的方法: “为了将输入实例的错误预测结果(比如疾病的高风险)转变为正确预测结果(比如疾病的低风险), 需要进行怎样的最小化改变”. 具体来说, 给定一个数据点x和从数据集学习到的机器学习决策模型f, 反事实解释找到一个改进的示例c, 该示例尽可能靠近数据点x, 并且其预测f(c)接近所需目标, 如图2所示.
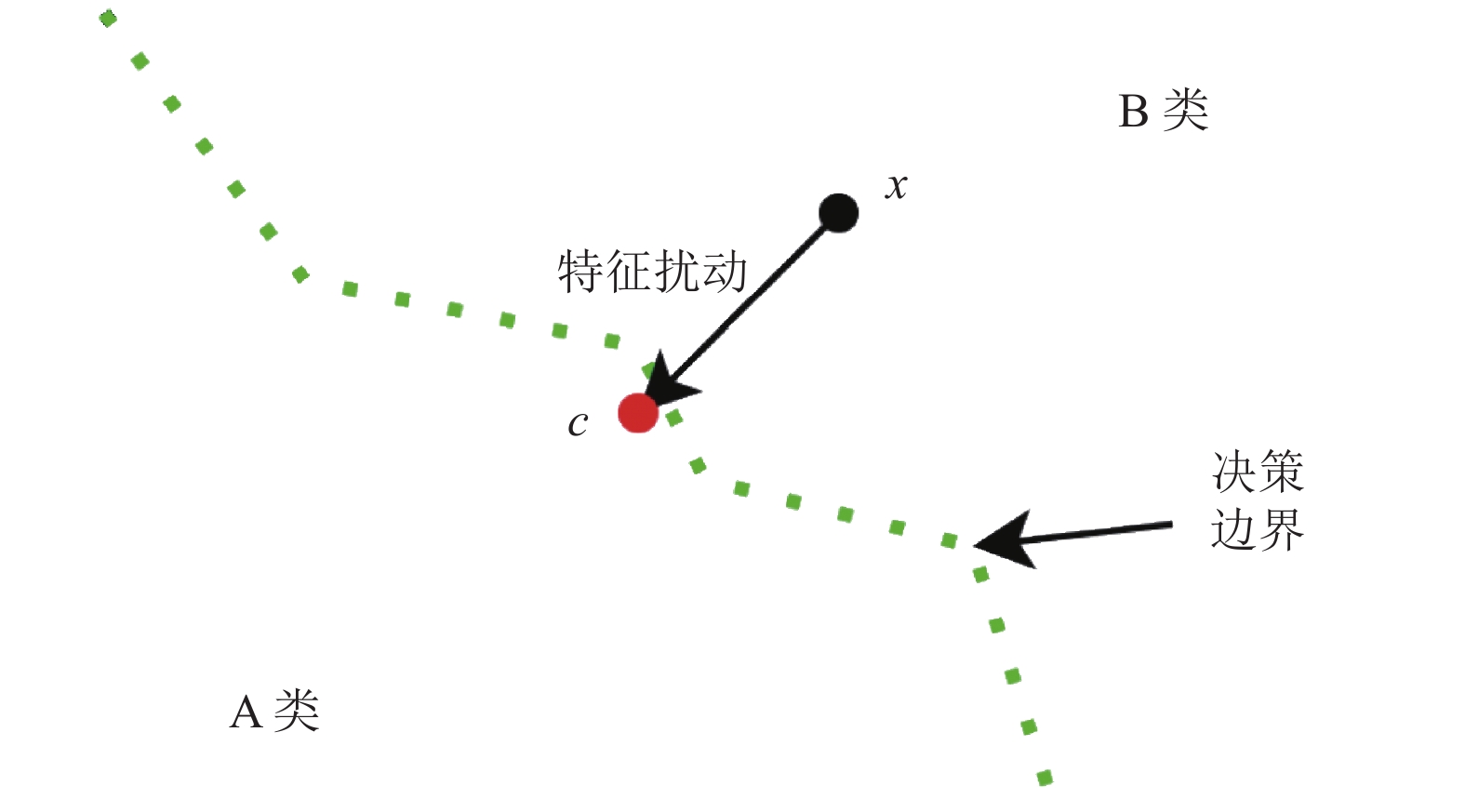
|
图 2 反事实解释示意图 |
图2中模型将数据划分为A类和B类, 模型将x预测为B类, 而x的反事实解释过程是对x进行特征扰动产生待选反事实c, 直至模型对c的预测结果是属于A类, 并且期间不断最小化待选反事实解释c到x的距离, 最终产生反事实解释c. 而x的反事实解释就是x和c的特征之间的差别, 这个差别可以解释为什么x属于B类而不属于A类, 即为什么模型将x预测为B类.
上述过程数学表达形式如下所示:
| argmincmaxλ<Λλℓ(f(c),y)+dist(x,c) | (1) |
其中,
经典反事实方法直接产生的反事实解释可能并不总是与现实相一致. 为了解决因果约束问题, Mahajan等人[12]提出了为分类模型生成强解释性的反事实解释方法. 该方法认为反事实解释可行性从根本上说是一个因果概念, 不能仅用统计约束来解决. 该方法基于输入特征之间的潜在结构因果模型正式定义了反事实解释, 提出了一种因果接近损失, 它可以添加到任何反事实生成方法中. 所提出的因果接近性损失时基于了特征之间的因果关系, 并由输入特征的结构性因果模型(SCM)进行建模.
如表1以及表2所示, 本文在Adult数据集上做了初步验证, 其中表1表示没有包含因果约束条件而修改后的特征, 而表2表示考虑了特征约束条件的修改后的特征. 从表1中可以明显看出, 年龄和婚姻状况特征之间存在矛盾. 生成的反事实解释显示其年龄在20岁左右, 但婚姻状况显示为“已婚”, 这种不一致与逻辑上的期望并不一致.
| 表 1 无因果约束时产生的反事实解释 |
| 表 2 有因果约束时产生的反事实解释 |
但是, 在表2中, 添加特征约束解决了这个问题. 纳入这些约束条件后产生的反事实解释反映了17岁和18岁的人是未婚的, 而30岁的人被描述为离异的.
然而, Mahajan等人[12]提出的方法在直接用于异常检测模型时仍然存在一些问题和挑战. 该方法认为如果特征之间存在的某种因果关系, 则特征的扰动必须按照这种因果关系去扰动. 例如, 年龄和学历之间是正相关, 如果要使年龄学历增加则年龄必须增加. 然而, 在异常检测的背景下这种因果关系是错误的, 因为异常对象的特征有可能完全不符合现实逻辑, 即年龄特征可能是
本文所解决的问题定义如下.
给定一个因果约束模型
为了解决上述问题, 本文提出了基于因果约束的异常对象反事实解释方法(IARC). IARC算法的基本流程如下.
如图3所示, 对于异常点首先将其输入到解释算法中, 然后判断其特征是否处于可以进行因果约束的范围, 如果符合则进行特征因果约束, 反之则进行异常特征约束直到特征处于正常区间.
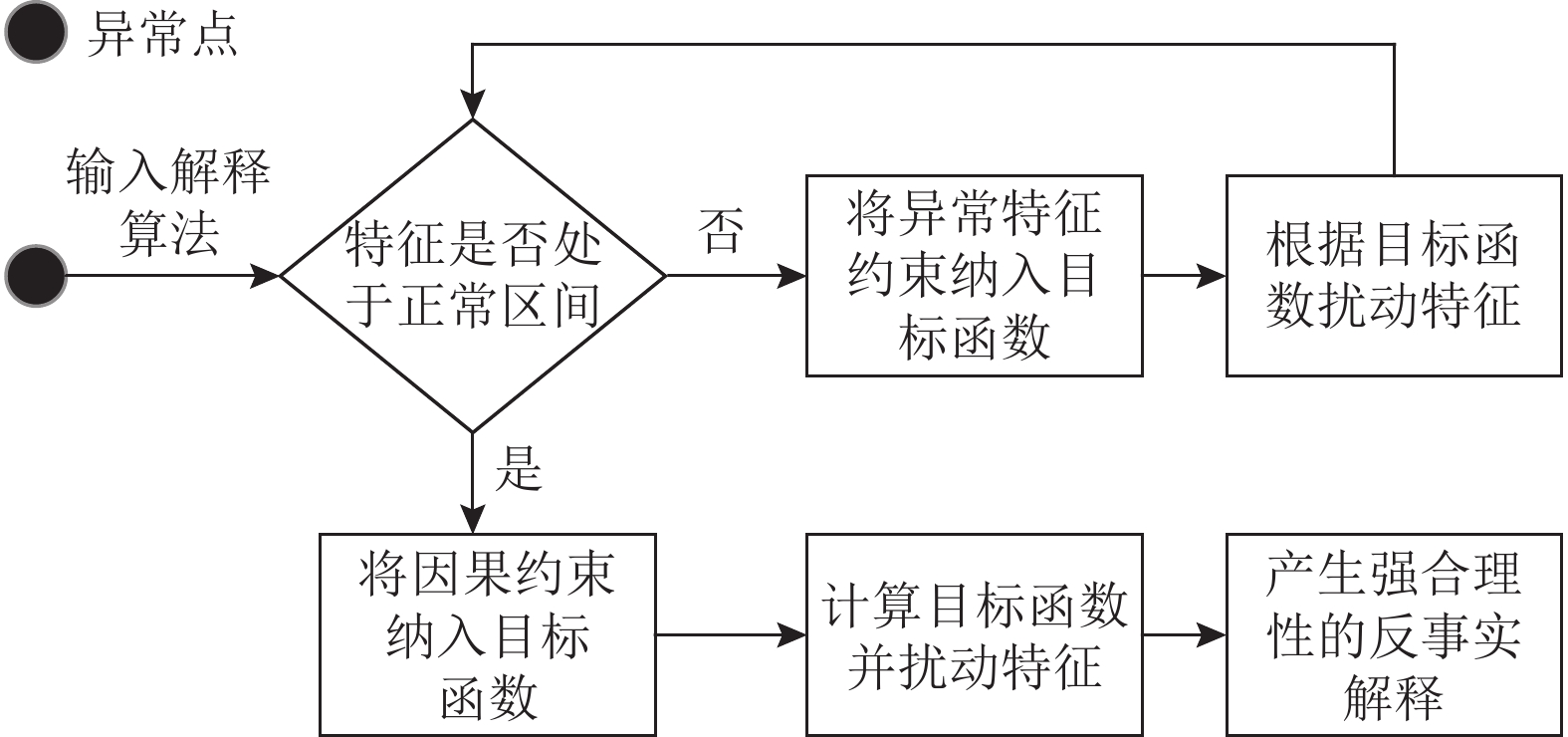
|
图 3 IARC的关键步骤 |
2.3.1 特征范围的确定
本节讨论的是待选反事实的异常特征处在怎样的范围才可以对待选反事实进行特征因果约束. 特征可以分为外因特征
若X为数据分布, 对于任意
| xf下=xfmin−αn∑i=1xfn | (2) |
其中, α是用于调节特征范围的参数,
| xf上=xfmax−αn∑i=1xfn | (3) |
其中, α是用于调节特征范围的参数,
通过在适当的范围开始对待选反事实进行特征因果约束才能确保某些违反因果模型的特征扰动能够进行.
此外, 除了外因特征和内因特征外, 还有一些只能呈仅增加或者仅减少的趋势, 比如汽车的里程数等, 对于这一类特征, 本文采取了一元约束对此进行约束:
异常特征约束的目的是将待选反事实的特征扰动到一个可以进行特征因果约束的范围, 即待选反事实应朝着密度高的区域移动, 因此本文复用了LOF得分作为评判密度的标准:
| density_loss=1kk∑i=1com_den(xi) | (4) |
但是仅有密度指标不足以将特征控制在可以使用特征因果约束的地步, 如果仅有密度则会导致待选反事实无条件地朝着高密度方向移动从而无法将特征扰动到特定的范围, 如图4所示. 图4中x为异常点, 显然该异常点是属于B类的异常, 因为可以很直观地从图中看出x距离B类集群更近, 但图中的待选反事实却不断地朝A集群靠近, 因为在仅有密度的情况下待选反事实会不断靠近高密度区域, 而B集群的密度显然要比A集群要高.
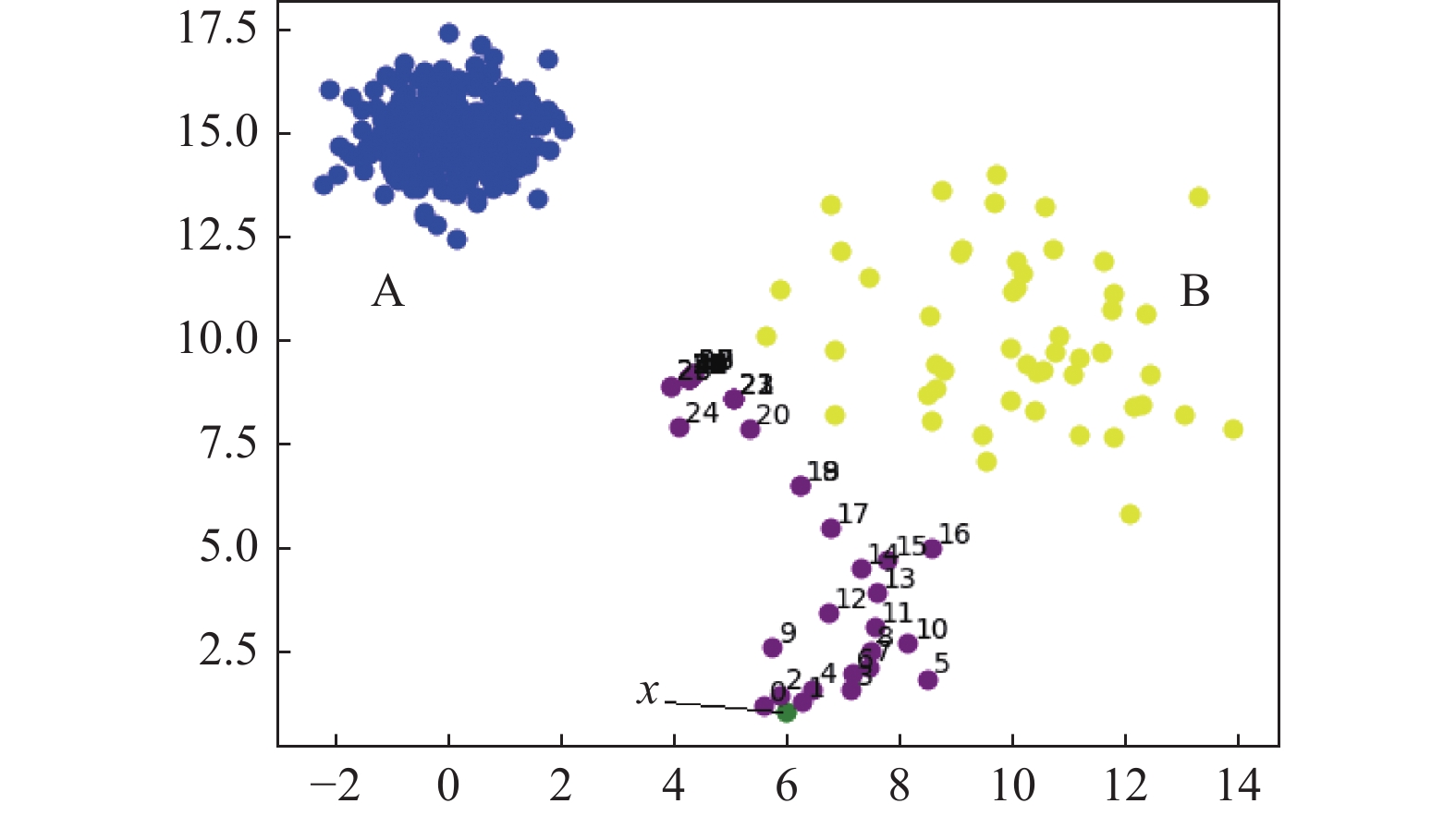
|
图 4 仅由密度控制下得待选反事实移动方向 |
为了解决这个问题, 本文在密度约束的基础上又添加了待选反事实到正常集群类中心的距离约束:
| dis_loss=d(xcf,1kk∑i=1xi) | (5) |
其中, k代表的是图4中所有B类的总数量,
综上, 最终本节提出的异常特征约束为:
| constraints=density_loss+λ1dis_loss | (6) |
然后将本节所提出的异常特征约束加入最初的反事实解释理论中可得式(7):
| C=argmincℓ(f(c),y)+λ2dist(x,c)+λ3constraints | (7) |
其中,
特征间的因果关系是指一个特征对另一个特征产生影响或导致变化的关系. 理解特征之间的因果关系对于模型的建立和解释至关重要, 这有助于识别特征之间真正的因果关系, 而不仅是相关性.
传统的机器学习方法通常更注重特征之间的相关性, 而较少关注因果关系. 通过使用因果推断方法, 人们可以更准确地识别哪些特征对结果产生了影响, 而不仅是表面上的相关性. 在处理特征间的因果关系时, 需要考虑因果推断的假设和限制, 确保推断出的因果关系是可靠和有效的. 此外, 了解特征之间的因果关系还可以帮助科研工作者更好地进行特征选择、模型解释和预测结果的解释. 因此, 在数据分析和机器学习中, 深入研究特征间的因果关系是至关重要的, 将有助于提高模型的稳健性和泛化能力. 通过深入研究特征间的因果关系, 用户可以更好地理解数据背后的机制和原因, 帮助用户进行更精准的预测和决策. 因果关系的探索还可以帮助解决相关性和因果之间的混淆, 从而避免误导性的结论.
而在本节中为了生成具有强合理性的反事实解释, 需要考虑到全局合理性[12].
全局合理性: 假设
此外, 如果待选反事实的特征已经处于正常区间, 则降低年龄的反事实实例是不可行的, 因为它违反了自然因果模型约束, 即年龄只能随着时间增长. 这样的因果约束无法仅通过数据学习到, 通常需要额外的信息才能学习到. 虽然其中一些可行性约束可以简单表述, 但是多个特征之间的因果关系可能导致复杂的约束条件. 但正如Mahajan等人[12]提到的方法, 可以使用结构性因果模型来形式化定义这些约束, 并将其实现为特征如何改变的约束.
接下来本文引用了Mahajan等人[12]提到的一个与合理性兼容的距离概念, 以限制对特征的独立扰动. 本文认为反事实案例与数据样本之间不仅基于它们之间的欧氏距离, 还要考虑特征之间的因果关系.
假设本文提供了观测数据的结构因果模型, 包括关于在
| DistCausalv(xv,xcfv)=Distv(xcfv,f(xcfvp1,⋯,xcfvpk)) | (8) |
其中,
这个距离度量由图5说明, 特征v的反事实值应取决于反事实案例中其父节点的值, 对于内因特征通过因果约束来控制特征的扰动, 而对于外因特征则仍然使用传统的距离度量. 一旦其父节点的反事实值确定, 它的值理想情况下应该是由结构因果模型函数f预测的值.
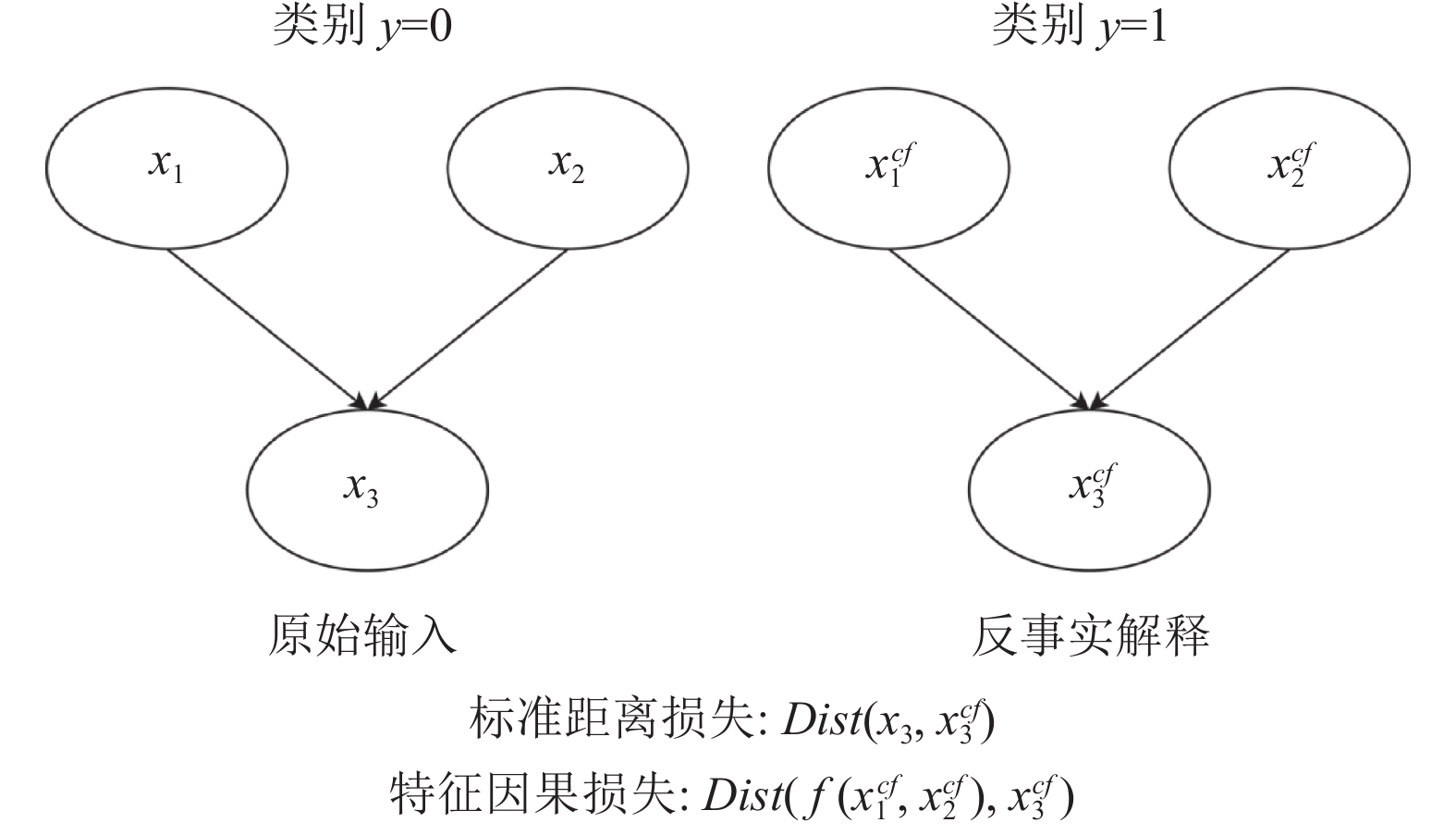
|
图 5 通过因果模型定义特征因果约束 |
需要注意的是这个距离度量并不用
| {Δv=xcfv−xvΔpredictedv=(f(xcfvp1,⋯,xcfvpk)+ε1)−(f(vp1,⋯,vpk)+ε2)E[Δpredictedv]=f(xcfvp1,⋯,xcfvpk)−f(vp1,⋯,vpk) | (9) |
当
| DistCausalv(xv,xcfv)=Dist(E[Δv],E[Δpredictedv]=ℓ2(xcfv,f(xcfvp1,⋯,xcfvpk)) | (10) |
因此, 传统的反事实生成损失函数中(式(1))的dist()项可被修改为式(11), 用以生成保持因果约束的反事实解释:
| DistCausal(x,xcf)=∑u∈UDistu(xcfu,xu)+∑u∈VDistCausalv(xcfv,xv) | (11) |
其中, U为外生节点(即在因果图中没有任何父节点的节点), 而V为其余特征, 之后再将式(1)的dist()项替换为因果约束可得式(12):
| argminxmaxλ<Λλℓ(f(x),y)+DistCausal(x,xcf) | (12) |
其中, x是待解释的异常对象, λ是控制各项之间平衡的参数, 在待选反事实的特征变动到特定范围后最小化式(12)即可生成具有强合理性的反事实解释.
2.3.4 目标函数的优化基于上述分析, 本文采取了改进后遗传算法[36]来对上述目标函数求解. 它通过模仿自然种群中观察到的遗传继承、交叉和突变过程来解决优化问题. 该算法不断进化并生成新解, 同时优化和改进现有解以逐渐接近最优解. 遗传算法的应用领域非常广泛, 它可以求解一些组合优化问题, 并且还可以求解复杂的多峰函数、优化控制器参数、参数优化、特征选择等.
遗传算法与进化论理论有相似的地方. 达尔文进化论保留了种群的个体性状, 而遗传算法则保留了针对给定问题的候选解集合(也称为individuals). 这些候选解经过迭代评估(evaluate), 用于创建下一代解. 更优的解会有着较大的概率被选择, 并将其特征遗传给其子代候选解集合. 随着代际更新, 候选解集合可以更好地解决当前的问题.
遗传算法的主要特点是遗传算法能够并行搜索解空间, 处理大规模问题, 并且遗传算法还根据个体的适应度来引导进化过程, 更有助于发现更优解, 遗传算法还具有较强的全局搜索能力, 能够跳出局部最优解. 除此之外遗传算法还不依赖于问题的特定性质, 所以其自适应性也较强.
但由于在异常对象周围的低密度数据需要解释, 遗传算法不能直接应用. 在算法执行的初始阶段, 对待处理的反事实解释特征的扰动对它们的密度影响很小, 导致优化目标变化微不足道. 生成的反事实解释往往会陷入局部最优解中, 并且生成的反事实点始终停留在异常区域附近, 无法充分逃离这些区域. 为解决上述问题, 在选择阶段对父代应用轻微的随机扰动. 在从父代生成后代的每次迭代中, 该算法在父代特征的基础上随机重置特征值, 重置范围为原始值的0.9–1.1倍, 之后新的父代经过交叉生成后代. 这种方法确保父代的特性保持不变, 同时能够迅速脱离局部最优解. 经过这一改进, 该算法持续产生有效的反事实解释.
基于上述分析, 本文提出了一种面向异常检测模型的生成强合理性的反事实解释的新算法(IARC), IARC算法的详细过程如算法1所示.
算法1. IARC
输入: 原始异常数据
输出: 反事实解释
1. 随机扰动原始异常
2. Repeat:
3. 将先前损失设置为当前损失;
4. 使用式(7)作为目标函数计算待选所有
5. 选取一定数量低损失的
6.
7. 如果当前待选反事实解释的内因特征和外因特征已经处于特定范围中, 则跳出当前循环;
8. Until |先前损失–当前损失|<α
9. 随机扰动原始
10. Repeat:
11. 将先前损失设置为当前损失;
12. 使用式(12)作为目标函数计算待选所有
13. 选取一定数量低损失的
14.
15. Until |先前损失–当前损失|<α
16. 输出反事实解释
首先输入原始异常数据
算法1的时间复杂度: 本算法的时间复杂度主要集中在计算两个目标函数上. 从步骤3–7计算了第1个目标函数, 在循环迭代寻找最小的损失, 同时还要在循环内遍历每一个特征, 因此, 时间复杂度是
对于每个数据集, 本文首先通过因果模型来建立特征之间的相互关系. 因此, 对于该实验, 本文假设特征之间的因果模型是预先知道的. 在了解了特征之间的相互关系后, 就可以计算出反事实的矛盾程度.
3.1.1 反事实解释度量指标本文定义了反事实解释特征的矛盾程度, 在本研究中, 特征之间的相互关系分为一致变化、不一致变化和不相关3类. 一致性变化是指特征的变化趋势在同一方向上的情况, 即如果特征A增加, 特征B也会增加, 如果特征A减少, 特征B也会减少. 另一方面, 不一致变化表明特征变化趋势相反; 特征A增加, 特征B减少, 特征A减少, 特征B增加. 最后, 不相关意味着这些特征之间没有关系; 它们的变化是独立的, 彼此之间没有影响.
本文假设特征之间的相互关系是事先已知的对于特征
| contradiction1={0, if Δf1×Δf2⩾0|Δf1|+|Δf2|2, else | (13) |
由式(13)可知, 如果特征
| contradiction2={0, if Δf1×Δf2⩽0|Δf1|+|Δf2|2, else | (14) |
上述方程的含义是, 如果特征
| contradiction=contradiction1+contradiction2 | (15) |
接下来本文使用上述度量指标在多个数据集上衡量了产生的反事实解释的矛盾程度, 数据集如下.
● Shuttle: 数据集名为“Shuttle”, 用于对太空飞船进行分类. 该数据集包含
● Glass: 数据集名为“Glass Identification”, 用于检测玻璃分类. 该数据集包含214个实例和10个特征.
● Page: 数据集名为“Page Block Classification”, 用于基于版面设计分类报纸版块. 该数据集包含
● Wine: 数据集名为“Wine Quality”, 用于评估白葡萄酒的质量. 该数据集包含
以上4个真实数据集皆来自UCI数据集仓库(https://archive.ics.uci.edu/dataset).
3.1.3 实验对比算法本文在以上4个数据集进行了实验, 并将实验结果与以下算法进行了比较.
WachterCF[22]: WachterCF是最早的反事实解释方法. WachterCF通过最小化原始实例与反事实实例之间的距离(距离损失)来生成反事实解释, 同时要求模型在反事实解释中尽可能地改变其预测(y损失). 在y损失之前有一个参数λ. 该方法通过最大化λ来平衡上述目标. 在实践中, 通过迭代求解xcf并增加λ直到找到足够接近的解来最大化λ.
DiCE[23]: DiCE在生成对抗解释时考虑了反事实解释的多样性. 作者在距离损失和多样性损失之前分别添加了λ1和λ2. 作者将λ1设为0.5, 将λ2设为1, 以平衡距离损失和多样性损失.
FACE[24]: FACE通过路径生成反事实解释. FACE使用路径算法确保FACE生成的所有用于反事实解释的路径由现有点组成. FACE主要有3种构建路径的方法, 本文采用性能最好的方法, 作者称其为KDE. 该方法的参数如下: 距离阈值
各个方法产生的反事实解释的平均矛盾程度如表3所示.
| 表 3 各算法的平均矛盾程度 |
● IARC vs. DiCE: 与DiCE相比, 可以观察到IARC的反事实解释在Shuttle、Glass和Wine中的特征矛盾水平明显较低. 这种矛盾的减少可以归因于目标函数中的特征因果约束的影响, 它倾向于产生具有较低矛盾程度的反事实. 然而, IARC在Page数据集上的性能不佳, 可能是由于该数据集具有因果关系的特征并没有出现异常, 而IARC在正常的特征上做了细微的扰动则导致了具有较高的矛盾程度.
● IARC vs. WachterCF: 与WachterCF相比, 同样可以观察到, IARC 在Shuttle、Glass和Wine数据集中表现出较低程度的矛盾. 这是因为WachterCF也没有考虑特性之间的特征之间的因果约束. 然而, 在Page数据集上, IARC和WachterCF显示出相似的矛盾程度. 这也可能归因于数据集具有因果关系的特征并没有出现异常.
● IARC vs. FACE: 与FACE相比, FACE生成的反事实解释具有相当低的矛盾程度, 直觉上这是因为FACE虽然没有考虑特征之间的因果约束, 但其考虑的生成反事实解释的路径是否可行, 即对特征的扰动所生成的待选反事实必须是现实中所存在的点, 所以矛盾程度低, 但事实上因为FACE无法在异常对象很少的数据集上生成反事实解释, 导致反事实解释的特征几乎没有改变, 故特征之间有着很低的矛盾程度.
上述实验证明, 本节所提出的反事实解释算法在大多数情况下都能生成合理的反事实解释, 故本文提出的基于因果约束的异常对象反事实解释方法是有效的.
3.3 真实案例分析本节分析了真实数据集上各个方法生成的反事实解释优劣. 表4和表5中每一行代表的是该特征在不同算法或场景下对应的特征具体数值, 而每一列代表的含义如列名所示, “特征”代表特征名称, “异常点”代表待解释异常的具体特征数值, 之后的算法名称代表的是不同算法生成的反事实解释的特征值具体数值如何. 如表4中IARC算法生成的反事实解释的Fixed acidity特征值为7.38.
| 表 4 Wine数据集上各方法产生的反事实解释 |
| 表 5 Glass数据集上各方法产生的反事实解释 |
对于Wine数据集, 如表4所示, 该数据集有以下特征, 依次是: 固定酸度, 挥发性酸度, 柠檬酸, 残糖, 氯化物, 游离二氧化硫, 总二氧化硫, 密度, 酸碱度, 硫酸盐, 酒精.
观察“Sulphates”特征, IARC方法产生的反事实解释相对于原异常提高了“Sulphates”的含量, 由于硫酸盐呈酸性, 理论上硫酸盐含量越高则溶液的pH值应越低, 反之越高, 而DiCE和WachterCF生成的反事实解释降低了硫酸盐的含量的同时却也降低了pH值, 这说明这两种方法生成的反事实解释所改动的特征存在矛盾, 反观IARC生成的反事实解释, 提高了硫酸盐的含量的同时也降低了pH值, 说明IARC对特征的改动是合理的. 另外, 很明显可以看出FACE方法产生的反事实解释的特征与异常对象的特征没有区别, 这就像本文先前提到的一样, 虽然FACE方法计算出来的矛盾程度得分很低, 但其低的原因并不是因为其在生成反事实解释时只选取真实存在的点作为解释, 而是因为其生成反事实解释失败, 并没有对特征做出扰动, 既然没有改动特征就不存在改动的特征之间存在矛盾的这种说法, 所以表4中FACE方法生成的反事实解释与异常对象的特征没有差别.
对于Glass数据集, 如表5所示, 该数据集有以下特征, 依次是: 折射率, 钠, 镁, 铝, 硅, 钾, 钙, 钡, 铁. 一般来说, 增加玻璃中的硅含量通常会导致折射率的升高[37]. 虽然IARC的硅含量降低的同时折射率Ri升高了, 但由于特征改变的幅度并不大, 并且DiCE和WachterCF的反事实解释也没有明显的优于IARC, 所以并不能说明特征因果约束完全无效. 产生这种情况的原因可能是因果模型中特征之间的关系有所欠缺, 因此出现了这种情况.
因此, 由表4和表5可知, 在真实数据集上, IARC与其他先进的算法相比能够生成更合理的反事实解释, 对于一些相互之间有因果关系的特征IARC成功阻止了特征扰动违背因果关系.
4 结束语在异常对象极度稀疏的异常检测任务中, 对异常检测结果做出具有强合理性的解释是一个实际且具有挑战性的问题. 为此, 本文提出了一个新的基于因果约束的异常对象反事实解释方法IARC. 所提出的方法主要由两个阶段性的目标函数组成: 第1个目标函数对异常特征进行约束, 使异常对象的特征大致处于相互之间具有因果关系的范围内; 第2个目标函数对特征的因果关系进行约束, 最终为异常对象生成具有强合理性的反事实解释. 最后, 在多个真实数据集下与其他先进的算法进行对比了各自生成的反事实解释之间的合理性, 并且与其他方法对比分析了反事实解释的合理性, 实验证明IARC算法为异常对象生成的反事实解释具有更强的合理性.
本文假设已经提前知道了特征之间的因果模型, 但在现实生活中特征之间的因果模型大多数情况下是无法获取的, 因此未来的工作可以考虑在无法获取特征之间的相互关系的情况下如何为异常点生成具有强合理性的反事实解释, 这是一个非常值得深入研究但同时也是非常具有挑战的问题.
| [1] |
Chandola V, Banerjee A, Kumar V. Anomaly detection: A survey. ACM Computing Surveys, 2009, 41(3): 15. |
| [2] |
Dal Pozzolo A, Caelen O, Le Borgne YA, et al. Learned lessons in credit card fraud detection from a practitioner perspective. Expert Systems with Applications, 2014, 41(10): 4915-4928. DOI:10.1016/j.eswa.2014.02.026 |
| [3] |
Porwal U, Mukund S. Credit card fraud detection in E-commerce: An outlier detection approach. arXiv:1811.02196, 2018.
|
| [4] |
Sithic HL, Balasubramanian T. Survey of insurance fraud detection using data mining techniques. arXiv:1309.0806, 2013.
|
| [5] |
Kim MH, Lee S, Lee KC. Kalman predictive redundancy system for fault tolerance of safety-critical systems. IEEE Transactions on Industrial Informatics, 2010, 6(1): 46-53. DOI:10.1109/TII.2009.2020566 |
| [6] |
Alom Z, Taha TM. Network intrusion detection for cyber security using unsupervised deep learning approaches. Proceedings of the 2017 IEEE National Aerospace and Electronics Conference. Dayton: IEEE, 2017. 63–69.
|
| [7] |
Ribeiro MT, Singh S, Guestrin C. Model-agnostic interpretability of machine learning. arXiv:1606.05386, 2016.
|
| [8] |
Ribeiro MT, Singh S, Guestrin C. “Why should I trust you?”: Explaining the predictions of any classifier. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 1135–1144.
|
| [9] |
Khan S, Liew CF, Yairi T, et al. Unsupervised anomaly detection in unmanned aerial vehicles. Applied Soft Computing, 2019, 83: 105650. DOI:10.1016/j.asoc.2019.105650 |
| [10] |
Gerstenberg T, Stephan S. A counterfactual simulation model of causation by omission. Cognition, 2021, 216: 104842. DOI:10.1016/j.cognition.2021.104842 |
| [11] |
Roese NJ. Counterfactual thinking. Psychological Bulletin, 1997, 121(1): 133-148. DOI:10.1037/0033-2909.121.1.133 |
| [12] |
Mahajan D, Tan CH, Sharma A. Preserving causal constraints in counterfactual explanations for machine learning classifiers. arXiv:1912.03277, 2019.
|
| [13] |
Ribeiro MT, Singh S, Guestrin C. Anchors: High-precision model-agnostic explanations. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press, 2018. 1527–1535.
|
| [14] |
Gilpin LH, Bau D, Yuan BZ, et al. Explaining explanations: An overview of interpretability of machine learning. Proceedings of the 5th IEEE International Conference on Data Science and Advanced Analytics. Turin: IEEE, 2018. 80–89.
|
| [15] |
Zhang Y, Tiňo P, Leonardis A, et al. A survey on neural network interpretability. IEEE Transactions on Emerging Topics in Computational Intelligence, 2021, 5(5): 726–742.
|
| [16] |
Jain S, Wallace BC. Attention is not explanation. Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Minneapolis: ACL, 2019. 3543–3556.
|
| [17] |
Lundberg SM, Lee SI. A unified approach to interpreting model predictions. Proceedings of the 30th International Conference on Neural Information Processing Systems. Long Beach, 2017. 4765–4774.
|
| [18] |
Corter JE, Gluck MA. Explaining basic categories: Feature predictability and information. Psychological Bulletin, 1992, 111(2): 291-303. DOI:10.1037/0033-2909.111.2.291 |
| [19] |
Guidotti R, Monreale A, Ruggieri S, et al. A survey of methods for explaining black box models. ACM Computing Surveys, 2019, 51(5): 93. |
| [20] |
Karimi AH, Barthe G, Balle B, et al. Model-agnostic counterfactual explanations for consequential decisions. Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics. Palermo: PMLR, 2020. 895–905.
|
| [21] |
Tan JT, Xu SY, Ge YQ, et al. Counterfactual explainable recommendation. Proceedings of the 30th ACM International Conference on Information & Knowledge Management. ACM, 2021. 1784–1793.
|
| [22] |
Wachter S, Mittelstadt B, Russell C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harvard Journal of Law & Technology, 2018, 31(2): 841-887. |
| [23] |
Mothilal RK, Sharma A, Tan CH. Explaining machine learning classifiers through diverse counterfactual explanations. Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency. Barcelona: ACM, 2020. 607–617.
|
| [24] |
Poyiadzi R, Sokol K, Santos-Rodríguez R, et al. FACE: Feasible and actionable counterfactual explanations. Proceedings of the 2020 AAAI/ACM Conference on AI, Ethics, and Society. New York: ACM, 2020. 344–350.
|
| [25] |
Kanamori K, Takagi T, Kobayashi K, et al. Counterfactual explanation trees: Transparent and consistent actionable recourse with decision trees. Proceedings of the 25th International Conference on Artificial Intelligence and Statistics. PMLR, 2022. 1846–1870.
|
| [26] |
Slack D, Hilgard S, Lakkaraju H, et al. Counterfactual explanations can be manipulated. Proceedings of the 35th International Conference on Neural Information Processing Systems. Curran Associates Inc., 2021. 6.
|
| [27] |
Carreira-Perpiñán MÁ, Hada SS. Counterfactual explanations for oblique decision trees: Exact, efficient algorithms. Proceedings of the 35th AAAI Conference on Artificial Intelligence. AAAI Press, 2021. 6903–6911.
|
| [28] |
Parmentier A, Vidal T. Optimal counterfactual explanations in tree ensembles. Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 8422–8431.
|
| [29] |
朱霄, 邵心玥, 张岩, 等. 面向数据库配置优化的反事实解释方法. 软件学报, 2024, 35(9): 4469–4492. [doi: 10.13328/j.cnki.jos.006977]
|
| [30] |
刘珈麟, 贺泽宇, 李俊. 反事实增强的对抗学习序列推荐. 计算机系统应用, 2024, 33(4): 235-245. DOI:10.15888/j.cnki.csa.009470 |
| [31] |
Blanc G, Koch C, Lange J, et al. A query-optimal algorithm for finding counterfactuals. Proceedings of the 39th International Conference on Machine Learning. Baltimore: PMLR, 2022. 2075–2090.
|
| [32] |
Tolkachev G, Mell S, Zdancewic S, et al. Counterfactual explanations for natural language interfaces. Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics. Dublin: ACL, 2022. 113–118.
|
| [33] |
Guidotti R. Counterfactual explanations and how to find them: Literature review and benchmarking. Data Mining and Knowledge Discovery, 2022. https://link.springer.com/article/10.1007/s10618-022-00831-6. (published online).
|
| [34] |
Tešić M, Hahn U. Can counterfactual explanations of AI systems’ predictions skew lay users’ causal intuitions about the world? If so, can we correct for that?. Patterns, 2022, 3(12): 100635. DOI:10.1016/j.patter.2022.100635 |
| [35] |
Moreira C, Chou YL, Hsieh C, et al. Benchmarking instance-centric counterfactual algorithms for XAI: From white box to black box. arXiv:2203.02399, 2022.
|
| [36] |
Holland JH. Genetic algorithms. Scientific American, 1992, 267(1): 44-50. |
| [37] |
Shelby JE. Introduction to Glass Science and Technology. 3rd ed., London: Royal Society of Chemistry, 2020.
|
 2024, Vol. 33
2024, Vol. 33



