随着城市化水平的不断提高, 大城市的交通流量急剧增加, 导致交通拥堵程度日益加剧. 交通拥堵作为一个重要的社会问题, 对城市乃至整个社会的发展有着深远影响, 不仅极大地降低了人们的出行体验, 还导致车辆不必要的燃油消耗, 加剧了环境污染, 造成了严重的直接或间接的经济损失^[1]. 为了解决交通拥堵问题, 城市规划人员已经尝试多种方法, 包括扩建道路、促进公共交通^[2]等. 然而, 这些方法大多有着应用局限, 成本较高, 效果不明显等缺点.

随着进入物联网时代, 智慧城市理念开始在城市规划与治理中崭露头角, 成为解决城市交通拥堵的新方向^[3]. 在智慧城市理论中, 通过广泛应用物联网技术, 交通系统变得更加智能和高效. 通过传感器、实时数据分析和智能算法, 管理者可以更准确地了解交通流量、道路状况以及城市居民的出行习惯, 并据此对整个城市的交通状况进行分析和针对性的优化. 其中, 交通信号控制算法的研究与应用是实现智慧城市的重要组成部分, 其对每个路口乃至整个路网的拥堵程度发挥了关键作用.

目前, 在交通信号灯控制领域中最为热门的方向是深度强化学习(DRL). 通过使用深度强化学习领域中的技术, 例如基于Q-Learning的方法, 交通信号灯调控系统可以学习在不同交通条件下最优的信号控制策略. 现如今, 学术界已经提出了许多基于深度强化学习的交通信号灯控制算法并取得了一定的成果. 然而, 尽管基于深度强化学习的交通信号控制方法相较于传统算法在控制效果上具有一些优势, 但这些方法通常需要大量的数据和长时间的训练, 这将持续消耗庞大的计算和存储资源, 显著超出了目前道路基础设施的能力. 因此, 它们一般只能通过离线训练交通信号控制模型, 这就导致其无法跟上不断变化的交通流, 缺乏适应实时动态应用场景的能力以及泛用性. 因此, 我们有必要研究一种能够在线学习的交通信号控制算法.

本文提出了一种基于上下文多摇臂赌博机模型的新型交通信号控制算法ISTSC (intellispine traffic signal control), 该算法使用多摇臂赌博机模型对单路口的交通信号灯控制问题进行建模求解, 并使用优先优化车流量大并对周围路口影响较大的路口的策略以实现快速高效的路口之间的协同. 最后通过在合成和真实的数据集上与多种已有交通信号灯控制算法进行多方位的对比, 从而验证了我们算法在多方面的优越性.

1 现有交通信号控制算法简介

根据目前的交通信号灯控制算法的原理以及发展历程, 我们大致可以将其分为两类: 传统交通信号灯控制算法和基于强化学习的交通信号灯控制算法.

1.1 传统交通信号等控制算法

在早期的研究中, 由于技术和硬件资源的限制, 人们只能使用一些较为简单的机制进行交通信号灯的控制. 这些算法通常基于交通工程学的原理和经验, 旨在最大程度地提高交通效率和减少拥堵. 传统的交通信号灯控制算法可以分为两大类: 定时控制和感应控制.

定时控制算法根据预先设定的信号灯时间表来调整信号灯策略. 定时控制算法简单易实现, 但是无法适应交通流量的实时变化. 感应控制算法则基于各种传感器数据, 如车流量、车辆等待队列长度等, 实时地调整交通信号灯策略. 相对于定时控制算法, 感应控制算法能够在一定程度上根据实时交通情况灵活地调整交通信号, 从而更有效地管理交通流量.

目前, 传统的交通信号灯控制算法如SCATS^[4]和SCOOT^[5] 已经广泛应用于实际场景中的交通信号控制. 然而以这两种方法为代表的传统控制算法一般都严重依赖于预先手动设计的交通信号方案和策略, 这使得它们难以适应复杂动态的交通情况.

1.2 基于强化学习的交通信号灯控制算法

随着人工智能技术的兴起和互联网、无线通信的持续发展, 数据获取变得更为方便和迅速, 机器学习技术在解决交通信号控制问题方面日益受到重视. 机器学习领域中的各种方法, 包括模糊逻辑^[6]、群体智能^[7]和强化学习^[8–14]等方法已在研究中被应用于交通信号灯控制问题上. 在这些方法中, 强化学习方法在智能交通信号控制研究中的应用最为广泛. 与传统的交通信号灯控制算法相比, 强化学习方法不依赖启发式假设和启发式方程, 不需要预设信号灯控制方案, 并且能够取得相对于传统算法更好的交通流调控效果. 然而, 基于强化学习的交通信号灯控制方法为了实现路口之间的协同工作, 需要大量的计算资源对多路口信号灯的合作决策建模. 此外, 为了使基于强化学习的交通信号灯控制算法具有更优秀的性能, 往往需要大量的数据以及计算资源作为支撑, 并且许多算法需要进行长时间的预训练而不能直接在线进行快速学习并收敛. 这些问题限制了基于强化学习, 尤其是基于深度强化学习的交通信号灯控制算法的广泛应用.

2 基于上下文多摇臂赌博机的交通信号控制算法

在对现有的交通信号控制算法进行研究和分析后, 本文提出了一种上下文多摇臂赌博机的交通信号控制算法ISTSC. 该算法使用上下文多摇臂赌博机模型对单路口的交通信号灯策略进行建模与控制, 再通过优先对车流量大的主干道上的车流进行优先优化控制来实现整体车流的优化, 同时实现主干道与周边路口之间的协同控制.

2.1 基于上下文多摇臂赌博机的单路口控制算法

首先, 我们使用上下文多摇臂赌博机模型对单路口交通信号灯控制问题进行建模. 多摇臂赌博机(multi-armed bandit, MAB)模型是一种用于解决在线学习问题的数学工具, 其名称来源于赌场的老虎机. 在MAB模型中, 每个“臂”代表一种可选的行动或策略, 而每次选择一个臂相当于在赌场拉动一台老虎机的手柄. 每个摇臂对应赌博机的期望收益互不相同, 我们的最终目标是通过在不同臂之间的选择来最大化累积奖励^[15].

而上下文多摇臂赌博机模型(contextual multi-armed bandit, CMAB)在MAB的基础上引入了上下文信息, 即在选择每个臂时考虑了当前的环境或背景条件. 这种模型的独特之处在于它能够根据不同的上下文动态地调整选择不同的臂, 从而更灵活地适应不同的情境. 为了使用CMAB模型对交通信号灯控制问题进行建模, 我们需要构建CMAB模型中的摇臂、收益、上下文信息等概念与信号灯控制问题中的概念之间的映射关系.

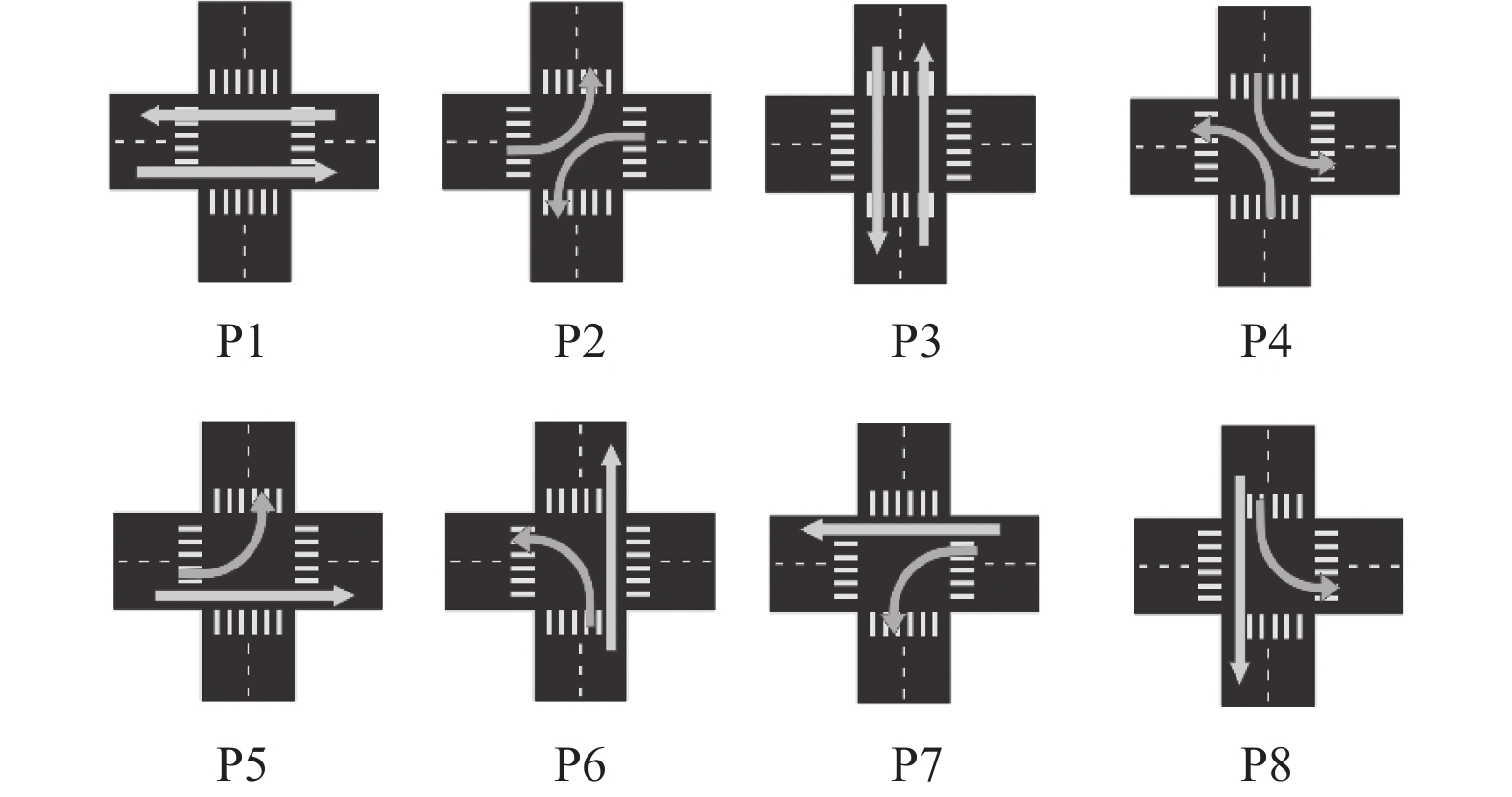
在交通信号灯控制问题中, 路口在每个时间段都需要从一些红绿灯设置方案中选择. 一般的方案是将几个互不冲突的车流方向放在一起, 称为一个相位. 如图1所示, 每个相位包含两个车流方向, 而这两个方向的车流同时通行时互不干扰, 因此可以放在一个相位中. 值得注意的是, 右转信号通常不会与其他信号冲突, 因此通常默认包含在每个相位中. 自然地, 我们可以将相位作为多摇臂赌博机模型中的摇臂, 并将路口中所有相位的集合记为$ {\mathbf{A}} $.

此外, 路口在每个决策回合$ t $都可以通过摄像头以及路口周边的传感器获取一个观察向量$ {{\mathbf{o}}_t} $, 该向量包含路口周围各个车道的等待车辆个数以及车辆平均速度等相关信息, 在多路口情况下还可以包括邻居路口的当前红绿灯设置等信息. 我们可以将$ {{\mathbf{o}}_t} $视为模型中的上下文信息.

最后, 我们还需要定义模型中每个摇臂对应的奖励值(reward). 在每个回合$ t $, 决策者在从摇臂集合$ {\mathbf{A}} $中选择一个摇臂后, 都会获得一个奖励值$ {r_t} $作为收益. 与许多现有研究类似(如文献[11]), 我们使用路口的压力值(pressure)来定义模型中的奖励值. 这里, 路口的压力指的是进入该路口的车辆数与离开该路口的车辆数之间的差值. 图2提供了路口压力的示例, 其中左侧路口的压力为4, 右侧路口的压力为3. 我们将一个交通信号灯策略对应的奖励值定义为在这个策略时间内的路口平均压力值的负数, 如式(1)所示, 其中$ {T_t} $表示第$ t $轮决策时的时间, $ \Delta t $表示每一轮决策后信号灯策略的持续时间, $ P(\tau ) $则表示在时刻$ \tau $路口对应的压力值. 由于压力值在设计上本身就考虑到了驶向周围路口的车辆数量, 因此相较于诸如等待车辆数量等其他常用指标, 使用压力值对模型的奖励值进行设计可以更好地实现路口之间的协同, 使得路口在决策时不会只考虑等待在本路口的车辆而是会在一定程度上兼顾周围路口的交通情况.

$ {{{r}}_{{t}}} = - \frac{1}{{{{\Delta}} {{t}}}}\int_{{{{T}}_{{t}}}}^{{{{T}}_{{t}}} + {{\Delta}} {{t}}} {{{P}}(\tau )} {\mathrm{d}}\tau $

(1)

至此, 如图3所示, 我们已经建立了描述单路口交通信号灯控制问题的上下文多摇臂赌博机模型的框架: 在每个时间段$ t $, 路口通过观察周边环境, 利用上下文信息$ {{\mathbf{o}}_t} $, 动态地选择最优的相位作为当前时间段的信号灯设置. 选择完成后, 将$ \Delta t $时间内路口的平均压力值的负数作为收益$ {r_t} $, 收益的大小即代表红绿灯设置方案的优劣. 通过过去的历史选择, 我们可以学习上下文信息$ {{\mathbf{o}}_t} $与收益$ {r_t} $的潜在关系, 从而在面对不同的环境时, 根据当前环境对应的上下文信息$ {{\mathbf{o}}_t} $判断每一种方案的预期收益$ {r_t} $. 该模型的数学形式如下:

$\left\{ \begin{array}{l}\text{Maxmize}:{\displaystyle \sum }_{t=1}^{N}{r}_{t}\left({a}_{t}, {\bf{o}}_{t}\right)\\ \text{s.t.}\;\;{a}_{t}\in A\end{array} \right.$

(2)

其中, $N$为总的决策轮数, ${a_t}$为第$ t $轮路口选择的相位, ${r_t}\left( {{a_t}, {{\mathbf{o}}_t}} \right)$则为在观察向量为$ {{\mathbf{o}}_t} $的情况下选择${a_t}$后所得到的奖励值.

现在我们需要通过过去的决策历史记录来对每个摇臂, 即相位, 对应的收益进行估计. 假设相位$a \in {\mathbf{A}}$已被选择$m$次, 生成了对应的$m$个观察向量和奖励值. 利用这些观察向量和奖励值, 我们可以使用岭回归(ridge regression)来估计上下文信息向量$ {{\mathbf{o}}_t} $与摇臂$a$的收益${r_t}\left( {a, {{\mathbf{o}}_t}} \right)$之间隐含的关系向量${{\mathbf{\theta }}_a}$. 我们将这些上下文向量系统地排列为行, 创建一个维度为$ m \times d $的矩阵, 表示为$ {{\mathbf{D}}_a} $, 其中$ d $是观察向量$ {{\mathbf{o}}_t} $的维度. 同样, 将$m$个奖励整合为一个大小为$m$的向量, 表示为$ {{\mathbf{c}}_a} $. 那么, 可以通过以下方程得到对关系向量${{\mathbf{\theta }}_a}$的估计值${{\mathbf{\hat \theta }}_a}$:

$ {{\mathbf{\hat \theta }}_a} = {({\mathbf{D}}_a^ \top {{\mathbf{D}}_a} + {{\mathbf{I}}_d})^{ - 1}}{\mathbf{D}}_a^ \top {{\mathbf{c}}_a} $

(3)

其中, ${{\mathbf{I}}_d}$为大小为$ d \times d $的单位矩阵, 我们可以使用公式${\hat r_t}\left( {{a_t}, {{\mathbf{o}}_t}} \right) = {{\mathbf{o}}^ \top_t} {{\mathbf{\hat \theta }}_a}$来获得一个对摇臂$a$对应奖励值的估计. 之后使用即可使用下面的公式得到对应的UCB (upper bound confidence)值.

$ \begin{split} & {\mathit{UCB} \left( {a\mid{{\mathbf{o}}_t}} \right) = } \\ & {\min \left\{ {\max \left\{ {{{\mathbf{o}}^ \top_t} {{{\mathbf{\hat \theta }}}_a} + \alpha \sqrt {{{\mathbf{o}}^ \top_t} {{({{\mathbf{H}}_a})^{-1}}}{{\mathbf{o}}_t}} , {r_{\min }}} \right\}, {r_{\max }}} \right\}} \end{split} $

(4)

其中, ${r_{\min}}$和${r_{\max}}$分别为奖励值的下界与上界, ${{\mathbf{H}}_a} = {\mathbf{D}}_a^ \top {{\mathbf{D}}_a} + {{\mathbf{I}}_d}$, $\alpha = 1 + \sqrt {\ln \left( {2 / \delta } \right) / 2} $, 其中$\delta $是一个指示置信水平的参数. 通过控制参数$\delta $的大小, 我们可以控制算法的行为, 以有效地平衡对探索新相位以收集信息和利用已知收益较高的相位以最大化奖励值. 算法的具体流程如算法1所示.

算法1. 基于CMAB的单路口交通信号灯控制算法

1) 路口通过传感器和摄像头获得观察向量$\scriptstyle {{\mathbf{o}}_t} $.

2) 对于该路口配置中所有的相位$\scriptstyle a \in {\mathbf{A}}$, 根据选择该相位所对应的历史奖励值通过式(3)计算出对关系向量$\scriptstyle {{\mathbf{\theta }}_a}$的估计值$\scriptstyle {{\mathbf{\hat \theta }}_a}$. 并根据式(4)计算对应的UCB值.

3) 得到所有相位$\scriptstyle a$对应的UCB值后, 选择UCB值最大的相位$\scriptstyle a$作为该路口接下来$\scriptstyle \Delta t $ s的相位, 其中$\scriptstyle \Delta t $为预先设定的相位持续时间.

4) $\scriptstyle \Delta t $ s后计算路口在这段时间内的平均压力值, 记录并保存对应相位$\scriptstyle a$的奖励值, 返回第1)步.

2.2 ISTSC算法

多路口交通信号灯控制问题中最困难的问题莫过于路口之间的协同问题. 为了解决这个问题, 本文从GreenWave算法^[16]中注重于优化城市道路中主干道的中心思想获取灵感提出了主干道提取算法, 即通过对车流量进行实时分析以从路网中分离出车流量高的主干道, 并优先对主干道路口进行信号灯策略决策和优化. 当高优先级的路口已经确定信号灯策略后, 则其驶向四周路口的车流情况在很大程度上可以预测, 因此利用这些预测的车流信息可以更好地使用第2.1节中提出的基于CMAB的单路口交通信号灯控制算法来确定周边路口的信号灯策略, 从而实现路口之间信号灯方案的协同. 与此同时, 由于周边路口的策略依赖于中心高车流量路口的决策, 因此能够根据中心路口的车流和决策情况动态调整自身策略, 从而缓解主干道上路口的交通压力.

通过使用主干道提取算法为路口划分优先级, 同时将已确定方案的路口的车流情况加入第2.1节中定义的周边路口的观察向量中, 以根据已确定车流情况进一步优化剩余路口的决策, 本文提出了ISTSC算法. 该算法的具体流程如下所示: 首先, 初始化一个空的初始集合$ {\mathbf{G}} $, 用于保存已经设定好当前信号灯方案的路口. 之后, 从所有路口中选出流入车流量最大的路口作为初始路口, 使用我们在第2.1节提出的算法1得到该路口的信号灯相位配置, 并将该路口放入初始集合$ {\mathbf{G}} $中. 由于集合$ {\mathbf{G}} $中所有路口的信号灯配置都已经确定, 因此我们可以计算出预计从这些路口流通到附近路口的车流量. 之后每次从不在集合$ {\mathbf{G}} $中的路口中选择一个路口$ x $, 使得该路口的自身车流量与接收集合$ \mathrm{G} $中路口车流量之和最大. 若路口$ x $与路口集合$ {\mathbf{G}} $中的路口相邻, 则其周围存在交通信号灯配置已知的路口, 因此可以将这些周边路口的配置信息以及车流情况加入路口$ x $的观察向量$ {{\mathbf{o}}_t} $中. 最后, 在使用算法1得到路口$ x $的相位配置之后, 将路口$ x $也加入集合$ {\mathbf{G}} $中. 该过程一直持续到所有路口都加入集合$ {\mathbf{G}} $中, 即所有的路口都已经配置完成交通信号灯相位为止. 该算法的具体流程如算法2所示.

算法2. ISTSC算法

1) 初始化空集合$ \scriptstyle {\mathbf{G}} $作为初始集合, 用于保存已经设定好当前信号灯方案的路口.

2) 找到车流量最大的路口, 使用算法1得到该路口的信号灯相位配置, 并将该路口其放入初始集合$\scriptstyle {\mathbf{G}}$中.

3) 从不在集合$\scriptstyle {\mathbf{G}} $中的路口中选择一个路口$\scriptstyle x $, 使得该路口是其自身车流量与接收路口集合$ \scriptstyle {\mathbf{G}} $中路口车流量之和最大的路口.

4) 若路口$ x $周围存在集合$ \scriptstyle {\mathbf{G}} $中的路口, 将这些路口的配置信息以及车流情况加入到路口$ \scriptstyle x $的观察向量$ \scriptstyle {{\mathbf{o}}_t} $中.

5) 使用算法1得到该路口的信号灯相位配置, 并将该路口其放入初始集合$\scriptstyle {\mathbf{G}} $中, 返回第3)步.

3 实验分析

本文使用开源的交通模拟器CityFlow^[17]分别在真实和合成数据集上进行了模拟实验, 并将结果与多个传统和基于DRL的算法在车辆平均通行时间和收敛速度等方面进行了详尽的对比.

3.1 实验设置

对于合成数据集, 本文配置了不同尺寸的网格网络: 1×3、3×3和4×4, 并假设网络中每条边路的车辆到达情况符合泊松分布, 每小时到达车辆数量期望为200. 这些路网中的道路长度和车辆的最高速度固定为300 m和30 km/h. 车辆在路口的转向比例设置为10%(左转)、60% (直行)和30% (右转), 这些比例基于对真实交通数据集的统计分析, 确保了合成数据集有足够的真实性. 本文为每种路网分别生成了1 h的车流数据, 1×3、3×3和4×4路网上的期望车流量分别为1600辆/h、2400辆/h和3200辆/h.

对于真实数据集, 本文将杭州(4×4大小)和曼哈顿(3×16大小)的部分真实道路网络数据导入到模拟器中, 并保留了路网中道路真实的长度. 另外, 本文使用了来自LibSignal^[18]的开源交通流数据集来作为实验中的车流数据. 曼哈顿数据集中的车流数据来源于纽约出租车行程数据, 杭州数据集则为通过路边摄像头等设备获取车辆轨迹, 从而得到交通流数据, 因此该数据集能够体现真实的交通情况. 本文通过采样分别为两种不同的路网配置生成了1 h的交通流数据, 相关统计信息如表1所示.

本文使用下面的几种算法与ISTSC算法进行对比.

● FixedTime: 一种最为传统的交通信号控制方法, 它为每个相位设置固定时间, 不考虑交通条件.

● MaxPressure^[19]: 一种经典的理论性能优异的传统交通信号控制方法, 它使用贪心策略, 总是选择能够使得当前交通压力最小的相位.

● IDQN^[18]: IDQN 是一种基于深度强化学习的方法, 每个代理根据自己的路口信息单独做出交通信号控制决策, 没有考虑任何路口之间的协作.

● PressLight^[11]: PressLight 将压力的概念整合到深度强化学习模型的状态和奖励设计中, 自主地实现了一定程度的跨路口的协调, 而无需任何先验知识.

● CMAB: 即前文中的算法1, 用于与改进后的ISTSC算法比较以检验改进的效果.

3.2 实验结果与分析 3.2.1 平均通行时间

本文使用车辆的平均通行时间作为算法效果的主要衡量标准. 平均通行时间是交通信号灯控制研究中最为常见的指标之一, 定义为所有车辆从起始位置出发到达目标位置所花费的平均时间. 一般而言, 较小的平均通行时间意味着较好的算法性能.

表2记录了6种算法分别在合成数据集和真实数据集上收敛后的最终平均通行时间. 显然传统算法的表现都远不如其他4种算法. 与基于深度强化学习的IDQN和PressLight相比较后可以看到, 除了在路网规模为1×3的合成数据集上ISTSC算法略逊于IDQN算法, 在其他4种数据集中ISTSC算法都是要优于其他所有算法.

此外, 比较ISTSC和改进前的CMAB算法可见, 改进后的ISTSC算法性能有了显著的提升, 在5种数据集上分别相对于改进前平均通行时间减少了3.16%、1.77%、2.61%、1.38%和4.55%, 这证明了本文对算法改进的有效性. 并且从数据中我们可以看出相较于其他算法, 在较为复杂的路网上ISTSC算法更能够发挥出更好的效果, 这是由于在较为复杂的路网中, ISTSC算法中提取主干道的策略能够有更为明显的效果, 能够更好地实现路口之间的协同.

3.2.2 收敛速度

算法的收敛速度定义为算法收敛到稳定状态所需的训练轮数. 在本文中我们定义连续20个训练轮次中算法的最终平均等待时间波动都不超过3%时算法收敛. 我们统计收集了每个算法的收敛所需轮次, 并将结果可视化在图4中.

通过图4可以十分明显地看出无论是CMAB还是改进后的ISTSC算法, 其收敛速度都显著快于另外两个基于深度强化学习的算法. 即使是在最为复杂的路网上, ISTSC算法也只需要6轮训练即可收敛, 而IDQN和PressLight两个基于深度强化学习的算法则普遍需要50轮以上的训练才能够收敛, 在曼哈顿3×16路网上甚至需要200轮以上的训练才能够收敛, 这显然没有达到能够不经过长时间的训练直接应用在真实路网上的要求. 由此可见, ISTSC算法可以实现快速的学习和收敛, 能够快速地适应复杂多变的环境.

4 结论与展望

本文提出了一种基于上下文多摇臂赌博机的交通信号控制算法(ISTSC), 旨在应对日益严重的交通拥堵问题. 本文通过在合成和真实数据集上进行广泛的模拟实验, 验证了ISTSC算法在平均通行时间和收敛速度方面的优越性. 不管是与传统算法还是与基于深度强化学习的算法比较, ISTSC在大部分情况下各项指标上均表现得更加出色, 特别是在收敛速度方面有着显著优势. 这为城市交通管理提供了一种创新的解决方案, 有望有效缓解交通拥堵问题, 提升交通系统的效率. 未来的工作方向包括进一步优化算法性能, 探索更多实际场景下的应用. 此外, 还需要考虑在路口之间沟通更加受限的情况下如何实现路口之间的协同.