高光谱图像(hyperspectral image, HSI)凭借丰富连续的窄光谱波段信息, 在许多视觉领域如矿产勘察[1]、蔬菜新鲜检测[2]等有着不可替代的优势和巨大的应用潜力. 但由于成像硬件的限制, 高光谱图像的高空间分辨率和丰富光谱信息往往无法兼得, 进而导致其无法得到许多对空间分辨率要求较高的计算机视觉任务的青睐. 所以如何从软件方面提升高光谱图像的空间分辨率(hyperspectral image super-resolution, HSISR)已然成为一个重要的研究课题.
传统的提升图像空间分辨率的方法包括插值法(如: 双三次插值、线性插值、双线性插值、最近邻插值)、稀疏表示法等. 这些传统机器学习方法往往对处理图像的先验假设较简单, 无法充分考虑和学习到图像的复杂空间信息规律, 致使最终重建效果差强人意. 随着硬件计算算力的不断提升, 越来越多复杂高效的深度学习方法被应用于图像超分辨率任务, 如卷积神经网络[3]、Transformer[4]和生成式网络[5]等, 不断提高图像重建质量. 但若将这些方法不加特定改动调整直接用于HSISR任务上不但会带来较差的空间重建效果, 光谱维度的规律也会被破坏. 这是因为相对于普通RGB图像的超分辨率重建而言, HSISR的目标不仅是从低空间分辨率图像(low resolution image, LR)中恢复出足够多的空间细节以得到高空间分辨率图像(high resolution image, HR), 还要保证HR的光谱维度规律的重建质量. 此外, HSI的空间信息在光谱维度上分布稀疏, 需要使用特定的方法策略才能达到较好的效果.
HSISR方法可以被划分为两大类, 分别是图像融合高光谱图像超分辨率和单幅高光谱图像超分辨率方法. 基于融合的高光谱图像超分辨率方法通过利用高光谱低空间分辨率图像的光谱信息和其对应的相同场景的高空间分辨率低光谱图像的丰富空间信息, 生成高光谱高空间分辨率图像. 采用的主流方法包括深度学习[6]、矩阵分解[7]和稀疏表示方法[8]等. 但基于融合的方法所需的高适配的同场景信息难以获得, 所以许多研究者更倾向于单幅高光谱图像超分辨率重建方法.
单幅高光谱图像超分辨率重建方法需要应对数据集规模小且数据维度大带来的困难, 许多研究者想到利用数据降维方法来降低数据维度[9]. 但是对于HSI来说, 因为HSI独特的光谱-空间特性, 在空间区域冗余的信息在光谱维度上确差异明显, 在光谱维度上冗余的信息在空间上却不一定相同. 因此, 传统的数据降维方法无法很好地处理HSI数据的特殊性.
为了解决这个问题, 一些研究者提出了基于光谱-空间联合降维的方法, 以更好地保留HSI数据的特征[10,11]. 这些方法将光谱和空间维度的信息进行联合建模, 并通过联合降维来减少数据维度. 例如, 一种常用的方法是将HSI数据表示为张量形式, 其中光谱维度和空间维度被同时考虑. 然后应用张量分解或张量低秩近似等技术, 将张量数据进行降维, 同时保留光谱和空间维度的相关性. 但数据降维依旧存在对HSI的有效信息进行丢失的情况, 进而影响到重建结果.
另有研究者从深度学习模型架构角度入手, 提出特定的光谱-空间特征提取策略并取得了可观的结果[12]. 受以上思路的启发, 本文提出了基于光谱强化Transformer和注意力卷积的特征强化高光谱图像超分辨率网络, 结合了Transformer捕捉高频特征和卷积神经网络空间特征提取能力的优势, 采用了双分支的网络架构, 增强对HSI高频信息重建能力的同时也保证了光谱-空间信息的重建能力. 本文主要贡献如下:
(1) 提出了具有额外监督的光谱强化Transformer高频特征分支, 使用拉普拉斯金字塔提取后的输入和标签的高频信息分别作为分支的输入与标签, 进而加强对HSI细节的重建能力.
(2) 提出了Multi-head ESSA注意力机制, 并结合提出的多尺度编码器层, 加强了对高频多样化特征的提取能力和对上下文特征信息的利用.
(3) 提出了双分支高频信息增强高光谱图像超分辨率网络(high-frequency enhanced dual-branch hyperspectral image super-resolution network, HFEDB-Net), 充分提取了HSI的空间和光谱信息, 在两个公开数据集上都获得了最先进的重建效果.
1 相关工作 1.1 基于卷积神经网络的高光谱图像超分辨率重建卷积神经网络(convolutional neural network, CNN)因具备的平移不变性和尺度不变性使得其备受许多研究者们的青睐, 在近年来产生了大量的不同架构如残差连接、密集连接、金字塔、U-Net网络等, 不断刷新各个计算机视觉任务的记录, 而对于HSISR任务也不例外. Liebel等人[13]提出了基于CNN的高光谱超分辨率图像重建方法. 他们将SRCNN[14]引申到高光谱超分辨率任务领域, 通过学习低分辨率和高分辨率图像之间的映射关系, 实现了高质量的超分辨率重建. 然而其网络深度有限, 限制了对高光谱图像的进一步表达能力. 之后Li等人[15]提出了基于深度残差网络的高光谱超分辨率图像重建方法. 他们引入了残差学习的思想, 设计了一个具有多个残差块的网络结构. 通过逐层的特征提取和重建, 他们有效地提高了超分辨率图像的质量. 但由于2D卷积无法捕捉通道间关系的限制, 导致重建图像的光谱失真情况比较严重.
为解决上述问题, 研究者们提出了一些方法, 例如, 使用3D卷积替代2D卷积, 进行高光谱图像的特征提取[16], 或引入通道注意力机制以增强整个网络对跨通道信息的关注[17], 从而提升对HSI光谱特征的表征能力. 然而, 卷积神经网络依靠滑动窗口机制来进行特征映射, 导致其在捕捉长距离依赖关系和适应数据方面的能力有限, 仍难以对复杂光谱信息进行利用和重建.
1.2 视觉TransformerTransformer最初由Vaswani等人[18]提出, 该模型在序列到序列的自然语言处理领域取得了重要的突破. 随后, Dosovitskiy等人[19]提出了Vision Transformer(ViT)将Transformer应用于图像处理领域, 并实现了端到端的视觉处理方法. 这引发了对ViT的广泛关注, 开始吸引许多计算机视觉任务研究者的兴趣.
在图像超分辨率任务中, Liang等人[20]提出了一个强大的图像超分辨率基准模型SwinIR, 该模型利用ViT架构进行深层特征提取, 包括多个SwinIR层和残差连接, 具有出色的性能和泛化能力. 接着, Li等人[21]提出了分层Swin Transformer (HST)网络来恢复低分辨率压缩图像, 该网络通过联合捕获分层特征表示并使用Swin Transformer来增强每个尺度的表示能力.
为了进一步提高恢复效果, Chen等人[22]提出了一种新的混合注意力Transformer (HAT), 该模型结合了通道注意力和基于窗口的自注意力方案, 以充分利用它们的互补优势, 激活更多的输入像素.
最早将ViT引入HSISR任务的是Hu等人[23]提出的Fusformer模型, 该模型在高光谱图像超分辨率任务中取得了巨大的成功, 然而, 其没有在注意力机制本身角度对HSISR任务进行适配, ESSAformer[24]提出了一种针对HSI的高效注意力机制, 充分考虑了高光谱领域的特点, 并引入了通道级归纳偏置, 进而提高了重建图像的光谱质量. 但其使用的注意力机制在映射Q、K、V三向量时的能力有限, 缺乏特征提取的多样性, 并且针对图像空间信息的利用不够充分, 缺少对上下文信息的交互.
为了解决上述存在的问题, 本文提出了一种基于高频信息强化的双分支高光谱图像超分辨率网络HFEDB-Net. 通过结合Transformer和卷积神经网络, HFEDB-Net能够有效地重建高光谱图像的高频信息和光谱-空间细节. 通过使用拉普拉斯金字塔提取输入和标签的高频信息, 并构建了基于多头ESSA的多尺度Transformer高频特征提取分支, 从而有效提升了对高频特征的提取能力和上下文特征信息的利用效果.
2 网络结构 2.1 整体架构基于深度学习的HSISR任务本质是通过损失函数Loss训练出一组能从低分辨率高光谱图像
| θ∗=argminθ(Loss(F(SLR;θ),SHR)) | (1) |
其中,
| {θ∗1=argminθ1(Loss1(F1(SLR,F2(SsharpLR;θ2);θ1),SHR)θ∗2=argminθ2(Loss2(F2(SsharpLR;θ2),SsharpHR)) | (2) |
其中,
| LSSTV=1N∑Nn=1(∇hF(SnLR)1+∇wF(SnLR)1+∇cF(SnLR)1) | (3) |
其中,
| Isharp=I−Up(Down(I)) | (4) |
其中,
为了提取HSI的空间和光谱特征, 主干分支由残差空间提取块与通道注意力空间-光谱块组成. 在空间提取块中, 使用3×3卷积来学习图像的空间上不同特征, 结合激活函数来为模块增加更多的非线性, 同时利用残差机制加强了特征的传递且缓解梯度爆炸和消失的问题. 值得注意的是, 使用单次上采样操作会不可避免地造成上下文细节的丢失情况, 所以在主干分支中我们将亚像素卷积上采样操作放在了每3个连续的空间提取块之后, 通过采用逐步上采样策略, 避免了只使用一次上采样带来的噪声影响过大问题. 且亚像素卷积具有重建质量高、参数量小和有效利用低分辨率信息的优点, 与反卷积上采样相比, 重建图像也会更少出现伪影的情况. 空间提取块如图1左上方所示.
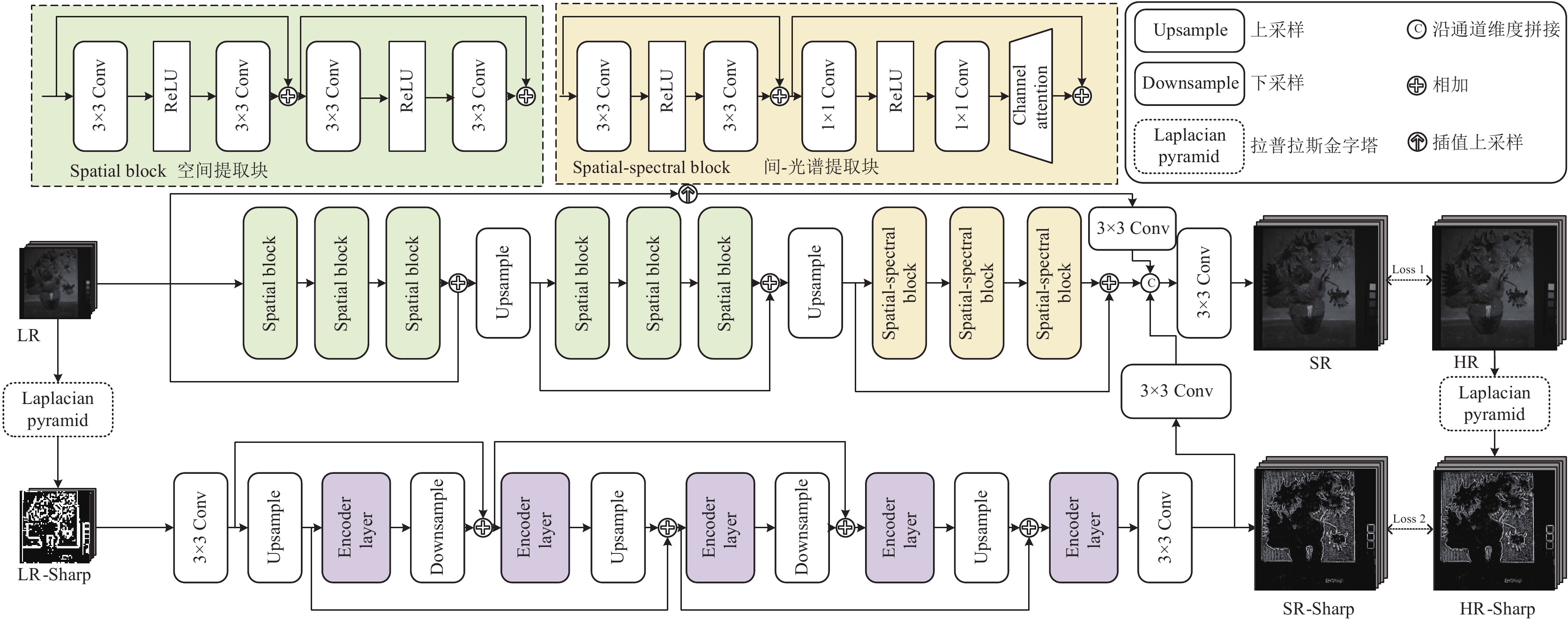
|
图 1 HFEDB-Net网络总架构 |
对于空间-光谱提取块而言, 本文引入擅长捕捉通道之间关系的通道注意力机制. 同样结合1×1卷积和激活函数, 增强了本块对空间和光谱特征的表达能力.
2.3 Transformer高频特征分支因HSI空间信息在光谱维度分布稀疏且不规律的特性, 卷积神经网络难以对其较高频的特征进行有效重建. 为了解决这个问题, 我们提出了具有额外监督的HSI高频特征超分辨率分支, 利用具有强自适应能力和擅于捕捉特征长距离依赖关系的Transformer方法. 本文设计了多头ESSA注意力机制, 采用光谱相关系数(SCC)用于替代原始的注意力矩阵, 并将归纳偏好引入模型中以便于训练. 并且将Q、K、V这3个向量的相乘顺序进行变换, 进而大幅减少了计算复杂度.
然而, ESSA无法有效地捕捉细粒度细节并充分利用多尺度的上下文信息. 这是因为其仅在一个空间尺度上进行操作, 并仅使用单个注意力头, 从而无法完全捕捉复杂HSI中存在的多样视觉模式.
为了解决这些问题并进一步增强Transformer分支的性能, 本文设计了多头ESSA和多尺度编码层. 通过引入多头注意力机制, 图像多样化的模式可以被分支所捕捉到, 且能够同时关注不同的区域. 此外, 编码层提取的多尺度特征还更好的整合了不同抽象层次的上下文信息.
多头策略使得高频特征分支能够学习多组注意力权重, 每组权重分别用于学习特定的高频特征模式规律、关注不同的空间特征位置. 而多尺度策略使得分支网络能够在不同空间分辨率上捕捉丰富的上下文信息, 有助于充分理解图像的高频局部细节和全局结构. 改进后的ESSA用公式表示如下:
| {ESSAi(Qi,Ki,Vi)=φ(Qi)(φ(Ki)TVi)Z=Concat(ESSA1,⋯,ESSAh)Wo | (5) |
其中,
另外, 我们在高频特征分支中还采用了逐步优化的结构策略, 通过多次迭代优化模型输出, 逐步提升上采样结果的质量. 每一轮迭代都可以对先前的输出进行细化和改进, 从而逐渐减小上采样后图像中的伪影和信息损失. 通过逐步优化, 高频特征分支可以更好地适应数据的细节和复杂性, 提高最终超分辨率重建图像的准确性和真实性. 高频特征分支的编码器层和多头ESSA注意力如图2所示.
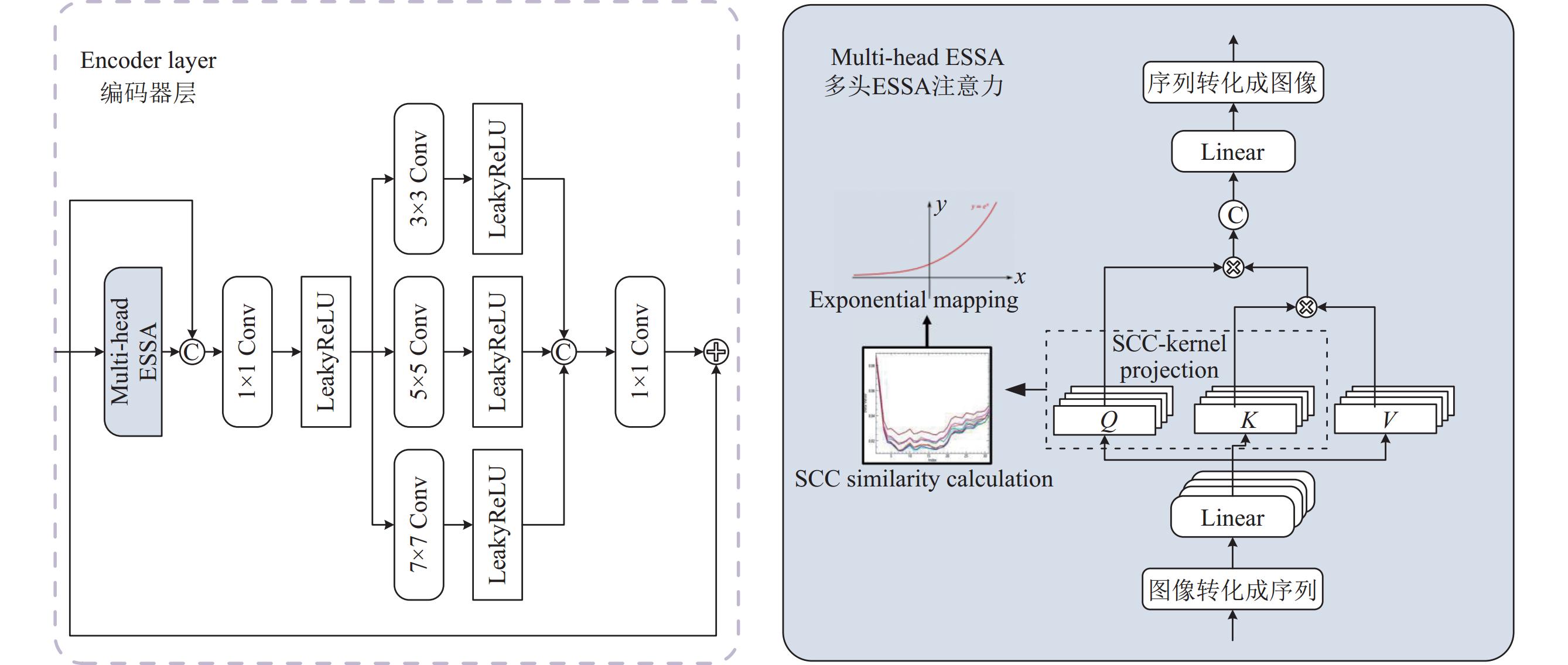
|
图 2 高频分支中的编码器层与多头ESSA注意力机制 |
3 实验分析 3.1 数据集
本文使用两个公开可用的高光谱数据集Harvard自然高光谱图像数据集[26]和Chikusei遥感高光谱图像数据集[27]进行了放大4倍和8倍的对比与消融实验, 证明了提出的HFEDB-Net的有效性.
Harvard数据集包含50个真实世界高光谱图像, 每个图像的尺寸为1392×1040×31. 所有的31个光谱波段是由420–720 nm范围内每隔10 nm采样得到. 其中我们将40个图像用作训练集, 10个图像用作测试集. 为了适应模型训练, 我们将训练集进行裁块处理. 在放大因子为4的情况下, 将每张训练集裁剪为64×64的互相重叠的图像块(重叠32个像素), 通道数保持不变; 最后将其降采样为1/4大小作为模型的输入. 在放大因子为8的情况下, 将每张数据集裁成128×128的重叠图像块(重叠64个像素), 通道数保持不变; 最后将其降采样为1/8大小作为模型的输入. Harvard数据集包含室内与室外的真实场景图像, 拍摄的物体和场景复杂多样, 蕴含丰富的空间和光谱信息.
Chikusei数据集是一张高光谱遥感图像, 图像尺寸为2517×2335×128, 光谱范围为363–1018 nm. 由于图像中存在边缘信息缺失不连续的情况, 所以我们首先将图像从中间裁剪为2304×2048的子区域. 然后, 从Chikusei图像的顶部选择4个尺寸为512×512×128的区域作为测试集, 剩余部分作为训练集. 同样, 裁块处理策略与Harvard相同. 与Harvard等自然高光谱图像数据集相比, Chikusei数据集具有更少数据、更多噪声、较小目标以及更多光谱波段的特点, 使针对其的重建任务更具挑战性.
3.2 评价指标和实验设置在对实验结果进行定量图像质量评价时, 我们选择使用以下6个主流评价指标: 互相关性度量(cross correlation, CC)、结构相似性(structural similarity, SSIM)、峰值信噪比(peak signal-to-noise ratio, PSNR)、相对全局精度误差(error relative global accuracy, ERGAS)、均方根误差(root mean square error, RMSE)和光谱角映射度量(spectral angle mapper, SAM)全面地评估了各个方法的性能. 另外, 为进一步从主观的角度评价重建图像的质量, 我们还将重建结果用多种方式进行呈现.
所提出的HFEDB-Net网络相关参数设置如下: 多头ESSA中的注意力头数量设置为3, 编码器层中的多尺度模块采用3×3卷积核、5×5卷积核与7×7卷积核的组合. 多头ESSA中每个注意力头的Q、K和V向量映射长度都设置为与输入向量长度相同.
3.3 对比方法设置为了证明提出的工作的优越性和有效性, 我们在两个数据集的两种放大因子上对比了4种先进的高光谱图像超分辨率方法, 从可视化和定量指标分析等方面对各个方法的重建结果进行分析. 以下是我们使用的对比方法.
(1) SSPSR[28]: SSPSR采用了一种有效的重叠分组策略的卷积神经网络, 强化了对光谱信息的捕捉能力, 从而实现了显著的重建效果.
(2) MCNET[29]: MCNET是一种混合卷积网络, 结合了2D和3D卷积, 能更有效地提取HSI图像的光谱空间特征.
(3) PDE-Net[30]: 一种使用概率启发的高光谱图像编码嵌入来进行高分辨率高光谱图像的迭代优化网络.
(4) ESSAformer: 使用了一种高效的基于光谱相关系数SCC核的自注意力(ESSA), 用于替代原始的注意力矩阵的Transformer方法.
3.4 实验结果与分析我们将提出的方法在两个数据集上与其余先进方法进行对比, 从定量评价指标表1可以得到, HFEDB-Net在两个公开数据集的4倍和8倍放大倍数下都取得了最好的结果. 其中在Harvard数据集上的优势最大, 尤其是在4倍放大倍数的条件下, MPSNR指标要高于ESSAformer 0.4 dB左右. 这是因为所提出的方法利用构造基于Transformer的额外监督高频分支来加强对高频信息的捕捉和重建, 同时从捕捉空间细节能力、上下文信息能力以及对多样特征的提取能力方面改进了ESSA注意力机制和编码器层, 进一步提升了总体网络的重建能力, 保证了重建图像的质量.
SSPSR、MCNet和PDE-Net都为基于卷积神经网络的方法, 从表1数据来看, 他们在大多数情况下要明显弱于基于Transformer方法的ESSAformer, 这是因为卷积神经网络的特性, 其特有的平移不变性的归纳偏置使得卷积神经网络很难构建长距离的依赖关系, 而长距离的依赖关系对于高光谱高维数据来说是非常重要的. 相反, Transformer利用自注意力机制, 能够对输入的各个位置进行全局范围的关联和交互, 从而更好地捕捉HSI中的长距离依赖关系, 这使得基于Transformer的方法如ESSAformer在处理高光谱高维数据时具有优势. 因此, 相对于基于卷积神经网络的方法, ESSAformer能够更好地建模HSI图像中的空间和光谱信息, 从而实现更准确的重建结果.
但是从空间提取能力角度分析, 卷积神经网络的空间提取能力要强于Transformer, 这是因为卷积神经网络局部感知和权值共享的特性. 卷积层通过滑动窗口的方式对图像的局部进行映射感知, 从而有效地捕捉到图像中的空间特征. 且卷积层中的权重共享也大幅度减少了网络的参数量, 进而一定程度上提高了网络的重建能力. 所以同样在表1中可以看到, 在放大因子为8的情况下, HSI空间信息的重建难度加大, ESSAformer的重建效果要略低于基于卷积神经网络的MCNet和PDE-Net. MCNet通过混合使用2D与3D卷积来对高光谱图像的高维特征进行捕捉, 与单使用3D卷积的方法相比, 减少了网络的参数量. PDE-Net则采用其提出的特征嵌入策略来对高光谱图像进行重建, 有效地保护了光谱信息, 避免了光谱失真现象的发生. 各个方法的重建可视化结果见图3、图4.
| 表 1 在Harvard与Chikusei两个数据集上放大倍数为4倍和8倍的重建结果 |

|
图 3 Image1重建图像的伪彩色图(波段31, 21, 11) |
从重建效果对比图中不难看出, 所提出的方法的超分辨率图像与其他方法相比更接近标签真实图像HR. 另外值得注意的是, 在高光谱图像的高频细节区域如砖块细节纹理和书本排列缝隙, HFEDB-Net重建的质量要明显优于其他方法. 因为在高频分支中, HFEDB-Net利用具有强自适应能力和捕捉特征长距离依赖关系的Transformer方法, 并利用提出的多头ESSA注意力和多尺度编码层, 丰富了对上下文信息和对空间细节的特征提取, 使得重建图像的质量进一步的提升.
为全面地对比各个方法的重建结果, 我们从光谱角度, 对比不同方法重建图像的质量. 我们利用平均误差图和平均误差曲线来从光谱角度对重建结果进行分析. 其中平均误差图的原理是通过将每个方法重建后的图像与标签真实图像做差, 并将结果沿着光谱维度求平均, 最后生成平均误差热力图, 图上越明亮越清晰的部分代表误差越大. 反之, 重建质量越高的部分则越暗无细节. 平均误差图热力图可见图5.

|
图 4 Image2重建图像的伪彩色图(波段31, 21, 11) |

|
图 5 Image3的平均误差热力图 |
从图5中可以看出, 提出的方法在光谱维度依然要比其他方法的重建质量要高, 并且从图5中观察到在图像的高频细节部分, 如百褶窗的纹理, 提出的方法的重建质量在空间和光谱两个维度都有明显的优势. 平均误差曲线图的原理为将重建后的图像与标签真实图像做差, 在空间维度求平均, 进而在每个光谱维度得到一个平均误差值, 将所有维度的平均误差值算出作为折线图的点, 最终得到平均误差折线图. 其中折线中的值越高说明重建后图像在该通道与真实标签的差距越大, 反之折线值越低则说明重建后图像在该通道与对应该通道的标签越接近. 平均误差折线图如图6所示.
从平均误差折线图也可以看出, 提出的方法在光谱维度依然要比其他方法的重建质量要高. 这是因提出的方法有效地利用并结合了卷积的空间提取能力和ESSA注意力对光谱的长距离依赖规律的捕捉.
同为基于Transformer方法的ESSAformer在光谱维度也同样有着不俗的表现, 其平均误差折线仅次于提出的方法排在第2名. 这证明了ESSA有效地捕捉了高光谱图像的光谱信息规律.
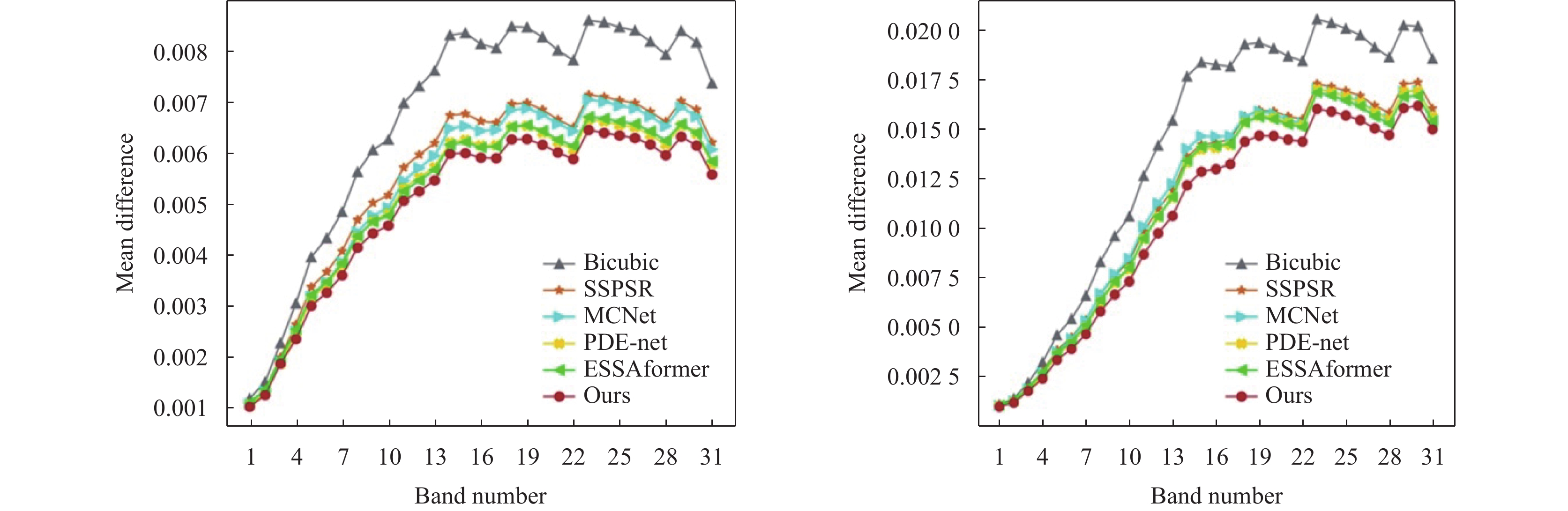
|
图 6 Image1与Image2的平均误差折线图 |
3.5 消融实验与分析
我们进行了不同组合的消融实验来证明所提出方法每个部分的贡献与有效性. 其中主要针对的部分为高频分支所使用的方法、主干分支所使用的方法以及改进后的多头ESSA与原始ESSA的差别. 消融实验结果如表2所示.
| 表 2 在4倍放大因子下Harvard数据集上不同模块的消融实验结果 |
从表2中可以看到, 完整的HFEDB-Net方法在4倍放大因子Harvard数据集上的重建能力是最好的, 而在将基于Transformer的高频分支与基于卷积神经网络的主干分支进行方法互换后对重建能力的影响最大, 结合单独将高频分支换成卷积神经网络以及单独将主干分支换成Transformer的结果, 我们可以得出以下结论: 针对图像高频信息的处理, 从自适应能力和捕捉长距离依赖, 来看Transformer有一定的优势. 而对于充分提取图像空间特征的目标, 卷积神经网络却是一个更好的选择.
同样从表2中显示, 对于ESSA和编码层的多头注意力机制和多尺度结构这两个改进方向是正确且有效的, 并且多头注意力机制的作用相对而言更大, 这是因为对于高光谱图像这种高维数据, 单头注意力机制难以捕捉足够多的特征和关系.
4 结论与展望本文提出了一种基于高频信息强化的Transformer与卷积神经网络的双分支高光谱图像超分辨率网络HFEDB-Net. 通过结合Transformer和卷积神经网络的优势, 双分支网络架构实现了对HSI高频信息和光谱-空间信息的有效重建. 本文通过使用拉普拉斯金字塔提取输入和标签的高频信息, 并构建了具有额外监督的光谱强化Transformer高频特征分支, 从而增强了对HSI空间细节的重建能力. 其次, 通过设计了多头ESSA注意力与多尺度编码层, 有效提升了对高频特征的特征提取能力和对上下文特征信息的利用. 在两个公开数据集的两种放大倍数下, 主观可视化和客观定量指标上均实现了最好的重建结果.
接下来可以开展的工作方向可以从光谱一致性以及高光谱空间信息的去噪方面来继续研究.
| [1] |
车永飞, 叶发旺, 张明林. 高光谱数据与航空伽玛能谱数据在砂岩型铀矿勘查中的应用. 地质论评, 2023, 69(S1): 341-342. DOI:10.16509/j.georeview.2023.s1.152 |
| [2] |
邵慧, 杨丽娟, 王程, 等. 利用高光谱图像实现生菜失水率和新鲜度预测. 光电子·激光, 1–13. http://kns.cnki.net/kcms/detail/12.1182.o4.20240325.1857.008.html. [2024-04-02].
|
| [3] |
Yamanaka J, Kuwashima S, Kurita T. Fast and accurate image super resolution by deep CNN with skip connection and network in network. Proceedings of the 24th International Conference on Neural Information Processing. Guangzhou: Springer, 2017. 217–225. [doi: 10.1007/978-3-319-70096-0_23]
|
| [4] |
Yang FZ, Yang H, Fu JL, et al. Learning texture Transformer network for image super-resolution. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 5790–5799. [doi: 10.1109/CVPR42600.2020.00583]
|
| [5] |
Wang XT, Yu K, Wu SX, et al. ESRGAN: Enhanced super-resolution generative adversarial networks. Proceedings of the 2018 European Conference on Computer Vision (ECCV) Workshops. Munich: Springer, 2018. 63–79. [doi: 10.1007/978-3-030-11021-5_5]
|
| [6] |
Xu YH, Hou JY, Zhu XJ, et al. Hyperspectral image super-resolution with ConvLSTM skip-connections. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 1–16. DOI:10.1109/TGRS.2024.3401843 |
| [7] |
Liu JJ, Wu ZB, Xiao L, et al. A truncated matrix decomposition for hyperspectral image super-resolution. IEEE Transactions on Image Processing, 2020, 29: 8028-8042. DOI:10.1109/TIP.2020.3009830 |
| [8] |
Dian RW, Li ST, Fang LY, et al. Hyperspectral image super-resolution via local low-rank and sparse representations. Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium. Valencia: IEEE, 2018. 4003–4006. [doi: 10.1109/IGARSS.2018.8519213]
|
| [9] |
Patel RC, Joshi MV. Super-resolution of hyperspectral images using compressive sensing based approach. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, I-7: 83-88. DOI:10.5194/isprsannals-I-7-83-2012 |
| [10] |
Hong DF, Yokoya N, Chanussot J, et al. Joint and progressive subspace analysis (JPSA) with spatial-spectral manifold alignment for semisupervised hyperspectral dimensionality reduction. IEEE Transactions on Cybernetics, 2021, 51(7): 3602-3615. DOI:10.1109/TCYB.2020.3028931 |
| [11] |
Huang H, Shi GY, He HB, et al. Dimensionality reduction of hyperspectral imagery based on spatial-spectral manifold learning. IEEE Transactions on Cybernetics, 2020, 50(6): 2604-2616. DOI:10.1109/TCYB.2019.2905793 |
| [12] |
Jia JR, Ji LY, Zhao YC, et al. Hyperspectral image super-resolution with spectral-spatial network. International Journal of Remote Sensing, 2018, 39(22): 7806-7829. DOI:10.1080/01431161.2018.1471546 |
| [13] |
Liebel L, Körner M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI-B3: 883-890. DOI:10.5194/isprs-archives-XLI-B3-883-2016 |
| [14] |
Dong C, Loy CC, He KM, et al. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. DOI:10.1109/TPAMI.2015.2439281 |
| [15] |
Li YS, Hu J, Zhao X, et al. Hyperspectral image super-resolution using deep convolutional neural network. Neurocomputing, 2017, 266: 29-41. DOI:10.1016/j.neucom.2017.05.024 |
| [16] |
Mei SH, Yuan X, Ji JY, et al. Hyperspectral image spatial super-resolution via 3D full convolutional neural network. Remote Sensing, 2017, 9(11): 1139. DOI:10.3390/rs9111139 |
| [17] |
Shi Z, Chen C, Xiong ZW, et al. Deep residual attention network for spectral image super-resolution. Proceedings of the 2018 European Conference on Computer Vision (ECCV) Workshops. Munich: Springer, 2018. 214–229.
|
| [18] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [19] |
Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16x16 words: Transformers for image recognition at scale. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [20] |
Liang JY, Cao JZ, Sun GL, et al. SwinIR: Image restoration using swin Transformer. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 1833–1844.
|
| [21] |
Li BC, Li X, Lu YT, et al. HST: Hierarchical swin Transformer for compressed image super-resolution. Proceedings of the 2022 European Conference on Computer Vision (ECCV) Workshops. Tel Aviv: Springer, 2022. 651–668.
|
| [22] |
Chen XY, Wang XT, Zhang WL, et al. HAT: Hybrid attention Transformer for image restoration. arXiv:2309.05239, 2023.
|
| [23] |
Hu JF, Huang TZ, Deng LJ, et al. Fusformer: A Transformer-based fusion network for hyperspectral image super-resolution. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 6012305. [doi: 10.1109/LGRS.2022.3194257]
|
| [24] |
Zhang MJ, Zhang C, Zhang QM, et al. ESSAformer: Efficient Transformer for hyperspectral image super-resolution. Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision. Paris: IEEE, 2023. 23016–23027.
|
| [25] |
Aggarwal HK, Majumdar A. Hyperspectral image denoising using spatio-spectral total variation. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 442-446. DOI:10.1109/LGRS.2016.2518218 |
| [26] |
Chakrabarti A, Zickler T. Statistics of real-world hyperspectral images. Proceedings of the 2011 Conference on Computer Vision and Pattern Recognition. Colorado Springs: IEEE, 2011. 193–200. [doi: 10.1109/CVPR.2011.5995660]
|
| [27] |
Yokoya N, Iwasaki A. Airborne hyperspectral data over Chikusei. Technical Report, SAL-2016-05-27. Tokyo: The University of Tokyo, 2016.
|
| [28] |
Jiang JJ, Sun H, Liu XM, et al. Learning spatial-spectral prior for super-resolution of hyperspectral imagery. IEEE Transactions on Computational Imaging, 2020, 6: 1082-1096. DOI:10.1109/TCI.2020.2996075 |
| [29] |
Li Q, Wang Q, Li XL. Mixed 2D/3D convolutional network for hyperspectral image super-resolution. Remote Sensing, 2020, 12(10): 1660. DOI:10.3390/rs12101660 |
| [30] |
Hou JH, Zhu ZY, Hou JH, et al. Deep posterior distribution-based embedding for hyperspectral image super-resolution. IEEE Transactions on Image Processing, 2022, 31: 5720-5732. DOI:10.1109/TIP.2022.3201478 |
 2024, Vol. 33
2024, Vol. 33



