在有监督学习和数据挖掘领域, 对不平衡数据集分类是普遍且具有挑战性的问题. 在一个二分类数据集中, 两类样本数量出现明显数量差异时, 称为类别不平衡数据集. 其中, 数量较多的类别称为多数类样本, 而数量较少的类别则被称为少数类样本. 将类别不平衡问题进一步划分为类间不平衡和类内不平衡^[1], 前者是指不同类别之间的样本数量存在明显差异; 后者则强调了同一类别内部样本在特征空间分布的不均匀性, 即某个类别的样本可能呈现出分散的分布模式, 导致了小间断问题. 当两种不平衡问题同时出现时, 传统机器学习分类算法难以有效捕捉到少数类的类别的特征和决策边界. 一方面, 传统分类器以优化整体分类误差为目标^[2], 导致在处理不平衡数据时往往偏向多数类样本, 而忽略对少数类样本的学习. 尤其在极端类不平衡的数据集中, 分类器的真实性能更容易被掩盖, 即使分类器无法正确预测任何一个少数类样本, 仍能达到极高的准确率. 另一方面, 不同类别样本数量差异越大, 越容易出现噪声、小间断、类重叠等复杂的数据结构, 造成分类器难以收敛而分类效果不佳的结果. 在实际应用中存在大量的不平衡问题, 比如信用卡欺诈、网络入侵、医学诊断和情感分析等^[3], 这些领域更重视少数类样本被正确分类的概率.

处理不平衡问题的主要方法有4类, 分别是数据层面、算法层面、代价敏感函数和集成学习层面^[4]. 其中, 数据层面的方法不受限于特定分类器, 成为最广泛使用的不平衡问题处理方法. 该方法主要分为过采样、欠采样和组合采样, 但欠采样通过舍弃多数类样本实现数据平衡易造成重要信息丢失, 并且在类别数量相差悬殊的情况下会严重影响分类器的性能, 故过采样成为较频繁使用的方法. 过采样有两种实施的方式: 一种是对所有少数类样本直接进行复制或生成; 另一种是先对样本进行聚类, 然后在每个簇中生成少数类样本. 大多数直接对少数类进行过采样的方法只是简单地解决了样本类间不平衡问题, 而基于聚类的过采样方法能够综合考虑类间和类内不平衡, 通过聚类的方式最大程度地保留原始数据的分布特征, 从而更有效地进行过采样.

合成少数过采样技术(synthetic minority over-sampling technique, SMOTE)是经典的过采样方法之一^[5], 通过随机选择一个少数类样本及其近邻样本, 然后在这两个样本之间进行线性插值生成新样本. SMOTE能够有效缓解过拟合问题, 但在选择参与合成的少数类样本时存在很大的随机性, 并且没有考虑到多数类的分布情况, 故而容易生成噪声样本. 考虑到SMOTE方法的局限性, 大量学者尝试对该方法进行改进^[6]. Han等提出的Borderline-SMOTE方法着重关注边界区域的少数类样本^[7], 在边界区域进行样本合成, 但忽略了少数类样本的稀疏区域, 而稀疏区域可能包含更多有效的信息. Lee等提出的LEE方法通过计算生成样本的同类近邻个数来过滤少数类^[8], 能够避免合成更多的噪声. Kunakorntum等根据两个类别的概率分布选择少数类样本来合成新的样本^[9], 提出SyMProD方法, 但该方法依赖于概率分布的准确性.

近年来, 基于聚类的过采样方法受到了广泛关注^[10,11]. Nekooeimehr等提出A-SUWO方法^[12], 它通过半监督的方式用层次聚类法对少数类和多数类进行聚类, 有效避免在类重叠区域合成样本, 但参数的确定较为复杂. Douzas等提出基于K-means的SMOTE方法^[13]和基于自组织映射神经网络的SOMO方法^[14]. 前者由于其简易性得到广泛应用, 它通过使用K-means聚类方法对所有样本进行聚类, 并根据每个簇中少数类的占比自主过滤部分簇, 但忽略了少数类样本中存在的小间断问题. SOMO方法利用自组织映射神经网络将数据聚类后映射到二维空间, 保持了原始数据的拓扑结构, 但会耗费大量计算资源.在现存的基于聚类的过采样方法中, 由于聚类算法本身的限制和原始数据集中存在的复杂数据结构, 小间断和类重叠问题仍未被解决. 综上, 本文提出一种基于共享近邻密度峰值聚类和集成过滤机制的过采样方法(shared nearest neighbor density peak clustering with oversampling followed by ensemble filtering, SNN-DPC-OF). SNN-DPC-OF算法的主要步骤为: (1)共享近邻密度峰值聚类; (2)自适应确定子簇过采样权重; (3)子簇内合成少数类样本; (4)消除噪声和部分边界样本.

1 相关理论 1.1 自适应共享近邻密度峰值聚类

2018年Liu等将共享近邻的概念引入传统的密度峰值聚类算法中, 提出一种基于共享近邻的密度峰值聚类算法(shared-nearest-neighbor-based clustering by fast search and find of density peaks, SNN-DPC)^[15]. 与密度峰值聚类算法^[16]相比, SNN-DPC中局部密度${\rho _i}$和相对距离${\delta _i}$是基于共享近邻计算的, 因此在处理高维和密度差异较大的数据更具优势. 任意两点之间共享近邻的计算公式如下:

$ {\textit{SNN}}({x}_{i}, {x}_{j})=\Gamma ({x}_{i})\cap \Gamma ({x}_{j}) $

(1)

其中, $ \Gamma ({x_i}) $为样本${x_i}$的K最近邻集合. 由两点间共享近邻数和平均距离的信息得到相似度的计算:

$ {\textit{Sim}}({x_i}, {x_j}) = \left\{ \begin{array}{*{20}{l}} {\dfrac{{{{\left| {{\textit{SNN}}({x_i}, {x_j})} \right|}^2}}}{{\displaystyle\sum\limits_{p \in {\textit{SNN}}({x_i}, {x_j})} {({d_{ip}} + {d_{jp}})} }}}, &{x_i}, {x_j} \in {\textit{SNN}}({x_i}, {x_j}) \\ 0 , &{\mathrm{otherwise}} \end{array} \right. $

(2)

其中, ${d_{ip}}$是样本${x_i}$和样本${x_p}$之间的欧氏距离. 那么, 可以得到由任意两个样本的相似度组成的二维矩阵. 按照相似度降序排列, 取排名前${k_1}$的样本作为样本${x_i}$的高相似度集合$L({x_i})$, 则${x_i}$的局部密度为:

$ {\rho _{{x_i}}} = \sum\limits_{{x_j} \in L({x_i})} {{\textit{Sim}}({x_i}, {x_j})} $

(3)

任意样本${x_i}$的相对距离${\delta _{{x_i}}}$利用近邻距离添加了一种补偿机制, 使得低密度聚类时点的$\delta $值也可能很高:

$ {\delta _{{x_i}}} = \mathop {\min }\limits_{{x_j}:{\rho _{{x_j}}} > {\rho _{{x_i}}}} \left[ {{d_{{x_i}{x_j}}}\left( {\sum\limits_{p \in \Gamma ({x_i})} {{d_{{x_i}p}}} + \sum\limits_{q \in \Gamma ({x_j})} {{d_{{x_j}q}}} } \right)} \right] $

(4)

为确保密度最大的样本能够被快速定位作为第1个聚类中心, 故它对应的$\delta $值被定义为由式(4)计算出的所有$\delta $值中的最大值.

SNN-DPC算法根据${\rho _i}$和${\delta _i}$手动确定聚类中心后再利用特定规则分配样本, 只需确定一个参数就可实行聚类. 然而, 对于大规模数据集而言, 手动确定聚类中心将花费大量时间, 而且存在一定人为主观性. 为了能够自动得到聚类中心, Lv等提出一种自适应SNN-DPC算法^[17]. 聚类中心具备较高${\rho _i}$值和${\delta _i}$值, 通过对局部密度${\rho _{{x_i}}}$平方进一步放大密度差异:

$ {\rho _{{x_i}}} = {\left( {\sum\limits_{{x_j} \in L({x_i})} {{\textit{Sim}}({x_i}, {x_j})} } \right)^2} $

(5)

设定决策值$ {\gamma _{{x_i}}} = {\rho _{{x_i}}} \times {\delta _{{x_i}}} $, 样本量设为$n$. 将$\gamma $按降序排序后得到${\gamma '}$, 那么拐点$kp$定义为:

$ kp = \max\{ i \mid {\left| {{\mu _{i + 1}} - {\mu _i}} \right| \geqslant \theta ,\; i = n - DN + 1, \cdots , n - 2\} } $

(6)

其中,

$ \left\{\begin{split} & DN = [\sqrt n ] \\ & \theta = \frac{1}{{DN - 2}}\sum\limits_{i = n - DN + 1}^{n - 2} {\left| {{\mu _{i + 1}} - {\mu _i}} \right|} \\ & {\mu _i} = \gamma '_{i + 1} - \gamma '_i,\; i = n - DN + 1, \cdots , n - 1 \end{split}\right. $

(7)

聚类中心即为决策值排名大于$kp$的所有样本. 聚类中心点确定后, 再将两点间共享近邻的个数大于等于$k/2$的样本划分到同一个簇中, 对不满足该条件的样本则根据邻域信息进一步确定它们所属的簇.

1.2 评价指标

在二分类任务中最常用的评价指标是准确率, 但它仅适用于平衡数据, 而在不平衡数据集中使用可能会造成很大的误差. 因此, 对于不平衡数据集, 需要综合考虑多数类和少数类的情况. 为此, 本文选取G-mean, F1分数和AUC作为评价指标. 本文实验过程中, 定义少数类样本为正类, 多数类样本为负类.

召回率: 全部正类样本被正确预测的比率:

$ Recall = \frac{{TP}}{{TP + FN}} $

(8)

特异度: 所有负类被正确预测的比率:

$ {\textit{Specificity}} = \frac{{TN}}{{TN + FP}} $

(9)

查准率: 全部被预测为正类样本中实际为正类的比例:

$ Precision = \frac{{TP}}{{TP + FP}} $

(10)

G-mean: 召回率和特异度的几何平均:

$ G {\text -} mean = \sqrt {Recall \times {\textit{Specificity}}} $

(11)

F1分数: 召回率和查准率的调和平均数:

$ F1 = \frac{{2 \times Recall \times Precision}}{{Recall + Precision}} $

(12)

AUC: ROC曲线下的面积, 该曲线横轴为假阳性率$FPR$, 纵轴为真阳性率${\textit{TPR}}$.

$ \left\{\begin{array}{l} AUC = \dfrac{{1 + {\textit{TPR}} - FPR}}{2} \\ {\textit{TPR}} = \dfrac{{TP}}{{FN + TP}} \\ FPR = \dfrac{{FP}}{{FP + TN}} \\ \end{array}\right. $

(13)

式(8)–式(13)中, TP代表正确预测为正类样本的数量, FP代表错误预测为正类样本的数量, FN代表正类样本被错误预测为负类样本的数量, TN代表正确预测为负类样本的数量.

2 本文方法 2.1 少数类聚类与过采样权重的设置

直接对少数类进行过采样的方法更注重处理样本的类别失衡问题, 而忽略了少数类样本密度分布不均所导致的类内不平衡问题. 基于聚类的过采样方法可以同时解决这两个问题, 聚类的结果直接影响到后续过采样的效果, 所以选择合适的聚类算法显得尤为关键. 传统的K-means算法不仅需要手动确定聚类个数, 而且在处理非团簇数据时存在限制. 在不平衡数据集中, 少数类由于缺乏有效样本导致分布不规则. 因此, 考虑到传统聚类算法的局限性以及少数类样本分布的独特性, 本文采用基于共享近邻密度峰值的聚类算法划分少数类样本为多个子簇.

不平衡数据分布中常见小间断问题, 少数类样本中的小间断数据呈数量少且较为密集的特点. 为每个子簇分别过采样数量时, 如果仅追求采样后各子簇大小一致只能解决由不同大小导致的不平衡问题, 而忽略了小间断簇的存在. 子簇的复杂情况可用密度和大小来描述, 越为稀疏的子簇说明分类器能够获得的有效信息越有限, 需要合成更多的新样本来增加特征信息. 换言之, 在合成样本时更为关注稀疏区域, 具体体现在对于较为稀疏的子簇会给予更高的过采样权重. 在之前为少数类聚类的步骤中已经计算了全部少数类样本的密度, 那么每个簇的密度和权重的计算公式为:

$ {\textit{SDE}}{_i} = \sum\limits_{j = 1}^{{\textit{SC}}{_i}} {\rho _{{x_i}}^{}} , \;i = 1, \cdots , C $

(14)

$ weigh{t_i} = \frac{1}{{{\textit{SDE}}{_i}}},\; i = 1, 2, \cdots , C $

(15)

其中, ${\textit{SC}}{_i}$为子簇的大小, $C$为子簇的个数. 子簇密度${\textit{SDE}}{_i}$是子簇中所有样本密度的总和; 权重$weigh{t_i}$取子簇密度的倒数, 以实现稀疏区域更高合成权重的目的, 从而得到每个子簇所需合成的样本数$O{S_i}$ 为:

$ O{S_i} = \frac{{weigh{t_i}}}{{\displaystyle\sum\limits_{i = 1}^C {weigh{t_i}} }} \times n,\; i = 1, \cdots , C $

(16)

其中, $n$为需要合成的少数类样本的数量. 通常情况下, 为了使两类样本数量最终达到1:1的平衡, $n$的取值设置为少数类样本数量与多数类样本数量之间的差值.

2.2 改进的合成新样本的方法

基于聚类的过采样算法在一定程度上能最大化保留原始样本的分布结构. 由于聚类不当或原本样本分布问题, 个别簇中可能出现局部稀疏的情况, 即子簇中个别样本与其他样本的距离明显过大. 若直接采用SMOTE在子簇内进行过采样, 合成样本极有可能大量分布在高密度区域, 而局部稀疏的样本可能会被忽视. 此外, SMOTE过采样时近邻个数的选择也会受到最小子簇大小的限制. 因此, 提出一种新的过采样策略, 包含3个主要步骤: (1)计算局部稀疏度确定每个少数类样本的最少合成次数; (2)根据局部多数类聚集度为近邻的选择分配概率; (3)比较局部多数类聚集度确立线性插值的权重范围.

首先, 少数类样本的局部稀疏程度用子簇内近邻距离来衡量. 以子簇$i$为例, 设任意一个属于该子簇的少数类样本$x_t^i$, 计算得到它在子簇$i$中的最近邻距离为$dnn_t^i$, 那么$x_t^i$的子簇内局部稀疏度为:

$ LS_t^i = \frac{{dnn_t^i}}{{\displaystyle\sum\limits_{j = 1}^{{\textit{SC}}{_i}} {dnn_j^i} }} $

(17)

在式(16)中已经计算出子簇$i$的合成样本数为$O{S_i}$, 再结合每个样本点的局部稀疏度, 得到$x_t^i$的最少合成次数计算公式为:

$ CS(x_t^i) = LS_t^i \times O{S_i} $

(18)

每个样本的最少合成次数是由局部稀疏度和子簇的合成样本数决定, 目的是保证子簇内较为密集样本的最少合成次数总是少于子簇内较为稀疏样本的最少合成次数.

其次, 本文引入局部多数类聚集度的概念, 从近邻选择概率和线性插值权重范围的确定两个方面避免生成类重叠样本. 对于少数类样本$x_t^i$ , 局部多数类聚集度的计算公式为:

$ m{d_{x_t^i}} = \frac{m}{{M{e_{d(x_t^i, x_v^{{\mathrm{maj}}})}}}} $

(19)

其中, $m$表示少数类样本$x_t^i$的${k_2}$近邻中多数类的数量, $d(x_t^i, x_v^{{\mathrm{maj}}})$代表少数类$x_t^i$与多数类${x_v^{{\mathrm{maj}}}}$的欧氏距离, $M{e_{d(x_t^i, x_v^{{\mathrm{maj}}})}}$是$m$个多数类的距离的中位数. 当$m = {k_2}$时, 说明少数类样本的${k_2}$近邻全是多数类, 不适合被选择作为合成样本点, 直接删除该样本.

根据$x_t^i$同属子簇$i$的其余少数类样本的$m{d_{x_s^i}}$值的大小, 为$x_t^i$选择合适的近邻合成新样本. 具体而言, $m{d_{x_s^i}}$值越大说明该样本周围的多数类聚集程度越大, 则被选中的概率就越小. 选中近邻$x_s^i$后, 根据线性插值原理, 即公式$x_{{\mathrm{new}}}^i = x_t^i + \omega \times (x_s^i - x_t^i)$生成新的少数类样本. 关于参数$\omega $的取值范围做如下规定:

$ \omega = \left\{ {\begin{array}{*{20}{l}} {(0, 0.5], }&{\begin{array}{*{20}{c}} {{\mathrm{if}}}&{m{d_{x_t^i}} < m{d_{x_s^i}}} \end{array}} \\ {(0.5, 1), }&{\begin{array}{*{20}{c}} {{\mathrm{if}}}&{m{d_{x_t^i}} > m{d_{x_s^i}}} \end{array}} \\ {[0, 1), }&{\begin{array}{*{20}{c}} {{\mathrm{if}}}&{m{d_{x_t^i}} = m{d_{x_s^i}}} \end{array}} \end{array}} \right. $

(20)

参数$\omega $的取值范围主要根据两个少数类样本点的局部多数类聚集度决定, 也就是新样本的生成总是靠近局部多数类聚集度低的方向. 重复新样本生成过程, 直到每个样本点得到最少合成次数, 最终每个子簇满足指定的样本合成数量.

不同于SMOTE随机选择少数类样本进行过采样的方法, 本文提出的过采样策略按照合成次数依次选择每一个少数类样本, 同时以局部多数类密度大小为概率选择近邻样本, 在进行线性插值时根据局部多数类聚集度确定权重大小来生成新样本. 该方法不仅考虑到子簇内局部稀疏样本, 增加了合成样本的多样性, 还避免了样本生成于多数类区域.

2.3 消除噪声和规范边界

过采样操作后的数据集仍存在两个问题: 一是噪声, 二是类重叠. 噪声样本普遍存在于实际数据集中, 噪声的存在会增加模型的复杂度而造成过拟合, 使得分类效果不佳. 在不平衡数据集中, 少数类样本的数量远少于多数类, 如果在过采样之前就进行去噪, 可能会导致噪声识别出现误差, 从而删掉高价值的样本. 类重叠问题可能本就存在于原始数据中, 而过采样策略虽然增加了合成样本的多样性, 但存在加重类重叠问题的风险. 类重叠现象指的是少数类和多数类样本在边界区域过于重叠, 导致分类边界不清, 加大分类器出现分类错误的概率. 因此, 提出一种基于C4.5分类器的集成过滤机制, 为了清理噪声和创建更为规则的类别边界.

过滤机制具体实施步骤如下: 在聚类步骤中, 少数类被划分为$C$个簇, 对应的子簇中心为${x_{{\mathrm{center}}{_i}}}$; 过采样后每个簇中包含原始样本和合成的新样本, 即每个簇中的样本数量为${N_{{\mathrm{old}} + {\mathrm{new}}{_i}}}$; 计算所有多数类与${x_{{\mathrm{center}}{_i}}}$的距离, 升序排列后选择与${x_{{\mathrm{center}}{_i}}}$距离最近的${N_{{\mathrm{old}} + {\mathrm{new}}{_i}}}$个多数类样本, 从而得到样本量为$2{N_{{\mathrm{old}} + {\mathrm{new}}{_i}}}$的类别平衡的数据集. 分别使用C4.5分类器对这些平衡数据集进行训练, 得到$C$个分类器后分别用来预测整个训练集的样本标签, 记第$i$个分类器预测错误的样本集合为${E_i}$, 那么所有分类器都预测错误的样本集合为:

$ E = {E_1} \cap {E_2} \cap \cdots \cap {E_C} $

(21)

集合$E$是所有分类器一致性分类错误的样本, 这些样本可以认为是噪声样本或是难以学习的边界样本, 理应把这些样本全部删除从而便于后续的学习阶段.

基于C4.5分类器的集成过滤机制是按照一致性规则认定噪声样本, 原因有两方面: 一是如果一个样本的特征与其标签一致, 那么大多数基于这些特征的分类器应该能够正确地预测其标签; 如果一个样本的特征与其标签不一致, 那么大多数分类器可能会根据这些特征做出错误的预测. 二是在对少数类聚类时, 聚类个数一般不会太多, 也就是构造的C4.5分类器数量较少, 故采用一致性规则认定噪声更为严谨.

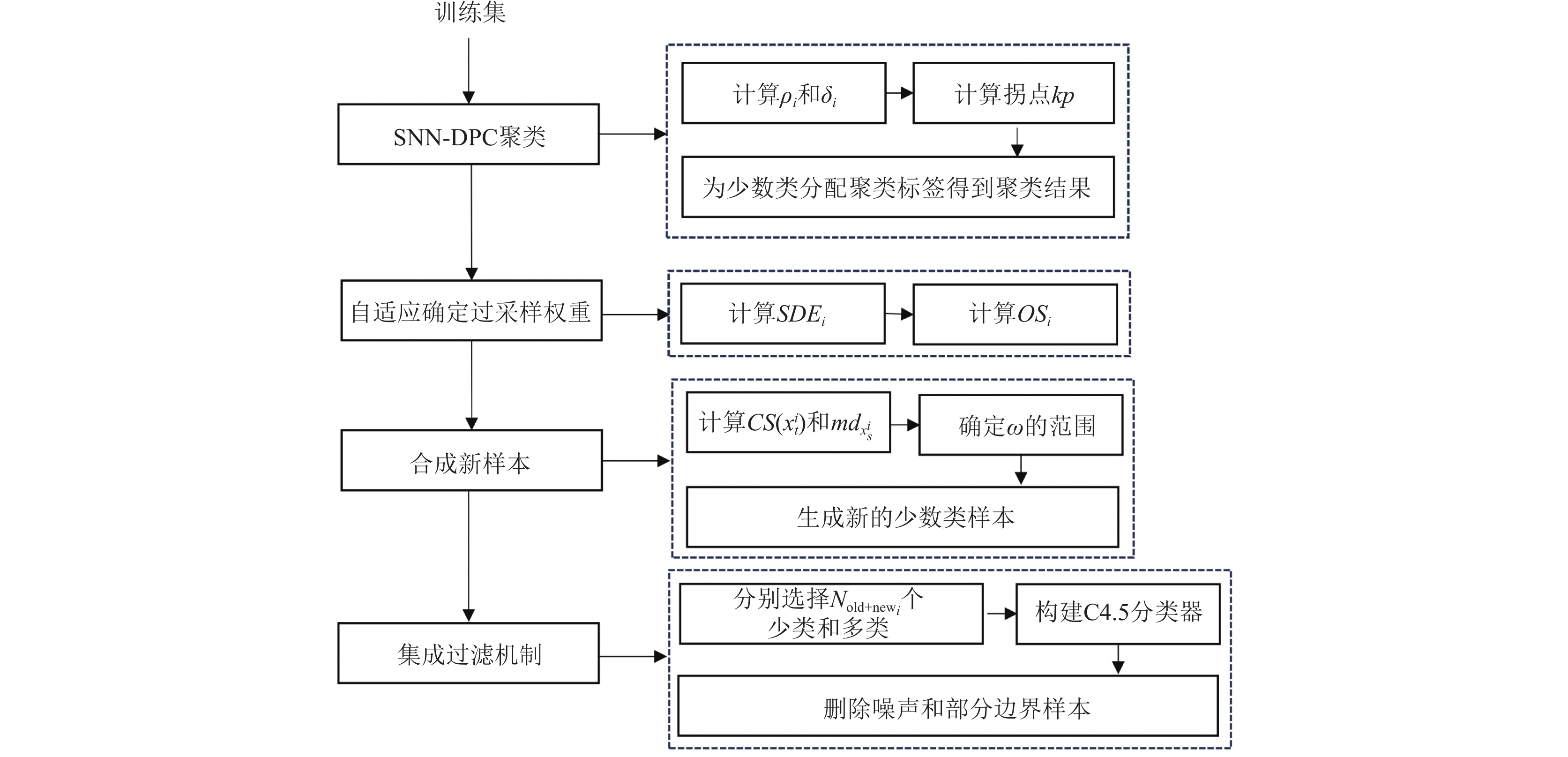
2.4 算法步骤

本文提出的基于共享近邻密度峰值聚类的过采样算法的具体步骤如算法1所示, 流程图如图1所示.

算法1. SNN-DPC-OF算法

输入: 训练集多数类样本集合$\scriptstyle {T_{{\text{maj}}}}$; 训练集少数类样本集合$\scriptstyle {T_{\min }}$; 聚类所需的近邻数$\scriptstyle {k_1}$; 局部多数类聚集度计算所需的近邻数$\scriptstyle {k_2}$.

输出: 平衡后的数据集.

1) 为避免计算距离时受到不同量纲的影响, 根据$\scriptstyle T_{\min }^{'} = \frac{{{T_{\min }} - \min ({T_{\min }})}}{{\max ({T_{\min }}) - \min ({T_{\min }})}}$归一化所有少数类样本;

2) 根据式(1)–式(5)计算每个少数样本的局部密度和相对距离, 再根据式(6), 式(7)确定聚类中心, 最后按照分配规则将少数类划分为$\scriptstyle C$个子簇;

3) 由式(14)–式(16)计算出每个子簇需要过采样的数量;

4) 对每个子簇, 由式(17), 式(18)计算簇中每个少数类样本的最少合成次数;

5) 根据式(19), 式(20)选择近邻样本和确定线性插值权重范围, 对子簇内所有少数类样本进行过采样, 将生成的新样本添加到新样本集合$\scriptstyle {T_O}$;

6) 重复步骤3)–5), 直到每个子簇都达到指定合成样本数量, 将$\scriptstyle {T_O}$放回训练集, 得到新样本集$\scriptstyle {T_{{\mathrm{new}}}}$;

7) 根据式(21)剔除噪声和难以学习的部分边界样本, 得到最终的数据集$\scriptstyle {T_{fb}}$.

3 实验结果及分析 3.1 实验数据及设计

实验数据: 为更全面评估过采样方法在处理不同级别的不平衡数据集的性能, 从UCI Machine Repository中选取8个不平衡率跨度较大的数据集进行实验, 数据集信息见表1. 每个数据集都只包含两个类别, 针对存在多个类别的数据集, 采用一对多的方法将多类数据转换为二类数据.

实验设置: 根据数据集特性, 为减少随机性带来的误差, 采用5折分层交叉验证方法进行实验. 具体来说, 对于每个数据集都划分为5折, 在每次交叉验证中, 选择其中4折为训练集, 而剩下的1折为测试集. 在训练集上使用SNN-DPC-OF方法, 再选择决策树(C4.5)、K近邻(KNN)和支持向量机(SVM)这3个分类器进行训练, 最后在测试集上评估分类结果. 因此, 训练集包含原始数据和合成的新数据, 而测试集中仅包含原始数据. 根据网格搜索的方法, 确定每个分类器的最佳参数设置. 分类器的建立和参数的选择基于Python中的scikit-learn包完成.

3.2 SNN-DPC-OF方法的验证与分析 3.2.1 过采样过程在二维数据的可视化展示

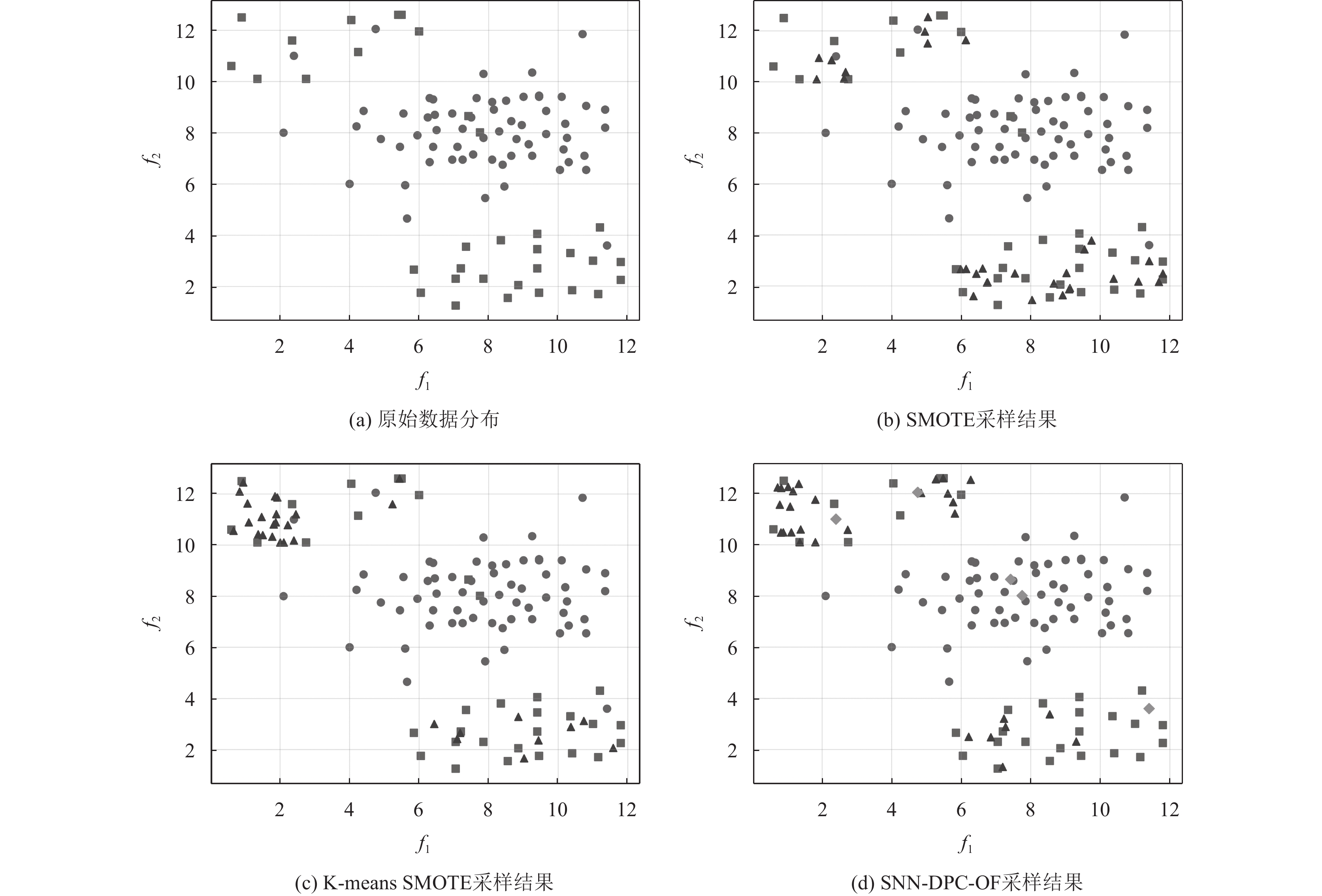
在二维数据集上能更直观地展示过采样后的结果, 从文献[13]中选择实验数据集b. 将SMOTE, K-means SMOTE和SNN-DPC-OF这3种过采样方法应用于该数据集, 实验中近邻个数设置为5, K-means SMOTE的聚类数量设置为3.

如图2所示, 其中实心圆代表多数类, 正方形代表少数类, 三角形代表新生成的少数类, 菱形代表被过滤的样本. SMOTE一方面受到噪声样本的影响, 从而合成大量的噪声数据; 另一方面在少数类聚集区域生成的样本明显多于稀疏区域, 容易造成过拟合. K-means SMOTE过采样后仍然存在原始噪声数据, 而且指定聚类数量对结果影响较大; SNN-DPC-OF方法不仅在少数类稀疏区域生成了更多样本, 还能够在过滤原始噪声数据的同时避免生成过多的类重叠数据.

3.2.2 多种过采样方法分类性能的对比分析

将SNN-DPC-OF方法与以下5个过采样方法进行比较: SOMO, SMOTE, Borderline-SMOTE, K-means SMOTE和SyMProD. 这5个过采样方法都基于Python的imblearn和smote_variants包^[18,19]实现. 表2–表4分别展示了SNN-DPC-OF算法与其他对比算法与3种分类器(C4.5, KNN, SVM)相结合在8个不平衡数据集上的G-mean指标对比结果, 表中加粗字体代表在该数据集中最优. G-mean能够更好地反映模型对于少数类别的预测效果, 对于不平衡数据集的评估更为合理.

表2展示的是C4.5的分类结果, SNN-DPC-OF在8个数据集中G-mean指标都达到最优, 说明本文算法与C4.5算法结合比其他过采样算法更能提高模型的分类性能. 从表3可以看出, 在采用KNN分类器时, SNN-DPC-OF算法在libra和wine数据集上不如SMOTE和Borderline-SMOTE算法, 但差距很小, 基本可以忽略不计. 从表4的分析结果看出, 本文算法结合SVM分类器在超半数的数据集上能达到最优分类结果.

综合表2–表4, SNN-DPC-OF方法和3种分类器结合在大多数数据集上都能取得好的分类效果. 在高维数据集libra和segment上, 本文算法在3个分类器上的G-mean指标上表现良好, 说明本文算法不仅适用于结构简单的数据, 还对高维的不平衡数据有较好的处理效果.

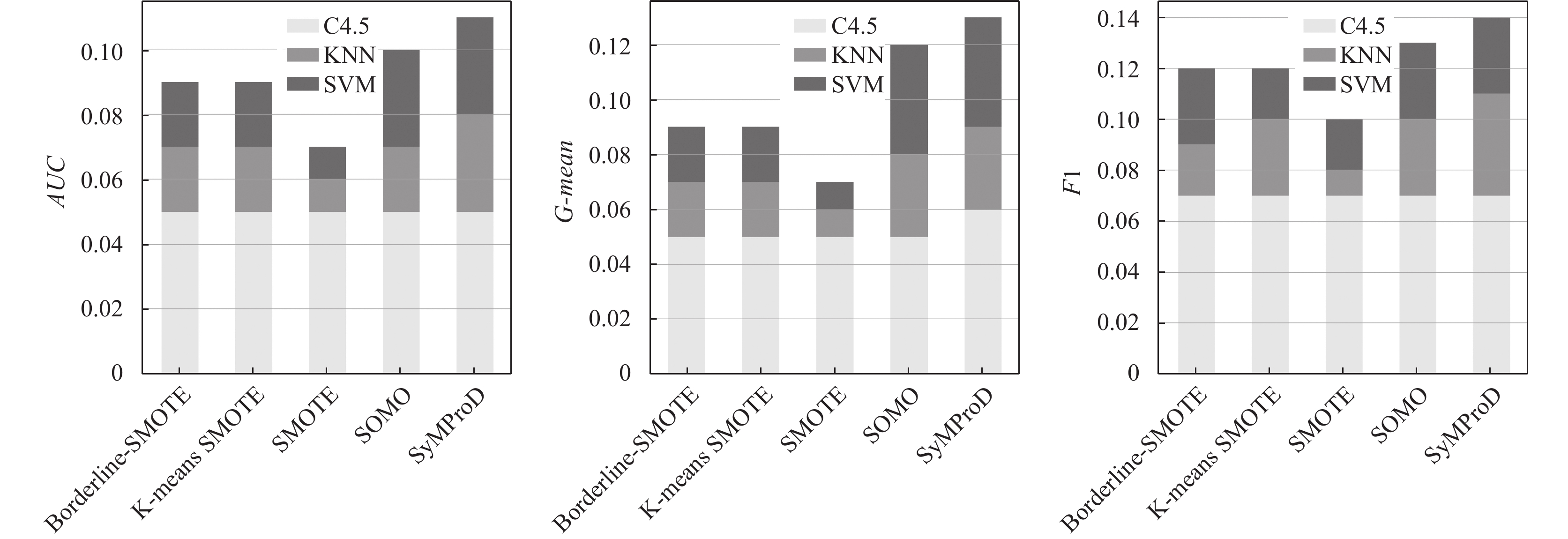
如图3所示, 该堆叠柱状图展现的是SNN-DPC-OF相对于其他算法在3个评价指标和3个分类器上提高的平均分数. 在3个不同的分类器中, 虽然本文算法比SMOTE算法的平均提高分数均低于其他算法, 但累计平均提升都在0.07以上, 仍能表现出本文算法的优势. F1分数在一定程度上反映模型对于数据重叠的处理能力. 当类别之间存在重叠时, 模型在准确率和召回率之间进行权衡, 以最大化F1分数. 图3中F1指标上的平均提升分数高于AUC和G-mean, 说明本方法能够有效处理类别重叠数据, 但一定程度上降低了对多数类的识别准确度. 总体而言, SNN-DPC-OF算法在不同分类器上表现较优, 能有效提高不平衡数据的分类效果.

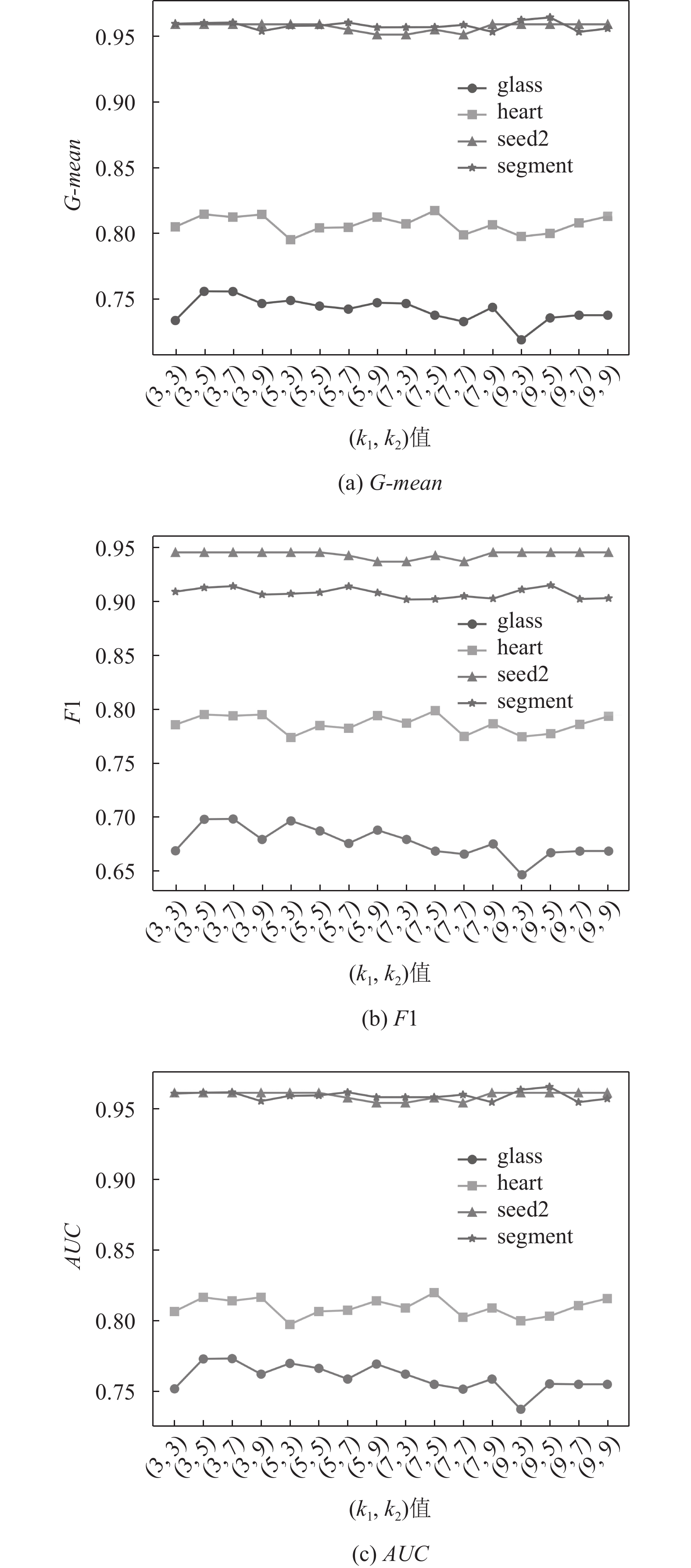
3.2.3 参数值的讨论

SNN-DPC-OF在聚类阶段使用了参数${k_1}$, 在局部多数类聚集度计算时使用了参数${k_2}$, 所以这两个参数的设置对各数据集各指标具有显著且关键的影响. 为了更好地评估两个参数对本文算法的影响, 在8个数据集中选择4个基准数据集实验, 从[3, 5, 7, 9]内选择最佳的参数组合. 为减少分类器的其他参数对结果的影响, 选择KNN分类器进行实验. 如图4所示, 横坐标为两个参数${k_1}$和${k_2}$的不同取值, 纵轴为各评价指标的值. 以glass数据集为例, 当参数${k_1}$取3时, 各项指标明显优于其他取值, 同时当${k_2}$取5时, 3个评价指标都达到最优.

4 结论与展望

本文提出了一种基于共享近邻密度峰值聚类的过采样方法, 该方法首先对少数类进行聚类, 进而确定子簇内过采样大小并实施过采样步骤, 最后引入集成过滤机制, 删除噪声和难以学习的边界样本, 从而有效提高分类器的性能. 在8个数据集上采用8种经典的过采样方法和SNN-DPC-OF算法对数据进行平衡化处理, 分别应用C4.5、KNN、SVM进行分类, 结果表明本文提出的方法分类效果显著优于其他方法. SNN-DPC-OF算法考虑了样本的类间平衡和类内平衡, 能关注到稀疏的少数类情况, 对较高不平衡数据集的处理效果也更好. 但是, 在运行时间上不及传统的SMOTE等过采样方法. 下一步将在对少数类聚类上寻找新的突破口, 使得少数类能更加准确地聚类并优化算法减少运行时间, 以便该方法能更好地应用于更多的分类器, 增强算法的泛化性和鲁棒性.