1 引言

物联网技术和5G网络的落地催生了大量新兴应用(如对象检测, 增强现实, 虚拟现实)的发展, 同时这些计算密集、时延敏感型应用也对终端设备提出了更高的计算需求. 但由于终端设备自身计算资源和电池能量的有限性, 若将任务全部本地执行, 会严重降低用户服务质量(quality of service, QoS).

移动边缘计算(mobile edge computing, MEC)通过将个性化服务器部署到网络边缘(如无线接入点或基站), 就近地为物联网设备和移动用户提供计算卸载服务, 不仅解决了传统云计算技术带来的核心网拥塞、隐私泄露等问题, 而且满足了终端用户低时延和低功耗的QoS需求.

然而, 在地面通信设施侧部署MEC带来了一些新的挑战. 首先, 由于MEC服务器高度定制化的特点, 位置固定的MEC服务器往往无法根据用户的需求灵活变换, 这会浪费MEC服务器的性能. 其次, 在偏远地区或受灾地区, 由于通信设施的缺失或受损, 用户往往难以得到可靠的通信和计算支持. 近年来, 无人机因其易部署、低成本、视距通信的特性逐渐被应用到通信领域, 通过为无人机配备个性化MEC服务器将有望解决上述问题^[1,2]. 文献[3]在车联网中引入无人机使能MEC系统, 解决了车联网中海量数据的交互和处理问题. 文献[4]针对海洋网络中的计算业务, 提出了一种安全、低功耗的无人机辅助多接入MEC系统, 弥补了海上通信、计算资源的不足. 文献[5]研究了一种灾害情景下多无人机协作的MEC系统, 并从功能和数据的角度详细说明了无人机边缘云的基本架构.

但是, 将无人机应用于MEC领域还存在着如下挑战, 首先, 由于无人机部署在三维空间, 需要考虑无人机部署位置对系统通信时延的影响; 其次, 为了延长无人机网络寿命, 需要制定更加苛刻的计算卸载策略以降低无人机的能耗, 对此, 国内外学者进行了广泛的关注研究.

文献[1]以最小化系统中用户和无人机的总能耗为目标, 使用K均值(K-means)聚类算法对物联网节点的位置进行聚类, 聚类所得的簇中心即为无人机部署的水平位置, 并将用户匹配问题总结为一个线性规划问题求解, 但在用户匹配后未调整无人机部署位置, 随着用户数量的增加, 用户公平性将会下降. 文献[6]以最小化所有用户完成计算卸载的总时延为目标, 将用户匹配问题和无人机部署优化问题建立为一个混合整数非线性规划问题, 并将原问题分解为3个子问题, 利用松弛变量法和连续凸优化将非凸问题转化为凸问题后迭代求解, 但仿真结果显示无人机群负载不均且所部署的无人机之间间隔过小, 这不仅容易带来无人机间通信干扰的问题, 而且容易引发安全问题. 文献[7]以最小化系统能耗为目标, 提出了一种两层优化方法, 上层由差分进化算法解决无人机的部署问题, 下层采用贪心算法解决了任务调度问题, 但忽略了无人机高度对系统效能的影响. 文献[8]以最小化系统中各用户的平均时延为目标, 提出了一种基于改进粒子群算法用以解决无人机在某一时隙的部署问题, 并用贪心算法解决卸载决策问题, 虽然该方法适用于多种场景, 但迭代次数多收敛速度慢, 在执行时间上略显不足. 文献[9]引入了概率视距无线传输信道模型, 以最小化系统中用户间的最大时延为目标, 通过凸优化和块坐标下降法联合解决了无人机的三维部署, 带宽分配等优化问题, 但缺乏了对无人机计算资源分配的考虑, 这是影响系统总时延和用户公平性的关键性因素之一. 文献[10]考虑到无人机基站的负载差异问题, 以最小化访问延迟为目标, 提出了一种基于K-medoids的帕累托边界搜索算法用以解决无人机基站的二维部署问题, 但缺乏了对无人机高度的优化, 这也是访问延迟的决定性因素之一. 文献[11]在无人机辅助MEC系统的基础上, 加入卫星节点, 提出了一种空-天-地一体化的MEC系统, 以最小化系统平均响应时延为优化目标, 提出了一种双层优化算法用以优化无人机部署位置和计算卸载方案, 但未考虑无人机计算资源分配和无人机高度优化问题, 且迭代次数较多. 文献[12]以最小化能耗和时延的加权和为目标, 将无人机部署和计算卸载转化为两个随机博弈过程, 并提出了两种基于策略选择概率的学习算法使之达到纳什均衡, 但该工作采用了完全卸载策略, 无法充分利用终端设备的计算资源. 文献[13]针对无人机辅助的车载边缘计算网络, 以最小化无人机能耗为目标, 提出了一种基于深度强化学习的能效自主部署策略, 但需要大量的数据来训练模型, 并且训练结果通常是不稳定的.

基于以上研究存在的用户公平性不足、影响因素考虑不充分等问题, 本文研究了一个无人机群作为空中计算平台辅助MEC的场景, 并充分考虑用户匹配, 无人机部署, 计算资源分配, 卸载因子对系统总时延和用户公平性的影响, 以最小化系统总时延为目标, 建立了一个多元优化问题, 提出了一种两阶段联合优化算法, 并通过仿真实验证实了所提算法的有效性.

2 系统模型 2.1 网络模型

无人机辅助MEC系统如图1所示, 该系统由无人机$K = \{ 1, 2 , \cdots , k\}$, 地面用户$I = \{ 1, 2 , \cdots , i\}$, 以及地面站软件定义网络(software defined network, SDN)控制器组成, 无人机上搭载有边缘服务器, 作为边缘云节点为覆盖区域内的地面用户提供个性化服务. 假设每一个地面用户都有一个时延敏感型任务$ {J_i} = \{ {l_i}, C, {\mu _i}\} $需要执行, 其中$ {l_i} $表示任务数据量大小, $ C $表示处理1比特任务数据所需的CPU周期数, $ {\mu _i} $表示卸载因子. 由于终端设备计算能力的有限性, 若将任务本地执行, 则会降低用户体验, 为了合理利用本地资源和边缘计算资源, 本文采用部分卸载策略, 即将用户任务根据卸载因子拆分为两部分, 一部分任务本地执行, 另一部分任务通过通信链路卸载至无人机执行. 该系统经由控制链路通过地面站SDN控制器进行集中式管理, SDN控制器可以获得网络资源视图, 包括用户坐标, 无人机坐标, 无人机计算资源等, 并利用搜集到的数据集中控制系统内的计算卸载与无人机部署^[14,15]. 由于本文的目的是最小化系统总时延, 而该时延与用户的通信时延和计算时延相关, 所以下文给出通信模型和计算模型以计算对应的两部分时延.

2.2 通信模型

系统采用三维笛卡尔坐标系表示用户和无人机的坐标, 第i个用户的坐标为$\left(s_i, 0\right), \; i \in I$, 其中$ s_i=\left[x_i, y_i\right]^{\rm{T}} \in \mathbb{R}^{2 \times 1} $表示用户i的二维坐标, 第k个无人机的坐标为$\left(q_k, {\textit{z}}_k\right), k \in {K}$, 其中$q_k=\left[x_k, y_k\right]^{\rm{T}} \in \mathbb{R}^{2 \times 1}$表示无人机k的二维坐标, $ {\textit{z}}_{k} $表示无人机k的垂直高度. 对于用户i, 与匹配无人机k之间的距离为:

$ {d_{i, k}} = \sqrt {{\textit{z}}_k^2 + {{\left\| {{q_k} - {s_i}} \right\|}^2}} $

(1)

为了更加准确描述信道特征, 本文引入概率视距信道模型^[16], 因此, 无人机k与用户i之间的建立视距通信的概率为:

$ P_{i, k}^{L{{oS}}} = {C_1} + \frac{{{C_2}}}{{1 + {{\rm{e}}^{ - ({B_1} + {B_2}{\theta _{i, k}})}}}} $

(2)

其中, $ {B_1} \lt 0 $, $ {B_2} \gt 0 $, $ {C_2} \gt 0 $, $ {C_1} $满足$ {C_1} + {C_2} = 1 $, 它们都是关于特定环境的常数, $ {\theta _{i, k}} $是用户i与无人机k之间的仰角, 表示为:

$ {\theta _{i, k}} = \frac{{180}}{\text{π} }\arctan \left(\frac{{{{\textit{z}}_k}}}{{\left\| {{q_k} - {s_i}} \right\|}}\right) $

(3)

相对的, 建立非视距通信的概率为$1 - P_{i, k}^{L{{oS}}}$, 用自由空间路径损耗模型评估无线信道, 则用户i与无人机k之间的视距和非视距信道增益系数分别为:

$ h_{i, k}^{LoS} = \beta d_{i, k}^{ - {\alpha _{LoS}}} $

(4)

$ h_{i, k}^{NLoS} = \lambda \beta d_{i, k}^{ - {\alpha _{NLoS}}} $

(5)

其中, $ \;\beta $表示单位距离$d=1 \; {\rm{m}}$时的信道功率增益, $ {\alpha _{LoS}} $和$ {\alpha _{NLoS}} $分别为视距和非视距状态下的路径损耗指数, $ \lambda $为非视距状态下的信道衰落因子. 为避免信道间干扰, 系统采用频分多址协议, 并为每架无人机分配不同的频段, 根据香农公式, 用户i与无人机k之间的数据传输速率有:

$ {r_{i, k}} = P_{i, k}^{L{{oS}}}r_{i, k}^{LoS} + (1 - P_{i, k}^{L{{oS}}})r_{i, k}^{NLoS} $

(6)

$ r_{i, k}^{LoS} = w{\log _2}\left(1 + \frac{{ph_{i, k}^{LoS}}}{{{n_0}w}}\right) $

(7)

$ r_{i, k}^{NLoS} = w{\log _2}\left(1 + \frac{{ph_{i, k}^{NLoS}}}{{{n_0}w}}\right) $

(8)

其中, $ w $表示信道带宽, $ p $表示用户发送数据时的传输功率, $ {n_0} $表示信道噪声功率谱密度. 但在实际场景中, 视距状态的传输速率远大于非视距状态, 所以忽略非视距状态下的传输速率^[16], 则用户i与无人机k之间的数据传输速率可以近似为:

$ {R}_{i, k}\triangleq {P}_{i, k}^{L{oS}}\cdot w{\mathrm{log}}_{2}\left(1+\frac{p{h}_{i, k}}{{n}_{0}w}\right) $

(9)

2.3 计算模型

在用户将任务计算卸载之前, 需要进行用户匹配, 有用户匹配矩阵 $ A \in {\left\{ {0, 1} \right\}^{i \times k}} $表示为:

$ A = \left( {\begin{array}{*{20}{c}} {{a_{1, 1}}}& \cdots &{{a_{1, k}}} \\ \vdots & \ddots & \vdots \\ {{a_{i, 1}}}& \cdots &{{a_{i, k}}} \end{array}} \right) $

(10)

其中, $ {a_{i, k}} \in \left\{ {0, 1} \right\} $为匹配因子, 当用户i与无人机k匹配时$ {a_{i, k}} = 1 $否则$ {a_{i, k}} = 0 $, 且一个用户在该时隙内只能和一架无人机进行匹配, 即:

$ \sum\limits_{k = 1}^{ K} {} {a_{ik}} = 1, \; \forall i \in I, \; \forall k \in { K} $

(11)

完成用户匹配后, 用户i会将任务按照通信模型式(9)的数据传输速率将任务部分卸载至匹配的无人机k执行. 假设设备的任务是逐位独立的, 并且可以通过卸载因子$ {\mu _i} $拆分为任意两部分, 用于移动设备的本地计算和无人机的边缘计算^[17]. 则用户完成计算卸载的时延由用户本地计算的时间、将任务卸载到无人机的传输时间、任务在无人机上计算的时间和任务计算结果回传时间组成, 由于回传数据较小, 且下行速率更快, 本文忽略任务回传时间. 用户i本地计算时延可以表示为:

$ T_i^{{\rm{local}}} = \frac{{(1 - {\mu _i}){l_i}C}}{{{f_{{\rm{local}}}}}} $

(12)

其中, ${f_{{\rm{local}}}}$表示用户i本地设备的CPU计算频率. 用户i卸载至无人机k的传输时延表示为:

$ T_{i, k}^{{\rm{up}}} = \frac{{{\mu _i}{l_i}}}{{{R_{i, k}}}} $

(13)

无人机k接收到用户i传来的数据后将进行任务计算. 计算时延为:

$ T_{i, k}^{{\rm{comp}}} = \frac{{{\mu _i}{l_i}C}}{{{f_{i, k}}}}, \; \forall {{i}} \in {\Phi _k} $

(14)

其中, $ \Phi_{k} $为与无人机k相匹配的用户集合, 对于系统来说有计算资源分配矩阵:

$ F = \left( {\begin{array}{*{20}{c}} {{f_{1, 1}}}& \cdots &{{f_{1, k}}} \\ \vdots & \ddots & \vdots \\ {{f_{i, 1}}}& \cdots &{{f_{i, k}}} \end{array}} \right) $

(15)

其中, $ {f_{i, k}} $为无人机k为用户i分配的计算资源. 由于无人机所搭载的边缘服务器拥有的计算资源是有限的, 所以存在以下约束:

$ \sum\limits_{i = 1}^I {f_{i, k}^{{\rm{alloc}}} \leqslant F_k^{\max }} , \; \forall i \in {\Phi _k}, \; \forall k \in { K} $

(16)

其中, $ F_k^{\max } $为无人机k搭载的边缘服务器的CPU计算频率. 则用户i将任务卸载至边缘端计算的时延为:

$ T_{i, k}^{{\rm{off}}} = {a_{i, k}}(T_{i, k}^{{\rm{up}}} + T_{i, k}^{{\rm{comp}}}) $

(17)

由于用户本地计算和卸载至无人机计算是并行的, 所以对于用户i来说, 完成计算卸载的总时延为:

$ {T_i} = \max \left\{ {{T_i}^{{\rm{local}}}, T_{i, k}^{{\rm{off}}}} \right\} $

(18)

2.4 问题建模

系统总时延主要受用户匹配矩阵, 无人机三维部署, 计算资源分配矩阵和卸载因子影响, 所以本文的目标是通过联合优化用户匹配矩阵$ A $, 无人机水平位置$ {q_k} $, 无人机高度$ {{\textit{z}}_k} $, 计算资源分配矩阵$ F $, 卸载因子$ {\mu _i} $, 在最小化系统总时延的同时, 保证用户公平性. 由于多无人机系统构成并行计算范式^[6], 系统总时延等价于系统内用户间最大时延, 所以该优化问题可以表述为P1:

$ \left\{\begin{gathered} \mathop {\min }\limits_{A, {q_k}, {{\textit{z}}_k}, F, {\mu _i}} \mathop {\max }\limits_{\forall i \in I} \left\{ {\mathop {\max }\limits_{} \left\{ {{T_i}^{{\rm{local}}}, T_{i, k}^{{\rm{off}}}} \right\}} \right\} \\ {\rm{s.t.}}{\text{ }}C1:\sum\limits_{k = 1}^{ K} {{a_{i, k}} = 1} , \forall i \in I, \forall k \in { K} \\ {\text{ }}C2:{a_{i, k}} = \left\{ {0, 1} \right\}, \forall i \in I, \forall k \in { K} \\ {\text{ }}C3:\sum\limits_{k = 1}^K {\left| {{N_k}} \right|} = I, \forall k \in { K} \\ {\text{ }}C4:\left\lfloor {\frac{I}{K}} \right\rfloor \leqslant {N_k} \leqslant \left\lceil {\frac{I}{K}} \right\rceil , \forall k \in { K} \\ {\text{ }}C5:{\theta _{i, k}} = \frac{{180}}{\text{π} }\arctan \left(\frac{{{{\textit{z}}_k}}}{{\left\| {{q_k} - {s_i}} \right\|}}\right) \\ {\text{ }}C6:{Z_{\min }} \leqslant {{\textit{z}}_k} \leqslant {Z_{\max }}, \forall k \in {\rm K} \\ {\text{ }}C7:0 \leqslant f_{i, k}^{} \leqslant F_k^{\max }, \forall i \in {\Phi _k}, \forall k \in {\rm K} \\ {\text{ }}C8:\sum\limits_{i = 1}^I {f_{i, k}^{} \leqslant F_k^{\max }} , \forall i \in {\Phi _k}, \forall k \in {\rm K} \\ {\text{ }}C9:0 \leqslant {\mu _i} \leqslant 1, \forall i \in I \\ \end{gathered} \right.$

(19)

其中, $ C1 $表示同一用户只能匹配至一架无人机, $ C2 $表示用户匹配矩阵内的元素为0或1, $ C3 $表示无人机群服务的用户总数量等于系统内用户数量, $ C4 $表示无人机负载均衡约束, 即每架无人机服务的用户数量应该是相同的或差值不超过1的, $ C5 $为非仿射仰角等式约束, $ C6 $表示无人机高度约束, $ C7 $和$ C8 $表示无人机为匹配用户分配的计算资源不能超过自身计算资源, $ C9 $是卸载因子约束.

3 问题求解 3.1 问题分析与转换

由于各优化变量之间相互耦合, 所以P1是一个在多项式时间内难以求解的非凸多元优化问题. 同时约束$ C2 $使得该问题成为一个混合整数非线性规划问题. 为降低求解难度, 本文将原优化问题解耦为5个子问题, 并将其优化过程分为两个阶段: 第1阶段通过一种平衡约束聚类算法解决用户匹配和无人机水平部署问题, 第2阶段使用凸优化结合块坐标下降法迭代求解无人机高度部署, 计算资源分配和卸载因子优化问题, 最终得到一个近似最优解.

同时为了方便解决问题, 减少内层max函数对求解难度的影响, 引入辅助变量$ {\eta _i} $来表示用户i的延迟, 即${\eta _i} = \max \left\{ {{T_i}^{{\rm{local}}}, T_{i, k}^{{\rm{off}}}} \right\}$, 则原问题可以等价为P2:

$ \left\{\begin{gathered} \mathop {\min }\limits_{A, {q_k}, {{\textit{z}}_k}, F, {\mu _i}} \mathop {\max }\limits_{\forall i \in I} {\text{ }}{\eta _i} \\ {\rm{s.t.}}{\text{ }}C10:{\eta _i} \geqslant T_i^{{\rm{local}}} \\ {\text{ }}C11:{\eta _i} \geqslant T_{i, k}^{{\rm{off}}} \\ {\text{ }}C1\sim C9 \\ \end{gathered}\right. $

(20)

其中, 约束$ C10 $和$ C11 $是${\eta _i} = \max \left\{ {{T_i}^{{\rm{local}}}, T_{i, k}^{{\rm{off}}}} \right\}$的变体, 目的是更好地通过凸优化求解器对其进行求解. 接下来本文将分别求解两阶段的5个优化子问题.

3.2 阶段1: 聚类 3.2.1 用户匹配和无人机水平部署优化

为了改善信道质量, 使无人机尽可能地靠近地面用户以提升上行速率, 在以往无人机网络的研究中, 大多使用K-means算法解决用户匹配和无人机水平部署问题^[18–20], 具体来说, 先对地面用户坐标进行聚类得到无人机水平部署位置, 再令簇内用户与各簇中心的无人机相匹配. 但在无人机辅助MEC系统中, 每架无人机的计算资源是有限的, 且与无人机相匹配的用户数与无人机为这些用户分配的计算资源之间是紧密耦合的, 常规的K-means算法不能约束每个簇内的用户数, 分簇结果可能导致无人机群负载失衡, 使得计算资源分配不均, 用户公平性下降.

本文沿用聚类算法最小化路径损耗的优点, 同时为了满足约束$ C3 $和$ C4 $, 让聚类后的各簇内用户数均衡, 使用了一种带有平衡约束的聚类算法^[21]对用户聚类, 聚类结果的簇心即为无人机水平部署位置, 并将簇内用户与该簇心无人机相匹配, 具体算法如算法1.

算法1. 基于Balanced K-means的用户匹配和水平部署算法

输入: 用户坐标集合$\scriptstyle S = \left\{ {{s_1}, {s_2} , \cdots, {s_i}} \right\}$, 簇数目即无人机数$\scriptstyle k $, 地面用户数$\scriptstyle i $

1) 使用K-means++算法从$\scriptstyle S $中确定出$\scriptstyle k $个数据点作为各簇初始中心点$\scriptstyle Q = \left\{ {{q_1}, {q_2} , \cdots , {q_k}} \right\}$

2) repeat

3) 为(i mod k), k–(i mod k)个簇心分别分配$\scriptstyle \left\lceil {i/k} \right\rceil $, $ \scriptstyle \left\lfloor {i/k} \right\rfloor $个总计$\scriptstyle i $个槽

4) 构建这$\scriptstyle i $个槽和$\scriptstyle i $个用户的完全二部图, 每条边的权值为用户$\scriptstyle i $到槽$\scriptstyle i $所属簇簇心的欧氏距离的平方, 使用匈牙利算法求解该指派问题

5) 根据分配结果更新簇心

6) until簇心位置不发生变化

7) 每个簇中心即为无人机水平部署位置, 用户与本簇心无人机相匹配

输出: 无人机水平部署坐标$\scriptstyle Q = \left\{ {{q_1}, {q_2} , \cdots , {q_k}} \right\}$, 用户匹配矩阵$\scriptstyle A $

此时每架无人机达到负载均衡, 并且用户与匹配无人机之间的距离最短, 进而达到传输时延在水平部署维度上的最小化.

3.3 阶段2: 凸优化

通过阶段1得到无人机水平部署位置和用户匹配矩阵后, 考虑到其他变量对系统时延的影响, 阶段2使用凸优化解决无人机高度部署, 计算资源分配和卸载因子优化问题, 具体来说, 使用块坐标下降法的思想, 迭代优化多个子问题, 直至目标值收敛以获得最优值.

3.3.1 无人机高度优化

固定用户匹配矩阵, 无人机水平位置, 无人机计算资源分配矩阵, 卸载因子, 单独优化无人机高度, 则无人机高度优化子问题可以表示为P3:

$ \left\{\begin{array}{l} \mathop {\min }\limits_{{{\textit{z}}_k}} \mathop {\max }\limits_{\forall i \in I} {\text{ }}{\eta _i}\\ {\rm{s.t.}}{\text{ }}C5, C6, C10, C11 \end{array}\right. $

(21)

其中, $ C5 $是关于$ {{\textit{z}}_k} $的非仿射函数, $ C6 $和$ C10 $是关于$ {{\textit{z}}_k} $的凸约束, $ C11 $关于$ {{\textit{z}}_k} $非凸非凹, 所以需要对约束$ C5 $和$ C11 $进一步处理.

由于约束$ C5 $是非仿射函数, 且目标函数关于仰角$ {\theta _{i, k}} $单调递减, 所以将$ C5 $中的仰角进行松弛处理:

$ {\theta _{i, k}} \geqslant \frac{{180}}{\text{π} }\arctan \left(\frac{{{{\textit{z}}_k}}}{{\left\| {{q_k} - {s_i}} \right\|}}\right) $

(22)

此时$ C5 $变为关于$ {{\textit{z}}_k} $的凸约束, 但由于CVXPY工具箱不支持arctan函数, 所以本文使用连续凸优化技术通过其在任意一点的一阶泰勒展开式来近似arctan函数^[22], 则原约束可以改写为:

$ \begin{split} {\theta _{i, k}} \geqslant & \frac{{180}}{\text{π} }\left(\arctan \left(\frac{{{\textit{z}}_k^r}}{{\left\| {{q_k} - {s_i}} \right\|}}\right)\right. \\ & \left. + \frac{{\left\| {{q_k} - {s_i}} \right\|}}{{{{({\textit{z}}_k^r)}^2} + {{\left\| {{q_k} - {s_i}} \right\|}^2}}}({{\textit{z}}_k} - {\textit{z}}_k^r)\right) \end{split} $

(23)

其中, $ {\textit{z}}_k^r $是$ {{\textit{z}}_k} $第$ r $次迭代时对应的值, 记不等式右侧为$ \mathop {{\theta _{i, k}}}\limits_\sim $.

对于约束条件$ C11 $, $T_{i, k}^{{\rm{up}}}$关于$ {{\textit{z}}_k} $非凸非凹. 令$X = 1 + {{\rm{e}}^{ - ({B_1} + {B_2}{\theta _{i, k}})}}$ , $ Y = {\left\| {{q_k} - {s_i}} \right\|^2} + {\textit{z}}_k^2 $, $ v = \dfrac{{p\beta }}{{w{n_0}}} $, 则约束$ C11 $可以转化为:

$ {\eta _i} \geqslant \frac{{{\mu _i}{l_i}}}{{\left({C_1} + \dfrac{{{C_2}}}{X}\right)w{{\log }_2}\left(1 + \dfrac{v}{{{{(Y)}^{{\alpha ^{LoS}}/2}}}}\right)}} \triangleq T_{i, k}^{{\rm{up}}}(X, Y) {\text{ + }}T_{i, k}^{{\rm{comp}}} $

(24)

由于$T_{i, k}^{{\rm{up}}}$关于$ X \gt 0 $, $ Y \gt 0 $的黑塞矩阵是正定的, 且$ X $, $ Y $是关于$ {{\textit{z}}_k} $的凸函数, 所以$T_{i, k}^{{\rm{up}}}$是关于$ X \gt 0 $, $ Y \gt 0 $的凸函数, 可以利用连续凸优化技术通过其在任意一点的一阶泰勒展开式作为下界来近似$T_{i, k}^{{\rm{up}}}$^[22]:

$ \begin{split} T_{i, k}^{{\rm{up}}} \geqslant &\dfrac{{{\mu _i}{l_i}}}{{\left({C_1} + \dfrac{{{C_2}}}{{{X^{{r}}}}}\right)w{{\log }_2}\left(1 + \dfrac{v}{{{{({Y^r})}^{{\alpha ^{LoS}}/2}}}}\right)}} \\ & + {\psi ^r}\left({{\rm{e}}^{ - ({B_1} + {B_2}{\theta _{i, k}})}} - {{\rm{e}}^{ - ({B_1} + {B_2}\theta _{i, k}^r)}}\right) \\ & + {\delta ^r}({\textit{z}}_k^2 - {({\textit{z}}_k^r)^2}) \end{split} $

(25)

$ {\psi ^r} = \frac{{\ln (2){\mu _i}{l_i}}}{{\ln \left(\dfrac{v}{{{{({Y^r})}^{{\alpha ^{LoS}}/2}}}} + 1\right)w{{({C_1}{X^r} + {C_2})}^2}}} $

(26)

$ {\delta ^r} = \frac{{\ln (2){\mu _i}{l_i}v\alpha {X^r}}}{{2w{Y^r}({C_2} + {C_1}{X^r}){{\ln }^2}\left(\dfrac{v}{{{{({Y^r})}^{{\alpha ^{LoS}}/2}}}} + 1\right)({{({Y^r})}^{{\alpha ^{LoS}}/2}} + v)}} $

(27)

其中, $ {X^r} $, $ {Y^r} $, $ \theta _{i.k}^r $, $ {\textit{z}}_k^r $是$ {{\textit{z}}_k} $第$ r $次迭代时对应的值, 记不等式右侧为$\mathop {T_{i, k}^{{\rm{up}}}}\limits_ \sim$. 经过松弛处理后, 约束条件$ C11 $可以改写为关于$ {{\textit{z}}_k} $的凸约束:

$ {\eta _i} \geqslant \mathop {T_{i, k}^{{\rm{up}}}}\limits_ \sim + T_{i, k}^{{\rm{comp}}}, {\text{ }}\forall i \in I, \; \forall k \in {\rm K} $

(28)

对约束$ C5 $和$ C11 $进行处理后, 问题P3可以转化为P4:

$ \left\{\begin{gathered} \mathop {\min }\limits_{{{\textit{z}}_k}, {\theta _k}} \mathop {\max }\limits_{\forall i \in I} {\text{ }}{\eta _i} \\ {\rm{s.t.}}{\text{ }}{C{12}}:{\theta _{i, k}} \geqslant \mathop {{\theta _{i, k}}}\limits_\sim \\ {\text{ }}{C{13}}:{\eta _i} \geqslant \mathop {T_{i, k}^{{\rm{up}}}}\limits_\sim + T_{i, k}^{{\rm{comp}}} \\ {\text{ }}{C6}, {C{10}} \\ \end{gathered}\right. $

(29)

至此, P3变成了一个关于$ {{\textit{z}}_k} $的凸优化问题, 可以通过CVXPY工具箱求得近似最优解.

3.3.2 计算资源分配优化

固定用户匹配矩阵, 无人机水平位置, 无人机高度, 卸载因子, 单独优化无人机计算资源分配矩阵, 由于计算资源分配直接影响计算时延$T_{i, k}^{{\rm{comp}}}$, 去除P1中与$ {f_{i.k}} $不相关的部分, 计算资源分配优化子问题可以表示为P5:

$ \left\{\begin{array}{l} \mathop {\min }\limits_F \dfrac{{{\mu _i}{l_i}C}}{{{f_{i.k}}}} \\ {\rm{s.t.}}{\text{ }}{C7}, {C8} \end{array}\right. $

(30)

P5的目标函数是关于$ {f_{i.k}} $的凸函数, 且约束条件都是关于$ {f_{i.k}} $的凸约束, 所以问题P5是一个凸优化问题, 使用拉格朗日乘子法求解. 引入拉格朗日乘子$ \xi $, 把目标函数转换成拉格朗日函数:

$ L\left( {f_{i, k}^{}, \xi } \right) = \frac{{{\mu _i}{l_i}C}}{{f_{i, k}^{}}} + \xi \left( {\sum\limits_{i \in {\Phi _k}} {f_{i, k}^{}} - F_k^{\max }} \right) $

(31)

通过KKT条件:

$ \frac{{\partial L\left( {f_{i, k}^{}, \xi } \right)}}{{\partial f_{i, k}^{}}} = 0 $

(32)

$ \xi \left( {\sum\limits_{i \in {\Phi _k}} {f_{i, k}^{}} - F_k^{\max }} \right) = 0 $

(33)

联立式(31)和式(32)可以解得P5的最优解为:

$ {}^*f_{i, k}^{} = \frac{{F_k^{\max }\sqrt {{\mu _i}{l_i}C} }}{{\displaystyle\sum\limits_{i \in {\Phi _k}} {\sqrt {{\mu _i}{l_i}C} } }} $

(34)

3.3.3 卸载因子优化

固定用户匹配矩阵, 无人机水平位置, 无人机高度, 无人机计算资源分配矩阵, 单独优化卸载因子, 则卸载因子优化子问题可以表示为P6:

$ \left\{\begin{array}{l} \mathop {\min }\limits_{{\mu _k}} \mathop {\max }\limits_{\forall i \in I} {\text{ }}{\eta _i} \\ {\rm{s.t.}}{\text{ }}{C9}, {C{10}}, {C{11}} \end{array}\right. $

(35)

P6是一个标准的线性规划问题, 使用CVXPY工具箱可以快速求得最优解.

3.4 整体算法设计

在第1阶段得到无人机水平部署位置和用户匹配矩阵后, 由于式(20)仍然非凸, 所以在第2阶段的3个小节中, 分别分析了无人机高度、计算资源、卸载因子对于式(20)的凹凸性, 由于式(20)关于无人机高度非凹非凸, 所以无法一次优化所有变量, 所以采用块坐标下降法的思想, 对式(20)的变体P4、P5、P6进行迭代求解, 直到优化目标小于一个阈值为止. 综合两阶段, 本文所提出的联合优化算法具体如算法2所示.

算法2. 联合优化算法

输入: 地面用户数量$\scriptstyle i $, 无人机数量$\scriptstyle k $, 地面用户坐标集合$\scriptstyle S = \left\{ {{s_1}, {s_2} , \cdots , {s_i}} \right\}$

阶段1:

1) 通过算法1得到无人机水平部署位置坐标 $\scriptstyle Q = \left\{ {{q_1}, {q_2} , \cdots , {q_k}} \right\}$和用户匹配矩阵$\scriptstyle A $

阶段2:

2)初始化无人机初始高度$\scriptstyle {Z^0} = \{ {\textit{z}}_k^0, \forall k \in {K}\}$, 计算资源矩阵$ \scriptstyle {F^0} $, 地面用户初始卸载因子$\scriptstyle {U^0} = \{ \mu _k^0, \forall k \in {K}\}$, 令$\scriptstyle r = 0 $

3) repeat

4) 固定$\scriptstyle {Z^r} $, $ \scriptstyle {F^r} $, 通过求解P6得到$\scriptstyle {U^{r + 1}} $

5) 固定$\scriptstyle {U^{r + 1}} $, $ \scriptstyle {Z^r} $, 通过求解P5得到$ \scriptstyle {F^{r + 1}} $

6) 固定$ \scriptstyle {U^{r + 1}} $, $ \scriptstyle {F^{r + 1}} $, 通过求解P4得到$\scriptstyle {Z^{r + 1}} $

7) 更新$\scriptstyle r = r + 1 $

8) until目标函数的增益小于一个阈值$\scriptstyle \varepsilon \gt 0 $

输出: 系统总时延, $\scriptstyle Q $, $\scriptstyle {Z^r} $, $\scriptstyle {F^r} $, $ \scriptstyle {U^r} $

4 实验与分析

本节给出仿真结果来说明本文提出的无人机辅助边缘计算中联合优化算法的性能. 假设存在一个基站损坏, 无人机辅助地面用户边缘计算的场景, 系统中无人机数量$ k = 3 $, 地面用户数量$ i = 30 $, 其水平位置随机分布在边长400 m的正方形区域, 令(2)中$ {B_1} = - 0.4568 $, $ {B_2} = 0.047 $, $ {C_1} = - 0.63 $, $ {C_2} = 1.63 $^[9]. 其余仿真参数设置如表1所示.

图2、图3分别展示了使用Balanced K-means和文献[18–20]的K-means进行用户匹配和水平部署的结果, 用同一颜色标明各簇用户和无人机之间的匹配关系. 使用Balanced K-means进行用户匹配和部署结果如图2所示, 系统内与每架无人机匹配的用户数都为10. 而传统K-means由于没有平衡约束, 难以达到无人机之间的负载均衡, 结果如图3所示, 无人机的用户匹配数分别为8, 8, 14. 同时由于使用了聚类算法解决无人机用户匹配问题, 在保证地面用户与匹配无人机间距离最短的同时, 避免了文献[6]中无人机部署距离过近导致的安全和干扰问题.

图4展示了用户匹配和无人机三维部署的结果, 其中无人机的高度分别为139 m, 140 m, 137 m, 它们都部署在适中的位置. 这是因为高度过低会降低视距通信概率, 而过高则会带来更多的路径损耗, 这都会降低用户与无人机之间的传输速率, 增加传输时延. 因此, 让无人机保持中等高度可以获得更好的通信链路.

为了验证本文所提算法在无人机辅助MEC系统中的性能, 将其与其他4个基准方法进行对比, 分别是: (1)文献[20]提出的无人机水平部署和用户匹配算法搭配本文凸优化算法; (2)不优化无人机高度, 固定无人机高度为50 m; (3)不优化计算资源分配, 计算资源平均分配; (4)不优化卸载因子, 固定卸载因子为0.6.

系统总时延随地面用户数量的变化如图5所示. 随着地面用户数量的增加, 每个用户分得的计算资源不断减少, 导致系统总时延不断增加, 同时, 本文所提联合优化算法的系统总时延均小于其他算法. 其中固定卸载因子算法的时延增量明显大于其他算法, 这是因为随着地面用户的增加, 固定卸载因子, 会使得边缘服务器的计算负载激增, 每个用户分配得到的计算资源减少, 进而导致边缘计算时延增加. 而使用算法1中贪心算法解决用户匹配问题时, 无人机间无法达到负载均衡, 导致用户计算资源分配不均, 使得匹配到高负载无人机的用户的时延升高, 系统总时延随之升高. 同时, 由于地面用户数据大小的随机性, 有针对性的资源分配算法优于平均分配算法. 固定高度使得用户无法平等建立视距通信, 也会对系统总时延造成影响. 上述分析表明, 在无人机辅助MEC系统中, 卸载比对系统总时延影响最大, 其次是计算资源分配和无人机高度.

图6展示了系统总时延随着无人机数量的变化. 随着部署的无人机数量的增加, 系统时延随之降低, 这是因为增加的无人机为系统带来了更多的计算资源, 使得分配给用户的计算资源增加, 边缘计算时延降低. 同时部署多架无人机可以使得其部署距离更接近地面用户, 进一步降低了传输时延. 但随着无人机数量的增加, 系统时延并不是呈线性下降的, 这是因为只有当无人机群中负载最大的无人机匹配的用户数下降时系统时延才会显著下降, 而在本系统中这个数量并不是随着无人机数量的增加而线性下降的, 并且系统的成本和能耗会随着部署无人机的数量而上升, 所以, 系统中无人机的数量并不是越多越好, 关于系统中无人机部署的数量还有待进一步的研究.

图7展示了各算法用户公平性的比较结果, 其中用户公平性由系统中各用户时延的标准差表示, 即:

$ {\textit{Fairness}} = \frac{1}{i}\sqrt {{{\sum\limits_{i \in I}^{} {\left( {{T_i} - \mathop T\limits^{\_\_} } \right)} }^2}} $

(36)

Fairness越低表明公平性越高. 如图7所示, 本文算法在地面用户数量不同的情况下都保持了良好的公平性, 同时也说明系统用户公平性与本文的各个优化变量都相关. 对于固定高度算法来说, 由式(2)和式(3)可知, 固定高度过低使得靠近无人机与远离无人机的用户间建立视距通信的概率差值过大, 进而使得数据传输速率差值过大. 对于算法1来说, 由于负载不均衡, 导致匹配至高负载无人机的用户获得的计算资源比匹配至低负载无人机的用户更少. 由于每个用户的任务数据量不同, 固定卸载因子和平均分配计算资源算法使得数据量大的用户的时延增加, 数据量小的用户的时延减少. 因此, 为了提升系统用户公平性, 联合优化各个相关变量是十分必要的.

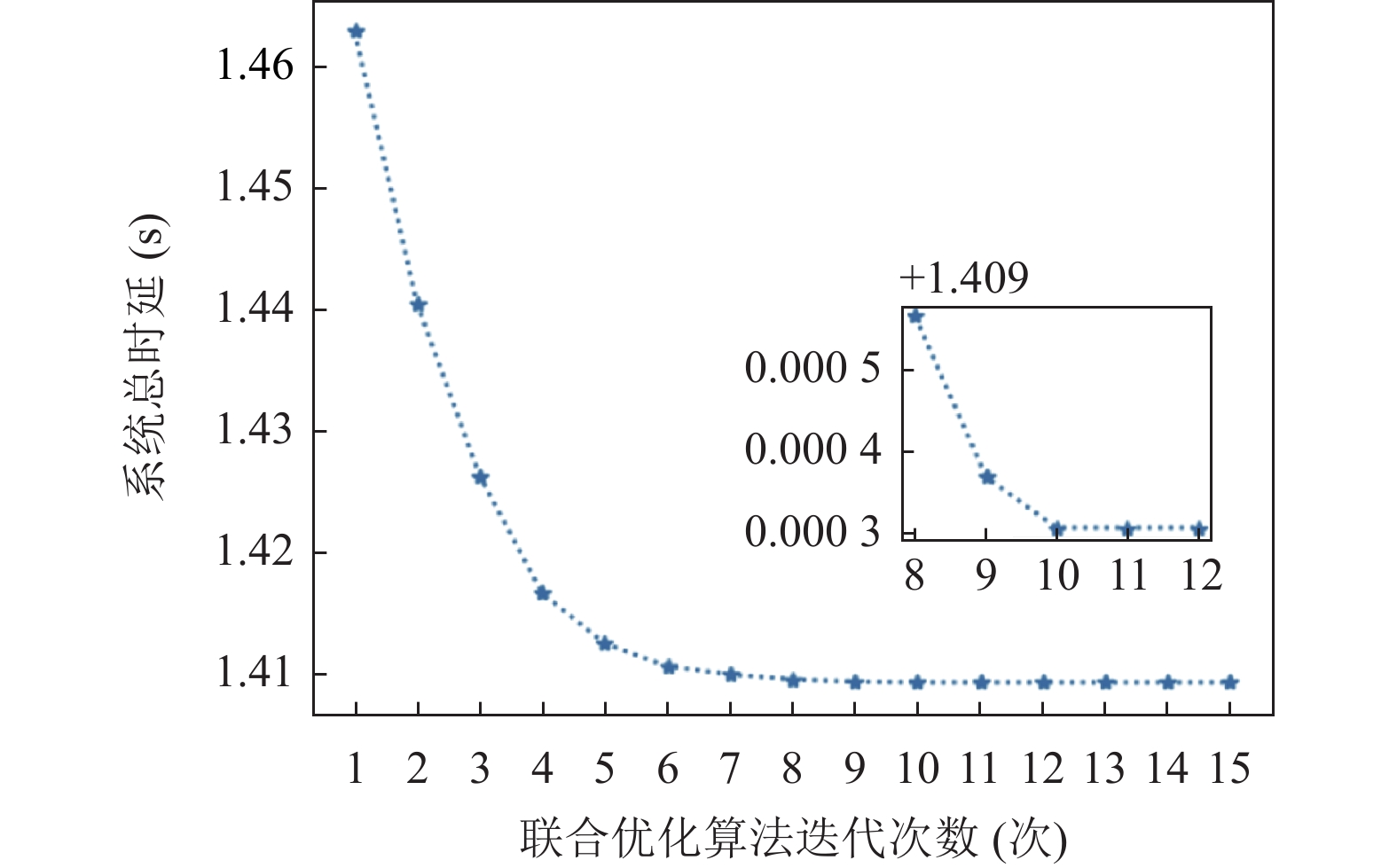
图8展示了本文所提算法的收敛性, 随着迭代次数的增加, 系统时延随之减小, 并且在第10次迭代处收敛. 由此可以得出本文算法具有良好的时效性, 能够在较短时间内获得近似最优解.

图9展示了随着地面用户数量的增加, 各用户平均卸载率的变化情况. 当无人机数量不变时, 随地面用户数量的增加, 平均卸载率不断下降, 因为系统中计算资源的数量是有限的, 用户数量的增加意味着分配给每个用户的计算资源的减少, 甚至会低于本地设备能提供的计算资源, 使得用户更倾向于本地计算更多的任务量. 随着系统无人机数量的增加, 系统拥有的计算资源增加, 平均卸载率则会上升.

5 结论

本文解决了无人机辅助MEC中面向用户公平性的计算卸载和三维部署问题. 以最小化系统时延为目标, 提出了一个两阶段联合优化算法, 在第1阶段通过平衡约束的聚类算法解决无人机用户匹配和无人机水平部署问题, 第2阶段通过凸优化迭代求解无人机高度部署、计算资源分配和卸载因子优化问题. 同时分析了各优化变量对用户公平性的影响. 仿真结果表明, 所提算法能够在最小化系统总时延的同时, 保证用户公平性. 未来工作主要考虑动态网络场景, 联合无人机轨迹优化, 进一步降低无人机辅助MEC场景中的能耗与时延.