由于3D扫描设备的快速发展, 获取三维点云(3D)数据已不再困难. 三维数据的容易获取, 使得深度学习已经不必限制在二维方面的研究与应用, 深度学习已经逐渐从二维跨向三维. 因此如何使用深度学习高效地处理三维点云数据, 已经成为一个盛行的话题. 在各种应用中, 比如: 自动驾驶、姿势估计、机器人零件拾取、医疗影像, 通常都需要将点云分割作为预处理步骤, 再以此为基础进行下一步骤. 在机器人领域中, 机器人零件拾取仍然是人们关注的热点. 在个体相互叠加、相互遮挡的场景下, 信息混杂, 如何达到很好的分割效果是一大问题.
深度学习在计算机视觉方面的4个经典应用: 识别、检测和定位、语义分割、实例分割. 实例分割是实例分割为属于同一类的对象的单独实例提供了不同的标签. 实例分割不光有语义分割的一部分特点, 需要不同类别之间进行分类, 还有目标检测的一部分特点, 需要定位出来不同的个体, 即使这些个体属于同一类物品. 实例分割大致分成两种方法: 自下而上和自上而下. 自上而下的实例分割方法先通过目标检测的方法找到个体所在的区域, 再在这一部分区域中进行语义分割, 分割出来的结果作为输出. 自上而下的方法通常实例分割的结果具有较好的对象性. 然而, 这些方法需要多阶段的训练和删除多余的建议. 因此, 它们通常是耗时并且计算成本高的[1–6]. 自下而上的实例分割方法通常认为实例分割是语义分割之后的后续步骤. 特别是, 大多数现有的方法都基于同一类别的点应该具有非常相似的特征的假设. 因此, 这些方法主要侧重于识别特征学习和点分组, 通常先进行像素级别的语义分割, 在通过聚类、度量学习等手段来区分不同的个体. 这些方法处理速度较快, 但相对而言并没有特别好的精度[7–11]. 两者之间最大的区别就在于是否需要找到个体所在的区域, 两种方法各有优劣, 但是在存在强烈遮挡的情况下, 自上而下的方法在寻找个体所在区域的效率不高, 因此性能较差.
1 FPCC网络原理现有的拾取场景实例分割方法可分为两类: 面向物流的方法和面向工业的方法. 前者是多类、多实例学习. 后者倾向于从杂乱的场景中进行一类多实例学习, 而不预测语义标签. 研究人员已采用主流的2D检测或2D实例分割网络来定位物流场景中的对象. 而在该工业场景下会存在多个同类物体相互堆叠、相互遮挡的问题、三维的分割速度问题以及三维数据标注难度问题. 因此, 很少有研究专注于工业拾取场景的实例分割. 而Xu等人[12]设计了针对此环境的三维实例分割网络(FPCC).
1.1 FPCC算法主要流程FPCC网络[12]是直接对点云进行处理的网络. 首先, 将点云数据的坐标
| $ \left\{\begin{gathered} \bar x = {x_i} - \min \{ {x_1}, {x_2}, \cdots, {x_n}\} \\ \bar y = {y_i} - \min \{ {y_1}, {y_2}, \cdots, {y_n}\} \\ \bar {\textit{z}} = {{\textit{z}}_i} - \min \{ {{\textit{z}}_1}, {{\textit{z}}_2}, \cdots, {{\textit{z}}_n}\} \\ \end{gathered} \right.$ | (1) |
FPCC网络输入的点云数据的格式为6维, 即
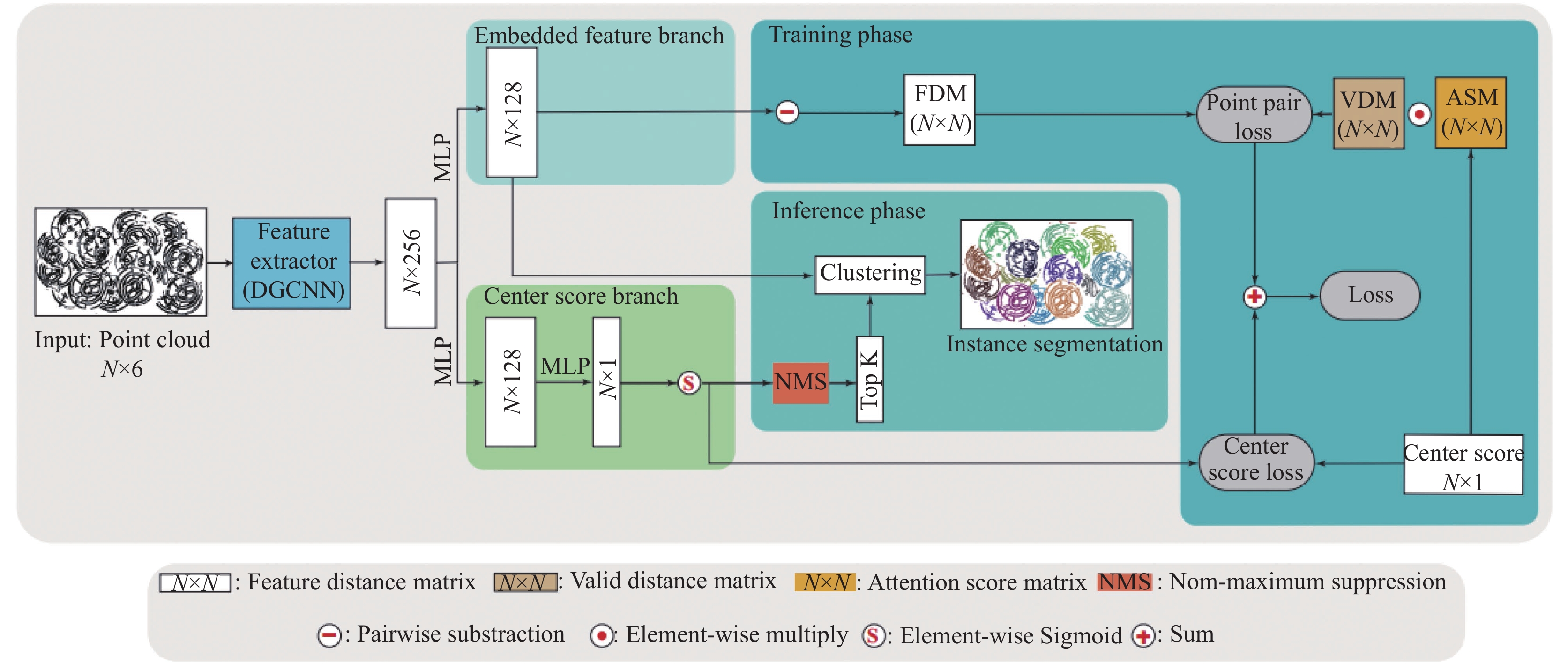
|
图 1 FPCC网络框架 |
1.2 中心点分支
该分支是通过训练得到不同个体的中心点, 该分支得到的中心点的准确度, 直接影响到后续实例分割的结果. 因此, 该分支训练的好坏是至关重要的.
中心点分数是指点与其物体中心点之间的距离. 物体中心的点的得分会比物体边界的点的得分高. 我们采用如式(2)的中心点分数定义:
| $ {C_{center(i)}} = 1 - {\left(\frac{{\parallel {p_i} - {c_i}{\parallel _2}}}{{d{}_{\max }}}\right)^\beta } $ | (2) |
其中,
在学习到的特征空间中, 同一实例的特征点在特征空间中应该非常接近, 而不同实例的特征点应该会被区分开, 因此我们采用距离公式来表示点与点之间的特征距离, 即:
| $ d(a, b) = \left\| a - b\right\| _2 $ | (3) |
其中,
| $ {d_{F(i, j)}} = {\left\| {e_F^{(i)} - e_F^{(j)}} \right\|_2} $ | (4) |
有效特征矩阵
| $ {d_{V(i, j)}} = \left\{ \begin{gathered} 1, \; {\text{ }}{\rm{if}} \; {\left\| {{p_i} - {p_j}} \right\|_2} \lt 2{d_{\max }} \\ 0, \; {\text{ }}{\rm{otherwise}} \\ \end{gathered} \right. $ | (5) |
式(5)表示判断
中心点被用作聚类的参考点, 所以更靠近中心位置的点对应该具有更高的权重. 因此引入注意力权重矩阵
| $ {S_{A(i, j)}} = {\rm{min}}(1, {s_{center(i)}} + {s_{center(j)}}) $ | (6) |
一对点
| $ {L_{EF}} = \sum\limits_i^N {\sum\limits_j^N {{w_{(i, j)}}{k_{(i, j)}}} } $ | (7) |
其中,
| $ {w_{(i, j)}} = {d_{V(i, j)}} \times {s_{A(i, j)}} $ | (8) |
而
| $ {k}_{(i, j)}=\left\{\begin{array}{l}\max(0, {d}_{F(i, j)}-{\varepsilon }_{1})\text{, }{\rm{if}}\text{ }{p}_{i}\text{ }{\rm{and}}\text{ }{p}_{j}是一个实例\\ \max(0, {\varepsilon }_{2}-{d}_{F(i, j)})\text{, }{\rm{otherwise}}\end{array}\right. $ | (9) |
其中,
对FPCC网络算法网络进行阅读理解以及实验验证, 发现模型中对于中心点不在物体本身的物体, 会存在中心点预测不准的问题, 这一问题也在该论文中提到过. 为了提升模型对于数据集的分割效果, 本文对FPCC算法改进主要为以下几个方面.
(1)改变了原网络模型结构. 对于中心点分支进行改进, 本文提出了新的中心点预测框架FEH, 该框架可以增强中心点预测的准确性. 该框架通过对中心点的预测, 再将预测结果放入网络与其余特征一起学习, 加强了对中心点这一特征的关注, 从而提高预测的中心点的正确率.
(2)改进了FPCC网络的损失函数. 针对中心点预测不准的问题, 要使得网络对中心点更加关注, 因此要修改网络的学习目标(损失函数), 修改了网络的损失函数, 添加了更多与中心点相关的值, 加强对中心点的监控, 从而提高中心点预测的准确度.
2.1 网络结构改进FEH网络是本文设计用于中心点的预测, 如图2所示, 该网络的输入为经过多层感知机(MLP)得到的128维特征向量(N×128)和点云数据(N×6), 将128维特征向量(N×128)通过多层感知机(MLP)得到预测的中心点得分(N×1), 再将该预测的中心点得分分别加入正在学习的特征空间中, 使得中心点在特征空间与其余点分离, 网络更容易学习中心点的特征. 其中, 本文设计的特征加强方法是FEH网络的重点. 而训练过程中的特征学习是使用DGCNN网络中的EdgeConv模块, 该模块因为有k-nn图表, 使得点云不仅仅有坐标点信息, 还将该点周围最近的k个点与该点联系到了一起, 从而加强了点与点之间的联系, 突显了局部信息, 达到更好的学习效果.
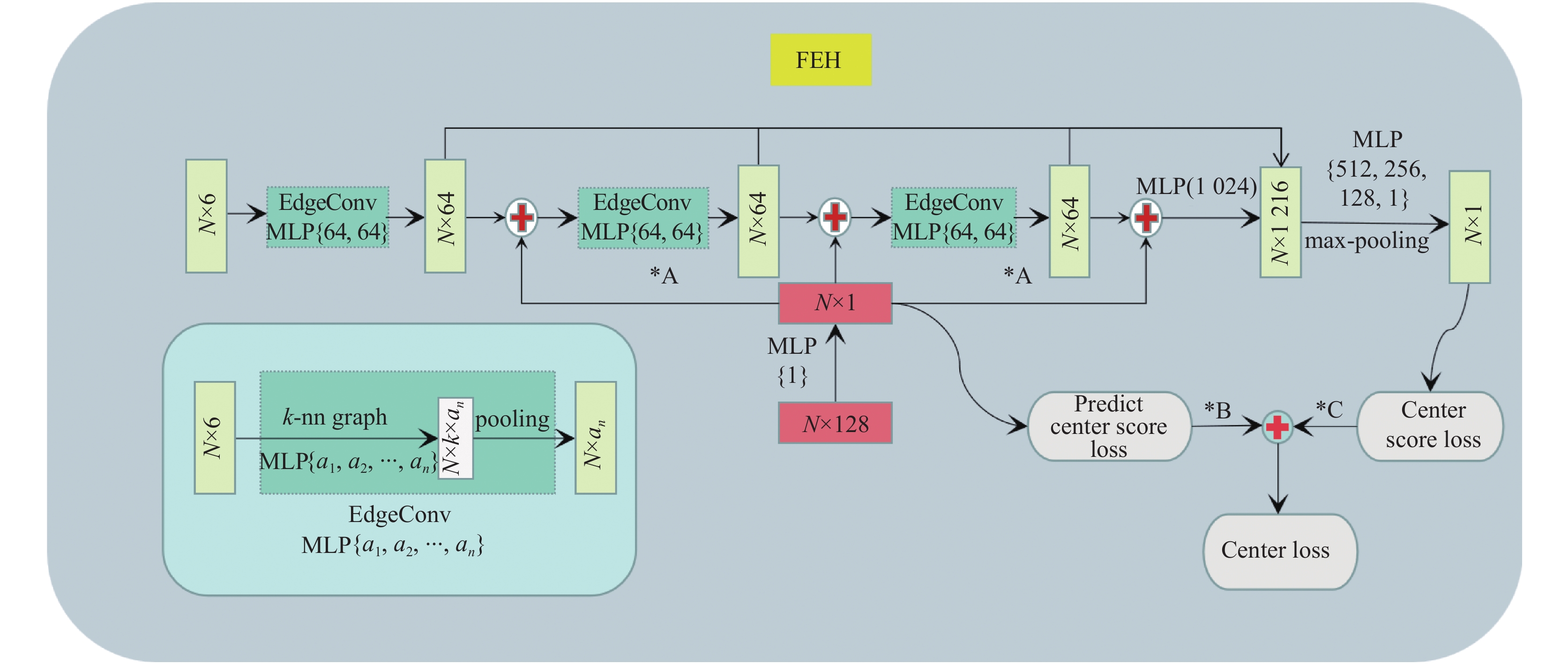
|
图 2 FEH网络框架 |
特征加强方法是如图3所示, 该方法是将得到的预测的中心点置信度通过加权的方法按照一定比例加入到点特征中, 从而突显中心点的特征, 达到更好的学习效果.
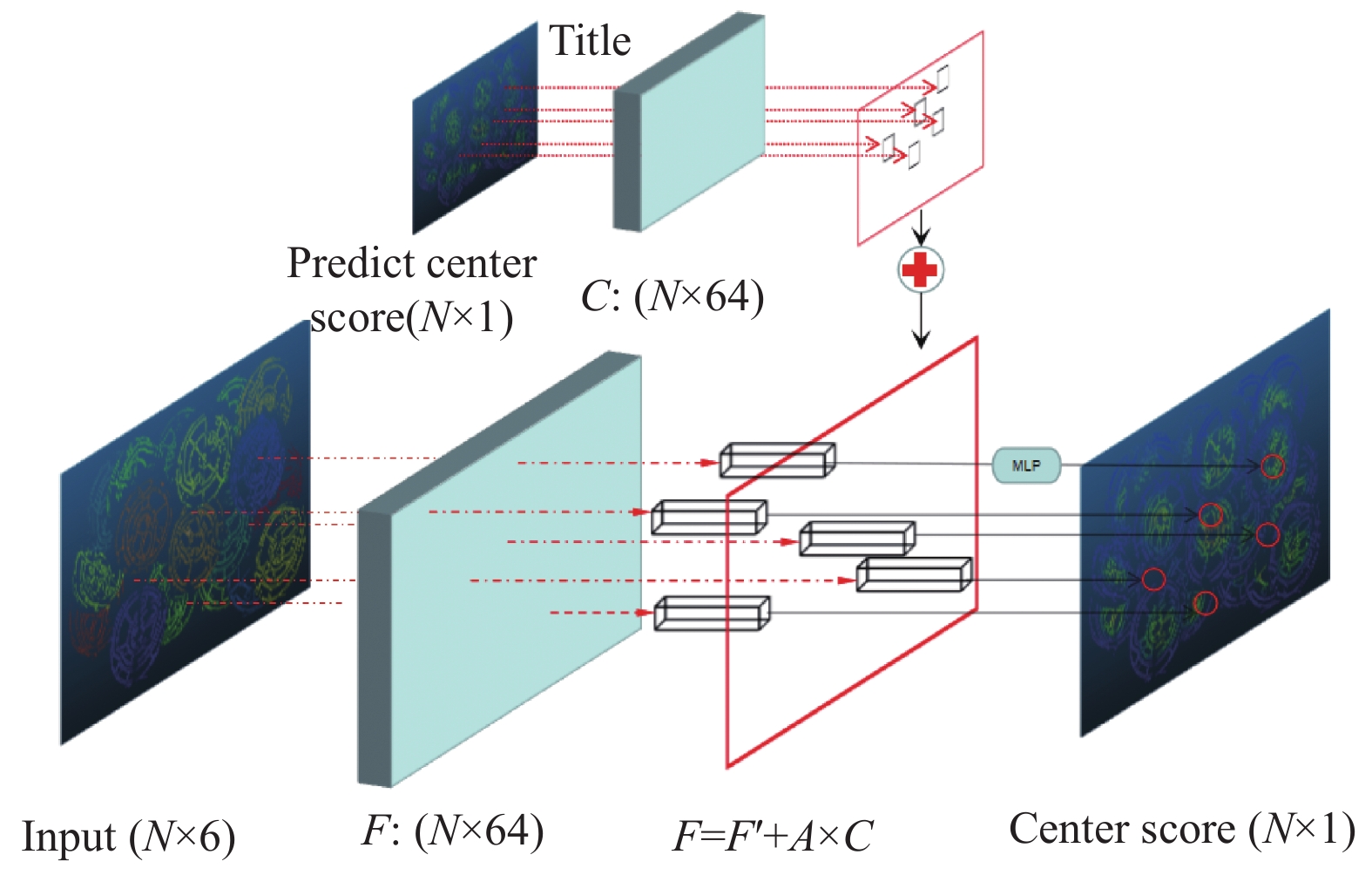
|
图 3 中心点特征增强方法 |
设点云数据为
中心点置信度是指该点是中心点的概率大小, 假设中心点置信度是两个极端, 只存在很大和很小的两种可能性, 即
新的特征向量如式(10)得出
| $ \left\{\begin{gathered} f'_0 = {f_0} + A \times {c_{m0}} \\ f'_1 = {f_1} + A \times {c_{n0}} \\ \qquad\quad \vdots \\ f'_{n - 1} = {f_{n - 1}} + A \times {c_{ms}} \\ f'_n = {f_n} + A \times {c_{nb}} \\ \end{gathered}\right. $ | (10) |
经过特征加强之后,
由于L1损失函数的鲁棒性, 平滑L1损失如式(11)所示被用作中心得分分支的损失函数[15].
| $ L1(x) = \left\{ \begin{gathered} 0.5{\left| x \right|^2}{\text{ }}, \;\;\;\, {\rm{if}}\; \left| x \right| \lt 1 \\ \left| x \right| - 0.5{\text{ }}, \; {\rm{otherwise}} \end{gathered} \right. $ | (11) |
预测的中心点得分损失
| $\left\{ \begin{gathered} {L_{{\rm{pre\_center}}}} = \frac{1}{N}\sum\limits_i^N {L1({S_{{\rm{pre\_center}}(i)}} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }_{{\rm{pre\_center}}(i)}})} \\ {L_{{\rm{center}}}} = \frac{1}{N}\sum\limits_j^N {L1({S_{{\rm{center}}(j)}} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} }_{{\rm{center}}(j)}})} \\ {L_{CL}} = B \times {L_{{\rm{pre\_center}}}} + C \times {L_{{\rm{center}}}} \\ \end{gathered}\right. $ | (12) |
其中,
本文实验所采用的数据集是开源的数据集IPA数据集[16]. IPA数据集: 这是第一个用于6D物体姿态估计和实例分割的公共数据集, 用于箱子拾取, 其中包含足够的注释数据, 可用于基于学习(learning-based)的方法. 数据集由合成场景和真实场景组成. 合成场景和真实场景中都提供了深度图像、3D点云、每个对象的6D姿势注释、可见性分数和每个对象的分割遮罩. 数据集包含10个不同的对象. 所有对象的训练场景都是合成的, 只有Ring-Screw和Gear-Shaft的测试场景才是真实的数据.
3.2 实验参数设置本文使用TensorFlow 1.1来构建我们的网络模型RFPCC, 并使用Adam[17]优化器进行培训, 初始学习率为0.0001, 批量大小为2, 动量为0.9. 所有训练和验证都在NVIDIA GeForce RTX 3080 GPU上进行. 在训练阶段, 设置
本文采用召回率(recall, R)和准确率(precision, P)以及两者的权重结合F1分数来评价网络模型的性能. 精确率是针对我们预测结果而言的, 它表示的是预测为正的样本中有多少是真正的正样本. 那么预测为正就有两种可能了, 一种就是把正类预测为正类(TP)另一种把负类预测为正类(FP), 也就是P=TP/(TP+FP). 召回率是针对我们原来的样本而言的, 它表示的是样本中的正例有多少被预测正确了. 那也有两种可能, 一种是把原来的正类预测成正类(TP), 另一种就是把原来的正类预测为负类(FN), 也就是R=TP/(TP+FN). 这两个衡量标准往往存在冲突; 当精度较高时, 召回率往往较低, 反之亦然. 为了平衡precision和recall之间的权衡, 通常使用F测度, 即precision与recall的加权谐波均值, 定义为F1=2×P×R/P+R. 表1是实例分割在IPA数据集上的数据结果. 在圆环这种中心点不在物体本身上的物体(Ring-Screw), 本文的改进方法很好地解决了这一问题, 并在精度上提升了12%, 并且本文方法并没有降低其他物体分割的效果.
| 表 1 实例分割的对比结果 (%) |
3.3.2 消融实验
表2给出了通过使用参数A的不同值进行特征加权而获得的分割结果. 当A的值设置得太大时, 中心点特征变得过于突出, 这会阻碍其他特征的学习, 并导致较差的分割性能. 相反, 当A的值设置得太小时, 中心点特征的突出效果不够明显, 这会使网络难以学习中心点特征, 并导致不好的学习效果. 因此, 选择合适的A值对于获得良好的分割性能是重要的.
| 表 2 A值的消融实验 |
参数B和C表示分配给两个中心点损失函数的权重, 它们的相对比例会显著影响网络的学习性能. 为了评估这些参数的有效性, 本文进行了4次消融实验, 如表3所示. 结果表明, 为这两种损失设置适当的权重对于改进网络的分割性能至关重要. 因此, 可以根据具体应用场景调整B和C值, 以优化网络的分割性能.
| 表 3 B值的消融实验 (A=0.3)(%) |
3.3.3 检测结果可视化
从检测结果可以清晰地看到, 改进后的算法较改进前的分割效果更好. 如图4所示, 可以清晰地看出, 改进后的中心点的预测更加集中. 从可视化可以看出, 本文提出的中心点增强的方法是有作用的.
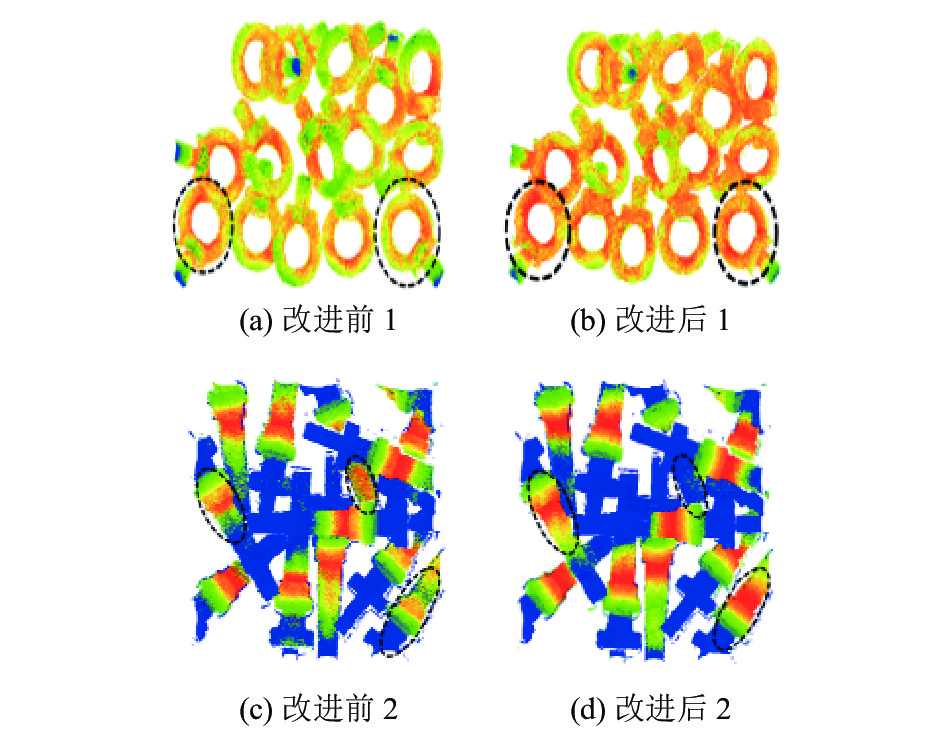
|
图 4 改进后中心点效果对比图 |
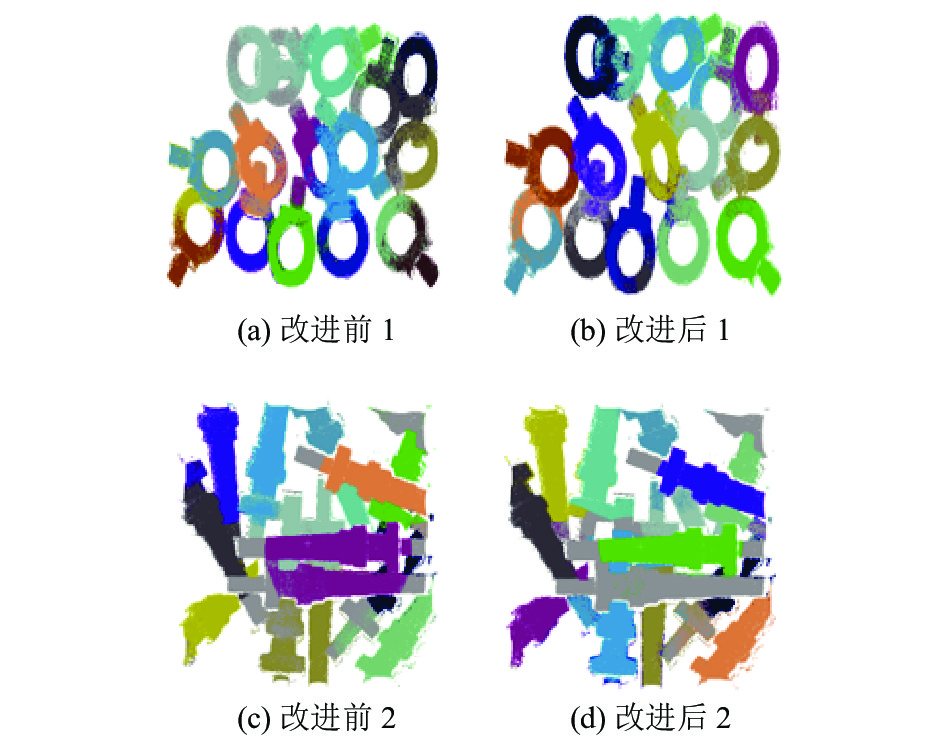
对于中心点不在物体上的物体, 如: Ring-Screw, 该物体的预测一直都不在实际的中心点上, 因此会降低分割的效果, FPCC网络不适合中心点不在物体本身上的对象. 但是, 如图5所示, 改进后的网络相比于原网络, 分割效果更好.
|
图 5 改进后分割效果对比图 |
4 结论与展望
本文根据FPCC网络改进出一个新的网络, 该网络增加了一个新的中心点预测模块, 可以更加准确地预测中心点. 本文也继承了FPCC网络的便捷性, 可以直接对点云数据进行处理. 在单一物体并且有大量遮挡以及堆叠的场景下, 本文取得了较好的实例分割结果.
本文还有一定的局限性, 会在之后的工作中尝试解决. (1)因为增加了FEH, 该网络的参数会增加, 导致计算量也会相对增加. (2)物体中心点预测得更加准确, 导致现在的聚类算法不能起到更好的聚类效果. 因此设计一种新的聚类算法是我们未来的工作.
| [1] |
Yang B, Wang JA, Clark R, et al. Learning object bounding boxes for 3D instance segmentation on point clouds. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 605.
|
| [2] |
Hou J, Dai A, Nießner M. 3D-SIS: 3D semantic instance segmentation of RGB-D scans. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 4416–4425.
|
| [3] |
Yi L, Zhao W, Wang H, et al. GSPN: Generative shape proposal network for 3D instance segmentation in point cloud. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3942–3951.
|
| [4] |
Narita G, Seno T, Ishikawa T, et al. PanopticFusion: Online volumetric semantic mapping at the level of stuff and things. Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems. Macao: IEEE, 2019. 4205–4212.
|
| [5] |
Zhang FH, Guan CY, Fang J, et al. Instance segmentation of LiDAR point clouds. Proceedings of the 2020 IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020. 9448–9455.
|
| [6] |
Engelmann F, Bokeloh M, Fathi A, et al. 3D-MPA: Multi-proposal aggregation for 3D semantic instance segmentation. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 9028–9037.
|
| [7] |
Wang WY, Yu R, Huang QG, et al. SGPN: Similarity group proposal network for 3D point cloud instance segmentation. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 2569–2578.
|
| [8] |
Charles RQ, Su H, Kaichun M, et al. PointNet: Deep learning on point sets for 3D classification and segmentation. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 77–85.
|
| [9] |
Liu C, Furukawa Y. MASC: Multi-scale affinity with sparse convolution for 3D instance segmentation. arXiv:1902.04478, 2019.
|
| [10] |
Mo KC, Zhu SL, Chang AX, et al. PartNet: A large-scale benchmark for fine-grained and hierarchical part-level 3D object understanding. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 909–918.
|
| [11] |
Liang ZD, Yang M, Wang CX. 3D graph embedding learning with a structure-aware loss function for point cloud semantic instance segmentation. arXiv:1902.05247, 2019.
|
| [12] |
Xu YJ, Arai S, Liu DY, et al. FPCC: Fast point cloud clustering-based instance segmentation for industrial bin-picking. Neurocomputing, 2022, 494: 255-268. DOI:10.1016/j.neucom.2022.04.023 |
| [13] |
Wang Y, Sun YB, Liu ZW, et al. Dynamic graph CNN for learning on point clouds. ACM Transactions on Graphics, 2019, 38(5): 146. DOI:10.1145/3326362 |
| [14] |
Li RK, Zhang YM, Niu DM, et al. PointVGG: Graph convolutional network with progressive aggregating features on point clouds. Neurocomputing, 2021, 429: 187-198. DOI:10.1016/j.neucom.2020.10.086 |
| [15] |
Girshick R. Fast R-CNN. Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV). Santiago: IEEE, 2015. 1440–1448.
|
| [16] |
Kleeberger K, Landgraf C, Huber MF. Large-scale 6D object pose estimation dataset for industrial bin-picking. Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Macao: IEEE, 2019. 2573–2578.
|
| [17] |
He KM, Gkioxari G, Dollár P, et al. Mask R-CNN. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2980–2988.
|
| [18] |
Wang XL, Liu S, Shen XY, et al. Associatively segmenting instances and semantics in point clouds. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 4091–4100.
|
| [19] |
Jiang L, Zhao HS, Shi SS, et al. PointGroup: Dual-set point grouping for 3D instance segmentation. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 4866–4875.
|
 2024, Vol. 33
2024, Vol. 33


