多变量时间序列的数据流反映了复杂系统中各变量随时间的变化过程, 这些数据通常由多个传感器收集, 网络流量数据是多变量时间序列的典型形式[1], 是容量规划、负载均衡、路径设置、异常检测和故障恢复等网络工程任务[2]的关键信息. 然而网络系统从固定和移动传感器测量流量数据的过程中存在局限性, 固定传感器(如环形探测器等)往往具有有限的空间覆盖范围, 而移动传感器则以高度不稳定的空间和时间分辨率收集数据, 这使得流量数据集具有一定的不完整性, 此外当网络系统遇到不良的监控条件时, 如网络拥塞、路由器错误行为和传输干扰等也会导致数据丢失. 网络流量数据缺失会导致多方面的问题, 从而影响网络的分析和管理. 首先, 缺失数据可能使得网络性能分析变得不准确和不全面, 从而影响对网络状况的准确把握. 其次, 缺失数据可能隐匿网络异常和安全威胁, 导致异常检测[3]和安全监控的效果下降. 此外, 缺失数据也会削弱对网络趋势的预测能力[4], 使得网络未来发展规划变得困难. 最后, 缺失数据可能导致网络可视化结果的不完整, 从而降低用户对网络状态和问题的理解, 因此修复缺失流量数据对于优化网络系统至关重要. 网络流量数据是多变量时间序列的典型形式, 具有时间特性, 同时由于路由方案的不确定性, 变量之间的相关性不断变化, 因此数据具有动态的空间特性, 如何设计合理有效的多维数据提取模式, 特别是设计数据动态空间特性的学习模型是目前的研究重点.
数据修复方法可分为两类: 传统方法和基于深度学习的数据修复方法. 传统的流量数据修复方法主要分为基于统计模型、机器学习和张量分解的3种算法, 但这些方法往往受限于对数据分布和特征的假设, 难以处理复杂的网络环境变化和未知的干扰. 与此同时, 深度学习作为近年来兴起的一种强大的机器学习技术, 具备从大规模数据中学习复杂模式和特征的能力, 为网络流量数据修复提供了全新的解决思路. 具体而言, 传统的数据修复方法如自回归移动平均(ARMA)[5]和自回归综合移动平均(ARIMA)[6]等统计模型可以估算缺失值, 但这些模型本质上是线性的, 可独立处理数据, 因此无法解决流量数据变量之间的相关性问题. 基于机器学习的插值方法通过学习历史数据建立预测模型, 并以此估算缺失数据, 如K-最近邻算法(KNN)[7]等, 此类方法需要从完整的历史数据集中学习, 当历史数据集中存在缺失数据时, 该方法同样不能建立变量之间的依赖关系. 目前有学者提出使用张量分解来解决变量之间的依赖性问题, 主要分为基于交替最小二乘(ALS)的局部张量分解(LTC)[8]算法和基于梯度的广义正则多项式张量分解(GCP)[9]算法, 其中LTC将流量矩阵表示为三维张量并将其划分为高度相关的子张量来挖掘多维数据之间的内在关系, 然而该方法假设数据空间特征为静态形式, 不符合数据空间特有的动态特性, 同时未考虑数据的时间关联性.
另一方面, 随着神经网络的不断发展及深度学习对数据理解能力的提高, 基于深度学习的缺失数据修复方法取得了一定的进展. 基于递归循环神经网络(recurrent neural network, RNN)[10]的方法具有挖掘时间序列中隐藏的时间关联信息的能力, 如Che等人提出GRU-D[11], 模型将缺失数据表示为最后一次观测值与平均值的组合. GRU-D为其他方法奠定了基础, 并在带有标签的医疗保健数据上展示了其显著的高性能, 但是这种方法不能以无监督的方式直接运用于没有标记的一般数据集. 继GRU-D之后, Cao等人提出基于双向RNN的插补模型(BRITS)[12], 通过引入衰减因子学习不规则数据的时空特征, 此方法考虑了空间特征, 但是只处理静态的变量相关性, 无法适用于流量数据. 生成对抗网络(generative adversarial network, GAN)可通过迭代训练过程捕获不完整、异构数据的分布和潜在结构并估计缺失值, 如Luo等人提出端到端生成对抗网络(E2GAN)[13], 该网络用于提取数据的时间特征并重构, 然而E2GAN只使用单向循环模型, 没有考虑数据变量之间的相关性, 因此应用于流量数据的插补任务中具有一定的局限性. 近年来国内外学者利用卷积神经网络(convolutional neural network, CNN)来处理数据的空间特性, 如Li等人提出利用三维卷积神经网络构建生成器和鉴别器以充分捕获交通数据的时空特征(3DConvGAN)[14]. Lei等人提出DCGAN模型[15], 生成器采用编-解码器体系结构来提取数据的时空特征并重构出完整数据; 鉴别器采用CNN提取时空特征来区分真实或虚假信号. Xie等人提出将三维卷积网络和张量补全算法相结合(NTC)[16], 实现对流量数据的补全. 然而, 模型通过将每个观测数据的索引作为输入, 当训练集中的观测数据数量较大时, NTC预测准确性将会降低. Spinelli等人提出使用图卷积神经网络(graph convolutional network, GCN)自编码器(GINN)对数据空间特性进行建模, 并由GCN解码器重建估算数据[17]. Le等人提出GCRINT模型[18]以处理流量缺失数据, 该模型使用双向LSTM和GCN来学习流量数据的时空相关性. 基于CNN的模型对各个类型数据的空间特性进行建模, 但这些方法同样只处理静态的相关性. 由于流量的路由方案不断变化, 不同变量之间的相关性随着时间的推移而发生显著变化, 数据具有明显的动态空间特性, 以上方法无法学习流量数据的多维特性.
针对此问题, 本文设计了一种并行双通道时空数据修复模型(ST-MFCN)来处理流量数据的丢失问题, 模型利用双向长短期记忆网络与多尺度卷积网络分别提取数据的时间特征和动态空间特征, 并采用双通道并行架构有利于捕捉数据特征的细节信息, 如吴敏忠等人提出一种融合多特征与时间序列的人群行为识别模型[19], 模型采用两个并行的网络层分别处理多特征相关性和时间序列依赖性对于人群行为的影响, 实现多方面捕捉数据特征的细节效果. 同时本文在原有的损失函数基础上添加对抗性损失函数以提高模型预测的精度. 实验结果表明, ST-MFCN能够有效地减少数据恢复的误差, 提升数据修复的精确度.
本文主要贡献如下.
1)针对流量数据的时间特性与动态空间特性, 提出了一种并行双通道时空数据修复模型(ST-MFCN). 该模型采用并行双通道架构捕捉数据特征的细节信息从而输出整体的流量数据.
2)针对流量数据前后时间信息的相关性, 采用双向LSTM进行特征的提取; 针对流量数据的动态空间特性, 采用两组不同尺度卷积核组成的扩展卷积模块, 并将两组扩展卷积模块采用传统连续卷积相结合的方式进行结合, 以多尺度卷积的方式实现对流量数据的动态空间特征的提取.
3)针对单一回归损失函数训练模型使得模型倾向于预测分布的平均值的问题, 本文设计了一种对抗性损失函数, 并将对抗性损失函数与回归损失函数组合进行模型的训练, 以提高模型预测的精度.
1 相关研究在本节中, 我们对目前缺失数据的修复方法进行分析, 主要分为传统数据修复方法及基于深度学习的数据修复方法两大类.
1)传统的数据修复方法
基于统计的插值方法通过利用已有数据的统计特征来预测缺失数据的值, 如Mehrotra等人提出使用均值法和中值法[20]分别利用观测数据的均值和中值对缺失值进行插补. Srebotnjak等人提出热卡填充法[21], 利用完整数据中最相似对象的值进行插补数据. 这类插补方法由于输入数据有限[22], 数据插补漏失率高, 导致预测不准确, 因此上述数据插值方法不适用于数据丢失较多情况下. Poulos等人[23]提出基于机器学习的插补方法, 提高预测性能的同时也补偿缺失数据的偏差. 这类方法通过挖掘数据间相关性来插补缺失数据, 如Zhang等人利用KNN模型[7]选择与丢失数据节点最邻近的K个节点的数据的平均值来填充缺失值, Shah等人通过链式方程(MICE)即迭代回归模型[24]来填充缺失值. 当缺失数据过多时, 数据间相关性较薄弱, 作为改进, García-Laencina等人提出最大期望算法(EM)[25], 尝试从不完全数据集中直接恢复出最大似然估计数据. 基于机器学习的数据插补方法无法学习数据的多维特征, 如忽略了数据的周期性和趋势性等多种固有特性.
目前提出的传统方法具有一定的局限性, 首先大多数方法通过对历史数据集进行训练形成预测模型, 当数据集缺失数据过多时, 数据间相关性较薄弱, 模型的建立过程中存在弊端; 其次传统方法受限于对数据分布和特征的假设, 难以处理复杂的网络环境变化和未知的干扰; 最后传统方法大多考虑数据的静态空间特征, 并不适用于具有动态特性的流量数据.
2)基于深度学习的数据修复方法
深度学习作为一种新型的、先进的数据驱动机器学习方法, 利用深度学习修复缺失数据及预测网络拥堵演化趋势等具有重要意义.
基于RNN的数据插补方法在时间序列数据处理中取得了较好的预测效果, 如Turabieh等人提出使用动态算法[26]训练RNN网络, 训练后的模型用于预测应用程序中的缺失值. Jeong等人通过双向循环神经网络模型(BRNN)[27]进行传感器数据重构, 该模型利用传感器数据之间的双向时间相关性来学习系统在积极(从过去到现在)和消极(从未来到现在)时间方向上的行为, 较单向的RNN模型效率较高. 基于RNN的数据修复模型通常假设数据集是连续的, 不能并行处理, 且很难直接建模具有不同时间戳的输入数据之间的相互依赖性.
GAN可通过迭代训练过程捕获不完整、异构数据的分布和潜在结构并估计缺失值, 且GAN是一种无监督学习方式, 具有直接生成样本的能力. Luo等人提出GAN-Z模型[28], 通过生成器与鉴别器的对抗训练将最佳噪声演化为完整的数据. 作为后续工作, Luo等人提出端到端生成对抗网络(E2GAN)[13], 该网络将缺失值部分用零值填充来避免“噪声”优化阶段, 同时编码器与解码器中采用GRU模块来提取数据之间的时间相关性, 具有直接修复缺失数据集的能力. 这类方法忽略数据的空间特征, 因此应用于流量数据的插补任务中具有一定的局限性.
近年来国内外学者利用CNN来处理数据变量之间的相关性. Li等人提出3DConvGAN模型[14]来解决交通数据缺失问题, 主要思想是利用三维卷积神经网络构建生成器和鉴别器以充分捕获交通数据的时空特征. Lei等人提出DCGAN模型[15], 生成器采用编-解码器体系结构来提取数据的时空特征并重构出完整数据; 鉴别器采用传统的CNN提取特征来区分真实或虚假信号. Yu等人提出了一种新的长短期上下文编码器模型(ILSCE)[29], 该模型是以CNN为内部结构的生成性对抗网络, 可以同时捕获空气质量数据集中的时空相关性和周期性变化, 并分层恢复缺失的空气质量值. 随着GCN的出现, 有学者利用GCN提取变量的相关性特征, 如Spinelli等人提出图插补神经网络模型(GINN)[17], 该模型使用GCN自编码器对数据空间特性进行建模, 并由GCN解码器重建估算数据. Le等人提出GCRINT模型[18]以处理网络流量缺失数据, 该模型使用双向LSTM和GCN来学习观测数据的时空相关性, 并估算网络流量数据的缺失值, 但是由于路由方案不断变化, 数据的空间特征具有动态特性, 上述模型均假设数据空间特征为静态形式, 因此无法充分学习数据的动态空间特征.
尽管国内外学者在数据输入方面做了很多努力, 但目前提出的基于深度学习的数据修复大多关注其时间特征, 未关注其空间特征, 而BRITS[12]等深度学习方法虽然考虑了流量的空间特征, 但仅限于静态空间相关性. 由于网络数据的动态性, 网络流量数据中变量之间的相关性随着时间显著变化, 数据存在动态空间特征, 因此如何将流量的动态空间特征与时间特征相结合是流量数据修复任务中需要解决的问题.
针对此问题, 本文提出了并行双通道时空数据修复模型(ST-MFCN), 模型使用双向LSTM和多尺度卷积模块分别学习时间特征和动态空间特征, 并且以双通道并行架构形式捕捉数据特征的细节信息来解决流量数据丢失问题. 此外本文借鉴GAN思想, 在回归损失函数的基础上引入了对抗性损失函数, 解决损失函数单一问题. 实验结果表明, 与现有方法相比, ST-MFCN在模拟网络流量分布方面效果明显的改善, 并能更准确地输入缺失值.
2 本文算法 2.1 问题描述数据的缺失值修复任务可以看作是一个矩阵补全任务. 本文使用矩阵
| X=(x0,⋯,xn−1)=[x00x10⋯xd−10x01x11⋯xd−11⋮⋮⋱⋮x0n−1x1n−1⋯xd−1n−1],X∈Rn×d |
该矩阵具体描述为分别在时间
| mji={0,ifxjiismissing1,otherwise | (1) |
时间序列的修复目标是尽可能正确地修复
针对网络流量数据的时间相关性和动态空间特性, 提出了一种并行双通道时空数据修复模型(ST-MFCN), 整体架构如图1所示.

|
图 1 ST-MFCN整体框架 |
ST-MFCN是BiLSTM和多尺度CNN的组合, 用于输入网络流量数据, 该模型可并行学习网络流量的时间特征与动态空间特征, 在空间和时间上分别实现对流量缺失数据的特征提取及预测修复. 具体而言, ST-MFCN有3个主要模块: 时间特征提取通道、空间特征提取通道和特征融合层. 时间特征提取通道通过BiLSTM学习数据中的时间特征, 空间特征提取通道采用多尺度卷积模块学习数据中动态空间特征, 特征融合层将时间特征与空间特征进行融合得到独特的时空特征. 传统的单向网络架构易受模型的参数影响, 需要大量时间匹配合适的模型参数, 造成数据特征细节信息丢失, 因此本文设计了时间特征提取通道和空间特征提取通道并行网络架构以减少模型参数间的影响和捕捉时间特征与空间特征细节信息, 下面将分别对各模块进行介绍.
2.2.1 时间特征提取通道网络流量数据作为时间序列数据, 时序之间存在较强相关性, 因此引入时间特征提取通道提取流量数据的时间特征, 如图2所示. 首先将缺失部分数据使用NAN值填充, 预得到完整的流量数据作为双向LSTM的输入并输出时间特征向量.

|
图 2 时间特征提取通道结构图 |
LSTM是RNN的一个分支, 通过在RNN中加入遗忘门、记忆门和输出门来处理输入的时间序列并解决长时间依赖问题, 传统LSTM结构如图3所示.

|
图 3 LSTM模块结构图 |
传统的LSTM按时间数据正序输入, 输出取决于之前时刻的时序信息. 由于相邻时间数据具有一定的相关性, 当前时刻的缺失数据不仅受前一刻时间的影响, 还与后续时刻的信息有关.
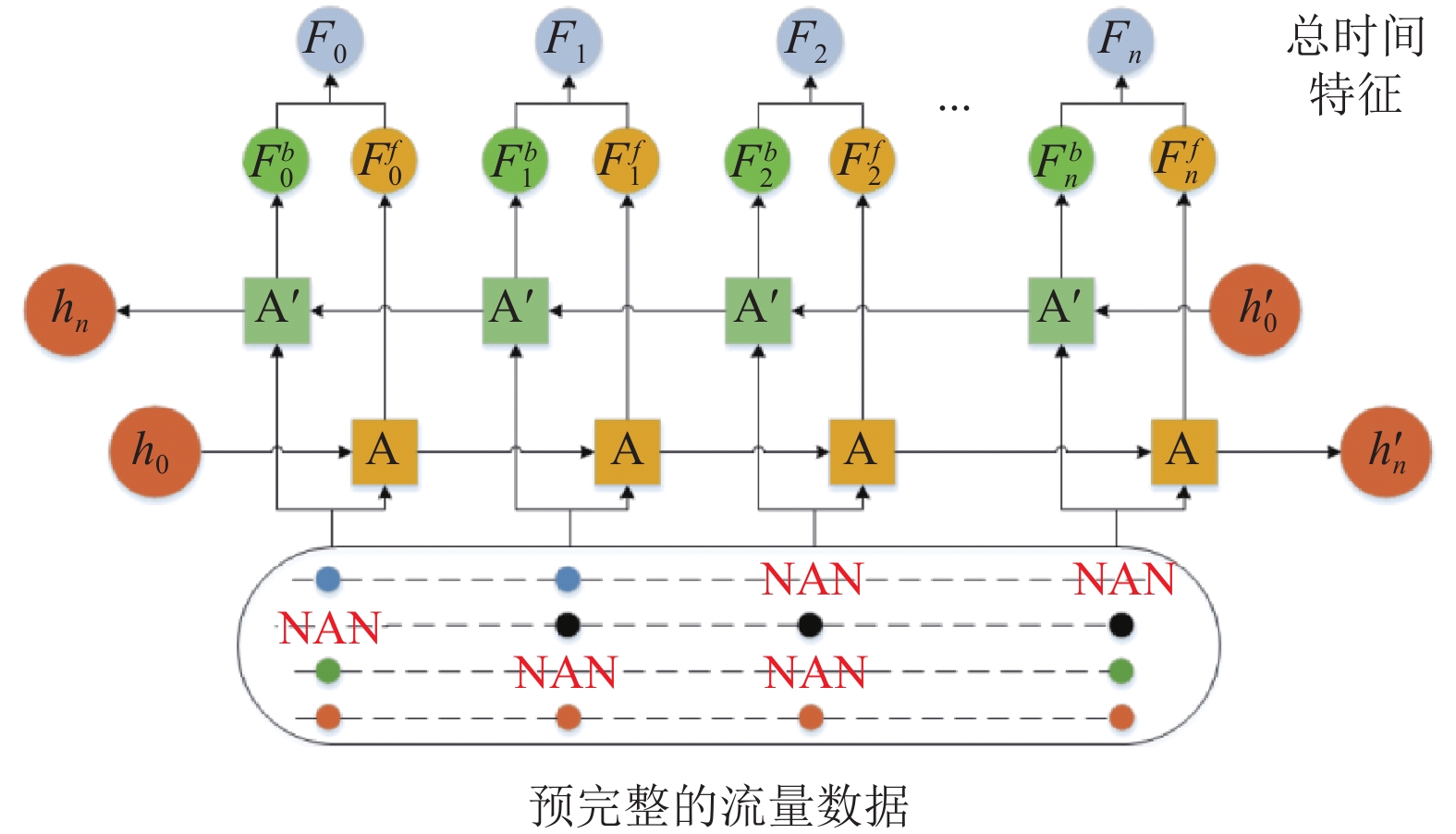
因此本文使用了双向LSTM数据特征提取模块, 通过对顺序和逆序数据的处理, 实现对数据历史时刻及未来时刻特征信息的提取, 结构如图4所示. 从图中可以看出, 该特征提取模块包含两个LSTM网络层, 其中
| Fft=LSTMf(X)Fbt=LSTMb(X) | (2) |
|
图 4 双向LSTM结构图 |
顺序特征和逆序特征经过权重参数的更新后即为总时间特征, 即
| Ft=w1Fft+w2Fbt | (3) |
其中,
数据不仅在时间上存在相关性, 不同类型的变量之间也存在相关性, 比如某网页中存在另一个网页的链接, 则两张网页的浏览量存在相关性. 此外, 由于路由方案的不同, 变量之间的相关性随之变化, 数据的空间特征具有动态特性, 因此本文设计多尺度卷积模块旨在从多个方面尽可能提取数据的空间特征, 如图5所示. 首先使用一组窗口大小为1的一维卷积核按变量顺序滑动并遍历所有时间段, 连接ReLU激活函数对序列进行初始特征提取; 其次利用多尺度卷积模块对初始特征进行处理得到多个特征图, 分别代表不同的空间特性, 多尺度卷积模块的如图6所示; 最后通过ReLU激活函数得到空间特征向量.

|
图 5 空间特征提取通道结构图 |
|
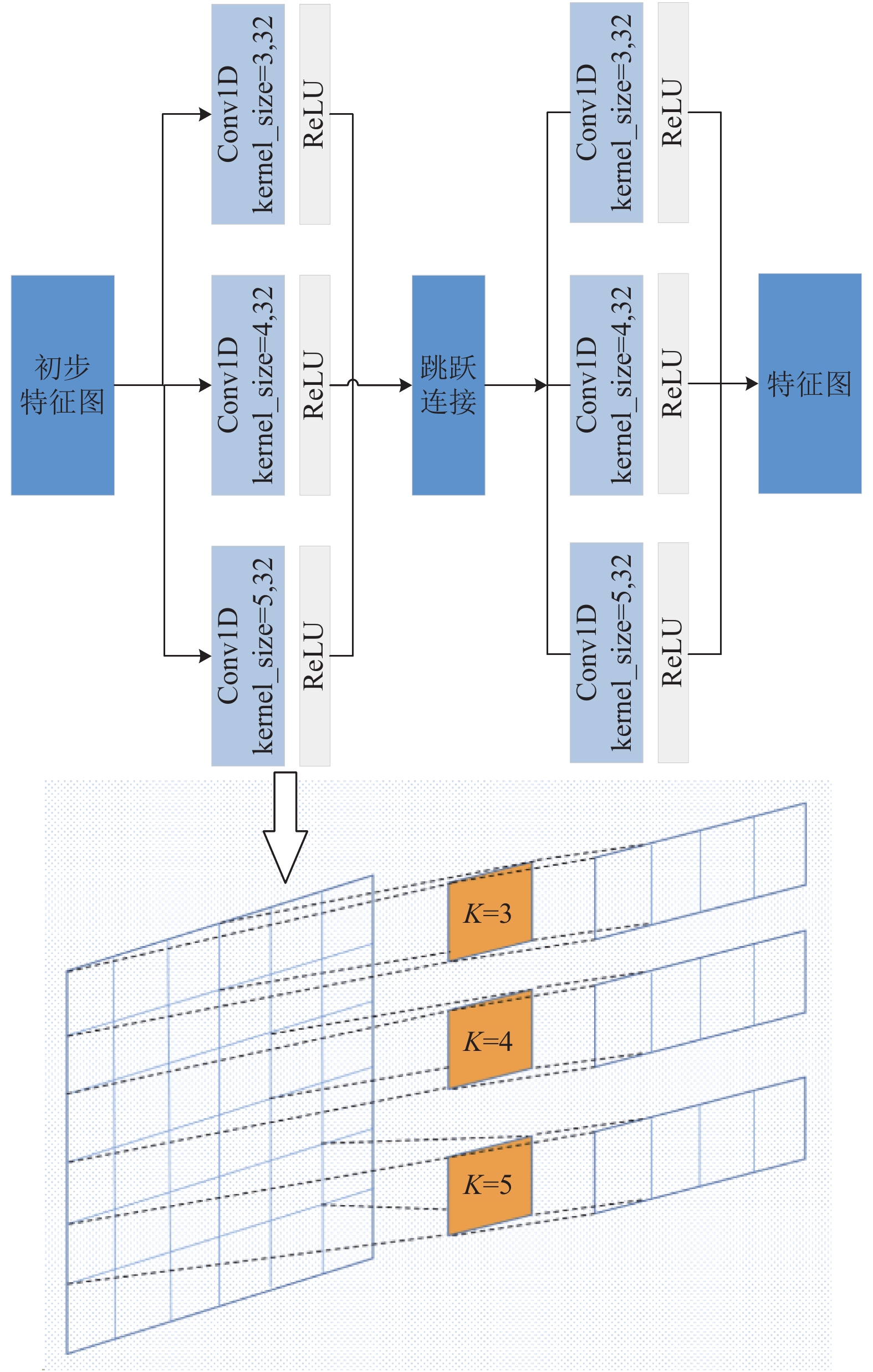
图 6 多尺度卷积模块结构图 |
从图6中可以看出, 模块中使用3个卷积分支构建一组扩张卷积层, 每个卷积分支采用长度分别为3、4、5的一维卷积核, 且每个分支使用32个卷积核. 同时设计了两组扩张卷积层增加网络的深度, 以提高数据预测的精度, 为防止梯度消失和梯度爆炸, 对于两组扩张卷积层采用跳跃连接的方式进行结合. 首先3个卷积分支中每个长度的一维卷积核在数据变量轴上从左向右以步数为1的方式遍历初步特征图并完成所有时间段的卷积运算, 输出变量轴方向上多个特征向量以表示不同的空间特征, 将提取到的多个特征向量分别在时间轴方向上进行拼接融合得到多个特征图, 即输出
| {Fi1=[f0i1,f1i1,f2i1,⋯,fd−1i1]Fi2=[f0i2,f1i2,f2i2,⋯,fd−1i2]Fi3=[f0i3,f1i3,f2i3,⋯,fd−1i3] | (4) |
其中,
| Fs=ReLU(Fi1, Fi2, Fi3) | (5) |
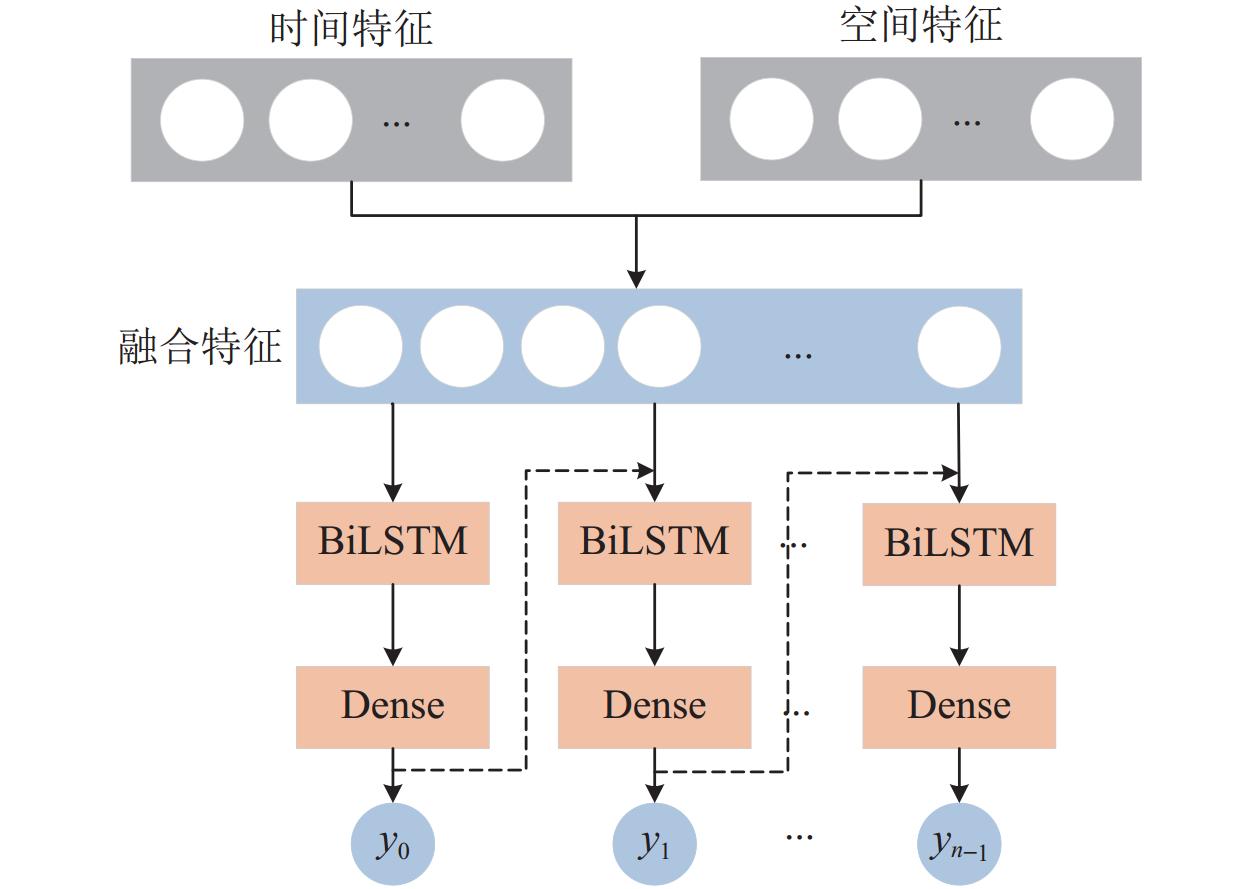
在数据生成阶段本文将时间特征提取通道提取到的时间特征
| Ffusion=Ft+Fs | (6) |
|
图 7 数据生成阶段细节图 |
同时, 采用双向LSTM模块对融合特征进行处理, 并在每个双向LSTM模块后连接一层全连接模块, 上一个Dense模块输出值将与融合特征共同作为下一个双向LSTM模块的输入值, 经过完整的数据生成过程得到输出数据
| Y=Dense(BiLSTM(Ffusion)) | (7) |
同时, 对于待修复的网络流量数据
| ˉX=X⊙M+Y⊙(1−M) | (8) |
在损失函数的设计过程中, 本文做出了改进: 数据修复模型中常用
GAN通常包含生成器与鉴别器两部分, 生成器学习从潜在空间到数据空间的映射, 鉴别器学习从数据空间到实值空间的映射, 实值空间表示鉴别器输入为真实数据的概率. GAN通过生成器与鉴别器的博弈游戏进行学习, 鉴别器同时接受生成器的输出和基础真实值, 并将它们区分, 生成器试图通过产生尽可能真实的数据来混淆鉴别器. 通过优化以下损失函数, 可以联合训练鉴别器和生成器:
| minGmaxDEx∈X[log(D(x))]+Ez∈Z[log(1−D(G(z)))] | (9) |
其中,
本文将并行双通道时空数据修复模型作为生成器的内部结构, 同时将网络流量修复模型中的并行特征提取通道连接Dense层与Sigmoid函数作为鉴别器的内部结构, 通过促进生成器尽可能生成真实数据, 鉴别器尽可能将假数据判断为真数据的对抗性训练设计对抗性损失函数, 整体结构如图8所示.
具体而言, 将输入的真实数据
| minGmaxDExi∈X[log(D(xi))]+Exi∈X[1−log(D(G(xi)))] | (10) |

|
图 8 对抗训练损失函数设计框架 |
对于基本的预测模型而言, 通常采取回归损失来收敛模型, 即均方误差, 该损失函数定义为:
| LMSE=1n∑n−1i=0(yi⊙mi−xi⊙mi)2 | (11) |
其中, n表示数据长度,
| L=λLMSE + (1−λ)Ladv | (12) |
其中,
通过损失函数权重的训练加快模型的收敛, 得到最优化模型, 有助于捕捉总体趋势, 解决单一
本文实验的主机配置: 操作系统为64位Windows 10操作系统, CPU为Intel core i7-9700H/3.00 GHz, 32 GB内存, 开发环境为Python 3.7.0, 所有实验均使用TensorFlow完成. 本文使用回归损失函数与对抗性损失函数的组合来衡量模型的性能, 模型具体参数如表1所示. 随机抽取88%的数据作为训练数据, 6%作为验证数据, 6%为测试数据. batch大小设置为64, 学习速率为0.0001, 训练回合数约为1 epoch. 由于神经网络经常会被过度训练, 因此对训练后的模型进行验证测试至关重要.
| 表 1 模型参数 |
3.2 实验数据集
本文采用2017年由谷歌主办的Kaggle维基百科网络流量时间序列预测数据集, 该训练数据集由大约145000个时间序列组成. 2015年7月1日–2016年12月31日, 每个时间序列代表不同维基百科文章的每日浏览量. 对于每个时间序列, 都会提供文章的名称以及该时间序列所代表的流量类型(all、mobile、desktop、spider). 每个页面和日期组合都有一个较短的ID. 页面名称和提交ID之间的映射在关键文件中给出. 该数据集格式如图9所示(来自Kaggle竞赛平台Web traffic time series预测数据集介绍界面), 纵坐标为网页类型名称, 横坐标为具体时间.

|
图 9 部分数据集 |
3.3 数据预处理
数据预处理包括缺失值设置、数据转化与数据裁剪, 本文采用的数据来源于公开数据集Web traffic time series中第2阶段的训练数据, 样本数据集为CSV格式的文件. 具体数据处理步骤如下.
1)缺失值设置: 数据缺失主要分为3种类型: 随机丢失、不完全随机丢失、有关联性丢失, 根据网络情景, 本文设计随机丢失模式, 并根据丢失率设计掩码矩阵, 0值代表丢失, 1值代表未丢失.
2)数据转换: 由于原始输入数据中的缺少数据以空白形式展现, 因此需要将网络流量数据集转换为标准格式, 网络流量数据集中存在零值, 因此采用–0.1值填充缺失部分, 保持数据集的整体趋势, 同时将数据集转变为一个三维张量, 作为ST-MFCN模型的输入.
3)数据整合: 网络页面浏览量以不同语言的形式展示, 并且每个页面都有不同的趋势, 因此语言将会对浏览量造成一定的影响, 因此添加语言变量对数据进行整合; 其次, 网络流量数据存在季节性规律, 即每季度、每年都存在重复趋势, 因此在数据中添加两个滞后变量与将重复趋势去除, 以此方法来缩短数据集的大小.
3.4 评价标准本文使用均方根误差(RMSE)和平均绝对误差(MAE)两个评价指标来衡量模型的数据修复能力. RMSE表示预测值和观测值之间差异(称为残差)的样本标准差, 而MAE表示预测值和观测值之间绝对误差的平均值. RMSE与MAE的公式分别为:
| RMSE = √1nn∑i=1(xi−yi)2 | (13) |
| MAE = 1nn∑i=1|xi−yi| | (14) |
其中,
为验证ST-MFCN模型在流量数据修复任务上的性能, 本文在Web traffic time series数据集上进行了3组实验. 第3.5.1节中为不同丢失率情况下ST-MFCN模型与LTC[8]、NTC[16]、BRITS[12]、GCRINT[18]模型的MAE值比较; 第3.5.2节为本模型的消融实验, 分析时间特征提取通道、空间特征提取通道和对抗性损失函数引入的合理性.
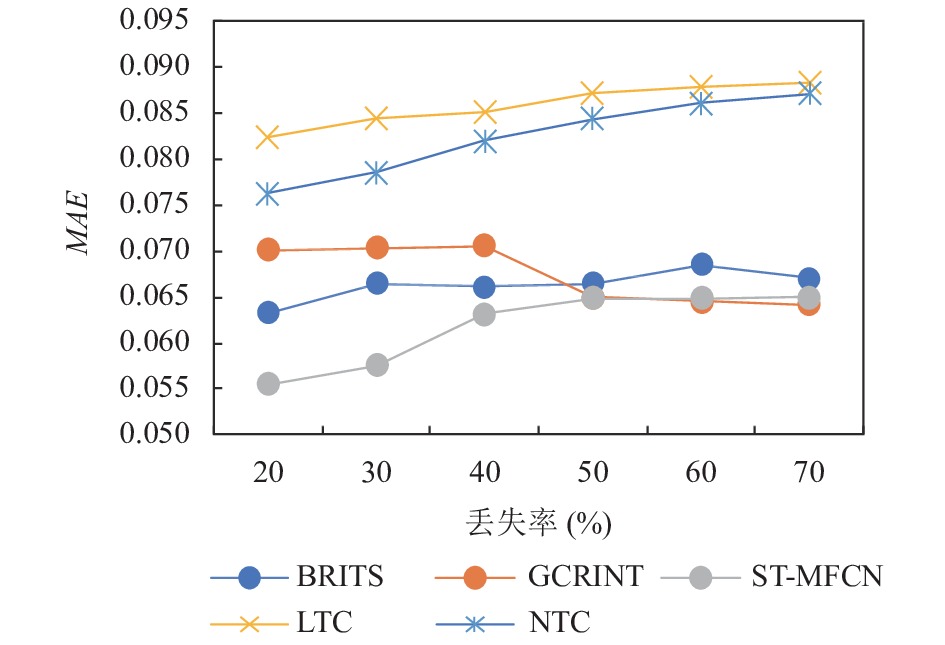
3.5.1 预测性能比较本文根据20%–70%缺失比率将缺失值引入数据集比较不同丢失率下LTC、NTC、BRITS、GCRINT与ST-MFCN模型的性能, 指标为MAE, 越低越好,
| 表 2 数据集上5种方法的性能比较 |
|
图 10 不同丢失率对应模型性能对比 |
总体而言, BRITS、GCRINT和ST-MFCN在网络流量插补问题上优于基于张量分解的方法, 其中ST-MFCN模型在所有模型中都展现了优质性能. 从图10可以看出, 当丢失率处于20%、30%、40%时, ST-MFCN模型修复后的MAE值始终处于其他4种模型之下, 与LTC和NTC相比, ST-MFCN可降低33%左右的MAE值, 说明深度学习模型相对于传统张量分解算法更能捕捉数据的趋势, 与 BRITS、GCRINT相比, ST-MFCN模型在低数据丢失率下具有较好的数据修复性能, 且验证了双通道网络架构和动态空间特征提取的优越性; 当数据丢失率在50%–70%时, LTC与NTC模型的MAE值有接近趋势, MAE值仍处于ST-MFCN上方. ST-MFCN与GCRINT模型接近, 比BRITS模型低, 且随着丢失率的上升, ST-MFCN模型的MAE值逐渐上升, 预测效果逐渐变差, 因此该模型在高丢失率情况下, 性能效果不显著, 但是调查发现[30], 高丢失率情况较少.
综合以上实验结果可以看出, 本文的数据修复模型相较于其他模型具有优越性, 相较于基于张量分解的模型, 深度学习方法具有较大优势. 以下将选取丢失率为20%时的基于深度学习的模型(BRITS、GCRINT和ST-MFCN)处理效果进行比较, 3个模型中某一段网络流量数据的修复效果如图11(a)–图11(c)所示, 其中绿色为真实数据, 红色为修复数据. 通过对3个模型修复效果进行比较, 发现在丢失率为20%的情况下, 本文的ST-MFCN模型相对于其他两个模型而言修复数据更贴合真实数据的变化趋势.

|
图 11 3种模型修复效果 |
3.5.2 消融实验
本节通过3个实验来探讨ST-MFCN模型设计的合理性, 第1个实验是验证时间特征提取通道的合理性; 第2个实验是验证空间特征提取通道的合理性; 第3个实验是验证对抗性损失函数引用的合理性, 并且每个实验都将丢失率设置为20%,
表3通过比较ST-MFCN和(w/o) BiLSTM的RMSE与MAE值验证时间特征提取通道的合理性, 其中(w/o) BiLSTM表示未采用时间特征提取通道, 且实验结果表示ST-MFCN优于(w/o) BiLSTM, 这表明时间特征提取通道提高了模型的修复能力. 表4对ST-MFCN和(w/o) MFCN进行了比较, (w/o) MFCN表示未采用空间特征提取通道, ST-MFCN的 RMSE与MAE值略低于(w/o) MFCN, 因此引入空间特征提取通道比传统的LSTM时间序列建模方法具有更好的修复性能. 同样, 表5对ST-MFCN、
| 表 3 时间特征提取通道消融实验结果 |
| 表 4 空间特征提取通道消融实验结果 |
| 表 5 对抗性损失函数消融实验结果 |
4 结论与展望
流量数据具有时间特性和复杂的动态空间特性, 造成现有的数据修复方法具有局限性, 本文提出了一种并行双通道时空数据修复模型, 采用双向长短期记忆网络与多尺度卷积网络分别提取数据的时间特征和动态空间特征, 并且时空特征提取通道为双通道架构以充分捕捉特征的细节信息, 本文在原有的损失函数基础上添加对抗性损失函数以提高模型预测的精度, 最终实现流量数据的修复. 在Web traffic time series数据集上进行实验, 实验结果表明, ST-MFCN能够有效地减少数据恢复的误差, 提升了数据修复的精确度. 但是当数据处于高丢失状态时, 模型的修复效果并不理想, 如何高效利用流量数据的时空特性, 改善网络架构, 实现高丢失率下数据的有效修复是后续需要探究的问题.
| [1] |
Xiao S, Yan JC, Farajtabar M, et al. Learning time series associated event sequences with recurrent point process networks. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(10): 3124-3136. DOI:10.1109/TNNLS.2018.2889776 |
| [2] |
Roughan M, Thorup M, Zhang Y. Traffic engineering with estimated traffic matrices. Proceedings of the 3rd ACM SIGCOMM Conference on Internet Measurement. Miami Beach: ACM, 2003. 248–258.
|
| [3] |
邓华伟, 李喜旺. 基于深度学习的网络流量异常识别与检测. 计算机系统应用, 2023, 32(2): 274-280. DOI:10.15888/j.cnki.csa.008989 |
| [4] |
刘春. 基于PSO-LSSVM的网络流量预测模型. 计算机系统应用, 2014, 23(10): 147-151. DOI:10.3969/j.issn.1003-3254.2014.10.025 |
| [5] |
Janacek G. Time series analysis forecasting and control. Journal of Time Series Analysis, 2010, 31(4): 303. |
| [6] |
Zhang GP. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing, 2003, 50: 159-175. DOI:10.1016/S0925-2312(01)00702-0 |
| [7] |
Zhang SC. Nearest neighbor selection for iteratively kNN imputation. Journal of Systems and Software, 2012, 85(11): 2541-2552. DOI:10.1016/j.jss.2012.05.073 |
| [8] |
Xie K, Wang XG, Wang X, et al. Accurate recovery of missing network measurement data with localized tensor completion. IEEE/ACM Transactions on Networking, 2019, 27(6): 2222-2235. DOI:10.1109/TNET.2019.2940147 |
| [9] |
Hong D, Kolda TG, Duersch JA. Generalized canonical polyadic tensor decomposition. SIAM Review, 2020, 61(1): 133-163. |
| [10] |
Bengio Y, Gingras F. Recurrent neural networks for missing or asynchronous data. Proceedings of the 8th International Conference on Neural Information Processing Systems. Denver: MIT Press, 1995. 395–401.
|
| [11] |
Che ZP, Purushotham S, Cho K, et al. Recurrent neural networks for multivariate time series with missing values. Scientific Reports, 2018, 8(1): 6085. DOI:10.1038/s41598-018-24271-9 |
| [12] |
Cao W, Wang D, Li J, et al. BRITS: Bidirectional recurrent imputation for time series. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 6776–6786.
|
| [13] |
Luo YH, Zhang Y, Cai XR, et al. E2GAN: End-to-end generative adversarial network for multivariate time series imputation. Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI.org, 2019. 3094–3100.
|
| [14] |
Li ZM, Zheng HF, Feng XX. 3D convolutional generative adversarial networks for missing traffic data completion. Proceedings of the 10th International Conference on Wireless Communications and Signal Processing. Hangzhou: IEEE, 2018. 1–6.
|
| [15] |
Lei XM, Sun LM, Xia Y. Lost data reconstruction for structural health monitoring using deep convolutional generative adversarial networks. Structural Health Monitoring, 2021, 20(4): 2069-2087. DOI:10.1177/1475921720959226 |
| [16] |
Xie K, Lu HL, Wang X, et al. Neural tensor completion for accurate network monitoring. Proceedings of the 2020 IEEE Conference on Computer Communications. Toronto: IEEE, 2020. 1688–1697.
|
| [17] |
Spinelli I, Scardapane S, Uncini A. Missing data imputation with adversarially-trained graph convolutional networks. Neural Networks, 2020, 129: 249-260. DOI:10.1016/j.neunet.2020.06.005 |
| [18] |
Le VA, Le TT, Le Nguyen P, et al. GCRINT: Network traffic imputation using graph convolutional recurrent neural network. Proceedings of the 2021 IEEE International Conference on Communications. Montreal: IEEE, 2021. 1–6.
|
| [19] |
吴敏忠, 王雷, 盛捷. 融合多特征与时间序列的人群行为识别模型. 计算机系统应用, 2022, 31(11): 268-274. DOI:10.15888/j.cnki.csa.008788 |
| [20] |
Mehrotra DV, Liu F, Permutt T. Missing data in clinical trials: Control-based mean imputation and sensitivity analysis. Pharmaceutical Statistics, 2017, 16(5): 378-392. DOI:10.1002/pst.1817 |
| [21] |
Srebotnjak T, Carr G, de Sherbinin A, et al. A global water quality index and hot-deck imputation of missing data. Ecological Indicators, 2012, 17: 108-119. DOI:10.1016/j.ecolind.2011.04.023 |
| [22] |
Zhuang YF, Ke RM, Wang YH. Innovative method for traffic data imputation based on convolutional neural network. IET Intelligent Transport Systems, 2019, 13(4): 605-613. DOI:10.1049/iet-its.2018.5114 |
| [23] |
Poulos J, Valle R. Missing data imputation for supervised learning. Applied Artificial Intelligence, 2018, 32(2): 186-196. DOI:10.1080/08839514.2018.1448143 |
| [24] |
Shah AD, Bartlett JW, Carpenter J, et al. Comparison of random forest and parametric imputation models for imputing missing data using MICE: A CALIBER study. American Journal of Epidemiology, 2014, 179(6): 764-774. DOI:10.1093/aje/kwt312 |
| [25] |
García-Laencina PJ, Sancho-Gómez JL, Figueiras-Vidal AR. Pattern classification with missing data: A review. Neural Computing and Applications, 2010, 19(2): 263-282. DOI:10.1007/s00521-009-0295-6 |
| [26] |
Turabieh H, Abu Salem A, Abu-El-rub N. Dynamic L-RNN recovery of missing data in IoMT applications. Future Generation Computer Systems, 2018, 89: 575-583. DOI:10.1016/j.future.2018.07.006 |
| [27] |
Jeong S, Ferguson M, Hou R, et al. Sensor data reconstruction using bidirectional recurrent neural network with application to bridge monitoring. Advanced Engineering Informatics, 2019, 42: 100991. DOI:10.1016/j.aei.2019.100991 |
| [28] |
Luo YH, Cai XR, Zhang Y, et al. Multivariate time series imputation with generative adversarial networks. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 1603–1614.
|
| [29] |
Yu YW, Li VOK, Lam JCK. Missing air pollution data recovery based on long-short term context encoder. IEEE Transactions on Big Data, 2022, 8(3): 711-722. DOI:10.1109/TBDATA.2020.2979443 |
| [30] |
Sowmya V, Kayarvizhy N. An efficient missing data imputation model on numerical data. Proceedings of the 2nd Global Conference for Advancement in Technology. Bangalore: IEEE, 2021. 1–8.
|
 2024, Vol. 33
2024, Vol. 33



