随着天然气的普及, 各大燃气公司逐步推进燃气资源的智能化管理. 为实现提前规划未来燃气用量, 优化决策方案, 降低运营成本的目的, 准确地预测未来燃气数据的用量成为国内外学者的研究热点. 近年来, 受新型冠状病毒以及油价波动的影响, 全世界的天然气产量下降. 2022年上半年, 国内天然气总供应量较历史同期减少了29亿立方米^[1]. 作为有限的清洁能源, 准确地预测未来燃气消耗, 对可持续发展有着重要的意义.

伴随深度学习模型的发展, Rumelhart等人^[2]提出了专门处理时间序列任务的循环神经网络(recurrent neural network, RNN)模型, 但传统RNN网络会出现梯度消失问题且无法处理数据中的长期依赖, 随后, Hochreiter等人^[3]提出长短期记忆网络(long short-term memory network, LSTM), 解决RNN存在的梯度消失问题, 同时能够较好地处理数据中的短期依赖与长期依赖. 由此, LSTM网络被广泛应用于时间序列预测任务中.

为进一步提高RNN类网络在机器翻译中的性能, Cho等人^[4]提出Encoder-Decoder架构, 该架构使用两个RNN类网络分别作为Encoder与Decoder, 输入数据通过Encoder编码成一个固定长度的上下文向量, Decoder依据该向量进行解码输出. 由于所有信息都是压缩到一个定长向量中, 当面对长输入数据时, 就会出现信息丢失问题, 模型表现性能迅速下降. 于是, Bahdanau等人^[5]提出基于注意力机制的Encoder-Decoder模型. 通过注意力机制筛选最重要的信息, 由此构成定长的上下文向量, 尽可能降低信息丢失带来的影响. 以提高模型的泛化能力. 随着注意力模型的成功, 在时间序列预测领域中也有通过注意力机制来提升模型预测效果. 例如, Qin等人^[6]提出基于双注意力机制模型, 通过特征注意力机制来选择最相关的特征数据, 利用时间注意力模块获取最相关的隐藏状态信息. Cui等人^[7]利用自注意力机制来提升模型的短期预测能力. 苏雅茜等人^[8]通过自注意力模块计算不同历史时间点上的数据权重信息来提高传统移动平均算法的预测能力. Li等人^[9]提出区域注意力机制, 通过合并相邻向量的方式来建模不同粒度的依赖. Sehovac等人^[10]利用注意力机制来提升Seq2Seq模型对电力负荷的预测精度. Yuan等人^[11]提出时空注意力机制来计算不同输入特征的重要程度与Encoder隐藏层输出中最相关的状态. Huang等人^[12]设计全局注意力机制与局部注意力机制来处理动态周期数据中的全局时间依赖与局部时间依赖. Du等人^[13]结合传统上下文向量与注意力向量设计注意力模块, 用于处理数据中长期依赖与隐藏特征.

然而, 传统注意力模型计算注意力权重的过程中, 每个资源通常是独立看待的, 不适用于燃气预测任务——通常燃气负载数据在时间维度上存在着多种时间依赖. 直接使用机器翻译领域中的注意力模型可能会导致时间依赖的丢失. 虽然, Li等人^[9]提出的区域注意力机制能够考虑不同的计算粒度, 但每次合并的相邻向量是固定的. 不适用于高频率突变的燃气负荷数据. 同时, 在采用基于注意力机制模型进行时间序列预测时, Decoder是平等地看待每一份输入的历史数据, 由于燃气负荷数据在短期内存在的随机突变性, 距离预测日期越近的历史燃气负载数据应该提供更多预测依据.

为解决上述提及的问题, 本文提出多维注意力机制Seq2Seq模型(multi-dimensional attention Seq2Seq, MA-Seq2Seq), 采用LSTM构建Encoder与Decoder. 基于区域注意力, 设计自适应合并步长计算. 提出多层次时间注意力模块, 从全局出发, 筛选Encoder编码信息中不同维度的时间依赖, 生成包含多维时间模式信息的上下文向量. 同时, 为解决模型无法关注重要历史信息的缺陷, 设计局部历史注意力模块, 依据短期依赖信息, 生成携带关注信息的历史数据, 最后Decoder依据多维时间上下文向量与携带专注信息的输入数据进行预测输出. 最终, 本文使用中国某市区的日燃气消耗数据与2016年电工数学建模竞赛A题的电力负荷数据来验证本文模型的有效性.

1 研究方法 1.1 符号定义

由于燃气负荷预测本质就是时间序列预测任务, 因此, 本文中时间序列数据, 历史数据, 燃气数据等都代指历史燃气负荷数据. 设定时间序列数据采集的间隔为每天, 则对于n天的历史数据表示为$ Y = ({y_1}, {y_2}, \cdots , {y_n}) $, 其中, ${y_t} \in R$. 相关特征数据表示为$X = ({x_1}, {x_2}, \cdots , {x_n})$, 其中, $X \in {R^{n \times m}}$, ${x_t} \in {R^{m \times 1}}$, m表示每次采样时特征数据的个数. Encoder产生的隐藏层输出表示为${h_i}$, $i \in [1, T]$, T表示输出窗口大小. 设上一时刻Encoder产生的隐藏状态为${h_{i - 1}}$, 上一时刻Decoder产生的隐藏状态为${d_{t - 1}}$, 长期状态为${c_{t - 1}}$. Encoder与Decoder的隐藏层维度设置为r.

1.2 注意力机制

注意力机制概念的起源是模拟人类对信息的认知过程——是一个在众多信息中检索重要信息的过程. 2016年, Bahdanau等人^[5]首次提出注意力模型来解决Encoder-Decoder模型在面对长输入数据时表现性能下降过快的问题——Encoder会将所有的输入数据都压缩到一个固定长度的上下文向量中, 输入数据过多时就会导致信息丢失. 而注意力模块会选择最为重要的信息来生成上下文向量, 从而尽可能地避免了信息丢失带来的影响. 该模型的成功让后续学者开发出不同版本的注意力模型. 但整体上, 注意力模型是利用对齐函数与分布函数进行数据查询的过程^[14–16].

注意力模型中, 通常会涉及3个表示向量, q, K, V, 其中, q通常代表信息检索的依据, 一般是与模型任务相关的数据向量, 例如, 上一时间步骤中Decoder的隐藏状态. K表示查询内容, 一般代表输入数据, 通常由多个向量组成. V是与K相互对应的数据矩阵, 可以是同一份数据, 也可以同一份数据经过不同处理得到K与V. 信息检索过程通过对齐函数实现——用于计算q与K中每个向量的初始相似程度, 或者能量权重. 将能量权重通过分布函数后便可得到注意力权重, 表示K中每个向量的重要程度. 分布函数通常用来将能量权重转化成注意力权重, 较为常见的分布函数是logistic Sigmoid与Softmax函数, 这两种函数能够确保所得到的注意力权重之和为1. 这样就可以将注意力权重的含义解释为重要程度的百分占比.

1.3 多层次时间注意力

在传统的注意力模型中, 通过对齐函数获取q与K之间的初始权重的过程是一个相互独立的过程, 即将K中的每个向量视作独立的个体与q进行权重计算, 而在时间序列任务, 采样数据之间是存在着一定的相关性的. 以独立计算方式生成的上下文向量, 可能会导致信息的丢失. 由此, 本文提出多层次注意力模块, 在全局上, 以既联合又独立的方式构建上下文向量. 先用传统的注意力计算方式获取一份上下文向量, 同时, 对同一份K, V矩阵内的数据进行自适应步长的相邻向量融合处理: 利用算法1遍历矩阵, 每次循环计算当前向量与后续向量间的相似度, 将相似度大于设定阈值的相邻向量与当前向量合并, 形成新K, V矩阵, 随后在新矩阵上进行注意力计算得到另一份上下文向量. 最后通过一层全连接网络融合两个上下文向量. 模型结构如图1所示.

算法1. 自适应合并粒度算法

$\scriptstyle \overline K $=[]

FOR i IN len(K)

　S = Similar($\scriptstyle {k_i}$, K[i:])

　$\scriptstyle {k_{sum}} = {k_i}$; inner=0

　FOR j IN len(S)

　　IF (S[j]$ \scriptstyle \geqslant \lambda $)

　　　$\scriptstyle {k_{sum}} + = {k_{i + j}}$; inner+=1

　　ELSE BREAK

　　END IF

　END FOR

　$\scriptstyle \overline K $.append($\scriptstyle {k_{sum}}$/(inner+1))

　IF (inner+1 == len(S))

　　 BREAK

　END IF

END FOR

在构建传统的单步注意力上下文向量的同时, 并行构建多步注意力上下文向量. 图1中, values矩阵与keys矩阵通常由Encoder产生的隐藏层输出${h_i}$构成. 为了更好地训练模型, 减少同一份数据的多次使用^[17], 对隐藏状态分别进行残差转换与非线性映射. 变换方式如下:

$ {k_i} = {W_k}{h_i} + {h_i},\; 1 \leqslant i \leqslant T $

(1)

$ {v_i} = {W_v}{h_i},\; 1 \leqslant i \leqslant T $

(2)

其中, ${W_k}$, ${W_v} \in {R^{r \times r}}$为可学习参数. ${h_i} \in {R^{r \times 1}}$.

图1中并行执行的两个注意力模块都使用全局依赖作为查询依据, 本文通过上一时间步骤中Decoder产生的隐藏状态${d_{t - 1}}$与长期状态${c_{t - 1}}$来构建与任务相关的全局依赖. 构建方式如下:

$ q = \frac{{{W_q}({d_{t - 1}} + {c_{t - 1}})}}{2} + \frac{{{d_{t - 1}} + {c_{t - 1}}}}{2} $

(3)

其中, ${W_q} \in {R^{r \times r}}$为可学习参数. ${d_{t - 1}}$, ${c_{t - 1}} \in {R^{r \times 1}}$.

在单步时间注意力中, 采用传统的注意力计算方式, 独立计算q与${k_i}$的相似度. 计算过程如下:

$ {e_i} = q{k_i},\; 1 \leqslant i \leqslant T $

(4)

$ {a_i} = \frac{{{\text{exp(}}{e_i}{\text{)}}}}{{\displaystyle\sum\nolimits_{j = 1}^T {\exp ({e_j})} }}, \;1 \leqslant i \leqslant T $

(5)

$ {c_1} = \sum\nolimits_{i = 1}^T {{a_i}} {v_i} $

(6)

其中, ${e_i}$代表初始权重, 即能量权重, ${a_i}$代表注意力权重. 使用的分布函数为Softmax. 上下文向量${c_1}$通过注意力权重与相应的value值进行加权求和得出.

在计算多步时间注意力模块中, 为让values矩阵与keys矩阵中包含不同步长的时间模式信息, 对两个矩阵分别进行自适应步长转化. 如图1所示. 对原矩阵中的数据进行遍历, 自适应的选择合并相邻向量的个数. 当某次合并中, 选择了后续所有向量, 则提前结束循环. 自适应选择是通过相似度算法与阈值配合实现, 当相邻向量的相似度超过阈值时, 则认为两者具有同一维度的时间模式需要进行合并. 最终, 新key值是通过对合并后的向量进行平均获得, 对应的value值则直接使用和向量. 获取新keys矩阵的算法过程如算法1.

算法1中, K表示原始的keys矩阵. Similar()为相似度算法, 用于计算当前key值与后续key值是否处于同一维度的时间模式, 本文采用余弦相似度配合Softmax函数的方式获取相似程度, $\lambda $为设定的阈值, 用于控制合并数量. 新values矩阵的计算过程同keys矩阵. 随后在新的keys矩阵与values矩阵上进行注意力计算, 方式如下:

$ \overline {{e_i}} = q\overline {{k_i}} ,\; 1 \leqslant i \leqslant \overline T $

(7)

$ \overline {{a_i}} = \frac{{\exp (\overline {{e_i}} )}}{{\displaystyle\sum\nolimits_{j = 1}^{\overline T } {\exp (\overline {{e_j}} )} }},\; 1 \leqslant i \leqslant \overline T $

(8)

$ {c_2} = \sum\nolimits_{i = 1}^{\overline T } {\overline {{a_i}} } \overline {{v_i}} $

(9)

其中, $\overline T $表示新矩阵中向量元素的个数. $\overline {{k_i}} $, $\overline {{v_i}} $分别表示新keys矩阵与新values矩阵中的元素. ${c_2}$为包含多维时间模式的上下文向量.

最终合并两个上下文向量${c_1}$与${c_2}$, 确保最终的上下文向量同时包含单步时间信息与多步时间信息, 合并方式如下:

$ c = \tanh ({W_1}{c_1} + {W_2}{c_2}) $

(10)

其中, ${W_1}$, ${W_2} \in {R^{r \times r}}$为可学习参数. 将该上下文向量代替Encoder原本的隐藏状态向后传递.

在燃气负荷预测中, 受大量外部因素影响, 数据特征存在着复杂的时间模式依赖, 提高了模型预测难度. 通过多层次时间注意力机制来提取不同时间模式特征, 以此优化模型对数据信息的捕捉能力.

1.4 局部历史注意力

在传统的注意力模型当中, 注意力机制模块通常只用来解决在长序列输入中信息丢失的问题, 在时间序列预测任务中, 该部分信息通常为特征数据的信息, 而对应的历史数据$ y = ({y_1}, {y_2}, \cdots , {y_T}) $是直接输入Decoder模块, 此时, Decoder在解码预测过程中会平等地看待所有历史数据, 而实际上, 与预测日期越接近的历史数据及与预测日期处于相同位置的数据所提供的信息更具有参考性. 由此引入局部历史注意力模块, 该模块建立在多层次注意力基础之上, 同时考虑近期特征数据与历史数据的情况下生成加权后的历史数据$\overline y $.

$ {e_i} = {W_q}{d_{t - 1}}\tanh ({W_k}{h_{t - 1}} + {W_h}[{h_i};{y_i}]),\; 1 \leqslant i \leqslant T $

(11)

$ {a_i} = \frac{{\exp ({e_i})}}{{\displaystyle\sum\nolimits_{j = 1}^T {\exp ({e_j})} }},\; 1 \leqslant i \leqslant T $

(12)

其中, ${W_k} \in {R^{r \times r}}$, ${W_h} \in {R^{r \times (r + 1)}}$为可学习参数, [;] 表示拼接操作. ${h_{t - 1}}$为上一时间步骤中Encoder隐藏状态, 通常为最后一个隐藏层输出或上下文向量. 通过短期特征记忆与当前隐藏层输出和历史数据建立短期变化信息, 在变化信息中查询重要程度较高的历史天数. 最终, 生成携带关注信息的历史数据$\overline y = ({a_1}{y_1}, {a_2}{y_2}, \cdots , {a_T}{y_T})$.

在燃气负荷预测过程中, 历史数据在短期内存在随机突变情况, 这使得一般的注意模型难以在一系列无规律变化中提取有效信息, 同时注意到哪些变化是重要, 哪些变化不那么重要. 通过局部历史注意力模块对数据的处理, 对Decoder输入窗口中的每份历史负荷数据计算出一个注意力权重, 注意力权重和为1, 对于预测有重要影响的历史负荷数据将分配更大的权重值, 从而通过 Decoder 计算时能够保留更多信息, 使模型能够察觉哪些变化是重要的, 哪些是可以忽视的, 更好应对数据中的随机事件.

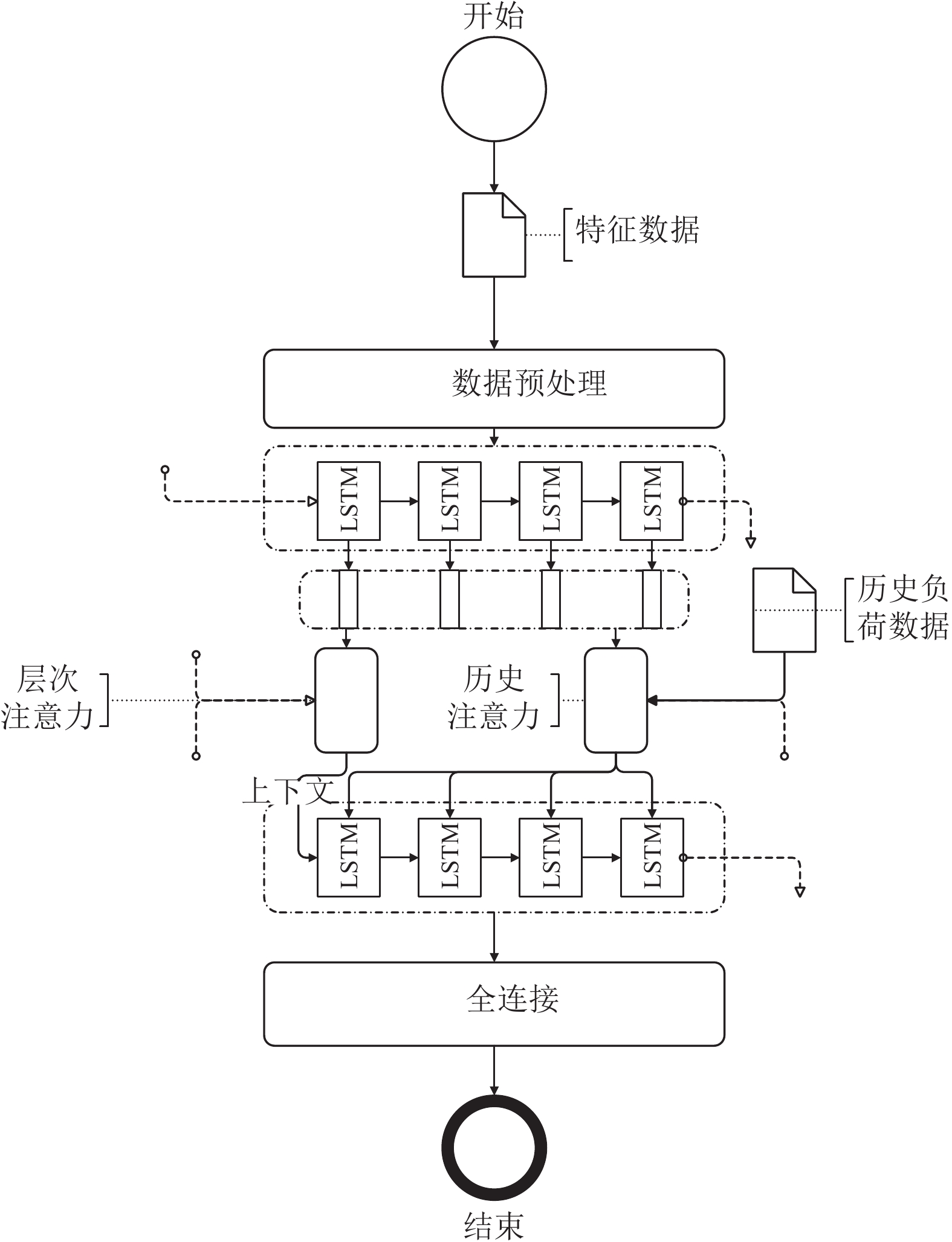
1.5 MA-Seq2Seq模型

为了应对燃气负荷数据中复杂的影响因素, 突变频率高幅度大的特点, 结合多层次时间注意力模块与局部历史注意力模块, 构建MA-Seq2Seq模型. 模型结构如图2所示.

该模型将Encoder编码结果通过多层次时间注意力模块生成包含多维时间信息的上下文向量, 同时将该上下文向量作为Encoder隐藏状态向后传递. 历史输入数据通过局部历史注意力模块, 生成携带关注信息的历史数据, Decoder根据两者内容进行解码, 最后, 通过单层全连接网络得到具体的预测结果.

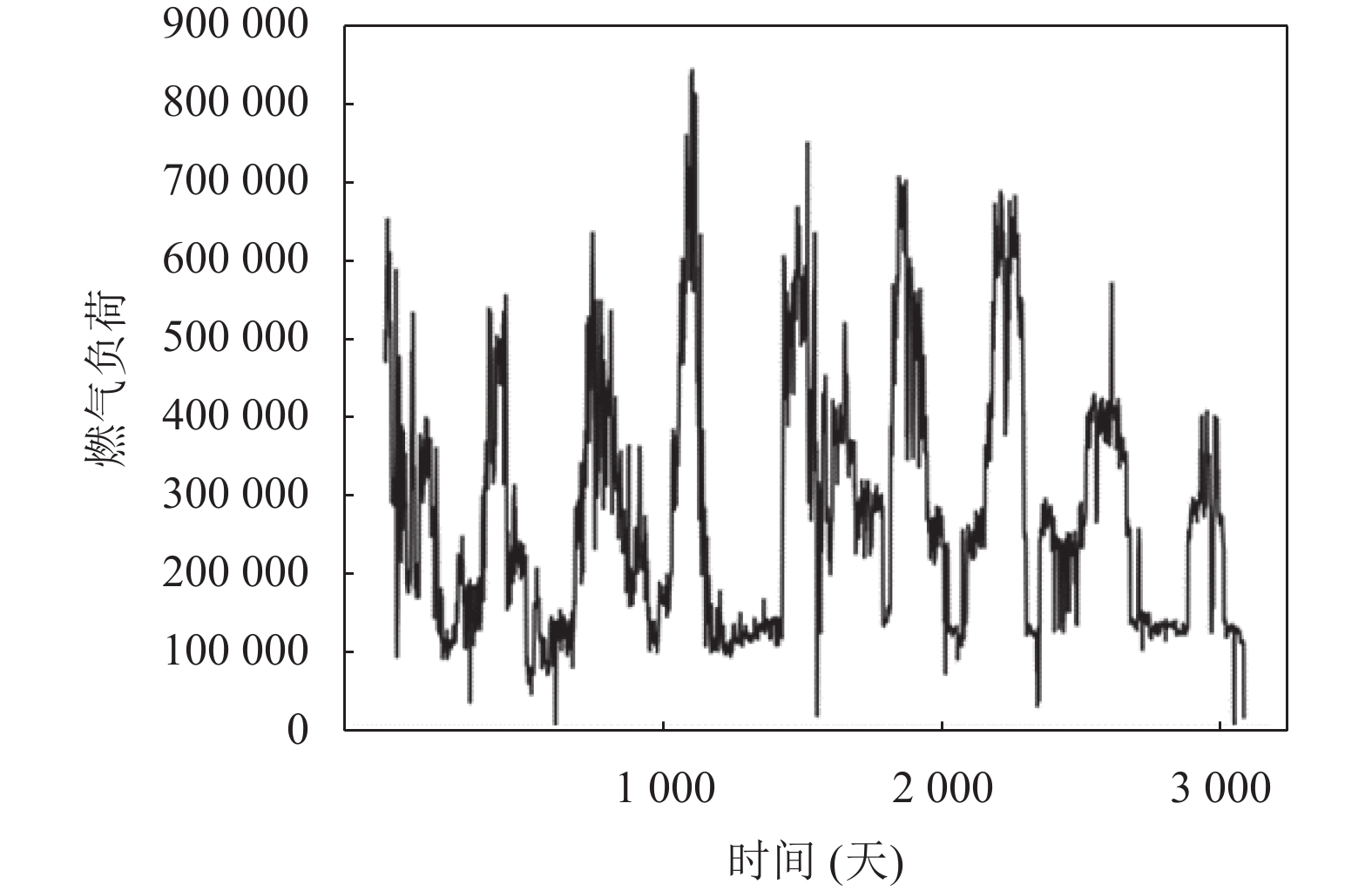
2 数据分析

本文使用中国某市区的燃气日使用数据集对模型的有效性进行验证, 数据中包含特征数据有最高温度、最低温度、星期等. 包含3083天历史燃气使用数据, 依据二八原则, 将数据的前80%作为训练集, 后20%作为测试集. 实验数据如图3所示.

2.1 训练设置

由于不同数据的取值范围各不相同, 为让模型更好收敛, 各阶段的输入数据都经过最大最小值法(Min-Max)进行处理. 本文模型MA-Seq2Seq采用单层LSTM构建Encoder与Decoder. 隐藏层的维度设置为64. 输入窗口T设置为14, $\lambda $设置为len(S)/2. 迭代次数为50次. 采用Adam优化算法. 损失函数采用平均绝对误差(mean absolute error, MAE). 学习率设置为0.0001, 采用L2正则化来避免模型过拟合.

2.2 评价函数

本文使用平均绝对误差(mean absolute error, MAE), 平均绝对百分比误差(mean absolute percentage error, MAPE), 均方根误差(root mean square error, RMSE)对模型的测试集数据进行评估, 计算公式定义如下:

$ MAE = \frac{1}{n}\sum\nolimits_{i = 1}^n {|{y_i} - \widehat {{y_i}}|} $

(13)

$ MAPE = \frac{1}{n}\sum\nolimits_{i = 1}^n {\left| {\frac{{{y_i} - \widehat {{y_i}}}}{{{y_i}}}} \right|} $

(14)

$ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{{({y_i} - \widehat {{y_i}})}^2}} } $

(15)

其中, ${y_i}$表示真实采样数据, 即一天的燃气消耗. $\widehat {{y_i}}$表示模型的预测数据, n表示测试样本数量.

2.3 燃气数据分析

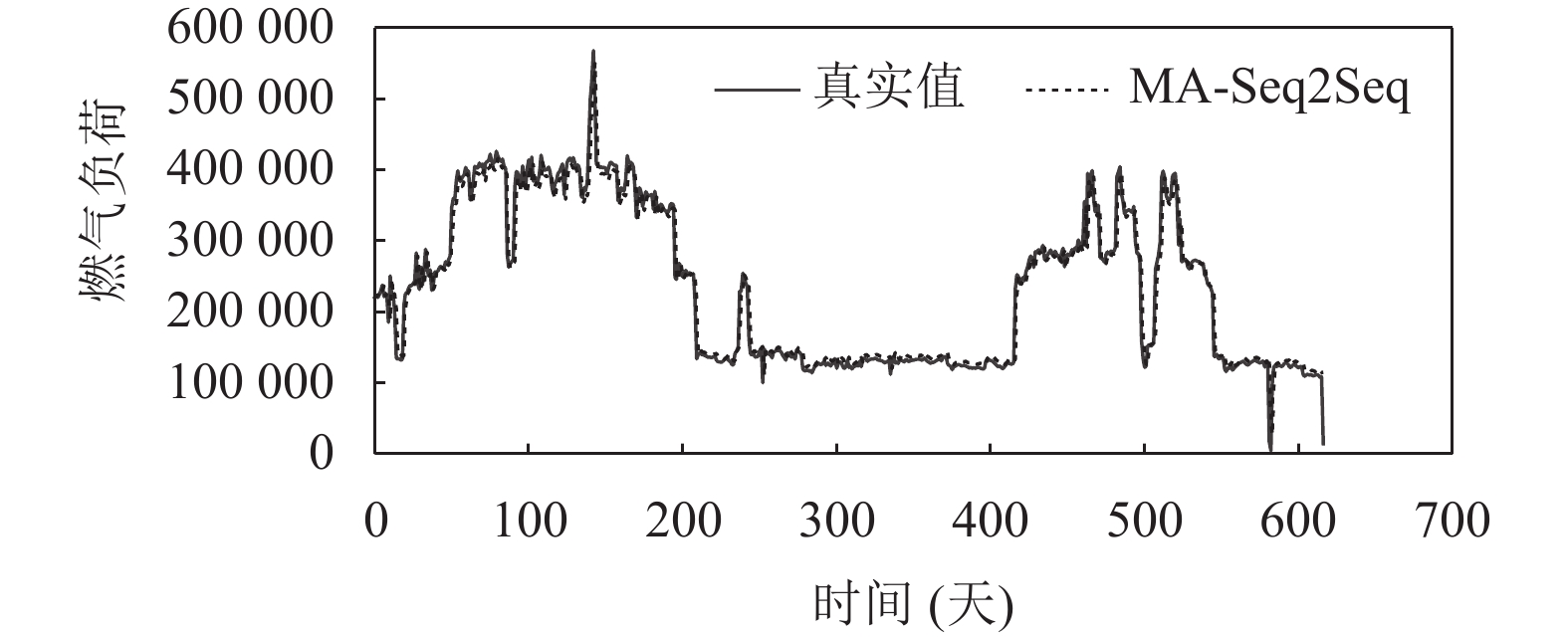
为验证本文模型的MA-Seq2Seq的可靠性, 本文使用传统LSTM模型, Seq2Seq模型, 基于注意力的Seq2Seq模型进行对比实验. 同时, 为尽可能地控制实验变量, 对比模型参数设置与MA-Seq2Seq模型相同. MA-Seq2Seq模型在测试集表现如图4所示.

从图4中可以看出, MA-Seq2Seq模型在测试集上拥有着不错的表现, 即便在数据突变部分也能有着良好的预测方向. 对比实验结果图如图5.

对比实验结果图5中可以发现, 在数据缺少较大波动的情况下, MA-Seq2Seq模型明显比其他模型有更精确的预测结果, 如图5中数据段300–400之间.

依据表1, MA-Seq2Seq模型在3个评价指标中都取得最优值, 表明提出的模型相较于常见的燃气预测模型, 能够取得更加精确的预测结果.

2.4 可解释性

相对于传统深度学习模型, 注意力模型一大特点是具有可解释性. 就局部历史注意力机制模块而言, 将某份测试数据(共14天输入数据)的权重信息划分成前7天与后7天. 由于每次输入两周的数据, 为方便分析, 假定该测试数据预测日期为周一. 结果如表2所示.

从表2中可以看出, 对于距离预测日期过于遥远的数据, 注意力机制会认为与预测日期处于相同位置的历史数据会有更高的参考价值, 当前预测日期为周一, 则同样处于周一位置的数据相较于其他数据而言拥有更高的权重.

表3中展现的是与表2相反的特性, 由于距离预测日期相对较近, 注意力机制认为前两天的数据会有更高的参考价值, 而是否在历史上处于同样的日期位置则不那么重要.

结合表2和表3, 总体上注意力机制认为距离预测日期最近的两天历史数据最能够决定预测日期的数据走向. 而这也符合燃气消耗数据的日常规律.

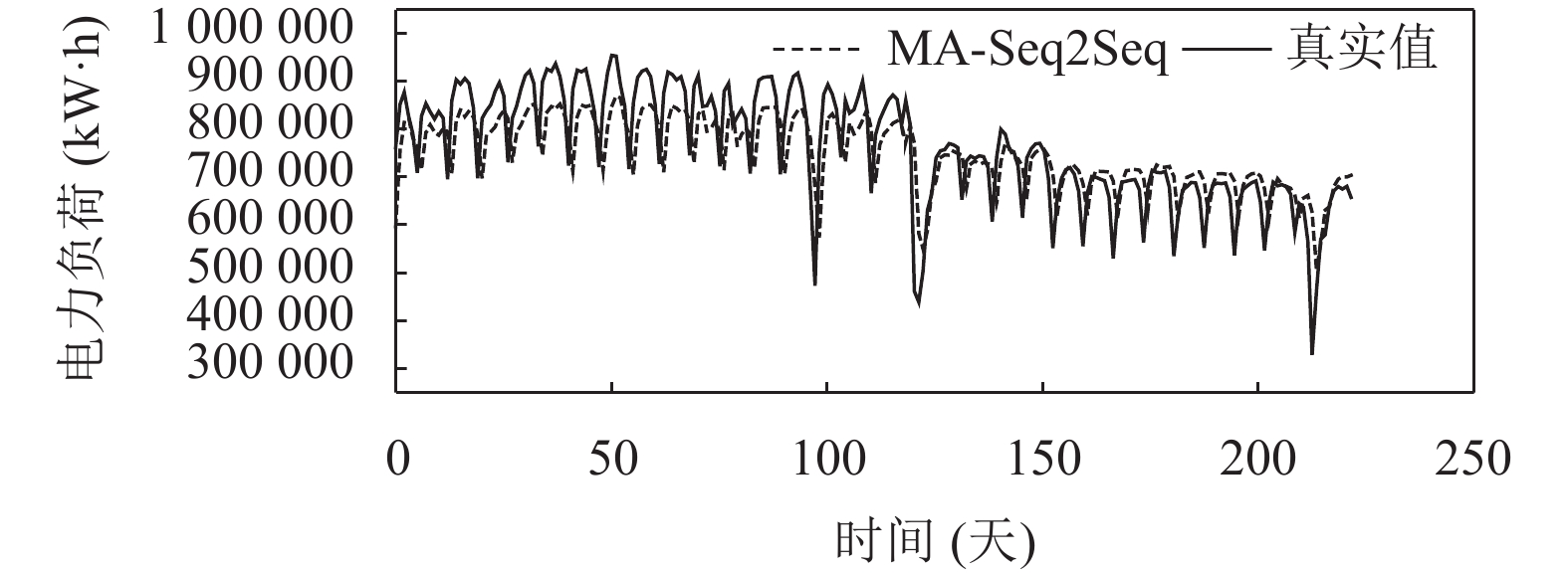
2.5 电力数据分析

为验证模型在其他相关数据集上的表现能力, 使用2016年电工数学建模竞赛A题中电力负荷数据进行实验. 包含的特征数据为最低温度、最高温度、平均温度、相对湿度、降雨量. 总共1106份数据, 其中885份作为训练数据, 221份作为测试数据. 同样, 为尽可能控制变量, 所有模型参数与第2.1节实验中保持一致. 实验结果如图6和图7.

从图6, 图7可以直观看出, 相较于其他模型, 本文模型在电力负荷测试集上的表现更加接近负荷数据的真实值. 同时, 表4的评价数据显示, 在MAE, MAPE及RMSE测评上, 本文模型依旧可以取得最优结果.

表5, 表6为某份测试数据的历史注意力权重信息, 总体上, 权重分布与燃气数据实验相似, 注意力模块认为与预测日期较近的数据应该占据更多权重. 表明本文模型在电力负荷数据集上依旧具备着可行性.

3 结论

本文提出一种多维注意力Seq2Seq预测模型, 研究设计了多层次时间注意力模块, 对Encoder隐藏层输出进行多时间步长对齐, 综合单时间步长、多时间步长计算, 生成包含多维时间模式信息的上下文向量, 为Decoder解码提供更多信息支持. 设计增加了局部历史注意力模块, 结合短期特征编码信息与输入的历史数据, 生成携带关注信息的历史数据, 以便Decoder在预测过程中能够关注更具有参考价值的输入数据. 通过两个注意力模块的处理, 能够让Decoder更具针对性地生成预测内容, 实验结果表明MA-Seq2Seq模型整体上有着良好的预测结果, 面对局部突变数据也能有不错的表现结果. 同时, 为验证模型在相似数据集上的可行性, 使用公开电力负载数据进行实验. 测试结果显示MA-Seq2Seq模型依旧可以取得较高的预测精度.