在地质勘探、石油开采、气象预测等领域需要绘制等值线图来进行可视化呈现, 克里金插值是绘制等值线的重要技术之一, 当采样点规模变大时, 克里金插值计算费时, 导致绘制等值线时间增多, 为了解决时间问题, 需要更好的并行方案.
当采样点的规模变大时, 可以采用Delaunay三角剖分, 将采样点构成三角网, 然后通过三角网快速搜索邻域点来进行克里金插值可以实现对插值点的并行计算, 并且该方法可以通过添加约束, 扩展到断层地质上使用. 王倩[1]提出一种基于DT三角网的并行克里金插值方法, 但是没有给出高效的GPU并行计算模型. 吴博等[2]将OpenMP和MPI结合基于CPU来实现克里金并行插值, 该方法虽然更好地利用集群的计算资源, 但是对于计算资源的要求也更高. Zhang等[3]提出一种将OpenCL框架CPU和GPU相结合, 并使用K-D树进行邻域搜索的克里金并行插值模型, 但是没有考虑GPU的资源负载以及CPU和GPU之间频繁通信时间损耗问题. 刘义[4]提出更高效的在CPU和GPU上进行克里金并行计算的模型, 获得比较好的提速效果, 但是没有提出较好的邻域搜索策略, 当插值点规模变大时, 仍需要对庞大的插值点不断计算周围采样点并进行拟合半变异函数和计算插值, 计算开销大. Pesquer等[5]提出一种能够自动拟合半变异函数的并且自适应不同空间的克里金插值方法. 使用局部点进行克里金插值时需要为插值点搜索邻域的采样点, 不同邻域搜索方法, 也会影响插值的效果和精度[6]. 在搜索采样点时, 往往需要通过距离[7]或者数目[8,9]来控制采样点的范围. 杜宇健等[10]提出一种使用固定距离滑动邻域来搜索采样点, 在避免外推的同时保证了搜索的邻域点的质量. 王金鑫等[11]提出了一种使用八叉树进行邻域搜索的改进克里金算法, 在三维空间上得到比较好的邻域搜索效果, 但是该方法构造树结构会造成额外的时间开销. 实际工程中的采样点空间分布并不一定是均匀的, 当空间分布不均匀时, 也会影响插值的效果[6].
针对以上问题, 本文提出以三角形为单位提前搜索邻域点并拟合半变异函数, 建立邻域索引表来迅速获得邻域采样点数据, 采用CPU-GPU负载均衡将部分计算优化, 提升了空间插值的速度. 对于不均匀分布的采样点集, 在正式插值前, 先通过三角网检测不均匀处需要补点的位置, 并使用克里金插值法计算属性, 保证了该方法在不均匀样本上也能应用.
1 基于三角网的克里金并行算法优化 1.1 普通克里金插值原理克里金插值是地质学上常用的一种空间插值技术, 它通过搜索空间内相关范围内的采样点来执行插值. 半变异函数是用于对有限范围内的属性值进行无偏和最优估计, 因此克里金插值法计算的插值点属性是线性无偏的最优估计, 且满足计算方差最小化.
假设Z(x0)为空间插值点x0处的属性值, 它是由周围邻域样本点属性值加权求和得到的, 如式(1)所示, 其中, 样本点记为xi (i = 1, 2, …, n), λi为待定权系数. 通常利用矩阵运算求解待定权系数, 如式(2)–式(4)所示, 其中γ(vi, vj)表示的是点vi和vj之间的变异函数值.
| $ Z({x_0}) = \sum\limits_{i = 1}^n {{\lambda _i}} Z({x_i}) $ | (1) |
| $ [K] \cdot [\lambda ] = [M] $ | (2) |
| $ [K] = \left[ {\begin{array}{*{20}{c}} {\gamma ({v_1}, {v_1})}&{\gamma ({v_1}, {v_2})}& \cdots &{\gamma ({v_1}, {v_n})}&1 \\ {\gamma ({v_2}, {v_1})}&{\gamma ({v_2}, {v_2})}& \cdots &{\gamma ({v_2}, {v_n})}&1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\gamma ({v_n}, {v_1})}&{\gamma ({v_n}, {v_2})}&{...}&{\gamma ({v_n}, {v_n})}&1 \\ 1&1&{...}&1&0 \end{array}} \right] $ | (3) |
| $ [M] = \left[ {\begin{array}{*{20}{c}} {\gamma ({v_1}, v)} \\ {\gamma ({v_2}, v)} \\ \vdots \\ {\gamma ({v_n}, v)} \\ 1 \end{array}} \right] $ | (4) |
数据量较大的采样点, 使用全部数据拟合半变异函数, 计算相关矩阵的计算开销很大. 为了节约开销, 先采用Delaunay三角剖分将采样点构网, 计算插值点时使用三角网快速搜索周围的采样点(如图1所示), 然后利用邻域点信息计算K矩阵和M矩阵, 并对K矩阵求逆, 求解系数矩阵, 最终计算插值点的属性值(如图2所示). 其中, 将适合并行实现的矩阵计算操作, 部署在GPU上并行执行[1].
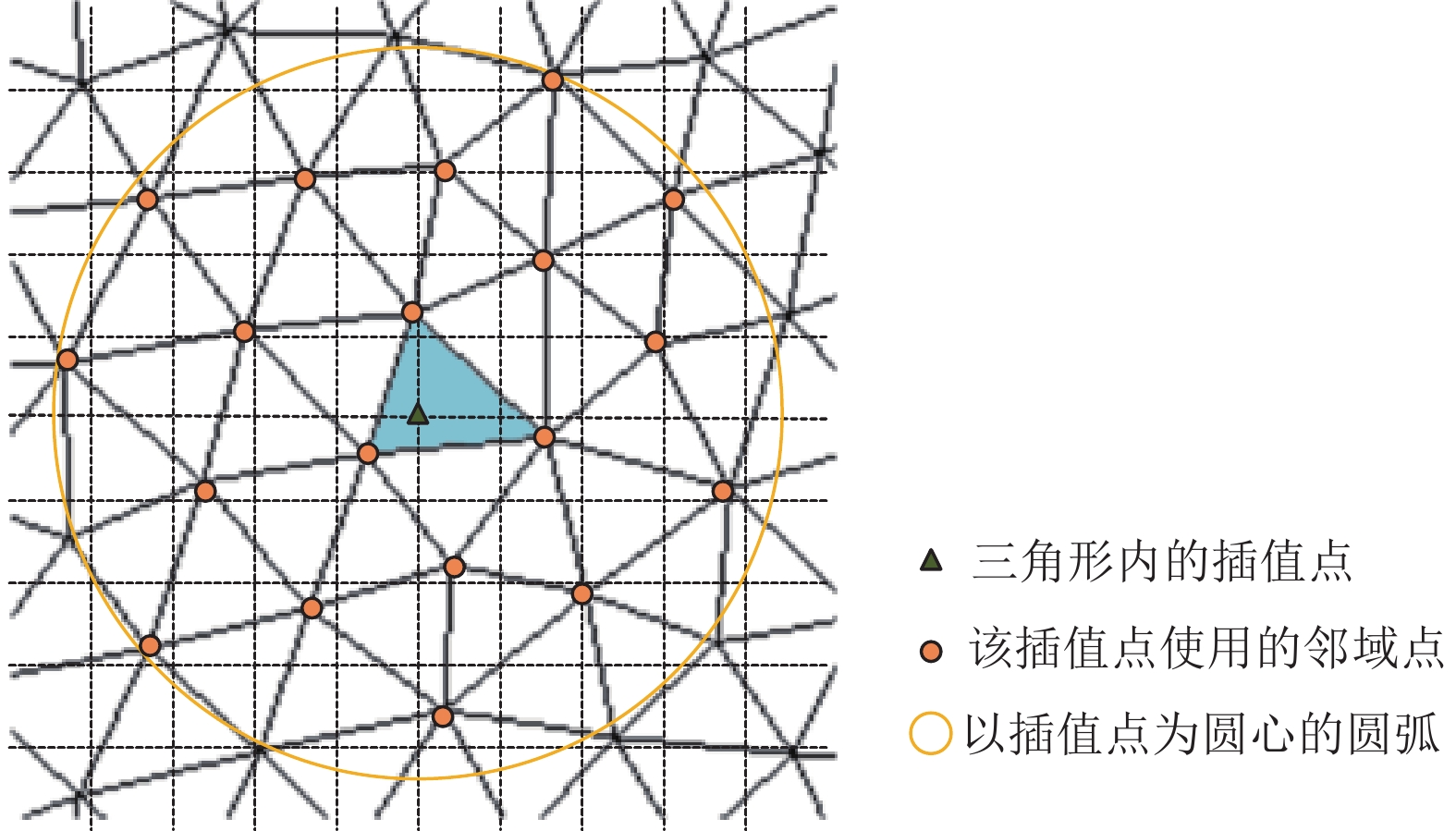
|
图 1 插值点搜索邻域采样点 |
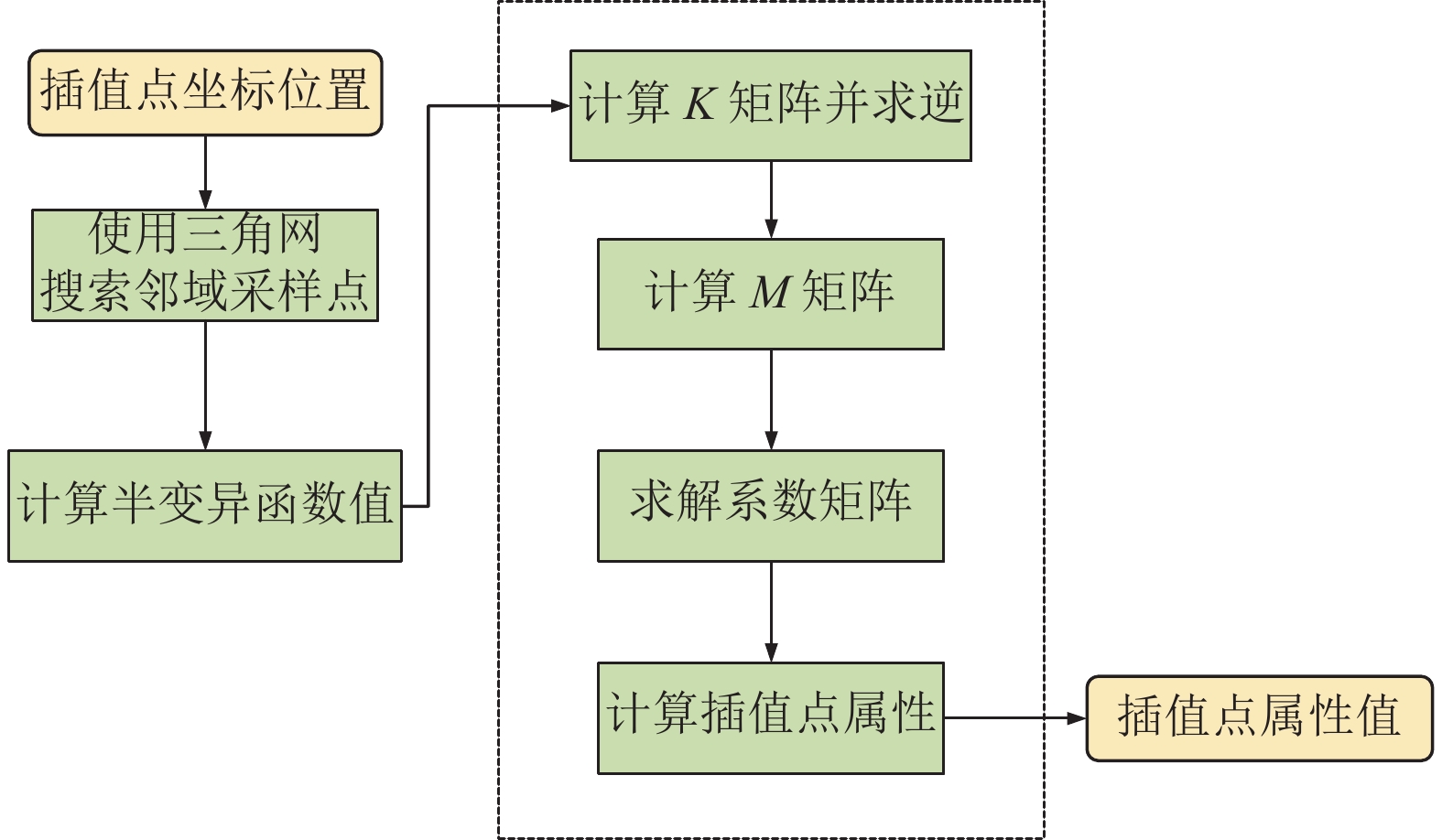
|
图 2 基于三角网的克里金插值并行计算流程 |
使用三角网确实能够极大程度的提升大规模样本的邻域搜索的速度, 但是当插值点的数量较大时, 需要对每一个插值点进行邻域搜索, 并拟合半变异函数, 造成较大时间开销. 实际上, 分布均匀、密集的采样点集, 可以将该三角形附近的采样点近似看成该三角形内全部插值点的邻域采样点(如图3所示). 在计算插值点属性值之前, 先搜索每个三角形的邻域采样点并拟合半变异函数, 再计算每个插值点所在的三角形id, 建立id到半变异函数的索引表. 计算属性值时, 直接通过三角形id寻找相应的半变异函数值进行计算.
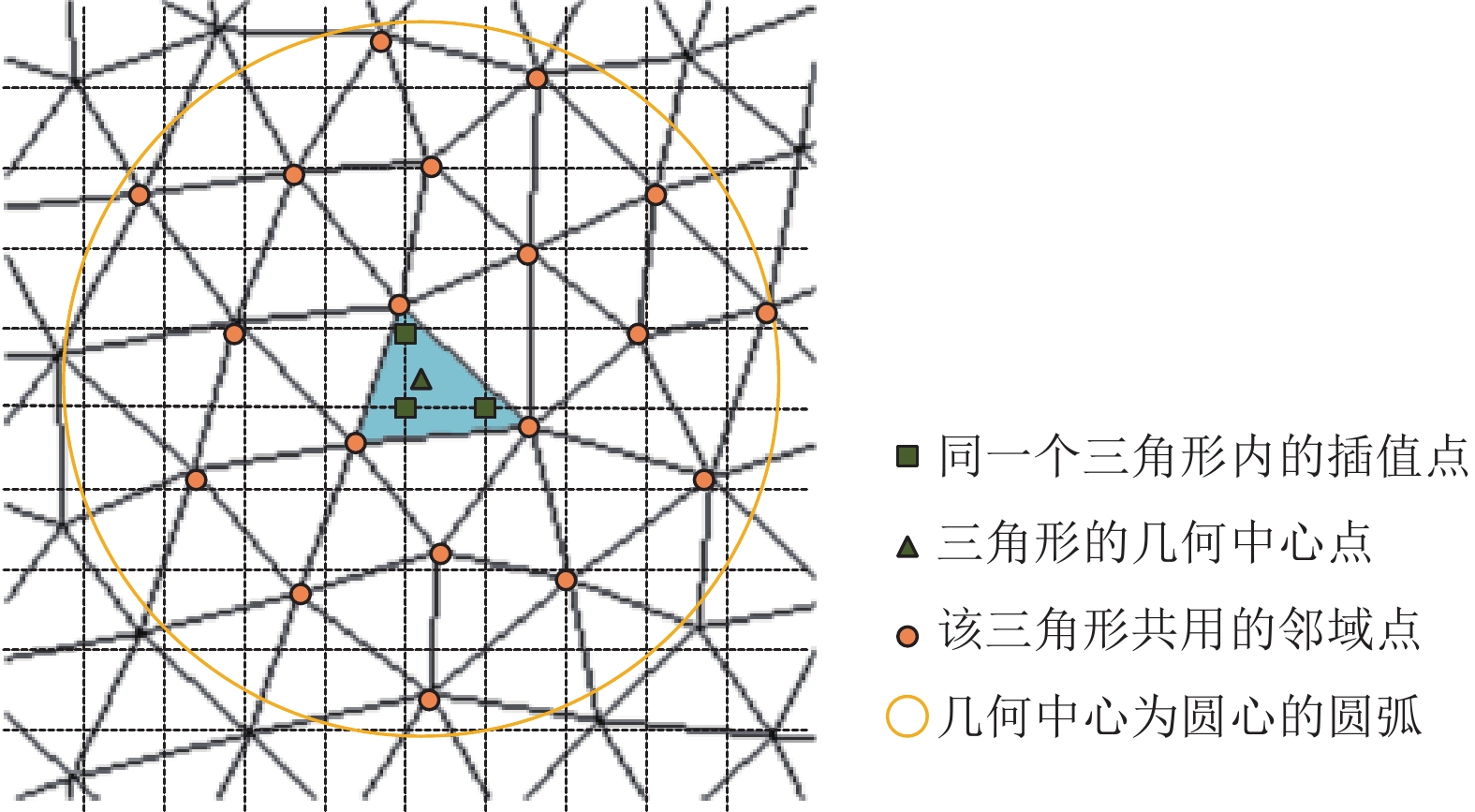
|
图 3 三角形内的插值点共用邻域采样点 |
使用索引表进行插值计算可以节省很多计算量, 但是当采样点数据分布不均匀时, 三角网中狭长或者过大的三角形内的插值点并不适合共用一份邻域采样点, 否则绘制出的渲染图会在三角形的边界处出现明显颜色变化(如图4所示). 因此使用该方法插值时, 需用确保采样点集是均匀分布的.

|
图 4 不均匀采样点集插值效果图 |
2 负载均衡的双层克里金插值模型
提前构建邻域索引表极大提升了插值点邻域搜索的复用, 且部分CPU和GPU的计算任务还可以通过负载均衡处理来进行加速, 但三角形区域内的插值点复用一份邻域数据的前提是, 该三角形的三个顶点物理距离相近, 也就要求空间内采样点的分布要平均且不稀疏. 因此需要一种可以将稀疏、不均匀的样本补充采样点, 并且可以进行高性能插值计算的方法.
2.1 基于索引表的负载均衡邻域搜索策略当采样点的数量较多时, 使用全部的采样点来拟合半变异函数会造成巨大的时间开销. 通常采用对插值点搜索邻域采样点的方法, 使用局部采样点来拟合半变异函数, 来提升插值速度. 王金鑫等[11]提出一种基于八叉树的邻域搜索策略, 先构建空间点的最小外包围盒, 然后对并对该外包围盒进行8等份剖分, 并自动填入采样点, 最后对插值点进行搜索. 王倩[1]提出一种基于空间索引的搜索方法, 该方法需要提前计算DT网中三角形内包含的空间插值点. 本文采用一种基于索引表的邻域搜索方法, 使用块结构存储DT网中三角形的相关信息.
当调用GPU来进行并行计算时, 只需要使用一个CPU内核来进行控制, 则在GPU计算期间, 所有剩余的CPU内核都在空闲等待, 这浪费了大量的CPU计算资源[12]. 姜春雷等[13]根据邻域点的性质将克里金算法中的任务分配CPU和GPU来同时执行, 提升了空间插值的效率. 可见, 将计算任务合理地分配给CPU和GPU的计算方式是协同并行计算的发展趋势[14].
基于索引表的邻域搜索方法, 虽然优化了克里金插值的计算量, 但是在GPU上构造树结构并为每一个插值点定位所在三角网中的位置时, CPU是空闲等待的, 这一定程度地浪费了计算资源. 本文提出一种改进的邻域搜索策略, 如图5所示, 在CPU上使用thread0在GPU上并行的构造四叉树, 并使用四叉树定位插值点的位置; 使用thread1构建三角网的共边表, 然后和其余线程搜索邻域采样点. 首先根据Coll等[15]提出的方法构建DT网, 在CPU上对DT网中的每一个三角形搜索邻域点, 建立索引表; 同时在GPU上并行的构建四叉树, 存储空间上网内的三角形, 并定位每个插值点所在的三角形id. 如图6所示, 进行插值点的邻域搜索时, 通过定位到的三角形id找到对应的邻域索引表, 该表内的信息即是该三角形内插值点所使用的邻域点. 计算的时间如式(5)所示, 总时间Ttotal为
| $ {T_{{\rm{total}}}} = \max \left( {T'_{{\rm{CPU}}}, {T'_{{\rm{GPU}}}}} \right) $ | (5) |
采样点的分布情况对克里金插值有着重要的影响, 甚至会影响计算模型设计和优化的成本和收敛性[16]. 实际工程上的采样点, 由于地形或者工程条件的制约, 经常出现采样稀疏或者不均匀的情况, 本文方法对样本稀疏的区域进行补充采样点. Zhai等[16]使用DT网内三角形的面积来表示采样点的离散度, 用三角形质心估计误差来表示区域误差来寻找勘测位置, 但是该方法的计算开销较大.

|
图 5 CPU-GPU负载均衡模型 |
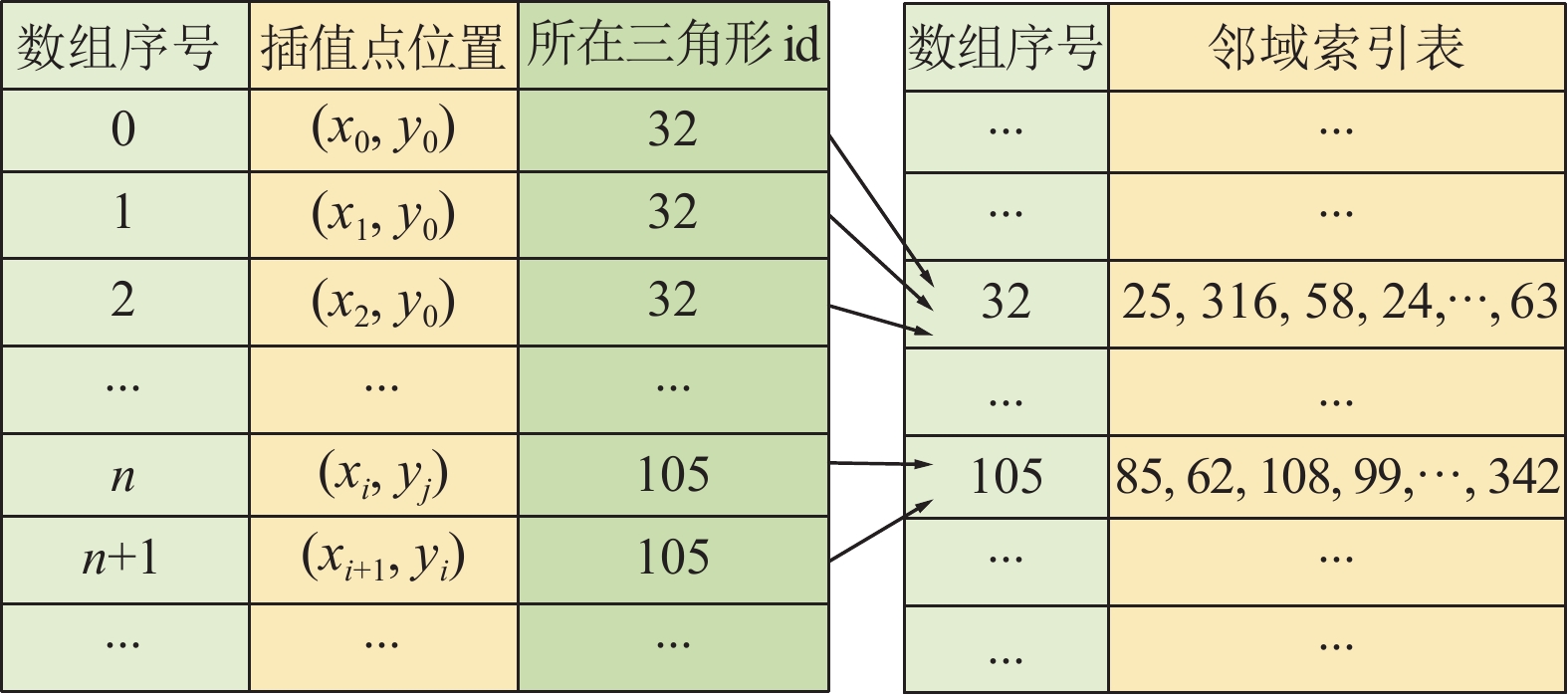
|
图 6 根据三角形id使用索引表 |
在DT网内三角形的质心进行补点, 可以均匀稀疏区域的采样点, 对于边界上的三角形, 如果不对在边界上的长边进行补点, 重新构造的三角网仍会产生狭长的三角形, 因此需要特殊处理. 本文提出一种利用三角网内三角形边长情况对三角网内部和边界分别进行补点的方法.
具体的实现步骤如下.
(1) 首先将区域内采样点坐标值映射到0–100之间, 构建DT三角网.
(2) 先找出与数据边界重合且边长超过阈值的三角形边, 对其进行补点(如图7所示), 补点个数按照式(6)计算, 插值点数NUM为边长length除阈值threshold向下取整.
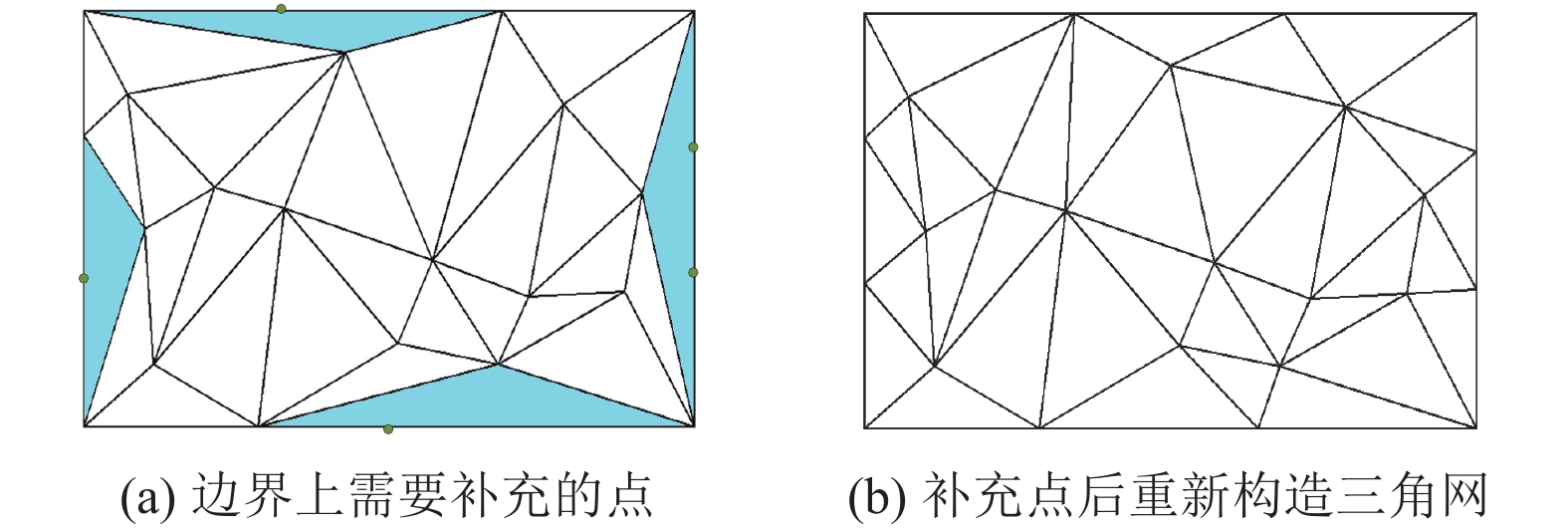
|
图 7 与边界重合的狭长边补充点 |
(3) 重新构建三角网, 遍历三角网中的三角形, 当边长超过设定阈值threshold的时候, 说明该三角形狭长或者过大, 将三角形id加入需补充点三角形集.
(4) 遍历待补充点三角形集, 计算三角形质心, 加入补充采样点集, 根据逐点插入法[17]调整三角网(如图8所示), 并将需补充点三角形集中受影响的三角形删除, 检查新构造的三角形, 将满足(3)中边长异常的三角形的id加入到需补充点的三角形集中. 当需补充点的三角形集为空时, 结束, 得到完整待补充采样点集.
| $ NUM = \left\lfloor {length/{\textit{threshold}}} \right\rfloor $ | (6) |
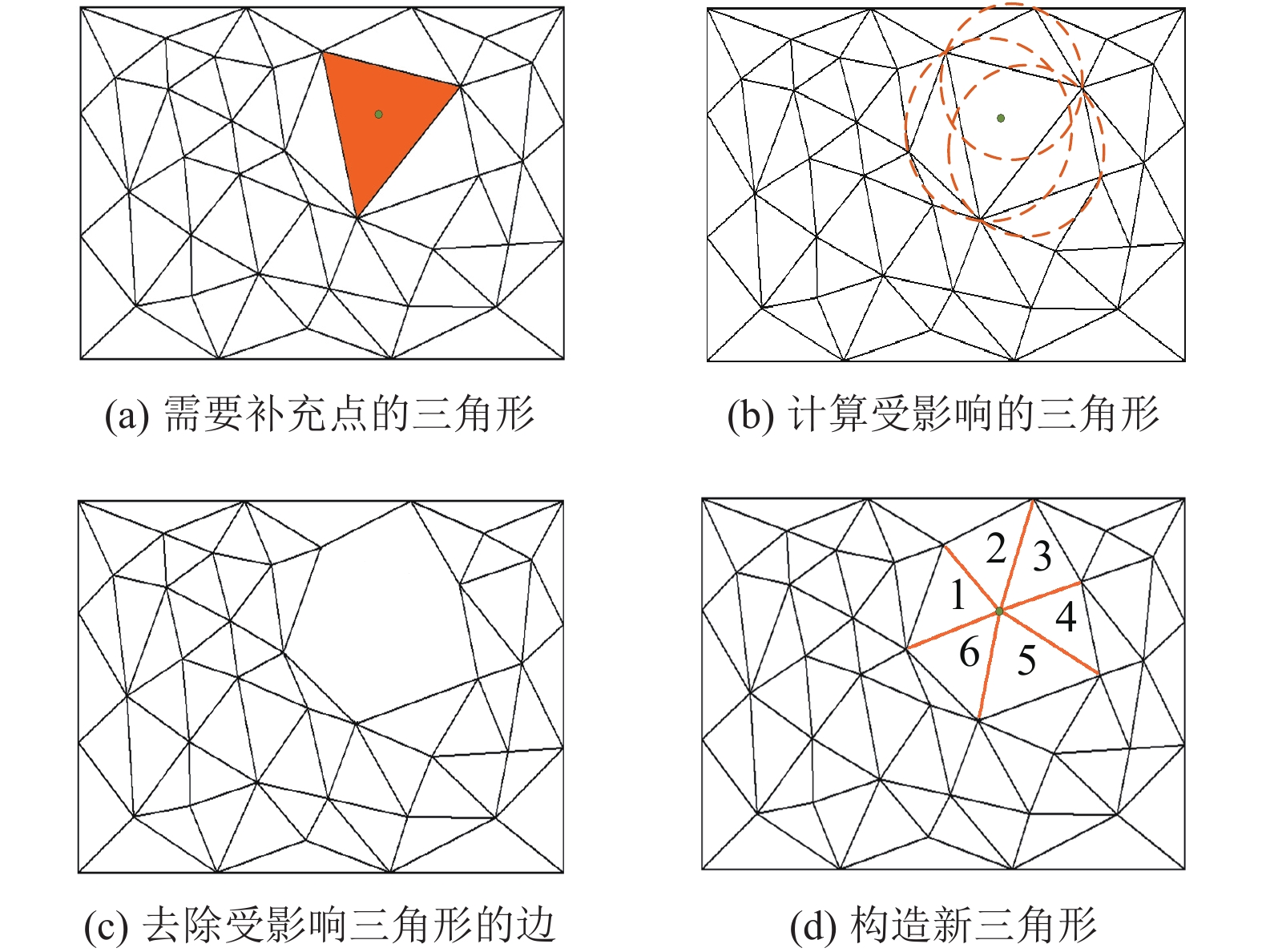
|
图 8 逐点插入法调整三角网 |
使用克里金法计算待补充采样点集的属性值, 并加入原始样本采样点集, 重新生成DT网, 网内不再存在狭长或者过大的三角形. 若计算得到的需要补点的位置为0, 就说明样本集已经均匀分布, 不需要补点.
2.3 双重克里金插值模型由于克里金插值中存在着许多矩阵计算, 因此适合使用并行计算的方法来实现加速. 单纯地使用并行手段对整体区域所构造的矩阵求解加速, 往往在大数据样本上不能取得很好的效果, 并且该方法不适用于对带断层的地质数据进行克里金空间插值, 因此很多学者采用以插值点为单位, 通过搜索邻域采样点, 并行计算插值点的属性值. 为了简化计算, 本文提出以三角形为单位拟合半变异函数, 同一个三角形上的插值点共用一份邻域采样点.
由于不均匀、稀疏的采样点会影响空间插值的效果, 本文提出了一种双重克里金插值模型, 如图9所示. 在正式空间插值之前, 先对采样点数据集进行一次预处理, 检测是否有不均匀和稀疏的区域, 并对稀疏区域进行补点, 然后将补充的点加入原始采样点集, 对新数据重新Delaunay三角剖分构网, 建立网内三角形的邻域索引表, 并提前拟合半变异函数. 具体功能板块如下.
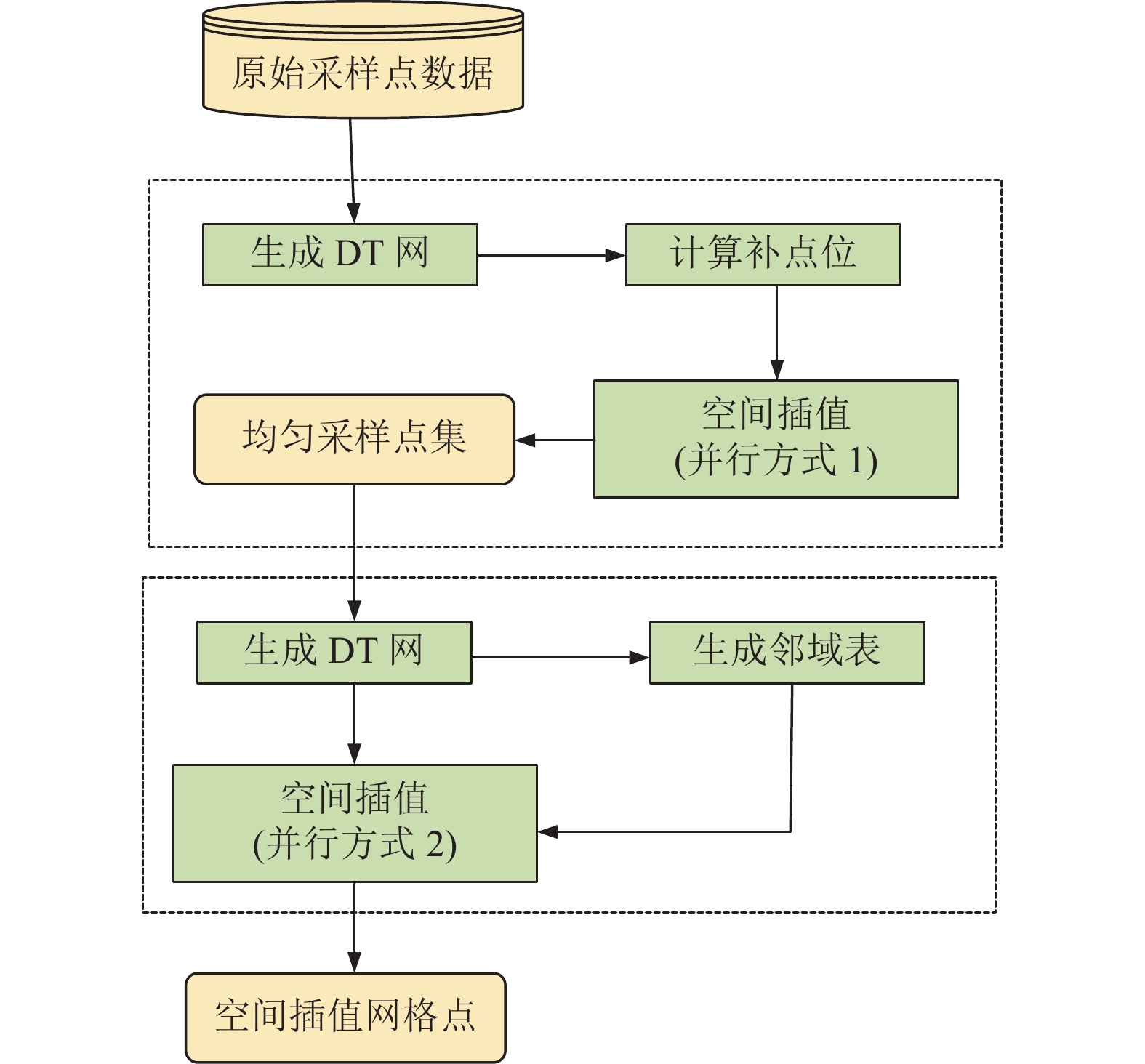
|
图 9 双层克里金并行插值模型 |
(1)第1层克里金模块
该模块的作用是对不均匀、稀疏的区域补充采样点. 首先需要生成DT三角网, 按照第2.2节中的方式找出待补点位置的坐标, 然后并行执行克里金空间插值. 该模块内每条线程代表一个补点位, 其执行的内容为:
1) 定位该点所在的三角形位置.
2) 外推搜索该三角形周围的邻域点, 并用距离和数量条件进行筛选.
3) 使用搜索出的邻域点拟合半变异函数.
然后在GPU上并行计算补充点的属性.
(2)第2层克里金模块
在第1层模块中已经准备好均匀、密集的采样点集, 用新采样点集构造三角网, 根据第2.1节中的方法并行的构建邻域索引表以及插值点所在三角形索引表, 然后在GPU上并行的进行克里金插值计算, 每条线程代表一个空间插值网格点, 该线程通过位置表中的id找到邻域点的相关数据, 使用该数据进行克里金插值计算插值点属性.
该模块内将邻域搜索提前并行执行, 将不适合在GPU上实现的邻域搜索剔除, 只将适合CUDA实现的矩阵计算等问题部署在GPU上, 并行效率高.
3 实验分析实验数据采用某物探院勘测数据, 本次实验使用Visual Studio 2015作为开发平台, 以OpenGL作为图像绘制工具, 以标准 C++作为开发语言, 使用C# MathNet库做为矩阵计算库, 使用CUDA C实现并行技术. 使用计算机配置为: Legion Y7000P2020, 处理器为Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz 2.59 GHz, 16 GB内存, Windows 10系统.
3.1 基于三角网的克里金并行算法优化效果该算法先检测样本集是否有不均匀区域, 并对稀疏区域补点, 再对生成的三角网进行邻域搜索并构建邻域索引表, 空间插值时使用邻域索引表可以迅速获得相关数据.
实验采用的原数据集为547个采样点, 生成三角网中含有三角形1094个, 进行边界补点和质心补点后, 补充采样点292个. 补充点后的数据集采样点个数为839个, 三角形个数为1656个.
原数据集生成的三角网如图10(a)所示, 网中存在很多较大以及狭长的三角形, 尤其是边界处容易产生狭长的三角形. 补点后的数据集生成的三角网如图10(b)所示, 网内三角形形状相对均匀, 对三角形进行邻域搜索得到的采样点集可以当做三角形内插值点的邻域采样点使用.
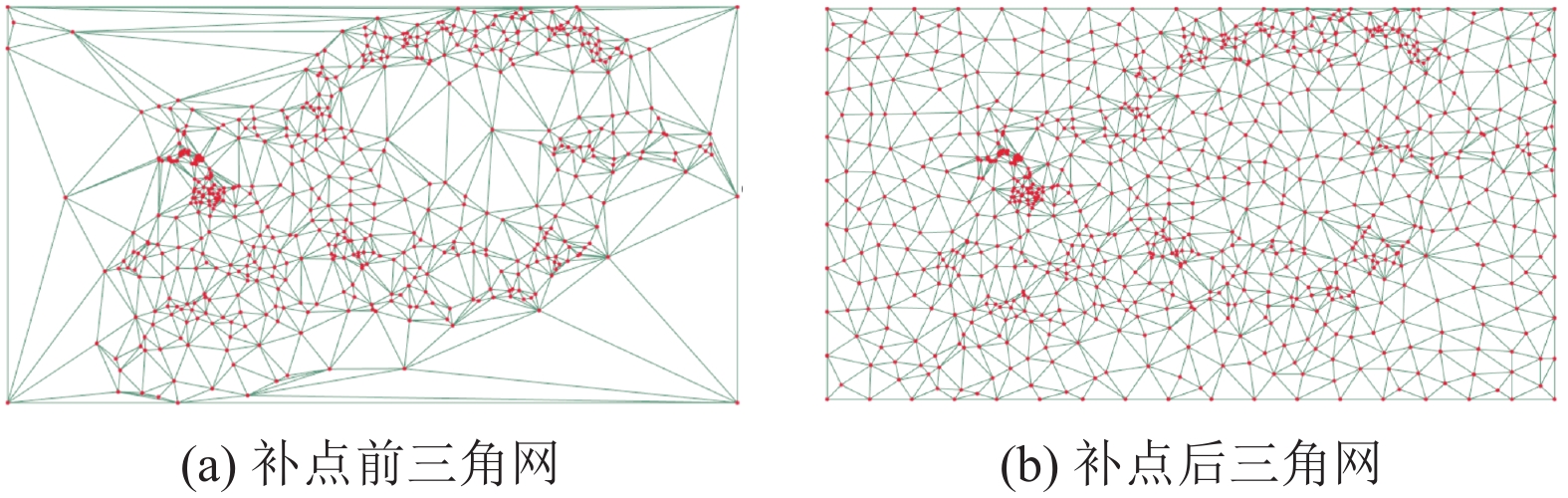
|
图 10 使用三角网补点效果对比 |
对原数据集数据使用双重克里金插值模型进行补点后再插值计算, 绘制的渲染图如图11所示, 可以看出, 该计算模型在不均匀样本集上依然具有较好的效果.
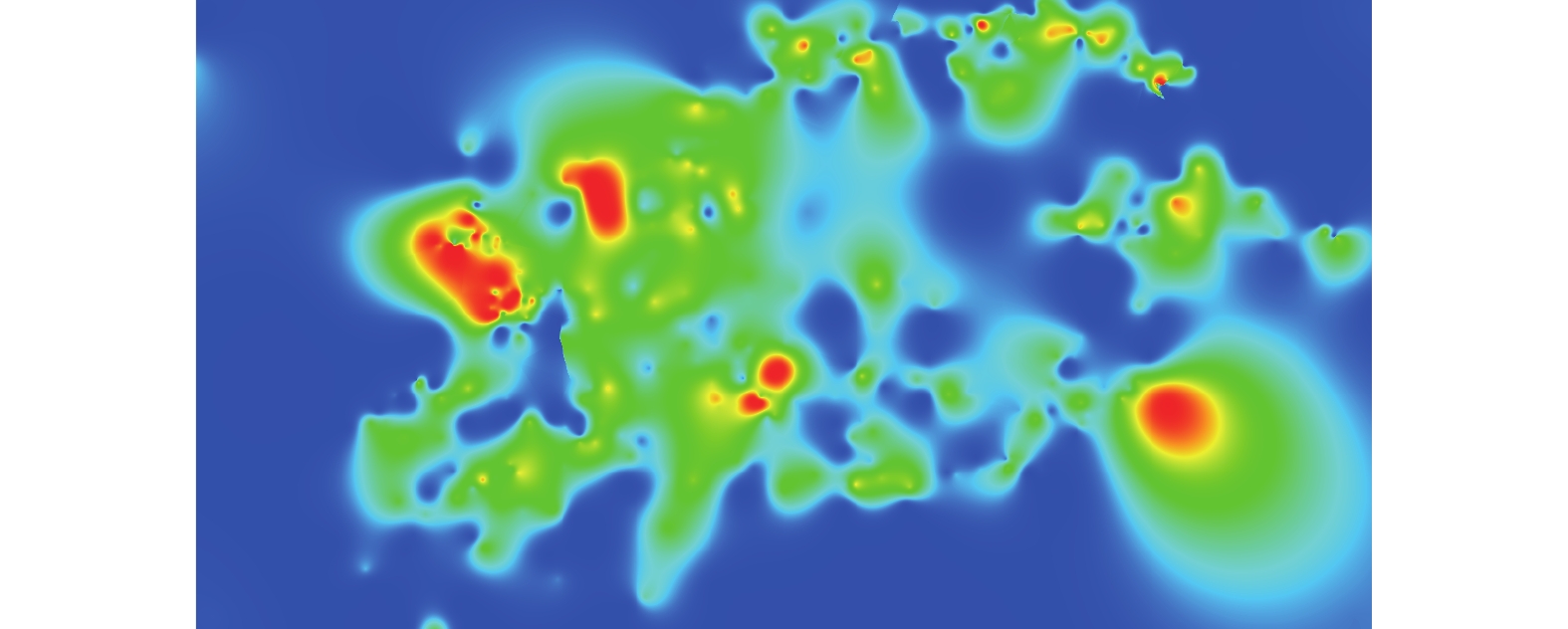
|
图 11 渲染效果图 |
3.2 负载均衡的双重克里金模型性能比较
实验使用547点采样数据, 负载均衡的双重克里金模型采用大量并行计算, CPU调用线程最多12条, GPU调用线程个数依据插值网格点的个数分配. 将搜索邻域采样点的个数固定为50个, 搜索邻域点和定位三角形采用负载均衡法所用时间与单线程方法对比如表1所示, 从表1中可以看出负载均衡法性能优于单线程法. 将搜索邻域采样点的个数固定为20个, 负载均衡双重克里金插值方法执行总时间如表2所示, 从表2中可以看出, 当插值点数为1万时, 基于三角网的克里金插值法性能更好, 这是因为双重克里金法需要在插值之前进行补点操作, 会消耗一定的时间. 当插值点大于5万点时, 负载均衡双重克里金插值时间优于前者, 并且随着插值点数量增加, 性能优势更加明显.
| 表 1 负载均衡时间比较 (s) |
| 表 2 插值总时间比较(s) |
3.3 插值算法精度验证
实验使用547点采样数据, 使用商业软件Surfer 15的克里金插值法进行网格插值, 网格大小为618×335, 共207030个网格插值点作为对照组数据, 实验组数据是使用双重克里金模型计算出的等规模网格插值点. 通过计算对照组和实验组对应的网格插值点的属性的误差来验证模型的精度. 统计学上常用的统计指标有标准均方根误差(RMSE)、平均相对误差(MRE). 标准均方根误差和平均相对误差越小, 说明精度越高.
经过误差计算, 两组数据插值点属性值的RMSE为0.016484, MRE为0.006331, 这表明双重克里金插值模型方法正确, 且具有较高精度.
4 结论本文提出了一种改进的基于Delaunay三角网的克里金并行插值方法, 提前以三角形为单位搜索邻域点并拟合半变异函数, 空间插值时通过邻域索引表迅速找到相关邻域数据, 设计CPU-GPU负载均衡的并行计算方案来优化插值性能; 另外, 提出对不均匀采样点数据的补点策略, 确保了该算法在不均匀样本上也能应用, 通过仿真实验证明了该方法有效地提升了插值计算的速度, 并且保证了插值精度.
| [1] |
王倩. 基于Delaunay的三维快速克里金插值[硕士学位论文]. 成都: 电子科技大学, 2015.
|
| [2] |
吴博, 高超, 谢健. 基于混合并行的Kriging插值算法研究. 计算技术与自动化, 2014, 33(1): 65-68. |
| [3] |
Zhang YH, Zheng XQ, Wang ZH, et al. Implementation of a parallel GPU-based space-time Kriging framework. ISPRS International Journal of Geo-information, 2018, 7(5): 193. DOI:10.3390/ijgi7050193 |
| [4] |
刘义. 基于GPU的三维克里金插值算法研究与开发[硕士学位论文]. 成都: 电子科技大学, 2021.
|
| [5] |
Pesquer L, Cortés A, Pons X. Parallel ordinary Kriging interpolation incorporating automatic variogram fitting. Computers & Geosciences, 2011, 37(4): 464-473. |
| [6] |
孙立双, 王恩德, 王井利, 等. 基于空间分布权系数Kriging邻域选点算法. 沈阳建筑大学学报(自然科学版), 2007, 23(3): 423-426. |
| [7] |
Bargaoui ZK, Chebbi A. Comparison of two Kriging interpolation methods applied to spatiotemporal rainfall. Journal of Hydrology, 2009, 365(1–2): 56-73. DOI:10.1016/j.jhydrol.2008.11.025 |
| [8] |
Cressie N, Johannesson G. Fixed rank Kriging for very large spatial data sets. Journal of the Royal Statistical Society: Series B: Statistical Methodology, 2008, 70(1): 209-226. DOI:10.1111/j.1467-9868.2007.00633.x |
| [9] |
Muhamad Ali MZ, Othman F. Selection of variogram model for spatial rainfall mapping using analytical hierarchy procedure (AHP). Scientia Iranica, 2017, 24(1): 28-39. DOI:10.24200/sci.2017.2374 |
| [10] |
杜宇健, 萧德云. Delaunay-固定距离滑动邻域Kriging算法. 工程图学学报, 2005, 26(2): 64-68. |
| [11] |
王金鑫, 秦子龙, 曹泽宁, 等. 基于八叉树的修正克里金空间插值算法. 郑州大学学报(工学版), 2021, 42(6): 21-27. DOI:10.13705/j.issn.1671-6833.2021.06.004 |
| [12] |
Wan LJ, Li KL, Liu J, et al. Efficient CPU-GPU cooperative computing for solving the subset-sum problem. Concurrency and Computation: Practice and Experience, 2016, 28(2): 492-516. DOI:10.1002/cpe.3629 |
| [13] |
姜春雷, 张树清. CPU-GPU协同加速Kriging插值的负载均衡方法. 国防科技大学学报, 2015, 37(5): 35-39, 148. DOI:10.11887/j.cn.201505006 |
| [14] |
卢风顺, 宋君强, 银福康, 等. CPU/GPU协同并行计算研究综述. 计算机科学, 2011, 38(3): 5-9, 46. |
| [15] |
Coll N, Guerrieri M. Parallel constrained delaunay triangulation on the GPU. International Journal of Geographical Information Science, 2017, 31(7): 1467-1484. DOI:10.1080/13658816.2017.1300804 |
| [16] |
Zhai ZM, Li HY, Wang XG. An adaptive sampling method for Kriging surrogate model with multiple outputs. Engineering with Computers, 2022, 38(1): 277-295. |
| [17] |
Bowyer A. Computing Dirichlet tesselations. Computer Journal, 1981, 24: 162-166. DOI:10.1093/comjnl/24.2.162 |
 2024, Vol. 33
2024, Vol. 33


