2. 山西省医学影像人工智能工程技术研究中心(中北大学), 太原 030051
2. Shanxi Medical Imaging Artificial Intelligence Engineering Technology Research Center (North University of China), Taiyuan 030051, China
脑肿瘤是大脑中异常细胞的团块或集合体, 其反过来破坏大脑的组织功能. 脑肿瘤可主要分为恶性肿瘤和良性肿瘤. 恶性脑肿瘤是目前最严重的癌症之一, 日益威胁着人类的健康[1]. 脑肿瘤被世界卫生组织划分为I–IV级, 脑肿瘤的级别越高, 患者的生存时间越短[2, 3], 所以对脑肿瘤早期的诊断和治疗十分重要. 手动分割脑肿瘤耗时长而且不同医生对同一病患的分割结果也参差不一, 因此脑肿瘤算法的研究对高效地诊断脑肿瘤具有重要的科学价值和临床意义.
随着深度学习方法的发展, 卷积神经网络成为诊断脑肿瘤区域的主要方法. 尤其是基于编码-解码结构的UNet[4]经典分割网络. 之后UNet类型的结构得到进一步发展, 如嵌套和密集连接的UNet++[5]、使用数据相关型上采样与残差块的改进UNet++[6] 、DenseNet[7]网络与UNet结合的DenseUNet[8]、用于体积分割Vnet[9]结构. 这些结构虽加强了对局部特征的提取, 但缺乏获取远程特征依赖和多尺度信息的能力.
对此, 文献[10]提出了TransBTS网络, 首次将Transformer集成到3D CNN的编码-解码结构中, 加强对全局特征的提取. 文献[11]提出了不同扩张率的分层卷积与肿瘤区域关系引导的注意力的轻量级的ADHDC-Net网络. 文献[12]设计了SDS-MSA-Net, 它分别从3D和2D输入中提取特征, 并使用选择性深度监督来辅助输出, 加快了模型的收敛速度, 但同时对 3D和2D资源处理, 加大了计算量. 以上改进的结构分别加强了全局特征和多尺度注意特征的提取能力, 但目前大多数网络都局限于多模态脑肿瘤数据输入级简单的拼接融合, 不能充分利用不同模态对之间互补的融合信息. 因此文献[13]设计了多模态图像的像素级融合与特征级融合的两阶段网络, 以实现对多模态信息更精细地利用, 但该网络核心肿瘤区域的分割精度还有待提升.
针对上述问题, 本文提出了一种跨模态融合的双注意力脑肿瘤图像分割网络(cross-modal fusion dual attention net, CFDA-Net). 为解决普通卷积感受野受限, 本文设计了密集并行大核注意力的新卷积块, 可以有效提取全局和局部信息; 为了加强不同模态对之间的深度融合, 提出了多模态深度融合模块, 更好地利用模态的互补信息; 为关注重要特征信息, 消除对冗余特征的关注, 在解码器分支使用Shuffle Attention[14]注意力以获取空间和通道注意重要特征. 针对类别不平衡问题, 本文使用了二进制交叉熵、Dice与L2 组成的混合损失函数, 进一步提升脑肿瘤分割精度.
1 本文方法 1.1 CFDA-Net网络总体结构本文提出的跨模态的双注意力脑肿瘤分割网络的整体结构如图1所示.

|
图 1 CFDA-Net网络结构 |
图1中左侧的编码器分支有5个密集并行大核注意卷积(dense parallel large kernel attention convolution, DPLC)模块, DPLC块一方面利用密集卷积加强特征重用, 防止梯度消失; 另一方面利用VAN视觉注意力网络提出的大内核注意力卷积(large kernel attention, LKA)块[15]来加强获取远距离特征依赖的能力, 将这两个模块并行相加融合, 可以很好解决普通卷积特征提取时的感受野不足的问题, 进而使局部与全局信息融合更充分. 然后在编码器的第2、3和4层左侧添加多模态深度融合(multimodal deep fusion module, MDFM)模块, 有效地利用不同模态对间的互补信息, 使信息融合更充分. 另外除了第3、第4层MDFM模块后的下采样采用特殊的步长为4、步长为8的3×3卷积外, 其余部分都使用步长为2的3×3卷积来进行下采样.
将编码器的各层级分支通过跳跃连接, 与右侧对应的解码器分支经过上采样后进行通道级拼接融合, 融合后使用SA (shuffle attention)注意力块进行分组后使用空间注意力和通道注意力, 为了加强对重要特征的关注, 最后再经过一个1×1卷积将对应通道数减半. 在最后一个解码器的SA模块后使1×1卷积与Softmax激活函数得到整体肿瘤区域、核心肿瘤区域和增强肿瘤区域的3通道网络模型预测图, 其中每个通道代表一个肿瘤分割区域.
1.2 密集并行大核注意卷积模块为了解决普通卷积特征提时感受野受限的问题, 本文设计了密集并行大核注意卷积(DPLC)模块, 如图2所示.

|
图 2 密集卷积并行大核注意模块结构图 |
首先第1个分支引用了经典的DenseNet网络的密集块, 它可以加强特征重用且能防止梯度消失, 本文为了减少参数和计算量, 将密集块中的层数设定为2层, 每个层将所有先前层的输出作为其输入, 并将其自身的特征传递给后续层. 然后再通过1×1卷积来降低通道数, 该密集块如式(1)所示:
| $ {X_l} = H\left( {\left[ {{X_0}, \cdots , {X_{l - 1}}} \right]} \right) $ | (1) |
其中, [X0, …, Xl–1]代表第0, …, l–1层输出特征图在通道维度进行拼合, 密集块分支的X0即为该模块初始的输入X . 非线性变换H(·)由3×3卷积、批归一化和ReLU激活函数组成. 然后将密集特征再经过1×1卷积降维通道以得到第1分支的输出特征图y1.
第2个分支使用视觉注意网络VAN[15]中提出降低参数量的大核注意力卷积(LKA)块, 该网络提出了一种适用于大核卷积的分解方式, 一个K×K的卷积核可以分解为3部分: 一个(2d–1)×(2d–1)的逐通道(DWConv)卷积; 一个K/d×K/d的逐通道膨胀(DW-D-Conv)卷积; 一个1×1卷积. 其中K为卷积核大小, d为膨胀率. LKA计算公式如式(2)所示:
| $ LKA = {\text{Conv}}_{1 \times 1}({\text{DW-D-Conv}}({\text{DWConv}}(X))) $ | (2) |
然后将LKA经过Sigmoid激活函数得到包含全局信息的注意力系数, 将注意力系数与第3个恒等连接分支进行元素级相乘得到特征图y2, 如式(3)所示. 其中
| $ {y_2} = X \cdot \sigma \left( {LKA} \right) $ | (3) |
最后将y1与y2特征图进行元素级相加生成该模块的最终输出, 如式(4)所示:
| $ y = {y_1} + {y_2} $ | (4) |
如今大多数网络模型针对多模态数据只是输入级的简单拼接, 不能有效利用模态间的互补信息, 为了更好地利用模态对之间的互补信息, 本文提出了多模态深度融合(MDFM)模块. 并在编码器的第2、3和4分支左侧分别添加了T1-T2、T2-T1ce与T1ce-Flair的模态对作为MDFM模块的输入, 这样可以对编码器主分支不断地补充空间特征信息, 使特征信息融合更加充分[16], 有利于提取脑肿瘤的增强和坏死区域的细节特征. 图3为MDFM多模态深度融合模块结构图.
图3以图1中第2层编码器左侧的MDFM模块为例, 该模块输入的ModelA为T1模态、ModelB为T2模态, 这两个模态的空间大小都为160×160、通道数为1, 本文首先将这两个模态进行拼接融合得到T1-T2的双通道特征, 将T1-T2的双通道特征分别输入到3个分支, 对3个分支开始处依次使用逐通道卷积、全局平均池化、全局最大池化, 同时对三分支的结尾处使用ReLU激活函数、1×1卷积进行通道升维得到特征图F1、F2和F3. 最后将3个分支的特征图相加, 再将相加后的特征图使用Sigmoid函数得到融合权重系数α. 将模态A使用1×1卷积升为C维后再与α相乘, 同理另一个模态B升维后与(1–α)乘积, 将两个乘积结果进行相加后, 得到该模块的输出特征S. 该模块如式(5)–式(9)所示:
| $ {F_1} = {\text{Conv}}_{1 \times 1}(\delta \left( {{\rm{DWConv}}\left[ {A, B} \right]} \right)) $ | (5) |
| $ {F_2} = {\text{Conv}}_{1 \times 1}\left( {\delta \left( {GAP\left[ {A, B} \right]} \right)} \right) $ | (6) |
| $ {F_3} = {\text{Conv}}_{1 \times 1}\left( {\delta \left( {GMP\left[ {A, B} \right]} \right)} \right) $ | (7) |
| $ \alpha = \sigma \left( {F_1 + F_2 + F_3} \right) $ | (8) |
| $ S = {\text{Conv}}_{1 \times {{1}}}(A) \cdot \alpha + {\text{Conv}}_{1 \times {{1}}}(B) \cdot (1 - \alpha ) $ | (9) |
其中, DWConv(·)是逐通道卷积, Conv1×1(·)目的是进行通道升维, δ(·)为ReLU激活函数,

|
图 3 多模态深度融合模块结构图 |
1.4 改进的Shuffle Attention注意力模块
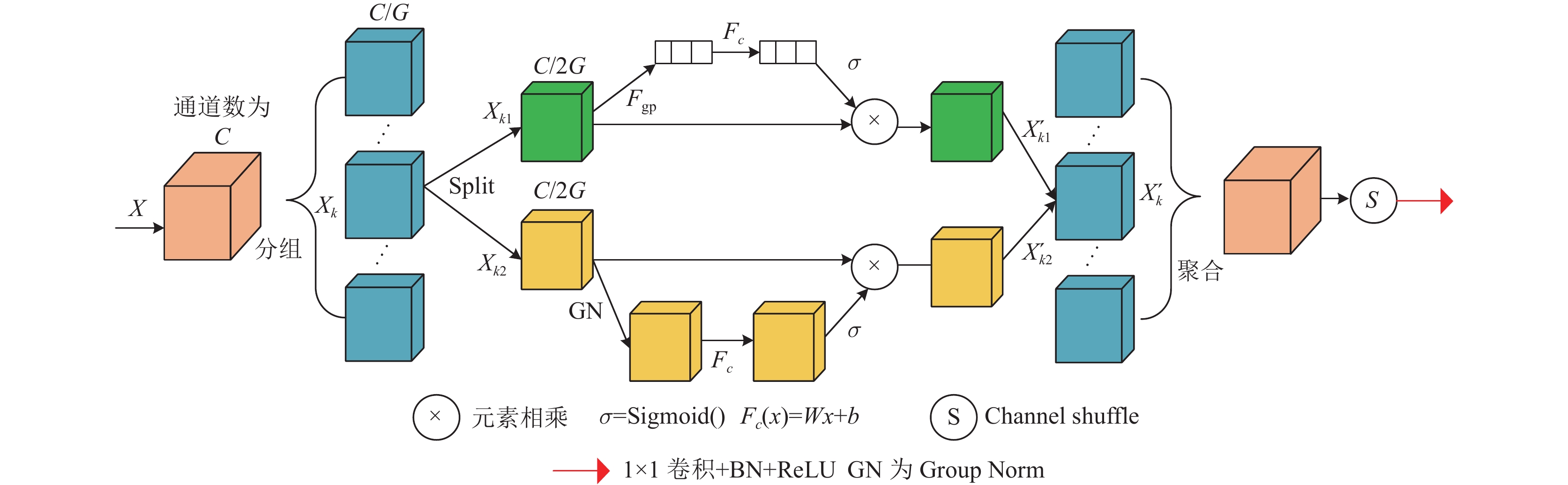
之前的大多数网络都是在跳跃连接处添加相应的注意力机制, 但是这样只加强了对应编码器分支重要的特征关注, 而忽视了对应解码器分支对后续特征的影响, 因此本文在解码器分支引入了轻量级的SA[14]注意力模块, 本文在SA模块的最后增加了1×1卷积、BN归一化和ReLU激活函数来对解码器分支进行降维. 改进后的SA模块结构如图4.
|
图 4 Shuffle Attention注意力结构图 |
对于输入特征映射X∈RC×H×W, 其中C是通道的数量, H、W分别为空间的高度和宽度, SA最初在通道维度上将X划分为G个组, 即X=[X1, …, Xk, …, XG], Xk∈RC/G×H×W. 然后, 分组的子特征Xk在信道维度中被分成两个分支: Xk1, Xk2∈RC/2G×H×W. 一个分支通过获取重要关注的信道序列, 另一个分支获取空间重点目标区域. 对于通道注意分支, 先使用全局平均池化来嵌入全局信息s∈RC/2G×1×1来产生信道统计量, 如式(10)所示.
| $ s = {F_{{\rm{gp}}}}({X_{k1}}) = \dfrac{1}{{H{{ \times }}W}}\sum\limits_{i = 1}^H {\sum\limits_{j = 1}^W {{X_{k1}}(i, j)} } $ | (10) |
这里通道注意分支结果为X'k1, 其中W1∈RC/2G×1×1, b1∈RC/2G×1×1用于缩放和移位来增强Xk1的特征表示, 如式(11)所示. 这里的
| $ X_{k1}^\prime = \sigma ({F_c}(s)) \cdot {X_{k1}} = \sigma ({W_1}s + {b_1}) \cdot {X_{k1}} $ | (11) |
对于空间注意分支, 首先对Xk2进行分组归一化(GN)得到空间统计量, 其中W2∈RC/2G×1×1, b2∈RC/2G×1×1用于缩放和移位来增强Xk2的特征表示如式(12)所示:
| $ X_{k2}^\prime = \sigma ({W_2} \cdot GN({X_{k2}}) + {b_2}) \cdot {X_{k2}} $ | (12) |
然后将通道和空间分支拼接得到子特征
本文数据来源为 (brain tumor segmentation, BraTS)竞赛2019年公开的数据集, 其中BraTS2019数据集有76例低级别脑胶质瘤病例与259例高级别脑胶质瘤病例, 本文将BraTS2019数据集按照8:2的比例对训练集和测试集的数据进行划分.
2.2 数据预处理由于使用 3D 格式图像进行训练时间周期长, 并且需要更好的 GPU 和更多内存, 因此选择使用 2D 切片训练本文提出的网络. 每个模态的3D数据大小为240×240×155, 由于脑肿瘤数据的外边缘区域有很多无用的背景信息, 会出现数据类别不平衡的问题. 所以本文首先将3D数据的空间大小裁减为160×160×155, 以消除无用空间背景信息, 然后再沿着通道方向对数据切片, 将3D数据变为155张160×160的2D切片以满足本文模型训练的需要.
因其成像机制不同, 不同模态的影像对比度也不同, 所以使用归一化操作让不同模态的数据强度变得均衡, 有利于模型利用不同模态间的互补信息. 归一化操作如式(13)所示:
| $ {\textit{z}} = \frac{{x - \bar x}}{\lambda } $ | (13) |
其中, x是裁减后的2D切片图像,
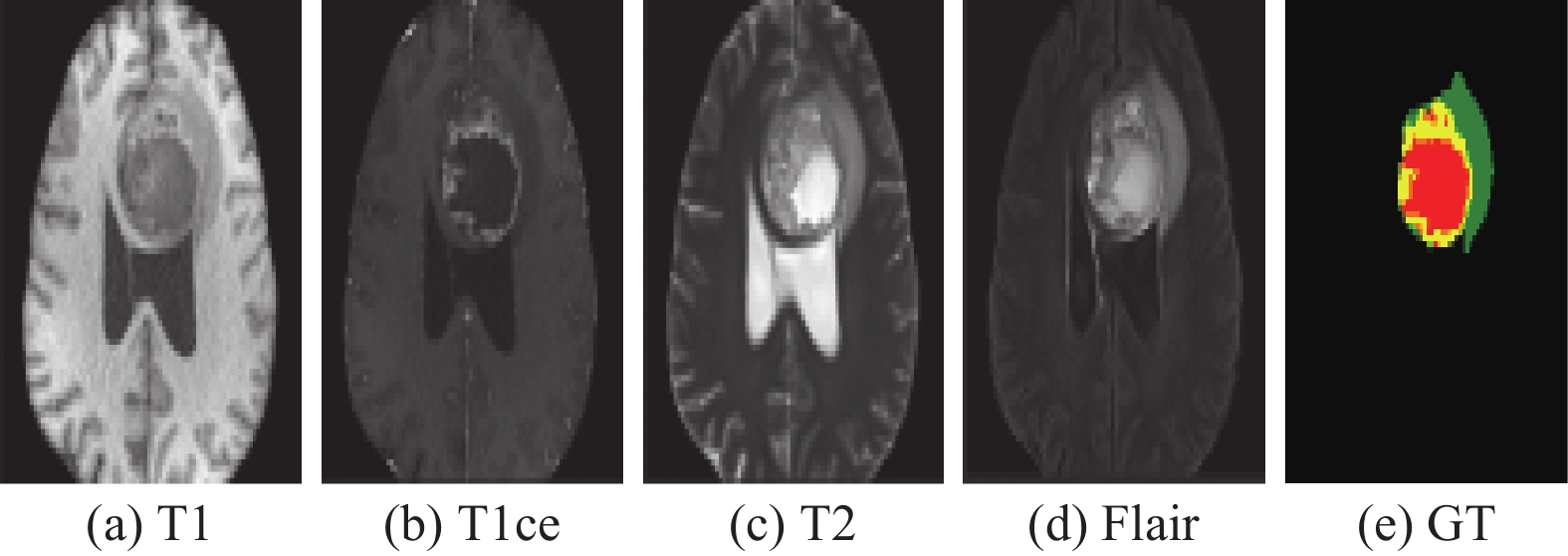
如图5所示, 经过本文预处理后的某一病例切片的4种模态和真实标签的图像, 从左到右依次为T1、T1ce、T2、Flair和GT (ground truth)标签. 其中网络模型预测图和真实标签中的绿色为整体肿瘤区、黄色为增强肿瘤区与红色为坏死和非增强肿瘤区域.
2.3 实验环境配置本文模型使用的深度学习框架是 PyTorch 1.11.0, Cuda 11.3的软件版本, 硬件环境为 CPU是15 vCPU AMD EPYC 7543 32-Core Processor、30 GB内存与使用的GPU是NVIDIA RTX A5000, 显存大小是24 GB. 网络模型使用Adam (adaptive moment estimation) 算法[17]作为优化器来更新模型的权值, 初始学习率为 0.003, 动量值设定为0.09, 权重衰减系数为1E–5. 设定的批量大小为 20, 训练周期数为100.
|
图 5 经过预处理后的4种模态图像与GT真实标签 |
2.4 评价指标
为评测模型的性能, 本文对整体肿瘤区域、核心肿瘤区域和增强肿瘤区域均使用Dice 相似系数(Dice similarity coefficient)来评测模型性能, 如式(14)所示. Dice数值越临近于1, 说明脑肿瘤分割结果与人工标签结果越相似, 分割效果也就越好. 而Dice数值越接近于0, 分割效果则越差.
| $ Dice = \frac{{2|Y \cap P|}}{{|Y| + |P|}} $ | (14) |
其中, Y为人工分割标签的集合, P为模型预测值的集合,
在不同医学数据集的分割任务上常使用(binary cross entropy, BCE)二进制交叉熵作为损失函数, 如式(15)所示:
| $ {L_{{{BCE}}}} = - \frac{1}{N}\sum\limits_{i = 1}^N {\left[ {{y_i}\log \left( {{p_i}} \right) + \left( {1 - {y_i}} \right)\log \left( {1 - {p_i}} \right)} \right]} $ | (15) |
其中, N是输出像素的总数, yi是对应于第i个像素的标签值, 并且pi是第i个像素的模型预测值. 由于BCE损失函数对前景像素和背景像素赋予相同权重, 但是多模态脑肿瘤的前景像素和背景像素比例差别大, 前景像素仅占其中的少数, 数据存在类别不平衡的问题, 为解决数据类别不平衡的问题, 本文在BCE损失函数的基础上增加了Dice损失函数, Dice损失函数如式(16)所示:
| $ {L_{{{Dice }}}} = 1 - \frac{{2\displaystyle\sum\limits_i^N {{p_i}} {y_i} + \varepsilon }}{{\displaystyle\sum\limits_i^N {{p_i}} + \displaystyle\sum\limits_i^N {{y_i}} + \varepsilon }} $ | (16) |
为了保证数据稳定性, 将参数ε的值设为10−6. 另外在模型训练过程中容易出现过拟合, 所以在此基础上又引入了L2损失来缓解训练模型过程中的过拟合问题, 有利于网络的收敛. L2损失函数如式(17)所示:
| $ {L_2} = \frac{1}{N}\Sigma _i^N{\left( {{y_i} - {p_i}} \right)^2} $ | (17) |
综上, 本文的混合损失函数如式(18)所示:
| $ L = {L_{{{Dice }}}} + \alpha {L_{{{BCE }}}} + \beta {L_2} $ | (18) |
本文使用控制超参变量的方法来试验最佳参数, 首先将β设置为0, 以试验最佳的超参α, 如图6所示, α的波动范围在0–1之间, 当α为0.5时, 本文模型在整体肿瘤(whole tumor, WT)、核心肿瘤(tumor core, TC)与增强肿瘤(enhancing tumor, ET)区域上达到最高峰值点, 说明此时模型性能达到最优.

|
图 6 超参α对模型性能的影响 |
在此基础上, 继续试验最佳的超参β, 如图7所示, 其中β的波动范围在0–0.1之间. 最终确定参数α为0.5, β为0.05时本文模型在WT、TC和ET区域上的Dice系数达到0.887、0.892与0.815, 模型预测性能达到了最好.
将最佳超参α=0.5与β=0.05带入混合损失函数中, 当模型训练迭代次数为100轮时, 模型的训练损失值和验证损失值达到最佳, 如图8所示.
2.6 消融实验为了验证本文设计和添加模块的有效性, 在UNet的架构上添加不同的模块, 使用相同的损失函数和参数实验. 结果如表1所示.
表1中DPLC代表密集卷积并行大核注意模块、MDFM代表多模态深度融合模块、SA代表Shuffle Attention注意力模块. 在将DLCB模块添加到UNet后, 在模型的整体肿瘤、核心肿瘤与增强肿瘤区域中分别增加了1.7%、3.6%和1.4%. 随着MDFM模块的加入, 模型在核心肿瘤区和增强区的表现也得到了进一步地提高. 最后, 增加了改进的 SA注意力. 该方法在3种不同类型的肿瘤中均取得了良好的分割效果, 证明了该方法的有效性.

|
图 7 超参β对模型性能的影响 |

|
图 8 模型训练Loss变化 |
| 表 1 模块消融对比实验 |
为了测试在解码器分支添加不同注意力的有效性, 本文将SA注意力机制分别与SE通道注意力[18]、CBAM通道空间注意力[19]、ECA高效通道注意力[20]进行对比, 如表2所示, 在解码器分支使用改进的SA注意力机制相比使用SE注意力, 在模型的整体肿瘤、核心肿瘤与增强肿瘤区域中分别增加了4.2%、3.5%和4.4%, 加强了模型捕获重要特征信息的能力.
| 表 2 添加不同注意力模块的实验 |
2.7 实验结果
为了进一步验证本文方法对多模态脑肿瘤MR图像分割的有效性, BraTS2019部分数据集作为测试集来与其他先进方法进行比较, 结果如表3所示.
相比与UNet、UNet++与DenseUNet的经典2D 网络, 本文模型在整体、核心与增强肿瘤区域都有较大的性能提升. 而与先进的TransBTS、ADHDC-Net与SDS-MSA-Net等3D模型对比时, 3D模型因其空间连续在整体肿瘤分割中占有优势, 但本文2D模型在核心与增强肿瘤区具有更好的分割性能, 且相较于3D模型, 降低了对高显存硬件资源的依赖.
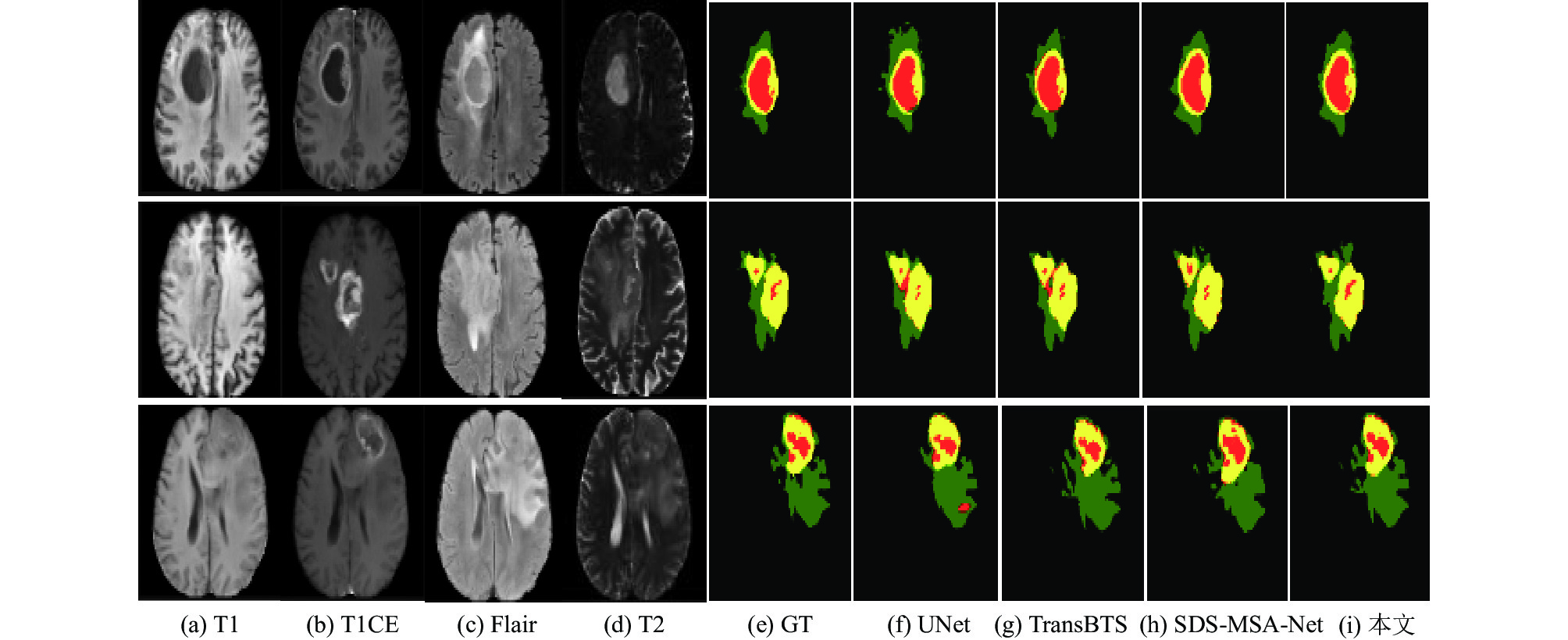
最后本文对BraTS2019测试数据集的样例进行分割对比, 模型的输入图像与分割结果对比如图9所示, 每一行代表一个病例患者, 第1–4列依次为T1、T1CE、Flair、T2的不同脑肿瘤模态, 第5列为高级医师的黄金分割标准. 从图9可以看出, UNet对第1个病例的水肿区域存在过分割现象; 当前先进的TransBTS与SDS-MSA-Net的3D网络因其空间连续, 对绿色的整体肿瘤区域分割效果良好, 但其在第2与第3病例上将部分水肿区域误分割为红色的核心肿瘤区域, 本文提出的分割模型在TC和ET肿瘤区域上, 比先进3D网络的SDS-MSA-Net分别提升了3.5%、1.9%, 相比之下本文方法对肿瘤核心和增强区域有更好的分割效果.
| 表 3 在BraTS2019测试集上与先进算法的比较 |
|
图 9 分割结果直观对比 |
2.8 网络模型复杂度对比分析
为了更好地检测模型的性能, 在相同输入大小的条件下, 对网络模型的参数量(Params)和计算量(FLOPs)进行对比, 如表4所示. 本文模型的参数量相比基础网络UNet减少了约55.17%, 计算量降低了约19.85%. 且与先进的3D模型SDS-MSA-Net相比, 本文的参数量减少了约45.42%, 计算量降低了约69.57%. 综上所述, 本文模型在具有较低参数量和计算量的条件下, 对脑肿瘤的核心和增强区域的分割性能达到了最优状态.
3 结束语为了解决脑肿瘤多模态信息融合不充分以及肿瘤区域细节信息丢失的问题, 本文在编码器-解码器结构的基础上进行改进, 将本文设计的多模态深度融合MDFM模块、密集并行大核注意卷积DPLC模块与改进的Shuffle Attention引入到架构中, 提出了一种跨模态融合的双注意力脑肿瘤分割方法. 其中MDFM模块可以增强不同模态对间的互补信息, 使肿瘤区域特征融合更充分; 编码器分支使用DPLC模块有效提取了全局和局部信息; 解码器分支使用改进的SA模块, 通道分组后一分为二地捕获重要的空间和通道特征; 设计了新混合函数, 缓解了脑肿瘤数据类别不平衡问题与网络训练时存在的过拟合问题. 实验结果证明, 本文模型在核心肿瘤和增强肿瘤区域优于其他先进模型; 在整体肿瘤区域, 虽然提高了检测效率, 但切片间的连续信息会有丢失. 因此在后续工作中, 将使用2.5D网络或者低参数的3D网络来进一步加强对整体肿瘤区域的分割, 提升对脑肿瘤的分割精度.
| 表 4 不同网络模型的复杂度对比 |
| [1] |
Ostrom QT, Cioffi G, Waite K, et al. CBTRUS statistical report: Primary brain and other central nervous system tumors diagnosed in the United States in 2014–2018. Neuro-Oncology, 2021, 23(S3): iii1-iii105. |
| [2] |
Zhou TX. Modality-level cross-connection and attentional feature fusion based deep neural network for multi-modal brain tumor segmentation. Biomedical Signal Processing and Control, 2023, 81: 104524. DOI:10.1016/j.bspc.2022.104524 |
| [3] |
Wang JJ, Yu ZS, Luan ZY, et al. RDAU-net: Based on a residual convolutional neural network with DFP and CBAM for brain tumor segmentation. Frontiers in Oncology, 2022, 12: 805263. DOI:10.3389/fonc.2022.805263 |
| [4] |
Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Munich: Springer, 2015. 234–241.
|
| [5] |
Zhou ZW, Rahman Siddiquee MM, Tajbakhsh N, et al. UNet++: Redesigning skip connections to exploit multiscale features in image segmentation. IEEE Transactions on Medical Imaging, 2020, 39(6): 1856-1867. DOI:10.1109/TMI.2019.2959609 |
| [6] |
侯奕辰, 彭辉, 谢俊章, 等. 改进UNet++在脑肿瘤图像分割的研究. 计算机工程与设计, 2022, 43(6): 1725-1731. |
| [7] |
Huang G, Liu Z, van der Maaten L, et al. Densely connected convolutional networks. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 2261–2269.
|
| [8] |
Kaku A, Hegde CV, Huang J, et al. DARTS: DenseUNet-based automatic rapid tool for brain segmentation. arXiv:1911.05567, 2019.
|
| [9] |
Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. Proceedings of the 4th International Conference on 3D Vision (3DV). Stanford: IEEE, 2016. 565–571.
|
| [10] |
Wang WX, Chen C, Ding M, et al. TransBTS: Multimodal brain tumor segmentation using Transformer. Proceedings of the 24th International Conference on Medical Image Computing and Computer Assisted Intervention. Strasbourg: Springer, 2021. 109–119.
|
| [11] |
Liu HX, Huo GQ, Li Q, et al. Multiscale lightweight 3D segmentation algorithm with attention mechanism: Brain tumor image segmentation. Expert Systems with Applications, 2023, 214: 119166. DOI:10.1016/j.eswa.2022.119166 |
| [12] |
Rehman A, Usman M, Shahid A, et al. Selective deeply supervised multi-scale attention network for brain tumor segmentation. Sensors, 2023, 23(4): 2346. DOI:10.3390/s23042346 |
| [13] |
Liu Y, Mu FH, Shi Y, et al. Brain tumor segmentation in multimodal MRI via pixel-level and feature-level image fusion. Frontiers in Neuroscience, 2022, 16: 1000587. DOI:10.3389/fnins.2022.1000587 |
| [14] |
Zhang QL, Yang YB. SA-NET: Shuffle attention for deep convolutional neural networks. Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Toronto: IEEE, 2021. 2235–2239.
|
| [15] |
Guo MH, Lu CZ, Liu ZN, et al. Visual attention network. Computational Visual Media, 2023, 9(4): 733-752. DOI:10.1007/s41095-023-0364-2 |
| [16] |
Zhou Y, Liang XF, Gu Y, et al. Multi-classifier interactive learning for ambiguous speech emotion recognition. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2022, 30: 695-705. DOI:10.1109/TASLP.2022.3145287 |
| [17] |
Wu XD, Huang FH, Huang H. Fast stochastic recursive momentum methods for imbalanced data mining. Proceedings of the 2022 IEEE International Conference on Data Mining (ICDM). Orlando: IEEE, 2022. 578–587.
|
| [18] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
|
| [19] |
Woo S, Park J, Lee JY, et al. CBAM: Convolutional block attention module. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 3–19.
|
| [20] |
Wang QL, Wu BG, Zhu PF, et al. ECA-net: Efficient channel attention for deep convolutional neural network. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 11531–11539.
|
 2024, Vol. 33
2024, Vol. 33


