网络科学是一个融合了数学、生物、统计学、社会学等多个学科思想与技术的交叉学科领域. 网络是由节点两两之间连边所构成. 例如交通枢纽与航线构成了交通运输网络, Zhang等[1]应用加入协变量的随机块网络模型分析了美国航空网络; 在生物上, 构建蛋白质之间的生化反应网络对于识别同源蛋白质或者蛋白质功能模块、蛋白质功能预测等方面具有十分重要的生物学意义[2]. 网络能够捕捉系统内部相互作用的模式, 是用来抽象并研究复杂系统的重要工具[3].
社区结构是网络数据最显著的特征之一, 是探索网络结构和功能的基本属性. 社区通常被定义为一个子网络, 子网络内部的节点之间连边较为密集, 不同子网络之间的连边相对比较稀疏[4]. 例如在文献引用网络中, 节点表示论文, 边表示论文之间的引用关系, 同一研究领域中的文献互相引用的频率往往比跨领域更高, 通过分析由相同研究领域的论文构成的社区结构, 可以帮助我们更好地了解当前的热门研究方向. 社区检测指将网络中的节点按照它们之间连边的密集程度进行聚类, 从而获得网络的社区结构, 它是近年来网络科学前沿领域十分热门的研究课题. Liu等[5]对fMRI数据构建网络模型, 同时实现了网络结构的恢复与社区检测, Ren等[6]则应用正则化网络嵌入的方法实现了对社区数目的相合求解, 并完成社区检测. 在实际中, 一方面, 社区检测可以作为揭示网络局部结构、挖掘相似模式的有力工具, 例如在对于消费者的购物信息构建的网络中进行社区检测可以发现具有相似购物倾向的消费者团体, 从而有利于企业进行针对性营销, 开发更高效的推荐系统[7]. 另一方面, 社区检测允许我们将大型网络有规律地划分为小型子网络, 并对它们分别进行研究. 大数据时代构建的网络规模常常会达到上万甚至上亿的规模, 对如此规模的网络进行整体研究是十分困难的事情, 因此社区检测能有效地将网络规模减小到可操作水平. 现有的大部分方法主要针对的是无向网络上的社区检测, 然而在实际应用中, 许多网络数据本质上是定向的, 例如在原核生物基因组序列数据中, 基因组之间的供体-受体关系是通过有向网络(横向基因转移网络-LGT)来建模的. 因此在有向网络中寻找社区结构是一项重要的任务, 在多个领域中有着广泛的应用.
目前常见的社区检测算法大致可以分为两类[1]: 第1类是对网络建立概率模型, 运用似然的方法完成社区检测任务, 具有代表性的是随机块模型[8]、度修正的随机块模型[9]、混合成员随机块模型[10]等. 第2类是定义一个用以衡量网络划分准确性的目标函数, 然后对其进行优化来获得网络的社区结构. 在第2类方法中, Paatero等[11]提出的非负矩阵分解(non-negative matrix factorization, NMF)以其计算简便、可解释性强等优点受到广泛关注. NMF的基本思想是用两个低秩非负矩阵来逼近目标非负矩阵, 能够对原始高维数据给出低维潜空间表示. Lee等[12]将NMF应用于图像处理, 取得了卓越的效果, 此后也被广泛应用于文档聚类[13,14]、推荐系统等[15,16]领域. Wang等[17]将NMF应用于网络社区检测, 并分别针对无向网络、有向网络、复合网络给出了对应的模型与求解方法; 其中针对有向网络, Wang等[17]提出采用非负矩阵三分解对标准NMF进行改进, 明确了社区之间的交互作用. 在现实世界的许多网络数据中, 来自专业领域知识的先验信息是可用的, 使用先验信息的社区检测方法称为半监督社区检测方法. 合理利用这些先验信息作为指导, 可以大大提升社区检测的准确性. Zhang[18]提出了一种半监督学习框架, 通过纳入ML (must-link)与CL (cannot-link)这两种先验信息来重建邻接矩阵以指导社区检测, 让社区结构更加清晰, 取得了较好的效果. 此后, Zhang等[19]在文献[18]的基础上, 在重建邻接矩阵的步骤中加入逻辑推断, 使得先验信息得到了更充分的利用, 同时验证了ML先验信息比CL先验信息更加有效. 文献[18]与文献[19]所提出的算法简洁高效, 但主要针对无向网络, 并且对于先验信息的运用仅限于重构网络拓扑. Yang等[20]通过在目标函数中增加了融入先验信息的图正则化项, 以约束具有ML先验信息的节点对在低维空间中的距离. 与文献[18]、文献[19]类似, 该工作主要考虑无向网络上的社区检测, 同时没有考虑节点度异质性对于目标函数的影响. Liu等[21]则进一步在目标函数中引入度对角矩阵, 消除了节点度异质性的影响. Liu等[21]所采用的对称NMF针对的是无向网络上的社区检测问题, 无法拓展到有向网络.
本文提出了一种基于非负矩阵分解的有向网络半监督社区检测算法, 与现有的基于非负矩阵分解的社区检测算法相比, 具有以下创新性.
(1) 本文采用非负矩阵三分解模型考虑有向网络上的社区检测问题, 与标准NMF相比, 可以发现社区之间的相互作用, 更类似于真实网络.
(2) 对先验信息的利用更加充分, 除了用先验信息重构邻接矩阵, 本模型还在目标函数中添加了融入先验信息的惩罚项, 从而使具有ML先验信息约束的节点对更有可能被分到同一社区.
(3) 本文考虑了网络中常见的节点度异质造成的影响, 通过对矩阵U施加行归一化约束提高了模型的适用性. 非负双奇异值分解初始化让算法计算效率更高.
后文组织如下: 第1节给出问题定义, 并介绍将非负矩阵分解用于社区发现的思路. 第2节阐述模型与求解方法. 第3节介绍实际数据模拟与实验结果分析. 第4节进行总结, 并给出下一步工作的想法.
1 社区检测与非负矩阵分解本节介绍社区检测的问题定义以及如何利用非负矩阵分解进行社区检测.
1.1 先验信息指导的有向网络社区检测问题给定一有向网络G = (V, E), 其中V为网络节点集合, 大小为n, E为节点之间连边集合, 并设节点vi对应编号i,
| $ A_{ij} = \left\{ {\begin{array}{*{20}{c}} {1, \; (i, j) \in E} \\ {0, \; (i, j) \notin E} \end{array}} \right. $ | (1) |
上述定义给出了网络的拓扑结构. 下面考虑用先验信息指导社区检测. 由于实际中ML先验信息比CL先验信息更容易获得, 且更加有效[19], 因此这里采用ML先验信息, 它是指节点对属于同一社区, 在进行划分时也要尽量把具有ML先验信息的节点对分到同一社区. 令ML先验信息集合为C, 如果(i, j)
我们的任务目标是: 基于给定的有向网络拓扑A与先验信息集合C, 求解网络G的社区结构.
1.2 利用非负矩阵分解进行社区检测考虑非负矩阵X
| $ \mathop {\min }\limits_{\boldsymbol U \geqslant 0, \boldsymbol V \geqslant 0} \left\| { \boldsymbol A - \boldsymbol U \boldsymbol V{ \boldsymbol U^{\rm{T}}}} \right\|_F^2 $ | (2) |
其中,
该模型中, 矩阵U提供了节点所属社区信息, V提供了社区之间的相互作用信息. U的n行可以看作网络中的n个节点在低维潜空间中的表示, Uij表示节点vi相对于社区j的隶属度, 即节点vi被划分到社区j的倾向性, 因此我们将vi分到社区l如果Uil = max{Uij | j
根据文献[17], 在下述迭代更新规则下, 目标函数非增:
| $ U_{ij} = U_{ij}\left( {\frac{{\left[ {\boldsymbol A_{}^{\rm{T}} \boldsymbol U \boldsymbol V + \boldsymbol {AUV}_{}^{\rm{T}}} \right]_{ij}}}{{\left[ {\boldsymbol {UVU}_{}^{\rm{T}}\boldsymbol{UV}_{}^{\rm{T}} + \boldsymbol{UV}_{}^{\rm{T}}\boldsymbol {U}_{}^{\rm{T}}\boldsymbol{UV}} \right]_{ij}}}} \right)_{}^{1/4} $ | (3) |
| $ V_{ij} = V_{ij}\frac{{\left[ {\boldsymbol U_{}^{\rm{T}}\boldsymbol{AU}} \right]_{ij}}}{{\left[ {\boldsymbol{U}_{}^{\rm{T}}\boldsymbol{UVU}_{}^{\rm{T}}\boldsymbol{U}} \right]_{ij}}} $ | (4) |
其中, 比例调整因子1/4是为了防止迭代更新过于激进. 根据式(3)、式(4)可获得优化问题的解. 以上即为利用非负矩阵分解进行社区检测的基本思想. 下面我们将介绍本文所提出的算法.
2 基于非负矩阵分解的有向网络半监督社区检测方法本节阐述本文所提出的模型, 首先利用先验信息重建网络拓扑, 然后在目标函数中加入由先验信息所指导的惩罚项, 同时对矩阵U进行行归一化来消除节点度异质性的影响, 最后给出求解算法.
2.1 利用先验信息重构网络拓扑考虑有向网络G = (V, E), 我们获得如第1.1节中所定义的邻接矩阵A以及ML先验信息集合C. 根据C可以构造ML先验指示矩阵M
| $ M_{ij} = \left\{ {\begin{array}{*{20}{l}} {\alpha , \; (i, j) \in C} \\ {0, \; 其他} \end{array}} \right. $ | (5) |
其中, α为权重参数, 它会影响模型中ML先验信息的重要性, α越大, 先验信息越重要. 如果α过大, 模型将过分依赖先验信息而忽略网络自身结构, 而当α过小时, 先验信息无法有效指导社区检测过程. 根据经验, 本文采用α = 2, 这在真实数据实验中取得了良好效果.
需要注意的是, 真实网络中的边往往非常稀疏, 仅使用观察到的节点之间的连接不足以表示节点之间的整体关联, 因此更好的做法是将先验信息整合到网络结构中, 使结果更清晰、更易于解释. 这里选择将ML先验信息整合到邻接阵A中, 获得重构邻接矩阵B, 如下所示:
| $ B_{ij} = \left\{ {\begin{array}{*{20}{l}} {M_{ij},\; (i, j) \in C} \\ A_{ij},\;\; 其他 \end{array}} \right. $ | (6) |
由此在式(2)基础上, 问题转化为如下形式:
| $ \mathop {\min }\limits_{\boldsymbol U \geqslant 0, \boldsymbol V \geqslant 0} \left\| {\boldsymbol B - \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}} \right\|_F^2 $ | (7) |
式(7)表示使用重构邻接矩阵B进行非负矩阵三分解. 与式(2)所使用的邻接阵A相比, 式(7)中的B融合了先验信息, 增强了网络社区内部节点之间的链接密集性, 因此分解获得的U和V所提供的节点隶属度信息和社区间的相互作用效应更加明确.
2.2 融入先验信息的惩罚项仅重构邻接矩阵对于先验信息的使用是不充分的, 这里进一步利用先验信息对节点的社区隶属度矩阵U进行约束.
如上文所述, U的行向量可以看作节点在低维潜空间中的表示, 其分量可以看作该行所对应的节点相对于各个社区的隶属度. 因此, 如果节点vi和vj属于同一社区, 那么U的第i行与第j行的最大值应该在同一列. 由这一想法, 我们可以在目标函数中添加融入先验信息的惩罚项:
| $ \mathop {\min }\limits_{\boldsymbol U \geqslant 0, {\boldsymbol V} \geqslant 0} \left\| {\boldsymbol B - \boldsymbol{UV}{\boldsymbol U^{\rm{T}}}} \right\|_F^2 + \lambda \sum\limits_{i, j = 1}^n {M_{ij}\sum\limits_{p = 1}^k {\sum\limits_{q = 1, q \ne p}^k U_{ip}U_{jq} } } $ | (8) |
其中, 正则化参数λ控制矩阵分解项与惩罚项之间的平衡.
利用简单的代数运算可以将问题转化为如下形式:
| $ \mathop {\min }\limits_{ \boldsymbol U \geqslant 0, \boldsymbol V \geqslant 0} \left\| { \boldsymbol B - \boldsymbol{UV}{\boldsymbol U^{\rm{T}}}} \right\|_F^2 + \lambda Tr\left( {\boldsymbol U_{}^{\rm{T}} \boldsymbol{MUQ}} \right) $ | (9) |
其中, Q = En −In, En为元素全为1的n阶方阵, In为n阶单位阵.
2.3 行归一化消除节点度异质性影响上述模型对于先验信息的利用已经较为完善, 但忽略了节点度异质性的影响, 而节点度的信息存储在矩阵U的行范数中. 因此考虑对U的行进行归一化, 于是在式(9)的基础上, 问题转化为如下形式:
| $ \mathop {\min }\limits_{\boldsymbol U \geqslant 0, \boldsymbol V \geqslant 0} \left\| {\boldsymbol B - \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}} \right\|_F^2 + \lambda Tr\left( {\boldsymbol U_{}^{\rm{T}}\boldsymbol{MUQ}} \right) + \eta \left\| {U{\mathbf{1}}_k - {\mathbf{1}}_n} \right\|_F^2 $ | (10) |
其中,
类似第1.2节, 固定U或者V时模型式(10)对这两者中的另一矩阵都是凸的, 因此采用交替迭代更新进行优化以获得局部最小值. 这里令Γ和Θ分别为约束条件U ≥ 0和V ≥ 0的拉格朗日乘子矩阵, 由此可定义如下拉格朗日函数L:
| $ L = \ell \left( {\boldsymbol U, \boldsymbol V} \right) + Tr\left( {\varGamma \boldsymbol U_{}^{\rm{T}}} \right) + Tr\left( {\Theta \boldsymbol V_{}^{\rm{T}}} \right) $ | (11) |
其中,
| $ \begin{split} \frac{{\partial L}}{{\partial \boldsymbol U}} =& 2 \boldsymbol U{\boldsymbol V^{\rm{T}}}{\boldsymbol U^{\rm{T}}}\boldsymbol {UV} + 2 \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U{\boldsymbol V^{\rm{T}}} + 2\eta \boldsymbol U{{\mathbf{1}}_k}{\mathbf{1}}_k^{\rm{T}} \\ & +2\lambda \boldsymbol {MUQ} - 2\boldsymbol {BU}{\boldsymbol V^{\rm{T}}} - 2{\boldsymbol B^{\rm{T}}}\boldsymbol{UV} - 2\eta {{\mathbf{1}}_n}{\mathbf{1}}_k^{\rm{T}} + \varGamma \end{split} $ | (12) |
| $ \frac{{\partial L}}{{\partial \boldsymbol V}} = 2{\boldsymbol U^{\rm{T}}}\boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U - 2{\boldsymbol U^{\rm{T}}}\boldsymbol {BU} + \Theta $ | (13) |
令式(12)与式(13)中的偏导数为0, 并由KKT条件, 对任意的i和j都有ΓijUij = 0和ΘijVij = 0, 得到以下关系:
| $ \begin{split} 0 = &\left[ {\boldsymbol U{\boldsymbol V^{\rm{T}}}{\boldsymbol U^{\rm{T}}}\boldsymbol {UV} + \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U{\boldsymbol V^{\rm{T}}} + \eta \boldsymbol U{{\mathbf{1}}_k}{\mathbf{1}}_k^{\rm{T}} + \lambda MUQ} \right]_{ij}U_{ij} \\ &- \left[ {\boldsymbol {BU}{\boldsymbol V^{\rm{T}}} + {\boldsymbol B^{\rm{T}}}\boldsymbol {UV} + \eta {{\mathbf{1}}_n}{\mathbf{1}}_k^{\rm{T}}} \right]_{ij}U_{ij} \end{split} $ | (14) |
| $ 0 = \left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U} \right]_{ij}\boldsymbol V_{ij} - \left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {BU}} \right]_{ij}\boldsymbol V_{ij} $ | (15) |
从而有更新规则:
| $ \begin{split} & U_{ij} =\\ & U_{ij}\left( {\frac{{\left[ {\boldsymbol {BU}{\boldsymbol V^{\rm{T}}} + {\boldsymbol B^{\rm{T}}}\boldsymbol {UV} + \eta {{\mathbf{1}}_n}{\mathbf{1}}_k^{\rm{T}}} \right]_{ij}}}{{\left[ {\boldsymbol U{\boldsymbol V^{\rm{T}}}{\boldsymbol U^{\rm{T}}}\boldsymbol {UV} + \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U{\boldsymbol V^{\rm{T}}} + \eta \boldsymbol U{{\mathbf{1}}_k}{\mathbf{1}}_k^{\rm{T}} + \lambda \boldsymbol {MUQ}} \right]_{ij}}}} \right) \end{split} $ | (16) |
| $ V_{ij} = V_{ij}\left( {\frac{{\left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {BU}} \right]_{ij}}}{{\left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U} \right]_{ij}}}} \right) $ | (17) |
与式(3)类似, 为了防止对于U的更新过于激进, 可以对其乘法更新系数添加非线性调整比例因子1/4. 因此最终的迭代更新规则如下:
| $ \begin{split} U_{ij} = U_{ij}{\left( {\frac{{\left[ {\boldsymbol {BU}{\boldsymbol V^{\rm{T}}} + {\boldsymbol B^{\rm{T}}}\boldsymbol {UV} + \eta {{\mathbf{1}}_n}{\mathbf{1}}_k^{\rm{T}}} \right]_{ij}}}{{\left[ {\boldsymbol U{\boldsymbol V^{\rm{T}}}{\boldsymbol U^{\rm{T}}}\boldsymbol {UV} + \boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U{\boldsymbol V^{\rm{T}}} + \eta \boldsymbol U{{\mathbf{1}}_k}{\mathbf{1}}_k^{\rm{T}} + \lambda \boldsymbol {MUQ}} \right]_{ij}}}} \right)^{1/4}} \end{split} $ | (18) |
| $ V_{ij} = V_{ij}\left( {\frac{{\left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {BU}} \right]_{ij}}}{{\left[ {{\boldsymbol U^{\rm{T}}}\boldsymbol {UV}{\boldsymbol U^{\rm{T}}}\boldsymbol U} \right]_{ij}}}} \right) $ | (19) |
对于迭代初始矩阵, 这里采用基于奇异值分解的非负双奇异值分解方法对U和V进行初始化[22]. 综上所述, 我们提出了惩罚非负矩阵三分解(PNMTF)算法, 如算法1所示.
算法1. PNMTF算法
Input: n阶邻接阵A, ML先验信息集合C, 社区数目k, 迭代次数iter
Output: 各节点vi的社区标签ci
1) 根据ML先验信息集合C构建ML先验信息指示矩阵M;
2) 基于式(6)构建重构矩阵B;
3) 对U、V进行初始化得到矩阵U0和V0;
4) while t ≤ iter do
基于式(18)更新U;
基于式(19)更新V;
5) end
6) (vi, ci) = arg maxj ≤ k Uij.
算法1具有以下特点: (1) 当先验信息较多时, 先验信息在算法中起主要作用, 而先验信息较少时, 主要基于网络本身的结构信息进行社区检测; (2) 我们采用的非负双奇异值分解初始化方法比通常使用的随机初始化方法计算效率更高, 只需要一次运行和较少次数的迭代就能保证算法收敛; (3) 式(18)、式(19)中的迭代更新规则能够保证目标函数非增, 并收敛到使目标函数满足KKT条件的稳态点. 我们对该算法的时间复杂度进行了一个简单的估计. 在每次迭代中, 根据对更新规则式(18)和式(19)的分析, 可以得出时间复杂度为O(n2k + nk2)的结论. 当邻接阵A具有稀疏性时, 时间复杂度可以降低到O(mk + nk2), 其中m表示边数. 由于k通常比n小得多, 因此这种情况下可以认为PNMTF算法的时间复杂度与网络的规模接近线性.
3 实验分析实验分为以下几部分: 第3.1节阐述PNMTF算法与其他方法的对比实验, 并分析消融实验结果; 第3.2节讨论ML先验信息比例对于社区发现结果的影响; 第3.3节进行参数调优, 分析惩罚项、行归一化项与矩阵分解项的平衡关系; 第3.4节分析算法的收敛性. 实验中, 我们使用了5个真实网络数据集: Cornell、Email、Texas、Washington和Wisconsin, 其中Cornell、Texas、Washington、Wisconsin来自4所大学的WebKB子网, 节点表示网页, 有向边表示网页之间的链接, 网页分为5类: 学生、教师、员工、课程、项目, Email来自欧洲大型研究机构42个不同部门的1005名员工之间的电子邮件交流网络, 节点表示员工, 有向边表示起始节点向末端节点发送了电子邮件. 表1给出了关于这5个网络的更详细信息.
3.1 方法对比与消融实验我们将本文的PNMTF算法与以下的半监督方法GNMF[20]、PSSNMF[21]、FSSNMF[19]和无监督方法K-means、ANMF[17]进行了对比, 并将消融实验的结果一并呈现在对比图中. 对于无监督的ANMF和K-means方法, 先类似FSSNMF将ML先验信息嵌入到邻接阵中, 然后使用ANMF和K-means进行无监督社区检测. 在消融实验中, 当惩罚项、行归一化项均不包含时, 模型退化为上述ANMF算法; 仅包含惩罚项时, 对应ABLATION曲线; 仅包含行归一化项时, 由于节点度异质性不会对目标函数产生影响, 故这种情况不予考虑.
| 表 1 真实网络数据描述 |
本文在实验中采用了两种广泛使用的评价指标: 聚类精度(clustering accuracy, AC)与归一化互信息[23](normalized mutual information, NMI)来衡量算法性能. NMI通过计算真实社区与由算法得到的社区之间的相似性来检验社区精度, 取值范围为[0, 1], NMI值越大, 算法性能越好. AC定义为社区归属划分正确的节点数与网络中节点总数之比, 取值范围为[0, 1], AC值越大, 算法性能越好.
由于实验中不知道哪些节点对具有ML先验信息, 因此我们从网络中所有可能的ML先验信息中随机选择一定比例用于指导社区检测. 例如, 给定一个具有n个节点、k个社区的网络, 社区i包含的节点数目为ni, 那么网络中所有可能的ML先验信息数量为:
| $ N = \sum\limits_{i = 1}^k {\frac{{{n_i}\left( {{n_i} - 1} \right)}}{2}} $ | (20) |
然后按一定比例从这N对中进行随机选择. 此外, Zhang等[19]引入了能使先验信息得到更充分利用的逻辑推断, 即: 令C为ML先验信息集合, 如果(i, j)
模拟中, 指定迭代次数为100次, 当损失函数的变化量小于10−5时, 迭代终止. 在每个数据集上, 设置先验信息的获取比例为2%、4%、6%、8%、10%、12%、14%, 并对每种方法重复运行10次, 计算每次的NMI值与AC值, 并分别取均值, 最终结果如图1所示.

|
图 1 5个数据集上不同方法及消融实验对比结果 |
不难看出, 在这5个数据集上所有的ML先验信息比例下, PNMTF算法均优于其他5个对比方法. 在先验信息比例较少如2%、4%时, 可以看到PNMTF在NMI值和AC值上相对于其他算法均具有优势, 说明PNMTF对于先验信息的利用率最高. 而当先验信息的获取比例达到10%时, PNMTF在Cornell、Washington、Wisconsin上的NMI值和AC值均逼近1, 而在Email和Texas上的NMI值和AC值也都超过0.9, 由此可以说明当先验信息比例达到10%的时候, 我们的方法已经具有较为出色的社区检测性能. 同时注意到当先验信息比例较大时, 非负矩阵分解及其拓展方法的效果普遍优于K-means算法, 而基于非负矩阵三分解的算法(PNMTF、ANMF、ABLATION)均优于非负矩阵二分解及其拓展算法(GNMF、PSSNMF、FSSNMF), 这是因为在进行有向网络社区检测时, 二分解所获得的两个矩阵分别蕴含从节点生成社区的出边与入边信息, 仅使用其中一个矩阵进行社区检测会忽略掉另一方信息; 而三分解方法中, V矩阵表示社区之间的相互作用, 已经蕴含连边的不对称性, 因此方向信息已经被分解出来, 再使用矩阵U进行社区检测会得到更准确的结果.
值得注意的是, 5个数据集中Email属于大规模网络, 与其他数据相比, Email数据包含的节点数和边数都显著增加, 因此算法的迭代更新速率较慢. 对比图1(i)、图1(j)与图1(a)到图1(h), 随着先验信息比例增加, PNMTF在Email上获得的NMI值与AC值的增加速率也显著低于其他4个数据集. 这是因为Email网络包含的社区数目较多, 社区结构更复杂, 平均社区规模较小, 因此提高先验信息的比例时, 算法的提升效果不如其他4个数据集.
此外, 消融实验探究的是模型中惩罚项与行归一化项的必要性, 与PNMTF进行对比的是ANMF曲线和ABLATION曲线. 注意到在5个数据集中的所有先验信息比例下, ABLATION的NMI值与AC值均优于ANMF, 因为ABLATION在ANMF的基础上考虑了对节点的社区隶属度进行约束的惩罚项, 对先验信息有更好的利用. 而PNMTF在社区检测性能上优于ABLATION, 原因就是本文模型在目标函数中添加了U矩阵行归一化项, 解决了节点度异质性的问题, 最终呈现出不错的结果.
3.2 先验信息的作用本节讨论不同的ML先验信息比例的影响. 我们不考虑网络本身的边, 仅基于先验信息来分析网络中的连接组件.
连接组件是指网络中一组可以通过路径互相连接的节点, 也就是说网络中任一连通子图所包含的节点都构成一个连接组件. 我们在这5个真实网络中计算了不同先验信息比例下由先验信息所导出的所有社区中连接组件的平均数量和平均规模, 结果如表2所示. 连接组件的平均数目定义为网络中连接组件个数除以社区数目, 表示平均每个社区中包含的连接组件数目. 连接组件的平均规模定义为所有连接组件包含的节点总数除以连接组件的个数, 表示平均每个连接组件包含的节点数目. 可以看出当先验信息比例较小时, 连接组件平均数量较大, 平均规模较小. 这意味着网络社区中包含许多由较少节点组成的小型连接组件, 这时PNMTF算法主要是决定合并哪些连接组件进行社区检测. Email数据在2%先验信息比例时, 连接组件的平均数量和平均规模都比其他4个数据集小, 所以先验信息在Email上对结果的提升不如其他4个数据集.
| 表 2 5个数据集上不同先验信息比例下所有社区中连接组件的平均数目和平均规模 |
随着先验信息比例的增大, 连接组件平均数量减小, 平均规模变大, 这意味着社区中的连接组件存在融合, 也就是多个由少数节点组成的连接组件融合为包含许多节点的大型连接组件. 当先验信息足够多时, 从表2中可以看到各个数据集中平均每个社区包含的连接组件数量都接近1, 而平均每个连接组件包含的节点数目都接近网络的平均社区规模, 这时网络中的社区结构更加清晰, 社区检测更加精确.
总的来说, 先验信息对社区检测具有较好的指导效果, 先验信息越多社区检测精度越高. 而先验信息在不同网络上起的作用受平均社区规模影响, 对比Email数据和其他4个数据可以发现, 平均社区规模越大, 先验信息对检测精度提升越明显.
3.3 调优参数分析本节分析模型中的平衡参数
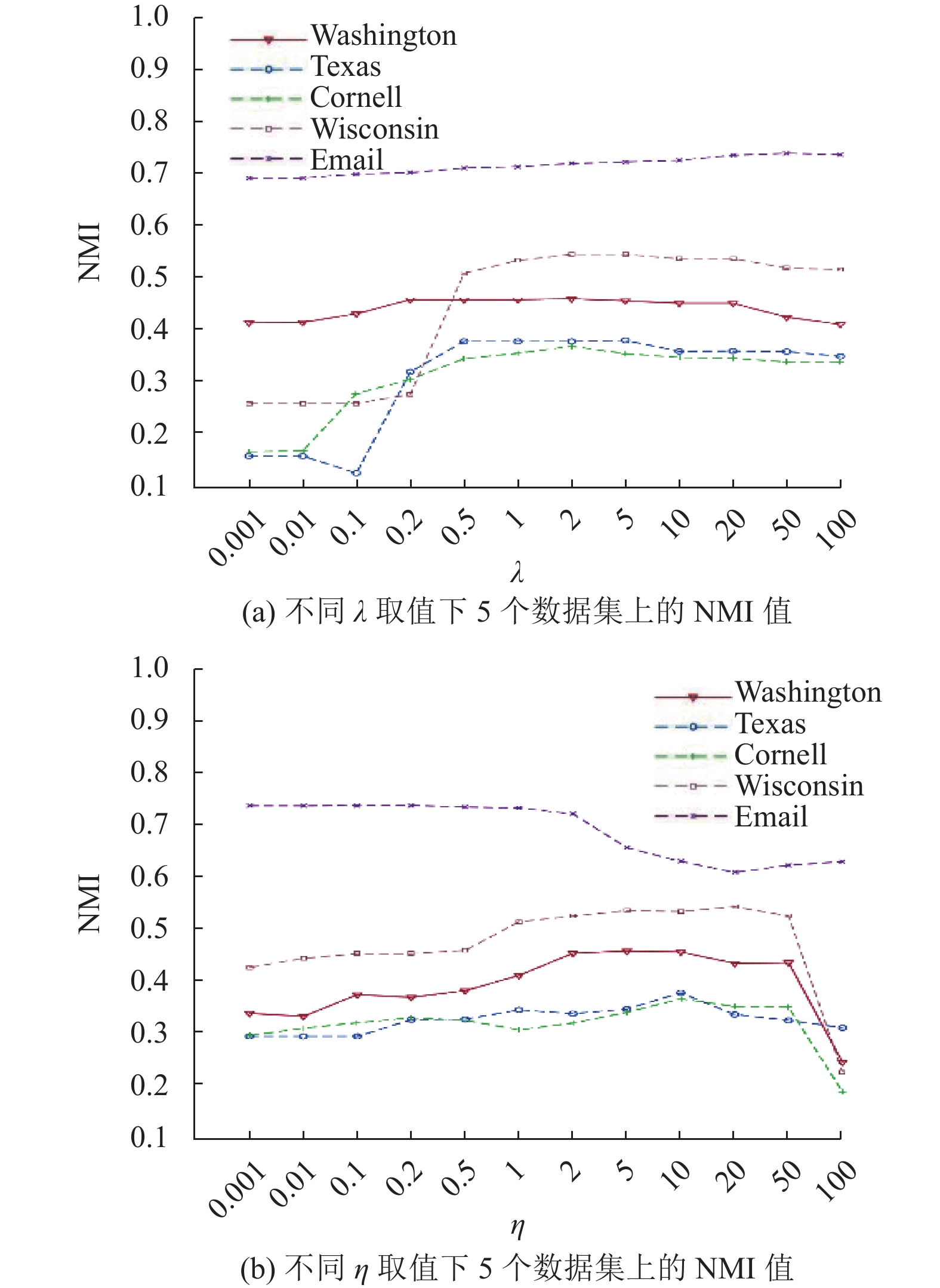
|
图 2 5个数据集上对于 |
不难看出, 在这5个数据集上, 当固定其中一个参数而增大另一个参数值的时候, NMI值均呈现出先增后降的趋势. 观察发现, 在Cornell、Texas、Washington和Wisconsin上,
本节分析PNMTF算法的收敛性. 我们在这5个真实网络数据集上运行PNMTF, 迭代次数为100次, 并记录每次迭代后目标函数的对数, 结果如图3所示.

|
图 3 5个数据集上目标函数的收敛情况 |
总体上, PNMTF的目标函数曲线收敛到平稳值的速度较快. 可以看到在Washington数据集上, 目标函数在5次迭代后已经几乎没有变化, 而在另外4个数据集上的迭代次数达到30次以后, 目标函数曲线也都已经趋于平稳. 因此PNMTF算法无论是在规模较大还是较小的网络上, 都具有较好的收敛性.
4 结论与展望本文针对有向网络上的社区检测问题, 提出了一种基于非负矩阵分解的有向网络半监督社区检测算法, 利用先验信息重构网络拓扑, 并在目标函数中添加由先验信息所指导的节点社区隶属度惩罚项, 同时考虑了节点度异质性影响, 实现了对有向网络社区结构的检测. 在多个真实网络数据集上的实验结果均证明了本文方法的有效性. 在接下来的工作中我们将考虑把该方法拓展到多层网络或者动态网络上, 基于多个网络结构提取出有说服力的部分结构信息作为先验信息来指导整体的社区检测. 此外, 在大规模矩阵上, 与所有基于非负矩阵分解的社区检测方法相同, 我们的算法仍然面临一定的挑战. 如果平均社区规模较小, 即平均每个社区包含的节点较少, 补充先验信息后, 会生成大量小型连接组件, 这时算法主要是对这些小的连接组件进行合并, 时间复杂度略有上升. 反之, 当平均社区规模较大时, 补充先验信息后会生成规模较大的连接组件, 使得网络稀疏性变小, 算法速率明显降低. 这时我们可以考虑采用并行或者分布式NMF算法[24,25], 这也将成为我们未来的工作方向. 同时, PNMTF算法需要提前指定社区数目k, 但在实际中k往往是未知的, 因此如何在NMF框架下弥补k的估计问题是一个值得讨论与研究的方向.
| [1] |
Zhang Y, Chen KH, Sampson A, et al. Node features adjusted stochastic block model. Journal of Computational and Graphical Statistics, 2019, 28(2): 362-373. DOI:10.1080/10618600.2018.1530117 |
| [2] |
陈悦, 陈璟. 一种基于遗传算法的PPI网络全局比对算法. 小型微型计算机系统, 2022, 43(7): 1494-1498. DOI:10.20009/j.cnki.21-1106/TP.2020-1089 |
| [3] |
Newman M. Networks. 2nd ed., Oxford: Oxford University Press, 2018.
|
| [4] |
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [5] |
Liu D, Zhao CW, He Y, et al. Simultaneous cluster structure learning and estimation of heterogeneous graphs for matrix-variate fMRI data. Biometrics, 2023, 79(3): 2246-2259. DOI:10.1111/biom.13753 |
| [6] |
Ren MY, Zhang SG, Wang JH. Consistent estimation of the number of communities via regularized network embedding. Biometrics. 2023, 79(3): 2404–2416.
|
| [7] |
Fernandes A, Gonçalves PCT, Campos P, et al. Centrality and community detection: A co-marketing multilayer network. Journal of Business & Industrial Marketing, 2019, 34(8): 1749-1762. |
| [8] |
Holland PW, Laskey KB, Leinhardt S. Stochastic blockmodels: First steps. Social Networks, 1983, 5(2): 109-137. DOI:10.1016/0378-8733(83)90021-7 |
| [9] |
Karrer B, Newman MEJ. Stochastic blockmodels and community structure in networks. Physical Review E, 2011, 83(1): 016107. DOI:10.1103/PhysRevE.83.016107 |
| [10] |
Airoldi EM, Blei DM, Fienberg SE, et al. Mixed membership stochastic blockmodels. The Journal of Machine Learning Research, 2008, 9: 1981-2014. |
| [11] |
Paatero P, Tapper U. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics, 1994, 5(2): 111-126. DOI:10.1002/env.3170050203 |
| [12] |
Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature, 1999, 401(6755): 788-791. DOI:10.1038/44565 |
| [13] |
马慧芳, 赵卫中, 史忠植. 基于非负矩阵分解的双重约束文本聚类算法. 计算机工程, 2011, 37(24): 161-163. DOI:10.3969/j.issn.1000-3428.2011.24.054 |
| [14] |
Li YT, Zhu RQ, Qu AN, et al. Topic modeling on triage notes with semiorthogonal nonnegative matrix factorization. Journal of the American Statistical Association, 2021, 116(536): 1609-1624. DOI:10.1080/01621459.2020.1862667 |
| [15] |
黄波, 严宣辉, 林建辉. 基于联合非负矩阵分解的协同过滤推荐算法. 模式识别与人工智能, 2016, 29(8): 725-734. |
| [16] |
贾俊杰, 姚叶旺, 陈旺虎. 基于非负矩阵分解的群组推荐算法. 计算机工程与科学, 2022, 44(5): 933-943. DOI:10.3969/j.issn.1007-130X.2022.05.020 |
| [17] |
Wang F, Li T, Wang X, et al. Community discovery using nonnegative matrix factorization. Data Mining and Knowledge Discovery, 2011, 22(3): 493-521. DOI:10.1007/s10618-010-0181-y |
| [18] |
Zhang ZY. Community structure detection in complex networks with partial background information. Europhysics Letters, 2013, 101(4): 48005. DOI:10.1209/0295-5075/101/48005 |
| [19] |
Zhang ZY, Sun KD, Wang SQ. Enhanced community structure detection in complex networks with partial background information. Scientific Reports, 2013, 3: 3241. DOI:10.1038/srep03241 |
| [20] |
Yang L, Cao XC, Jin D, et al. A unified semi-supervised community detection framework using latent space graph regularization. IEEE Transactions on Cybernetics, 2015, 45(11): 2585-2598. DOI:10.1109/TCYB.2014.2377154 |
| [21] |
Liu X, Wang WJ, He DX, et al. Semi-supervised community detection based on non-negative matrix factorization with node popularity. Information Sciences, 2017, 381: 304-321. DOI:10.1016/j.ins.2016.11.028 |
| [22] |
Boutsidis C, Gallopoulos E. SVD based initialization: A head start for nonnegative matrix factorization. Pattern Recognition, 2008, 41(4): 1350-1362. DOI:10.1016/j.patcog.2007.09.010 |
| [23] |
Danon L, Díaz-Guilera A, Duch J, et al. Comparing community structure identification. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005(9): P09008. |
| [24] |
He CB, Fei X, Li HC, et al. Improving NMF-based community discovery using distributed robust nonnegative matrix factorization with SimRank similarity measure. The Journal of Supercomputing, 2018, 74(10): 5601-5624. DOI:10.1007/s11227-018-2500-9 |
| [25] |
He CB, Li HC, Fei X, et al. A topic community-based method for friend recommendation in large-scale online social networks. Concurrency and Computation: Practice and Experience, 2017, 29(6): e3924. DOI:10.1002/cpe.3924 |
 2024, Vol. 33
2024, Vol. 33


