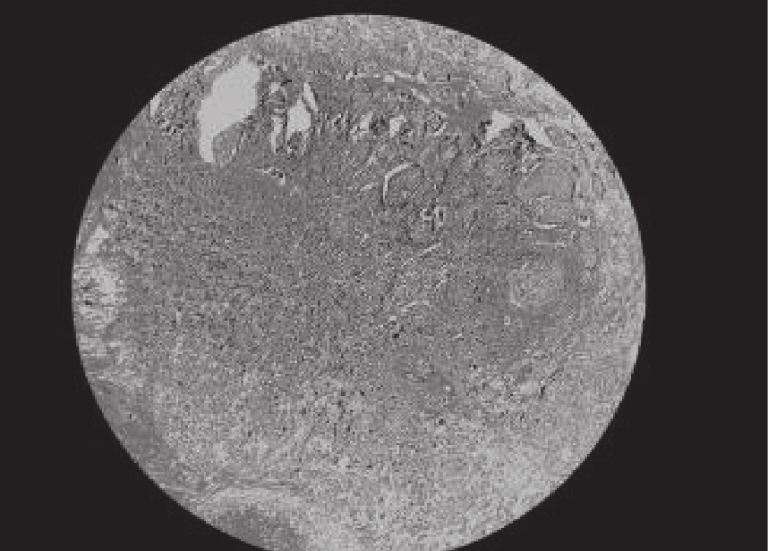
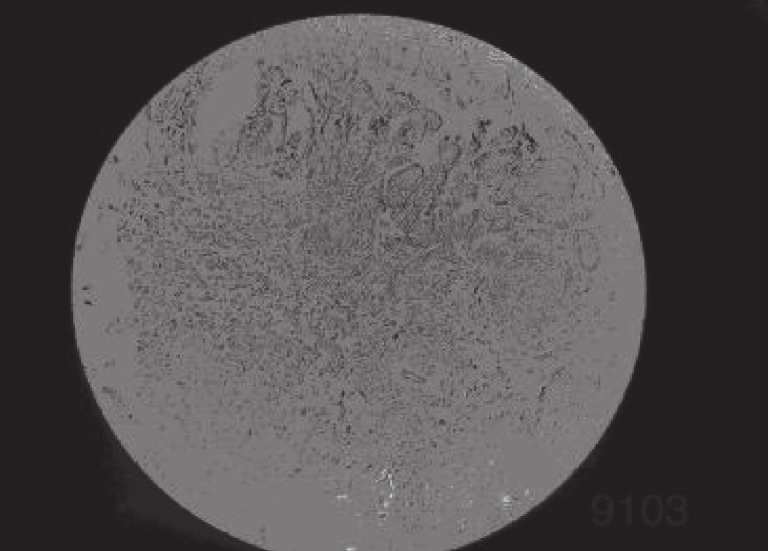
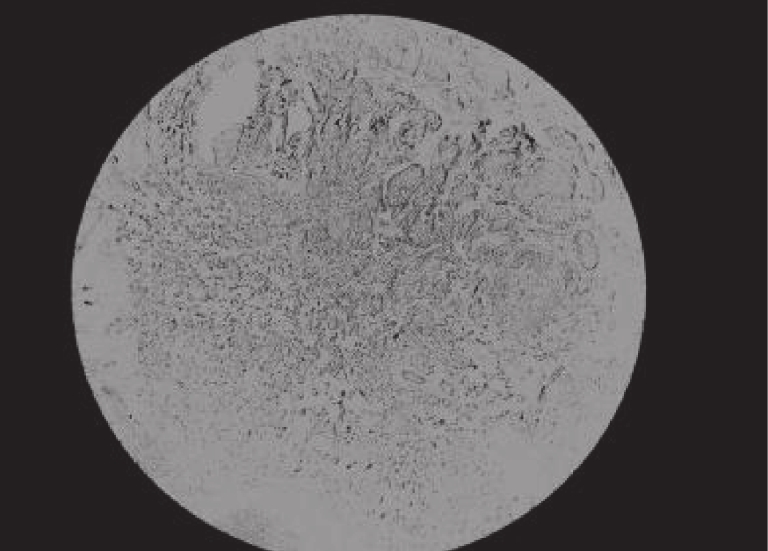
乳腺癌已取代宫颈癌成为威胁妇女身体健康的最常见恶性癌症. 如果能在乳腺早期检查中识别出异常, 将会提高医生治疗成功率并降低患者死亡风险^[1]. 浸润性乳腺导管癌(IDC)是乳腺癌症中最常见的类型, 但因为乳腺结构的复杂和IDC的细微性质, 导致人工诊断效率低下, 甚至出现误诊的情况^[2]. 随着医学技术的发展与人工智能的兴起, 越来越多的医院利用计算机辅助技术对乳腺癌症医学图像进行分析检测, 帮助医生提高诊断率. 图像分割是计算机辅助技术的关键环节, 高质量的医学分割图像可以提高病变区域检测的准确性^[3,4].

因为阈值分割相对于其他的分割技术更加简单与便捷, 而且阈值分割方法中最大化类间方差法(Otsu)因为图像分割效果好, 操作简单, 所以我们选择阈值分割和Otsu用于图像处理^[5,6]. 但传统的阈值分割需要通过穷举法来列举排除出一个合适阈值, 效率低下, 过程复杂, 为减小计算量, 文献[7]和文献[8]提出利用鲸鱼算法来寻找Otsu的合适阈值, Wang等人提出了一种基于改进金枪鱼群优化(ITSO)的混合森林冠层图像分割方法, 将对称交叉熵方法引入到森林冠层图像阈值分割中以获取各种植物种群参数^[9], 在文献[10]中, 采用狮子优化和猫群优化的混合算法, 为有效的多级图像阈值分割提供了最优阈值, Agrawal等人采用了主色分量和自适应WOA对彩色图像进行多级阈值处理^[11], Sharma等人使用Kapur、Tsali和模糊熵的目标函数, 提出了一种有效的基于对立的改进萤火虫算法, 用于多级图像分割^[12], 文献[13]提出一种基于多目标海洋捕食者算法的多级阈值分割算法, 该算法以9DKapur熵函数作为目标函数, 得到图像分割效果良好, 但这些方法要么计算复杂, 实用性较为欠缺, 要么本身算法的收敛能力不足, 无法获得最佳阈值.

所以我们引入增强的蒲公英优化算法(IDO)来探索出最合适的阈值, IDO在探索阈值的阶段结合布朗运动和莱文(Levy)飞行, 以其强大的局部优化能力和对立式学习本身的全局优化能力完美的胜任了探寻最佳阈值的任务. 本算法寻到的最佳阈值后得到的图像分割效果通过实验证明满足了我们的需求.

1 相关工作 1.1 最大化类间方差法(Otsu)

最大化类间方差法由Otsu提出^[14], 在一张图片的二维直方图上通过最大化阈值两侧像素数据的类间方差, 使我们分割的各部分区域相差最大^[15–17]. 假设一张图片大小为M×N, 其灰度级为[0, L], 计算灰度i的频率P_i:

$ {P}_{i}=\frac{{{n}}_{{i}}}{{M}\times {N}} $

(1)

其中, ${{{n}}_{{i}}}$是图片中灰度值为i的像素数量, i=0, 1, 2, …, L. 如果阈值个数为m, 0<m<L–1, 则分割部分数量为m+1, 记为[0, T₁, T₂, …, T_m, 255], T_(m+1)=255. 统计每个分割部分灰度级的平均灰度:

$ {{{u}}_{{k}}} = \frac{1}{{{\omega _{{k}}}}}\mathop \sum \nolimits_{{{j}} = {{{T}}_{{k}}}}^{{{{T}}_{{{k}} + 1}}} {{j}}{P_j} $

(2)

其中, k=0, 1, 2, …, m, j表示的是两个阈值之间的灰度值, 参数${\omega _{{k}}}$计算如式(3)所示:

$ {\omega _k} = \mathop \sum \nolimits_{{{j}} = {{{T}}_{{k}}}}^{{{{T}}_{{{k}} + 1}}} {P_j} $

(3)

图片整体的平均灰度值${\mu_{{T}}}$为:

$ \mu_{{T}}={{\displaystyle \sum }}_{{i}=0}^{{L}}{{iP}}_{{i}} $

(4)

其总体类间方差计算公式为式(5):

$ {\sigma }_{B}^{2}={{\displaystyle \sum }}_{k=0}^{m}{\omega }_{{k}}{\left[{{u}}_{{k}}-{\mu }_{T}\right]}^{2} $

(5)

1.2 对立式学习(opposition-based learning, OBL)

许多受自然群体影响的启发式算法将函数逼近视为给定问题的答案^[18,19]. 在许多情况下, 算法起点的初始化位置通常是随机选择的, 包括神经网络的权重、群智能优化算法的初始种群和增强剂的主动策略^[20]. 当起点接近理想的最佳解时, 收敛发生得更快. 但是, 如果它离理想解的距离很远, 比如在最差的情况下, 处于和最佳解完全相反的位置, 收敛将需要的时间更长, 或者获得解可能是无法收敛的不可解^[21]. 对立解的数学表现形式如式(6)所示:

$ {\bar x_0} = a + b - {x_0} $

(6)

其中, ${x_0}$是属于[a, b]范围内的一个实数, ${\bar{x}}_{0}$就是它的对立解. 将它放入直角坐标系中, 对立解就是[a, b]范围内的一个实数关于中心直线$ {x}=\dfrac{a+b}{2} $对称.

在D维度决策空间中, 某一个体$x={x}_{1}, {x}_{2}, {x}_{3},\cdots , {x}_{D}$, 它的对立解表现形式$\bar{x}=[{\bar{x}}_{1}, {\bar{x}}_{2}, {\bar{x}}_{3}, \cdots , {\bar{x}}_{D}]$, 群体的对立解为${\bar{x}}_{k}={a}_{k}+{b}_{k}-{x}_{k}$, 其中$ k=\mathrm{1, 2}, 3, \cdots , $D^[22].

2 蒲公英优化算法(DO) 2.1 算法基本原理

蒲公英优化算法(DO)是一种用于解决连续优化问题的新型元启发式算法^[23]. 元启发式算法简单来说就是模仿自然群体在决策空间内通过个体的探寻和群体的配合不停地迭代搜索可行解, 并且优胜劣汰^[24]. 在元启发式算法中, 探索和开发是值得重点关注的因素. 过度关注探索新解会导致算法本身最后收敛困难, 但过度关注开发却又会导致算法陷入到局部最优^[25]. 所以如何在探索和开发之间取得一个平衡是决定元启发式算法性能优劣的关键指标.

蒲公英优化算法(DO)是受到蒲公英种子依靠风力长途飞行传播的灵感而诞生的算法, 蒲公英种子在传播过程中经过3个阶段: 第1个阶段是上升阶段, 如果是在晴天多风的天气, 种子会借助风力向更远的地方传播, 如果是在阴天多雨的天气, 种子就会漂浮在附近; 第2个阶段是下降阶段, 种子上升到一定高度时开始逐渐向下降落; 第3个阶段是着陆阶段, 种子会在天气与风力的影响下落到一个随机位置孕育出下一代蒲公英. 而蒲公英算法正是通过这3个阶段更新个体的位置, 并且在上升阶段通过服从正态分布的随机数来决定探索和开发, 同时通过动态调节种子传播半径来控制蒲公英种子位置的变更.

DO算法框架大致为种群初始化, 计算种群适应度, 更新种群, 挑选全局最优4部分, 其包含2个主要参数, 分别为种子传播半径α, 局部搜索系数K. 种子传播半径α和局部搜索系数K在迭代过程中随着时间变化而变化, α用于调节全局搜索步长, 局部搜索系数K用于调节局部搜索步长, 通过服从正态分布的随机数用于调整由探索到开发过程以及避免局部最优.

2.2 初始化阶段

定义一个N粒d维度决策空间的蒲公英种群矩阵seed, 其第i粒种子可以表示为X_i=[X_i¹, X_i², …,$ X_i^d $], i=1, 2, …, N. 对该种群进行初始化, 初始化为式(7):

$ {{X}}_{{i}}={lb}+{{r}}_{{i}}\times \left({ub}-{lb}\right) $

(7)

其中, ${{{r}}_{{i}}}$是服从正态分布的(0, 1)间的随机数字, ub为决策空间最大值, lb是决策空间的最小值, N是种群矩阵的最大行数值, d是种群矩阵的最大列数值, 后文同字符皆为同义.

2.3 上升阶段

通过一个服从正态分布的随机数r决定全局搜索或者局部开发, 记为r~N(0, 1).

1) 如果r<1.5, 天气晴朗时上升, 为全局搜索, 种子此时的位置为式(8):

$ {X}_{t+1}={X}_{t}+\alpha \times {v}_{x} \times {v}_{y} \times {\ln}Y \times \left({X}_{s}-{X}_{t}\right) $

(8)

其中, ${X_s}$表示初始化的种子位置, 如式(9)所示; ${v_x}$和${v_y}$表示水平与垂直的风力系数, 如式(11)所示; $\alpha $表示的是种子传播半径, 如式(10)所示; ${\text{ln}}Y$表示服从均值为0, 方差为1的对数正态分布.

$ {X_s} = {{rand}}\left( {1, {{d}}} \right){\times}\left( {ub - lb} \right) + lb $

(9)

$ \alpha = {{rand}}(){\times}\left( {\frac{1}{{{T^2}}}{t^2} - \frac{2}{T}t + 1} \right) $

(10)

其中, T是总迭代次数, t是当前迭代次数, t=1, 2, 3, …, T.

$ {v}_{x}=r \times \text{cos}\theta \text{, }{v}_{y}={{r}} \times \text{sin}\theta \text{, } {{r}} = \frac{1}{{{{\text{e}}^{{\theta }}}}} $

(11)

其中, θ是介于[−π, π]之间的随机数.

2) 如果$ r \geqslant 1.5 $, 天气下雨时上升, 为局部搜索, 种子此时的位置如式(12):

$ {{{X}}_{{{t}} + 1}} = {{{X}}_{{t}}} \times {{k}} $

(12)

其中, 局部搜索系数k如式(13)所示:

$ {{k}} = 1 - {{rand}}() \times {{q}} $

(13)

$ {{q}} = \frac{1}{{{{{T}}^2} - 2{{T}} + 1}}{{{t}}^2} - \frac{2}{{{{{T}}^2} - 2{{T}} + 1}}{{t}} + 1 + \frac{1}{{{{{T}}^2} - 2{{T}} + 1}}$

(14)

2.4 下降阶段

经过上升一定距离后, 此时算法仍然侧重于探索, 种子开始根据布朗运动逐渐下降, 种子位置如式(15)所示:

$ {X_{t + 1}} = {X_t} - \alpha {\times}{\beta _t}{\times}\left( {{X_{{\text{meant}}}} - \alpha {\times}{\beta _t}{\times}{X_t}} \right) $

(15)

其中, ${\beta _t}$是布朗运动, 服从正态分布的随机数; ${{X}}_{\text{meant}}$是为了反映蒲公英下降的稳定性, 采用了上升阶段后的平均位置信息, 表示为式(16):

$ {{{X}}_{{\text{meant}}}} = \frac{1}{{{N}}}\mathop \sum \limits_{{{i}} = 1}^{{N}} {{{X}}_{{i}}} $

(16)

2.5 着陆阶段

蒲公英此时开始着陆, 根据莱文飞行在陆地随机选择着路地点, 算法开始收敛进入开发阶段. 种子位置表示为式(17):

$ X_{t+1}=X_{\rm {elite }}+{levy}(\lambda) \times \alpha \times \left(X_{ {{\rm{elite}} }}-X_{t} \times \delta\right) $

(17)

其中, ${X_{{\text{elite}}}}$表示种群的最佳个体; ${{levy}}\left( \lambda \right)$代表莱文飞行, 可由式(18)表示, $\lambda $是服从${{levy}}$分布函数的随机数; 线性函数$\delta $如式(20)所示.

$ {{levy}}\left( \lambda \right) = s \times \frac{{w \times \sigma }}{{{{\left| t \right|}^{\frac{1}{\beta }}}}} $

(18)

$ \sigma =\left(\frac{\Gamma \left(1+\beta \right)\times \text{sin}\left(\dfrac{{{\text{π}}} \beta }{2}\right)}{\Gamma \left(\dfrac{1+\beta }{2}\right)\times \beta \times {2}^{\left(\frac{\beta -1}{2}\right)}}\right) $

(19)

$ \delta = \frac{{2{{t}}}}{{{T}}} $

(20)

其中, s=0.01, $\;\beta $=1.5, $w$和t都是0–1之间的随机数字, Γ是伽马函数.

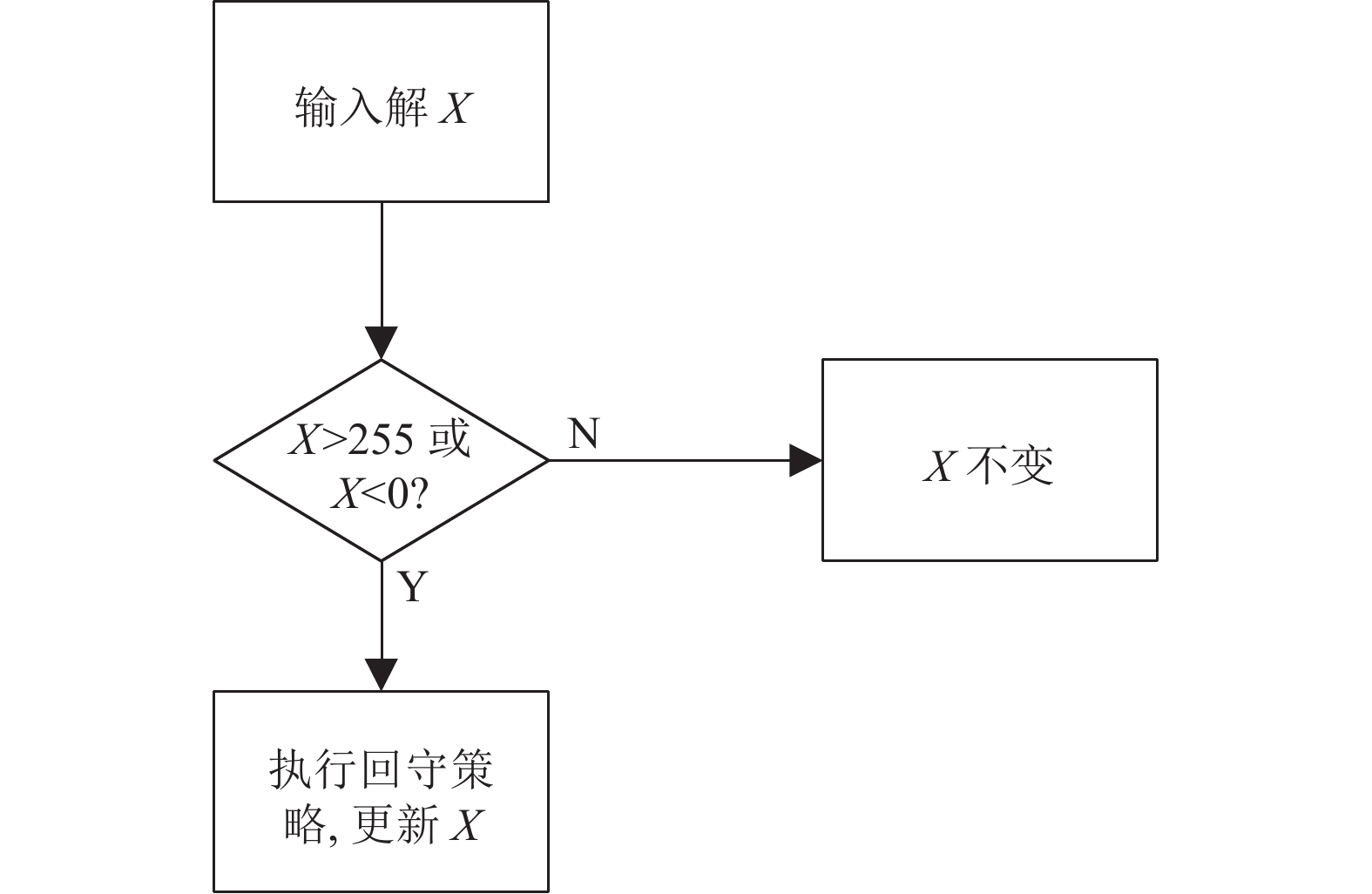
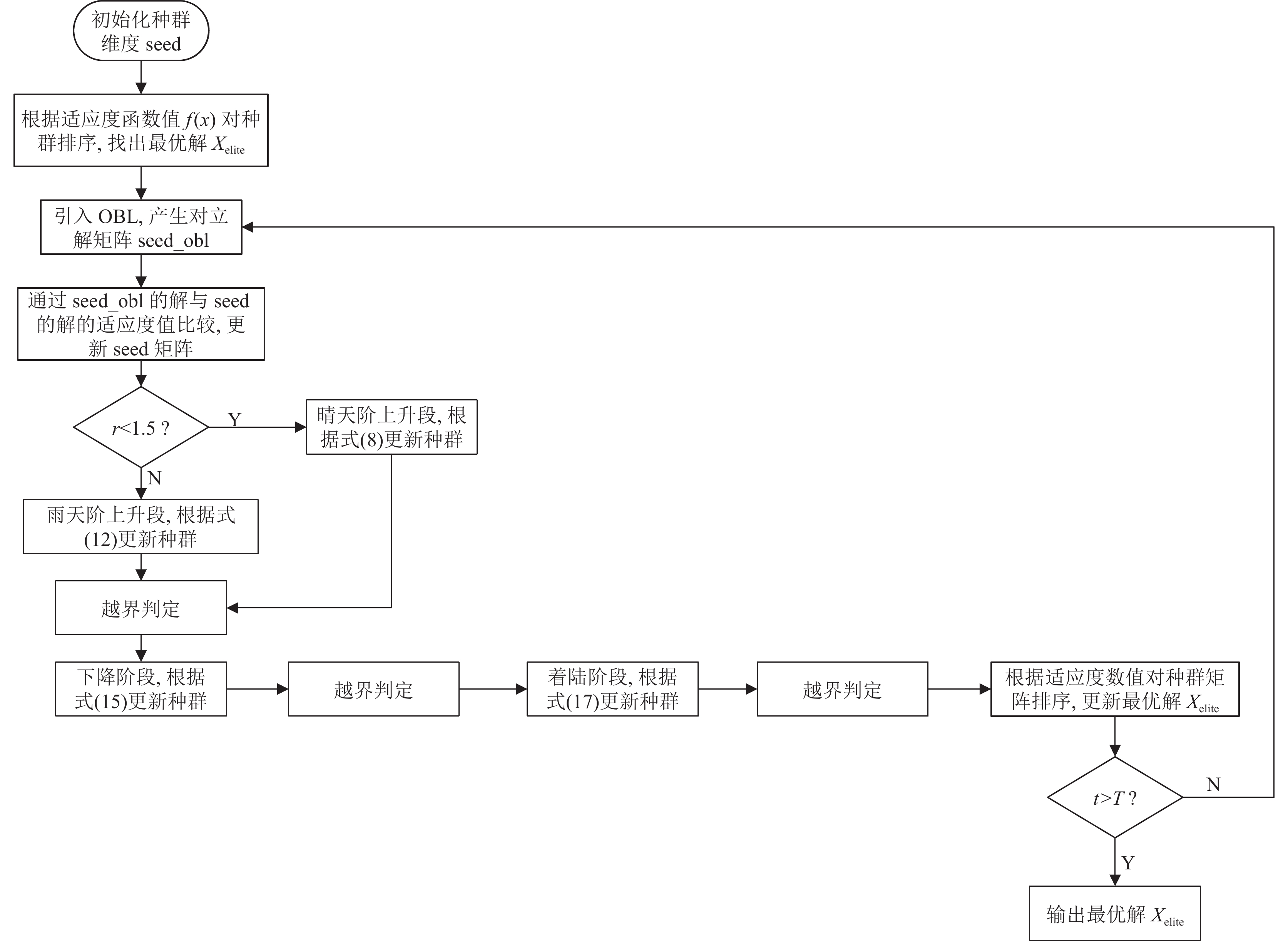
越界判定流程如图1所示, 增强的蒲公英优化算法流程图如图2所示.

3 增强蒲公英优化算法(IDO) 3.1 IDO的OBL优化

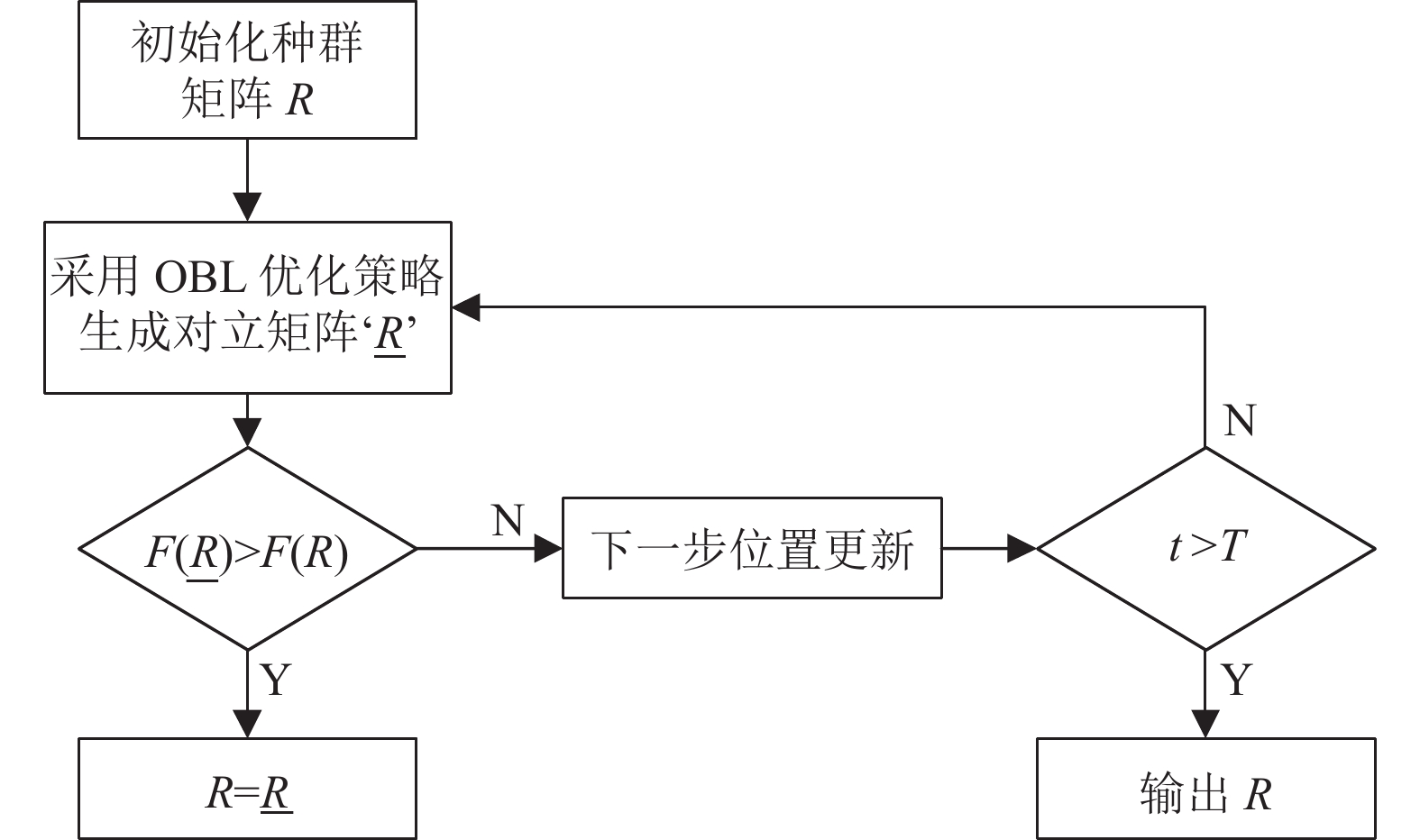
本节对所提出的技术IDO进行了全面的解释. 最初只是扩展了DO算法的应用, 将它引入乳腺肿瘤图像分割邻域, 以Otsu法为适应度函数. IDO引入了OBL规则, 在解R迭代更新之前都会与反向解R相比较, 如果R的适应度值)大于R, R保持不变, 否则R的值更新为R. 相比原算法在决策空间的孤军奋战, OBL通过对立解的产生, 相当于在决策空间的两个方向同时探索, 增加了解的多样性, 避免算法陷入局部最优, 提高了算法的收敛性. 它的大致流程如图3所示.

3.2 回守策略

蒲公英传统算法探索解时超出范围, 会强制等于上下界限[0, 255], 但在图像分割上会导致图片信息丢失, 模糊不清, 如图4所示. IDO建立的回守策略却会在解X超出范围时, 在范围内通过服从正态分布的随机数随机生成一个新解, 然后将新解与X的适应度值比较, 优胜劣汰. 通过回守策略, 就可避免阈值取到0或255的极端情况, 保证图片信息完好.

3.3 IDO算法操作步骤

IDO算法操作步骤如算法1.

算法1. IDO算法

1)定义一个N粒d维度决策空间的蒲公英种群矩阵seed, 其第i粒种子可以表示为X_i=[X_i¹, X_i², X_i³, …, X_i^d], i=1, 2, 3, …, N. 对该种群进行初始化, 初始化为式(7).

2) 引入OBL规则, 通过式(6)产生seed的对立解矩阵seed_obs.

3) 通过OBL优化规则将对立解矩阵seed_obs和种群矩阵seed比较, 更新种群矩阵seed.

4) 对种群seed进行评估, 挑选种群的最佳个体.

5) 通过一个服从正态分布的随机数r决定全局搜索或者局部开发:

如果r<1.5, 天气晴朗时上升, 为全局搜索, 种子此时的位置为式(8);

如果r$\scriptstyle \geqslant$1.5, 天气下雨时上升, 为局部搜索, 种子此时的位置为式(12).

6) 经过上升一定距离后, 此时算法仍然侧重于探索, 种子开始根据布朗运动逐渐下降, 种子位置如式(15)所示.

7) 蒲公英此时开始着陆, 根据莱文飞行在陆地随机选择着路地点, 算法开始收敛进入开发阶段. 种子位置表示为式(17).

8) 更新最佳个体X_elite .

9) 如果迭代没有结束, 返回第2)步, 否则输出X_elite.

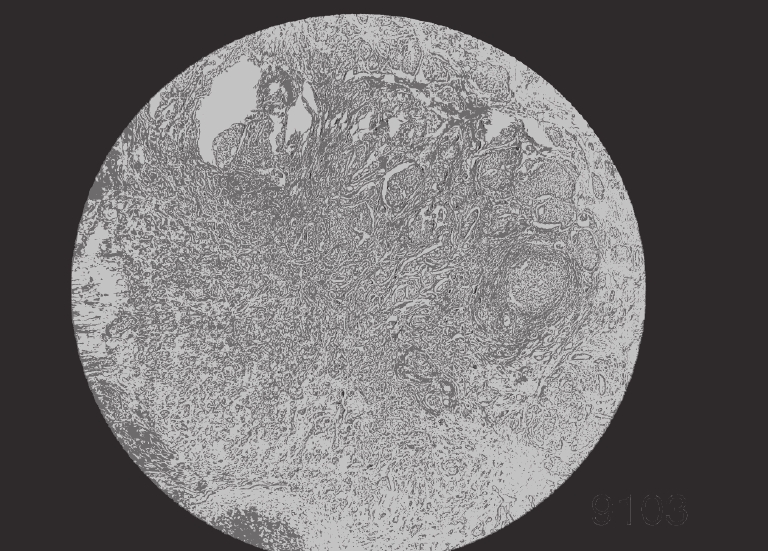
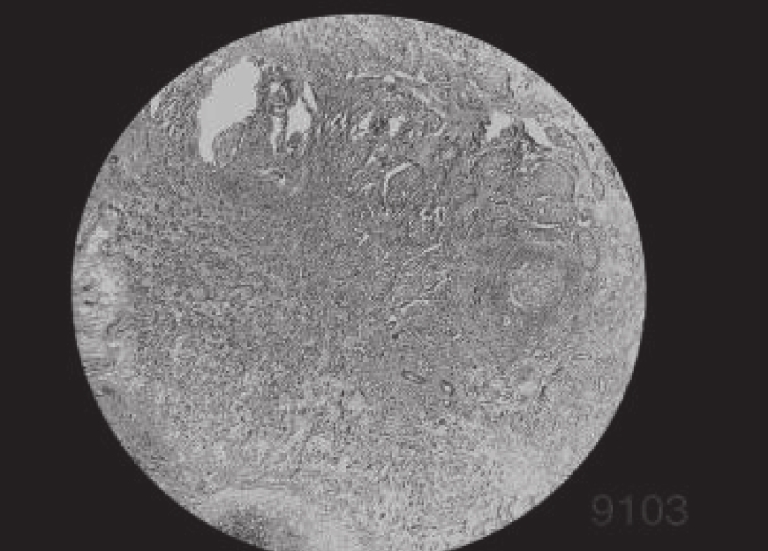
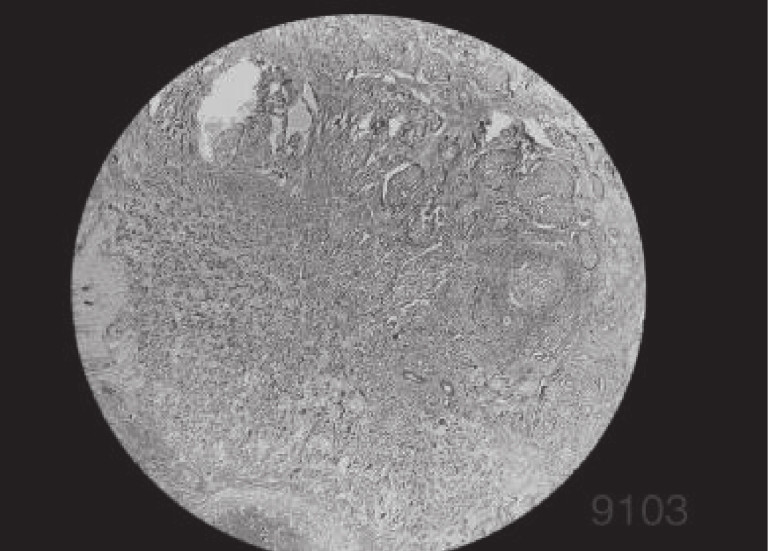
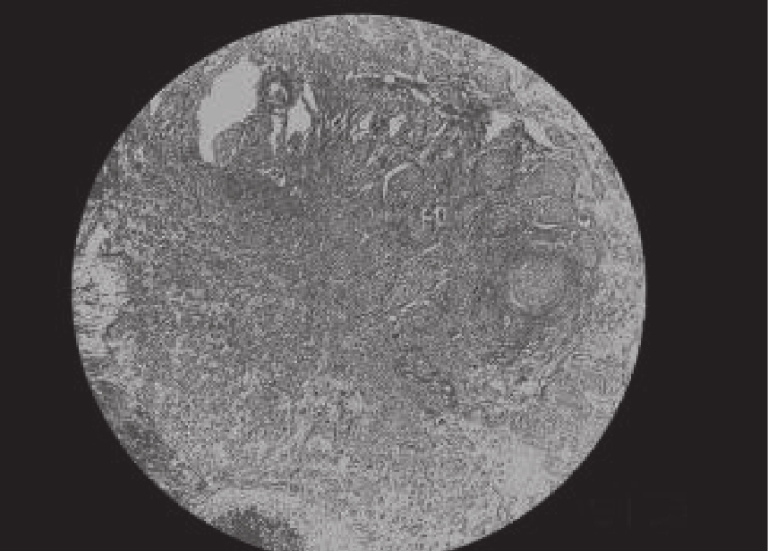
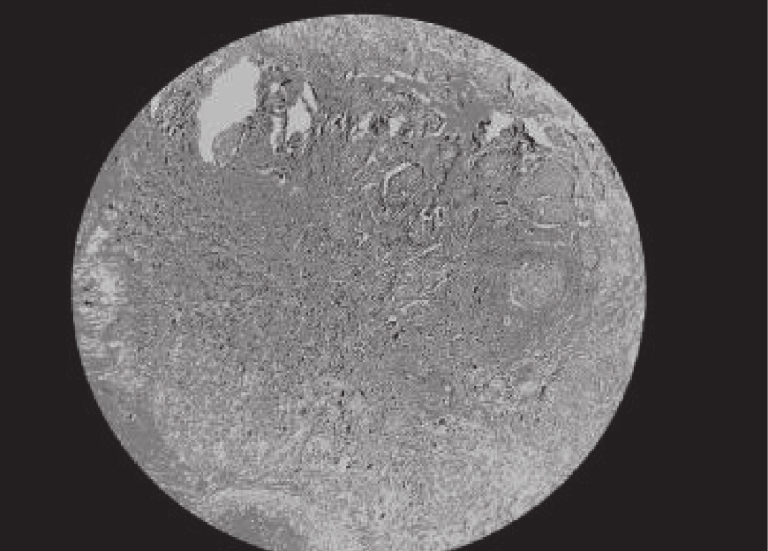
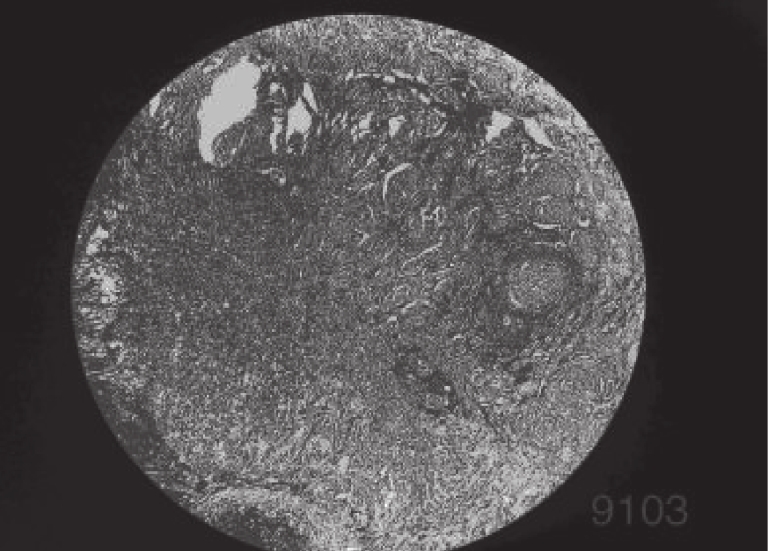
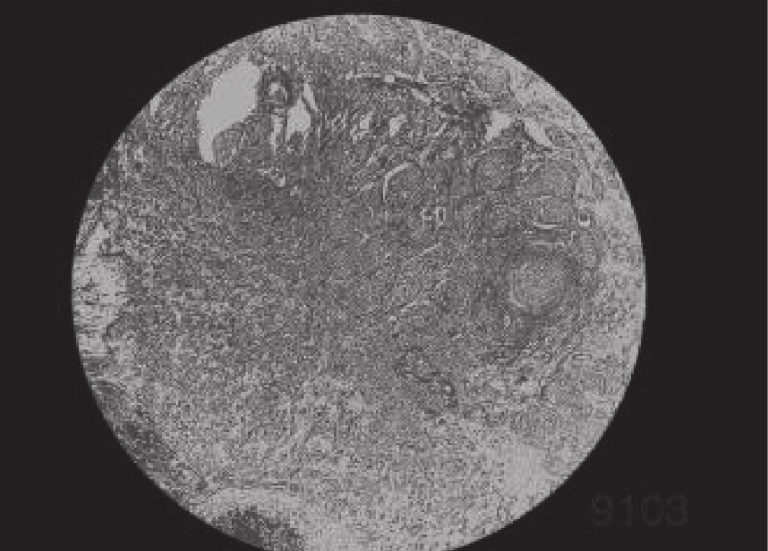
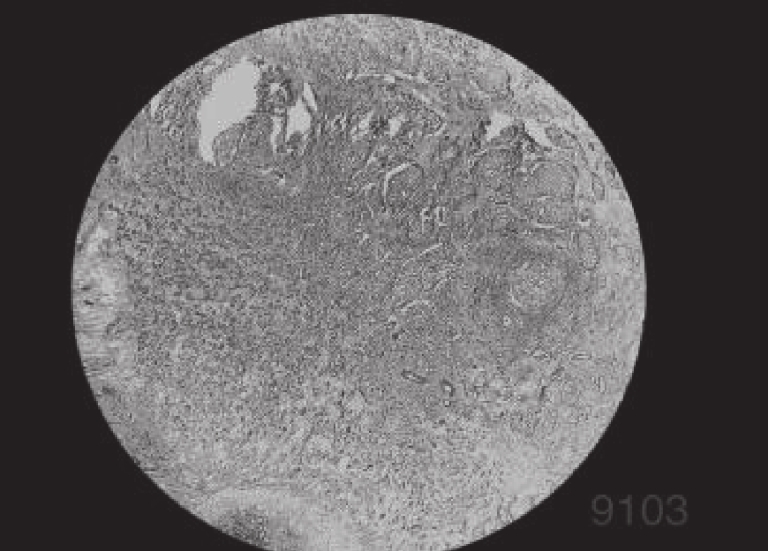
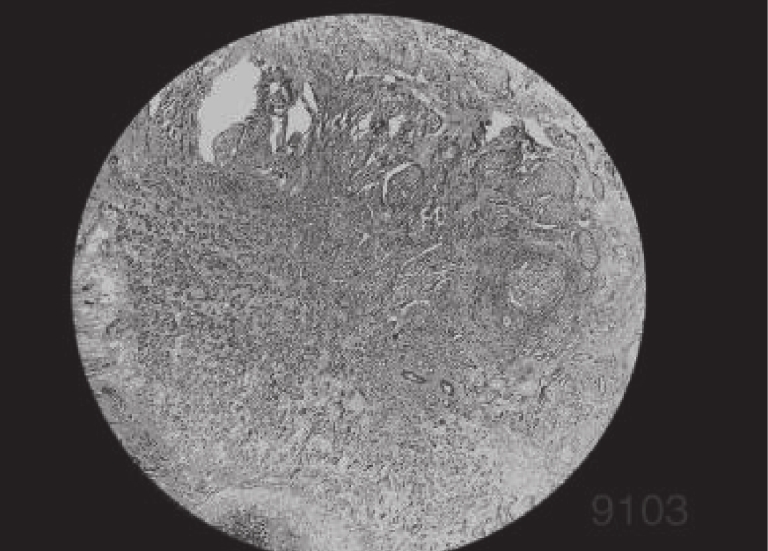
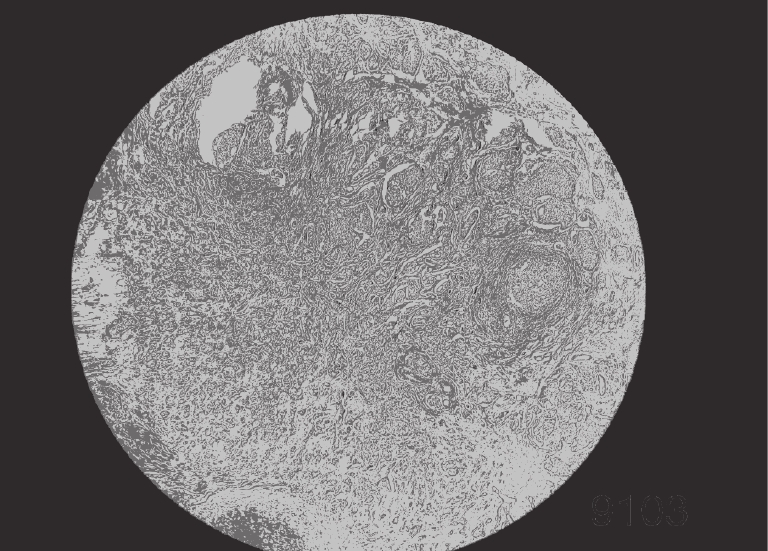
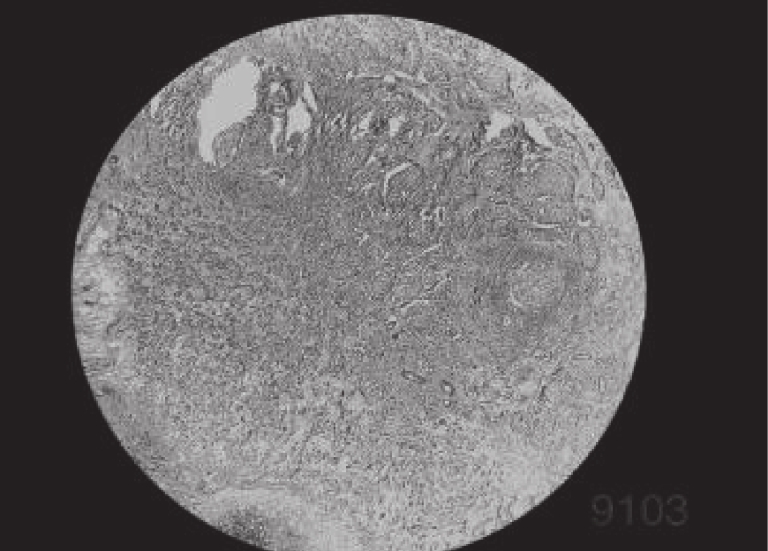
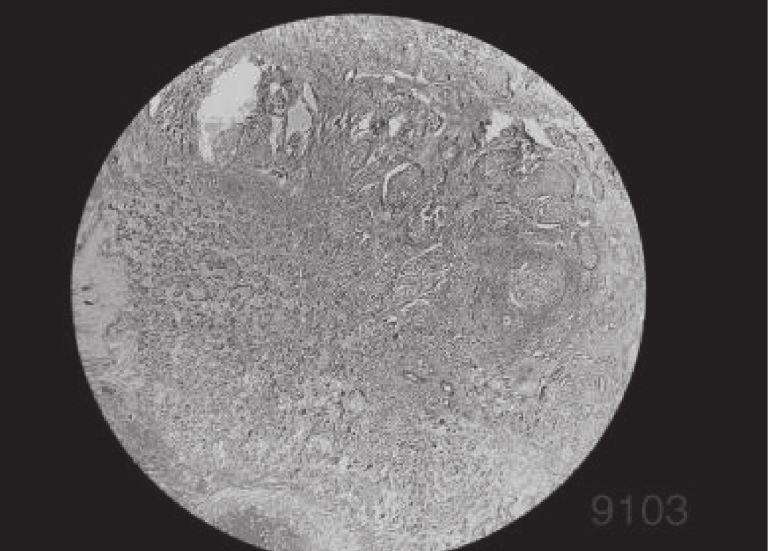
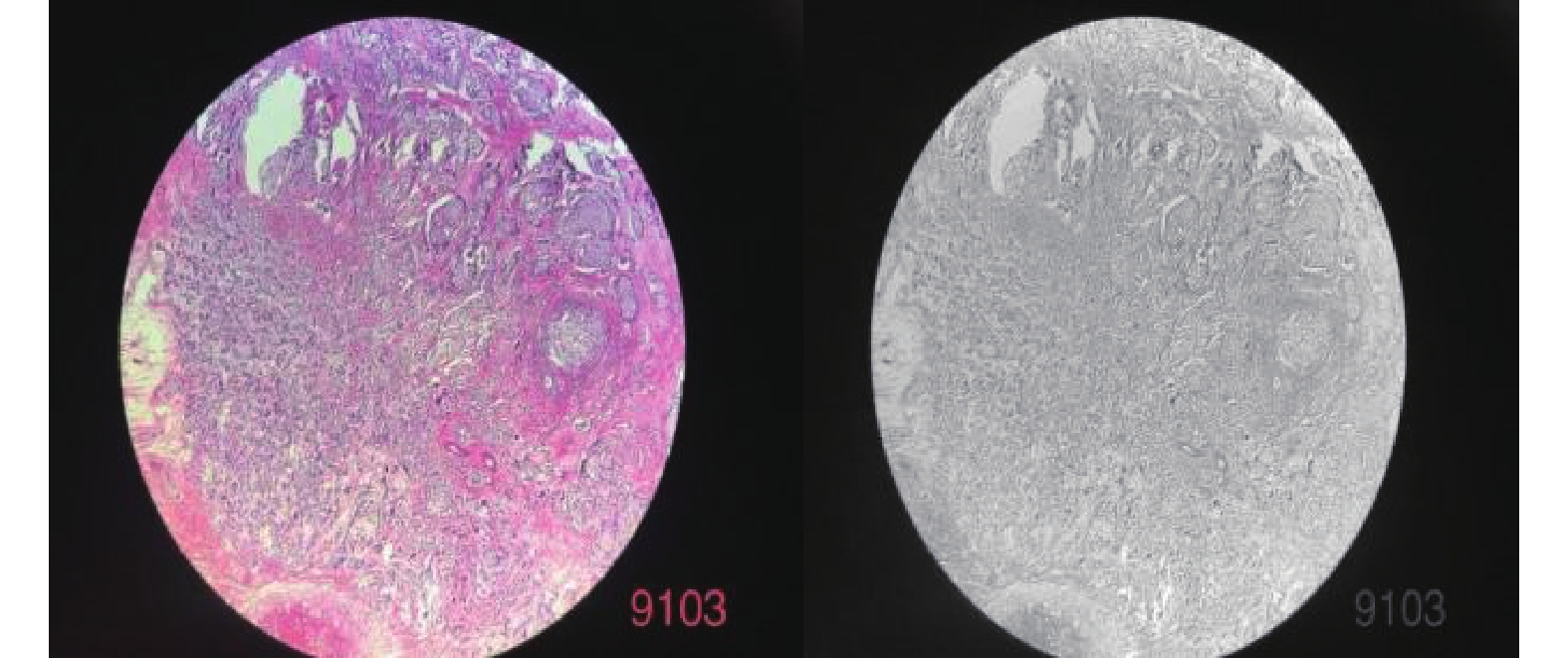
4 实验分析

为了验证IDO算法对乳腺癌图像分割的准确性, 需要将它与经典算法哈里斯鹰算法(HHO)^[26], 人工猩猩部队优化算法(GTO)^[27], 传统蒲公英优化算法(DO), 海洋捕食者算法(MPA)^[28]在相同阈值下用于图像分割领域, 通过峰值信噪比(PSNR), 结构相似度(FSIM), 特征相似度(SSIM)对比, 分析算法的性能优劣. 本实验是在PyCharm的2019专业版本, 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30 GHz, 2.30 GHz, Windows 10 64位系统平台上运行, 本文乳腺细胞图像来自文献[29]中的数据集, 数据集中的标本是用苏木精和伊红染色的乳腺组织, 取自2019–2014年间在伊朗伊斯法罕医科大学Poursina Hakim研究中心诊断出的124名患者, 共有922张JPEG格式的图片, 本文选取4X倍数的其中一张. 其原始图像和灰度图如图5所示, 数据网址链接https://databiox.com/.

4.1 参数设置

所有的算法我们将种群大小N设为20, 最大迭代次数T设为350, 选取阈值个数为k=2, 3, 4, 我们得到的最终实验数据是在每一个算法单独执行100次后取得的平均数. 我们对实验中算法的参数设置如表1所示. IDO和DO算法以及HHO算法中使用莱文飞行部分的参数设置为1.5, MPA算法涡流效应参数FADs设为0.2, 步长p1设为1.5, 参数C设为0.05设为1.5.

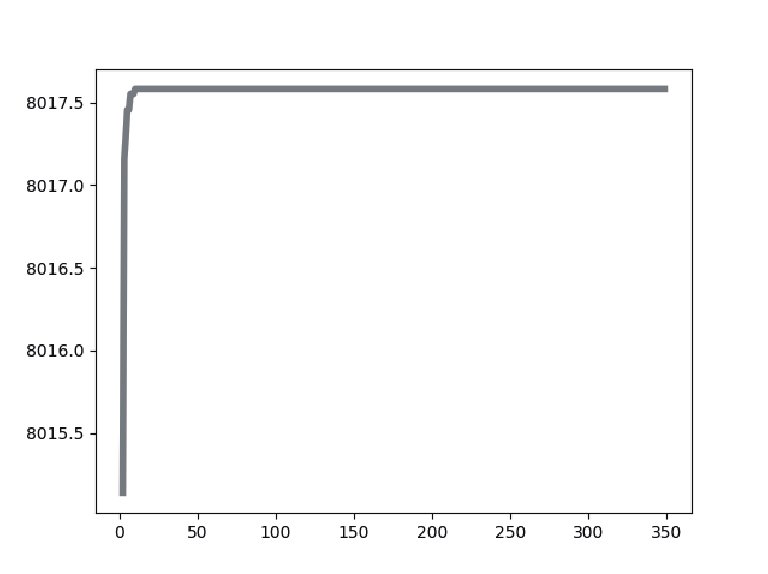
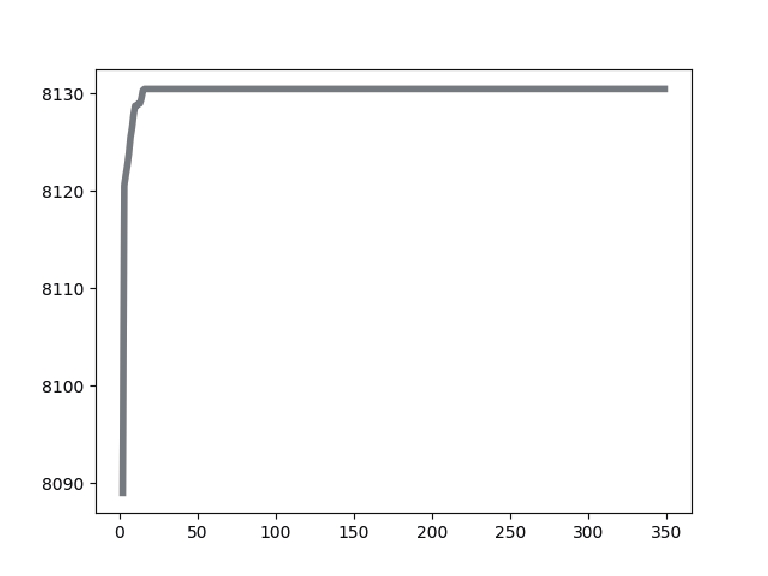
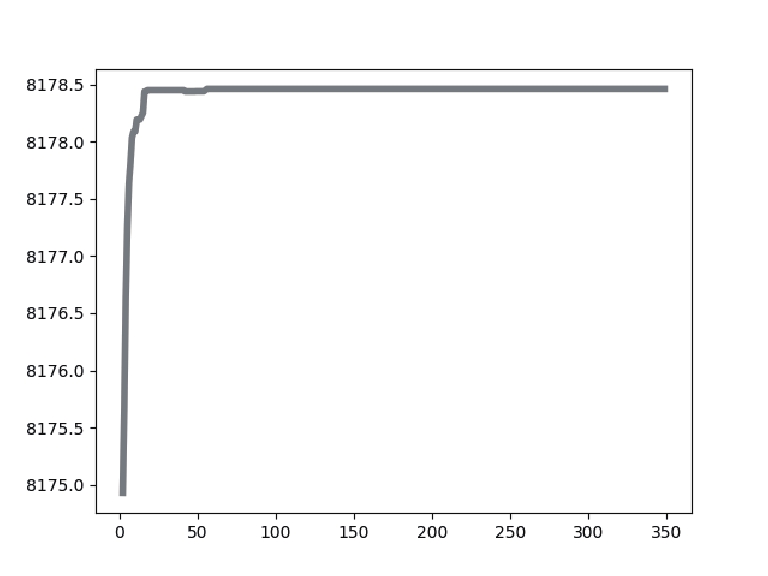
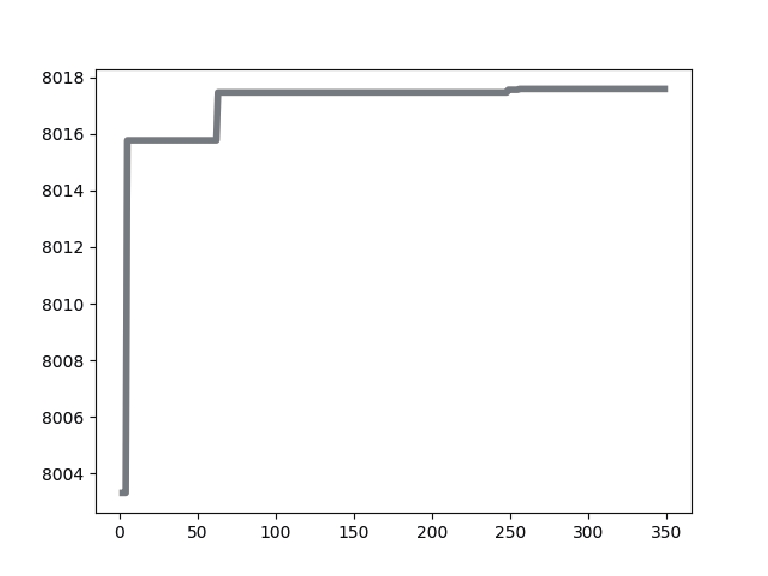
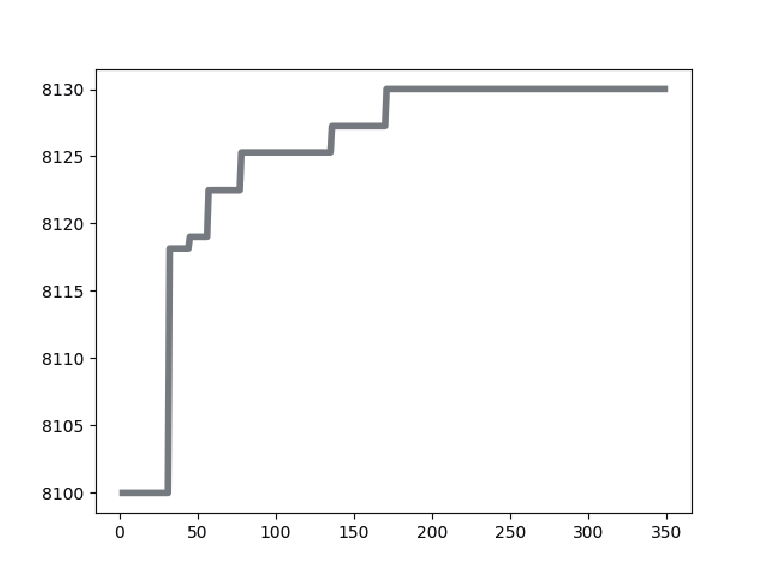
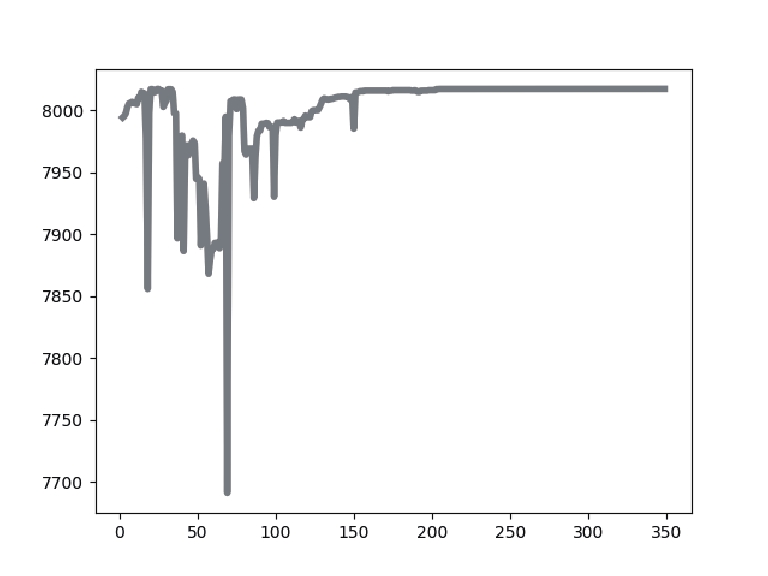
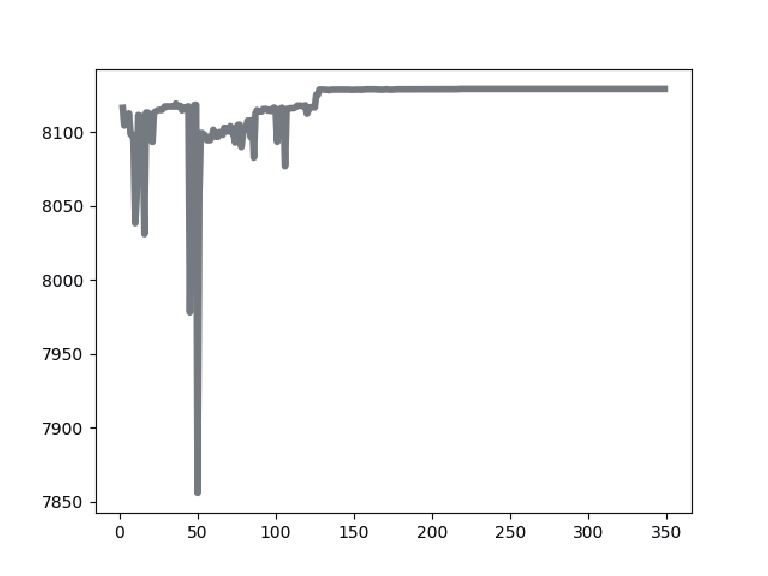
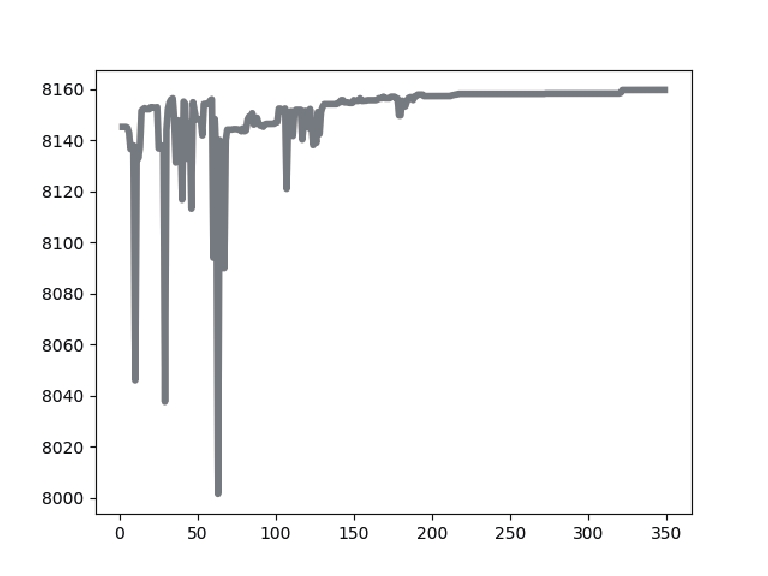
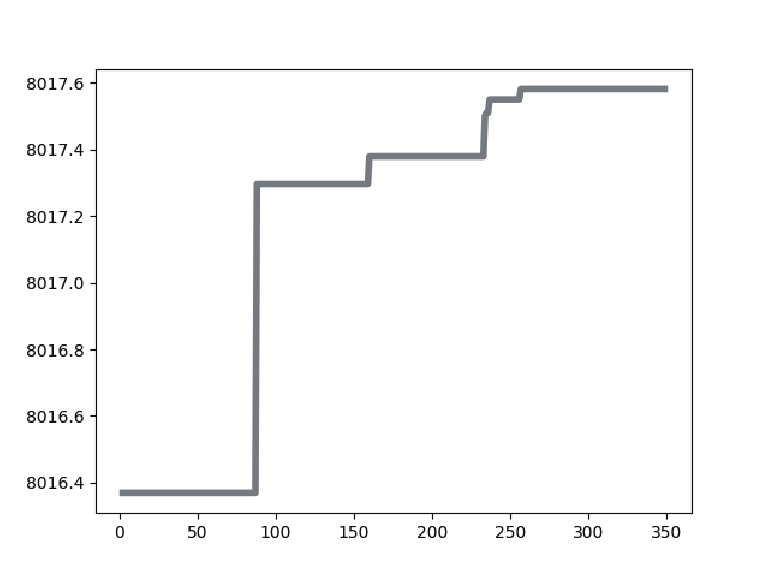
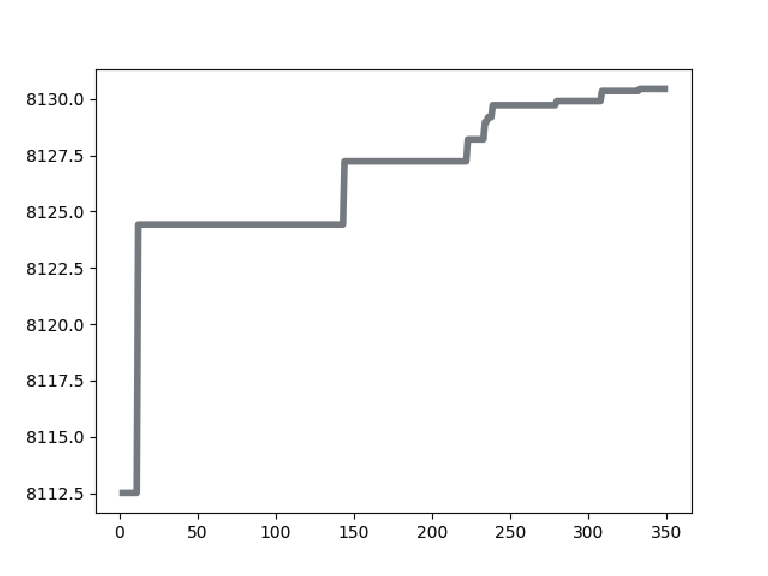
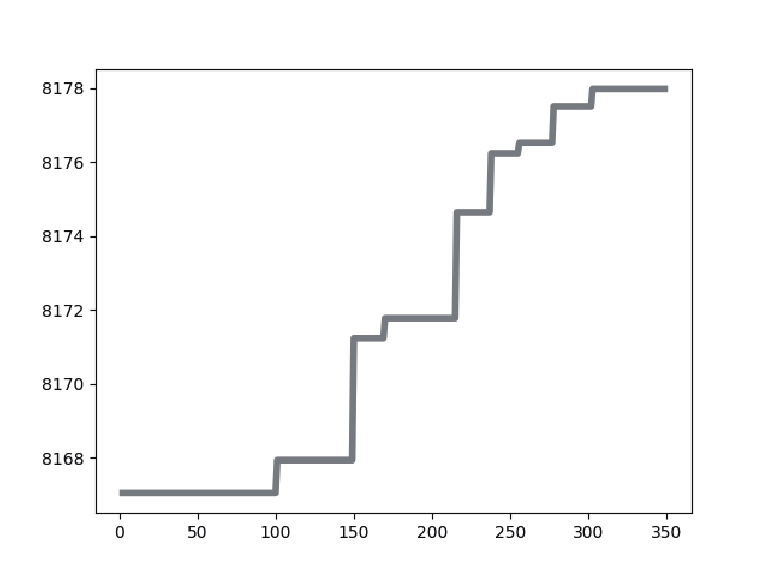
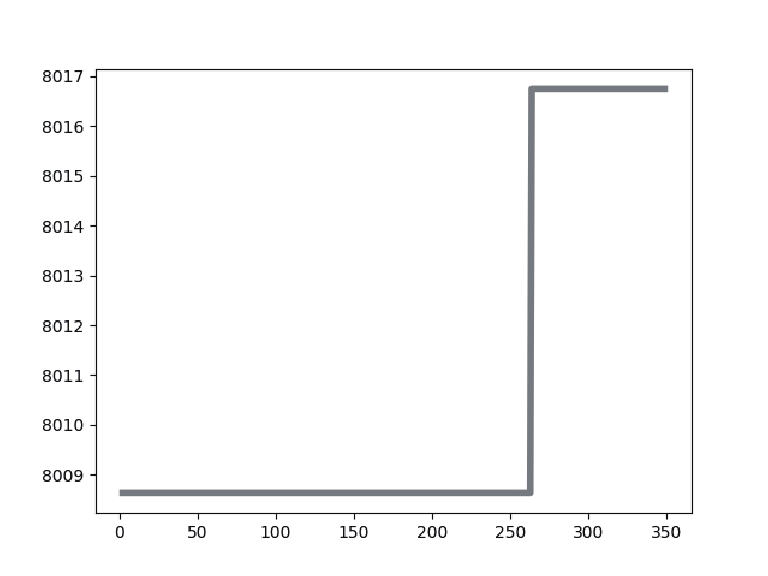
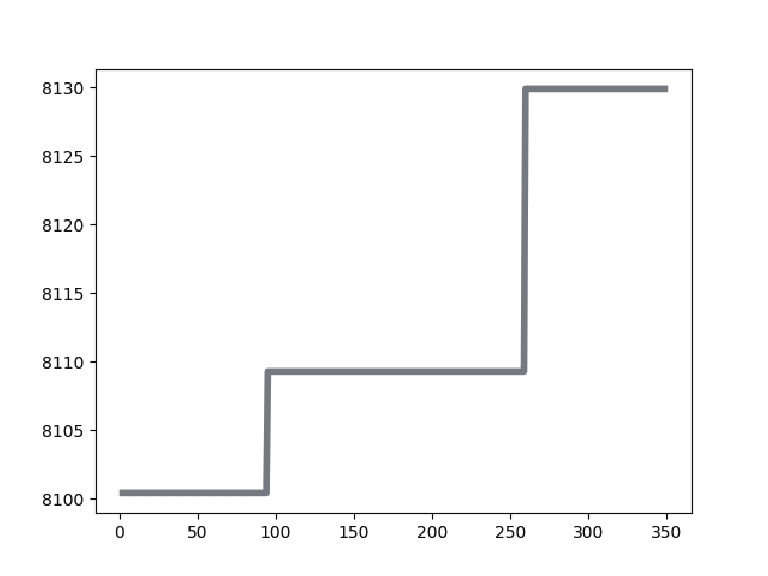
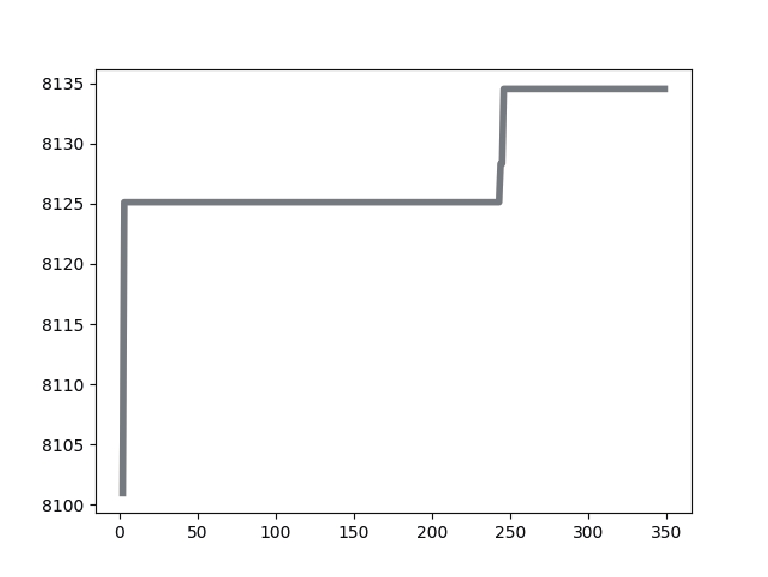
4.2 数据分析

表2展示了针对实验中使用的乳腺癌测试图像, 使用不同阈值[k=2, 3, 4]的IDO算法、DO算法、HHO算法、MPA算法、GTO算法分割后的图像以及它们的最佳阈值取值大小. 表3表示了使用不同阈值[k=2, 3, 4]时IDO算法、DO算法、HHO算法、MPA算法、GTO算法的适应度值曲线和适应度值.

从表3的各算法适应度图中可以看出, IDO算法, 在k=2, 3, 4任意阈值时, 它的收敛速度都快于其他算法, 并且它获得的适应度值要比其他算法高. 在阈值个数k=2时, IDO算法在50次迭代以内便开始完成收敛, GTO算法在迭代次数达到250次时开始收敛, HHO算法适应度曲线波动起伏大并且在迭代次数达到150次后才开始收敛, DO算法和MPA算法在迭代次数达到250次后才开始收敛, 而且相较于其他算法, IDO算法和MPA算法所获的适应度值最高. 在阈值个数k=3时, IDO算法仍然在50次迭代以内便开始完成收敛, 但收敛时的时间开始增加, GTO算法在迭代次数达到150次时开始收敛, HHO算法适应度曲线波动起伏大并且也在迭代次数达到150次后才开始收敛, MPA算法在迭代次数达到300次后开始收敛, DO算法在迭代次数达到250次后开始收敛, 而且相较于其他算法, IDO算法和MPA算法所获的适应度值最高. k=4时, IDO算法在50次迭代以内便开始完成收敛, GTO算法在迭代次数达到150次时开始收敛, HHO算法适应度曲线波动起伏大并且在迭代次数达到200次后才开始收敛, MPA算法在迭代次数达到300次后开始收敛, DO算法在迭代次数达到250次后开始收敛且适应度值最低, 而且相较于其他算法, IDO算法所获的适应度值最高. 这些充分证明了IDO算法的收敛能力比其他算法更强, 搜索最佳阈值更快, 实时性更好.

4.3 性能指标

我们很难通过肉眼对分割后的图像质量进行主观评价, 所以需要通过峰值信噪比(PSNR), 结构相似度指数(SSIM), 特征相似度指数(FSIM)这3个指标进行衡量^[30].

PSNR计算公式如式(21)所示:

$ {\textit{PSNR}} = 20 \times {\text{lo}}{{\text{g}}_{10}}\left( {\frac{{255}}{{{\textit{RMSE}}}}} \right) $

(21)

$ {\textit{RMSE}} = \sqrt {\frac{{\displaystyle\mathop \sum \nolimits_{{{i}} = 0}^{{{M}} - 1} \displaystyle\mathop \sum \nolimits_{{{j}} = 0}^{{{N}} - 1} {{\left( {{{{I}}_{{{ij}}}} - {{}}{{{{\textit{Seg}}}}_{{{ij}}}}} \right)}^2}}}{{{{M}} \times {{N}}}}} $

(22)

其中, RMSE是每个像素的均方根误差, M×N表示图像的大小, ${{{I}}_{{{ij}}}}$表示原始 图像的像素灰度值, ${{\textit{Seg}}_{{{ij}}}}$表示分割后的图像中的像素灰度值^[31].

SSIM计算公式如式(23)所示:

$ {\textit{SSIM}} = \frac{{\left( {2{\mu_I}{\mu_{{\text{seg}}}} + {{{c}}_1}} \right)\left( {2{{{\sigma }}_{{{I}}, {\text{seg}}}} + {{{c}}_2}} \right)}}{{\left( {\mu_I^2 + \mu_{{\text{seg}}}^2 + {{{c}}_1}} \right)\left( {{{\sigma }}_I^2 + {{\sigma }}_{{\text{seg}}}^2 + {{{c}}_2}} \right)}} $

(23)

其中, ${\mu_I}$和${\mu_{{\text{seg}}}}$是原始图像和分割图像的像素平均值, ${\sigma{}}_I^{}$和${\mathrm{\sigma }}_{{{\rm{seg}}}}$是原始图像和分割图像的标准差, ${{{\sigma}}_{{{I}}, {\text{seg}}}}$是原始图像和分割图像的协方差, c₁和c₂是用来保证稳定性的常数^[32].

FSIM计算公式如式(24)所示:

$ {\textit{FSIM}} = \frac{{\displaystyle\mathop \sum \nolimits_{{{I}} \in {{\Omega }}} {S_L}\left( X \right)P{C_m}\left( X \right)}}{{\displaystyle\mathop \sum \nolimits_{{{I}} \in {{\Omega }}} P{C_m}\left( X \right)}} $

(24)

$ {\textit S_L}\left( X \right) = {\textit S_{PC}}\left( X \right){ \textit S_G}\left( X \right) $

(25)

$ {\textit S_{PC}}\left( X \right) = \frac{{2{{P}}{C_1}\left( X \right){{P}}{C_2}\left( X \right) + {T_1}}}{{{{PC}}_1^2\left( {{X}} \right){{PC}}_2^2\left( {{X}} \right) + {T_1}}} $

(26)

$ \textit {S}_{G}\left(X\right)=\frac{2{G}_{1}\left(X\right){G}_{2}\left(X\right)+{T}_{2}}{{{G}}_{1}^{2}\left({X}\right){{G}}_{2}^{2}\left({X}\right)+{T}_{2}} $

(27)

$ {{G}} = \sqrt {{{G}}_{{x}}^2 + {{G}}_{{y}}^2} $

(28)

$ \textit {{PC}}\left( {{X}} \right) = \frac{{{{E}}\left( {{X}} \right)}}{{{{\varepsilon }} + \displaystyle\mathop \sum \nolimits_{{m}} {{{A}}_{{n}}}\left( {{X}} \right)}} $

(29)

其中, Ω代表原始图像的所有像素域. ${S_L}\left( X \right)$表示相似度得分. T₁和T₂是常数, G₁和G₂分别为原始图像和分割图像的梯度, E(X)是位置X和尺度n中的向量大小. 此外, $ \mathrm{\varepsilon } $是一个小数, ${{{A}}_{{n}}}\left( {{X}} \right)$是尺度n中的局部大小, 采用文献[33]的参数设置.

表4给出了使用不同阈值[k=2, 3, 4]的IDO算法、DO算法、HHO算法、MPA算法、GTO算法分割图像后性能指标PSNR、SSIM、FSIM的平均结果.

从表4观测数据得知, 在阈值个数k=2, 3时IDO算法, MPA算法的SSIM值同占第1位; 在阈值个数k=4时, IDO算法的SSIM值独占第1位, 超过了MPA算法. 在阈值个数k=2, 3时IDO算法, MPA算法的FSIM值占第1位; 在阈值个数k=4时, IDO算法的FSIM值占第2位, 稍逊MPA算法一筹. 在阈值个数k=2时, IDO算法, MPA算法的PSNR值同占第3位, GTO算法占第1位, HHO算法占第2位; 在阈值个数k=3时, IDO算法的PSNR值占第4位, MPA算法的PSNR值占第3位, DO算法占第1位, HHO算法占第2位; 在阈值个数k=4时, IDO算法的PSNR值超越了其他算法占第1位. 从数据的纵向看, IDO在3个指标中总体比其他算法更具优势, 并且随着阈值个数的增加, IDO的优势在不断地增加.

5 结论与展望

通过实验数据可知, 本文提出的基于增强蒲公英优化算法(IDO)的乳腺癌图像多阈值分割方法通过传统蒲公英优化算法结合布朗运动和莱文飞行的三阶段搜索过程快速寻找最佳阈值, 提升了图像分割的效率, 并且建立的回守策略解决了传统蒲公英算法(DO)在图像分割领域无限制搜索, 超出像素范围的问题; 引入的对立式学习(OBL)避免算法陷入局部最优. IDO的性能超越了对比的4种算法: GTO算法、HHO 算法、DO算法、MPA算法, 我们提出对传统蒲公英优化算法的改进是合理的, 对其他启发式算法的改进具有借鉴意义, 并且IDO算法在图像分割的优良性能, 也让它具有较好的推广价值.

虽然IDO算法在数据上显示有很大的优势, 但其仍然有不足之处, 首先本算法使用优化策略调高了算法的复杂度, 其次本算法还不能处理其他高难度的分割任务, 并且本算法只测试了部分低阈值个数的情况, 没有测试高阈值情况, 没有找到最佳阈值个数, 这些将是我们今后的重点研究方向.