聚类是一种寻找数据内在结构之间的一些规律并按照这种规律将数据组成若干相似的不同类别的组, 被划分在相同小组内的数据样本之间彼此相似度较高, 而被划分在不同小组之间的数据相似度较低. 随着网络的迅速发展, 人们的各种行为都可以以数据的形式进行表达, 加上5G时代的普及, 每天都会有海量的网络数据产生, 聚类是传统的数据分析方法之一, 对从这些海量数据中发现数据之间的规律起着重要作用. 聚类技术是以一种无监督的方式对数据进行划分的技术, 因为它不需要数据有额外的标签信息, 日常生活中聚类分析无处不在. 例如: 对于新兴起的电商领域, 聚类可以通过分析消费者的消费行为数据, 从而将消费者的消费偏好进行划分, 有助于商家对自己的产品进行定位与改进, 从而可以寻找到新的潜在的市场, 聚类分析是商家对消费市场进行细致划分的有效工具: 在生物医学领域, 聚类分析可以用来分析生物物种的基因数据, 然后将生物物种的类别进行区分, 以便于人们对生物种群的快速认知; 在互联网行业上, 聚类分析可以用于对来自网络上的东西进行划分, 将各种图片进行分类以及各种文档类别的区分; 在保险行业领域, 保险销售员可以根据购买保险的人所居住的地理位置以及购买保险金额的大小来向固定区域的人推荐适合他们的保险套餐等.

传统的聚类分析方法主要是以机器学习技术去解决聚类问题. 传统的机器学习技术在针对海量高维的数据时首先对高维数据的多种特征进行特征选择(一般主要采用一些传统的降维方式及其一些改进的高维数据降维方法, 如: 主成分分析、Lasso特征映射等方法), 然后再对所选择出来的数据特征运用聚类算法进行聚类. 但目前存在的方法有些许不足, 在处理的数据维数较低时, 传统的一些聚类方法可以正确的将数据样本划分到它所属类别, 但网络的发展使得数据的维度与复杂度与日俱增, 传统的特征选择方式已经不能很好地应用于聚类, 限制了聚类方法的性能.

近几年, 深度聚类方法兴起, 并在聚类效果方面取得了良好的结果. 现阶段聚类方法主要为利用深度学习方法去进行聚类. 目前所研究的深度聚类方法主要有两大类: 一类是将数据降维过程与数据聚类过程分开进行, 降维过程使用的是深度学习技术, 而聚类过程采用传统的聚类方法, 上述方式被称为两步策略; 另一类是在联合学习数据的低维表示和聚类过程中均采用深度学习技术, 这种方法称为一步策略. 其中, 在两步策略中, 无监督的深度嵌入聚类(unsupervised deep embedding for clustering analysis, DEC)算法^[1]首先采用线性自动编码器通过最小化输入数据与输出数据之间的均方误差来提取数据的低维特征, 然后摒弃解码器通过使用KL散度作为损失函数来进行聚类数据的分配与数据低维表示优化; 利用成对数据相似度进行深度聚类(deep clustering with self-supervision using pairwise data similarities, DSCC)算法^[2], 首先使用线性自动编码器提取数据的低维特征然后再使用一个MNet网络将数据低维特征空间映射到一个K维空间上完成数据簇的分配; 利用完全卷积自动编码器进行判别增强的图像聚类(discriminatively boosted image clustering with fully convolutional autoencoders, FCAE-DBC)算法^[3]通过使用卷积自编码器提取原始高维数据的低维特征表示, 提出一个基于完全卷积自动编码器和软K-means的统一聚类框架来迭代更新数据低维表示与聚类分配; 在一步策略中, 利用局部结构保持改进的深度嵌入聚类(improved deep embedded clustering with local structure preservation, IDEC)算法^[4]将DEC中的数据低维特征提取损失函数与聚类损失函数以一定的权重联合起来进行优化, 省去中间过程, 通过迭代优化来得到最优的数据低维表示与最优的聚类集群; 利用卷积自动编码器的深度聚类(deep clustering with convolutional autoencoders, DCEC)算法^[5]在IDEC的基础上将IDEC中的线性自编码器中的线性层替换为卷积层, 然后采用与IDEC相同的策略去学习数据低维表示与聚类分配; 半监督深度嵌入聚类(semi-supervised deep embedded clustering, SDEC)算法^[6]在IDEC的基础上在聚类损失函数中加入成对距离约束损失函数, 同时学习低维数据表示与聚类分配; 基于非对称残差自编码器的深度嵌入式聚类(deep embedded clustering with asymmetric residual autoencoder, ADREC)算法^[7]将卷积自编码器的编码部分替换为4个残差块, 将对称的卷积自编码器改变为非对称的自编码器, 增强了自编码器的编码能力从而保证了自编码器所提取特征的可靠性, ADREC同样采用一步策略来优化数据低维表示与聚类分配; 通过收缩特征表示和焦点损失进行的无监督深度聚类(unsupervised deep clustering via contractive feature representation and focal loss, DCCF)算法^[8]在特征学习过程中引入收缩表示并在聚类层中利用焦点损失, 用端到端机制添加的收缩惩罚项使得该算法能够学习到更多的区别性特征; 深度嵌入K-means聚类(deep embedded K-means clustering, DEKM)算法^[9]采用对称卷积自编码器提取数据低维空间, 然后将数据低维空间转换为包含聚类结构的新空间, 用熵来衡量聚类的好坏, 以此来进行迭代更新数据低维表示与聚类结果; 在相似性和重构约束下的深度聚类(deep clustering under similarity and reconstruction constraints, DCSR)算法^[10], 通过利用适应性涅罗损失来使深度神经网络将相似或不相似的成对样本加以区分, 获得数据可解释的one-hot表示^[11], 然后将重构损失与涅罗损失联合起来进行优化从而形成了端到端式的深度聚类. 虽然上述深度聚类方法已经取得了较好的结果, 但上述方法大都是对数据预处理部分或者聚类算法部分的改进以提升聚类性能, 很少有对高维数据进行特征提取^[12]部分的改进. 对于高维数据的聚类, 数据的低维特征提取对聚类结果的好坏影响至关重要, 因此本文着重对深度聚类方法特征提取部分进行改进以提升深度聚类算法性能.

基于以上, 本文提出一种基于跳跃连接的深度嵌入K-means聚类(deep embedded K-means clustering with skip connections, SDEKC), 该模型通过在对称的卷积自编码中加入两个跳跃连接, 弱化了卷积编码器的解码器对编码器的要求, 使得到的低维数据表示更多的保留原始数据的聚类信息结构; 然后在聚类阶段使用一个标准正交矩阵将现有的低维数据空间转化为一个包含聚类信息的新空间, 使用贪婪算法同时优化数据低维表示与聚类信息; 最后, 在6个公开真实数据集上与多种算法进行对比实验, 验证了本文所提算法的有效性.

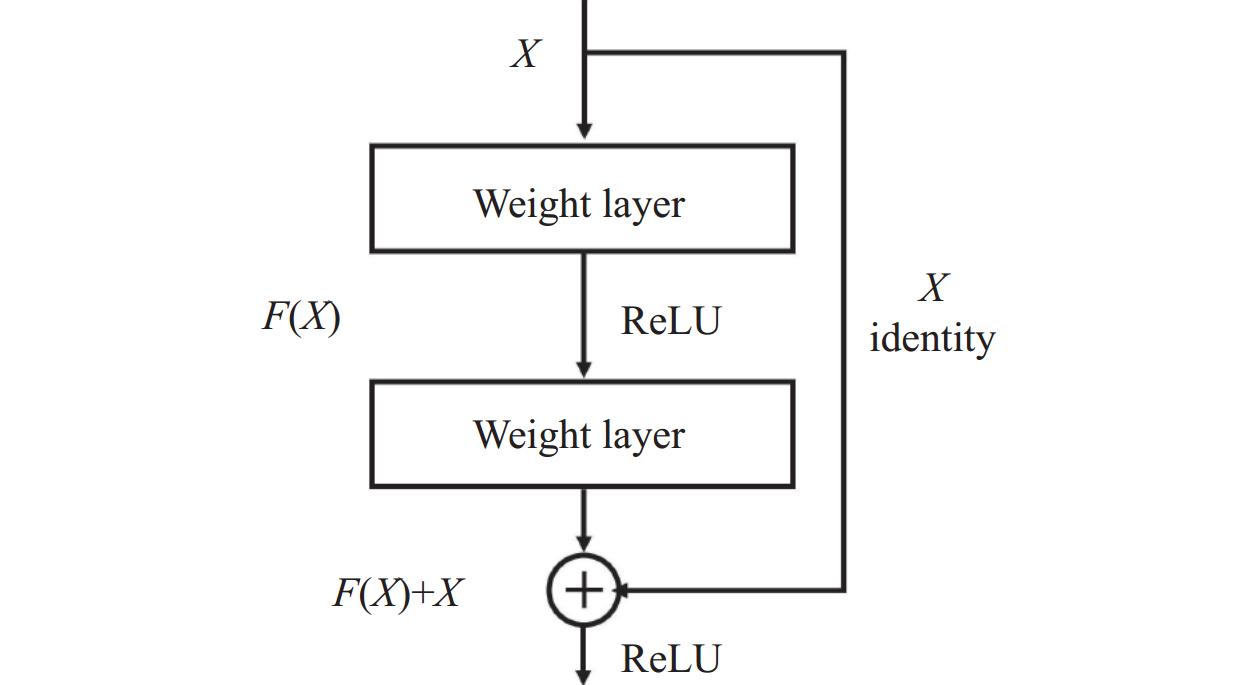
1 SDEKC算法

随着深度学习的发展, 在较深层次的网络中加入跳跃连接开始兴起, 在网络中加入的跳跃连接会跳过神经网络中的几个层相当于对跳过的几层链接作了恒等映射, 同时将数据通过这几层的输出结果与通过恒等映射的信息相加作为接下来那一层网络的输入. 跳跃连接的恒等映射原理解决了深层次网络中出现的网络退化问题. 跳跃连接有两种连接方式: 加法和串联. 以加法方式的跳跃连接典型例子为ResNet^[13]. ResNet使用加法方式的跳跃连接解决了网络中随着网络层数的不断增加而出现的网络“退化问题”. 具体ResNet网络的短路连接机制如图1所示.

如图1中ResNet构建块所示, ResNet网络中下一层的输入等于通过恒等映射的X加上X经过Weight layer层后得到的F(X). 以串联方式的跳跃连接典型例子为DenseNet^[14]. 相比于ResNet, DenseNet提出了一个更加密集的跳跃连接机制: 将前面网络得到的图像信息传递给它之后的每一层网络, 也就是在DenseNet中的每一层网络都会串联它之前的所有层的输出结果作为其向下一层网络所传递的输入. DenseNet直接串联来自不同层的特征图, 实现了网络特征重用, 提升了网络的效率. 跳跃连接的使用也拓展到了自编码器中, 典型的例子为U-Net^[15]. U-Net源于生物医学领域, 用于生物医学图像的分割. 它包含一个编码器-解码器部分, 跳跃连接将其对应的编码与解码部分连接, U-Net中的跳跃连接方式为串联. 在自编码器提取数据低维特征的过程中扭曲了原始数据的特征空间, 而跳跃连接具有数据特征重用功能^[16], 在自编码器中加入跳跃连接可以很大程度上缓解自编码器对原始数据特征空间的扭曲.

本文受到深度残差网络与U-Net网络的启发, 在自动编码器中加入跳跃连接. 原因如下: (1)在编码器部分, 图像细节可能会被遗失, 使得解码器恢复图像能力变弱, ResNet中使用的跳跃连接技术解决了缩小维数时的信息丢失现象导致图像还原时分辨率下降的问题. 本文采用与ResNet相同形式的跳跃连接, 将编码器提取的特征以对称连接的方式传递给解码器的反卷积层, 有助于解码器提高图像的重构能力. (2)使用自编码器重构原始图像的过程中, 随着损失函数的值越来越小, 解码器对编码器要求的数据低维表示越来越抽象, 会扭曲数据的低维表示, 加入跳跃连接, 编码器每层提取的特征会在解码器重构图像的过程中提供一定原始数据细节, 弱化了解码器对编码器的编码要求, 编码器产生的低维表示更能表示出原数据特征, 从而可以更加有效提升聚类性能.

本文提出的SDEKC主要包括两个部分: 高维数据的特征提取部分和聚类部分. 本文所提出的SDEKC网络结构图如图2所示.

1.1 高维数据的低维特征提取

自编码器是一种将输入数据(可以是数字、图像以及文本类型) x输入到所建立的网络模型中, 先对原始高维数据进行低维压缩得到输入数据x的低维潜在特征表示z, 然后再对z进行解压缩得到重构数据x'的过程. 从整体来看, 自编码器包含两部分: 一部分为对原始数据进行压缩的编码器E_W(·)部分, 另一部分为对所提取的低维特征进行高维特征恢复解码器D_U(·)部分. 使用编码器来提取低维数据特征是深度学习领域的主要降维方法之一, 主要目的是得到高维数据在低维空间上的数据表示便于后续对数据进行分析. 自编码器通常通过最小化输入数据与重构数据之间的均方误差(mean squared error, MSE)来优化低维特征表示z. 最小化MSE的过程表示如下:

$ \mathop {\min }\limits_{W, U} \frac{1}{n}\sum\limits_{i = 1}^n {||{x^\prime_i} - {x_i}||_2^2} $

(1)

其中, $x'_i$= D_U (E_W (x_i)).

经过自动编码器训练得到x的低维特征表示z. z可表示如下:

$ {E_W}(x) = \sigma (Wx) \equiv {\textit{z}} $

(2)

其中, $\sigma $为Sigmoid或ReLU等的激活函数, x与z均为向量.

为了使自动编码器能更好地提取图像特征, 本文将自动编码器的编码部分的线性层全都替换为卷积层, 将自动编码器的解码部分的线性层全都替换为反卷积层. 所替换后的自编码器仍为对称结构, 卷积操作能很好的提取图像的空间结构信息. 提取图像低维特征的过程如式(3)所示:

$ {E_W}(x) = \sigma (x * W) \equiv {\textit{z}} $

(3)

其中, “$* $”表示卷积算子, 反卷积解码过程定义如式(4)所示:

$ {D_U}({\textit{z}}) = \sigma ({\textit{z}} * U) $

(4)

自编码器中编码部分z=E_W(x)和解码部分x'=D_U(z)中的参数利用神经网络中反向传播算法来进行参数更新. 重构过程损失函数定义如式(5)所示:

$ {L_r} = \frac{1}{n}\sum\limits_{i = 1}^n {||{D_U}({E_W}({x_i})) - {x_i}||_2^2} $

(5)

其中, n是数据集的数量, x_i表示第i个数据.

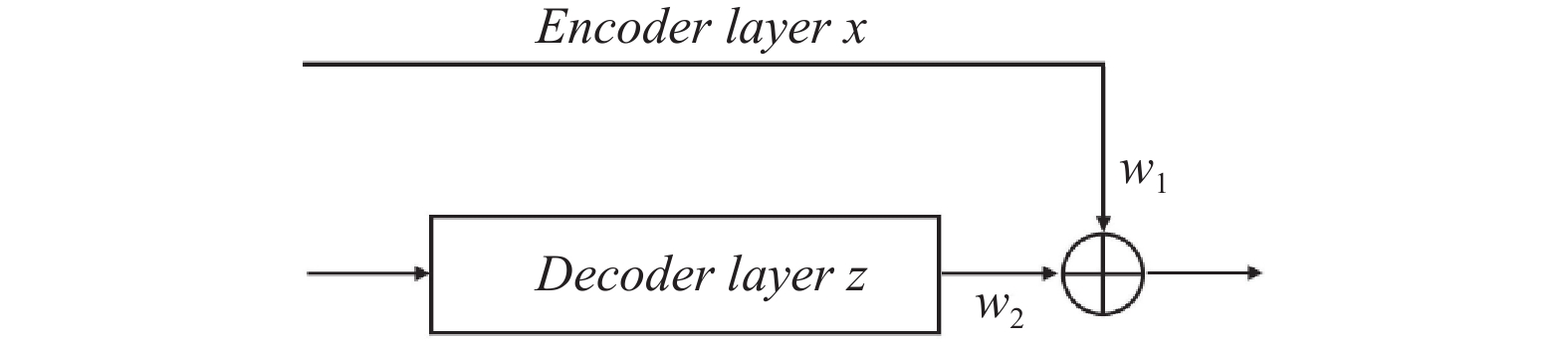
在本文中, 在卷积自编码器中加入两个跳跃连接来提取图像的低维特征. 跳跃连接被用来向前传递特征图, 为了提高重构质量同时突出编码器的编码能力, 在自编码器的编码部分和解码部分之间以一定权重对称增加了两个跳跃连接. 加入跳跃连接的反卷积层的下一层输入如图3所示.

图3中, 下一层反卷积输入为w₁×Encoder layer x+w₂×Decoder layer z.

1.2 聚类

经上述通过带有跳跃连接的卷积自编码对高维数据特征的提取, 可得到了数据的低维特征, 接下来对数据的低维特征z进行聚类. 上述过程所提取的数据低维特征可能不包含任何聚类信息. DEC在使用线性自编码器通过最小化输入数据与重构数据之间的均方误差损失提取数据的潜在特征后, 给定初始聚类中心, 其次使用t分布来计算每个数据样本被分配到每个聚类集群的软分配的概率^[4], 然后根据软分配概率计算出辅助目标分布, 使用KL散度来衡量上述两者之间的差异, 最后通过最小化KL散度来更新低维空间中的数据表示及聚类集群间数据样本的分配. DEC的思想是属于统一集群的数据有相同的分布. DEC属于深度聚类中的两步策略, 将特征提取过程与聚类过程分开进行. 改进的DEC版本IDEC使用了一步策略, 将特征提取过程与聚类过程联合进行优化. IDEC想要优化聚类集群的同时优化数据的低维特征表示, 于是以一定的权重将重构损失与聚类损失联合起来, 但权重参数不同聚类结果也会有所不同. 权重参数只能人为定义因此聚类结果有很大的不确定性.

在本文中, 使用K-means对数据的低维特征进行聚类, 聚类目标函数如下:

$ \min {L_C} = \sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {||{\textit{z}} - {\mu _i}|{|^2}} } $

(6)

其中, $\;{\mu _i} = \dfrac{1}{{|{C_i}|}}\displaystyle\sum\nolimits_{{\textit{z}} \in {C_i}} {\textit{z}} $. 这里z表示卷积自编码提取的数据低维特征, k为聚类的集群个数, C_i表示第i个聚类簇, μ_i表示第i个聚类簇的聚类中心. 为了揭示数据的低维特征中所蕴含的聚类结构信息, 本文用标准正交变换矩阵V将数据的低维特征空间Z转换成为一个新的空间Y, Y= VZ^[9]. 则上述损失函数变为:

$ \begin{split} \min {L_C} &= \sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {||V{\textit{z}} - V{\mu _i}|{|^2}} } \\ & = \sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {{{(V{\textit{z}} - V{\mu _i})}^{\rm{T}}}(V{\textit{z}} - V{\mu _i})} } \\ & = \sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {{{({\textit{z}} - {\mu _i})}^{\rm{T}}}{V^{\rm{T}}}V({\textit{z}} - {\mu _i})} } \\ & = \sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {Trace({{({\textit{z}} - {\mu _i})}^{\rm{T}}}{V^{\rm{T}}}V({\textit{z}} - {\mu _i}))} } \end{split} $

(7)

因为V^TV=I, 将上述等式进行变形, 式(7)最后一步可化成如下形式:

$ \begin{split} & {\textit{Trace}}\left( {V\left[ {\sum\limits_{i = 1}^k {\sum\limits_{{\textit{z}} \in {C_i}} {({\textit{z}} - {\mu _i}){{({\textit{z}} - {\mu _i})}^{\rm{T}}}} } } \right]{V^{\rm{T}}}} \right) \\ &\quad = {\textit{Trace}}(V{S_W}{V^{\rm{T}}}) \end{split} $

(8)

则损失函数式(7)变为式(9):

$ \min {L_C} = {\textit{Trace}}(V{S_W}{V^{\rm{T}}}) $

(9)

其中, ${S_W} = \displaystyle\sum\limits_{i = 1}^k {\displaystyle\sum\limits_{{\textit{z}} \in {C_i}} {({\textit{z}} - {\mu _i}){{({\textit{z}} - {\mu _i})}^{\rm{T}}}} }$. S_W为K-means的类内散度矩阵. V是一个标准正交矩阵, 最小化上述聚类损失函数是一个标准的迹最小化问题.

Rayleigh-Ritz定理^[17]表明: V的解包含具有特征值上升的S_W的特征向量. 特征值表明了特征向量在变换空间Y=VZ中对聚类簇结构贡献的重要性, 特征值越小, 其对应的特征向量对变换空间中的聚类簇结构的贡献就越重要. S_W是对称的, S_W可正交对角化. 式(6)–式(9)的合理性如下.

定理1^[18]. 若向量v是方阵A的特征向量, 则可以表示为如下形式:

$ Av = \lambda v $

(10)

其中, λ为方阵A中的向量v对应的特征值. 则对于任意一个方阵A来说:

$ A\left( {{v_1}, {v_2}, \cdots , {v_m}} \right) = \left( {{\lambda _1}{v_1}, {\lambda _2}{v_2}, \cdots, {\lambda _m}{v_m}} \right) $

(11)

$ \left( {{\lambda _1}{v_1}, {\lambda _2}{v_2}, \cdots, {\lambda _m}{v_m}} \right) = \left( {{v_1}, {v_2}, \cdots, {v_m}} \right)\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}& \cdots &0 \\ \vdots & \ddots & \vdots \\ 0& \cdots &{{\lambda _m}} \end{array}} \right] $

(12)

则有AV=VΛ, 则矩阵A的特征分解公式A=VΛV⁻¹, V为正交矩阵. 根据矩阵的相似与合同定义, 矩阵A与矩阵Λ既相似又合同, 必有相同的特征值与特征向量. 从式(6)到式(9)的过程可以认为是矩阵特征分解的过程. 在任意一个矩阵的特征值中, 特征值越大, 包含可解释原始数据的信息就越多. 主成分分析中的特征值分解方法与上述原理一致, 主成分分析主要是根据特征值的大小来反映其对应的向量对所包含矩阵信息的多少. 主成分分析原理见图4. 矩阵A中大的特征值所对应的特征向量包含原始数据的信息越多.

因此, 找到一个标准正交矩阵V使得聚类损失函数式(9)成立是可行的.

1.3 算法优化

直接通过标准正交变换矩阵将得到的数据低维空间Z转换为蕴含有聚类结构信息的空间Y, 得到的Y是仅通过特征提取部分得到数据的聚类结构信息空间, 并不能真正反映原始数据的聚类信息结构, 因此, 将数据的低维表示与聚类结果进行联合优化使得到的数据低维表示包含原始数据中更多的聚类结构信息同时得到的聚类结果更加准确, 优化过程如下.

首先, 在数据的低维空间Z中直接运用K-means得到S_W, 然后对S_W进行特征分解得到正交矩阵V, 最后将数据的低维空间Z转换成一个新的空间Y, 以此来揭示数据的聚类信息. 对于新空间Y, Y中的每个维度都蕴含着聚类簇的结构信息, 而Y的最后一个维度蕴含最少的聚类簇结构信息. 我们将式(9)转换为如下形式:

$ \min {L_3} = \sum\limits_{i = 1}^k {\sum\limits_{y \in {c_i}} {||y - {m_i}|{|^2}} } $

(13)

其中, y=Vz且m_i=Vμ_i. 本文中我们采用熵^[19]来衡量聚类的簇结构信息, 因为数据的熵越小表明其包含的聚类簇的结构信息越高. 一个聚类集群i的熵(Entropy)的计算公式为:

$ {\textit{Entropy}}_i = - \sum\limits_{j = 1}^L {{p_{ij}}{{\log }_2}{p_{ij}}} $

(14)

在式(14)中p_ij=m_ij/m_i, m_ij表示聚类集群i中真实标签与聚类集群i一致的数据样本个数, m_i表示所划分的第i个聚类集群中总共包含的数据样本的个数. L为数据中所包含类别的个数, p_ij范围为0–1. 于是得到所有聚类集群的熵总和计算公式为:

$ {\textit{Entropy}} = \sum\limits_{i = 1}^k {\frac{{{m_i}}}{m}{\textit{Entropy}}_i} $

(15)

式(15)中, k表示聚类集群的数目, m是整个数据中所需聚类的样本数. 从式(14)中可以看出当p_ij在[0, 1]范围内变化时, 以2为底的log函数为增函数, 而熵的整体公式为减函数, 即聚类结果越好(p_ij越大), 熵值越小; 当聚类结果较差时(p_ij越小), 熵值反而越大. 因此, 通过最小化熵来优化聚类结果及数据的低维表示.

在本文中, 希望K-means发现的聚类簇中的数据点更靠近聚类簇的中心点, 即单个聚类簇是聚拢的而不是分散的. 该思想等价于式(6). 本文应用贪婪算法使得聚类簇中的数据点靠近其聚类簇中心y的最后一个维度, DEKM中的实验结果表明使数据点靠近聚类簇中心的最后一个维度的聚类效果更好, 且更容易优化数据的低维表示. 贪婪方法的具体步骤如下: 首先我们将得到的初始的y复制为y', 然后用m_i的最后一个维度去替换y'的最后一个维度. 目标函数如式(16):

$ \min {L_4} = \sum\limits_{i = 1}^k {\sum\limits_{y \in {c_i}} {||y - y'|{|^2}} } $

(16)

本文使用小批次更新策略, 每次只移动一小部分数据点去靠近它们簇的质心. 通过上述过程得到了一个新的数据低维表示z之后, 再次对z运用K-means来获得聚类簇及其各自的质心, 重复上述贪婪算法的过程, 直到聚类的过程中需要更新簇的数据点数量小于其原来数据点数量的0.1%后, 停止上述过程. SDEKC模型算法过程如算法1所示.

算法1. SDEKC

输入: 数据$\scriptstyle x$, 聚类数$\scriptstyle k$, 自编码器训练次数$\scriptstyle {\textit{z}} {\textit{-}} epoch$, 聚类更新次数$\scriptstyle c {\textit{-}} epoch$, 跳跃连接权重$\scriptstyle {w_1}$, $\scriptstyle {w_2}$, 学习率$\scriptstyle lr$.

输出: 数据低维表示$\scriptstyle {\textit{z}}$, 聚类簇$\scriptstyle C = \left\{ {{c_1}, \cdots , {c_k}} \right\}$.

1) for $\scriptstyle i$ in $\scriptstyle range({\textit{z}} {\textit{-}} epoch)$:

2) 　使用式(5)训练加入跳跃连接的卷积自编码器

3) end

4) for $\scriptstyle i$ in $\scriptstyle range(c {\textit{-}} epoch)$:

5) 　使用卷积自编码器的编码部分生成数据$\scriptstyle x$的低维表示$\scriptstyle {\textit{z}}$;

6) 　使用K-means算法得到初始的聚类簇与聚类中心$\scriptstyle \left( {C, U} \right)$;

7) 　使用式(9)得到类内散度矩阵$\scriptstyle {S_W}$;

8) 　对类内散度矩阵$\scriptstyle {S_W}$进行特征值分解得到标准正交矩阵$\scriptstyle V$;

9) 　使用式(16)优化数据低维表示$\scriptstyle {\textit{z}}$;

10) end

11) return $\scriptstyle {\textit{z}}$, $\scriptstyle C$

2 实验结果与分析 2.1 实验环境配置与参数设置

(1) 二分类数据集的实验设置

对于二分类问题, 卷积自编码器的编码部分使用了3层卷积, 紧跟一个线性的全连接层, 跟着编码部分之后的是一个嵌入层. 编码部分的3个卷积层的通道数分别为4、2、1, 3个卷积层的卷积核大小都采用3×3的卷积核, 所有卷积操作中的步幅都设为2. 在嵌入层中神经元的个数为2. 在解码器部分, 解码器首先为一个全连接层, 神经元数量与编码部分的全连接层神经元数量一致, 然后使用3个反卷积层, 反卷积的每一层均为对应的解码器部分卷积层的镜像, 解码器的每一层输出用零填充以匹配相应的编码器层的输入大小. 整个卷积自编码器的激活函数均使用tanh函数. 聚类方法与IDCEC中的聚类方法一致.

(2) 多分类数据集的实验设置

在多分类问题中, 卷积自编码器的编码部分也使用了3层卷积, 3层卷积层之后紧跟着一个全连接层, 然后是一个嵌入层. 3个卷积层的通道数分别为32、64、128, 3层卷积的卷积核大小分别为5×5卷积核、5×5卷积核和3×3卷积核, 所有卷积层的步幅与二分类实验步幅设置一致. 将低维数据空间中神经元的个数设置为每个数据集中所需划分的类别数. 解码器部分, 解码器首先设置一个全连接层, 这个全连接层与编码部分的全连接层一致, 然后依次连接3个反卷积层, 反卷积的每一层均为对应的解码器部分卷积层的镜像, 解码器的每一层输出用零填充以匹配相应的编码器层的输入大小. 整个卷积自编码器的激活函数均使用ReLU函数. 聚类方法采用本文所提聚类方法.

所有层的权值都使用Xavier方法^[20]初始化, 采用Adam ^[21]优化器, 初始的学习率lr=0.001, β₁=0.9, β₂=0.999, w₁=0.999, w₂=0.001. 所有的实验均在Google Colab (GPU100)上进行. 以上实验中, 自编码器训练阶段次数均设置为200, 聚类阶段训练次数均设置为1000, 但当聚类数据中所需要更新簇的数据小于原来数据的0.1%时, 停止聚类阶段的训练.

(3)对比实验设置

本文中所有对比的方法所使用的超参数值都与之前论文中的最优参数设置一致.

2.2 实验数据集

为了评估加入跳跃连接的性能, 本文首先在二分类数据集上与原分类方法结果做了比较, 再次为了更精确地评估本文所提出的SDEKC模型的性能, 又进一步在5个真实数据集上与其他基准方法进行了比较. 为了展示本文所提出的方法能够很好地应用于不同类型图片的聚类, 我们选择了不同类型的图片包括手写类数据集、人脸类数据集、物品数据集以及时尚商品类数据集.

(1) 二分类数据集

地震信号数据集^[22]: 地震信号分为远距离信号与局部信号. 数据集是以图片形式进行记录的, 来自南加州地震网络的宽带和强运动以及日本K-NET和KiK-net强运动网络(仅地面站)的记录. 本文中仅使用9.2k的垂直分量地震图(几乎同等包含远距离和局部波形).

(2) 多分类数据集

MNIST数据集^[23]: 数据来源于美国国家标准与技术研究所, 由250个人(一半高中, 一半工作人员)手写数字0–9组成的灰度图像数据集, MNIST总共包含10个类别70000张图片, 训练集与测试集按6:1划分, 单张图片的大小为28×28像素. Fashion-MNIST数据集^[24]: 由Zalando (德国的时尚科技公司)旗下的研究部门提供, 图片内容为不同时尚商品, 其与MNIST一样分为10种类别, 同样有60000张训练数据集与10000张测试数据集, 单张图片的大小也为28×28像素. USPS数据集^[25]: 由美国邮政提供, 内容为0–9的手写数字, 是从信封中扫描出来的灰度图像, USPS总共包含9298张图片, 7291张为训练数据集, 2 007张为测试数据集, 单张图片为16×16像素, 包含10个类别. COIL-20数据集^[26]: 包含20个类别, 每个类别有72张图片, 在数据预处理时将数据集中单张图片重置为28×28像素的灰度图像. FRGC数据集^[27]: 彩色图片数据集, 该数据集有50000张20个不同人脸数据图片, 我们将图片的大小重置为32×32像素.

数据汇总描述如表1所示.

2.3 评价指标

(1) 准确率(accuracy, ACC)

准确率用于衡量某一数据集在运用某种聚类或者分类算法以后, 数据集中可以被正确地归类到它所属标签的类别的数据样本量占总体数据样本量的比例. ACC的计算公式如式(17):

$ ACC = \mathop {\max }\limits_m \frac{{\displaystyle\sum\nolimits_{i = 1}^n {1\left\{ {{l_i} = m({c_i})} \right\}} }}{n} $

(17)

其中, l_i代表第i个数据点所属的真实标签类别, c_i表示第i个数据被划分到的聚类集群结果, m为映射函数, 它包含整个数据集真实标签和聚类结果之间的一对一映射, 上述映射函数基于匈牙利算法^[25].

(2) 归一化互信息(normalized mutual information, NMI)

归一化互信息主要是用来评估将某一数据集进行相似度划分后的结果, NMI用于比较数据集进行划分后在聚类集群内的数据标签与该聚类集群标签是否一致, NMI的范围为0–1, NMI值越接近于1表明数据集中的样本几乎都被正确的划分到它所属的类别, NMI的计算公式如下:

$ NMI = \frac{{I\left( {T;C} \right)}}{{\dfrac{1}{2}\left[ {H\left( T \right) + H\left( C \right)} \right]}} $

(18)

其中, T代表数据的真实类别标签, C表示数据所被划分到的聚类集群的标签, H(·)表示交叉熵函数表达, I(T;C)=H(T)-H(T|C)表示互信息表达公式.

2.4 基准方法

在多分类数据集中, 我们将本文的方法与一些基准的方法和最先进的方法进行比较, 本文所进行比较的方法如下.

(1) K-means^[28]: 先对原始数据进行处理(若为图片与文本类型, 则需转化为数字类型数据), 再使用K-means进行聚类.

(2) AE+K-means: 先使用线性层全连接自动编码器提取数据的低维特征, 然后再进行聚类.

(3) CAE+K-means: 将AE中的线性层用卷积层代替然后提取数据的低维特征, 最后运用K-means进行聚类.

(4) ARAE+K-means: 将自编码器的编码层替换为4个残差块, 解码层为反卷积层构成自动编码器, 最后对所提取的低维数据运用K-means算法进行聚类.

(5) DEC: 使用与AE中相同的方法提取高维数据的低维特征, 然后去掉AE中的解码部分, 最后以KL散度为损失函数来衡量聚类损失迭代更新低维数据聚类以及数据的低维表示.

(6) IDEC: 在DEC的基础上考虑了自编码器的重构损失, 在一定程度上缓解了编码器对原始数据的扭曲, 在聚类过程中采用端到端的方式联合优化聚类和数据的低维表示.

(7) DCEC: 将DEC的线性编码层替换为卷积层, 线性解码层替换为反卷积层. 聚类过程中采用与DEC相同的更新策略.

(8) IDCEC^[29]: 将IDEC中的线性自编码器替换为卷积自编码器, 然后采用与IDEC相同的更新策略.

(9) SIDCEC: 在IDCEC的基础上在卷积自编码器的基础上加入两个跳跃连接.

(10) DEKM: 采用卷积自编码器提取数据低维空间, 然后将数据低维空间转换为包含聚类结构的新空间, 用熵来衡量聚类的好坏, 以此来进行迭代更新数据低维表示与聚类结果.

2.5 实验结果

二分类数据集聚类结果如表2所示.

多分类数据聚类结果如表3所示, 加粗字体表示各指标的最优表现.

2.6 低维数据空间可视化

(1)二分类数据低维数据空间的比较

对于二分类型数据: 地震信号数据, 分别将IDCEC方法与SIDCEC方法所提取的数据低维空间使用t-SNE^[30]进行可视化, 结果如图5与图6. 图5是使用IDCEC方法对地震信号数据集的高维空间进行低维特征提取后使用t-SNE对提取的低维数据空间进行可视化后的结果; 图6是在IDCEC方法的基础上在IDCEC中对称的卷积自编码器上以本文所提出的加入跳跃连接的方式加入两个跳跃连接后所提取的地震信号数据的低维特征使用t-SNE可视化后的结果. 通过图5与图6的结果可以看出在卷积自编码器提取数据低维特征的过程中加入跳跃连接有助于提取到的数据低维特征更能反映出数据集本身的类别特征, 有助于数据更好地进行聚类. 验证了本文所提的加入跳跃连接思想的有效性. 为了更好地应用于聚类, 本文进一步改进了IDCEC的聚类方法并在多分类数据集上验证了所提出方法的有效性.

(2)多分类数据低维数据空间的比较

在多分类数据集中, 本文仅展示了不同嵌入算法在MNIST数据集上的低维数据空间的可视化. 共选取MNIST数据中前2 000个数据使用t-SNE进行可视化. 结果如下.

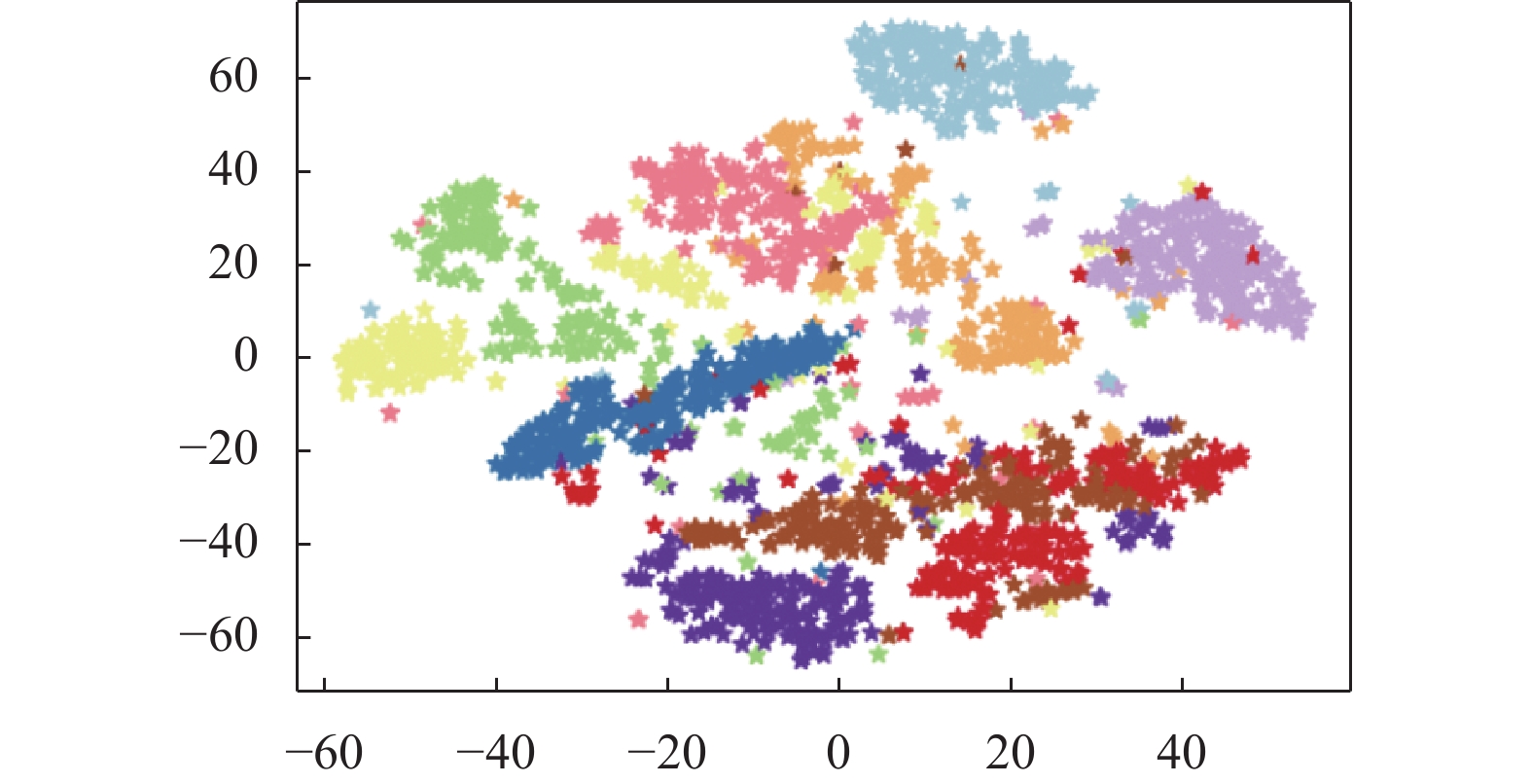
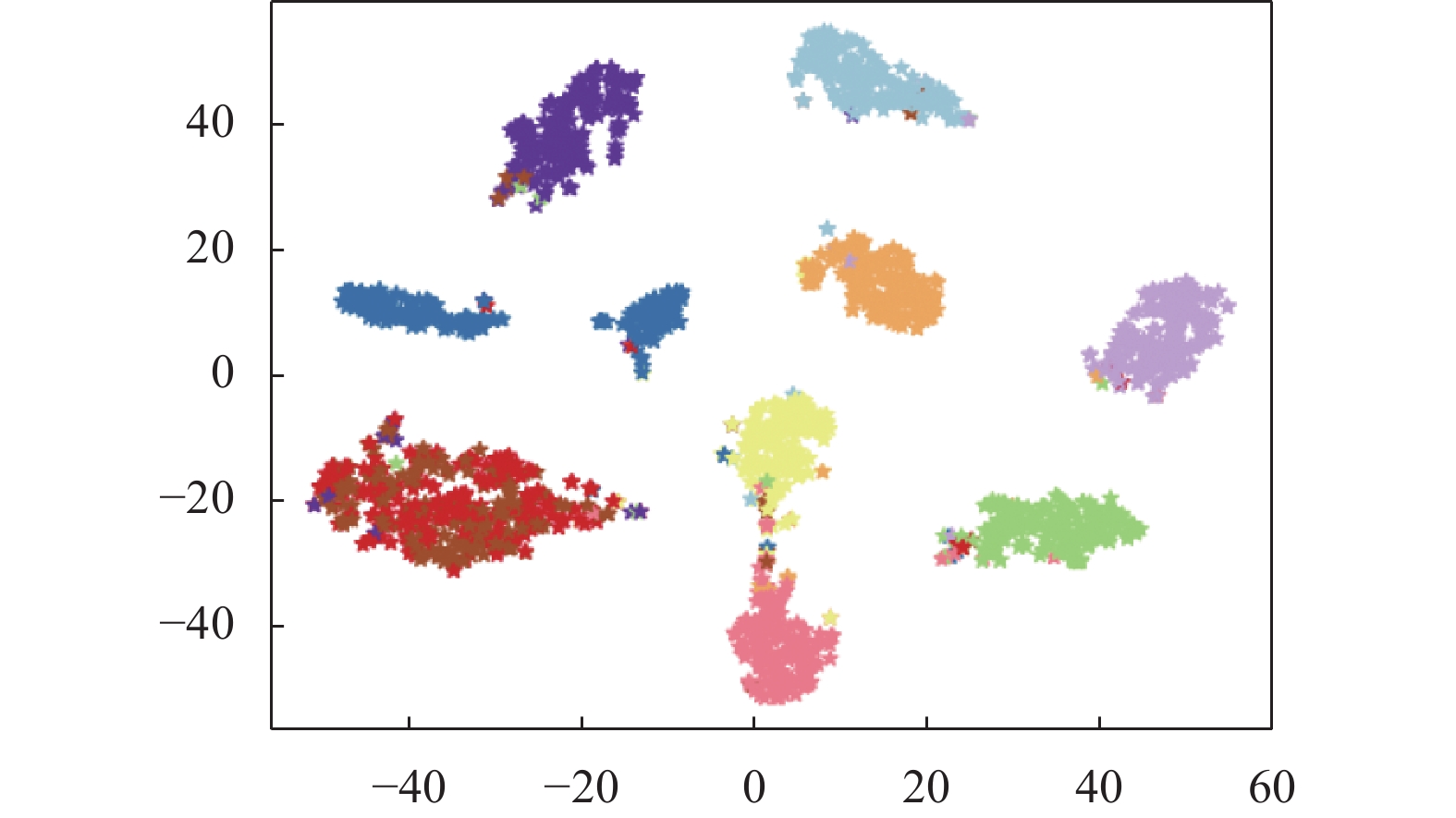
图7展示了MNIST数据集直接进行t-SNE可视化后的结果, 虽然大部分数据的类别可以很容易进行区分但仍有部分数据的类别不明确; 图8展示了MNIST数据集经过线性自编码器提取低维数据特征空间后再使用t-SNE进行可视化后的结果, 从图8中可以看出聚类结果并不理想; 图9展示了DEC算法的MNIST数据低维空间, DEC提取出的数据低维空间可以很好地应用于聚类, 但不足的是有两个类别还没完全区分开来; 图10展示了DEKM的MNIST数据低维空间, 经过DEKM模型训练提取的数据低维空间可以很好地将数据类别区分开来, 但每个类别中都混有一些其他类别的数据; 图11展示了本文算法SDEKC的MNIST数据低维空间, 本文提出的算法SDEKC提取的数据低维空间可以很好地用于聚类并且类与类之间可以进行很明显的区分, 图11中有3个类别是没有掺杂其他类别的数据, 提高了聚类的准确率.

从多分类的t-SNE的可视化图中可以看到本文提出的SDEKC聚类算法优于其他聚类算法.

3 结束语

本文提出了一种新的深度聚类方法SDEKC. SDEKC首先使用卷积自编码器提取高维数据的低维表示, 通过在卷积自编码器中加入两个带有权重的跳跃连接, 提高卷积自编码器的编码能力的同时弱化了卷积自编码器的解码能力, 使得卷积自编码器能产生更多包含数据本身结构的低维特征表示, 使得接下来的聚类算法能更好地挖掘数据中潜在的聚类簇; 在聚类阶段我们首先使用K-means对带有跳跃连接的卷积自编码器所提取的数据低维特征进行聚类, 然后对K-means的类内散度矩阵进行特征分解得到一个标准的正交变换矩阵, 使用这个标准正交变换矩阵将提取到的数据低维特征空间转换为一个新的能够揭示数据聚类结构信息的空间, 得到的标准正交变换矩阵的每一个行向量均表示类内散度矩阵的特征向量, 其特征值表示了对应的特征向量对新得到的包含聚类结构的新空间中聚类信息的贡献大小; 最后使用贪婪算法来迭代优化数据的低维表示以及聚类簇. 实验结果表明, 本文提出的SDEKC优于所比较的方法, 充分验证了新SDEKC算法的有效性.