2. 福建省网络安全与密码技术重点实验室 (福建师范大学), 福州 350117;
3. 福州职业技术学院 信息工程系, 福州 350108;
4. 台湾中山大学 平行处理实验室, 高雄 510275
2. Fujian Provincial Key Lab of Network Security & Cryptology (Fujian Normal University), Fuzhou 350117, China;
3. Department of Information Technology Engineering, Fuzhou Polytechnic, Fuzhou 350108, China;
4. Parallel Processing Lab, Taiwan Sun Yat-sen University, Kaohsiung 510275, China
现实生活中无处不存在数据, 无时无刻也不在产生数据, 而这些随时间变化的连续数据就是时序数据, 如金融数据, 天气数据, 交通数据, 运动数据等. 这些时序数据中通常会存在异常数据, 在金融数据中, 异常数据可能对应着欺诈事件的发生, 在工业数据中, 异常数据也可能对应着机器故障的发生, 因此, 对时序数据中的异常数据进行检测以避免带损失就极具意义. 但是异常通常是不常见, 并且隐藏在大量的正常数据中, 这也使得数据标记变得困难且昂贵, 因此, 现在的大量工作都是基于无监督的时间序列异常检测, 本工作也是基于此.
无监督时间序列异常检测是一个有挑战性的工作, 在这个复杂的工作面前, 传统的机器学习算法很难取得好的表现, 于是越来越多的深度学习方法出现, 以期好的完成这个工作. 无监督时间序列异常检测工作的难点在于训练数据中包含正常数据和异常数据, 对模型学习数据的特征信息会产生不利影响, 同时, 还需要模型习得一个好的判据, 以此来区分正常数据和异常数据. 因此, 上述两个问题就是解决无监督时间序列异常检测的重点, 也是难点所在. 由于时间序列具有时间模式的特性且RNN具有序列建模的能力, 很自然地就想到使用RNN建模, 但RNN的局限在于模型更注重的是当前时间点的数据信息和前一时间点的数据信息的关系, 而当前时间点的数据信息并非只与前一时间点的数据信息有关, 往往与前一段时间点的数据信息有关, 这就限制了RNN的特征表示能力. 随着近年来Transformer模型[1]在计算机视觉和自然语言处理等领域的不错表现, 许多学者开始尝试将Transformer模型运用在时间序列数据中, CAT[2]、DCT-GAN[3]、anomaly Transformer[4]、TranAD[5]等工作对Transformer模型针对时间序列的特性做了各种改进, 提升了其计算性能, 也得到了好的表现. 但最近Zeng等人[6]的工作质疑了基于Transformer的模型对时间序列建模的有效性, 其实验表明 Transformer中的核心模块self-attention在时序数据建模上并没有取得作用. self-attention模块是为了提取长序列的语义信息, 其特征提取是没有考虑顺序的, 但时序建模中顺序是一个重要因素. 尽管使用Transformer架构的模型增加了positional embedding和temporal embedding模块弥补时序的顺序特殊性, 但其实验得出的结论是这些模块并没有保留时序数据的顺序. 与此相反, 线性模型体现出了对顺序关系的极度敏感, 调换输入数据的顺序会对结果产生非常大的变化, 同时, 线性模型也较好地保留了趋势性和周期性. 基于Zeng等人[6]的工作, MTS-Mixers[7]、TSMixer[8]基于线性结构的模型在时间序列预测任务上取得优于基于Transformer模型的效果, 也验证了线性结构在时间序列数据上的有效性. 鉴于此, 本文提出了UMTS-Mixer模型, 其中并没有用到RNN和self-attention结构, 而只用到了线性层. 通过线性层的堆叠, 先缩放后扩展(类似编解码器的结构), 在数据的时间相关上学习特征表示; 然后依旧是线性层的堆叠, 先缩放后扩展, 在数据的通道相关上学习特征表示, 使模型从两个维度学习, 得到好的信息表征.
本文的贡献如下: (1) 本文提出了基于时间相关性和通道相关性的时间序列异常检测方法, 通过对顺序敏感的线性模型来习得数据在时间和通道两个维度上信息表征, 使正常数据区别于异常数据, 更容易为模型所表示. (2) 对4个数据集进行了实验, 结果表明本方案与基线方法相比, 提升了对异常的检测准确率, 在F1 值和召回率两个异常检测指标上优于基线方法.
本文第2节介绍了相关工作. 第3节介绍本文提出的基于时间相关性和通道相关性的时间序列异常检测方法. 第4节在4个现实数据集上评估本文的方法. 第5节总结本文的工作.
2 相关工作无监督多变量时间序列异常检测作为一个重要的现实问题, 得到了广泛的关注. 有大量的基于神经网络的方法被提出, 这些方法大致可以分为两类, 一类是基于自回归的方法, 另一类则是基于重构的方法.
基于自回归的方法, 通常将过去时间段的数据作为模型的输入, 模型产生的输出与当前时间点的数据的差值作为预测误差, 通过预测误差检测异常. 基于自回归的方法有时序预测模型 ARIMA [9] , 该方法需要将时间序列转换为平稳、突变较少的序列, 使用前一时间段内的样本点来预测下一时刻的样本输入值. VAR[10]扩展了 ARIMA, 并根据滞后相关的协方差预测未来. 自回归模型也可以替换为 LSTM[11].
基于重建的方法, 通常将当前时间点的数据作为模型的输入, 模型对数据降维, 然后还原到原始维度重建数据, 模型输入和输出之间的差值作为重建误差, 通过重建误差检测异常. 基于重建方法的模型一般通过编解码器的结构来实现, 自编码器也被称为自相关神经网络, 具有非线性降维能力. 为了捕获更多的信息并能更好的表示信息, 对传统的自编码器做了相应特性的改变, 如稀疏自动编码器 [12]、去噪自动编码器[13]、卷积自动编码器[14]. VAE (variational autoencoder)[15]将神经网络自动编码器与mean-field variational Bayes相结合. Park等人提出了LSTM-VAE模型[16], 该模型替换了原始VAE中的FFN, 采用LSTM主干进行时间建模, LSTM 使用去噪自动编码进行训练以提高表示能力. Su等人提出的OmniAnomaly[17]进一步扩展了具有归一化流的LSTM-VAE模型, 并使用重构概率进行检测. 随着Transformer兴起, 将Transformer中的结构引入时序数据的建模中, 提出了anomaly Transformer, 同时使用高斯核学习先验关联, 用自注意力学习序列关联, 并用MINMAX方法突出关联差异, 但该方法未考虑变量之间的关系. TranAD是另一个基于Transformer的异常检测模型, 它具有自调节和对抗训练, 在处理长序列时, 训练和测试效率很高, 同时保持稳定性. 虽然已经有部分基于Transformer的方法取得了不错的表现, 但其复杂的架构和其核心模块在顺序结构建模的无效性, 不得不重新对其进行审视.
因此, 针对上述问题, 本文通过采用线性模型对数据的时间维度和通道维度建模, 从而使得模型对正常数据有强大的表征能力, 区别于异常数据的难以表征, 以此来进行正常数据和异常数据的区分, 达到异常检测的目的.
3 模型构造 3.1 问题描述给定一个多变量时间序列数据的实例, 表示为Xt = [x1, x2, x3,…, xn] ∈
Zeng等人[6]通过实验证明了线性模型能更好地捕获时间依赖关系, 因此本文提出了一种线性结构模型UMTS-Mixer以实现高效的时间序列的异常检测. 模型的整体架构如图1所示.
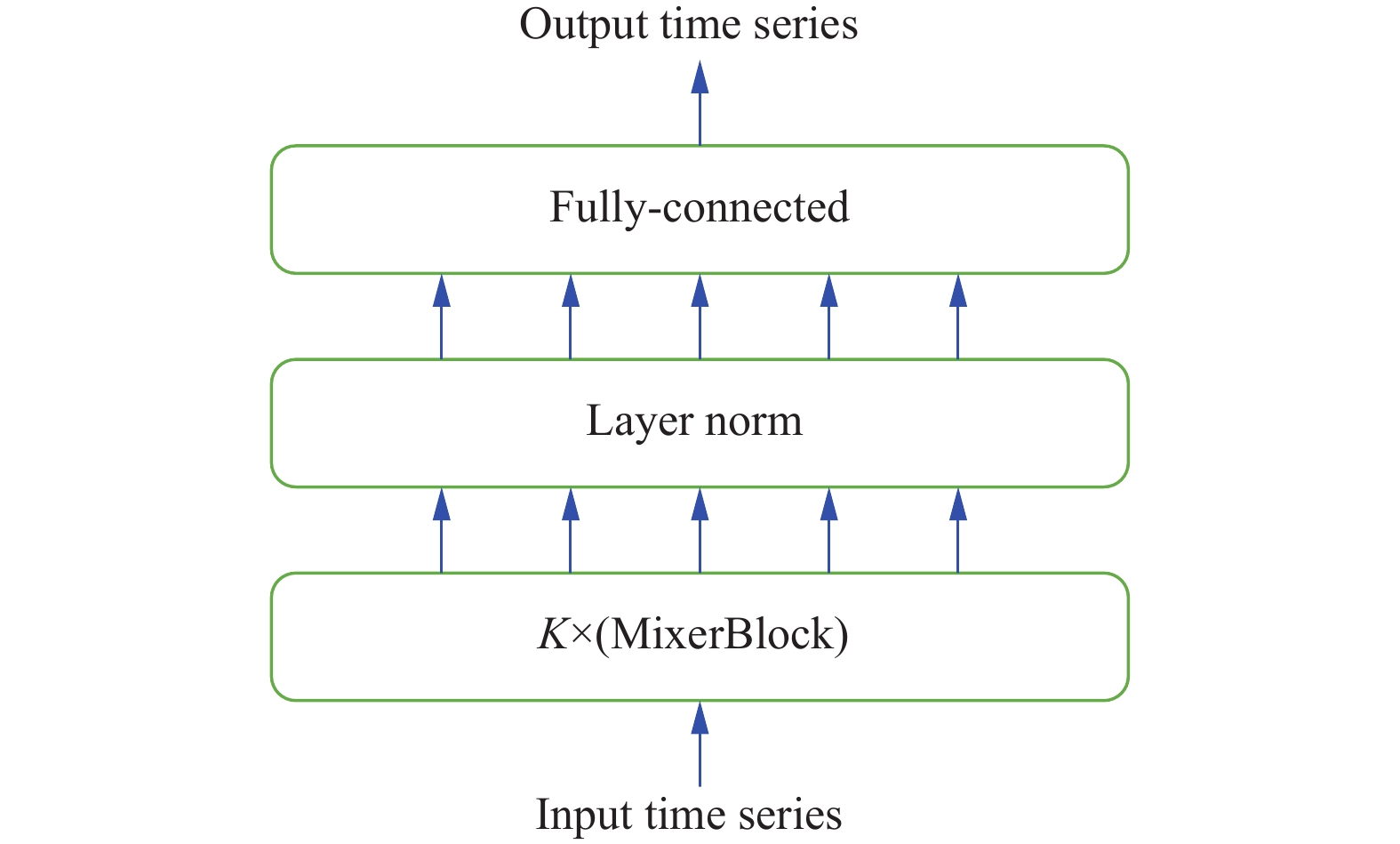
|
图 1 UMTS-Mixer 整体架构 |
UMTS-Mixer模型主要由MixerBlock模块构成, MixerBlock模块包含两个子模块分别为time-mixer和channel-mixer, 其中time-mixer模块用来学习时序数据中的时间依赖关系, channel-mixer模块用来学习时序数据中变量之间的依赖关系, 而time-mixer和channel-mixer模块组成核心是MLP, layer norm层对数据进行归一化处理, time-mixer与channel-mixer的衔接中需要完成T转置操作, 使得模型可以交替进行对时间依赖和变量依赖学习, MixerBlock模块的结构如图2 .
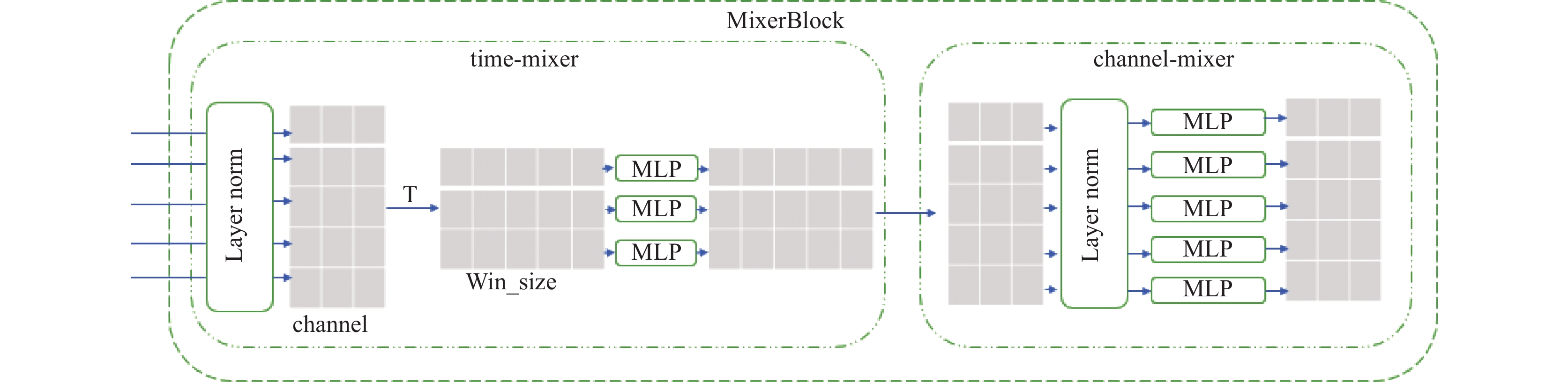
|
图 2 MixerBlock模块结构图 |
time-mixer与channel-mixer中最基本的组成单元MLP的构成如图3所示. MLP其中包含了fully-connected层, GELU激活层, dropout层, 最后由一个fully-connected层结束. 训练模式下时间序列重建的过程如下:
| $ \left\{\begin{array}{l} X_{{\rm{in}}}^{\rm{T}} = MLP(rearrange(norm({X_{{\rm{in}}}}))) + {X_{{\rm{in}}}} \\ X_{{\rm{in}}}^{\rm{C}} = MLP(norm(rearrange(X_{{\rm{in}}}^{\rm{T}}))) + X_{{\rm{in}}}^{\rm{T}} \\ {X_{{\rm{out}}}} = Linear(norm(X_{{\rm{in}}}^{\rm{C}})) \end{array} \right.$ | (1) |
其中, Xin表示输入模型的时间序列数据, norm表示layer norm层, rearrange表示时间维度和变量维度的一个转换,
| $ loss = ||{X_{{\rm{in}}}} - {X_{{\rm{out}}}}||_F^2 $ | (2) |
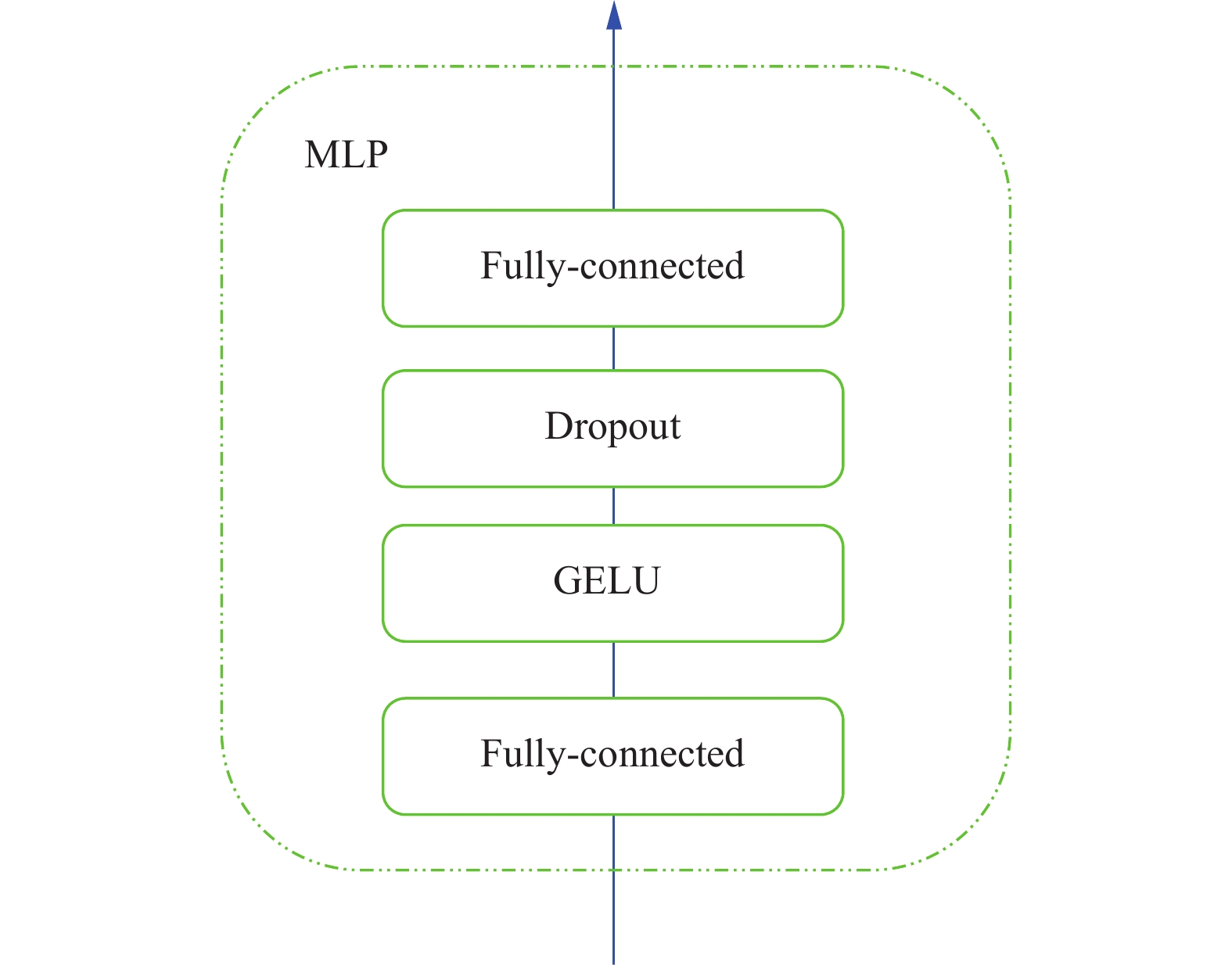
|
图 3 MLP构成图 |
训练模型, 算法流程如算法1.
算法1. 训练算法
Input: 输入样本Xin.
Output: 输出值Xrec.
1. for i = 1 to epoch do
2. for j = 1 to batch do
3. for k = 1 to K do
4. Xk = MixerBlock(Xk–1)
5. end for
6. Zk = norm(Xk)
7. Xrec = Linear(Zk)
8. 更新模型参数
9. end for
10. end for
算法1中epoch表示模型迭代训练次数, 每个epoch将数据划分为等份的若干个batch, 1个batch数据通过计算loss值和优化器更新1遍模型参数, K表示UMTS-Mixer模型中有K个MixerBlock模块.
测试模型, 异常检测算法流程如算法2.
算法2. 测试算法
Input: 训练数据Xtrain, 验证数据Xval, 测试数据Xtest.
1. for i = 1 to batch do
2. predtrain = UMTS-Mixer(Xtrain)
3. losstrain = predtrain – Xtrain
4. end for
5. for i = 1 to batch do
6. predval = UMTS-Mixer(Xval)
7. lossval = predval – Xval
8. end for
9. thresh = np.percentile(losstrain, lossval, 99)
10. for i = 1 to batch do
11. predtest = UMTS-Mixer(Xtest)
12. losstest= predtest – Xtest
13. if losstest > thresh
14. 判定为异常
15. else
16. 判定为正常
17. end for
算法2中Xtrian表示训练数据, Xval表示验证数据, Xtest表示测试数据, 先将训练数据输入模型, 得到模型重建的训练数据, 然后计算出训练数据和重建数据之间的误差值, 验证数据重复训练数据的操作, 得到验证数据和重建数据之间的误差值, 将得到的训练数据的误差值和验证数据的误差值按比例划分, thresh为误差值最高1%与剩下99%的分界线, 最后计算测试数据的误差值, 将误差值高于thresh的数据判定为异常数据, 误差值低于或等于thresh的数据判定为正常数据.
| $ {\textit{thresh}} < ||pre{d_{{\rm{test}}}} - {X_{{\rm{test}}}}||_F^2 $ | (3) |
| $ {\textit{thresh}} \geqslant ||pre{d_{{\rm{test}}}} - {X_{{\rm{test}}}}||_F^2 $ | (4) |
本文在4个基准数据集上评估UMTS-Mixer的异常识别效果. 4个数据集分别是SMD、PSM[18]、MSL、SMAP, 以下是对4个实验数据集的描述: (1) SMD是从一家大型互联网公司收集的服务器数据, 具有38个通道, 异常占比为4.2%. (2) PSM是从eBay 的多个应用服务器节点内部收集的数据信息, 具有26 个通道, 异常占比为27.8%. (3) MSL 和 SMAP都是来自 NASA[11]的公共数据集, 分别有 55 个通道和 25 个通道, 异常占比分别为10.5%和12.8%. 其中包含从航天器监控系统的事件报告得出的遥测异常数据. 数据集具体信息表1所示.
| 表 1 4个数据集具体信息 |
4.1 实现细节
本文采用滑动窗口来获得一组子序列. 对于SMD数据集, 滑动窗口的大小为 200, 滑动步长为100, 其他3个数据集滑动窗口大小为100, 滑动步长为1. 阈值thresh被确定为使标记为异常的验证数据集的 r 比例数据. 对于最终结果, 本文设置SMD 的 r = 0.5%, 其他数据集设置为 1%. 训练模型时, 用到了提前停止训练方法, 当连续3个epoch的验证集loss没有降低时, 则停止训练, 并将loss值最低的模型作为最终的模型, 同时, 每个epoch的学习率会根据epoch的变化而变化. 在异常检测时, 使用调整策略[19], 如果检测到某个连续异常段中的时间点, 则认为该异常段中的所有异常被准确检测. 这种策略是合理的, 因为一个异常时间点会导致警报, 将使整个时间段被注意到[20]. UMTS-Mixer 包含 3个MixerBlock模块, 本文将隐藏状态 dmodel 的通道数设置为 512, 使用初始学习率为 10−4 的 Adam优化器[21], 批量大小为 64. 所有实验均以 Python 3.8 作为编程基础, PyTorch 1.10.0、cuda 11.1实现和测试. 使用 Windows 10、Intel(R) Core(TM) i7-10750H CPU、RTX3060、16 GB 内存的计算机运行程序.
4.2 对比实验本文将模型与 9个基线进行比较, 包括以下模型: anomaly Transformer (2022)、TranAD (2022)、InterFusion (2021)、BeatGAN (2019)、OmniAnomaly (2019)、LSTM-VAE (2018)、THOC (2020)、LSTM (2018)、VAR (1976); 其中InterFusion (2021)、THOC (2020)是当年发表的最先进的深度模型.
4.3 评估指标通过准确率(P)、召回率(R)和F1值来评估一个异常检测算法的好坏, TP表示算法将异常样本识别出来的个数, FN表示算法将异常样本识别为正常样本的个数, FP表示算法将正常样本识别成异常样本的个数. 根据公式理解, P表示算法识别为异常的样本中有多少比例是识别正确的, P越接近1则说明算法误报越少, P越接近0说明算法误报越多, R表示算法在所有的异常样本中有多少比例是将异常样本识别为异常的, 也即算法识别出异常样本的比例, R越接近1则说明算法漏报越少, R越接近0则说明算法漏报越多, F1值则是P和R综合考虑, 权衡出的准则, F1越接近1说明算法的效果越好.
| $ \left\{\begin{array}{l} P=\dfrac{T P}{T P+F P} \\ R=\dfrac{T P}{T P+F N} \\ F 1=\dfrac{2 P \times R}{P+R} \end{array}\right. $ | (5) |
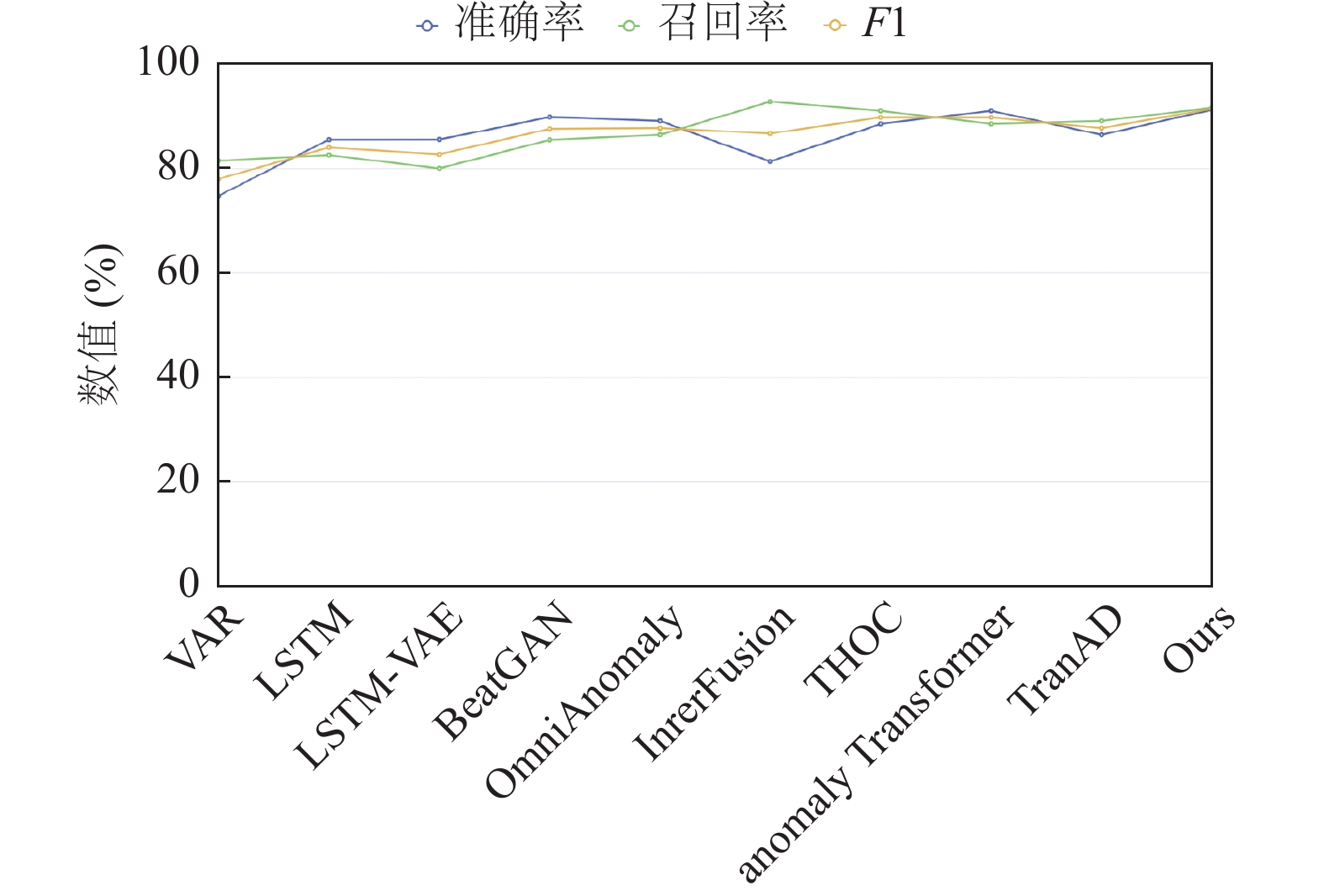
为了衡量本文模型UMTS-Mixer的有效性, 模型在4个数据集上做了检验, 并与9个基准模型进行对比, 对比结果如表2, 图4, 图5所示. 表2中, 其中加粗表示该项的最大值. 由表2可知, 本文提出的模型在MSL、PSM这两个数据集上, F1值为最高, 取得了最好的表现, 在MSL、SMAP数据集中, 模型的准确率也是对比模型中最高的, 在SMD、SMAP数据集中, 模型的F1值分别位于对比模型的第3位和第4位. 在MSL、SMD这两个数据集上, 本模型取得的准确率和召回率都是比较接近的, 说明模型的thresh取值是较为准确的, 但模型在SMAP、PSM这两个数据集中准确率和召回率相差较远, 说明模型没有找到更好的thresh分界线, 若准确率高于召回率(相差10%左右)说明模型更倾向于判定为异常, 若准确率低于召回率(相差10%左右)说明模型更倾向于判定为正常. 从图4也能更直观地看出本文提出的模型要优于基线模型. 图6给出了 PSM 数据集时间序列、已知的异常数据点、模型判定的异常数据点, 其中feature_0表示时间序列数据, Model-pred表示模型判定的异常数据点, Known-label表示已知的异常数据点, Known-label与Model-pred的匹配度越高, 说明模型的异常检测效果越好. Known-label与Model-pred不匹配的时间点, 说明模型在该时间点进行了误判或漏判, Model-pred不在Known-label区域代表误判, Known-label区域中是feature_0代表漏判. 从图6中的匹配度可以得出模型在PSM数据集上异常检测的表现是优异的.
| 表 2 本文提出的模型与9个基线在4个数据集上的性能对比 (%) |
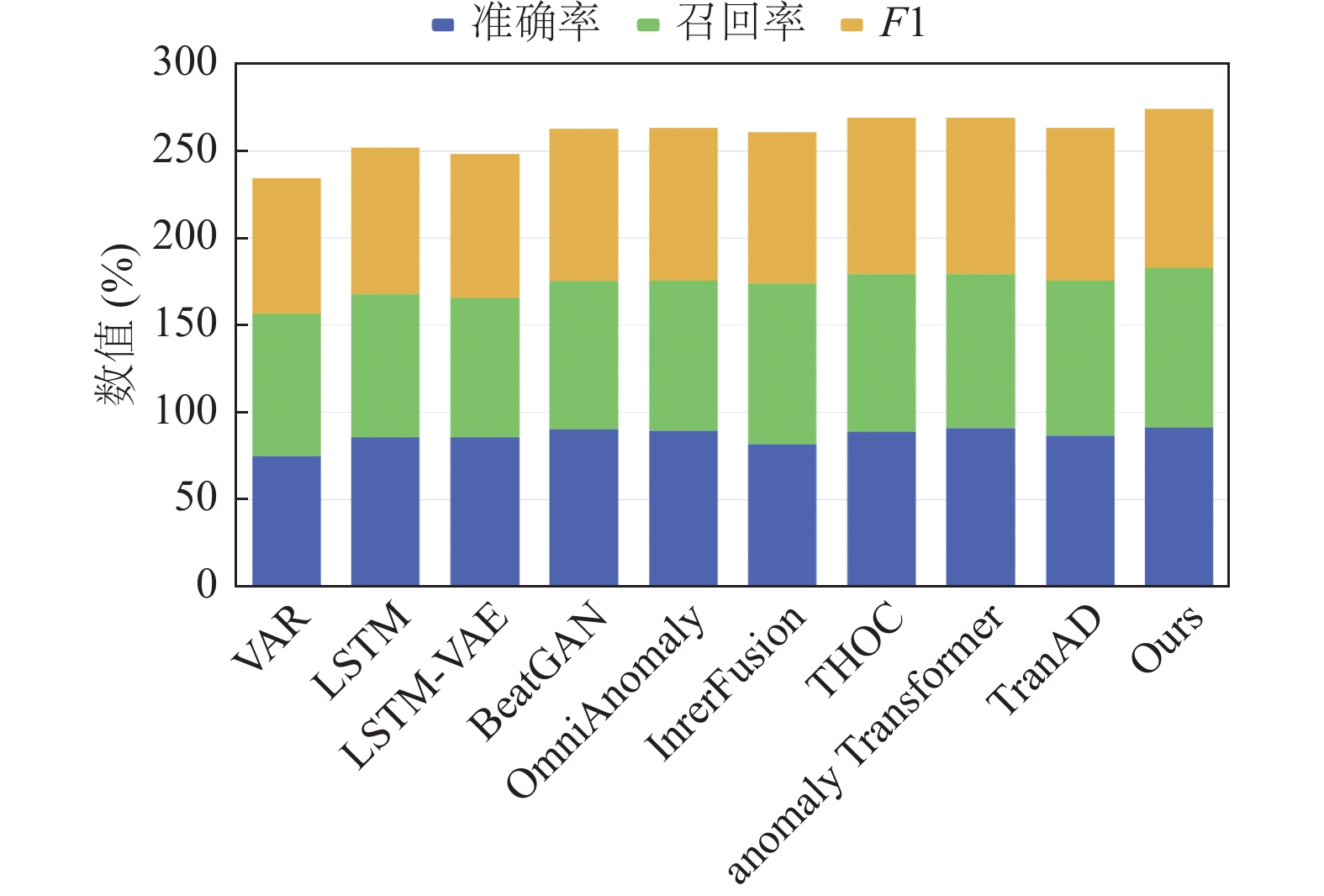
|
图 4 各个模型在MSL数据集上3个评估指标的矩形堆叠图 |
|
图 5 各个模型在MSL数据集上的准确率, 召回率, F1 |

|
图 6 PSM数据集已知异常与模型给定异常对比图 |
5 结语
本文通过研究无监督多变量时间序列异常检测问题, 提出了一种更适合时间序列领域的模型范式, 即基于MLP的异常检测模型UMTS-Mixer, 由于线性结构对顺序敏感的特性, 模型使用MLP学习数据中的时间依赖关系和各变量之间的关联关系获得更好的数据表征. UMTS-Mixer 在一组详尽的实证研究上, 与其他模型相比, 取得更好表现, 但依旧存在改进空间, 即如何在提高准确率或召回率的同时缩小准确率和召回率的差值. 未来工作需要在模型的学习策略上展开大量的研究, 以使得模型不仅有好的重建能力, 也具备强的正异常界定的能力.
| [1] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2017. 6000–6010.
|
| [2] |
Zhang SM, Liu YC, Zhang XC, et al. CAT: Beyond efficient Transformer for content-aware anomaly detection in event sequences. Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. Washington: ACM, 2022. 4541–4550.
|
| [3] |
Li YF, Peng XY, Zhang J, et al. DCT-GAN: Dilated convolutional Transformer-based GAN for time series anomaly detection. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(4): 3632-3644. DOI:10.1109/TKDE.2021.3130234 |
| [4] |
Xu JH, Wu HX, Wang JM, et al. Anomaly Transformer: Time series anomaly detection with association discrepancy. Proceedings of the 10th International Conference on Learning Representations. ICLR, 2022.
|
| [5] |
Tuli S, Casale G, Jennings N R. TranAD: Deep Transformer networks for anomaly detection in multivariate time series data. Proceedings of the VLDB Endowment, 2022, 15(6): 1201-1214. DOI:10.14778/3514061.3514067 |
| [6] |
Zeng AL, Chen MX, Zhang L, et al. Are Transformers effective for time series forecasting? Proceedings of the 37th AAAI Conference on Artificial Intelligence. Washington: AAAI Press, 2023.
|
| [7] |
Li Z, Rao ZW, Pan LJ, et al. MTS-Mixers: Multivariate time series forecasting via factorized temporal and channel mixing. arXiv:2302.04501, 2023.
|
| [8] |
Chen SA, Li CL, Yoder N, et al. TSMixer: An all-MLP architecture for time series forecasting. arXiv:2303.06053v5, 2023.
|
| [9] |
Moayedi HZ, Masnadi-Shirazi MA. ARIMA model for network traffic prediction and anomaly detection. Proceedings of the 2008 International Symposium on Information Technology. Kuala Lumpur: IEEE, 2008. 1–6.
|
| [10] |
Anderson O, Kendall M. Time-series. Journal of the Royal Statistical Society (Series D), 1976, 25(4): 308–310.
|
| [11] |
Hundman K, Constantinou V, Laporte C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 387–395.
|
| [12] |
Ng A. Sparse autoencoder. CS294A Lecture Notes, 2011, 72(2011): 1-19. |
| [13] |
Vincent P, Larochelle H, Bengio Y, et al. Extracting and composing robust features with denoising autoencoders. Proceedings of the 25th International Conference on Machine Learning. Helsinki: ACM, 2008. 1096–1103.
|
| [14] |
Noh H, Hong S, Han B. Learning deconvolution network for semantic segmentation. Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 1520–1528.
|
| [15] |
An J, Cho S. Variational autoencoder based anomaly detection using reconstruction probability. Special Lecture on IE, 2015, 2(1): 1-18. |
| [16] |
Park D, Hoshi Y, Kemp CC. A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder. IEEE Robotics and Automation Letters, 2018, 3(3): 1544-1551. DOI:10.1109/LRA.2018.2801475 |
| [17] |
Su Y, Zhao YJ, Niu CH, et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage: ACM, 2019. 2828–2837.
|
| [18] |
Abdulaal A, Liu ZH, Lancewicki T. Practical approach to asynchronous multivariate time series anomaly detection and localization. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. Singapore: ACM, 2021. 2485–2494.
|
| [19] |
Xu HW, Chen WX, Zhao NW, et al. Unsupervised anomaly detection via variational auto-encoder for seasonal KPIs in Web applications. Proceedings of the 2018 World Wide Web Conference. Lyon: International World Wide Web Conferences Steering Committee, 2018. 187–196.
|
| [20] |
Shen LF, Li ZC, Kwok JT. Timeseries anomaly detection using temporal hierarchical one-class network. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 13016–13026.
|
| [21] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv:1412.6980, 2014.
|
 2024, Vol. 33
2024, Vol. 33


