计算机系统应用  2024, Vol. 33 Issue (1): 177-184   PDF    
引用本文
孟繁林, 何晓曦, 刘应浒, 李茄濡, 朱群. 基于自注意力机制的点云分类分割. 计算机系统应用, 2024, 33(1): 177-184.http://www.c-s-a.org.cn/1003-3254/9341.html   
Meng FL, He XX, Liu YH, Li JR, Zhu Q. Point Cloud Classification and Segmentation Based on Self-attention Mechanism. Computer Systems and Applications, 2024, 33(1): 177-184(in Chinese).http://www.c-s-a.org.cn/1003-3254/9341.html   
基于自注意力机制的点云分类分割
孟繁林1,2, 何晓曦1,2, 刘应浒1,2, 李茄濡1,2, 朱群1,2     
1. 成都信息工程大学 软件工程学院, 成都 610225;
2. 四川省信息化应用支撑软件工程技术研究中心, 成都 610225
收稿日期：2023-05-24; 修改日期：2023-06-26; 采用时间：2023-08-08; csa 在线出版时间：2023-11-28
基金项目：四川省科技厅重大专项(2022ZDZX0001); 四川省科技厅重点研发项目(2022YFG0033, 2022YFG0037); 四川省信息化应用支撑软件工程技术研究中心开放课题(2021RJGC-Y01)
通讯作者：何晓曦, E-mail: microwest@cuit.edu.cn.
摘要：3D点云由于其无序性以及缺少拓扑信息使得点云的分类与分割仍具有挑战性. 针对上述问题, 我们设计了一种基于自注意力机制的3D点云分类算法, 可学习点云的特征信息, 用于目标分类与分割. 首先, 设计适用于点云的自注意力模块, 用于点云的特征提取. 通过构建领域图来加强输入嵌入, 使用自注意力机制进行局部特征的提取与聚合. 最后, 通过多层感知机以及解码器-编码器的方式将局部特征进行结合, 实现3D点云的分类与分割. 该方法考虑了输入嵌入时单个点在点云中的局部语境信息, 构建局部长距离下的网络结构, 最终得到的结果更具区分度. 在ShapeNetPart、RoofN3D等数据集上的实验证实所提方法的分类与分割性能较优.
关键词: 深度学习    自注意力机制    分类    分割    点云    
Point Cloud Classification and Segmentation Based on Self-attention Mechanism
MENG Fan-Lin1,2, HE Xiao-Xi1,2, LIU Ying-Hu1,2, LI Jia-Ru1,2, ZHU Qun1,2     
1. School of Software Engineering, Chengdu University of Information Technology, Chengdu 610225, China;
2. Sichuan Province Informationization Application Support Software Engineering Technology Research Center, Chengdu 610225, China
Abstract: Due to the disorder and lack of topological information, the classification and segmentation of 3D point clouds is still challenging. To this end, this study designs a 3D point cloud classification algorithm based on the self-attention mechanism to learn point cloud feature information for object classification and segmentation. Firstly, a self-attention module suitable for point clouds is designed for feature extraction. A neighborhood graph is constructed to enhance the input embedding, and the local features are extracted and aggregated by utilizing the self-attention mechanism. Finally, the local features are combined via multi-layer perceptron and encoder-decoder approaches to achieve 3D point cloud classification and segmentation. This method considers the local context information of individual points in the point cloud during input embedding, constructs a network structure under local long distances, and ultimately yields more distinctive results. Experiments on datasets such as ShapeNetPart and RoofN3D demonstrate that the proposed method performs better in classification and segmentation.
Key words: deep learning     self-attention mechanism     classification     segmentation     point cloud    

随着3D传感器的迅速发展, 3D数据变得无处不在, 其中具有代表性的3D数据有网格(mesh), 体素(voxel)以及点云(point cloud). 其中, 点云因其为多种设备如无人机、LiDAR采集空间数据的原始通用格式而受到广泛关注, 同时, 对点云数据的进一步识别解析与重建, 使其可应用于环境识别[1]、城市空间重建[2]、虚拟现实物体重建[3]等领域. 然而, 点云本身具有的无序性与不规则性[4]且缺少拓扑信息, 使得直接对点云进行处理具有一定挑战性. 相较于图像是排列在规则的像素网格上, 三维点云是嵌入在连续空间中的, 这使得三维点云在处理方法上与图像存在较大差异, 因此也无法应用计算机视觉中常用的深度学习网络设计, 例如基于离散卷积的网络.

为了将深度学习成功应用于点云上, 研究人员进行了许多尝试. Tchapmi等人[5]、Wang等人[6]将点云体素化后进行空间卷积, 这造成了大量的计算与内存开销; 文献[7,8]直接对点云进行卷积, 之后使用池化运算进行特征聚合以此传播信息; Wang等人将点集连接成图, 在图上使用卷积运算进行信息的传递[9]. 在众多的研究方法中, 值得注意的是点云与Ashish等人提出的Transformer模型[10]的结合. Transformer模型具有的长距离依赖建模能力在自然语言处理(NLP)领域表现出优异的效果, 而其在处理一连串的点时所具有的交换不变性和全局特征学习能力使其非常适合用于点云学习[11].

本文的主要贡献为: 1)提出了一个基于自注意力机制的网络, 通过自注意力机制对点云特征进行聚合, 以提高网络的特征提取能力. 2)使用可训练的位置嵌入函数对点云进行位置特征描述. 3)联合局部特征和长距离依赖提升网络对点云特征的提取能力. 4)本文算法在RoofN3D屋顶分类数据集上表现优异, 并在ModelNet40和ShapeNetPart数据集上显示出良好的泛化能力.

1 相关工作

对于二维图像来说, 像素在成网格规则排列, 因此直接对图像使用卷积具有良好的效果. 而对三维点云来说, 若直接对其在空间中使用三维卷积运算, 由于点云的稀疏性, 将不可避免地造成大量的无效计算与数据冗余, 对最终的结果将产生巨大影响. 因此, 一般将深度学习应用于点云上时可大致分为3种网络结构: 基于视图的网络、基于体素的网络以及基于点的网络.

1.1 基于视图的网络

为了处理无序的点云, 一个直接的想法是将其投影到多个二维平面上, 再对其使用类似图像上的卷积运算以提取特征, 然后进行多视图融合以进行最后的输出表示, 如文献[12–14]中所提到的方法, 均将多个点云视图作为输入源以供类似CNN架构的网络进行点云研究任务. 然而此种类型的处理方式所存在的缺陷也较为明显, 即极大地依赖于所投影的平面, 这导致若三维点云中存在遮挡, 将对结果造成较大影响.

1.2 基于体素的网络

使用体素可较大程度地对点云的数据结构和空间分布状态进行保留. 由于无法在空间中直接使用卷积操作, Graham 等人[15]使用稀疏卷积来适应体素的稀疏性. 八叉树是一种用于描述三维空间的树状数据, Wang等人[6]便利用了八叉树表示三维形状并对其表面进行离散化, 仅对三维形状边界的稀疏八叉树进行卷积运算, 对存储和运算均有较大提升, 但其存储和运算开销随八叉树深度的增长呈2次方增长. 这些方法相较基于视图的网络具有更好的准确性, 但由于体素与点存在差异, 在几何细节上仍存在缺失的可能.

1.3 基于点的网络

无论是基于视图或是基于体素的网络均会对点云信息本身造成影响, 但直接对点云进行处理即可避免此种影响, 其优势十分明显.

PointNet[7]开创了直接对点云进行学习, 其通过多层感知器(MLPs)和最大池化运算来对点集进行特征聚合, 虽然对点云的全局特征提取效果较好, 但对局部特征的提取上仍有欠缺; 在此基础上, PointNet++[8]使用查询求分组和层次化的PointNet, 提高了网络对局部特征的敏感性. 受以上网络的启发, 衍生出了一些类似的网络结构[16–18].

相较于PointNet的结构, 一些研究则致力于对不规则的三维点云重新定义卷积运算. Li等人[19]使用特殊的运算符对输入的无序点云进行重新排序; Wang等人[9]在动态图上设计了边卷积(EdgeConv)算子, 恢复了点云的拓扑信息以进行学习; Tatarchenko等人[20]设计了切面卷积(tangent convolution), 对点做切平面并将该点附近的每个点均投影到切平面上, 在该切平面上进行卷积运算, 很好地保留了局部信息、空间关系与位置信息.

1.4 Transformer与计算机视觉

Transformer模型自提出后即在NLP领域取得巨大成果. 由于其出色的长距离依赖模型, 也同时受到了计算机视觉领域的关注, 有许多网络结构也开始将注意力机制引入到相关的视觉任务中. 目前在计算机视觉中采用Transformer的相关工作主要有两种模型架构, 一种为仅使用Transformer的架构, 另一种为混合了卷积神经网络(CNN)与Transformer的架构. Wu等人提出的Vision Transformer[21]直接将Transformer架构应用于一系列图像块上的分类任务, 相较最先进的卷积神经网络, 取得了更优异的结果, 同时大幅缩减了计算资源. Carion等人提出的DERT[22]将卷积神经网络与Transformer相结合, 使用CNN来提取图像的特征, 再辅以位置编码, 将其输入到Transformer模型的编码器中, 最后以Transformer模型的解码器输出到前馈神经网络中来预测目标类别和包围盒. 相较传统的目标检测方法, 该结构显著地简化了物体检测的流程.

由于Transformer模型固有的交换不变性和其强大的全局特征学习能力, 使得在三维空间中的Transformer非常适合点云的处理和分析. Guo等人[23]将点云的空间坐标嵌入到特征空间中以生成特征, 然后输入到注意力模块中以进行区分并学习每个点的语义信息. Zhao等人[24]为点云设计了自注意力层, 提出了“矢量自注意力”和“减法关系”以进行局部特征聚合. 以上两种为点云设计的Transformer模型对捕捉长距离依赖关系仍存在一定困难, Lai等人[25]据此设计了一种新颖的采样策略, 对点附近进行密集采样, 对远处的点进行稀疏采样, 以达到扩大有效感受野的目的.

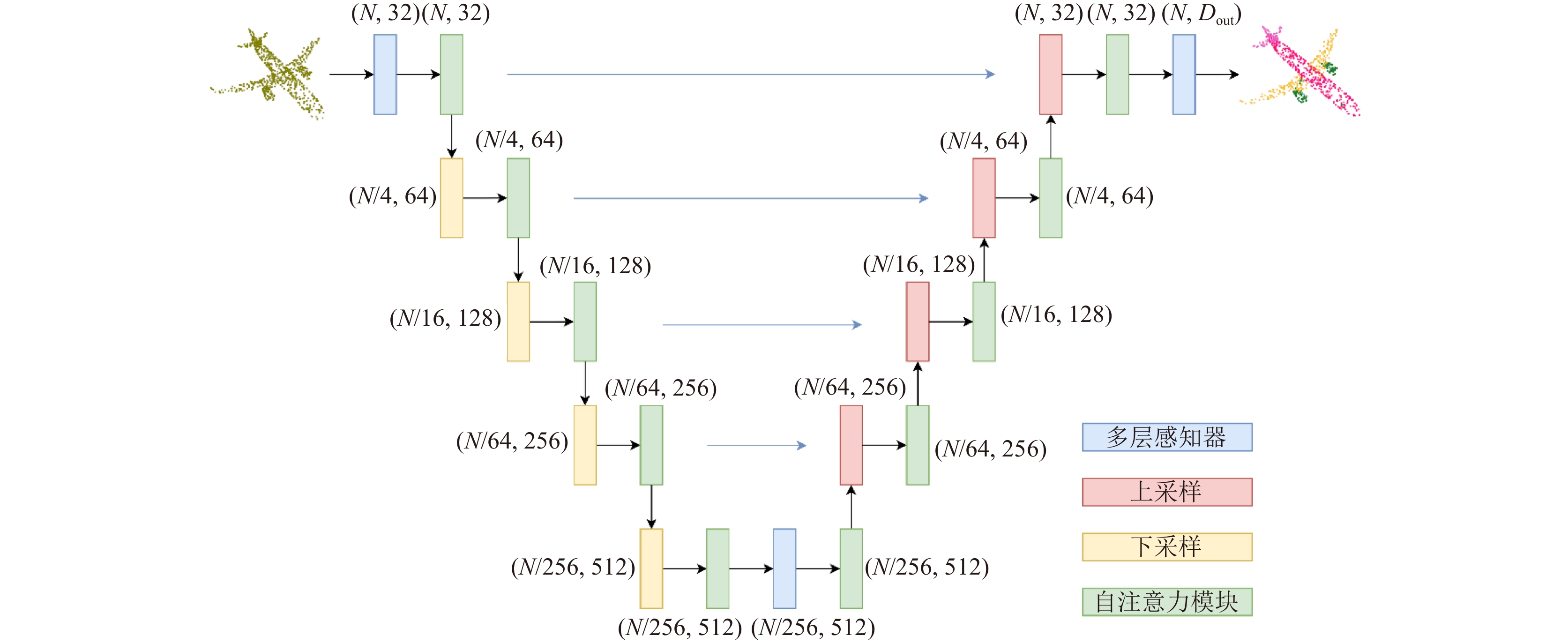
2 基于自注意力机制的三维点云分类算法

受以上3种为点云设计的Transformer模型启发, 本文在自注意力模块的基础上使用Lambda attention[26]用以提升计算效率, 同时对空间中的每个点构建K-NN图, 以获取局部长距离依赖和局部特征. 将经过以上两种运算后的信息送入自注意力模块中进行特征聚合, 在每个自注意力模块或前馈网络前均使用LayerNorm[27]来替代BatchNorm以实现更好的归一化. 同时使用类似U-Net[28]的编码器-解码器结构以实现特征的汇总, 网络结构如图1所示.

图 1 本文算法网络结构图

2.1 自注意力模块

类比NLP中的词嵌入, 则每个点的空间位置天然地可以看作这个点的位置嵌入. 但为了对点的位置嵌入进行特征描述, 本文引入了可训练的位置嵌入函数, 如式(1)所示:

$ {F_{{\text{pe}}}} = \rho \left( {{x_i}} \right) $ (1)

其中, xi为每个输入点的空间坐标, 位置嵌入函数$\; \rho $为一个由两个线性层和一个ReLU激活层所组成的多层感知器(MLP). 得到位置嵌入Fpe后上采样测试, 即可按照原始Transformer模型[10]中所做的那样, 通过线性变换分别构建Q、K、V矩阵, 即查询、键、值矩阵. 将位置嵌入Fpe与Q、K、V矩阵进行如下运算以得到特征向量Fatt:

$ {F_{{\rm{att}}}} = {\textit{Softmax}} \left( {\frac{{Q{K^{\rm{T}}}}}{{\sqrt {{d_k}} }}} \right)V $ (2)

其中, dk为Q、K矩阵的维度, Q、K、V的计算分别如下:

$ \left\{ {\begin{array}{*{20}{c}} {Q = {F_{{\rm{pe}}}} \cdot {W_q}} \\ {K = {F_{{\rm{pe}}}} \cdot {W_k}} \\ {V = {F_{{\rm{pe}}}} \cdot {W_v}} \end{array}} \right. $ (3)

其中, Wq、Wk、Wv分别为由线性变换组成的共享参数的可学习矩阵. 式(2)中将Q矩阵与K矩阵的转置做矩阵的点乘以得到注意力强度, 再将其做归一化后使用Softmax计算注意力系数, 最后与V矩阵相乘后得到特征向量Fatt.

虽然原始注意力公式可以很好地获取特征, 但其运算效率仍较低. 在参考Lai等人的研究[25]后, 可将式(2)简单地修改为:

$ {F_{{\rm{att}}}} = Q\left( {{\textit{Softmax}} {{\left( K \right)}^{\rm{T}}}V} \right) $ (4)

其中, K矩阵由Softmax函数进行归一化, ${\textit{Softmax}} {\left( K \right)^{\rm{T}}}V \in {\mathbb{R}^{{d_k} \times {d_v}}}$被称为Lambda[26], dk和dv分别为K、V矩阵的维度. 如此, 时间和空间复杂度分别为$ {\rm O}\left( {N{d_k}{d_v}} \right) $和$ {\rm O}\left( {N{d_k} + N{d_v} + {d_k}{d_v}} \right) $, N为点云中的个数. 当$ {d_k} \ll N $时, 可大大降低计算成本.

由于Q、K、V矩阵由共享参数的可学习矩阵和输入的位置嵌入Fpe所决定, 且Softmax和归一化均不影响排列, 因此整个自注意力过程具备排列不变性, 使其非常适合用于无序的、不规则的点云学习. 在获得Fatt后将输入到LBR网络中, 与Fpe一同运算以得到最终的Fout:

$ {F_{{\rm{out}}}} = LBR\left( {{F_{{\rm{att}}}}} \right) + {F_{{\rm{pe}}}} $ (5)
2.2 局部特征与长距离依赖

虽然使用每个点经过线性变换的位置嵌入已经能够很好地对点云特征进行捕捉, 但是点云中, 局部的邻域信息同样也至关重要. 在参考了PointNet[7]和PCT[23]中相关的局部特征捕获运算后, 本文对点云中的每个点进行K最邻近运算, 以此将点周围的局部领域信息纳入网络考虑范围. 具体来说, 本文对每个点采用K最邻近算法, 对该点周围采样K个最邻近点, 后将与该点一同构成新的位置嵌入. 由相对位置所构成的位置嵌入能帮助网络更好地获取局部的领域信息, 如式(6)所示:

$ {F_{{\text{pe}}}} = \rho \left( {{x_i} - {F_{{\rm{knn}}}}} \right) $ (6)

其中, 函数$\; \rho $与式(1)中相同, Fknn为K最邻近算法.

为了不仅对局部特征进行捕捉, 本文同样参考Stratified Transformer[25]中所提出的思想, 加强网络对长距离依赖的提取能力. 具体来说, 本文对每个点云使用FPS算法[8]进行最远端采样, 将整个点云最远端的点纳入网络考虑范围, 以此实现长距离依赖的提取, 据此可将式(6)修改为式(7):

$ {F_{{\text{pe}}}} = \rho \left( {{x_i} - concat\left( {{F_{{\rm{knn}}}}, {F_{{\rm{fps}}}}} \right)} \right) $ (7)

其中, Ffps为最远点采样算法.

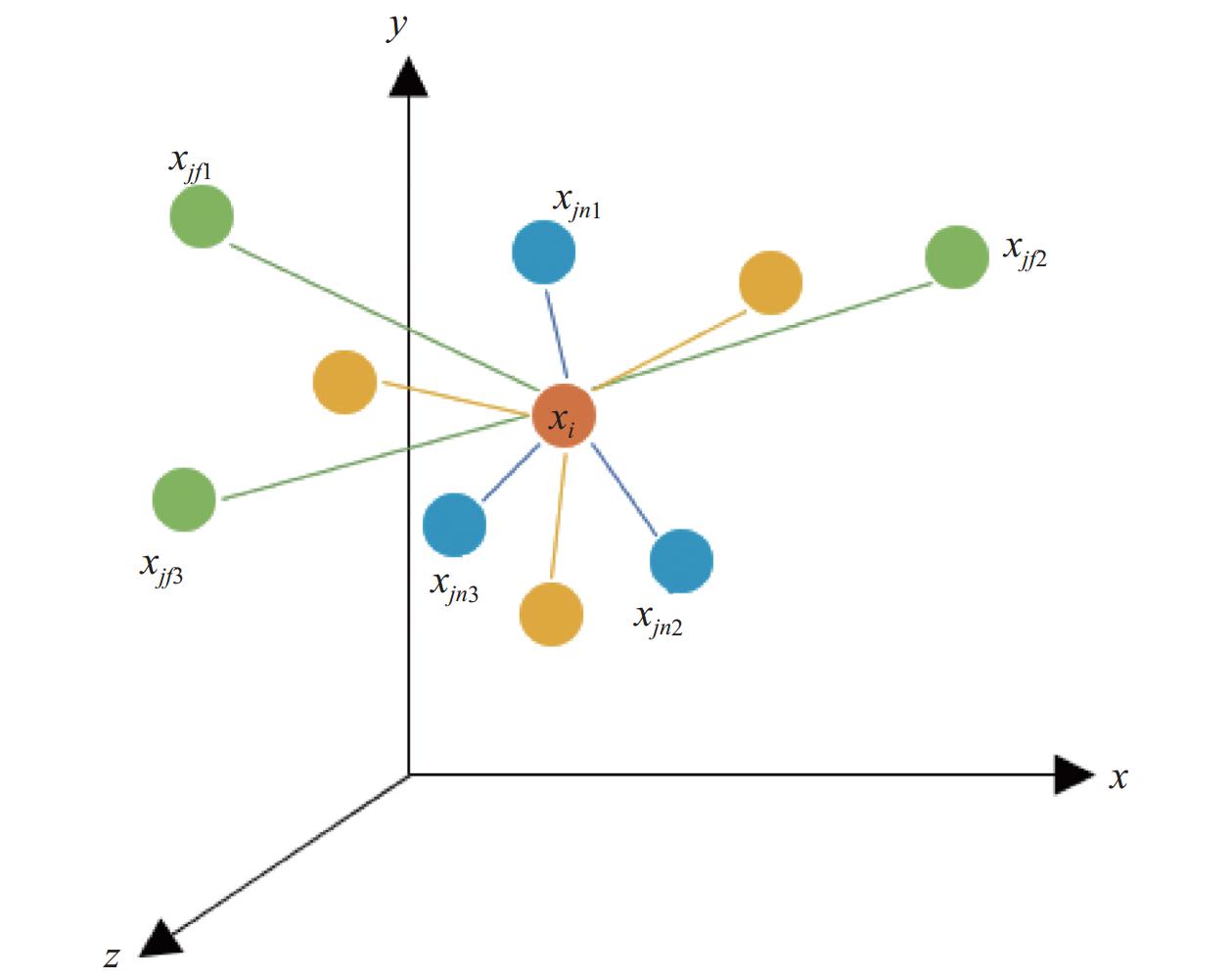
2.3 邻域图

第2.2节中所述方法能够对点云中每个点的局部特征与长距离特征进行较好地捕捉, 但考虑到点云中单个点的影响范围应仅在该点附近而不应辐射至整个点云, 故在受文献[9]中关于边卷积的启发后, 考虑对点云中的每个点构建邻域图, 即对每个点考察其周围点对其的欧氏距离, 使用一定距离内的点构建无向图, 在该无向图内考虑考察点的最邻近点和相对远端的点, 如图2所示. 对点$ {x}_{i}\in {\mathbb{R}}^{c} $, c为点的维度, 以欧氏距离建立邻域图, 获得点集xj={xj1, xj2, …, xjn}, 将点集xj中距离考察点xi最近的点形成点集n={xjnk | k=1, 2, …, n}, 距离考察点xi最远的点形成点集f={xjfk | k=1, 2, …, n}, 将点集n作为局部特征信息, 点集f作为局部长距离依赖信息.

图 2 领域图示例

2.4 网络结构

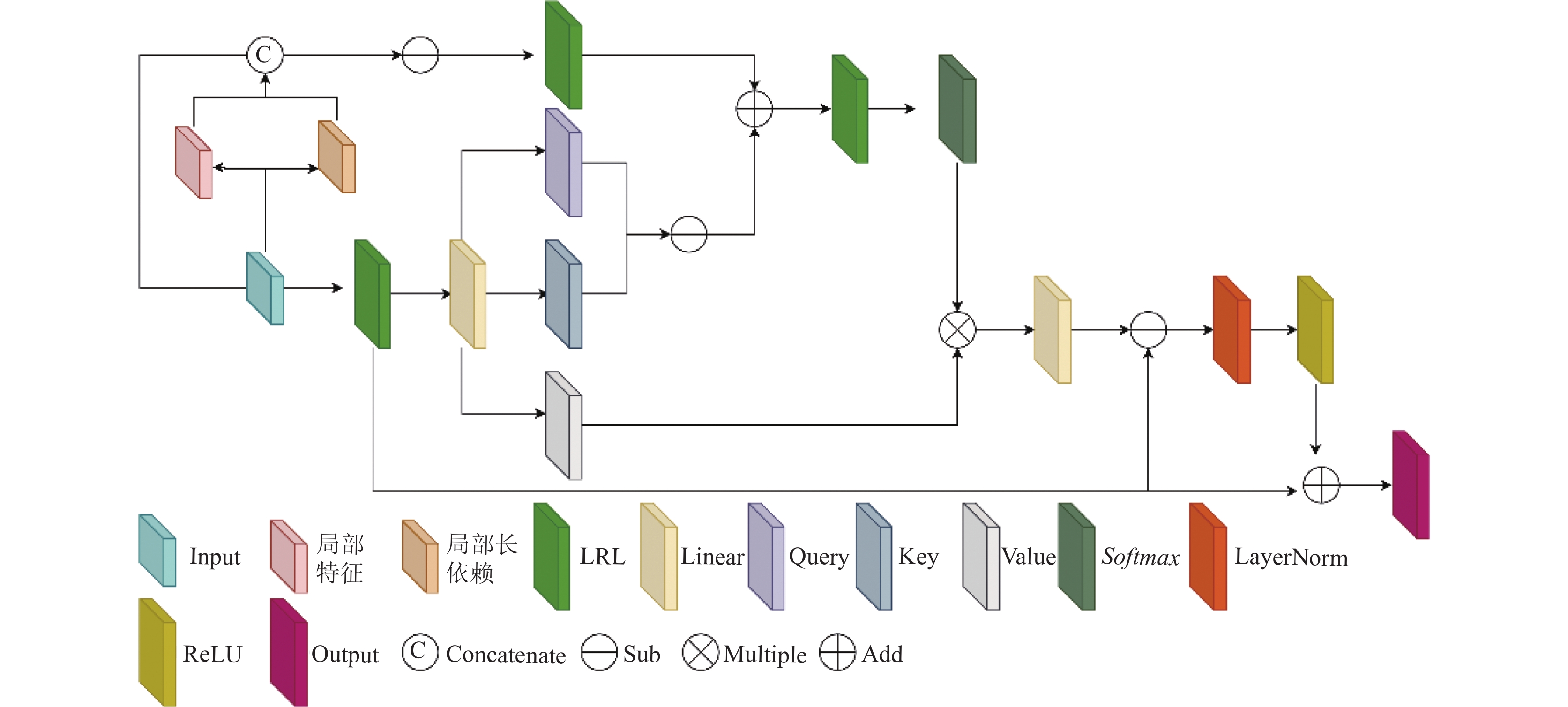
原始的Transformer模型为编码器-解码器结构, 据此, 本文参考U-Net[28]网络结构以及Point Transformer[24]中的网络结构, 搭建编码器-解码器结构. 具体来说, 首先将点云输入到自注意力模块中, 获得特征之后将其输入到下采样模块中, 下采样点的个数为输入点云中点个数的1/4, 之后再输入到自注意力模块中. 以上步骤重复4次后, 将获得的特征进行上采样, 每上采样一次后均需输入到自注意力模块中, 最后经过两次LBR层, 获得整个网络的输出结果. 与图像分割任务类似, 点云分类任务因其仅需提取点云的特征, 因此仅需编码器部分即下采样部分即可. 自注意力模块结构如图3所示.

图 3 自注意力模块结构图

3 实验

本文在点云分类和点云分割领域和任务上评估了所提出算法的有效性. 对于点云分割任务, 本文采用ShapeNetPart数据集[29]. 对于点云分类任务, 本文使用广泛采用的ModelNet40数据集[30]和RoofN3D数据集[31], 前者来自普林斯顿大学的ModelNet项目, 后者来自柏林大学.

3.1 点云分割

ShapeNetPart数据集[29]被用于三维物体部分分割. 该数据集由16个形状类别的16880个模型组成. 其中, 14006个三维模型用于训练, 2874个用于测试. 每个类别下的部件数在2–6个之间, 总共有50个不同的部件. 本文使用Qi等人[8]制作的采样点集, 以此与之前的工作进行比较. 本文使用类别均交并比Class mIoU和实例均交并比Instance mIoU来评判点云分割算法的性能. 因PointNet[7]、PointNet++[8]是深度学习应用于点云分割任务上的先驱, DGCNN[9]首次将图卷积引入深度学习上的点云分类分割, 而PCNN[32]、PointConv[33]则是将卷积应用于点云相关的任务上, 以上几种方法具有一定代表性, 故选择以上方法作为对比方法, 实验结果列于表1, 可见本文算法在实例均交并比上表现较优. 部分分割可视化结果见图4, 图4中上半部分为真实值, 下半部分为预测值.

表 1 ShapeNetPart数据集点云分割领域性能比较 (%)

图 4 ShapeNetPart数据集部分分割的部分结果

3.2 点云分类

RoofN3D数据集[31]由机载LiDAR采集的纽约市的房屋屋顶点云, 该数据集主要用于建筑物重建. 该数据集由3个形状类别的107440个模型组成, 其中, 95632个模型用于训练, 11808个用于测试. 由于至今极少有工作在该数据集上进行, 而建筑物重建又具有较多使用场景, 例如数字孪生、虚拟现实、自动驾驶, 因此, 本文采用该数据集对本文所提出的算法进行验证, 以期对深度学习在建筑物重建上应用有所帮助. 本文使用总体精度(overall accuracy, OA)作为点云分类的评估指标, 在采样1024个点的情况下取得了97.7%的准确率. 因KPConv[34]和PCT[23]对本文内容具有启发作用, 故在第3.1节所述对比方法的基础上添加以上两种方法作为对比方法. 实验结果列于表2, 可见本文在总体精度上表现较优.

表 2 RoofN3D数据集点云分类领域性能比较 (%)

ModelNet40数据集[30]由12311个通用对象的三维合成模型组成, 具有40个类别的9843个训练样本和2468个测试样本. 本文使用Qi等人[8]的数据准备程序, 并统一采样来自每个三维模型的点. 同RoofN3D一样, 本文采用总体精度OA作为评估指标, 采样点为1024个. 因PAT[35]、Set Transformer[36]、A-SCN[37]均采用了自注意力机制作为点云相关任务的处理方法, 与本文在自注意力机制对点云相关任务的判断上较为一致, 故将上述3种方法作为对比方法与本文结果进行对比, 实验结果列于表3, 可视化部分结果见图5, 图5首列为输入的查询点集, 其余为查询出来的点集结果. 需要注意的是, 该结果为未考虑法线作为网络输入的情况, 若考虑法线作为输入将进一步提高网络性能.

表 3 ModelNet40数据集点云分类领域性能比较 (%)

图 5 ModelNet40数据集部分可视化结果

以上实验结果表明, 在点云分类领域, 本文算法虽然未在ModelNet40数据集上表现最优, 但其准确率仍然较高, 且本文算法在RoofN3D数据集上表现优异; 在点云分割领域, 本文算法在ShapeNetPart数据集上表现较优, 达到较为先进水平. 综合来看, 本文算法准确率较高, 但仍面临一些问题, 如参数量较大.

3.3 消融实验

本节进行了一系列对照实验以检测本文设计的算法的有效性和最优的参数选择. 以下实验均基于ModelNet40点云分类数据集.

局部特征点与局部长距离依赖点数选择. 本实验旨在研究所设计的自注意力机制模块中局部特征点和局部长距离依赖点的个数对算法结果的影响. 为了使所提取特征均匀表示, 局部特征点和局部长距离依赖点的个数均设置为相同个数, 实验以总体精度OA作为评估指标, 实验结果见表4.

表 4 局部特征点与局部长距离依赖点数选择 (%)

以上实验结果表明, 在局部特征点与局部长距离依赖点数均选择为10个时, 总体精度达到最大为92.0%.

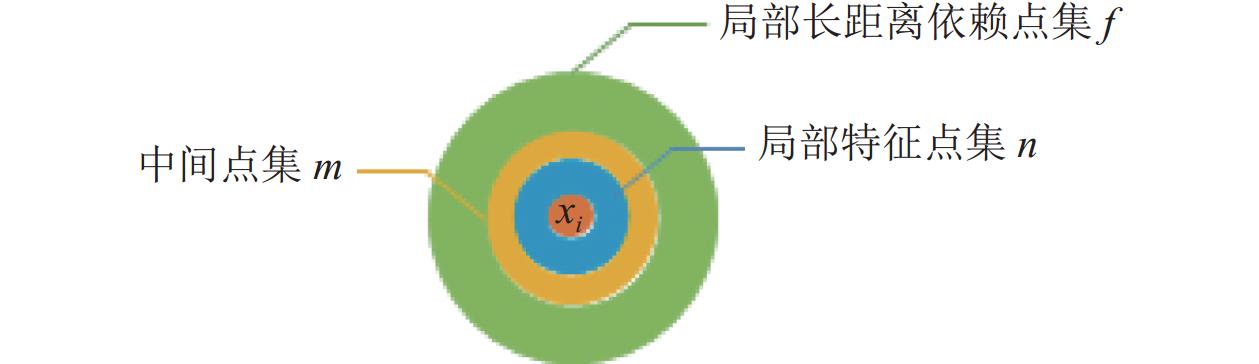
领域范围距离选择. 领域范围, 即对于查询点所选择的周围点的个数, 决定了局部特征点集和局部长距离依赖点集的距离, 如图6所示. 本实验旨在研究所设计的自注意力机制模块中领域范围的大小对算法结果的影响, 实验以总体精度OA作为评估指标, 实验结果见表5.

图 6 领域范围示例

表 5 领域范围选择

以上实验结果表明, 在领域范围为3时, 总体精度达到最大为92.0%.

模块有效性验证. 本实验旨在研究所设计的自注意力机制模块对算法的有效性, 实验在以上两个实验的基础上进行, 实验以总体精度作为评估指标, 实验结果见表6.

表 6 模块有效性验证

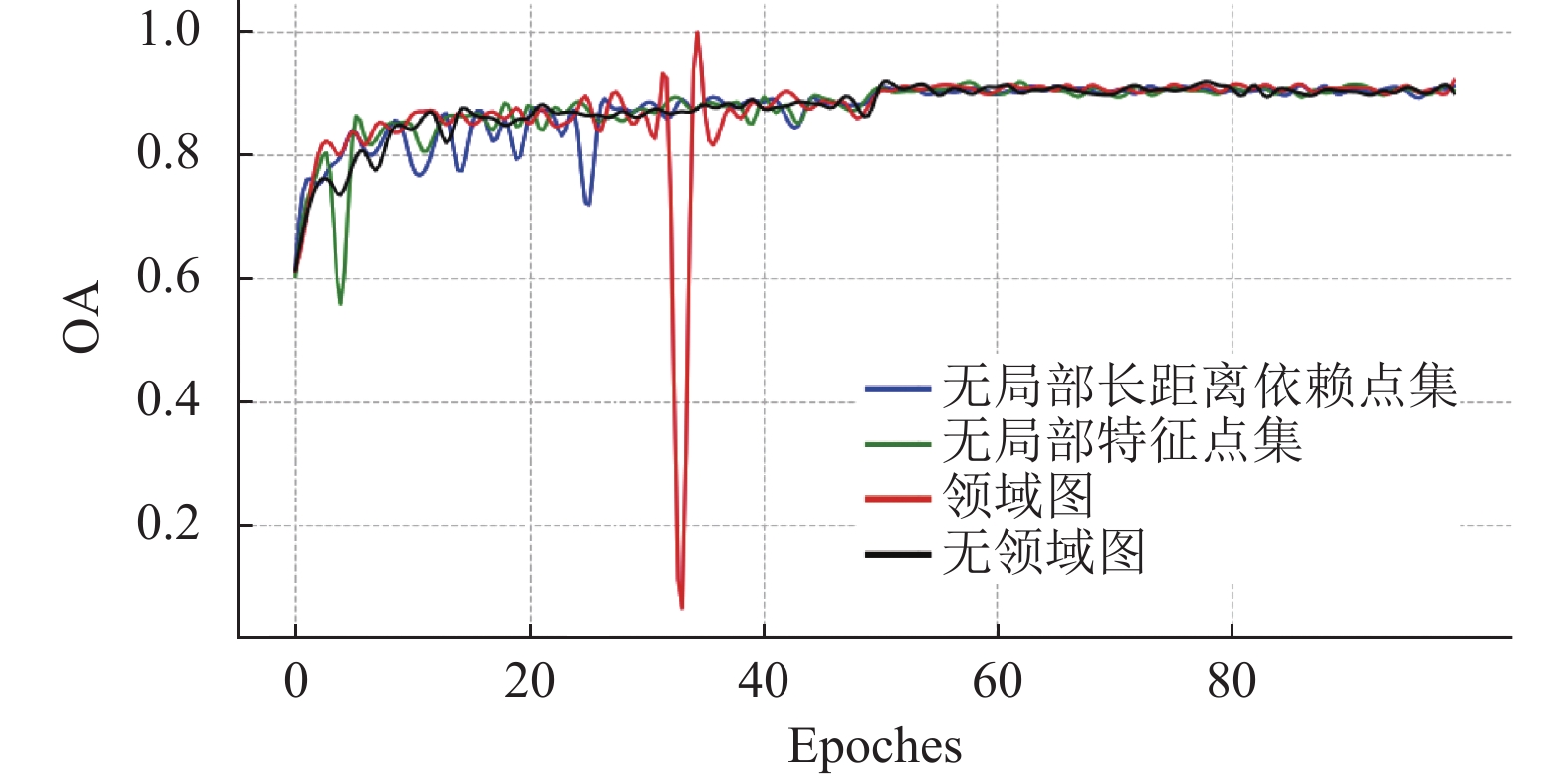
通过表4的结果可见, 当网络仅包含局部特征点集时总体精度为91.1%, 仅包含局部长距离依赖点集时总体精度为90.4%, 不包含领域图模块时总体精度为89.9%, 当包含领域图模块且局部长距离依赖点集与局部特征点集均存在时总体精度达到最大为92.0%, 实验结果表明完整的领域图模块对点云模型分类性能有较大提升, 总体精度对比折线图如图7所示.

图 7 总体精度对比折线图

4 总结

为有效提高点云分类和点云分割的精确度, 本文提出了一种基于自注意力机制的点云分类分割算法. 本文在RoofN3D数据集上达到了较高的分类精度, 同时在ModelNet40上也达到了较好的精度, 在ShapeNetPart分割数据集上也到达了较优的实例均交并比. 综上所述, 通过使用局部特征与长距离依赖以及自注意力机制, 可以有效提高点云分类和点云分割的精度, 为建筑物重建提供了有效的前置条件.

参考文献
[1]
Guo YL, Wang HY, Hu QY, et al. Deep learning for 3D point clouds: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(12): 4338-4364. DOI:10.1109/TPAMI.2020.3005434
[2]
李晶晶, 范大昭, 耿弘毅, 等. 城市点云的区域生长三角网构建方法. 测绘科学技术学报, 2016, 33(1): 65-70.
[3]
Rahman MM, Tan YH, Xue J, et al. Notice of violation of IEEE publication principles: Recent advances in 3D object detection in the era of deep neural networks: A survey. IEEE Transactions on Image Processing, 2020, 29: 2947-2962. DOI:10.1109/TIP.2019.2955239
[4]
李娇娇, 孙红岩, 董雨, 等. 基于深度学习的3维点云处理综述. 计算机研究与发展, 2022, 59(5): 1160-1179. DOI:10.7544/issn1000-1239.20210131
[5]
Tchapmi L, Choy C, Armeni I, et al. SEGCloud: Semantic segmentation of 3D point clouds. Proceedings of the 2017 International Conference on 3D Vision. Qingdao: IEEE, 2017. 537–547.
[6]
Wang PS, Liu Y, Gou YX, et al. O-CNN: Octree-based convolutional neural networks for 3D shape analysis. ACM Transactions on Graphics, 2017, 36(4): 72.
[7]
Charles RQ, Su H, Kaichun M, et al. PointNet: Deep learning on point sets for 3D classification and segmentation. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 77–85.
[8]
Qi CR, Yi L, Su H, et al. PointNet++: Deep hierarchical feature learning on point sets in a metric space. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 5105–5114.
[9]
Wang Y, Sun YB, Liu ZW, et al. Dynamic graph CNN for learning on point cloud. ACM Transactions on Graphics, 2019, 38(5): 146.
[10]
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
[11]
Engel N, Belagiannis V, Dietmayer K. Point transformer. IEEE Access, 2021, 9: 134826-134840. DOI:10.1109/ACCESS.2021.3116304
[12]
Lawin FJ, Danelljan M, Tosteberg P, et al. Deep projective 3D semantic segmentation. Proceedings of the 17th International Conference on Computer Analysis of Images and Patterns. Ystad: Springer, 2017. 95–107.
[13]
Zhou WG, Jiang X, Liu YH. MVPointNet: Multi-view network for 3D object based on point cloud. IEEE Sensors Journal, 2019, 19(24): 12145-12152. DOI:10.1109/JSEN.2019.2937089
[14]
Jaritz M, Gu JY, Su H. Multi-view PointNet for 3D scene understanding. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshops. Seoul: IEEE, 2019. 3995–4003.
[15]
Graham B, Engelcke M, van der Maaten L. 3D semantic segmentation with submanifold sparse convolutional networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 9224–9232.
[16]
Xu MY, Zhou ZP, Qiao Y. Geometry sharing network for 3D point cloud classification and segmentation. Proceedings of the 34th AAAI Conference on Artificial Intelligence, the 32nd Innovative Applications of Artificial Intelligence Conference, the 10th AAAI Symposium on Educational Advances in Artificial Intelligence. New York: AAAI, 2020. 12500–12507.
[17]
Xu MT, Zhang JH, Zhou ZP, et al. Learning geometry-disentangled representation for complementary understanding of 3D object point cloud. Proceedings of the 35th AAAI Conference on Artificial Intelligence, the 33rd Conference on Innovative Applications of Artificial Intelligence, the 11th Symposium on Educational Advances in Artificial Intelligence. AAAI, 2021. 3056–3064.
[18]
Hu QY, Yang B, Xie LH, et al. RandLA-Net: Efficient semantic segmentation of large-scale point clouds. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 11105–11114.
[19]
Li YY, Bu R, Sun MC, et al. PointCNN: Convolution on X-transformed points. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 828–838.
[20]
Tatarchenko M, Park J, Koltun V, et al. Tangent convolutions for dense prediction in 3D. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 3887–3896.
[21]
Wu HP, Xiao B, Codella N, et al. CvT: Introducing convolutions to vision transformers. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 22–31.
[22]
Carion N, Massa F, Synnaeve G, et al. End-to-end object detection with transformers. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 213–229.
[23]
Guo MH, Cai JX, Liu ZN, et al. PCT: Point cloud transformer. Computational Visual Media, 2021, 7(2): 187-199. DOI:10.1007/s41095-021-0229-5
[24]
Zhao HS, Jiang L, Jia JY, et al. Point Transformer. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 16239–16248.
[25]
Lai X, Liu JH, Jiang L, et al. Stratified transformer for 3D point cloud segmentation. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 8490–8499.
[26]
Bello I. LambdaNetworks: Modeling long-range interactions without attention. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
[27]
Ba JL, Kiros JR, Hinton GE. Layer normalization. arXiv:1607.06450, 2016.
[28]
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Munich: Springer, 2015. 234–241.
[29]
Yi L, Kim VG, Ceylan D, et al. A scalable active framework for region annotation in 3D shape collections. ACM Transactions on Graphics, 2016, 35(6): 210.
[30]
Yang Z, Wang LW. Learning relationships for multi-view 3D object recognition. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 7504–7513.
[31]
Wichmann A, Agoub A, Schmidt V, et al. RoofN3D: A database for 3D building reconstruction with deep learning. Photogrammetric Engineering & Remote Sensing, 2019, 85(6): 435-443.
[32]
Wang SL, Suo S, Ma WC, et al. Deep parametric continuous convolutional neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 2589–2597.
[33]
Wu WX, Qi ZG, Fuxin L. PointConv: Deep convolutional networks on 3D point clouds. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 9613–9622.
[34]
Thomas H, Qi CR, Deschaud JE, et al. KPConv: Flexible and deformable convolution for point clouds. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 6410–6419.
[35]
Yang JC, Zhang Q, Ni BB, et al. Modeling point clouds with self-attention and gumbel subset sampling. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3318–3327.
[36]
Lee J, Lee Y, Kim J, et al. Set transformer: A framework for attention-based permutation-invariant neural networks. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 3744–3753.
[37]
Xie SN, Liu SN, Chen ZY, et al. Attentional shapeContextNet for point cloud recognition. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 4606–4615.