在大数据时代背景下, 教育数据挖掘领域相关研究迅速发展, 其目的是从大规模的教育数据中提取有价值的信息. 教育数据挖掘的关键任务之一就是利用学生的考试数据进行建模, 从而获知学生的潜在认知状态[1]. 其中, 认知状态是指学生在学习过程中对所学知识的学习情况.
传统的考试评估通常只报告一个笼统的总分或能力分数, 而忽略了个体之间存在的认知状态差异. 但是即使考试成绩相同的学生, 也有可能具有不同的认知状态[2]. 为了解决传统考试评估的缺陷, 最新的研究提出了认知诊断模型, 该模型能把认知过程与测量手段结合起来, 不仅能对学生的整体水平做出评估, 同时还可以将学生的认知结构模式化. 其利用合适的测量模型对不同的认知结构模式进行诊断, 从而定量地考察学生的认知状态与个体差异[3].
具体来说, 认知诊断模型的有效性是通过预测学生表现(predict student performance, PSP)来实现的. 此外, PSP可以进一步应用于许多方向, 如个性化的补救建议和教学计划的改进[4]. 由于认知诊断结果具有很强的可解释性, 研究人员投入了大量精力来设计合适的认知诊断模型, 以提高个性化学习的质量[5].
目前常见的认知诊断模型可以分为两类: 离散型和连续型. 离散型认知诊断模型包括DINA模型(deterministic inputs, noisy and gate), 连续型认知诊断模型包括IRT模型(item response theory). 最近, 也有许多新的模型被提出, 如FuzzyCDF[6], R-FuzzyCDF[7]和NeuralCDM[8].
然而, 在上述认知诊断模型中仍存在一些限制. 首先, 现有的认知诊断模型考虑了对客观题和主观题的预测情况, 但缺少对这两类题目的细化研究. 例如, 编程题属于主观题, 但是和传统意义上的主观题又存在差异, 编程题具有更加严格的约束性和限制性. 因此, 现有的认知诊断模型在分析编程题时存在精度不足的问题. 其次, 尽管传统的认知诊断模型在小规模数据环境中具有良好的性能, 但是由于收敛速度慢, 此类模型在处理大规模数据时的执行效率显著降低.
为了解决这些问题, 本文提出了一种基于编程表现的模糊认知诊断模型P-FuzzyCDF (programming-performance-based fuzzy cognitive diagnosis framework). 具体来说, 该模型首先基于学生的潜在特质来模糊化学生对特定知识点的掌握程度. 随后, 该模型基于编程题掌握知识点越多, 分数越高的特性, 模糊化了学生对问题的掌握程度. 此外, 该模型会基于学生由于抄袭而答对题目的情况, 生成学生在每道题目上的最终得分. 其中, 我们使用了学生在校期间的学习数据以及编程数据来分析学生的认知状态, 从而得到模型中的重要参数.
为了评估提出的方法, 本文在4个真实的数据集上进行了实验. 实验结果表明, 本文提出的方法与现有经典方法相比, 在保证预测准确性的基础上, 减少了时间开销. 综上所述, 本文的贡献如下.
(1)提出了一种基于编程表现的模糊认知诊断模型P-FuzzyCDF, 并将该模型应用在了学生表现预测方面, P-FuzzyCDF弥补了传统认知诊断模型在程序设计教育领域研究的不足.
(2)引入了学生在校期间的编程数据信息, 将其应用在P-FuzzyCDF中, 从而提高模型的准确率.
(3)多个数据集上的实验结果表明, 本文提出的 P-FuzzyCDF方法优于基准方法.
2 相关工作本节介绍了现有的几种被广泛应用的认知诊断模型: DINA, IRT, FuzzyCDF (fuzzy cognitive diagnosis framework).
2.1 DINA模型DINA模型是一种典型的离散型认知诊断模型. 该模型将学生描述成一个多维的知识点掌握向量, 从学生实际作答结果入手进行诊断. DINA模型简单, 参数的可解释性较好, 且 DINA 模型的复杂性不受属性个数的影响[9].
式(1)展示了DINA模型定义的学生
| ηij=KΠk=1αqjkik | (1) |
其中,
DINA模型联合试题知识点关联矩阵
式(2)表示在已知学生
| Pj(αi)=Pj(Xij=1|αi)=g1−ηijj(1−sj)ηij | (2) |
其中,
由于DINA模型在客观题的预测中准确性高, 可解释性强, 所以被广泛应用在认知诊断中. 但是, DINA模型只能把学生的潜在认知状态分为两类, 即完全未掌握(0)或完全掌握(1). 这并不符合编程题目需要多级评分的特点, 从而使得DINA模型在预测学生在编程题的认知状态时的准确性和精度都有所下降[11].
2.2 项目反应理论项目反应理论(IRT)是一种典型的连续型认知诊断模型, 被广泛应用在心理学和教育测量领域. IRT根据学生回答问题的情况, 通过对题目特征函数的运算, 来推测学生的能力. IRT的题目参数有: 区分度
式(3)展示了IRT的双参数模型:
| α=1/1(1+exp[−D×a×(θ−b)](1+exp[−D×a×(θ−b)]) | (3) |
其中,
IRT模型相比于DINA模型可以进行多级评分, 使用潜在变量来描述一个学生. 但是, IRT模型对测验条件要求较为严格, 样本容量要大, 被试者的能力分布范围要广, 测试题目数量要多, 这些条件如果没被满足则会影响其精确性[14].
2.3 FuzzyCDFFuzzyCDF模型将模糊理论应用到认知诊断中, 可以同时对学生作答客观题和主观题进行诊断, 解决了传统认知诊断模型无法有效诊断主观题的问题[5]. FuzzyCDF模型假设在客观题作答中, 学生要掌握题目所涉及的全部知识点才能掌握题目. 而在主观题作答中, 学生仅需掌握题目所涉及的部分知识点即表明该学生掌握该题目.
在FuzzyCDF模型中, 学生正确回答客观题和主观题的概率公式分别为式(4)和式(5):
| P(Xij=1|ηij,sj,gj)=(1−sj)ηij+gj(1−ηij) | (4) |
| P(Xij|ηij,sj,gj)=N(X|[(1−sj)ηij+gj(1−ηij)],σ2) | (5) |
其中,
FuzzyCDF模型相比于传统的认知诊断模型, 考虑了客观题和主观题的不同情况, 但是缺少对编程题这一特殊类型的题目的考虑. 此外, FuzzyCDF模型需要应用采样算法进行参数估计, 所以面临着高计算复杂度的问题和需要大量训练数据的问题[15].
3 个性化的模糊认知诊断模型本节将介绍本文提出的基于编程表现的模糊认知诊断模型(P-FuzzyCDF). 如图1所示, P-FuzzyCDF由4个部分组成, 自上而下分别是学生的潜在特质、学生对知识点的掌握程度、学生对问题的掌握程度以及预测得到的问题得分. 其中, 我们使用了学生在校期间的学习数据以及编程数据来分析学生的认知状态, 从而得到模型中的重要参数. 为了更好地说明, 表1展示了建模过程中的一些重要的数学符号, P-FuzzyCDF 的每个步骤将在第3.1–3.4节中详细说明.
3.1 模糊化知识点掌握程度本节将展示如何获知学生对特定知识点的掌握情况. 在基于DINA的认知诊断模型中, 其把学生对知识点的掌握程度假设为完全掌握和完全未掌握, 该模型适用于只有正确和错误两种选项的客观题目[16]. 然而, 在计算机编程课程中, 对于仅满足了部分题目要求的编程题, DINA模型并不适用. 因此, 为了解决这个问题, P-FuzzyCDF将模糊集合理论引入认知诊断模型中, 从而使二元变量(0或1)模糊为
| αjk=μk(j)=1/(1+exp[−1.7×ajk×(θj−bk)]) | (6) |
式(6)表明学生对知识点的掌握程度受到学生的潜在特质(
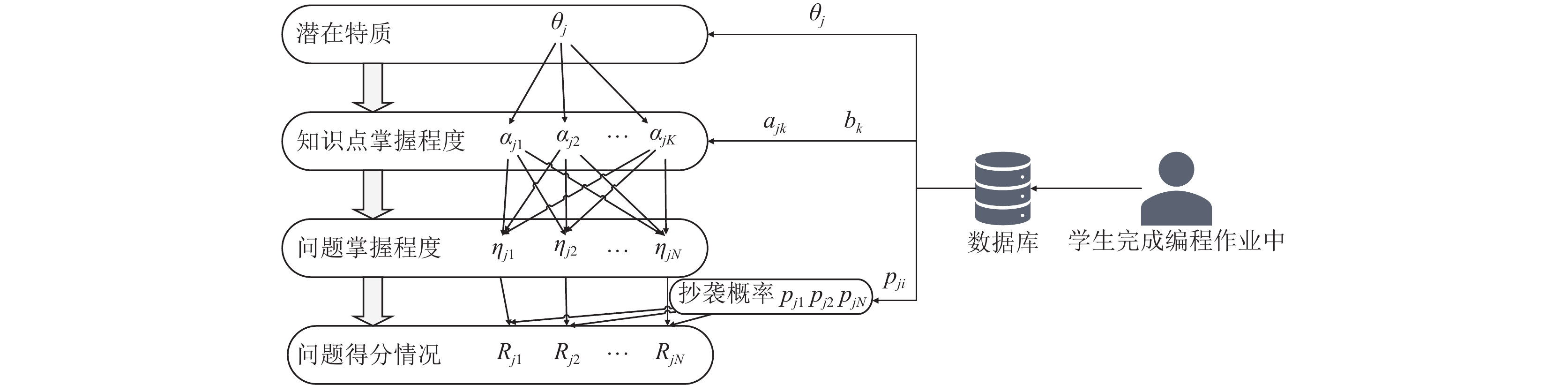
|
图 1 4层模糊认知诊断模型的框架 |
| 表 1 一些重要的数学符号 |
假设1: 学生的高阶潜在特质可以由学生当前的学业GPA决定.
学生的高阶潜在特质指学生的能力水平, 而学生的能力水平一般表现在学生的考试成绩(即GPA). 因此,
假设2: 学生对知识点的潜在认知程度可以由含有该知识点的题目的历史通过率决定.
相比于传统的线下教育, 在编程教育领域中, 教师可以得到详细的学生在编程过程中的学习数据. 因此,
假设3: 知识点的难度系数可以由教师对知识点的难易程度进行人工评级来决定.
教师作为知识的传播者对每个知识的都有着很深入的认识, 因此,
基于第3.1节中模糊化的知识点掌握程度, 我们可以进一步模糊化学生对问题的掌握程度(即能够解决问题的概率). 在模糊认知诊断模型中, 学生对问题的掌握程度受到学生对该问题所需知识点的掌握程度的影响.
知识点在问题上的相互作用主要分为联结型和补偿型[18]. 联结型是指学生只有掌握了解决问题所需要的全部知识点才能答对问题, 补偿型是指学生只要掌握了解决问题所需要的部分知识点就可以获得该题目的部分分数. 对于编程题而言, 学生掌握的知识点越多, 在这道题目上的得分就越高. 因此, 我们假设知识点对编程题的相互作用是补偿型的. 那么学生在这一道题目上的掌握程度就是学生对这道题目所需知识点的掌握程度的并集. 学生
| ηji=μ∪1⩽k⩽K,qik=1k(j) | (7) |
其中,
| μA∪B(x)=max | (8) |
由第3.2节可以确定学生在问题上的掌握程度. 在本节中, 考虑了一种例外情况(即学生在作答题目的过程中存在抄袭行为), 并采用高斯分布预测编程题的分数. 在实际答题过程中, 学生的题目分数不仅与学生对题目的掌握程度有关, 还与学生是否抄袭有关. 同时考虑到编程题具有多级评分的需求, 将题目的得分划分为[0, 1]之间的连续变量来归一化编程题的分数. 然后, 假设学生在编程题上的得分服从高斯分布, 这在研究中被广泛应用[6,7,15]. 结合学生对题目的掌握情况以及抄袭因素可以得到学生的真实作答得分:
| P({R_{ji}}|{\eta _{ji}}, {p_{ji}}) = { N}({R_{ji}}|{p_{ji}}(1 - {\eta _{ji}}), {\sigma ^2}) | (9) |
其中,
假设4: 学生在一道题目上的抄袭概率可以由学生历史答题的抄袭比率决定.
在计算机编程教育领域, 可以通过在线编程平台获得每个学生在每道题目上的抄袭概率, 当抄袭概率大于等于80%时, 学生的抄袭可能性较高. 因此, 如果学生在一道题目上的抄袭概率大于等于80%, 则假定该学生通过抄袭来回答题目. 那么
为了更好地说明本文提出的P-FuzzyCDF模型, 使用如图2所示的模型图来表示. 得分矩阵
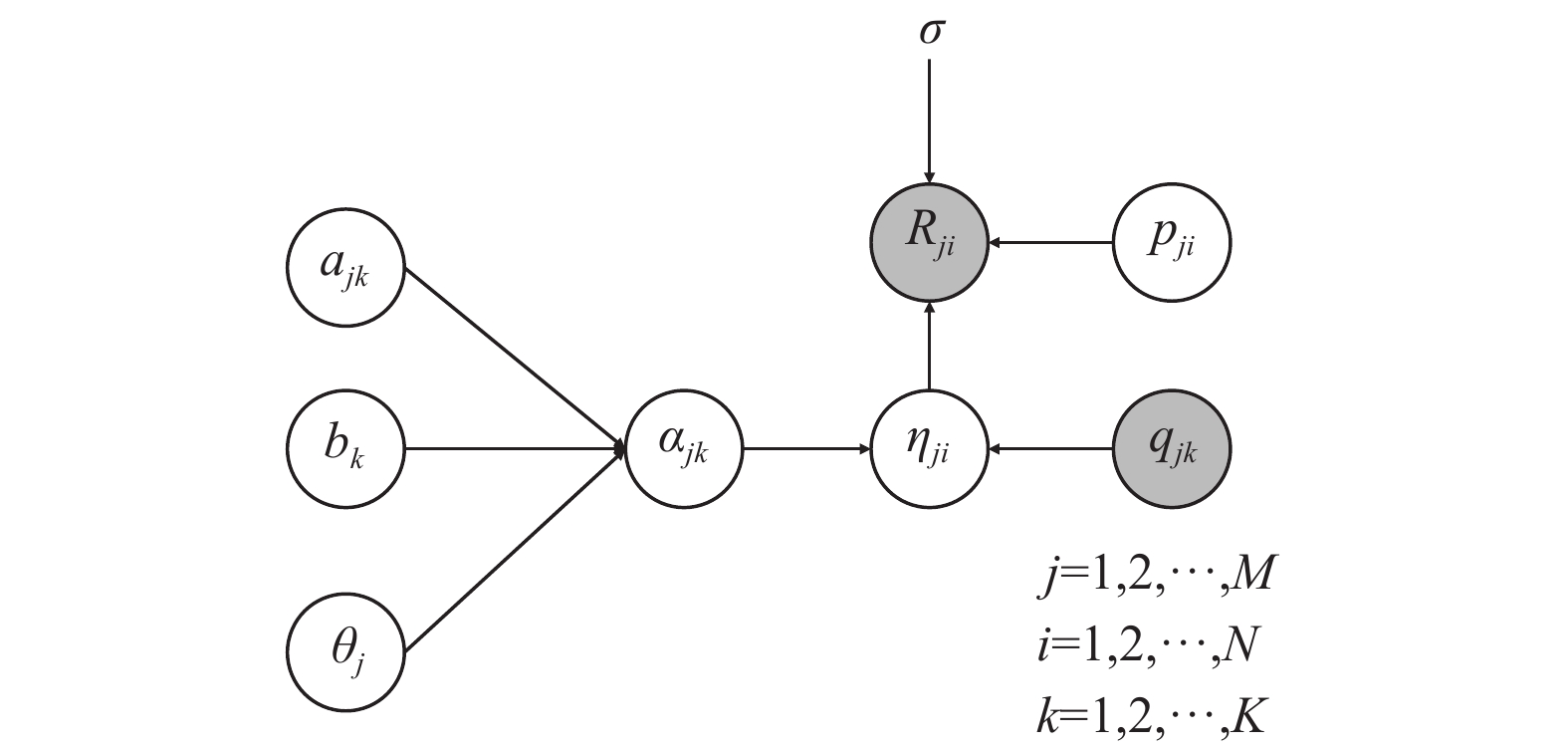
|
图 2 P-FuzzyCDF模型 |
4 实验设计
为了验证P-FuzzyCDF方法的有效性, 在真实数据集上设置了对比实验. 本节首先在PSP任务上, 将P-FuzzyCDF与基准方法进行对比. 其次, 使用假设检验验证了P-FuzzyCDF方法的有效性. 最后, 通过案例分析评估预测结果的可解释性.
4.1 数据集实验数据来自北京化工大学在教学过程中学生与OJ系统交互所产生的学习行为数据以及教务管理系统中的学生基础数据. 如表2所示, 共包含4个数据集, 分别来自4门编程课程, 共有206道编程题, 总计531名学生参与. 每个数据集中包括了得分矩阵
| 表 2 数据集信息汇总 |
| 表 3 得分矩阵示例 |
| 表 4 知识点矩阵示例 |
4.2 标签
由于在OJ系统中学生每道编程题的得分情况只有两种(完全正确和完全错误), 只是用OJ系统中的得分不符合编程题作为主观题的特性. 因此, 我们提出了一种计算得分矩阵
首先, 根据提交次数与题目是否正确之间的关系来定义编程题的初始分数
其次, 我们根据学生在OJ系统中的排名对学生的编程题得分进行二次定义. 按照排名顺序将分数定义为等差数列, 排名第一的学生分数定义为
最后, 通过将上述两个得分加和取平均即可得到学生的最终分数
| 表 5 定义初始分数 |
4.3 评价指标
我们使用3种不同的指标(即MAE、MSE和RMSE)来评估性能. 这3个性能指标在现有关于认知诊断的研究中被广泛使用[15].
如式(10)所示, MAE是预测得分和实际得分之间的绝对差值的平均值, 它衡量的是预测误差的大小. MAE值越小, 表示预测误差越小. 如式(11)所示, MSE是预测得分与实际得分之差平方的期望值, 它可以评价数据的变化程度,MSE值越小, 说明预测模型具有更好的精确度. 如式(12)所示, RMSE是MSE的算数平方根, 用于指示模型在预测中会产生的误差规模, 对于较大的误差, 权重较高, RMSE越小越好.
| MAE = {{\sum _{{{j}} = 1}^m|{y_{\text{j}}} - {{\overline y }_j}|} / M} | (10) |
| {\textit{MSE}} = {{\sum _{{{j}} = 1}^m{{({y_j} - {{\overline y }_j})}^2}} / M} | (11) |
| {\textit{RMSE}} = \sqrt {{{\sum _{{{j}} = 1}^m{{({y_j} - {{\overline y }_j})}^2}} / M}} | (12) |
在实验中考虑了3个方法进行对比实验, 分别是DINA, IRT和FuzzyCDF, 它们参数都是通过参数估计算法得到的[15]. 具体描述如下:
(1) DINA[7]: 一种经典的离散型认知诊断模型. 该模型在给定知识点矩阵的情况下, 对学生的认知状态进行建模, 结合回答问题时的例外情况(失误因素
(2) IRT[13]: 一种经典的连续型认知诊断模型. 该模型通过评估学生的潜在特征
(3) FuzzyCDF[15]: 该模型将模糊理论应用到认知诊断中, 基于学生的潜在特征
为了评估P-FuzzyCDF的有效性, 使用第4.1节描述的数据集, 将其与基准方法(如第4.4节所述)进行了对比. 使用3个评价指标来评估P-FuzzyCDF的有效性: MAE, MSE和RMSE. 这3个评价指标的值越接近0, P-FuzzyCDF在PSP任务上就越准确.
表6为在不同的数据集上, P-FuzzyCDF与基准方法的对比实验结果. 从表中数据可知, P-FuzzyCDF的表现优于所有基准方法. 具体来说, 在程序设计基础数据集中, 相比于DINA, P-FuzzyCDF在MAE,MSE和RMSE上效果分别提升了58.8%, 55%和75%. 相比于IRT, P-FuzzyCDF在MAE, MSE和RMSE上效果分别提升了58.8%, 55%和75%. 相比于FuzzyCDF, P-FuzzyCDF在MAE,MSE和RMSE上效果分别提升了63.2%, 62.5%和83.3%.
| 表 6 Python国际化课程数据集实验结果 |
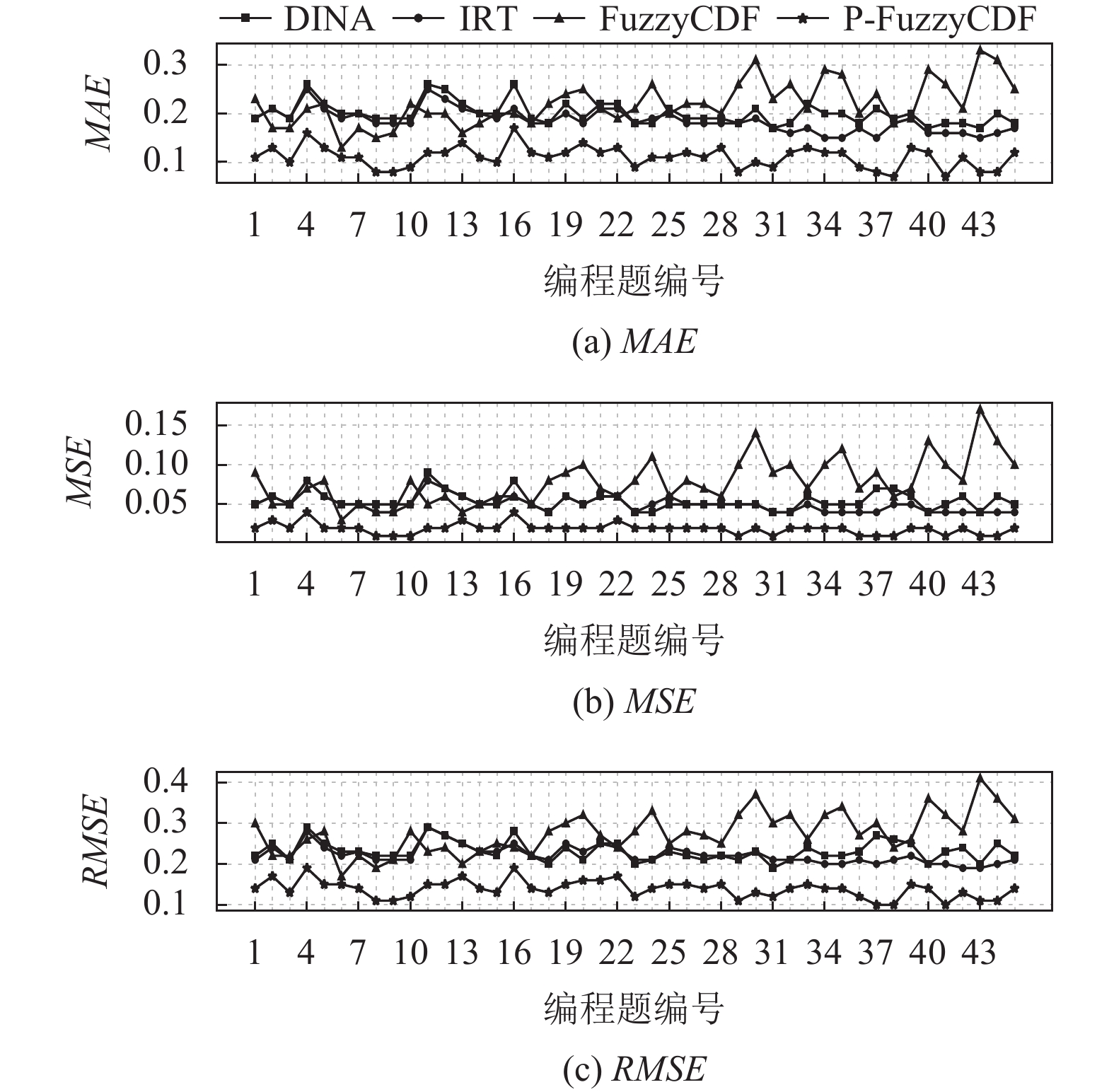
图3–图6为P-FuzzyCDF与基准方法在每一道编程题上的详细对比. 如图4所示为程序设计基础数据集下的实验结果, 该数据集共包含56道题目, 与基准方法相比, P-FuzzyCDF在每一道题目的预测结果上均有显著优势. 从图4–图6中可以看出, 在程序设计基础数据集, ACM/ICPC程序设计竞赛方法与实践数据集和数据结构数据集上, P-FuzzyCDF明显优于基准方法.
具体来说, P-FuzzyCDF利用在线编程教育数据精确性的特点, 提出了4个教育假设进行参数估计, 该参数估计方法更符合编程题的特征, 因此, 相比于基准方法, P-FuzzyCDF在预测编程题的成绩时表现更好. 此外, P-FuzzyCDF在对学生的学习认知状态的诊断结果为连续变量(即学生对知识点的掌握程度为[0, 1]区间内的连续值), 而DINA模型的诊断结果为离散值(1表示完全掌握, 0表示完全没有掌握). IRT模型没有考虑学生对知识点的掌握情况, 仅使用一个潜在的连续型数值变量对学生成绩进行表示. FuzzyCDF模型虽然可以将学生的认知状态表示为连续变量, 但缺少对编程题的具体分析, 忽略了编程题的自身特点. 而P-FuzzyCDF在预测学生成绩时, 考虑了学生在答题时的抄袭因素, 使预测结果更接近实际作答结果. 因此, 相较于传统的认知诊断方法, P-FuzzyCDF模型不仅提高了预测的准确性还保证了结果的可解释性.

|
图 3 Python 国际化课程数据集的详细实验结果 |

|
图 4 程序设计基础数据集的详细实验结果 |
4.5.2 假设检验
从图3中可以看出, 在Python国际化课程数据集上, P-FuzzyCDF没有明显的优势. 因此, 在本节进行了Wilcoxon符号秩检验[20], 以验证P-FuzzyCDF的竞争力. 表7显示了上述假设检验在Python国际化课程数据集的结果. 注意, 我们实现了3种现有方法, 因此我们只能对这3种方法进行假设检验. 我们研究中使用的假设如下: H0: P-FuzzyCDF和其他方法在MAE, MSE和RMSE方面没有显著差异. 该检验的显著性水平设置为0.05. 表7显示, 所有P-value均低于0.05, 则统计结果导致拒绝零假设. 这些结果表明, 我们提出的方法与其他方法在MAE, MSE和RMSE度量方面存在显著差异. 需要注意的是, 图4–图6中展示的结果表明, P-FuzzyCDF比其他现有方法在评估指标MAE、MSE、RMSE上取得了显著的优势, 因此可以安全地得出结论, P-FuzzyCDF可以比基准方法显著获得更好的性能.
|
图 5 ACM/ICPC 程序设计竞赛方法与实践数据集的详细实验结果 |
4.5.3 案例分析
为了验证PEP结果的可解释性, 使用了DINA和P-FuzzyCDF给出了一个学生在数据结构数据集上每个知识点的可视化诊断结果的示例. 可视化结果如图7所示, DINA和P-FuzzyCDF都可以获得有意义的诊断结果. 但是, DINA只能区分学生是否掌握了一个知识点(1完全掌握, 0完全未掌握). 而P-FuzzyCDF可以得出一个学生对知识点的具体掌握程度. 因此, 根据诊断结果, 学生可以准确地了解自己的优点和不足. 老师也可以根据我们的诊断结果给出个性化的教学建议. 相比于DINA和P-FuzzyCDF, IRT方法使用潜在变量来描述一个学生, 因此, 不能为每个学生提供直观可解释性的结果. 另外, 虽然FuzzyCDF 也可以给出学生对知识点掌握程度的描述, 但是由第4.5.1节可知, FuzzyCDF在PEP的准确性方面低于DINA.

|
图 6 数据结构数据集的详细实验结果 |
| 表 7 第4.5.2节中假设的P-value |
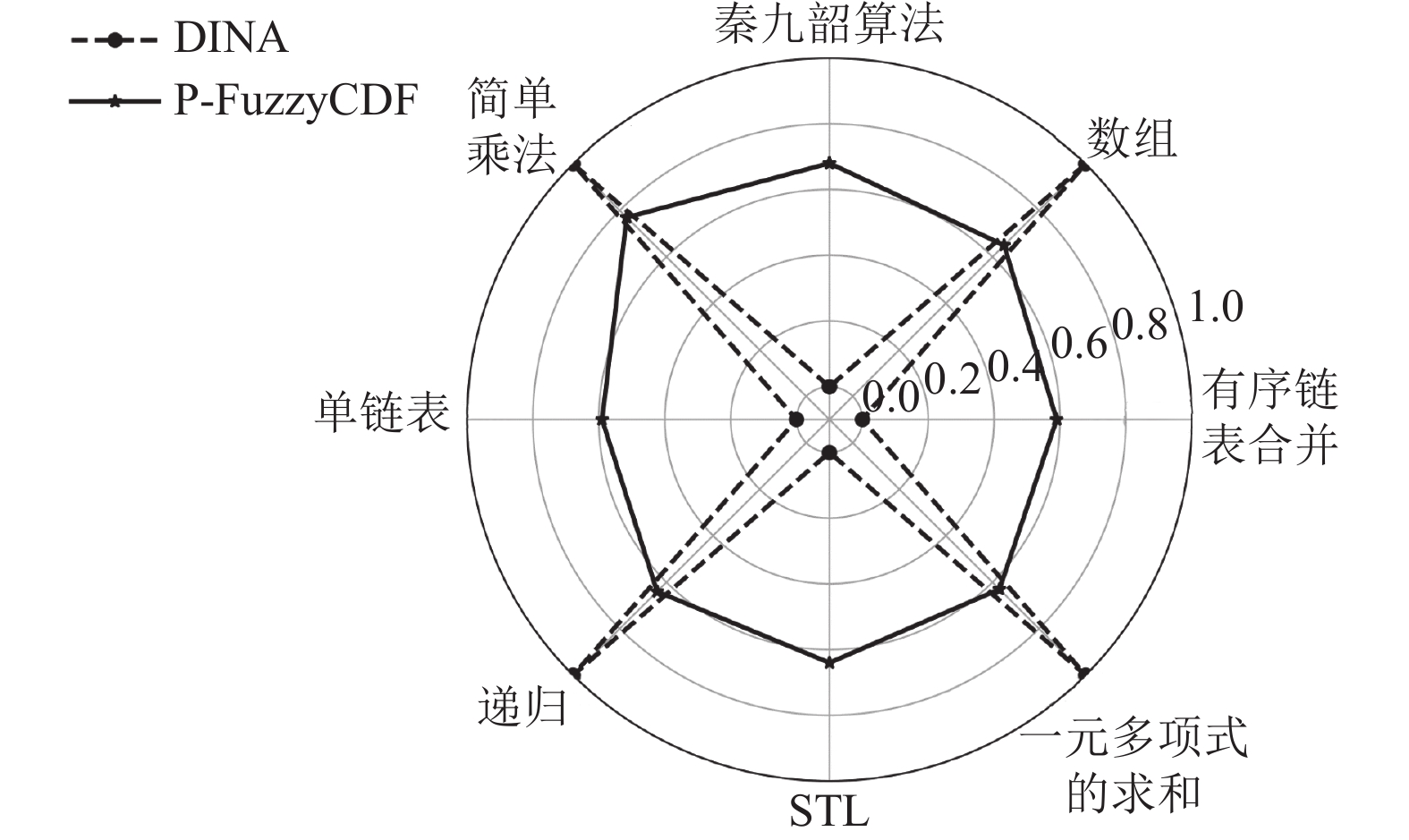
|
图 7 学生在每个知识点上的诊断结果 |
5 结论与展望
在本文中, 设计了一个个性化的模糊认知诊断框架P-FuzzyCDF, 以探索认知诊断模型在编程题上的表现. 首先基于模糊集假设模糊化学生对知识点的掌握程度, 然后通过模糊集运算模糊化学生对编程题的掌握程度, 接下来通过考虑学生抄袭因素来对认知诊断进行建模. 此外, 在4个数据集上进行了评估, 大量的实验结果表明, P-FuzzyCDF能够定量的, 可解释的分析每个学生的特征, 从而获得更好的预测性能. 今后, 将根据学生量化的学习状态为学生推荐个性化的学习路径和学习活动.
| [1] |
Xu CJ, Zhu GB, Ye J, et al. Educational data mining: Dropout prediction in XuetangX MOOCs. Neural Processing Letters, 2022, 54(4): 2885-2900. DOI:10.1007/s11063-022-10745-5 |
| [2] |
刘淇, 陈恩红, 朱天宇, 等. 面向在线智慧学习的教育数据挖掘技术研究. 模式识别与人工智能, 2018, 3(1): 77-90. |
| [3] |
Zhou SQ, Traynor A. Measuring students’ learning progre-ssions in energy using cognitive diagnostic models. Frontiers in Psychology, 2022, 13: 892884. DOI:10.3389/fpsyg.2022.892884 |
| [4] |
江培超, 王川, 胡富珍, 等. 基于阅读认知诊断的学生表现预测. 计算机工程与应用, 2022, 58(11): 160-170. |
| [5] |
李忧喜, 文益民, 易新河, 等. 一种改进的模糊认知诊断模型. 数据采集与处理, 2017, 32(5): 958-969. |
| [6] |
Liu Q, Wu RZ, Chen EH, et al. Fuzzy cognitive diagnosis for modelling examinee performance. ACM Transactions on Intelligent Systems and Technology, 2018, 9(4): 1-26. |
| [7] |
Liu J, Tang WS, He XP, et al. Research on DINA model in online education. Proceedings of the 6th International Conference on E-learning, E-education, and Online Training. Changsha: Springer, 2020. 279–291.
|
| [8] |
Wang F, Liu Q, Chen EH, et al. Neural cognitive diagnosis for intelligent education systems. Proceedings of the 34th AAAI Conference on Artificial Intelligence, the 32nd Innovative Applications of Artificial Intelligence Conference, and the 10th AAAI Symposium on Educational Advances in Artificial Intelligence. New York: AAAI Press, 2020. 6153–6161.
|
| [9] |
范士青, 刘华山. 常见的认知诊断模型及其比较. 教育测量与评价, 2015(7): 4-9. |
| [10] |
Tatsuoka K K. Rule Space: An approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 1983, 20(4): 345-354. DOI:10.1111/j.1745-3984.1983.tb00212.x |
| [11] |
De La Torre J, Minchen N. Cognitively diagnostic assessments and the cognitive diagnosis model framework. Psicología Educativa, 2014, 20(2): 89-97. |
| [12] |
张兆远, 陶剑. 项目反应理论(IRT)甄选试题方法研究. 伊犁师范学院学报(自然科学版), 2018, 12(3): 10-14. |
| [13] |
Janssen R, Tuerlinckx F, Meulders M, et al. A hierarchical IRT model for criterion-referenced measurement. Journal of Educational and Behavioral Statistics, 2000, 25(3): 285-306. DOI:10.3102/10769986025003285 |
| [14] |
刘彦楼, 辛涛, 田伟. 项目反应理论与认知诊断模型的参数估计: 模型整合视角. 北京师范大学学报(自然科学版), 2017, 53(6): 742-748. DOI:10.16360/j.cnki.jbnuns.2017.06.017 |
| [15] |
Wu RZ, Liu Q, Liu YP, et al. Cognitive modelling for predicting examinee performance. Proceedings of the 24th International Conference on Artificial Intelligence. Buenos Aires: AAAI Press, 2015. 1017–1024.
|
| [16] |
蔡艳, 赵洋, 刘舒畅, 等. 一种优化的多级评分认知诊断模型. 心理科学, 2017, 40(6): 1491-1497. DOI:10.16719/j.cnki.1671-6981.20170632 |
| [17] |
刘彬彬. 几种基于IRT (项目反应理论)模型的参数估计方法研究. 硅谷, 2010(22): 80. |
| [18] |
Yamaguchi K, Okada K. Hybrid cognitive diagnostic model. Behaviormetrika, 2020, 47(2): 497-518. DOI:10.1007/s41237-020-00111-x |
| [19] |
熊超, 马华. 结合认知诊断和答题行为分析的试题推荐方法. 计算机时代, 2022(12): 85-88. |
| [20] |
Divine G, Norton HJ, Hunt R, et al. A review of analysis and sample size calculation considerations for Wilcoxon tests. Anesthesia & Analgesia, 2013, 117(3): 699-710. |
 2023, Vol. 32
2023, Vol. 32



