21世纪被认为是脑科学时代, 探索和揭示脑的奥秘已成为当代自然科学研究所面临的最重大的挑战之一. 脑电图(electroencephalogram, EEG)是一种记录脑电波的电生理监测方法. 而基于脑电信号实现的脑机接口(brain computer interface, BCI)可以在人脑和计算机或其他外部设备之间建立直接的信息交互和控制通道, 是人类了解和提高脑功能的重要手段, 正成为脑科学、生物医学及康复工程、智能信息处理等领域的一个研究热点.

但是脑电具有个体差异性、非稳态等特性. 针对同一个任务, 脑电信号会随着被试的变化而变化即每个被试的信号是不太一样的, 存在协变量偏移(covariate shift)现象. 即使是同一个任务同一个被试, 也会随着时间的变化而呈现不同的脑电信号, 后一种的典型是同一个被试不同时间分段之间的偏移. 一个时间分段通常时间较长, 时间分段之间存在休息.

传统脑电分类的方法按照是否独立于被试, 可分为两种. 第1种, 针对每个被试(subject specific)的方法, 即用每一个被试的数据训练一个模型用于分类. 这种方法的优点在于可以针对每个被试训练一个独特的模型, 适应性更好. 然而, 由于心理学实验中收集到的每个被试的数据量通常很少, 样本数量通常不超过1 000个, 因此存在样本偏少的问题. 这使得使用深度学习方法进行训练变得困难. 第2种, 对于所有被试通用(subject independent)的方法, 即用所有被试的数据训练一个统一的模型. 这种方法的优点在于, 集合了所有数据后, 可以使用深度学习方法进行训练. 然而, 这种方法不能针对每个被试进行个性化优化.

迁移学习方法能够结合上述两种方法的优点. 因此本文提出基于域对抗迁移的方法. 本文所提出的迁移学习方法总体网络框架是先用MMCNN^[1]作为骨干网络提取信号特征, 再将源域被试上学习到的特征迁移到目标域被试上. 传统迁移学习方法通常都是单源的迁移, 即从一个源域迁移到一个目标域, 而心理学实验采集到的脑电信号是来自多个被试的, 可以理解为多个域, 在进行迁移的时候, 需要从众多被试中选择一个和目标被试脑电信号最相似的被试, 即从多个源域中选取一个最佳源域用于迁移.

本文提出了一个新的迁移框架, 来提高运动想象任务的分类准确率. 该框架由一个源域选择算法MSTE和一个迁移算法ToSAN组成. 本文的贡献在于: (1) 提出了一个新的源域选择算法MSTE, 同时考虑了类别和时间子域上源域和目标域的距离以及源域内部时间子域之间的距离, 从而计算出最佳的“源域—目标域”配对. (2) 提出了一个新的基于域对抗神经网络的迁移方法ToSAN, 该方法不仅利用了目标域信息还将特征分解, 对齐对分类任务有关的特征. (3) 本文所提出的迁移算法和源域选择算法在两个经典数据集上进行了广泛的实验. 实验结果表明, 所提出的框架在分类准确率方面明显优于对比方法.

1 相关工作

脑电波是一种使用电生理指标记录大脑活动的方法. 大脑在活动时, 大量神经元同步发生的突触后电位经过总和后形成的. 它记录大脑活动时的电波变化, 是脑神经细胞的电生理活动在大脑皮层或头皮表面的总体反映^[2]. 目前关于脑电信号分类任务有众多研究算法提出.

机器学习利用一套数学模型和算法来逐步提高任务的性能. 它将训练数据集作为输入, 在验证集或者测试集上进行预测来优化模型. 脑电信号分类任务中, 常用的机器学习算法包括支持向量机(SVM)、K最近邻算法(KNN)、贝叶斯网络和随机森林等. Chatterjee等人^[3]利用基于统计、基于小波的能量熵和基于RMS、PSD的平均功率和不良功率形成相应的特征向量, 然后使用SVM、MLP进行分类. Tang等人^[4]设计了一个基于KNN的平滑自动编码器来实现对运动想象脑电信号的精准识别. Blankertz等人^[5]优化了空间过滤器用于鲁棒的信号分析.

近年来, 伴随着深度学习在计算机视觉、语音识别、自然语言理解等领域的不断突破, 虽然大多数脑机接口系统仍然依赖于手动提取的特征, 但最近的许多工作已经探索了深度学习在脑电信号中的应用. Craik等人^[6]系统回顾了深度学习在脑电信号分类任务中的历史和发展. Schirrmeister等人^[7]提出了著名的Deep ConvNet, Shallow ConvNet以及Hybrid ConvNet, 这3个网络分别从网络结构和训练策略两方面探讨了卷积神经网络在运动想象数据集分类任务上的表现. EEGNet^[8]是第1个用于各种脑电信号分类任务的标志性网络. MMCNN^[1]采用了多分支多尺度的结构, 利用不同尺度的卷积核大小来捕获特征提高分类准确率. Zhang等人^[9]同时考虑了脑电信号在时间和空间上的特征, 有效利用了电极的相对位置信息, 提高了脑电信号分类准确率.

但上述这些方法不能在各种脑机接口范式中发挥全部威力, 原因是脑电信号的特征高度受年龄、心理等不同个体差异的影响, 不同个体的脑电信号对于同一事件可能存在不同^[10]. 且脑电信号存在非平稳, 低信噪比, 对特定任务敏感的信息难以过滤等特性. 此外, 每次心理学实验收集的样本量有限, 限制了模型的训练. 在计算机视觉以及语音领域, 迁移学习飞速发展. 迁移学习能够有效优化脑电信号信息提取的不足, 同时减少对数据量的需求, 学界开始研究在脑电信号上应用迁移方法. Dagois等人^[11]应用10个个体的正则化判别分析得分来学习不同被试之间的类条件分布, 用于运动想象任务中的时间环节校准. Li等人^[12]借鉴了DANN^[13], 通过在每个源域上训练一个DANN模型, 然后根据各个模型在测试数据上的表现加权集成, 将集成后的结果作为最终结果输出. Demsy等人^[14]同时利用欧几里得对齐(Euclidean alignment, EA)和迁移成分分析(transfer component analysis, TCA)^[15]进行被试间的迁移学习. 传统方法关注频域信息而忽略了多模态信息. 为此, Tan等人^[16]把EEG转变为脑电光流信息, 有效保留了多模态的信息, 在此基础上将脑电光流和图片一块进行训练提取特征, 联合训练可以强制网络学习具有迁移性的通用特征, 从图片中获得知识并把它转移到脑电光流中. Fahimi等人^[17]采用了经典的预训练微调的方式进行迁移. Wu等人^[18]介绍了脑机接口的整个训练流程, 以及各种迁移方法如CSP、RCSP、EA、PS、wAR、LDA方法的组合, 并做了详尽的实验说明迁移方法在流程上的应用和效果.

但并不是所有的迁移都能造成积极影响. Agarwal等人^[19]详细阐述了源域和目标域的数据分布不同可能造成负迁移. 同样在脑电数据中, 不同被试间的分布差异并不均衡, 某些被试数据之间的分布差距可能过于巨大, 当这些被试被选为源域和目标域进行迁移时迁移效果反而会下降, 即发生负迁移现象. 因此需要慎重选择合适的源域和目标域进行迁移.本文收集了广泛的源域选择算法, 发现主要有以下这几种类型的方法用于源域选择.

(1)聚类方法. Wu等人^[18]通过K-means聚类方法, 选出聚类后与目标域最接近的源域进行迁移. Song等人^[20]提出了P3 map聚类方法用于源域选择.

(2)基于模型的方法. Li等人^[12]提出了一个多源域选择算法, 假设有标签的源域数据和无标签的目标域数据分布相似, 枚举了N个在源域上训练的分类器, 然后选出分类准确率最高的 ${{N}}_{{s}}$ 个分类器, 认为这 ${{N}}_{{s}}$ 个分类器训练用的源域数据就是最佳源域. Zuo等人^[21]提出了ABMSDA方法, ABMSDA首先训练一个域识别模型来计算目标图像属于每个源域的概率. 基于域相关性, 提出了加权矩距离(WMD), 以更加关注相似性较高的源域.

(3)距离度量方法. Cui等人^[22]提出使用推土机距离(earth mover’s distance, EMD)评估域相似性, 进而根据域相似性选择源域. Chen等人^[23]提出了分层距离(stratified distance), 通过使用分层距离评估相似性选择源域, 不同于其他方法只关注全局的信息, 该方法同时关注了局部信息.

(4)特征相似性方法. Gong等人^[24]提出了ROD算法选择源域, ROD算法能同时集成几何和统计特征信息. 几何上, 主角度越小说明几何上越对齐; 统计上, 当两种不同数据集映射到子空间后的对称KL散度越小说明统计上越接近. Jeon等人^[25]根据被试在静息状态脑电信号中的功率谱密度特征选择合适的源域. Zhang等人^[26]提出了DTE的源域选择算法. DTE算法通过计算源域内部类间散度矩阵与源域目标域之间类间散度矩阵来获得域之间的相似性进而选择源域.

2 方法

运动想象任务的脑电信号被定义为 $X = \left[ {{{{x}}_1}, {{{x}}_2}, \cdots, {{{x}}_n}} \right] \in $ ${R^{n \times C \times T}} $ , 其中 $n$ 表示样本量个数, $C$ 表示采集的脑电信号通道数, $T = t \times f$ 表示采集的脑电信号的时间点数, $t$ 表示运动想象任务进行的时长, $f$ 表示脑电信号的采样率.

给定源域 ${D_s} = \left\{ {\left( {{{x}}_i^s, y_i^s} \right)} \right\}_{i = 1}^{{n_s}}$ , 目标域 ${D_t} = \left\{ {\left( {{{x}}_i^t, y_i^t} \right)} \right\}_{i = 1}^{{n_t}}$ , 其中 ${n_s}, {n_t}$ 分别是是有标签的源域样本数量和目标域样本数量. ${D_s}$ 和 ${D_t}$ 有着相同特征空间和标签空间. 两个域之间的边缘分布和条件分布是不一致的, 即 ${P_s}\left( {{{{x}}^s}} \right) \ne {P_t}\left( {{{{x}}^t}} \right), {P_s}\left( {{{{x}}^s}|{y^s}} \right) \ne {P_t}\left( {{{{x}}^t}|{y^t}} \right)$ . 迁移学习框架的目的就是设计一个深度神经网络来学习一个迁移分类器 $y = {{f}}({{x}})$ 减少域之间的分布漂移, 最终使得目标域上的风险 ${\epsilon }_{t}({f})={\mathbb{E}}_{(x, y)\sim{P}_{t}} [{f}(x)\ne y]$ 可以被控制进而实现更好性能, 其中 ${\mathbb{E}_{({{x}}, y)\sim{P_t}}}$ 表示在服从 ${P_t}$ 分布的数据 $({{x}}, y)$ 上的期望值.

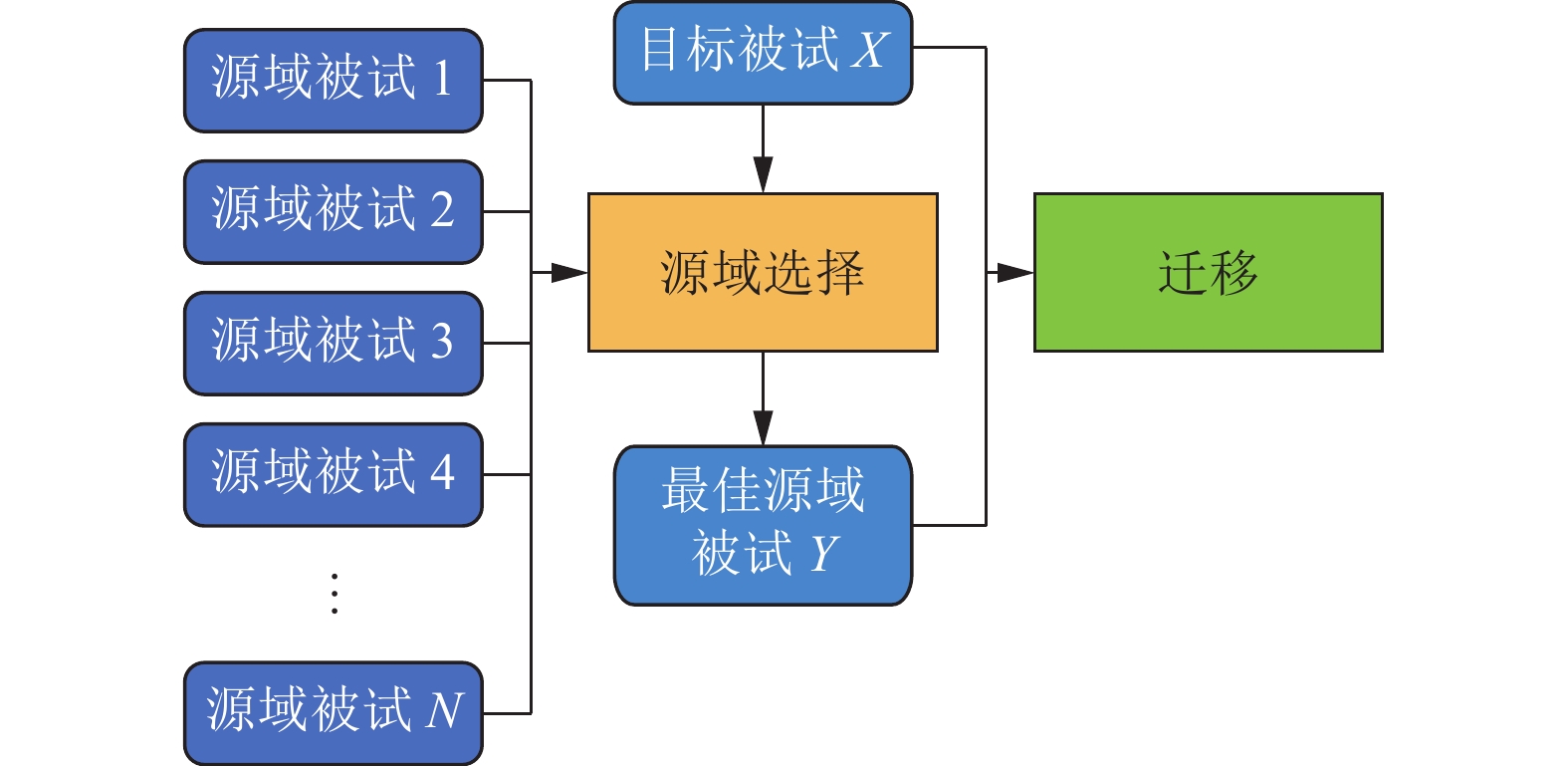
本文所提出的迁移学习整体框架如图1所示, 主要有源域选择和迁移两部分组成. 本节将详细介绍用于脑电信号分类任务的单源域选择方法MSTE以及任务导向的子域对抗神经网络ToSAN.

2.1 源域选择算法

本节提出了一个新的单源域选择方法MSTE (multi-subdomain transferability estimation).

2.1.1 最大均值差异

最大均值差异 (maximum mean discrepancy, MMD)^[27]是一个核学习方法. 该方法通过在样本空间中寻找一个映射函数, 将样本映射到高维空间, 再计算两个不同分布 $p$ 和 $q$ 的样本均值差, 取最大值即为MMD. 最后用MMD作为检验统计量, 判断两个分布 $p$ 和 $q$ 是否相同. MMD值越小说明两个分布越接近, 当MMD值为0时两个分布完全一致, 而MMD值越大说明两个分布越不相同. MMD按如下公式定义了差异度量:

$ {d_\mathcal{H}}(p, q) \triangleq \left\| {{\mathbb{E}_p}\left[ {\phi \left( {{{{x}}^s}} \right)} \right] - {\mathbb{E}_q}\left[ {\phi \left( {{{{x}}^t}} \right)} \right]} \right\|_\mathcal{H}^2 $

(1)

其中, $\mathcal{H}$ 是具有特征核 $k$ 的再生希尔伯特空间(RKHS). 这里 $\phi ( \cdot )$ 表示将原始样本映射到RKHS的特征映射函数, 核 $k$ 表示 $k\left( {{{{x}}^s}, {{{x}}^t}} \right) = \left\langle {\phi \left( {{{{x}}^s}} \right), \phi \left( {{{{x}}^t}} \right)} \right\rangle$ , 其中 $\langle \cdot , \cdot \rangle $ 表示向量内积. MMD的具体计算公式如下所示:

$ \begin{split} {{\hat d}_\mathcal{H}}(p, q) =& \left\| {\frac{1}{{{n_s}}}\sum\limits_{{{{x}}_i} \in {D_s}} \phi \left( {{{{x}}_i}} \right) - \frac{1}{{{n_t}}}\sum\limits_{{{{x}}_j} \in {D_t}} \phi \left( {{{{x}}_j}} \right)} \right\|_\mathcal{H}^2 \\ = &\frac{1}{{n_s^2}}\sum\limits_{i = 1}^{{n_s}} {\sum\limits_{j = 1}^{{n_s}} k } \left( {{{x}}_i^s, {{x}}_j^s} \right) + \frac{1}{{n_t^2}}\sum\limits_{i = 1}^{{n_t}} {\sum\limits_{j = 1}^{{n_t}} k } \left( {{{x}}_i^t, {{x}}_j^t} \right) \\ & - \frac{2}{{{n_s}{n_t}}}\sum\limits_{i = 1}^{{n_s}} {\sum\limits_{j = 1}^{{n_t}} k } \left( {{{x}}_i^s, {{x}}_j^t} \right) \end{split} $

(2)

其中, ${\hat d_\mathcal{H}}(p, q)$ 是 ${d_\mathcal{H}}(p, q)$ 的无偏估计. 在本文中, 使用多项式核函数 $ k(u, v) = {(\alpha < u, v > + c)^d} $ 来估计MMD, 其中 $\alpha $ 和 $c$ 是两个超参数用来调整核函数的形状, 分别设置为1和0, $d$ 是多项式次数, 用来控制复杂度, 设置为2.

2.1.2 相似度度量

启发于MSDAN^[28], 本文提出了一个新的源域选择方法MSTE. 不同于MSDAN独立考虑了时间子域和类别子域, MSTE同时考虑了时间子域和类别子域之间的相互影响, 此外MSTE还考虑了源域单被试内部的时间漂移问题, 使得源域和目标域数据之间的相似性得到准确度量. MSTE与其他方法的核心差异在于源域和目标域的相似度度量的设计. MSTE的相似度度量函数的表示如下:

$ \begin{split} {d_L}\left( {{D_s}, {D_t}} \right) =& \frac{1}{{C\times T}}\sum\limits_{c = 1}^C {\sum\limits_{\tau = 1}^T {\left\| {\frac{1}{{n_s^{c, \tau }}}\sum\limits_{{{{x}}_i} \in D_s^{c, \tau }} \phi \left( {{{{x}}_i}} \right) - \frac{1}{{n_t^{c, \tau }}}\sum\limits_{{{{x}}_j} \in D_t^{c, \tau }} \phi \left( {{{{x}}_j}} \right)} \right\|_\mathcal{H}^2} } \\ & + \frac{{{\lambda _1}}}{{C\times (T - 1)}}\sum\limits_{c = 1}^C {\sum\limits_{\tau = 1}^{T - 1} {\left\| {\frac{1}{{n_s^{c, \tau }}}\sum\limits_{{{{x}}_i} \in D_s^{c, \tau }} \phi \left( {{{{x}}_i}} \right) - \frac{1}{{n_s^{c, \tau + 1}}}\sum\limits_{{{{x}}_j} \in D_s^{c, \tau + 1}} \phi \left( {{{{x}}_j}} \right)} \right\|_\mathcal{H}^2} } \\ \end{split} $

(3)

其中, $C$ 分别代表分类任务的种类数目, $T$ 表示分割的时间段数, BCI Competition IV 2a和BCI Competition IV 2b两个数据集中每个被试都进行若干时间分段的实验, 每个时间分段之间都有一小段的休息时间. 由于脑电信号的非稳态特性, 即便是同一被试同一实验背景下执行相同任务, 可能由于时间的不同导致脑电信号的漂移. 针对这一点, 本文把每个被试的试次在时间上粗略地分为两部分, 即 $T = 2$ . $n_s^{c, \tau }$ 表示源域的类别为 $c$ 同时时间段为 $\tau $ 的试次数量, $D_s^{c, \tau }$ 表示源域的类别为 $c$ 同时时间段为 $\tau $ 的细分域, $n_t^{c, \tau }$ 表示目标域的类别为 $c$ 同时时间段为 $\tau $ 的试次数量, $D_t^{c, \tau }$ 表示目标域的类别为 $c$ 同时时间段为 $\tau $ 的细分域, ${\lambda _1}$ 是一个折中的系数, 用于平衡源域同一类不同时间段之间距离以及源域和目标域每一类每一时间段之间的距离.

MSTE相似度度量函数包含了两部分. 第1部分是源域和目标域在时间和类别子域上的MMD距离, 第2部分是源域内部不同时间分段之间的MMD距离. 第1部分表示源域和目标域在每一类每一时间段之间的MMD距离, 该部分越小说明源域和目标域在每一类每一时间段上的差异越小. 第2部分表示源域中每一个被试所做试次的前后时间段之间的MMD距离均值, 该部分越小说明每个被试在执行运动想象分类任务时的时间漂移越小. 两部分相结合, MSTE的相似度度量函数的值越小, 说明源域和目标域之间差异越小, 更适合作为迁移配对.

2.2 迁移方法

本节提出了一个新的迁移方法ToSAN (task-oriented subdomain adversarial transfer network).

2.2.1 用于域适应的对抗学习框架

生成对抗网络 (generative adversarial network, GAN)^[29]包含了一个生成网络和一个鉴别网络, 其中生成网络不断生成类似于真实样本的样本最大化地迷惑鉴别网络, 而鉴别网络则尽可能地区别真实样本和生成样本. 启发于GAN, 域对抗适应网络能够有效地学习可迁移特征. 域对抗神经网络也类似于双人博弈, 包含了特征提取器 ${G_f}$ 和域鉴别器 ${G_d}$ . 特征提取器 ${G_f}$ 试图从源域和目标域中提取域不变特征来混淆域鉴别器 ${G_d}$ , 域鉴别器 ${G_d}$ 则被训练鉴别输入的特征是源自源域还是目标域, 得益于梯度反转层GRL^[13], 特征提取器和域鉴别器能够同时训练. 域对抗神经网络的整体损失函数如下:

$ \begin{split} L\left( {{\theta _f}, {\theta _y}, {\theta _d}} \right) =& \frac{1}{{{n_s}}}\sum\limits_{{{{x}}_i} \in {D_s}} {{L_y}} \left( {{G_y}\left( {{G_f}\left( {{{{x}}_i}} \right)} \right), {y_i}} \right) \\ & - \frac{{{\lambda _2}}}{{{n_s} + {n_t}}}\sum\limits_{{{{x}}_i} \in \left( {{D_s} \cup {D_t}} \right)} {{L_d}} \left( {{G_d}\left( {{G_f}\left( {{{{x}}_i}} \right)} \right), {d_i}} \right) \end{split} $

(4)

其中, ${G_y}$ 表示类别标签分类器, ${L_y}$ 和 ${L_d}$ 分别表示标签分类损失和域鉴别损失, ${\lambda _2}$ 是一个权衡参数, ${\theta _f}, {\theta _y}, {\theta _d}$ 分别表示 ${G_f}, {G_y}, {G_d}$ 的参数. 域对抗适应网络是一个无监督的方法, 因此目标域数据没有标签, ${d_i}$ 表示输入样本的域标签 (当 ${d_i}$ 为0时表示来自源域, ${d_i}$ 为1时表示来自目标域). 当训练达到收敛状态, 参数 ${\hat \theta _f}, {\hat \theta _y}, {\hat \theta _d}$ 将会使下式达到平衡状态:

$ \left( {{{\hat \theta }_f}, {{\hat \theta }_y}} \right) = \arg {\min _{{\theta _f}, {\theta _y}}}L\left( {{\theta _f}, {\theta _y}, {\theta _d}} \right) $

(5)

$ {\hat \theta _d} = \arg {\max _{{\theta _d}}}L\left( {{\theta _f}, {\theta _y}, {\theta _d}} \right) $

(6)

2.2.2 ToSAN的具体组成

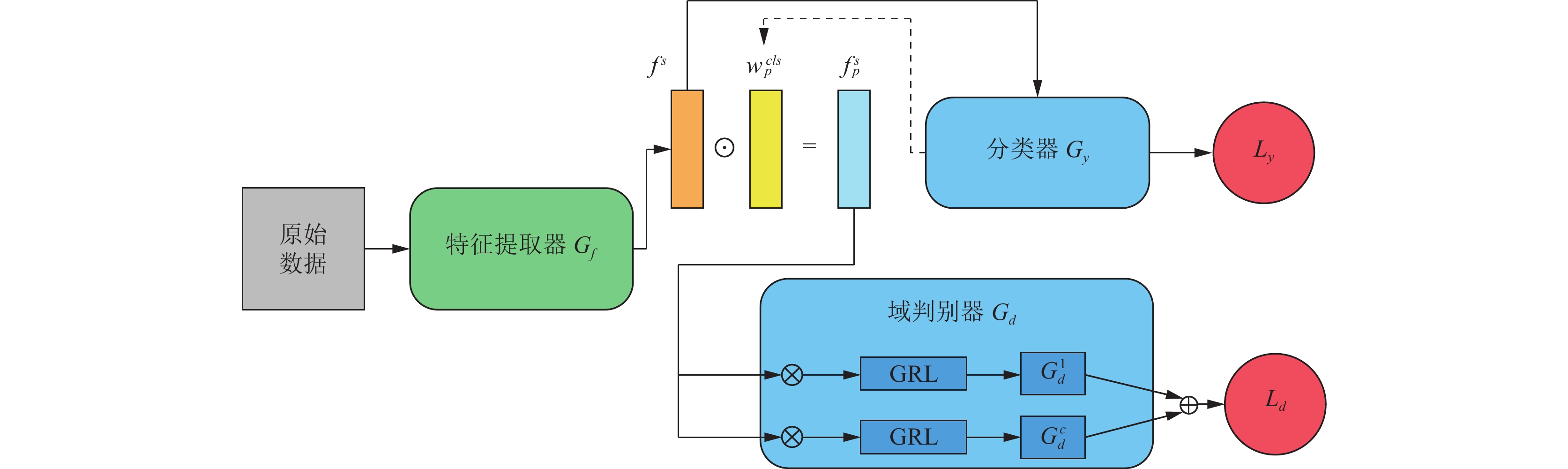
ToSAN的具体框架如图2所示. 主要包含以下几个组件.

(1)特征提取器 ${G_f}\left( {{\theta _f}} \right)$ , 这里本文使用MMCNN^[1]作为脑电信号特征提取网络.

(2)分类器 ${G_y}\left( {{\theta _y}} \right)$ , 用于对提取后的特征进行分类. 现有迁移方法, 如MSDAN^[28]、MTDANN^[30]等仍然把运动想象任务看作无监督的任务, 实际在任务进行过程中, 运动想象的实验范式保证了这是一个有监督任务. 图3展示了运动想象的具体实验流程. 如图3所示, 每个运动想象试次都由一个中央注视点开始, 接着是线索呈现, 然后是被试的运动想象, 最后是一个休息. 呈现的线索代表着实验设计者想要被试进行的具体的运动想象任务类型. 假设有4种类型的线索提示, 总共120个试次, 每种类型进行30个试次, 在实验开始前设计好120个试次对应的类型顺序, 这样我们就获得了120个试次的标签信息, 无论是离线还是在线场景, 实验者都能获取试次的标签信息. 所以在进行运动想象任务的过程中, 能够同步获取具体试次的标签. 因此分类器能够获取源域和目标域的标签信息, 其训练的损失函数如下:

$ \begin{split} {L_y} =& - \frac{1}{{{n_s}}}\sum\limits_{{{{x}}_i} \in {D_s}} {\sum\limits_{c = 1}^C {{P_{{{{x}}_i} \to c}}} } \log {G_y}\left( {{G_f}\left( {{{{x}}_i}} \right)} \right) \\ & - \frac{1}{{{n_t}}}\sum\limits_{{{{x}}_i} \in {D_t}} {\sum\limits_{c = 1}^C {{P_{{{{x}}_i} \to c}}} } \log {G_y}\left( {{G_f}\left( {{{{x}}_i}} \right)} \right) \end{split} $

(7)

其中, $C$ 是类别个数, ${P_{{{{x}}_i} \to c}}$ 是 ${{{x}}_i}$ 属于类别 $c$ 的概率.

(3)域判别器 ${G_d}\left( {{\theta _d}} \right)$ , 包含了 $C$ 个子域判别器, 用于进行条件分布适配. 子域判别器用于判断输入的每一类的特征来自源域还是目标域, 其训练损失函数如下:

$ {L_l} = \frac{1}{{{n_s} + {n_t}}}\sum\limits_{c = 1}^C {\sum\limits_{{{{x}}_i} \in {D_s} \cup {D_t}} {L_d^c} } \left( {G_d^c\left( {\hat y_i^c{G_f}\left( {{{{x}}_i}} \right)} \right), {d_i}} \right) $

(8)

其中, $G_d^c$ 和 $L_d^c$ 是类别 $c$ 的域判别器以及其交叉熵损失. $\hat y_i^c$ 是在输入样本 ${{{x}}_i}$ 的基础上预测为类别 $ c $ 的可能性, ${d_i}$ 是输入样本 ${{{x}}_i}$ 的域标签.

还有其他一些符号解释如下, 图2中 $ \oplus $ 表示相加操作, $ \otimes $ 是乘法操作. ${f^s}$ 是特征提取网络提取出的特征, ${L_y}$ 和 ${L_d}$ 分别是分类损失以及域损失. 以往的方法大多专注于特征在源域和目标域之间的整体对齐, 但实际上这种域对齐不直接服务于分类任务. 通过特征分解, 分解出对分类任务有关的特征, 然后在这些特征上进行进一步对齐. 借鉴于ToAlign^[31], 从骨干网络得到特征向量 ${f^s} \in R_ + ^{T \times C}$ , 其中 ${f^s}$ 表示非负的张量, $T$ 表示时间序列长度, $C$ 为通道数. 将源域样本的特征向量 ${f^s}$ 重新加权获得任务相关特征向量 $f_p^s$ , $w_p^{cls}$ 是加权系数. $w_p^{cls}$ 由式(9)获得:

$ {w^{cls}} = \frac{{\partial {y^c}}}{{\partial {f^s}}} $

(9)

其中, ${w^{cls}} \in {R^C}$ , ${y^c}$ 是预测为类别 $c$ 的预测分数. ${w^{cls}}$ 作为一种通道注意力机制, 有助于捕获和分类相关的特征.

$ {f_p} = w_p^{cls} \odot {f^s} = {\textit{z}}{w^{cls}} \odot {f^s} $

(10)

其中, $ \odot $ 表示逐元素点积, $w_p^{cls} = {\textit{z}}{w^{cls}}$ , ${\textit{z}}$ 是一个调整因子用来调节 $\mathcal{E}\left( {{f_p}} \right) = \left\| {{f_p}} \right\|_2^2$ , 使得 $\mathcal{E}\left( {{f_p}} \right) = \mathcal{E}({f^s})$ . ${\textit{z}}$ 的计算公式如下:

$ {\textit{z}}=\sqrt{\frac{\Vert {f}^{s}{\Vert }_{2}^{2}}{{\Vert {w}^{cls}\odot {f}^{s}\Vert }_{2}^{2}}}=\sqrt{\frac{{\displaystyle \sum _{c=1}^{C}{({f}_{c}^{s})}^{2}}}{{\displaystyle \sum _{c=1}^{C}{\left({w}_{c}^{cls}{f}_{c}^{s}\right)}^{2}}}} $

(11)

3 实验结果与分析

本节将在BCI Competition IV 2a和BCI Competition IV 2b数据集上比较ToSAN算法与其他迁移算法, 验证ToSAN算法的有效性. 在实验中, 不同的被试将作为源域或者目标域, 所提出的ToSAN方法也将在源域和目标域被试上进行迁移. 此外, 本文还比较了一些源域选择算法, 评估了本文所提出的源域选择算法MSTE的有效性. 考虑到源域选择算法可能对迁移方法的结果存在一定技巧的影响, 本节先介绍了迁移方法, 并用随机期望这一指标评估了迁移方法的有效性, 然后再在迁移方法上应用了源域选择方法.

3.1 实验环境和参数设置

实验过程中所使用的软硬件环境配置如下: 中央处理器: Intel(R) Xeon(R) Gold 6240R CPU @ 2.40 GHz; 显卡: Tesla V100s-PCIE-32 GB; 内存: 250 GB; 操作系统: Ubuntu 18.04LTS. 本节的所有的深度迁移方法均采用相同的实验参数, 批量大小为128, 最大的epoch数量为500, 并设置早停技术防止过拟合, 早停阈值数目为30. 选用随机梯度下降方法(SGD)作为优化器. L2正则惩罚项被用于防止模型过拟合, 具体数值为0.000 5. 考虑到随机梯度下降方法的训练收敛速度较慢, 以及可能掉入局部极值点, 不能找到全局最优极值点, 本文在SGD的基础上增加了动量(momentum), 并设置动量值为0.9. 初始学习率是0.001, 并按式(12)进行迭代:

$ lr = \frac{\omega }{{{{\left( {1 + 10\delta } \right)}^\beta }}} $

(12)

其中, $\omega $ 是初始学习率, $\delta $ 是当前迭代轮次与总迭代次数的比值, $\;\beta = 0.75$ . 为了增加实验的可复现性, 随机数种子被固定设置为2 022.

3.2 数据集

在本节实验中总共用到了如下两个数据集.

(1) BCI Competition IV 2a数据集: 从 9 名健康被试中收集, 其中包含 4 种不同的运动想象任务(分别是左手、右手、双脚和舌头的运动想象). 具体实验流程图如图3所示, 对于每个任务, 由1.25 s的线索提示和3 s的运动想象组成, 这里我们选择由线索提示和运动想象组成的4 s任务时间进行分析. 实验由22个 Ag/AgCl电极记录, 采样频率为250 Hz. 此外, 信号在 0.5 Hz和100 Hz之间进行带通滤波. 每个被试有2个时间分段. 每个时间分段由6次运行组成. 因此, 每个被试有576个试次, 总共有5 184试次.

(2) BCI competition IV 2b数据集: 采集自9名健康被试, 与BCI Competition IV 2a数据集相比, BCI Competition IV 2b数据集考虑了2种不同的运动想象任务(左手和右手运动的想象). 另外, 不同的是每个被试有5个时间分段. 前两个时间分段没有反馈. 每个时间分段包含120个试次. 最后3个时间分段有反馈, 每个时间分段包含160个试次. 这里我们也选择了由线索提示和运动想象组成的4 s任务时间进行分析. 实验由3个Ag/AgCl 电极记录, 分别为C3、Cz和C4. 采样频率和带通滤波器与BCI Competition IV 2a数据集相同. 总共有6 480个试次.

在本节实验中, 两个数据集均选取左右手的运动想象任务数据.

3.3 实验设置

为了验证已有迁移算法和提出的ToSAN算法的有效性, 本文针对BCI Competition IV 2a和BCI Competition IV 2b数据集中的9个被试每2个被试进行了双向跨被试实验. 总共有 ${\rm{A}}_9^2 = 72$ 个分类任务, 例如S1→S2 (被试1作为源域, 被试2作为目标域), S1→S3, S1→S9, …, S9→S8. 对于本文提出的ToSAN, 使用MMCNN^[1]作为骨干网络提取特征. 两个数据集都按照7:3的比例划分为训练集和测试集, 每一个被试都有70%数据在训练集中, 30%数据在测试集中.

本文提出的源域选择算法与如下方法进行了比较: DTE^[26]、Symmetrical KL^[32] 、ROD^[24]、1-Wasserstein Distance、2-Wasserstein Distance、最差选择、随机选择期望. 本文进行比较的源域选择算法具体如下.

(1) DTE^[26]: 一个经典的基于脑电信号的运动想象任务的源域选择算法. DTE是一种在无监督场景下对二维数据( $C \times T$ )的相似度进行评估的算法. 考虑到脑电信号是3维数据( $N \times C \times T$ ), 其中 $C$ 表示通道数, $T$ 表示采样的时间点数, $N$ 表示样本数, 将每个样本的通道数都压缩成1来降维, 目前的做法是将某一采样点时间上的所有通道都加在一起.

(2) Symmetrical KL^[32]: 一种经典的相似性度量算法. 对称形式的KL散度作为距离度量. 最短的距离作为相应的源域选择算法结果.

(3) ROD^[24]: 第1个经典的源域选择算法.

(4) 1-Wasserstein Distance: 一种经典的相似性度量算法. 用1阶推土机距离作为源域和目标域的距离度量. 最短的距离作为相应的源域选择算法结果.

(5) 2-Wasserstein Distance: 一种经典的相似性度量算法. 用2阶推土机距离作为源域和目标域的距离度量. 最短的距离作为相应的源域选择算法结果.

(6)最差选择: 根据提出的源域选择算法MSTE选出的最差下限结果.

(7)随机选择期望: 所有源域和目标域被试组合的分类结果平均值.

本文提出的ToSAN方法与如下方法进行了比较: MMCNN^[1]、joint distribution adaptation (JDA)^[33]、multi-subdomain adaptation network (MSDAN)^[28]、manifold embedded knowledge transfer (MEKT)^[26]、PS-RCSP-wAR^[18]. 本文进行比较的迁移算法具体如下.

(1) MMCNN^[1]: 一种非迁移的深度神经网络用于运动想象的脑电信号分类. 作为JDA、MSDAN以及ToSAN的特征提取网络.

(2) JDA^[33]: JDA同时考虑了边缘分布适配和条件分布适配. 由MMCNN^[1]提取出来的脑电信号特征作为输入.

(3) MSDAN^[28]: 一种用于运动想象脑电信号分类的深度迁移算法. 由MMCNN^[1]作为骨干网络提取运动想象任务的脑电信号特征.

(4) MEKT^[26]: 一种基于流形的传统迁移算法.

(5) PS-RCSP-wAR^[18]: 融合了PS、RCSP以及wAR三种方法的迁移方法.

本文使用准确率作为模型性能的评价指标. 准确率的计算公式如下:

$ ACC = \frac{{TP + TN}}{{TP + TN + FP + FN}} $

(13)

其中, $TP$ 是正例预测正确的个数, $TN$ 是负例预测正确的个数, $FP$ 是正例预测错误的个数, $FN$ 是负例预测正确的个数.

3.4 实验结果

ToSAN以及其他对比的方法在BCI Competition IV 2a和BCI Competition IV 2b数据集上的分类结果都呈现如下. 表1和表2分别展示了ToSAN在BCI Competition IV 2a和BCI Competition IV 2b数据集上8×9=72个配对迁移结果. 每个迁移结果都是由源域被试迁移到目标域被试. 表2的每一列代表目标域被试, 每一行代表源域被试. 对于每个目标域被试, 最佳的源域被试对应的迁移结果都用加粗表示.

表3展示了JDA, MSDAN, MEKT, PS-RCSP-wAR以及ToSAN在BCI Competition IV 2a和BCI Competition IV 2b数据集上的随机期望准确率. 这里随机的含义是对于每一个目标域被试, 随机选择一个非本身的源域被试进行迁移, 而随机期望表示所有目标域被试的迁移结果的期望值即将每个源域迁移到目标域的结果取平均.

表4和表5分别展示了源域选择算法在BCI Competition IV 2a和BCI Competition IV 2b数据集上的结果. 表4和表5的第1行1–9数字表示目标域序号, 随后几行分别给出了对于每一个目标域, 每种源域选择方法下的源域选择结果. 表4和表5最后一列展现了ToSAN与各种源域选择算法结合后的平均准确率. 不难看出本文所提出的源域选择算法在两个数据集上均表现优异, 优于所有比较的算法, 进一步证明了本文提出的方法的优越性.

3.5 消融实验

为了进一步说明迁移方法和源域选择方法成分的有效性, 本文进行了深入的消融实验. 图4依次对ToSAN的成分进行消融实验, 可以看出, 随着任务导向的特征对齐, 目标域标签信息逐步去除, ToSAN在BCI Competition IV 2a和BCI Competition IV 2b数据集上的随机期望准确率也在逐步下降, 说明每一个成分都必不可少, 都对分类结果产生积极影响.

本文提出的源域选择方法MSTE含有两个部分, 一个是时间和类的混合距离, 还有一个是源域内同一类不同时间之间的距离, 图5展现了仅有时间与类的混合距离作为源域选择方法在BCI Competition IV 2a和BCI Competition IV 2b数据集上的结果以及完整的源域选择方法在BCI Competition IV 2a和BCI Competition IV 2b数据集上的结果. 显然, 完整的源域选择算法的性能更加优秀, 说明源域选择算法各个成分的有效.

3.6 收敛性分析

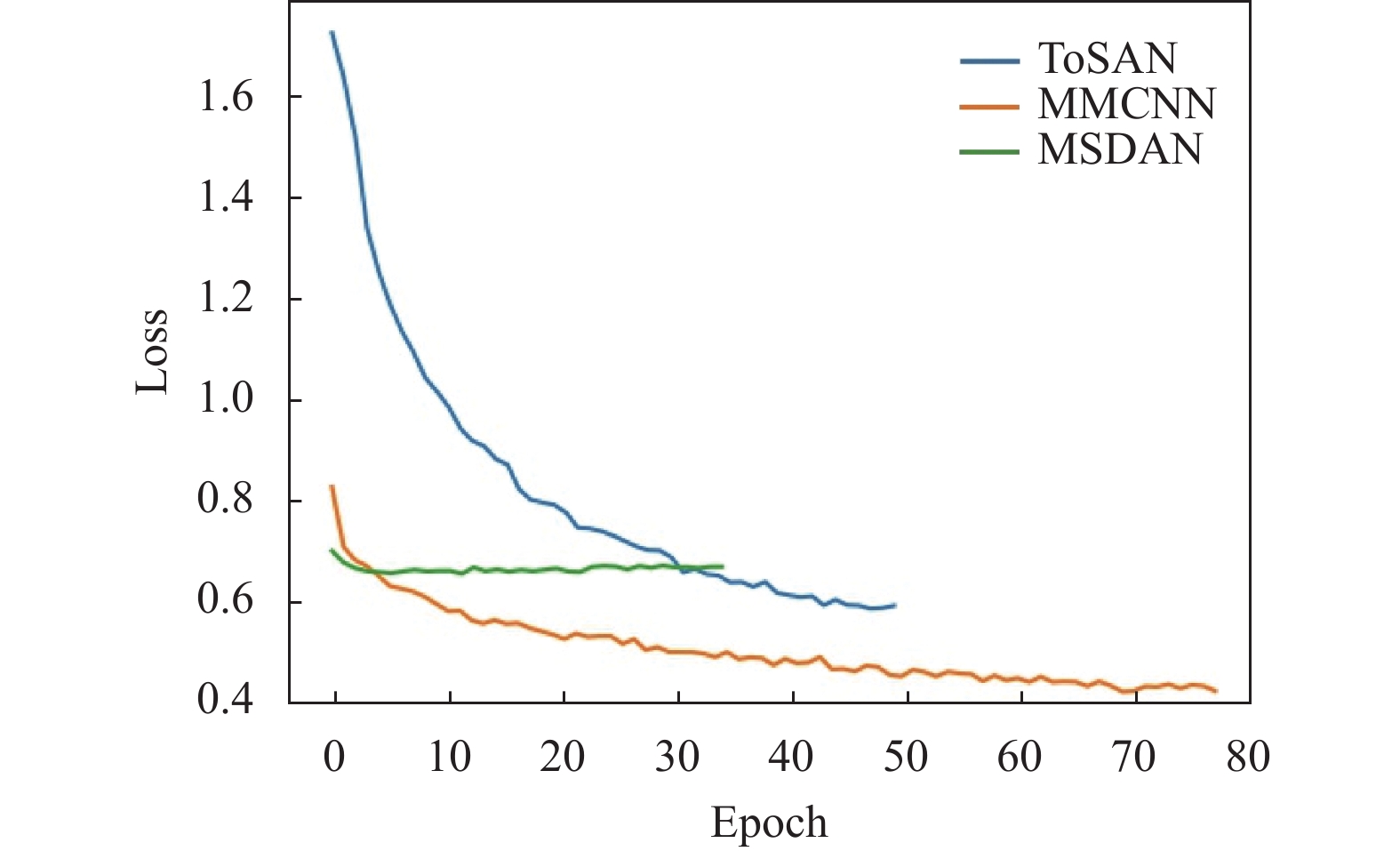
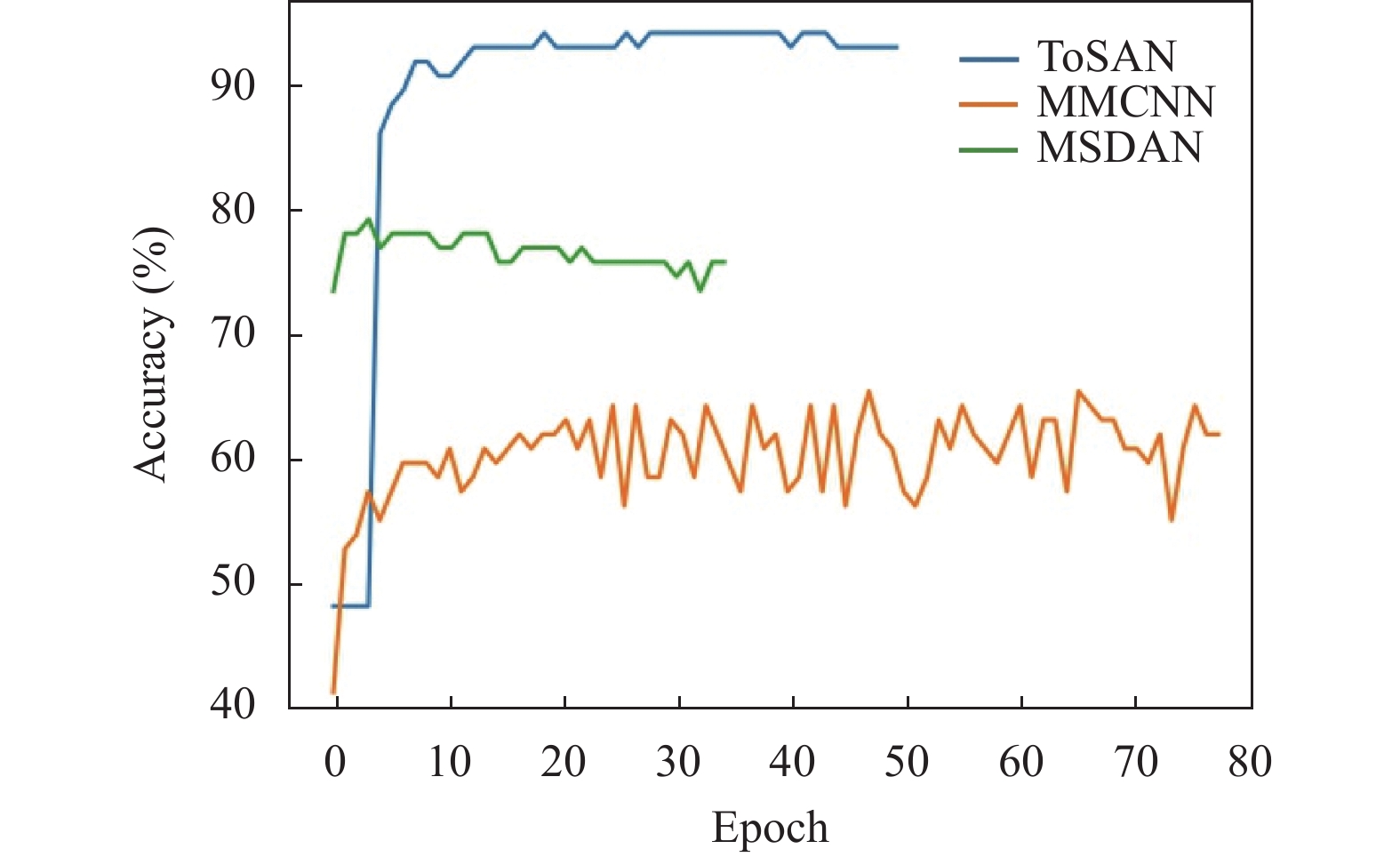
此外, 本文给出了ToSAN的收敛性相关分析, 以BCI Competition IV 2a数据集上被试4到被试3的迁移为例, 其训练损失曲线和测试准确率曲线如图6和图7所示. 从图6和图7可以看出, 在相同的迭代次数下, ToSAN比MMCNN^[1]和MSDAN^[28]收敛得更快更稳. 值得注意的是, 相比于其他方法, MMCNN在训练过程中只用到了源域数据, 而在测试过程中使用了目标域数据. 由于源域数据和目标域数据分布并不完全相同, 会导致图中MMCNN的训练集损失收敛曲线较低, 同时测试集准确率不高的情况. 图6和图7结果表明, 所提出的ToSAN不仅可以达到良好性能, 而且可以很容易地训练出稳定的结果.

4 结论与展望

在这项工作中, 对于运动想象的脑电信号分类任务, 本文提出了一个新的迁移算法ToSAN和一个新的单源域选择算法MSTE. ToSAN使用了对抗域神经网络作为基础网络框架, 在迁移的过程中不仅利用了源域的信息还有效利用了目标域的标签信息. ToSAN细化了以往特征迁移的粒度, 把源域的特征进行分解, 筛选出与分类任务有关的特征, 然后在此基础上对这些特征进行对齐, 忽略和分类无关的特征. 新的源域选择算法MSTE同时考虑了时间和类别子域上源域和目标域的距离, 以此作为源域选择的依据. ToSAN与MSTE两个算法相辅相成. 为了验证所提出的ToSAN以及MSTE的有效性, 本文在2个经典的运动想象数据集BCI Competition IV 2a和BCI Competition IV 2b上进行了细致全面的实验. 实验结果表明ToSAN算法优于所有比较的算法, 提出的源域选择算法MSTE也优于其余的算法, 两者结合, 分类效果突出.

在未来的工作中, 将ToSAN和MSTE方法扩展到更多的运动想象数据集上是一个实际可行的目标. 更进一步地, 将这些运动想象方法扩展到其他脑机接口范式的数据集中则是一个具有挑战性的目标.