2. 四川省机械研究设计院(集团)有限公司, 成都 610041
2. Sichuan Machinery Research & Design Institute (Group) Co. Ltd., Chengdu 610041, China
随着计算机技术的快速发展, 人机交互(HMI)系统也越发趋于智能化、数字化, 并广泛应用于航空航天、医疗、家电、核电等领域. 但由此带来的是人机交互界面的信息量不断增加, 操作员则通常需要在较短的时间内加工信息并做出正确的反应和决策, 容易造成过高的脑力负荷进而影响任务的可靠性和安全性.
脑力负荷也被称作为心理负荷或者认知负荷, 是指任务期间的大脑资源利用率, 反映了人在工作中的精神状态[1]. 现有的研究表明, 认知资源与脑力负荷有着非常密切的联系, 认知负荷理论由Sweller等人最先提出, 主要体现在人的工作记忆的容量是有限的, 如果各种认知加工活动所需要的认知资源超过了人所具有的认知资源的总量, 便会造成认知负荷[2].
现有的关于脑力负荷的评估方法主要有主观量表法、任务绩效法和生理参数法3种. 其中主观量表法在实际测量中使用最多的是NASA开发的NASA-TLX[3]量表, 它通过脑力需求、体力需求、时间需求、主观绩效、努力程度、挫败感这6个维度来综合评估, 最终结果是6个维度的分值与其权重加权求和. 主观量表法的缺陷主要有: 评价结果有偏差; 方法应用存在局限性; 评价结果易混淆. 任务绩效法分为主任务绩效法和辅助任务绩效法, 任务绩效法的缺陷在于任务和个体的参照性弱, 因而在实际的研究中采用得较少. 生理测量法通过记录生理指标数据来客观地反映用户完成任务的状况, 不会干扰实验, 且可以连续地记录信息的, 常用的生理信号有脑电(EEG)、心电(ECG)、眼电(EOG). 脑电信号具有高时间分辨率、非侵入式的特点, 并且现有研究表明EEG在脑力负荷这方面可以比眼部, 外周生理提供更加丰富的信息, 是当前使用最为广泛、灵敏度最高的一种手段[4].
时域特征指的是从EEG的时间序列中包含的特征信息, 事件相关电位(ERP)是脑力负荷评估最常用的, 相关的成分一般包含P300[5]等. 虽然ERP特征相对直观, 但是需要多个时间点信息描述, 特征维数高[6].
频域是时域经过傅里叶或者小波等变换得来的. 与脑力负荷一般高度相关的频段有θ(4–8) Hz, α(8–13) Hz, β(13–30) Hz. 有学者发现低顶叶部位的α波段功率的降低和额叶部位的θ波功率增加有关[7]. β波段和γ波段能量的增加则与更高的任务需求相关[8].
脑力负荷研究的一大关键点是建立关于脑力负荷分类模型, 早期主要是利用判别分析、回归分析等传统的统计学方法[9-11]. Blanco 等人对比了 13 种不同的分类器, 并使用了嵌套的十倍交叉验证方法来估计分类模型的泛化性能, 最终发现在模拟飞行环境的任务中, 利用线性判别分析(LDA)进行脑力负荷分类会取得最好的分类结果, 此外, 特征集合和学习器的个性化组合可以有效地提高模型的分类精度[12]. 支持向量机(SVM)是一种广义的二元分类器, Garrett 等人通过对比发现, 在利用 SVM、LDA 以及对脑力负荷进行分类时, 应用 SVM 算法的分类模型准确率更高[13]. 张洁等人采集了被试在低、中、高这3种负荷条件下的脑电数据, 以其功率谱密度作为输入特征, 结合 SVM算法训练出了准确可靠的脑力负荷分类模型[14].
传统的机器学习方法需要手工制作特征, 而深度学习则可以从数据中自动提取特征, 且能够学习到相比于手工提取更为高级的特征, 因此在基于EEG的脑力负荷研究中流行起来. Almogbel等人采集驾驶员在不同工况模拟场景下驾驶的脑电信号, 使用卷积神经网络对其进行训练[15], 得到了良好的分类效果. Lee等人提出了一种多特征块的卷积神经网络(multiple feature block-based convolutional neural network)来识别模拟飞行环境下的飞行员的疲劳、脑力负荷、分心以及正常的4种心理状态[16].
本文亦采用深度学习的方法, 在卷积神经网络EEGNet的结构上进行改进, 将原来的单个卷积核串行改进为多个卷积核并行由此来学习到更多的特征, 并添加SENet模块在自建的被试数据测试集上实现3类n-back范式脑电信号的准确分类, 并与现有的EEG的深度学习分类模型在测试集上作性能对比.
2 数据采集及预处理本文使用64通道脑电设备在n-back实验范式下采集脑电数据, 并使用Matlab中的eeglab工具包进行预处理获得模型训练的数据.
2.1 n-back范式n-back范式是诱发不同水平脑力负荷的常用范式[17, 18], 它需要被试者将当前呈现的信息与n个之前呈现的信息进行比较并作出相应判断, 而通常n值的增大意味着脑力负荷的增大. 基于目前大多数研究仅有视觉或者仅有听觉的n-back任务维度较为单一的问题, 本实验设计同时采用了听觉与视觉的刺激来使得诱发脑力负荷的过程更加完整. 听觉的任务需要将当前听到的数字与n个之前的作比较, 视觉的任务需要将蓝色小方块在九宫格的位置与n个之前的位置作比较.
已有研究指出n-back主要用于成年人工作记忆训练[19, 20], n-back任务具有一定难度尤其是当n>1时, 并且该实验需要n-back诱发一定的脑力负荷, 因此试验选取8名20–25岁的智力正常, 身体健康的年轻人作为研究对象, 其中男性和女性各占一半. 试验过程中需要避免有较大肢体运动且尽量减少吞咽眨眼等动作, 受试者需要在正式实验之前接受训练熟悉n-back的记忆模式并能够达到一定的准确度. 实验中播放的数字和显示的九宫格图持续时间为500 ms, 两次刺激间隔为3 s, 在整个实验过程中目标所占比大概为50%. 每名被试需要完成3个系列, 每个系列又包含听觉的2-back, 听觉的3-back, 视觉的2-back三类范式如图1所示, 红色为目标. 被试人员每个系列的准确度必须达到80%才记作有效试次否则将重新实验.

|
图 1 试验中的3类n-back范式 |
每类范式的出现的次数大致相等, 这样保证了3类样本的均衡性. 为避免持续较高脑力负荷给被试者会带来的疲劳与不适让其能顺利完成整个实验, 每类范式结束后被试者有1 min的休息时间, 而在每个系列结束后有2 min的休息时间.
2.2 数据预处理脑电数据采集使用的是ANT Neuro公司的eego设备, 总共有64通道, 电极材料为Ag/AgCl, 其电极分布遵循的是国际10-20标准. 但64通道数据量在预处理时计算效率低, 故根据常用的32通道模板选取了其中的29个通道, 其分布如图2所示.
数据预处理使用的工具包是eeglab2020. 数据预处理的流程如图3所示.
首先是对电极进行定位, 图1已展示, 选用的参考电极是双侧乳突M1和M2; 然后对raw data使用0.5–40 Hz的巴特沃斯带通滤波器去除掉直流信号和高频信号; 巴特沃斯滤波器可以使用式(1)表示振幅的平方与频率的关系: 其中n是滤波器的阶数, ωc是截止频率, ωp是通频带边缘频率.
| |H(ω)|2=11+ε2(ωωp)2n | (1) |

|
图 2 29电极分布2d图 |

|
图 3 EEG数据预处理流程 |
接着是将数据进行降采样到128 Hz减少数据量; 试验时在n-back任务出现匹配目标时打下标记, 因此接着根据标记提取epochs将连续的EEG数据进行分段, epochs区间取[−1, 2] s, 并进行基线矫正; 通过独立成分分析(ICA)列出数据的所有成分, eeglab中的扩展包AAR可识别出哪些大概率是伪迹由此过滤掉这些伪迹成分, 常见的伪迹干扰有心电, 眼电, 肌电等. ICA的原理如下文所述. 原信号可以认为是所需脑电信号和噪声的线性混合, 从原数据分离出干净的脑电数据称为盲源分离, 可通过式(2)表示:
| x=As | (2) |
其中, x是观测到的多通道信号, s是原始的多通道信号, A是混合矩阵, 对于此问题关键在于求解A的逆矩阵W, 使得变换后的结果y趋于源信号s如式(3)所示:
| y=Wx=WAs≈s | (3) |
对于某一具体通道yi则有:
| yi=WTiAs | (4) |
下一步则是通过电压极值来过滤掉一些不良epochs; 最后对各个电极的数据进行检测判断, 坏电极则进行插值修补.
2.3 ERP分析由于n-back任务也是外加一种特定刺激来实现的, 所以可以进行事件相关电位(ERP)的分析. 以出现刺激为时刻的零点, 取[−1, 2]将3类n-back范式的在此时间区域进行数据的平均叠加. 得到3类n-back范式各自的29个通道的ERP波形以及某些时刻的脑地形图如图4所示.

|
图 4 ERP及脑地形图 |
对3种n-back范式对比分析, 在听觉上数字的2-back记忆和3-back记忆的ERP及脑地形图较为相似, 但3-back的波峰延后而波谷提前, 说明其加工信息的时间更为集中. 而同为2-back任务的基于听觉的数字记忆和基于视觉的位置记忆, 两者的波峰波谷出现的时刻相对于零点则是相反的. 若采用传统的机器学习模型如SVM则需手动输入3类范式的ERP特征; 而CNN则可以通过卷积操作自动提取.
3 网络模型深度学习表现出了优秀的泛化性能, 但是需要充足的数据量并且会耗费较大的计算资源. 因此Lawhern等人设计出了一种轻量紧凑的用于EEG分类的卷积神经网络EEGNet[21], 在有限的数据集上依然有较高的分类准确率. 但由于该模型使用串行的卷积模式并且未区分不同特征的重要程度, 本文拟基于EEGNet进行改进, 以此提升在自建的数据集上的分类效果.
脑电数据集的通道数为C, 1个epochs中的样本点数为T, 输入的数据
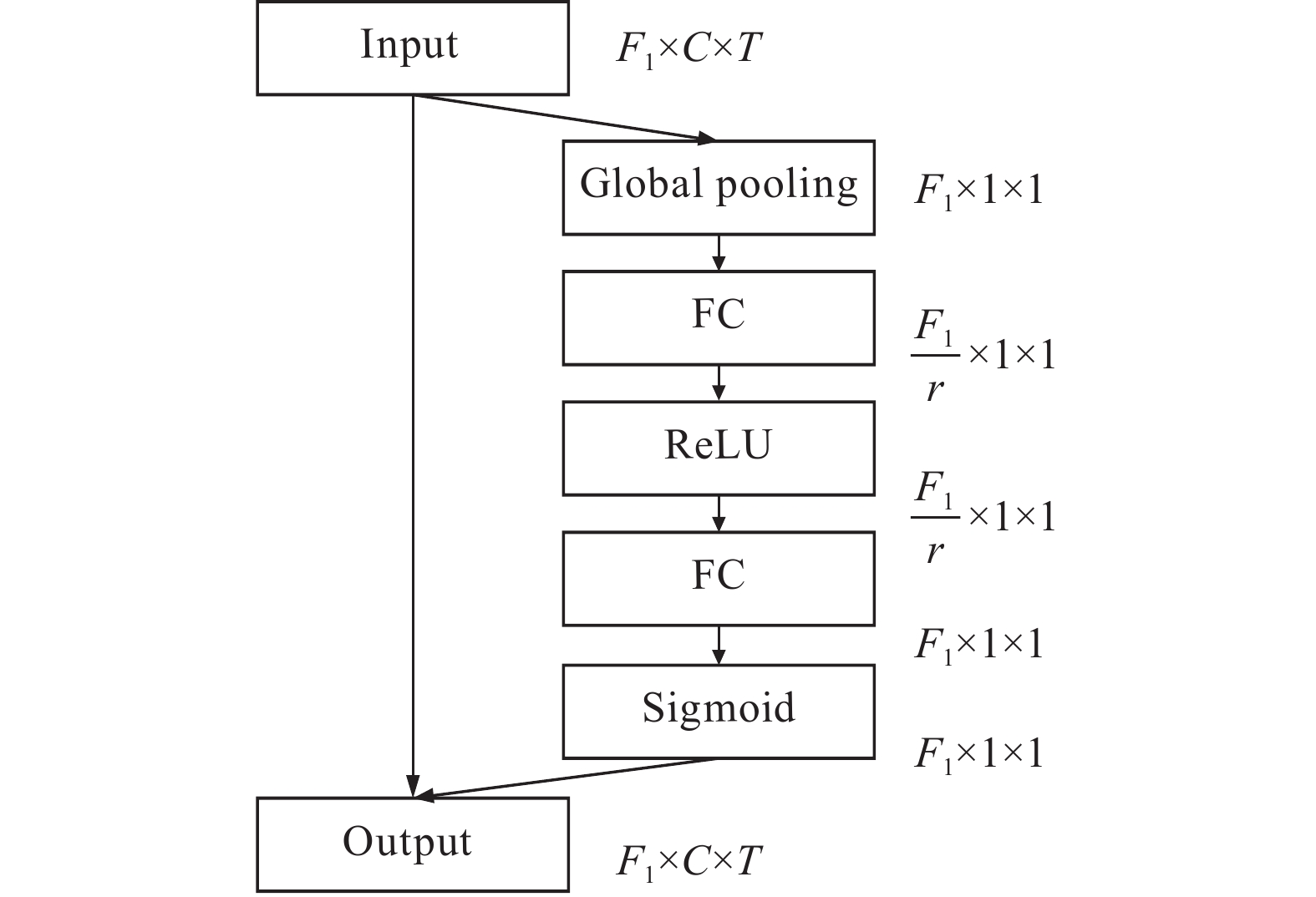
注意力机制是为了突出显著有用的特征而去抑制或者忽略掉无关特征. 在Conv2D输出的结果后面添加SENet (squeeze and excitation)模块如图5所示. Squeeze是通过全局平均池化来完成的:
| Fsq(uc)=1H×WH∑i=1W∑j=1uc(i,j) | (5) |
经压缩后的size为(8, 1, 1). 接着进行的是excitation的操作, 通过两个全连接层对应的激活函数分别是ReLU和Sigmoid.
| s=σ(g(z,W))=σ(W2δ(W1z)) | (6) |
其中, s是权重, 将其赋给uc即完成最后的权重更新.
| ⌣Xc=Fscale(uc,sc)=uc×sc | (7) |
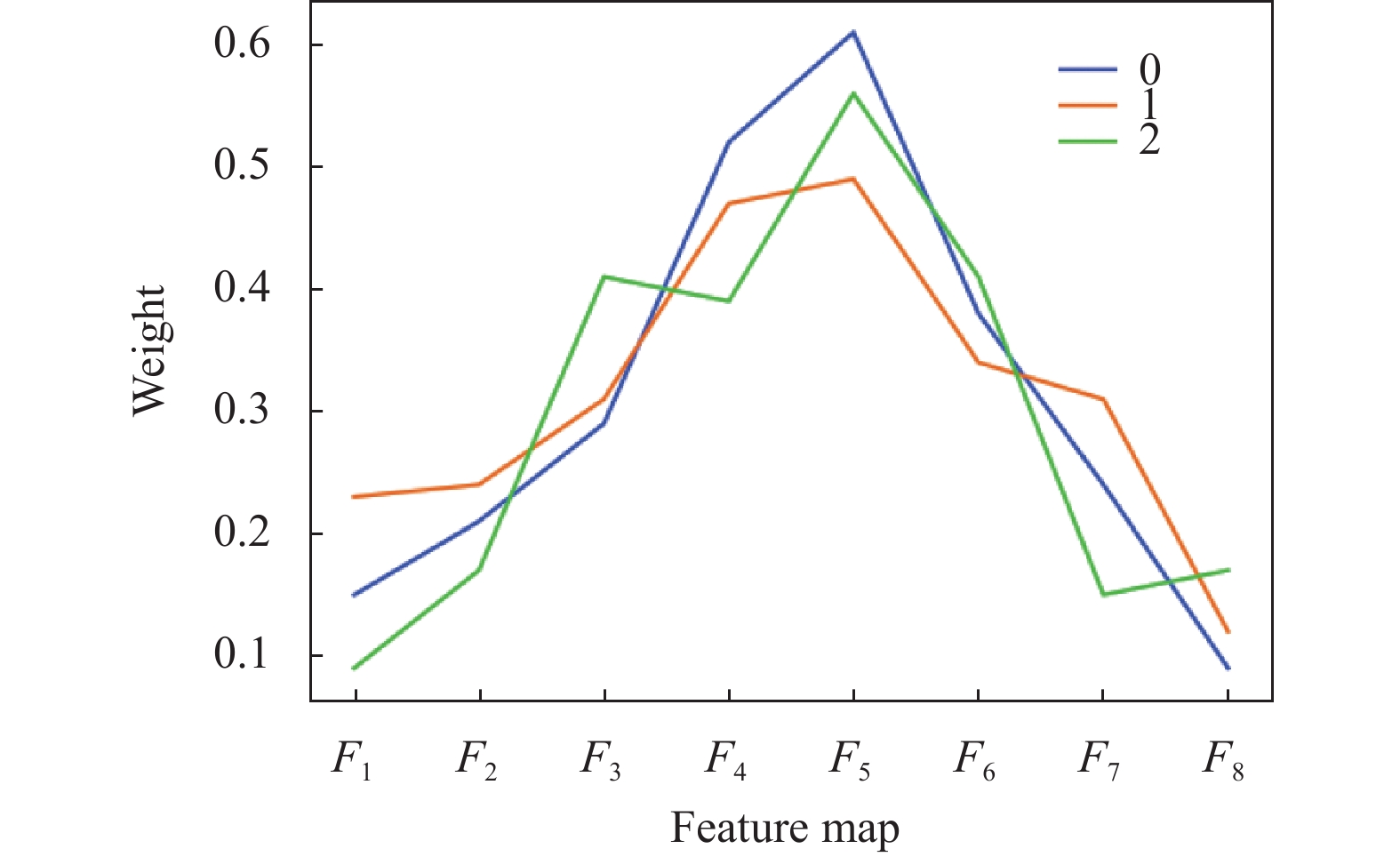
图6展示了各个feature map的权重分布, 经Sigmoid函数激活后值均在0–1之间. 它体现了特征与各个类别的相关性, 即权重越大特征与标签的相关性越高. 由图6可知, 3类n-back范式中, 中间的feature map对最终分类结果的贡献较大, 而两端的贡献较小.
|
图 5 SENet模块 |
|
图 6 Feature map权重分布 |
然后执行的是深度卷积(depthwise convolution)操作用来学习空间滤波器, 其卷积核的大小为(C, 1), 其特点是只改变feature map的大小不改变通道数. 深度参数D控制每个特征映射要学习的空间滤波器的数量, 一般取值为2. 深度卷积的主要好处是减少了拟合的可训练参数的数量, 因为这些卷积并没有完全连接到所有先前的特征映射. 该操作同时提供了一种为每个时间滤波器到空间滤波器的学习方法, 从而让空间滤波器能够提取到特定频率的特征. 对应两个卷积未使用非线性激活函数, 是由于在使用非线性激活时性能没有显著提高. 之后, 沿着特征图维度应用批量归一化. 归一化后的激活函数选择的是ELU, 其计算公式如式(8)所示:
| f(x)={x,x⩾0α(ex−1),x<0} | (8) |
输入大于0部分的梯度为1, 输入小于0的部分无限趋近于−α, 超参数取值一般为1. 使用Dropout概率为0.5. 接着进行卷积核大小为(1, 4)的平均池化操作, 将信号的采样率降低到32 Hz, 同时通过对每个空间滤波器的权值使用1的最大范数约束对其进行正则化.
在block2用的是可分离卷积(separable convolution), 其实际上是depthwise convolution和pointwise convolution的组合. Depthwise convolution的卷积核大小为(1, 16), 代表在32 Hz上的500 ms的脑电图活动. Pointwise convolution的特点是使用大小为(1, 1)的卷积核, 不改变feature map的大小只改变通道数. 设置pointwise convolution的卷积核数量F2 = D×F1 (时间滤波器及其相关的空间滤波器的数量, 之后的操作类似于block1中的深度卷积后的操作: 批量归一化后用ELU激活函数, 然后进行卷积核大小(1, 8)的平均池化降采样, 仍使用dropout概率为0.5.
在分类block中, 这些特征直接传递给一个N个单元的Softmax分类, 由于是3类范式, 所以N=3. 改进后的EEGNet模型的整体架构如图7所示.
4 实验结果分析本节内容包括以下部分: 首先是对改进的EEGNet在训练集上进行训练, 再在验证集上进行参数调整得到最佳模型, 训练和验证过程的性能评价指标主要是损失函数(loss)准确率(accuracy, acc). 然后将模型与现有的EEG分类的CNN模型在测试集上的性能对比.
4.1 模型训练与验证开发环境为Python 3.7.10, 操作系统为Windows 10, 深度学习使用的框架是PyTorch 1.9.0. 损失函数选用的是Softmax计算后的交叉熵, 其公式如式(9)所示:
| L=−1MM∑c=1yiclog(pic) | (9) |
其中, M是类别的数量, yic是标签的one-hot编码, 如果该类别和样本i一样就是1, 否则为0. 训练的Batch_size设置为32, epoch设置为200, 选用的优化器为Adam如式(10)所示, θ是更新后的参数, 学习速率α设置为8E–4, 第1次估计的指数衰减率β1为9.
| θt+1=θt−η√vt+ε×mt | (10) |
第2次估计的指数衰减率β2为999. 由于3类n-back范式的数据较为均衡, 故采用的评价指标为准确率(acc)如式(3)所示:
| acc=TP+TNTP+TN+FP+FN | (11) |
其中, T/F表示预测的正确与否, F/P表示预测的结果为正例与负例. 若一个实例是正类, 并且被预测为正类, 即为真正类TP; 若一个实例是正类, 但是被预测为负类, 即为假负类FN; 若一个实例是负类, 但是被预测为正类, 即为假正类FP; 若一个实例是负类, 并且被预测为负类, 即为真负类TN. 每名被试在经预处理后约包含1000个样本, 将其按照6:2:2的比例划分为训练集、验证集和测试集. 这里随机选取的某名被试, 训练和验证过程中改进的EEGNet的loss与acc随epochs变化如图8所示. 验证集的损失函数和准确率在epochs上的变化相较于训练集都更平滑, 但两者均在100个epochs左右达到收敛, 说明数据集本身和模型的参数选择结果良好. 在EEG领域大多使用数据集的多数为几百至几千条的小样本数据, 改进EEGNet属于轻量级网络, 在此基础上设有dropout值为0.5以及对每个空间滤波器权值使用1的最大范数约束正则化来避免过拟合, 由图8可知无过拟合现象.

|
图 7 改进EEGNet的整体结构 |

|
图 8 改进EEGNet的训练与验证的loss与acc变化 |
4.2 模型评估与对比
在每名被试者脑电数据上经训练和验证得到的模型只在该被试的测试集上检验分类的acc效果, 混淆矩阵是一种直观地显示预测与实际分类结果的矩阵, 由于样本即n-back范式有3类, 所以此处的混淆矩阵为3×3的方阵, EEGNet在8名被试测试集的混淆矩阵如图9所示标签0, 1, 2分别对应3类n-back范式. 混淆矩阵的对角线元素即为测试集中实际标签与预测标签相符合的个数, 矩阵的其余的位置的元素都 是预测错误的结果. 由图9可知, 改进的EEGNet模型在不同的被试测试集上对3类n-back范式都具有良好的分类效果.

|
图 9 改进EEGNet在被试测试集的混淆矩阵 |
本文还将改进后的EEGNet与现有的常用在EEG分类的以下CNN模型在8名被试者的测试集作比, 这4种模型都运用到了滤波器组共空间模式(FBCSP)的思想. (1) FBCNet[23]包含一个新的方差层, 可以有效地聚合EEG时域信息. (2) ShallowConvNet是一种经典的浅层CNN. (3)本文的基础模型EEGNet. 4种模型的参数大小和设置如表1所示.
| 表 1 各模型参数设置 |
各个模型在8名被试的准确率acc如图10所示.
由图10可知4种模型在n-back三分类任务上均有稳定的性能, 这4种应用在EEG的CNN分类模型在8名被试测试集上的(max_acc, min_acc)分别为(84%, 74%), (79%, 66%), (72%, 65%), (69%, 63%). 本文还计算了各个模型在测试集上的Kappa系数, 其值同样反映分类准确度, 表达式如下式所示:
| Kappa=p0−pe1−pe | (12) |
表2进一步展示了各个模型的参数大小和在8名被试的测试集上的分类效果.

|
图 10 被试测试集上的模型acc对比 |
在时序滤波阶段, 改进EEGNet不同于其他列举出的模型, 使用两种不同大小的卷积核能够提取到多个尺度的特征进而增强模型的泛化能力. 添加SENet模块可通过学习权重来使模型关注重要的特征并抑制不相关的特征, 同时SENet不会对模型的计算和存储带来更大的开销.
| 表 2 模型性能对比 |
由表2可知, 改进EEGNet在并未显著增加模型参数量和提取特征的滤波器个数的情况下, 在8名被试的测试集的平均acc和平均Kappa分别为78.88%和72.36%, 均是4种模型最高, 表明改进EEGNet拥有最优的分类准确性. 同时分类acc和Kappa的标准差为2.85%和2.45%可说明在被试测试集上有较高稳定性.
在完成人机交互的主任务中, n-back范式可以充当次任务来做分心等研究, Yan等人[24]采用2-back范式的替代次要任务诱导视觉或听觉分心. 通过对22名被试的脑电图信号进行分析, 以区分驾驶员的专注状态和分心状态. 结果表明, 基于EEGNet和长短期记忆(LSTM)的3类分类平均准确率为71.1%. 本文相较与此则设计了能诱导更高脑力负荷的3-back范式并且对EEGNet做了进一步改进.
5 结论与展望本文在诱发脑力负荷的记忆任务n-back上设计了包含视觉和听觉感知的3种范式, 基于EEGNet改进, 在卷积层增添了并行卷积核来获取更多的时域及频域特征同时增添通道注意力机制(SENet)来筛选与关键特征密切相关的通道, 在8名被试测试集上取得了84%, 74%, 79%的最大、最小及平均准确率, 均高于本文提到的其他的脑电CNN分类模型. 下一步的研究内容是构建在线的脑力负荷识别系统能够实时地监测人机交互时人的脑力负荷状况来提高完成任务的安全性和可靠性.
| [1] |
Lim LG, Ung WC, Chan YL, et al. Optimizing mental workload estimation by detecting baseline state using vector phase analysis approach. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2021, 29: 597-606. DOI:10.1109/TNSRE.2021.3062117 |
| [2] |
Sweller J, Chandler P, Tierney P, et al. Cognitive load as a factor in the structuring of technical material. Journal of Experimental Psychology General, 1990, 119(2): 176-192. DOI:10.1037/0096-3445.119.2.176 |
| [3] |
Hart SG. NASA-task load index (NASA-TLX); 20 years later. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 2006, 50(9): 904-908. DOI:10.1177/154193120605000909 |
| [4] |
Kumar N, Kumar J. Measurement of cognitive load in HCI systems using EEG power spectrum: An experimental study. Procedia Computer Science, 2016, 84: 70-78. DOI:10.1016/j.procs.2016.04.068 |
| [5] |
Causse M, Fabre E, Giraudet L, et al. EEG/ERP as a measure of mental workload in a simple piloting task. Procedia Manufacturing, 2015, 3: 5230-5236. DOI:10.1016/j.promfg.2015.07.594 |
| [6] |
Wang SY, Gwizdka J, Chaovalitwongse WA. Using wireless EEG signals to assess memory workload in the n-back task
. IEEE Transactions on Human-Machine Systems, 2016, 46(3): 424-435. DOI:10.1109/THMS.2015.2476818 |
| [7] |
Dehais F, Duprès A, Blum S, et al. Monitoring pilot’s mental workload using ERPs and spectral power with a six-dry-electrode EEG system in real flight conditions. Sensors, 2019, 19(6): 1324. DOI:10.3390/s19061324 |
| [8] |
Fitzgibbon SP, Pope KJ, Mackenzie L, et al. Cognitive tasks augment gamma EEG power. Clinical Neurophysiology, 2004, 115(8): 1802-1809. DOI:10.1016/j.clinph.2004.03.009 |
| [9] |
Taylor G, Reinerman-Jones L, Cosenzo K, et al. Comparison of multiple physiological sensors to classify operator state in adaptive automation systems. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 2010, 54(3): 195-199. DOI:10.1177/154193121005400302 |
| [10] |
Fu RR, Tian YS, Shi PM, et al. Automatic detection of epileptic seizures in EEG using sparse CSP and fisher linear discrimination analysis algorithm. Journal of Medical Systems, 2020, 44(2): 43. DOI:10.1007/s10916-019-1504-1 |
| [11] |
Arora A, Lin JJ, Gasperian A, et al. Comparison of logistic regression, support vector machines, and deep learning classifiers for predicting memory encoding success using human intracranial EEG recordings. Journal of Neural Engineering, 2018, 15(6): 066028. DOI:10.1088/1741-2552/aae131 |
| [12] |
Blanco JA, Johnson MK, Jaquess KJ, et al. Quantifying cognitive workload in simulated flight using passive, dry EEG measurements. IEEE Transactions on Cognitive and Developmental Systems, 2018, 10(2): 373-383. DOI:10.1109/TCDS.2016.2628702 |
| [13] |
Garrett D, Peterson DA, Anderson CW, et al. Comparison of linear, nonlinear, and feature selection methods for EEG signal classification. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2003, 11(2): 141-144. DOI:10.1109/TNSRE.2003.814441 |
| [14] |
张洁, 庞丽萍, 完颜笑如, 等. 基于脑电功率谱密度的作业人员脑力负荷评估方法. 航空学报, 2020, 41(10): 123618. DOI:10.7527/S1000-6893.2019.23618 |
| [15] |
Almogbel MA, Dang AH, Kameyama W. EEG-signals based cognitive workload detection of vehicle driver using deep learning. Proceedings of the 20th International Conference on Advanced Communication Technology. Chuncheon: IEEE, 2018. 256–259.
|
| [16] |
Lee DH, Jeong JH, Kim K, et al. Continuous EEG decoding of pilots’ mental states using multiple feature block-based convolutional neural network. IEEE Access, 2020(99): 1. DOI:10.1109/ACCESS.2020.3006907 |
| [17] |
Jonides J, Schumacher EH, Smith EE, et al. Verbal working memory load affects regional brain activation as measured by PET. Journal of Cognitive Neuroscience, 1997, 9(4): 462-475. DOI:10.1162/jocn.1997.9.4.462 |
| [18] |
Scharinger C, Soutschek A, Schubert T, et al. When flanker meets then-back: What EEG and pupil dilation data reveal about the interplay between the two central-executive working memory functions inhibition and updating
. Psychophysiology, 2015, 52(10): 1293-1304. DOI:10.1111/psyp.12500 |
| [19] |
Costers L, Van Schependom J, Laton J, et al. Spatiotemporal and spectral dynamics of multi-item working memory as revealed by the n-back task using MEG
. Human Brain Mapping, 2020, 41(9): 2431-2446. DOI:10.1002/hbm.24955 |
| [20] |
Pergher V, Wittevrongel B, Tournoy J, et al. Mental workload of young and older adults gauged with ERPs and spectral power during n-back task performance
. Biological Psychology, 2019, 146: 107726. DOI:10.1016/j.biopsycho.2019.107726 |
| [21] |
Lawhern VJ, Solon AJ, Waytowich NR, et al. EEGNet: A compact convolutional neural network for EEG-based brain-computer interfaces. Journal of Neural Engineering, 2018, 15(5): 056013. DOI:10.1088/1741-2552/aace8c |
| [22] |
梁椰舷, 李婷, 姬昊余. 多通道连续卷积神经网络脑电信号情绪识别. 计算机系统应用, 2023, 32(1): 399-405. DOI:10.15888/j.cnki.csa.008897 |
| [23] |
Mane R, Chew E, Chua K, et al. FBCNet: A multi-view convolutional neural network for brain-computer interface. arXiv:2104.01233, 2021.
|
| [24] |
Yan LR, Chen Y, Zhang JW, et al. Distraction detection of driver based on EEG signals in a simulated driving with alternative secondary task. Proceedings of the 2nd IEEE International Conference on Human-machine Systems (ICHMS). Magdeburg: IEEE, 2021. 1–3.
|
 2023, Vol. 32
2023, Vol. 32



