近几十年来, 视频监控系统以其安全、直观、丰富以及生动形象的特点, 被广泛应用于各行各业中^[1]. 塔机吊钩可视化系统通过在起重臂小车上安装摄像装置, 向塔机司机实时提供吊钩视频图像, 有效解决了塔机司机在隔山吊等复杂施工工况下的盲吊、视觉不清晰等安全隐患问题. 然而, 在实际应用过程中, 由于摄像装置受塔机运动及外界环境因素影响会发生机械振动, 导致监控视频出现晃动、不清晰, 这不仅会对塔机司机造成视觉疲劳, 而且还会导致司机误判、漏判. 因此, 对塔机吊钩视频的稳像至关重要.

数字稳像技术是利用数字图像处理技术去除视频帧画面的抖动, 实现稳像. 近年来, 基于深度学习的视频稳像方法^[2-4]开始兴起, 但是其稳像效果受限于稳像训练数据集和计算机硬件配置, 仍处于初步阶段. 目前, 大多数视频稳像还是以传统稳像方案为主. 传统的视频稳像算法主要包括运动估计、运动滤波和运动补偿3个阶段^[5], 其中, 运动估计和运动滤波是稳像算法中的研究热点. 基于ORB算法的运动估计是一种常用的方法^[6], 具有稳定性好, 且不易受外界环境干扰, 但是对于塔机吊钩视频, 由于背景复杂、场景多变, 经典ORB算法的特征点提取会导致特征点分布不均匀、特征匹配精度差; 同时, 视频中的局部运动目标会对运动估计造成较大的误差, 在稳像算法中需要剔除局部运动目标^[7]. 稳像算法中的运动滤波是将视频全局运动参数中的主观运动和随机抖动分离, 得到补偿参数. 目前常用的运动滤波方法主要有低通滤波、曲线拟合法以及Kalman滤波. Sánchez等^[8]采用高斯低通滤波对得到的运动轨迹进行平滑, 该方法平滑效果依赖于滤波窗口大小; Grundmann等^[9]采用L1范数对相机轨迹进行约束优化生成稳定视频, 该方法处理速度较慢, 无法满足塔机监控的实时性要求; Kalman滤波^[10]在实时稳像领域应用广泛.

针对塔机吊钩视频的特点, 本文提出了将改进ORB特征匹配与固定滞后Kalman滤波相结合的吊钩视频稳像算法. 在吊钩视频的运动估计阶段, 在经典ORB算法中采用图像分块与自适应阈值FAST特征点提取方法, 并引入图像四叉树算法提高图像特征点分布均匀性, 在此基础上, 采用背景补偿结合帧间差分法, 快速识别局部运动目标并进行剔除; 在运动滤波和补偿阶段, 本文采用固定滞后Kalman滤波算法, 分离全局运动参数中的主观运动和随机抖动, 最后, 根据摄像机的主观运动对图像进行运动补偿, 即可得到稳定的塔机吊钩视频.

1 塔机吊钩视频的运动估计 1.1 预处理

塔机吊钩视频存在抖动、光照不均匀、噪声等问题, 而且塔机吊钩可视化系统视频分辨率高, 直接进行处理, 会导致特征点提取难度大、匹配精度低, 且计算时间开销大. 本文对输入吊钩视频图像进行了降采样、灰度直方图均衡化处理, 提高了图像对比度, 使图像清晰, 降低了程序运行时间.

1.2 改进ORB特征匹配算法

经典ORB (oriented FAST and rotated BRIEF) 算法由FAST特征点提取和BRIEF特征描述两部分组成. 由于塔机施工现场环境复杂, 吊钩视频场景中有各种颜色、特征纹理丰富和形状交织、层叠的钢筋、模板等建筑器材, 还有地面、混凝土墙面等弱纹理区域, 经典的FAST特征点提取算法采用固定阈值, 对于塔机吊钩视频图像容易检测出大量聚集以及冗余特征点, 本文采用图像分块与自适应阈值特征点提取方法, 并结合图像四叉树算法, 对经典ORB算法进行改进, 在特征点提取基础上, 构建BRIEF特征描述符, 并采用k近邻算法加PROSAC算法对特征点进行粗、精匹配, 为后续稳像算法提供了较好的特征基础. 本文改进ORB特征匹配算法步骤如下.

(1) 构造图像金字塔

为使特征点具有尺度不变性, 首先通过高斯卷积核对输入图像进行下采样处理, 构造6层图像金字塔, 并按照尺度缩放因子 $ \rho $ 计算每层需要提取的期望特征点数量, 特征点数量的计算如式(1)所示:

$ {N}_{j}\text=\frac{K({1-}{\rho }^{2})}{(1-{({\rho }^{2})}^{m})}{({\rho }^{2})}^{j}, \text{ }j=1, 2, \cdots, 6\text{ , }m=6 $

(1)

其中, $ {N_j} $ 代表第 $ j $ 层的期望特征点数量, $ K $ 代表总共需要提取的特征点数量, $ m $ 代表金字塔层数.

(2) 图像分块与自适应阈值的FAST特征点提取

将构造的每层图像金字塔进行分块, 分块的目的是保证特征点在整个图像上均匀分布. 首先取块边长像素大小为40像素的正方形, 再根据图像实际分辨率计算图像块数量; 并设定FAST特征点提取的初始阈值 ${T_{{\rm{iniFast}}}}{\text{ = 25}}$ , 根据初始阈值对每个图像块提取FAST特征点; 如果某个图像块内没有提取到特征点, 就按比例降低初始阈值, 继续在该图像块内查找特征点, 直到遍历完所有图像块为止.

(3) 引入图像四叉树算法均衡特征点分布

四叉树是一种具有快速检索功能的空间索引树, 其每一个节点都表示一个矩形区域, 通过该算法可以将步骤(2)提取的所有特征点均匀地分布在图像上的每一个节点, 并去除节点内的其他冗余特征. 算法首先是以原始图像作为四叉树的根节点, 然后将根节点分裂为4个子节点, 得到4个等间距的图像块, 接着判断每个子节点区域内的特征点数量, 如果特征点数量大于1, 则继续将该节点分裂成4个新的子节点; 如果等于1, 则不再分裂并保存该节点; 如果小于1, 则舍去该节点, 然后重复上述过程, 当图像节点数量达到要求的节点最大数量时, 结束节点分裂, 并保留每个节点内质量最好的特征点. 这时所获得的特征点不仅能在图像中均匀地分布, 而且减少了大量冗余特征.

(4) 构建BRIEF特征描述符

获得特征点后, 使用灰度质心法对得到的每个特征点计算方向信息, 使特征点具有旋转不变性和抗噪性能. 为进行图像特征匹配, 需要对特征点构建描述符, 本文采用经典ORB算法中的BRIEF特征描述算法为每个特征点构建二进制特征描述符.

(5) 特征点粗匹配

吊钩视频相邻帧图像进行特征点提取和描述后, 采用k近邻算法进行特征点粗匹配, 得到粗匹配特征点集. k近邻算法的详细流程参见文献[11].

(6) 特征点精匹配

采用渐进样本一致性PROSAC 算法从粗匹配特征点集中筛选出误匹配的点, 得到精匹配特征点集. PROSAC算法的详细流程参见文献[12].

从塔机吊钩视频中抽取了一段视频, 对图像进行特征点提取. 图1和图2分别是采用经典ORB算法与本文改进ORB算法提取特征点的结果, 由图可见: 经典ORB算法提取的特征点容易集中在纹理更强的区域, 对于弱纹理区域无法提取足够的特征点, 而本文改进ORB算法提取的特征点分布更均匀.

1.3 局部运动目标识别

在塔机吊装过程中, 摆动的吊钩、吊物形成了视频图像中的局部运动目标, 给视频的全局运动参数估计带来了较大误差. 因此, 需要识别并剔除局部运动目标, 朱娟娟等^[13]利用时空一致性, 采用3帧间差分剔除运动目标, 该方法无法剔除动态场景下的运动目标; 吉淑娇等^[14]以及Yu等^[15]则采用光流法去除局部运动目标, 光流法会消耗大量的计算资源, 且难以实现实时稳像; 尹丽华等^[16]结合时空显著性目标检测技术识别运动目标并剔除, 但要求局部运动目标特征显著. 目前常采用帧间差分法进行局部运动目标识别, 该方法具有实现简单、速度快的优点, 广泛应用在实时性要求高的工业领域. 但是对于吊钩视频来说, 视频中背景也会随摄像装置的运动发生动态变化, 直接采用帧间差分法会产生很大误差.

综合考虑吊钩视频中吊钩局部运动特点, 本文将背景补偿与帧间差分法相结合, 首先对背景运动进行补偿, 在此基础上进行帧间差分, 可以对动态场景下的复杂局部运动目标进行快速识别. 本文局部运动目标识别的算法流程如算法1所示.

算法1. 局部运动目标识别算法

1) 首先, 建立仿射变换模型, 根据相邻帧匹配的特征点集计算前一帧I_t–1到当前帧I_t 的仿射变换运动矩阵H , 仿射变换模型如式(2)所示:

$ \left[ \begin{gathered} {{x'}} \\ {{y'}} \\ {1} \\ \end{gathered} \right] = {H}\left[ \begin{gathered} {x} \\ {y} \\ {1} \\ \end{gathered} \right] = \left[ \begin{gathered} { {a_1}}{\text{ }}{a_2}{\text{ }}{t_{{x}}} \\ {{a_3}}{\text{ }}{a_4}{\text{ }}{t_y} \\ {0}{\text{ }}{\text{ }}{\text{ 0 }} {\text{ }}{\text{ 1 }} \\ \end{gathered} \right]{\text{ }}\left[ \begin{gathered} {x} \\ {y} \\ {1} \\ \end{gathered} \right]{\text{ }} $

(2)

其中, $\scriptstyle{(x', y')}$ 代表当前帧I_t的特征点坐标, $\scriptstyle{(x, y)}$ 代表前一帧I_t–1的特征点坐标, H代表仿射变换矩阵, $\scriptstyle{({a}_{1}, {a}_{2}},{a}_{3},{a}_{4})$ 代表旋转和缩放运动矢量, (t_x, t_y)代表平移运动矢量.

2) 利用仿射变换矩阵H对前一帧I_t–1进行运动背景补偿, 即 $\scriptstyle{{I'_t}} = H{I_{t-{\text{ 1}}}}$ , 得到背景运动补偿后的图像 $\scriptstyle{{I'_t}}$ .

3) 将背景运动补偿后图像 $\scriptstyle{{I'_t}}$ 与当前帧 $\scriptstyle {I_t} $ 进行帧间差分, 得到含有局部运动目标的差分灰度图像I_obj.

4) 依次对差分灰度图像I_obj进行二值化阈值处理、形态学开运算操作, 并采用图像边缘检测算法提取图像中的局部运动目标.

图3是本文局部运动目标识别算法与直接采用帧间差分法处理结果的对比, 由图3可见: 直接采用帧间差分法处理后的图像信息丢失严重, 无法进行后续局部运动目标提取, 而本文算法处理后图像的吊钩、吊物运动目标更加突出, 有助于后续局部运动目标提取和特征点剔除.

图4为剔除局部运动目标区域特征点后的背景特征点分布图, 由图4可见: 本文算法的局部运动目标识别结果准确、局部运动目标特征点剔除效果良好.

1.4 全局运动参数估计

根据上述算法得到吊钩视频背景的匹配特征点后, 将其代入仿射变换模型, 利用最小二乘法求解仿射变换矩阵, 提取相邻帧的平移、旋转运动参数, 然后将相邻帧的运动参数分别进行累加处理, 得到视频当前帧相对于第1帧的全局运动参数 $ {C_t} $ . 对于吊钩视频前n帧的原始运动轨迹则可以表示为 $\left\{ {{C_1}{\text{, }}{C_2}{\text{, }} \cdots , {C_n}} \right\}$ , 该轨迹包含旋转、水平和垂直方向上的全局运动参数.

2 运动滤波与补偿 2.1 固定滞后Kalman滤波算法

吊钩视频的原始运动轨迹包含随塔机运动的低频主观运动, 以及由于塔机振动引入的高频随机抖动. 为了进行稳像, 需要对原始运动轨迹进行滤波平滑处理, 去除高频抖动. Kalman滤波算法是一种常用的滤波算法, 具有计算量少、运算速度快等优势. Kalman滤波算法包括预测和更新校正两个过程, 通过不断地循环迭代得到目标下一刻的滤波估计值.

(1) Kalman滤波的预测过程, 通过状态预测方程计算当前时刻的预测值 $ \hat C_t^{\sim f} $ 和协方差矩阵的预测值 $ P_t^{\sim f} $ , 状态预测方程为:

$ \left\{ \begin{gathered} \hat C_t^{\sim f} = F{{\hat C}}_{t - 1}^f + B{u_{t - 1}} \\ P_t^{\sim f} = FP_{t - 1}^f{F^{\rm{T}}} + Q \\ \end{gathered} \right. $

(3)

其中, $ \hat C_t^{\sim f} $ 是 $ (t - 1) $ 时刻的滤波估计值 $ {{\hat C}}_{t - 1}^f $ 对 $ t $ 时刻的预测值, $ F $ 是状态转移矩阵, $ B $ 是控制矩阵, $ {u_{t - 1}} $ 是 $ (t - 1) $ 时刻的系统控制量, $ P_t^{\sim f} $ 是 $ (t - 1) $ 时刻协方差矩阵 $P_{t{{ - 1}}}^f$ 对 $ t $ 时刻的预测值, $ Q $ 是过程噪声的协方差.

(2) Kalman滤波的更新校正过程, 通过状态更新方程计算当前时刻的滤波估计值 $ \hat C_t^f $ 和协方差矩阵 $ P_t^f $ , 状态更新方程为:

$ \left\{ \begin{gathered} K_t^f = P_t^{\sim f}{H^{\rm{T}}}{(HP_t^{\sim f}{H^{\rm{T}}} + R)^{ - 1}} \\ \hat C_t^f = \hat C_t^{\sim f} + K_t^f({C_t} - H\hat C_t^{\sim f}) \\ P_t^f = (I - K_t^fH)P_t^{\sim f} \\ \end{gathered} \right. $

(4)

其中, $ K_t^f $ 是Kalman增益, $ H $ 是系统参数, $ {C_t} $ 是 $ t $ 时刻的观测值(全局运动参数), $ \hat C_t^f $ 是 $ t $ 时刻对 $ {C_t} $ 的滤波估计值, $ P_t^f $ 是 $ t $ 时刻协方差矩阵的校正值, $ I $ 是单位矩阵.

固定滞后Kalman滤波算法是在Kalman滤波的基础上增加了后向递推平滑处理. 根据Kalman滤波算法计算出的滤波估计值进行回代计算, 并对已有的滤波估计值进行修正, 从而得出平滑估计值. 该算法提高了原始运动轨迹的平滑效果, 固定滞后Kalman滤波算法的运动滤波过程如下.

(1) 参数初始化

初始化全局运动参数 $ {C_{\text{1}}}{\text{ = 0}} $ , 回代步长 $ N{\text{ = 4}} $ , 假设 $ t $ 表示系统的当前时刻, 其初值为 $ t{\text{ = 0}} $ .

(2) 执行Kalman滤波算法

执行式(3)和式(4)得到滤波估计值 $ \hat C_{t - i}^f $ , $i = 1, {\text{2}}, \cdots , N$ .

(3) 判断是否开始进行后向递推平滑处理

当 $ t < N $ 时, $ t{\text{ = }}t{\text{ + 1}} $ , 返回执行步骤(2).

当 $ t \geqslant N $ , 开始后向递推, 执行步骤(4).

(4) 后向递推平滑处理

后向递推是对前向滤波估计值 $\hat C_{t-i}^f$ 的进一步平滑处理, 其基本过程是, 由 $ t $ 到 $t-N$ 时刻的滤波估计值不断回代 $ N $ 次, 从而得到 $t-N$ 时刻的平滑估计值 $\hat C_{t-N}^s$ , 这个过程可用式(5)描述:

$ \left[ \begin{gathered} \hat C_t^s \\ \hat C_{t - 1}^s \\ \;{\text{ }}{\text{ }} \vdots \\ \hat C_{t - N}^s \\ \end{gathered} \right] = \left[ \begin{gathered} I \\ 0 \\ \vdots \\ 0 \\ \end{gathered} \right]\hat C_t^f + \left[ \begin{gathered} 0{\text{ }} \cdots {\text{ 0}} \\ I{\text{ }}{\text{ }} {\text{ 0 }}{\text{ }} \vdots \\ \vdots {\text{ }} \ddots {\text{ }} \vdots \\ 0{\text{ }} \cdots {\text{ I}} \\ \end{gathered} \right]\left[ \begin{gathered} \hat C_{t - 1}^f \\ \hat C_{t - 2}^f \\ \;{\text{ }} {\text{ }}\vdots \\ \hat C_{t - N}^f \\ \end{gathered} \right] + \left[ \begin{gathered} {K^{{\text{(1)}}}} \\ {K^{{\text{(2)}}}} \\ \;{\text{ }} {\text{ }}\vdots \\ {K^{{\text{(}}N{\text{)}}}} \\ \end{gathered} \right]({C_t} - H\hat C_t^f) $

(5)

其中, $ \hat C_{t - i}^s $ 是分别进行 $ N $ 次后向递推的平滑估计值结果, $i = 1, {\text{2}}, \cdots , N$ , 第 $ N $ 次递推结果 $\hat C_{t-N}^s$ 为 $t-N$ 时刻的平滑估计值; $ I $ 是单位矩阵; $ {K^{(i)}} $ 是固定滞后Kalman平滑增益, $ {K^{(i)}} $ 的计算如式(6)所示:

$ {K^{(i)}} = {P^{(i)}}{H^{\rm{T}}}{[HP_t^f{H^{\rm{T}}} + R]^{ - 1}} $

(6)

其中, $ {P^{(i)}} $ 是固定滞后Kalman平滑协方差矩阵, ${P^{(i)}}{\text{ = }} P_t^f[{(F - K_t^fH)^{\rm{T}}}]$ .

得到的平滑估计值 $\hat C_{t{{ - }}N}^s$ 即为塔机吊钩视频的主观运动.

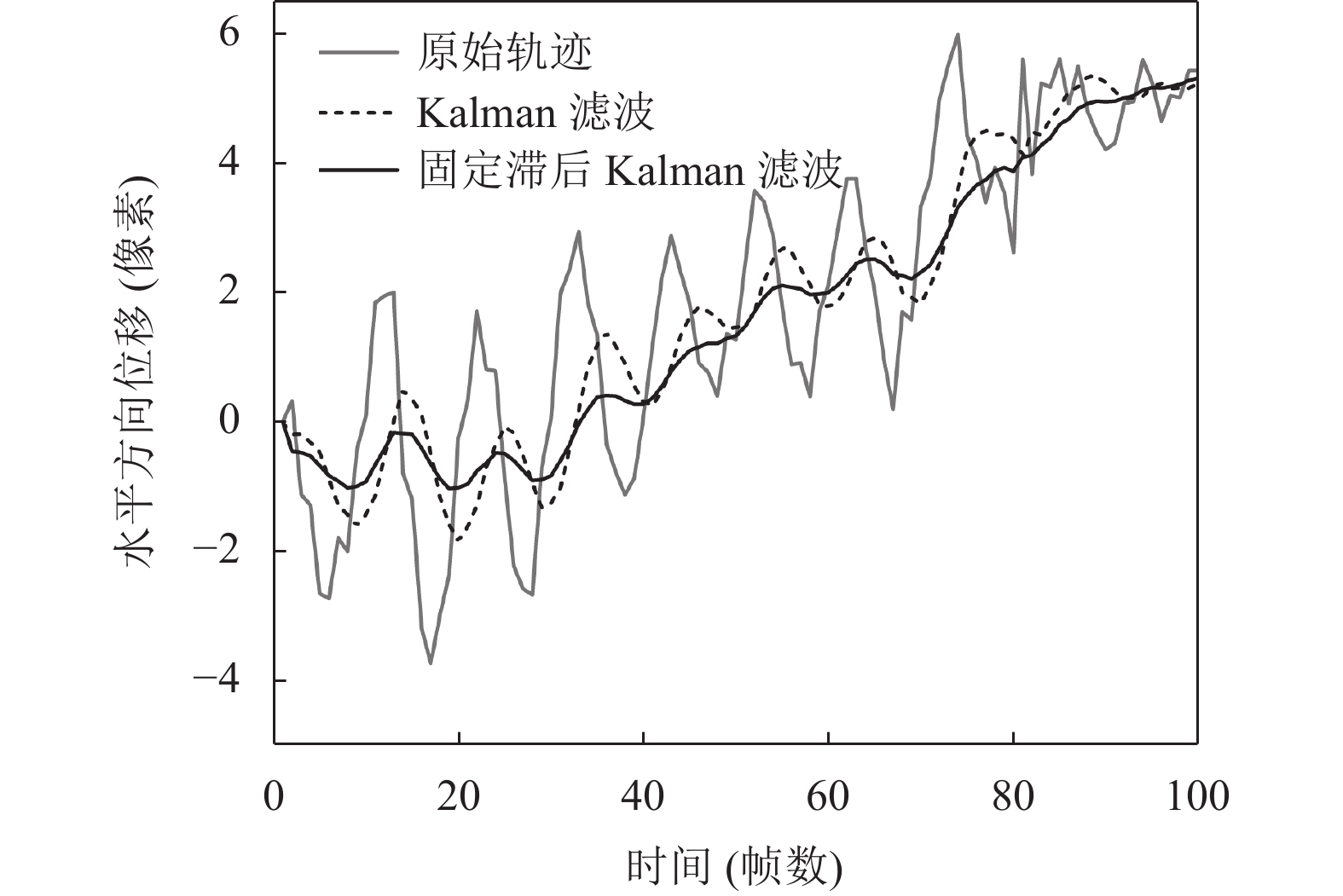
图5是采用固定滞后Kalman滤波算法和Kalman滤波算法对某段吊钩视频水平方向原始运动轨迹进行平滑处理的结果比较, 由图5可以看出: 采用固定滞后Kalman滤波算法能够很好地滤除高频随机抖动噪声, 处理后的轨迹更加平滑.

2.2 运动补偿

对原始运动轨迹 $\left\{ {{C_1}{\text{, }}{C_2}{\text{, }} \cdots , {C_n}} \right\}$ 进行滤波处理后, 得到平滑后的主观运动轨迹 $\left\{ {\hat C_{\text{1}}^s{\text{, }}\hat C_{\text{2}}^s{\text{, }} \cdots , \hat C_n^s} \right\}$ , 利用平滑轨迹对视频帧进行补偿. 假设第 $ t $ 帧图像的补偿矩阵为 $ {B_t} $ .

$ {B_t} = \hat C_t^sC_t^{ - 1} $

(7)

利用 $ {B_t} $ 对第 $ t $ 帧图像进行几何变换, 即可得到稳定后的视频图像.

3 实验分析

为了验证本文算法的稳像效果, 实验采用了某塔机上现场采集的吊钩视频进行测试, 视频分辨率为 $ {\text{1920}} \times {\text{1080}} $ . 选取了4种不同工况场景下的抖动视频进行实验分析. 4种视频工况的特点如表1所示.

工况1与工况2, 塔机无主观运动, 且吊钩的局部运动均不明显, 但两种工况不同, 工况1的视频背景存在大面积的弱纹理地面区域; 工况2的视频背景复杂, 有钢筋、模板等物料堆放, 图像的纹理特征较为丰富. 工况3与工况4, 塔机分别在做变幅、回转运动, 此时吊钩的局部运动明显.

图6展示了工况1视频序列的稳像前后效果, 在图像画面中添加橙色十字形参考线, 观察背景目标相对于十字形参考线的位置变化, 可以反映出视频的抖动情况. 图像的右下角对视频的细节进行了放大, 图6中给出了静止“斗车”相对参考线的位置变化, 从图中可以看出: 稳像前视频图像中斗车位置发生了明显偏移, 而经过本文算法稳像后, 其视频图像中的斗车参照物与参考线的距离基本保持一致, 表明经过本文算法稳像后, 视频的抖动得到了有效去除.

本文采用帧间变换保真度ITF^[10]、结构相似度平均值 $ \overline {{\text{SSIM}}} $ ^[17]以及帧处理速率FPS这3个指标来定量评价本文改进算法的吊钩视频稳像效果. ITF用于衡量帧间的平滑度, $ \overline {{\text{SSIM}}} $ 衡量帧间的整体相似度(取值范围 $ [0, 1] $ ). ITF值越大或 $ \overline {{\text{SSIM}}} $ 越接近1, 表明视频的帧间差异越小, 视频的稳像效果越好; 帧处理速率FPS反映了算法的实时性, 单位是f/s.

针对上述4种工况的塔机吊钩视频, 采用经典算法(即经典ORB算法+Kalman滤波算法)与本文改进算法进行稳像对比测试. 表2给出了两种算法对不同工况视频稳像处理前后的帧间变换保真度ITF值、结构相似度平均值 $ \overline {{\text{SSIM}}} $ 以及帧处理速率FPS的实验结果.

由表2的评价指标可见: (1)本文改进算法稳像后视频与经典算法稳像后视频相比, ITF平均值由24.091 dB提高到26.289 dB, 提升约9.12%; $ \overline {{\text{SSIM}}} $ 平均值由0.801提高到0.823, 提升约2.75%, 可见本文改进算法比经典算法的稳像效果更好; (2)经典算法的FPS平均值约为51.69 f/s, 较经典算法, 本文改进算法的FPS平均值下降了42.63%, 对于塔机吊钩视频, 速度达到25 f/s就可以满足监控要求, 而本文改进算法的FPS平均值约为29.65 f/s, 满足塔机吊钩可视化系统监控视频的实时性要求.

4 结论与展望

面向塔机吊钩可视化系统监控的视频稳像需求, 本文提出改进ORB特征匹配与固定滞后Kalman滤波相结合的视频稳像算法. 针对塔机吊钩视频背景的复杂情况, 采用图像分块与自适应阈值特征点提取方法, 并引入图像四叉树算法提高图像特征点分布均匀性; 考虑吊钩与吊物的局部运动, 采用背景补偿结合帧间差分法, 快速识别局部运动目标并进行剔除, 提高了全局运动参数估计的准确性; 在上述运动估计基础上, 采用了固定滞后Kalman滤波算法对原始运动轨迹进行平滑, 很好地滤除了吊钩视频的高频随机抖动; 最后根据摄像机的主观运动对图像进行运动补偿, 实现对塔机吊钩视频的稳像, 实验结果表明: 与经典ORB加Kalman滤波的稳像算法相比, 本文所提出的稳像算法帧间变换保真度ITF提升了约9.12%, 结构相似度平均值 $ \overline {{\text{SSIM}}} $ 提升了约2.75%, 获得了更好的稳像效果; 改进稳像算法的帧处理速率FPS可达到29.65 f/s, 满足塔机吊钩可视化系统的实时监控要求.

本文算法依然存在一些不足, 当局部运动目标覆盖视频图像的区域较大时, 本文采用的局部运动目标识别算法效果不理想; 另外本文没有考虑夜间工况下塔机吊钩视频的稳像, 这需要后期进行更深入的研究.