随着我们对海洋探索的不断推进, 对水下传感网络(underwater sensor networks, UWSNs)的研究越来越受到研究者的青睐. 陆地通信与海洋通信有着本质的不同, 陆地通信所用的电磁波在水下传输具有严重的衰减, 水下环境更适用于声波进行传输. 并且水声通信在水中遭受着严重的频率相关衰减, 这就导致声学调制解调器的传输功率消耗要比陆地通信高得多^[1-3]. 因此传统的陆地通信协议, 并不适用于水声通信. 此外, 在水下实现通信, 还会有声波的传输高延时; 水中节点会动态漂移造成链路断裂; 水下节点能量有限等问题.

为了克服UWSNs的问题, 已经提出了许多路由协议来解决在水下传感网络中数据传输的问题. 许多经典传统算法被提了出来, 如基于向量的转发协议^[4]、定向洪泛基于路由协议^[5]和基于深度的协议DBR^[6]等. 然而, 传统的优化方法受到在实践中难以获得的先验信道统计知识的限制, 很容易陷入局部最优和水下路由空洞问题^[7,8]. 因此, 转向智能自适应的在线学习方法非常重要.

为了解决水下路由局部最优和水下路由空洞问题, 研究员们开始转向对智能算法的研究, 例如蚁群优化(ant colony optimization , ACO)和(Q-learning, QL)强化学习算法^[9]. ACO 是 Dorigo等人在1996年引入的一种基于群体的元启发式方法^[10]. 蚁群可以通过跟踪信息素来找到它们的巢穴和食物来源之间的最短路径. 然后, 较短路径上的蚂蚁比较长路径上的蚂蚁更早到达目的地. 此外, 强化学习算法(reinforcement learning, RL)^[11]作为一种自适应算法, 可以通过学习训练解决水下路由局部最优和水下路由空洞问题, 实现水下更节能高效的路由机制. 目前, 强化学习已被证明是解决无线通信网络中各种问题的有效在线学习技术. 通过即时与外部环境交互的奖励反馈, RL智能体可以在没有任何先验系统知识的情况下学习最优策略. 如基于 Q-learning 的节能和生命周期感知路由协议(Q-learning-based energy-efficient and lifetime-aware routing protocol, QELAR)^[12], 该协议根据节点的能量定义了其奖励函数. QELAR虽然在能效方面表现良好, 但缺乏深度和延迟信息来优化路由程序, 使得节点容易陷入局部最优. 基于Q学习辅助的蚁群算法 (Q-learning aided ant colony routing protocol, QLACO)^[13], 该协议根据节点能量、深度和节点连接稳定系数定义奖励函数, 并通过给单个节点添加等待时间的方式解决空洞问题, 但是由于数据传输经过节点的等待时间是不同的, 容易使得节点陷入局部最优, 降低网络性能.

因此, 本文基于蚁群优化(ACO)算法以及QL强化学习算法, 提出一种基于Q学习辅助的蚁群算法(Q-learning ant colony optimization, QACO), 用以实现水下通信路由协议. 将节点深度、能量、传输延迟信息和水深链路质量(link quality indicator, LQI)^[14]加入到奖励参数中, 使得奖励机制的评判更加全面. 并运用ACO实现信息的路由以及链路奖励的更新, 使得网络能在更短的时间找到最优路径, 提升网络的性能.

1 系统模型及问题表述 1.1 水下传感网络系统模型

水声网络传感器的水下部署见图1, 分别有水底数据采集节点、水中移动AUV, 以及水面数据接收节点构成. 假设水下网络一共有 $W$ 个传感器节点, 在每个时隙中, 源节点将采集的数据从有限集 $F = \left\{ {{f_1}, {f_2}, \cdots , {f_h}} \right\}$ 发送数据到有限集为 $P = \left\{ {{p_1}, {p_2}, \cdots , {p_m}} \right\}$ 的中继节点, 数据包再经过中继节点被传递到水面目标节点 $Z = \{ {{\textit{z}}_1}, {{\textit{z}}_2}, \cdots , {{\textit{z}}_l} \}$ . ${F_h}$ 、 ${P_m}$ 、 ${Z_l}$ 分别表示为源节点、中继节点、目标节点. 每类节点对应的个数为 $\left| {{F_h}} \right| \triangleq {W_h}$ 、 $\left| {{P_m}} \right| \triangleq {W_m}$ 、 $\left| {{Z_l}} \right| \triangleq {W_l}$ , 即有 $W = {W_h} + {W_m} + {W_l}$ . 假设每个传感器节点的初始能量为 ${E_{{\text{init }}}}$ . 则 ${d_{i, j}}$ 为空间节点 $i\left( {{x_1}, {y_1}, {{\textit{z}}_1}} \right)$ 和节点 $j\left( {{x_2}, {y_2}, {{\textit{z}}_2}} \right)$ 之间的距离为欧氏距离, 公式为:

$ {d_{i, j}} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2} + {{\left( {{{\textit{z}}_1} - {{\textit{z}}_2}} \right)}^2}} $

(1)

且每个节点的发射功率和接收功率分别为 ${P_s}$ 和 ${P_r}$ , 当节点处于空闲状态时其功率为 ${P_k}$ , 每个节点都配置有声波调制解调器, 其最大可传输距离为 ${R_0}$ .

1.2 水下声学信道分析

不同于陆地通信, 水下是靠水声信道传输数据的. 因此, 水声信道的传输路径选择尤为重要. 不同的传输路径会导致不同的平均信噪比(SNR)^[15]和链路吞吐量, 从而影响链路的能量消耗.

水声信道增益通常由距离和频率相关的大尺度衰落和时变多径衰落来描述. 信道增益 $A$ 是传播距离 $d\;({\rm{m}})$ 的函数, 频率 $f\;({\rm{kH}}{\textit{{\rm{z}}}})$ , 以及一个随机变量 $\gamma $ (小规模衰落). 水声信道的路径传输损耗可表示为:

$ A(d, f) = \gamma \bar A(d, f) $

(2)

其中, $\bar A(d, f)$ 称为平均信道功率增益. 根据Deng等人^[16]的研究得:

$ \bar A(d, f) = {d^k}a{(f)^d} $

(3)

其中, $a(f)$ 为吸收损耗系数, 单位为 ${\rm{dB/km}}$ , 与频率有关. $k$ 为描述传播几何形状扩展因子. 根据 $ {\text{Throp}} $ 传输模型的经验公式^[17], $a(f)$ 可以表示为:

$ 10\lg a(f) = \frac{{0.11{f^2}}}{{1 + {f^2}}} + \frac{{44{f^2}}}{{4100 + {f^2}}} + 2.75 \times {10^{ - 4}}{f^2} + 0.003 $

(4)

$\lg a(f)$ 为以10为底的对数函数. 因此, 每次传输的瞬时信道增益随机变化, 从而影响瞬时接收信噪比和误码率(BER). 假设节点在时隙 $t$ 以频率 $f$ , 传输距离 $d$ , 发送一个数据包, 则成功传输的概率为:

$ {\theta _{{f, d}}} = \Pr \left\{ {{{BE}}{{{R}}_{{f, d}}} \leqslant \delta } \right\} $

(5)

其中, $\delta $ 为接收器可接受的最大误码率.

除了水下路径损耗之外, 环境噪声也会对节点的能量消耗造成影响. 水下环境噪声主要分为4种类型: 湍流噪声、船舶噪声、海浪噪声和热噪声. 假设4种噪声的功率谱密度和为: $N(f)$ , 因此, 一个节点以频率 $f$ , 功率 $P$ , 发送数据, 声波传输距离为 $d$ 的平均窄带SNR为:

$ {\textit{SNR}} (d, f) = \frac{{P/A(d, f)}}{{N(f)\Delta f}} $

(6)

其中, $\Delta f$ 为节点噪声带宽, 通常近似为一个常数. 根据通信理论可知, BER会随着 ${\textit{SNR}} (d, f)$ 的增加而降低, 这样就有了传输距离 $d$ 、频率 $f$ 和传输成功率概率的关系:

$ {P_{{\text{success }}}} = 1 - \frac{1}{2}\left( {1 - \sqrt {\frac{{{\textit{SNR}} (d, f)}}{{1 + {\textit{SNR}}(d, f)}}} } \right) $

(7)

1.3 水深链路质量

水声网络中, 有可能存在某一节点失效, 或者某一节点能量耗尽, 造成链路断裂的情况. 并引发路有空洞问题. 因此建立一个数学模型, 及时的评估链路质量, 以便尽早地发现问题, 提高系统的稳定性. 根据第1.2节定义的水下网络模型, 假设 ${M_{i, j}}$ 为节点 ${p_i}$ 和节点 ${p_j}$ 之间的链路质量, 且 ${d_{i, j}} < {R_0}$ . 需要考虑节点间水声链路质量, 否则链路断裂, 质量指标为零, 无需考虑链路影响. 为了评估节点链路的优劣, 本文使用链路质量链路LQI越大, 则反映出该链路的质量越佳. 节点 ${p_i}$ 和 ${p_j}$ 的链路质量可以表示为:

$ {M}_{i, j}=\left\{\begin{array}{*{20}{l}} 0,& {d}_{i, j} > {R}_{0}\\ {a}_{1}\times \left[\mathrm{ln}\left({R}_{0}/{\left({b}_{1}^{2}\cdot {d}_{ij}\right)}^{2}+{b}_{1}\right.\right], & 0 < {d}_{i, j}\leqslant{R}_{0}\\ {a}_{1}\cdot {b}_{1}& {d}_{i, j}=0 \end{array} \right. $

(8)

其中, ${a_1} \in {N^*}, \;{b_1} \in {N^*}$ 分别为链路调节系数.

1.4 问题描述

在UWSNs的数据传输过程中, 一条合适的传输路径受到传输节点深度、能量、延时的影响. 因此, 本文的设计的路由协议优化目标将围绕以上3点展开. 将路由协议基于蚁群算法的实现方式, 运用QL的决策设计理念. 将网络中央处理器看成一个集中式智能体, 在数据传输过程中, 不断地从环境中获取经验, 给出决策, 实现最优的动作. 最终实现一种路由, 以较低的数据传输延时均衡网络中的能量消耗. 假设 $N$ 次传输数据所每次经过的节点组成的动作空间集合为 ${\zeta _e}$ , 其中第 $n$ 次传输经过了 ${n_{{\zeta _e}}}$ 个节点. 本节制定了一个评定指标 $V$ 来评估在 $t$ 时隙, 合集 ${\zeta _e}$ 中节点深度、能量和延时所对应的网络性能, 即:

$ {V_n} = \sum\limits_{n = 1}^N {{D_{(n, t)}}} /{E_{(n, t)}}{T_{(n, t)}} $

(9)

其中,

$ {D_{(n, t)}} = {D_{\textit{z}}}\Bigg/\sum\limits_{i = 1, j = 2}^{{n_{\zeta e}}} {{d_{ij}}} $

(10)

$ EX = \sum\limits_{j = 1}^{{n_{\zeta {\text{e}}}}} {\left( {{E_{(j, t)}} - {E_{{\rm{init}}}}} \right)} /{n_{{\zeta _e}}} $

(11)

$ {E_{(n, t)}} = \sum\limits_{j = 1}^{{n_{\zeta e}}} {{{\left( {\left( {{E_{{\rm{init}}}} - {E_{(j, t)}}} \right) - EX} \right)}^2}} /{n_{{\zeta _e}}} $

(12)

$ {{{T}}_{(n, t)}} = \left( {\sum\limits_{j = 1}^{{n_{\zeta e}}} {\left( {1 - \left( {{E_{(j, t)}}/{E_{{\text{init }}}}} \right)} \right)} \times {T_{\max }} + \eta } \right)/{n_{{\zeta _e}}} $

(13)

其中, $ {D}_{(n, t)}\text{ }、{E}_{(n, t)}\text{ }、{T}_{(n, t)} $ 为第 $n$ 次传输的节点深度、能量、延时的评定指标, ${D_{\textit{z}}}$ 为源节点的垂直深度, ${E_{{\text{init }}}}$ 为节点初始能量, ${T_{\max }}$ 为最大持续时间, $\eta $ 为随机值, $EX$ 为节点平均能量和平均延时. 本算法研究就是找到一种合适的路由转发策略, 使得每条传输链路的 ${V_n}$ 值最大, 表达式为:

$ {\pi _*} = \arg \max \sum\limits_{n \in N} {{V_n}} $

(14)

2 基于QACO的强化路由协议

QACO的实现主要有两部分, 第1部分为做决策部分, 由QL强化学习算法完成; 第2部分为路由行为的实现, 由蚁群算法完成. 本节将对这两部分进行详细阐述.

2.1 强化学习及奖励机制 2.1.1 强化学习框架

RL是机器学习的一个重要分支, 它为马尔可夫决策过程(MDP)提供了最优策略. 具体来说, 在MDP范式中, 智能体在时隙 $t$ 观察环境状态 ${s_t}$ , 然后在策略 $\pi $ 下决定其动作 ${a_t}$ . 受根据执行的 ${a_t}$ 的影响. 环境将即时奖励 ${r_{t + 1}}$ 反馈给智能体, 并以转移概率 $P_{{s_t}{s_{t + 1}}}^{{a_t}}$ , 进入到新的状态 ${s_{t + 1}}$ , 其奖励 ${r_t}$ 定义为:

$ {r_t} = P_{{s_t}{s_{t + 1}}}^{{a_t}}r_{{s_t}{s_{t + 1}}}^{{a_t}} $

(15)

MDP的目标是找到最优策略 ${\pi ^*}$ , 使得长期累积奖励最大化, 长期累积奖励定义为:

$ {R_t} = \sum\limits_{k = t + 1}^\infty {{\gamma ^{k - t - 1}}} {r_k} $

(16)

其中, $\gamma \in [0, 1]$ 为折扣因子. 由于智能体通常不知道先验概率的情况下, 就能够做出决策, 因此, QL算法广泛用于解决概率未知的环境模型中. QL使用 $Q$ 表存储动作值函数 $Q(s, a)$ . 在每个时隙 $t$ 智能体根据状态 ${s_t}$ 采取行动 ${a_t}$ , 通过使用 $\epsilon {\textit{-}}greedy$ 策略^[18], 获得奖励 ${r_{t + 1}}$ , 进入新状态 ${s_{t + 1}}$ , 其中对应的 $Q(s, a)$ 更新公式如下:

$ {Q_\pi }(s, a) = {R_t} + \gamma \sum\limits_{{s_{t + 1}} \in S} {P_{{s_t}{s_{t + 1}}}^{{a_t}}} Q\left( {{s_{t + 1}}, {a_t}} \right) $

(17)

通过策略学习, $Q$ 值最终收敛于最优 $Q$ 函数, 定义为 ${Q^*}(s, a)$ .

2.1.2 QACO奖励机制

在水声环境中, 数据的传输包括成功和失败. 因此环境分别对成功和失败反馈奖励. 因此, 本文定义在某个时隙 $t$ , 数据从节点 $i$ 传输到节点 $j$ 时, 奖励为:

$ R_{i, j}^* = {P_{i, j}}{R_{i, j}} + {\widetilde P_{i, j}}{\text{ }}{\widetilde R_{i, j}} $

(18)

其中, $ {P}_{i, j}\text{ }、{R}_{i, j} $ 分别为数据成功从节点 $i$ 传输到节点 $j$ , 对应的转移概率和奖励. $ {\tilde{P}}_{i, j}\text{ }、{\tilde{R}}_{i, j} $ 分别为数据节点 $i$ 传输到节点 $j$ 发送失败, 对应的转移概率和奖励. 由于数据只有成功和失败两种情况, 因此 ${P_{i, j}} = 1 - {\widetilde P_{i, j}}$ , 由此得出环境转移概率为:

$ P_{{s_t}{s_{t + 1}}}^{{a_t}} = \sum\limits_{i = 1, j = 1, i \ne j}^{{n_{{\zeta _e}}}} {{P_{i, j}}} /{n_{{\zeta _e}}} $

(19)

由式(7)得 ${P_{i, j}} = {P_{{\text{success }}}}$ . 当信息包成功转发时, 在奖励函数中同时考虑了发送节点和接收节点的情况. 定义奖励为:

$ {R_{i, j}} = {\alpha _1}{E_{i, j}} + {\alpha _2}D + {\alpha _3}{T_{i, j}} + {M_{i, j}} $

(20)

其中, ${E_{i, j}}$ 为剩余能量, $D$ 为节点深度, ${T_{i, j}}$ 为节点传输延时. ${M_{i, j}}$ 为节点之间链路质量. ${\alpha _1}, \;{\alpha _2}, \;{\alpha _3}$ 为各个奖励的权重系数. 其中 ${E_{i, j}}$ 定义为:

$ {E_{i, j}} = - \left( {{c_i} + {c_j}} \right) $

(21)

其中,

$ {c_i} = 1 - \frac{{{E_i}}}{{{E_{{\text{init }}}}}} $

(22)

式(21)中, ${c_i},\; {c_j}$ 分别为节点 $i,\; j$ 的剩余能量价值, ${c_i}$ 的剩余价值计算如式(22)所示, 同理可得 ${c_j}$ . $D$ 定义为:

$ D = - \frac{{\left| {{D_{ix}} - {D_{jx}}} \right|}}{{{D_{ij}}}} $

(23)

其中, ${D}_{ix},\; {D}_{jx}$ 分别为节点 $i,\; j$ 分别在 $x$ 轴方向上的投影. ${D_{ij}}$ 为节点 $i, j$ 的欧氏距离. 节点传输延时为:

$ {T_{ij}} = {T_i} + {T_j} $

(24)

$ {{{T}}_i} = \left( {1 - \left( {{E_i}/{E_{{\text{init }}}}} \right)} \right)\times{T_{\max }} + \eta $

(25)

其中, ${E_i}$ 为当前节点能量, ${E_{{\rm{init}}}}$ 为节点初始能量, ${T_{\max }}$ 为最大持续时间, $\eta $ 为随机值. 当传输失败时, 将不会再考虑节点 $j$ 的能量作为奖励, 以及 $j$ 点的延时信息, 因此节点传输失败奖励为:

$ {\widetilde R_{i, j}} = {\alpha _1}{c_i} + {\alpha _2}D + {\alpha _3}{T_i} + {M_{i, j}} $

(26)

综上所述, 第 $n$ 次传输经过了 ${n_{{\zeta _e}}}$ 个节点, $Q$ 网络的奖励为:

$ {R_t} = \sum\limits_{i = 1, j = 1, i \ne j}^{{n_{\zeta e}}} {R_{i, j}^*} $

(27)

2.2 QACO路由行为

QACO通过将进行节点之间信息交互的数据包看作蚂蚁, 在网络中进行传播, 维护网络环境. 路由行为的实现, 主要分为4个阶段: 向前蚂蚁阶段、回溯蚂蚁阶段、路由维持阶段、数据传输阶段.

2.2.1 向前蚂蚁阶段

向前蚂蚁阶段: 发生在路由发现, 建立网络拓扑结构期间. 是一个全链路探测阶段, 蚂蚁由源节点出发, 采用 $\varepsilon {\textit{-}}greedy$ 算法不断地向前探查, 以找到通往目的节点的路径. 向前探索蚂蚁作为一种智能体去建立从源节点到目的节点的信息素轨迹. 蚂蚁经过空间节点 $i, j$ 携带的节点信息为:

(1)经过节点的剩余能量 ${E_{i, j}}$ .

(2)蚂蚁经过节点的累积队列延迟 ${T_{i, j}}$ , 以及节点的深度信息 ${D_i}$ 、 ${D_j}$ .

节点 $j$ 能否作为节点 $i$ 的转发节点由到达指标 $\Lambda $ 决定.

$ \Lambda = \left\{ {\begin{array}{*{20}{l}} 0,&{{d_{i, j}} > {R_0}或 {d_{i, j}} = 0} \\ 1,&{0 < {d_{i, j}} \leqslant {R_0}} \end{array}} \right. $

(28)

$ {d_{i, j}} $ 为节点 $i, j$ 之间的欧氏距离, 若 $\Lambda $ 为1则节点 $i$ 将节点 $j$ 加入邻居表, 否则不加入. 为了找到一条合适的路径, 蚂蚁需要带着数据包, 并不断地进行广播. 如图2为一个蚂蚁经过一个节点的过程图. 当一个蚂蚁经过一个节点, 首先判断达指标 $\Lambda $ , 若满足则将节纳入邻居节点, 继续向下传播, 否则直接丢弃. 若到达目的节点, 则是直接产生回溯蚂蚁, 更新链路信息素, 否则继续搜集信息向下转发.

2.2.2 回溯蚂蚁阶段

在 $t$ 时隙向前蚂蚁携带数据信息到达目的节点时, Q网络立即采用评估模型对第 $g$ 条路径进行评估, 如式(29)所示:

$ {\Psi _g} = \hat \Gamma \times {{\rm{e}}^{Q\left( {{s_t}, {a_t}} \right) + \gamma \sum\limits_{{s_{t + 1}}{\in S}} {P_{{s_t}{s_{t + 1}}}^{{a_t}}} Q\left( {{s_{t + 1}}, {a_t}} \right)}} $

(29)

其中,

$ \hat \Gamma = {{\sum \Lambda } \mathord{\left/ {\vphantom {{\sum \Lambda } {{n_{{\varsigma _e}}}}}} \right. } {{n_{{\varsigma _e}}}}} (\Lambda = 1) $

(30)

其中, $Q({s_t}, {a_t})$ 为第 $g$ 条路径的 $Q$ 值奖励, $\gamma $ 为挥发系数, $ P_{_{{s_t}{s_{t + 1}}}}^{{a_t}} $ 为转移概率, $\hat \Gamma $ 为平均邻居节点系数. 回溯蚂蚁通过评价模型对 ${\Psi _g}$ 值进行评估. 最后选择最优的路径将数据发送相应数据包, 表达式为:

$ {\psi _*} = \arg \max \sum {{\Psi _n}} $

(31)

其他向前蚂蚁变为回溯蚂蚁, 将路径的 $Q$ 值信息带回链路中, 并更新链路的信息素.

2.2.3 路由维持和数据传输阶段

当源节点以一定的流量不断地发送数据时, 向前蚂蚁周期性地产生, 由于水下网络拓扑环境不是单一固定的, 是实时变化的, 因此在路由维持阶段, 还要处理网络拥堵问题. 网络拥堵情况由指标 $\phi $ 决定, 计算方式如下:

$ \phi = 1 - \left( {{N_{{\rm{receive}}}}/{N_{{\text{send }}}}} \right) $

(32)

其中, ${N_{{\rm{receive}}}}$ 为接收节点个数, ${N_{{\rm{send}}}}$ 为源节点发送节点数, $\phi $ 值越大, 说明网络越空闲, 可以适当增加发送节点数, 否则应该降低节点数. 在算法1中概括了QACO算法, 数据的传输是选择式(27)最优决策进行数据的传输. 详细的传输方法及决策过程如算法1所示.

3 仿真实验与结果分析 3.1 仿真参数设置

为了评估QACO协议的性能, 本文构建了水下传感网络仿真环境, 并将传统DBR算法与本节中的算法相比较. 具体的仿真参数设置如下: 空间为一个 $3000 \times 3000 \times 3000\;{{\rm{m}}^3}$ 的水下传输模型, 并设置200–600个传感器节点, 不规则地分布于环境模型中. 每个节点的最大传输半径为1 000 m; 在水面和底部分别设置一个源节点和目的节点. 维护蚂蚁周期性的广播数据包以维护传感网络, 网络仿真参数如表1所示. ${\alpha _1}, {\alpha _2}, {\alpha _3}$ 分别为节点能量、深度、延时的调整系数, ${\alpha _1}$ 水深系统设计的调整参数, 用于将数据从源节点传到目的节点.

算法1. QACO路由决策算法

输入: 初始化Q-learning参数: 折扣因子 $\scriptstyle \gamma $ , 奖励值 $\scriptstyle R$ , 选择概率 $\scriptstyle P$ , 权重系数 $\scriptstyle {\alpha _1}, \;{\alpha _2},\; {\alpha _3}$ .

输出: 式(14)得出的路由决策.

● 初始化阶段

1. 初始化节点参数: 中继节点 $\scriptstyle {W_m} $ , 节点传输范围 $\scriptstyle {R_0}$ , 节点初始能量 $\scriptstyle {E_{{\rm{init}}} }$ , 网络节点发射功率 $\scriptstyle {P_s}$ 和接收功率 $\scriptstyle {P_r}$ , 以及空闲时的功率 $\scriptstyle {P_k}$ .

2. 初始化Q网络相关参数: 折扣因子 $\scriptstyle \gamma $ , 奖励值 $\scriptstyle R$ , 选择概率 $\scriptstyle P$ , 权重系数 $\scriptstyle {\alpha _1},\; {\alpha _2},\; {\alpha _3}$ , 以及初始 $\scriptstyle Q$ 矩阵, 数据包转发次数 $\scriptstyle {G_0}$ .

● QACO路由及决策

3. $\scriptstyle {\rm{for}}\; episode = 1, 2, 3, \cdots , {G_0} \;{\rm{do}}$ //设置数据传输次数

4. $\scriptstyle {\rm{for}}\; t = 1, 2, 3, \cdots , T \;{\rm{do}}$ //传输时隙

5. 向前蚂蚁依次从源节点出发, 广播节点 $\scriptstyle {W}_{n}, {W}_{l} $ 包头信息.

6. 基于 $\scriptstyle \varepsilon {\textit{-}} greedy$ 访问节点, 并将已访问节点加入自己的禁忌表.

7. 计算相邻 $\scriptstyle i, j$ 节点之间的欧氏距离 $\scriptstyle {d_{ij}}$ .

8. 若 $\scriptstyle 0 < {d_{ij}} < {R_0}$ , 则将节点分别纳入自己的邻居表. 否则将不加入邻居表.

9. 计算第 $\scriptstyle n$ 次传输的环境状态 $\scriptstyle {s}_{(n, t)}=[{D}_{(n, t)}, {E}_{(n, t)}, {T}_{(n, t)}] $ , $\scriptstyle n \in {G_0}$ .

10. 将状态输入Q网络计算Q值

11. 根据评估模型对第传到目的节点的 $\scriptstyle {{g} }$ 条路径进行评估得出 $\scriptstyle {\psi _*}$ .

12. 最优路径回溯蚂蚁向源节点传回响应信息, 其余回溯蚂蚁则分别返回更新链路信息.

13. 信息更新完成, 选择动作 $\scriptstyle {a_t}$ 选出的最大Q值的路径进行下一次数据的发送.

14. 以式(27)更新计算动作的奖励 $\scriptstyle R_{ij}^* $ , 且状态转变为 $\scriptstyle {s_{t + 1}}$ .

15. $\scriptstyle {\rm{end}}\; {\rm{for}}$

16. $\scriptstyle {\rm{end}}\; {\rm{for}}$

3.2 仿真结果分析

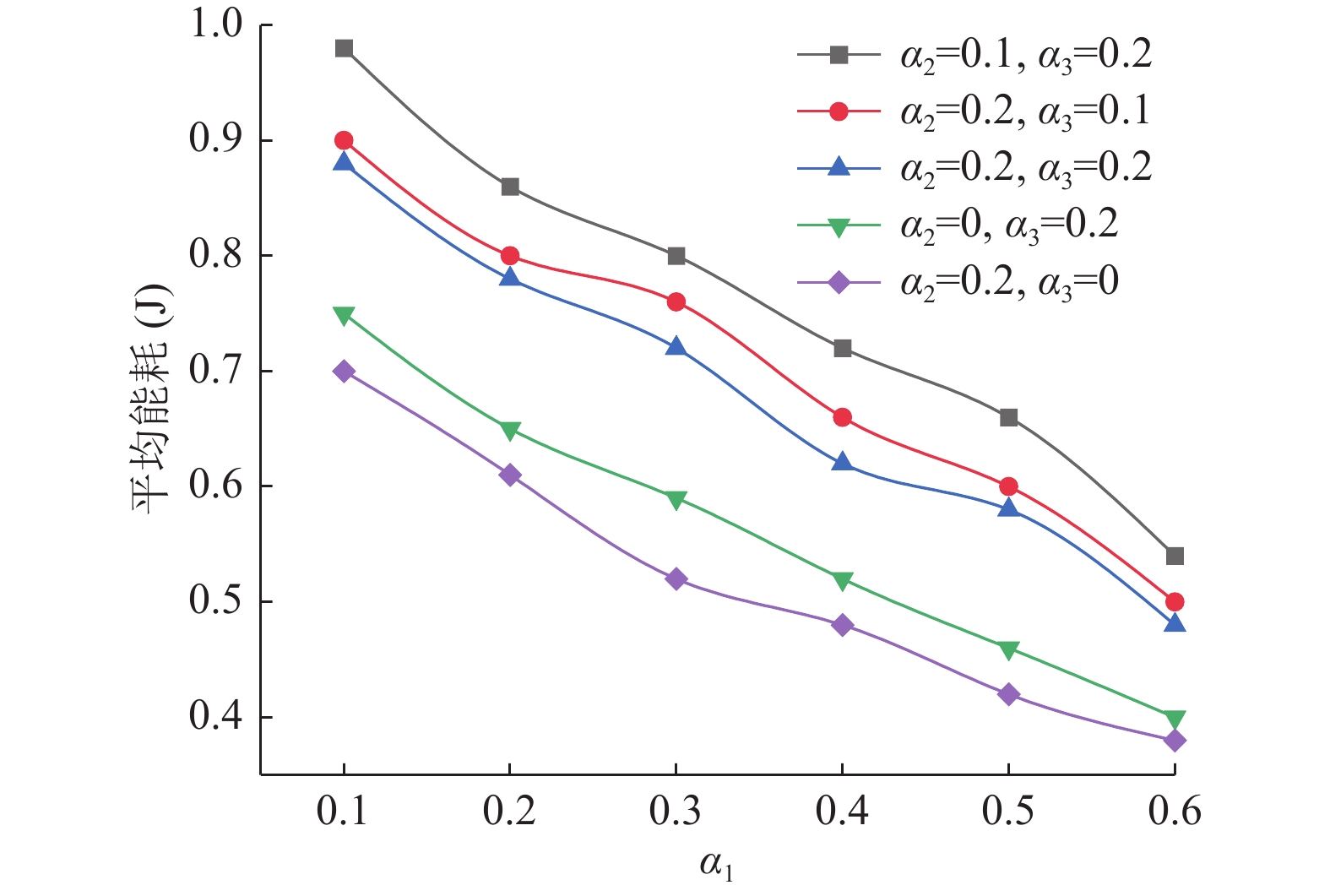
如图3所示, 首先对不同 ${\alpha _1}$ 下的算法的平均能耗进行实验, 平均能耗进行归一化为 $(0, 1)$ . 在进行模拟实验中 ${\alpha _1} \in [0, 0.6]$ 、 ${\alpha _2} = \{ 0, 0.1, 0.2\} $ 、 ${\alpha _3} = \{ 0, 0.1, 0.2\} $ . 通过对比不同的参数进行仿真实验, 可以得出结论: ${\alpha _1}$ 越高, 并且 ${\alpha _3}$ 越低, 会使得网络的平均能耗越低, 网络的寿命越长.

由图3可知, 得出了不同权重下对网络能耗的影响情况, 为了使得网络性能更加, 取 ${\alpha _1} = {\alpha _2} = {\alpha _3} = 0.2$ 作为QACO的权重系数, 分别与其他同类算法相互比较. 由图4显示了不同节点密度情况下, 网络中节点平均延时情况. 由于QACO引入了水深链路质量因子LQI, 相比于QLACO单个节点添加等待时间的方式解决空洞的方式, QACO带来了更低的节点延时信息. 并且随着节点的增加, QACO的优势显得更加明显. 同时与考虑单一影响因素的协议相比, QACO协议更稳定且延时更低.

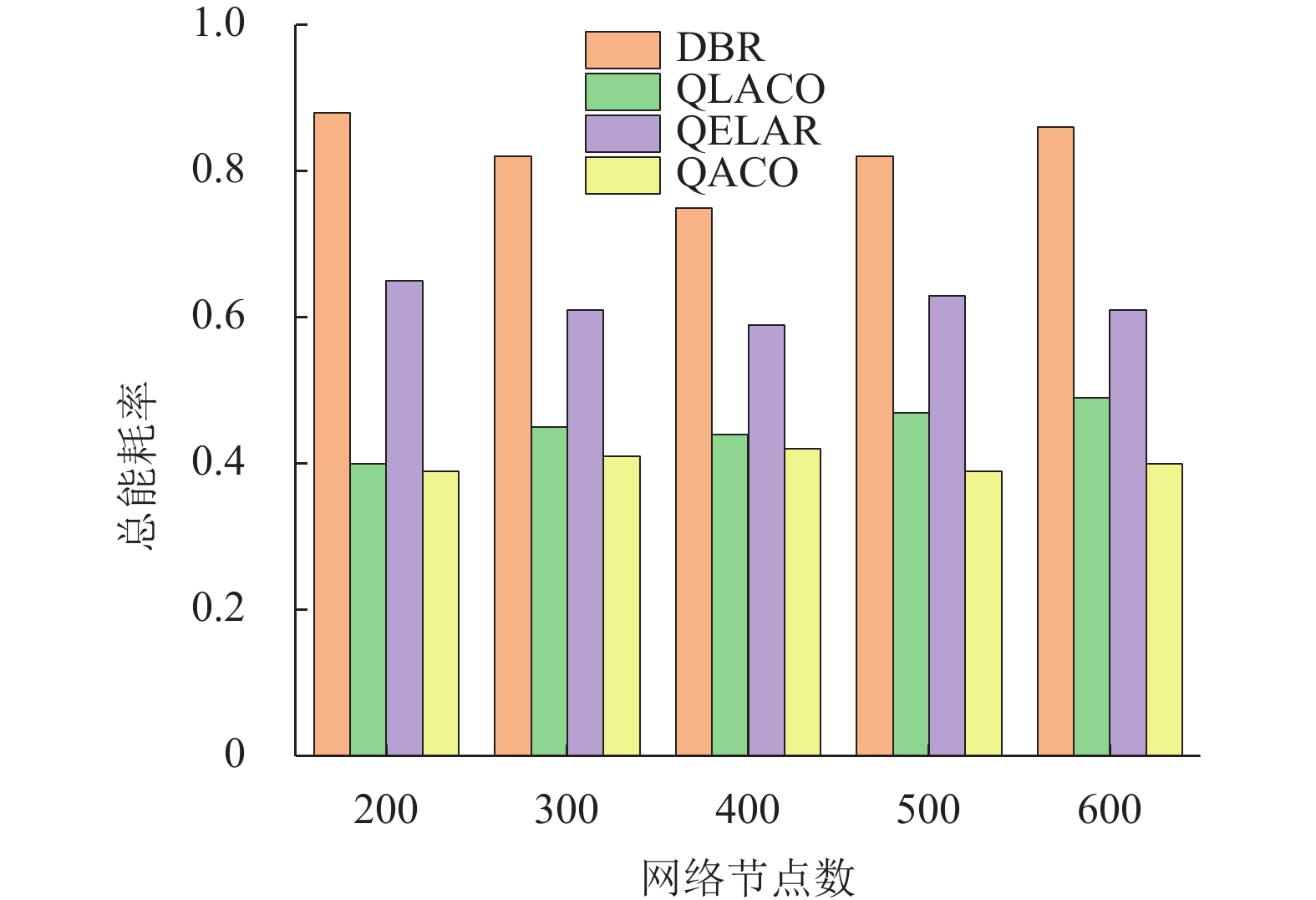
结合图5和图6, 随着网络节点数量的增加, 采用QACO路由协议和与QELAR、QLACO和DBR协议相比, 具有更长的网络生命周期和最少的能耗. 由于QLACO在处理路由空洞时会造成节点长时间的等待, 增加节点能量的消耗, 容易使节点陷入局部最优, 并且在节点数量增加时这一弊端显得更为明显. 而QACO通过链路质量因子LQI来判断链路好坏, 并兼顾考虑节点深度、能量、延时, 使得路由得出全局最优选择, 避免了路有空洞问题. 同时QACO采用智能蚂蚁进行路由行为, 优化了链路的传输效率, 降低了系统能耗, 延长了网络的生命周期.

4 结论

本文提出了一种基于Q学习优化的蚁群智能水声网络路由协议, 利用Q学习进行确定全局路由最优选择, 并设计基于延迟、剩余能量、深度和链路质量相关奖励函数. 并将蚁群算法应用于水声传感网络的路由行为, 实现水下数据的稳定可靠传输, 并解决了路有空洞问题, 分别从网络的延时、能量消耗、生命周期方面对协议进行了仿真实验, 实验证明, QACO算法在延时, 能耗以及网络的生命周期方面都明显优于QELAR、QLACO和DBR算法.