2. 上海第二工业大学 智能制造与控制工程学院, 上海 201209
2. School of Intelligent Manufacturing and Control Engineering, Shanghai Polytechnic University, Shanghai 201209, China
现代工业对汽车行业生产安全的要求越来越高, 这使得生产厂商越来越注重汽车相关产品及配件的质量和精度[1, 2]. 在汽车生产过程中, 油封是一种重要的机械元件, 主要用于隔离传动机构和受力机构, 以防止机油进入排气管和避免机油流失. 然而, 油封的生产过程中存在很多影响产品尺寸的因素, 包括人为因素和自然因素. 因此, 需要对加工完的油封进行尺寸检测. 目前, 传统的人工检测可能无法满足检测精度的要求. 因此, 边缘检测技术逐渐被应用于工业生产检测中.
边缘检测的实质是提取图像背景和前景目标的分界线, 其分割边界即为图像边缘. 传统的边缘检测通常基于微分算子进行计算, 例如Laplace算子和Canny算子等, 但只能达到像素级检测精度[3]. 随着工业生产的精度提高, 像素级的边缘检测精度受到了局限. 因此, 越来越多的专家学者致力于研究亚像素边缘检测算法. 目前, 亚像素边缘检测算法主要分为3类: 插值法、拟合法和矩方法[4]. 插值法具有计算复杂度低和计算量小优点, 但其对噪声敏感, 会使图像轮廓模糊. 拟合法能够有效降低噪声的敏感度, 并可以减小灰度误差, 但其算法模型复杂和计算量大. 在亚像素检测算法中, 矩方法边缘检测算法不受图像旋转变化的影响, 具备良好的抗噪性, 因此受到广泛关注. 目前, 由于Zernike矩的独特优点, 国内外学者对其进行了大量研究. 刘悦等[5]提出基于Zernike矩的光斑图像亚像素边缘检测方法, 主要是通过Sobel算子的粗定位, 再用Zernike矩进行亚像素定位, 减小边缘检测的误差和时间. 程敏杰等[6]提出利用一种形态学滤波方式细化边缘的Zernike矩边缘检测算法, 并结合直方图的最大类间方差来优化, 以满足直齿轮检测的精度要求.
本文以气门油封为研究对象, 提出一种基于Zernike矩优化的亚像素级检测算法. 首先采用Canny边缘检测算法进行粗定位, 然后采用改进的Zernike矩算法进行图像的亚像素级定位, 再通过最小二乘法进行圆拟合, 最后进行实验分析以验证检测精度是否满足要求.
1 检测系统的设计 1.1 系统构成与工作原理气门油封组装机主要由上料机构、抓取机构和视觉检测机构3部分组成. 在组装过程中, 油封和弹簧分别通过振动盘进行上料, 随后由抓取机构完成弹簧的抓取, 并横移至油封上方进行组装. 最后, 检测机构对产品进行合格性检验, 并剔除不合格品, 确保出厂产品的合格率. 视觉检测模块不仅需要完成产品的分类, 还需与运动控制进行信息传输. 图1为气门油封组装机的示意图.
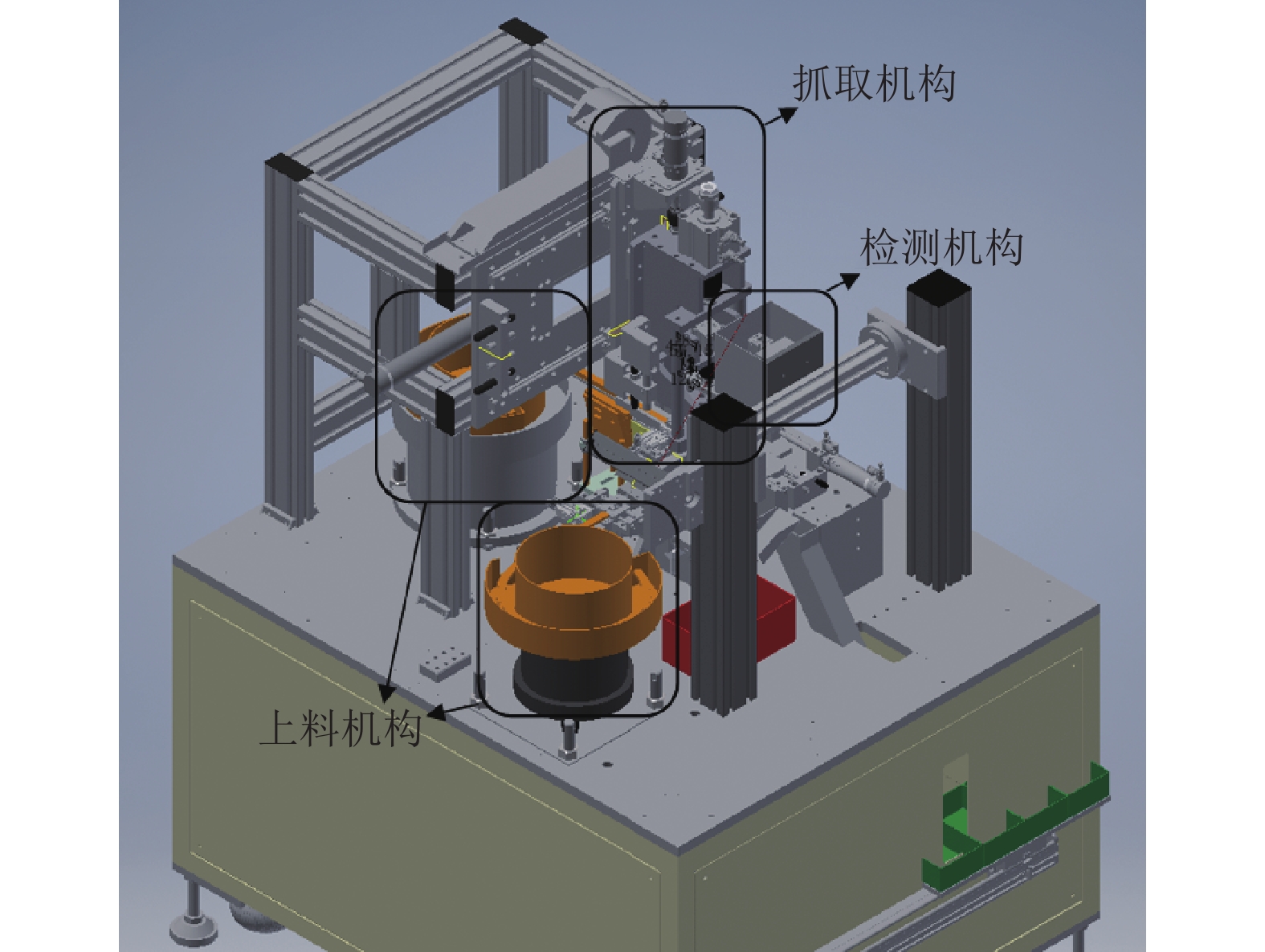
|
图 1 生产线工艺流程图 |
1.2 工件检测要求
本文中检测的产品尺寸数据为: 外径为11 mm, 内径为6 mm, 高度为8 mm. 在工件组装时, 需要将弹簧安装在油封的径口部, 以满足发动机气门的密封性要求. 目前, 气门油封制造企业已经制定了相应的标准, 例如: 零件尺寸误差应小于±0.15 mm, 每个零件检测时间不得超过0.5 s, 检测准确率应大于95%, 漏检率应小于1%, 过检率应小于0.1%.
2 图像滤波 2.1 高斯滤波高斯滤波是一种线性滤波, 它本质上是加权平均滤波. 该滤波利用二维高斯分布对目标图像进行加权平均值替换中心点像素值[7]. 二维高斯函数在各个方向上的平滑程度相同, 因此可以保留原图像的边缘特征. 高斯滤波对于正态分布的噪声有着很好的抑制效果. 在滤波过程中, 使用的高斯函数如式(1)所示:
| $ G(x, y) = \frac{1}{{2{\text{π}} {\delta ^2}}}{{\rm{e}}^{ - \frac{{{x^2} + {y^2}}}{{2{\delta ^2}}}}} $ | (1) |
其中,
双边滤波是一种基于高斯滤波改进的去噪方法[7]. 该方法综合考虑了模板范围内像素与目标像素的像素值灰度和空间距离. 双边滤波是由两个高斯滤波组成, 分别计算空间信息和像素的灰度值信息, 这既考虑到邻域的概念, 又解决了灰度值相似的问题. 因此, 双边滤波能够避免其他像素点对边缘点的干扰, 有效保护图像边缘的真实信息. 每个像素所占的权重比例是根据值域高斯函数计算得到. 双边滤波公式如式(2)所示:
| $ g(x, y)=\frac{\displaystyle\sum_{(x, y) \in M(x, y)} f(k, l) \omega(x, y, k, l)}{\displaystyle\sum_{(x, y) \in M(x, y)} \omega(x, y, k, l)} $ | (2) |
其中,
权重系数中
| $ {\omega _s} = \exp \left( { - \frac{{{{(x - k)}^2} + {{(y - l)}^2}}}{{2\delta _s^2}}} \right) $ | (3) |
权重系数中
| $ {\omega _r} = \exp \left( { - \frac{{\parallel f(x, y) - f(k, l)\parallel }}{{2\delta _r^2}}} \right) $ | (4) |
将加权系数进行相乘, 如式(5)所示:
| $ \omega (x, y, k, l) = {\omega _s} \times {\omega _r} $ | (5) |
其中,
综上所述, 针对气门油封进行了两种滤波方法的对比实验, 实验结果如图2所示. 图2中可以看出: 在原图中的方框区域表示图像噪声, 高斯滤波处理后的图像清晰度降低, 虽然可用于正态分布噪声的滤波, 但对其他噪声的滤波效果一般, 且对边缘信息的保护效果较差; 相比之下, 双边滤波具有更好的边缘保护效果, 图像处理后更加清晰, 且保留了大量的图像边缘信息. 因此, 本文选用双边滤波方法对油封数据集进行图像滤波处理.

|
图 2 滤波实验对比图 |
3 基于Zernike矩的亚像素尺寸检测 3.1 传统的Zernike矩原理
矩方法是一种积分算子, 利用矩的旋转、平移、伸缩不变特性. 根据图像的局部矩特征信息进行计算, 其中的矩特征信息主要包括大小、位置、方向、形状等. 常见的有灰度矩、空间矩和Zernike矩等. 其中Zernike矩具有定位精度高和抗噪性强的特点, 被广泛的应用[8]. Zernike矩对于图像T
| $ {Z_{nm}} = \frac{{n + 1}}{{\text{π}} }\mathop \int \int \nolimits_{{x^2} + {y^2} \leqslant 1} V_{nm}^ * (d,\theta )T(x,y)dxdy $ | (6) |
其中,
Zernike矩的理想模型, 如图3所示. 图中的阴影表示边缘轮廓外侧, L表示实际边缘位置, d表示边缘带原点的距离, 图像背景和边缘的灰度值分别为h和h+k, d与x轴的夹角为θ.

|
图 3 Zernike矩的理想模型 |
由于Zernike矩具有旋转不变性, 旋转θ后的关系式
| $ Z'_{nm} = {Z_{nm}}{{\rm{e}}^{ - im\theta }} $ | (7) |
其中, i表示虚数单位. 利用
| $ \left\{ \begin{gathered} Z'_{00} = {Z_{00}} \\ Z'_{11} = {Z_{11}}{{\rm{e}}^{ - i\theta }} \\ Z'_{20} = {Z_{20}} \\ \end{gathered} \right. $ | (8) |
旋转θ角度后, 关于x轴对称, 如式(9)所示:
| $ \mathop \int \int \nolimits_{{x^2} + {y^2} \leqslant 1} T(x,y)dxdy = 0 $ | (9) |
由于
| $ Im\left[ {Z'_{11} } \right] = \sin (\omega ){Re} \left[ {{Z_{11}}} \right] - \cos (\omega )Im\left[ {{Z_{11}}} \right] = 0 $ | (10) |
其中,
| $ \theta = {\tan ^{ - 1}}\left( {\frac{{{Re} \left[ {{Z_{11}}} \right]}}{{Im\left[ {{Z_{11}}} \right]}}} \right) $ | (11) |
推导出
| $ \left\{ \begin{gathered} Z'_{00} = h{\text{π}} + \frac{{k{\text{π}} }}{2} - k{\sin ^{ - 1}}d - kl\sqrt {1 - {d^2}} \\ Z'_{11} = \frac{{2{k^3}\sqrt {{{\left( {1 - {d^2}} \right)}^2}} }}{3} \\ Z'_{20} = \frac{{2k{d^3}\sqrt {{{\left( {1 - {d^2}} \right)}^2}} }}{3} \\ \end{gathered} \right. $ | (12) |
根据式(12), 求得参数h、k、d的值, 计算方法如式(13)所示:
| $ \left\{ \begin{gathered} h = \frac{{\left[ {{Z_{00}} - \dfrac{{k{\text{π}} }}{2} + k\arcsin d + kd{{\left( {1 - {d^2}} \right)}^{\frac{3}{2}}}} \right]}}{{\text{π}} } \\ k = \dfrac{{3{Z_{11}}{{\rm{e}}^{ - i\omega }}}}{{2{{\left( {1 - {d^2}} \right)}^{\frac{3}{2}}}}} \\ d = \dfrac{{{Z_{20}}}}{{{Z_{11}}{{\rm{e}}^{ - i\omega }}}} \\ \end{gathered} \right. $ | (13) |
用M×M的模板检测, 求解亚像素坐标(X, Y)计算公式, 如式(14)所示:
| $ \left\{ \begin{gathered} X = x + \frac{M}{2}d\cos \theta \\ Y = y + \frac{M}{2}d\sin \theta \\ \end{gathered} \right. $ | (14) |
传统的Zernike矩用5×5模板检测边缘精度不高, 可以采用7×7的模板进行优化, 进而提升边缘检测的精度, 抗噪性也得到增强.
3.2 基于Zernike 矩的亚像素边缘检测优化(1) Canny算子的粗定位
Canny边缘算子是一种多级检测算法[9]. 目前常见的一节微分算子和二阶微分算子都是基于灰度值的突变来确定边缘点, 而边缘附近的噪点对检测精度产生不同程度的影响. 相比之下, Canny边缘算子检测具有精度高、强抗噪性和快速的运算速度. Canny算子边缘检测步骤, 如图4所示.
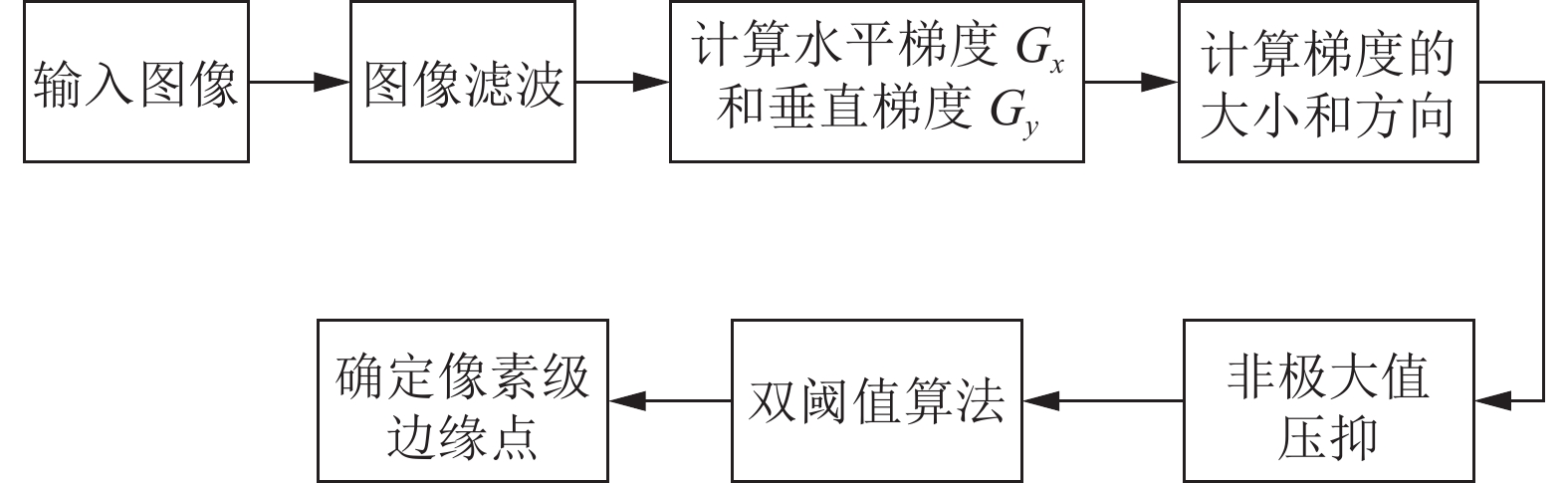
|
图 4 Canny算子边缘检测流程图 |
① 图像滤波. 对图像
| $ I(i, j) = g(i, j) \times f(i, j) $ | (15) |
② 利用Sobel算子求解x和y两个方向上梯度
| $ G(i, j) = \sqrt {G_x^2(i, j) + G_y^2(i, j)} $ | (16) |
| $ \delta (i, j) = \arctan \left[ {\frac{{{G_x}(i, j)}}{{{G_y}(i, j)}}} \right] $ | (17) |
③ 非极大值限制. 通过比较每个像素点在不同梯度方向上的幅值大小, 剔除某些局部最大值的像素点, 有利于提升边缘检测的精度.
④ 双阈值算法检测. 对每个像素点进行判断, 高于高阈值的像素点保留, 小于低阈值的像素点舍弃, 其余像素点需要分析与高阈值联系的程度.
由于Canny算子在梯度方向上采用非极大值抑制来获取真实的边缘, 达到了降低错误检测的概率; 采用双阈值算法避免双边缘出现, 能够检测出准确的边缘点.
(2)理想模型优化
对实际图像中边缘区域像素点灰度值的变化进行分析, 实际上的大多数的边缘都是逐渐变化的过程. 这是由于光线的衍射现象会导致图像边缘与背景产生衍射区域, 进而影响边缘的灰度值变化规律. 为了符合实际的边缘灰度值变化规律, 国内外学者提出了三灰度边缘模型[10], 如图5所示. 图5中的实线表示三级灰度边缘模型, 虚线表示经典的理想模型. 其中, h、h+∆k、h+k分别表示为背景灰度值、衍射区域的灰度值、边缘灰度值, d2表示中心到正式边缘的距离, d1表示中心到衍射区域边缘的距离. 由于采用7×7的Zernike矩检测模板, 因此

|
图 5 三灰度过渡模型 |
根据三灰度过度模型, 求解Zernike矩的
| $ \begin{split} {Z_{00}} =& {{\Delta }}k\left[ {{d_1}\sqrt {1 - d_1^2} + {{\sin }^{ - 1}}\left( {{d_1}} \right) - {d_2}\sqrt {1 - l_1^2} - {{\sin }^{ - 1}}\left( {{d_2}} \right)} \right] \\ & + k\left[ {\frac{{\text{π}} }{2} - {d_1}\sqrt {1 - d_1^2} - {{\sin }^{ - 1}}\left( {{d_1}} \right) + h{\text{π}} } \right] \end{split} $ | (18) |
| $ {Z_{11}} = \frac{2}{3}{{\Delta }}k\left[ {{{\left( {1 - d_2^2} \right)}^{\frac{3}{2}}} - {{\left( {1 - d_1^2} \right)}^{\frac{3}{2}}}} \right] + \frac{2}{3}k{\left( {1 - d_2^2} \right)^{\frac{3}{2}}} $ | (19) |
| $ {Z_{20}} = \frac{2}{3}{{\Delta }}k\left[ {{{\left( {1 - d_2^2} \right)}^{\frac{3}{2}}} - {d_1}{{\left( {1 - d_1^2} \right)}^{\frac{3}{2}}}} \right] + \frac{2}{3}k{d_1}{\left( {1 - {d_2}^2} \right)^{\frac{3}{2}}} $ | (20) |
| $ \begin{split} {Z_{31}} = &\frac{2}{3}{{\Delta }}k\left[ {{{\left( {1 - {d_2}^2} \right)}^{\frac{3}{2}}} - {{\left( {1 - d_1^2} \right)}^{\frac{3}{2}}}} \right] + \frac{4}{5}k{\left( {1 - {d_2}^2} \right)^{\frac{3}{2}}} \\ & - \frac{4}{5}{{\Delta }}k{\left( {1 - {d_2}^2} \right)^{\frac{3}{2}}} + \frac{2}{{15}}k{\left( {1 - {d_2}^2} \right)^{\frac{3}{2}}}\left( {6{d_1}^2 - 1} \right) \end{split} $ | (21) |
联立求解参数
| $ \left\{ \begin{gathered} {d_2} = \frac{{6{{\textit{Z}}_{00}} - 3a{{\textit{Z}}_{00}} + \sqrt {\left( {9{a^2} - 6} \right){{\textit{Z}}_{00}}^2 - 30{{\textit{Z}}_{31}}{{\textit{Z}}_{11}} + 36{{\textit{Z}}_{20}}^2} }}{{6{{\textit{Z}}_{11}}}} \\ {d_1} = {d_2} + a \\ {{\Delta }}k = \frac{{3\left( {{d_1}{{\textit{Z}}_{11}} - {{\textit{Z}}_{20}}} \right)}}{{2a{{\left( {1 - d_2^2} \right)}^{\frac{3}{2}}}}} \\ k = \frac{{\dfrac{3}{2}{{\textit{Z}}_{11}} - {{\Delta }}k\left[ {{{\left( {1 - {d_2}^2} \right)}^{\frac{3}{2}}} - {{\left( {1 - d_1^2} \right)}^{\frac{3}{2}}}} \right]}}{{{{\left( {1 - {d_1}^2} \right)}^{\frac{3}{2}}}}} \\ \end{gathered} \right. $ | (22) |
故边缘参数
| $ d = {d_1} - \frac{{{{\Delta }}k}}{k}\left( {{d_1} - {d_2}} \right) $ | (23) |
(3)自适应阶跃阈值
传统的Zernike矩亚像素算法中, 主要是通过计算
针对灰度阈值
(4) Zernike矩优化后的检测流程
针对Zernike矩的不足之处, 本文采用了“粗细定位”结合的方式对其进行了优化. 具体的检测流程如下.
Step 1. 对图像进行预处理, 例如双边滤波等操作.
Step 2. 利用Canny算子进行像素级的粗定位, 获取边缘点集.
Step 3. 通过7×7的模板进行卷积计算, 求解Zernike矩的
Step 4. 求解边缘角度θ、背景灰度值h、边缘的灰度值h+k、边缘到原点的距离d.
Step 5. 通过Otsu法自动选取灰度阈值
Step 6. 求解亚像素边缘点的坐标.
由于Canny算子边缘检测具有很好的抗干扰能力, 且在像素级边缘定位精度方面表现优异, 经过Canny算子的粗定位后, 可以除部分噪点和干扰边缘点, 有效降低亚像素边缘检测的边缘点的计算. 本文采用了Otsu法来自动选取合适的灰度阈值, 以确保Zernike矩算法的检测精度稳定, 同时避免了人工选择阈值的困难.
(5)实验结果分析
为了验证改进的Zernike矩的算法优势, 进行实验对比分析, 如图6所示.
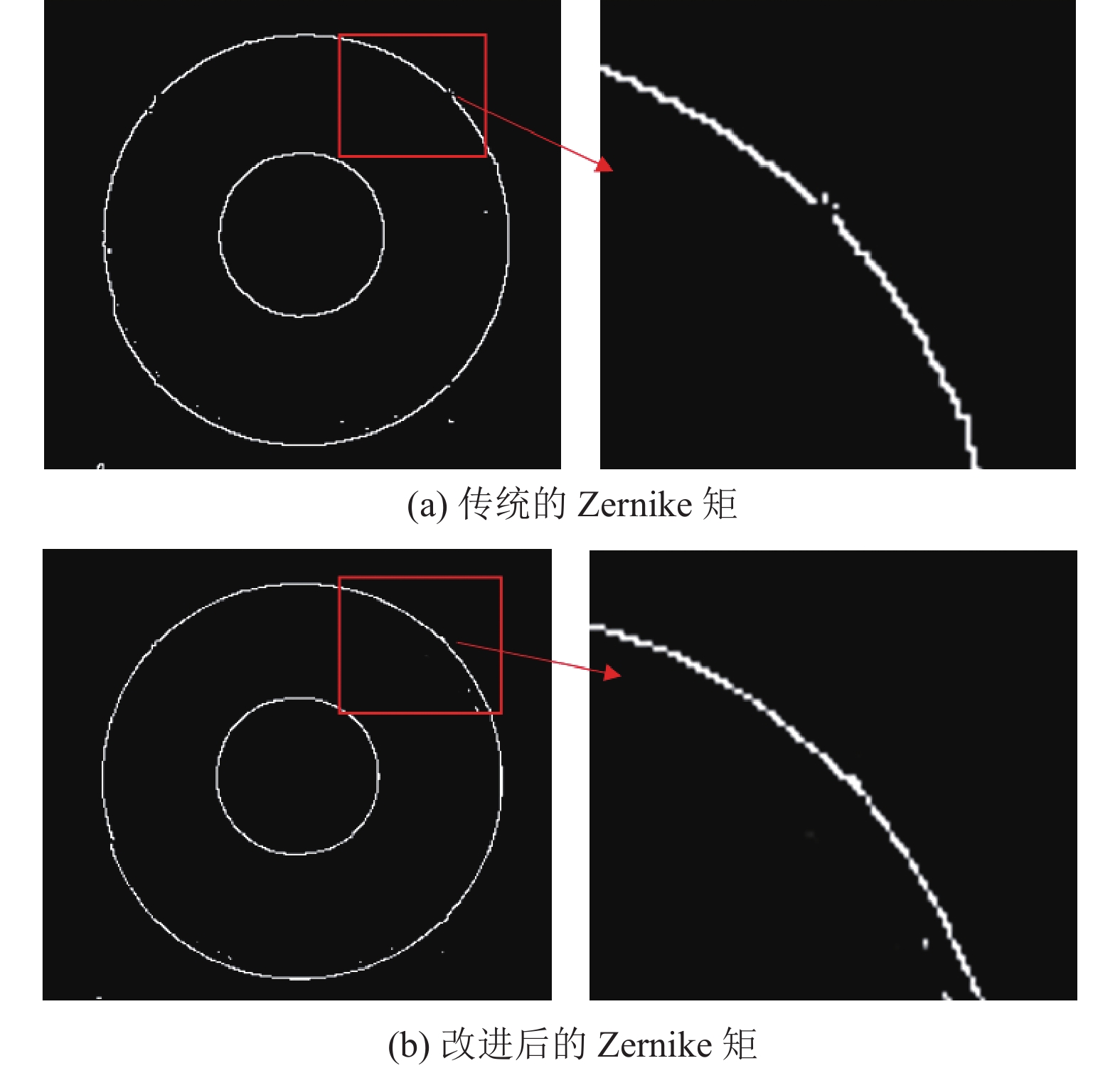
|
图 6 改进Zernike矩算法效果对比图 |
从图6中可以看出, 传统的Zernike矩边缘检测会出现断边现象, 可能是采用了理想阶跃模型; 优化后的Zernike矩边缘检测有着完整边缘信息, 并且提升了边缘点的定位精度. 优化算法采用Canny算子进行粗定位, 对图像有着明显的降噪作用. 在算法的检测时间上, 优化后的Zernike矩边缘检测也是有着明显的优势, 减少了人工阈值选择的重复实验时间.
4 边缘拟合算法边缘检测算法得到边缘点的坐标, 再根据坐标的位置信息进行特征圆的识别. 常见的识别检测方法为: Hough圆变换和最小二乘拟合法. Hough圆变换是采用几何空间像素点特征信息与参数空间的网格点进行多对一的映射, 再对参数空间内所有点特征信息遍历求, 以确定圆心坐标、半径等信息. 其检测精度主要与参数空间的网格有关, 若要求检测精度高, 需要将网格细化, 这样会增加大量的计算量, 从而识别速度变慢, 时间复杂度增加, 不符合工业检测的高精度、时效性的要求. 相比之下, 最小二乘拟合法则是通过最小化所有像素点到圆心距离的平方和来实现圆的拟合. 其具有精度高、计算速度快、识别精度高等优点. 所以, 本文采用最小二乘拟合法进行特征圆的拟合检测.
4.1 最小二乘拟合圆法将亚像素边缘坐标作为采样点, 利用最大似然估计的思想来求解气门油封的圆心坐标和我半径等相关参数. 最小二乘拟合圆法求解中, 首先确定圆的曲线公式, 如式(24)所示:
| $ \begin{split} {R^2} = {(x - A)^2} + {(y - B)^2} = {x^2} - 2Ax + {A^2} + {y^2} - 2Bx + {B^2} \end{split} $ | (24) |
设
| $ {x^2} + ax + by + {y^2} + c = 0 $ | (25) |
取气门油封的亚像素边缘点坐标点记为样本
| $ d_i^2 = {\left( {{X_i} - A} \right)^2} + {\left( {{Y_i} - B} \right)^2} $ | (26) |
距离平方和半径平方的差
| $ \begin{split} {\delta _i}& = d_i^2 - {R^2} = {\left( {{X_i} - A} \right)^2} + {\left( {{Y_i} - B} \right)^2} - {R^2} \\ & = X_i^2 + Y_i^2 + a{X_i} + b{Y_i} + c \end{split} $ | (27) |
令
| $ Q(a, b, c) = \sum \delta _i^2 = \sum {\left( {X_i^2 + Y_i^2 + a{X_i} + b{Y_i} + c} \right)^2} $ | (28) |
对式(28)的a, b, c求偏导, 使得
| $ \left\{ \begin{gathered} A = \frac{a}{{ - 2}} \\ B = \frac{b}{{ - 2}} \\ R = \frac{1}{2}\sqrt {\left( {{a^2} + {b^2} - 4c} \right)} \\ \end{gathered} \right. $ | (29) |
将边缘点
为了验证本文采用的优化后的Zernike矩边缘检测和加最小二乘法对气门油封的检测效果. 本实验采用以下步骤: 首先对图像进行预处理; 然后使用Canny算子进行边缘粗定位, 并实现边缘点扩充与筛选; 再利用Zernike矩法提取图像亚像素边缘; 最后使用最小二乘法计算出半径和圆心坐标等信息. 实验分析优化后的Zernike矩进行最小二乘法拟合效果, 如图7所示. 从图中可以看出, 优化后的Zernike矩进行拟合误差更小, 有效地降低了噪声对边缘拟合的影响.
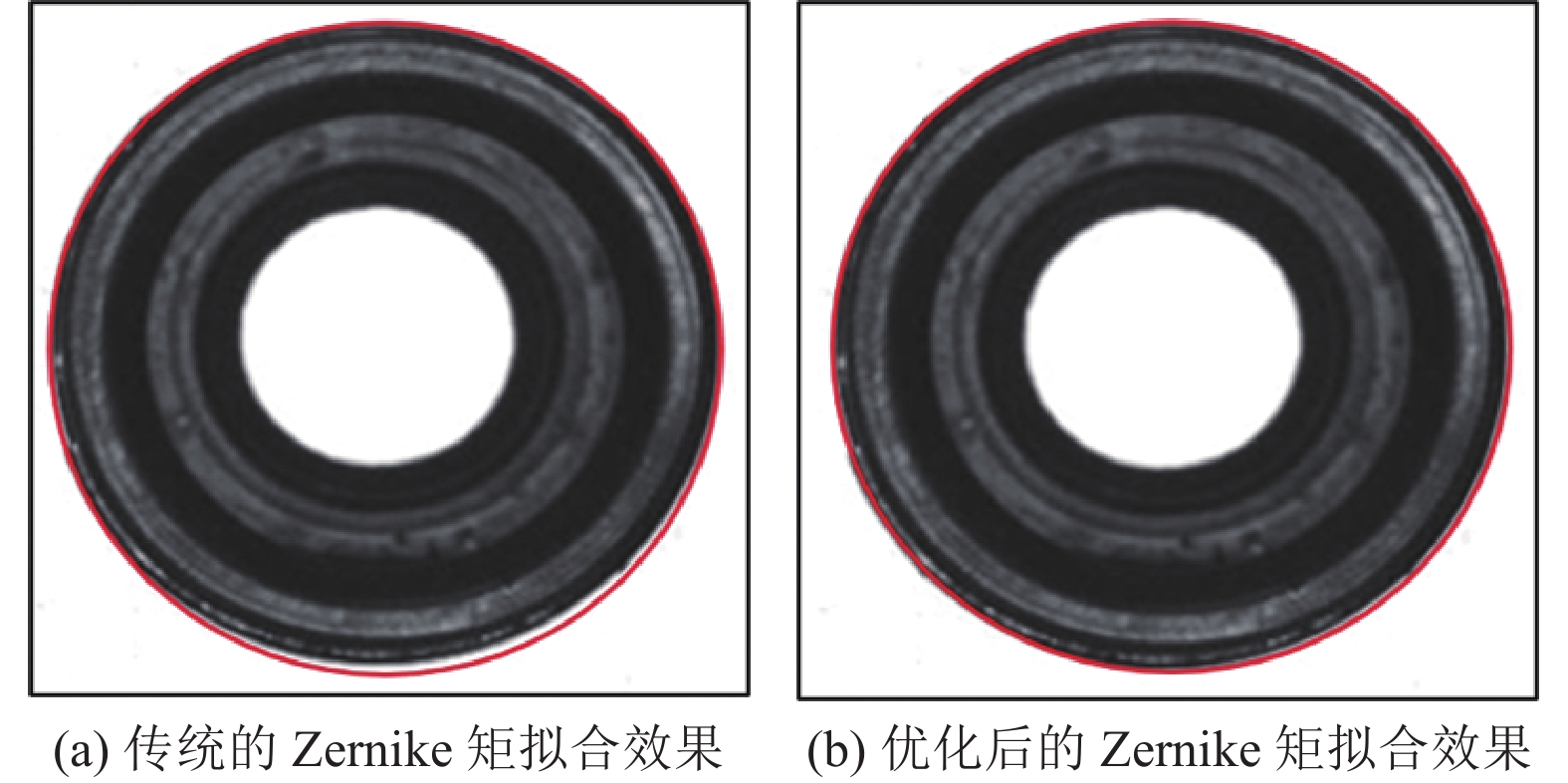
|
图 7 最小二乘法的拟合效果图 |
为了更加直观展现最小二乘法的拟合精度, 选取20组数据进行对比分析, 制作320×320的二值图像, 其图中圆心坐标为(157.5, 164.3), 半径为120. 采集目标图像的圆心坐标和半径数据, 如表1、表2所示. 表中可以看出, 传统的Zernike矩拟合圆心X坐标的平均误差为0.2999, Y坐标的平均误差为0.2763, 半径的平均误差为0.5221; 而优化后Zernike矩拟合圆心X坐标的平均误差为0.2055, Y坐标的平均误差为0.1897, 半径的平均误差为0.3997. 优化后的Zernike矩算法标准差更小, 说明边缘拟合更准确.
5 结语本文针对气门油封的尺寸检测问题, 提出了一种基于Zernike矩改进算法的亚像素边缘检测方法. 在图像预处理阶段, 对高斯滤波和双边滤波进行了比较分析, 得出双边滤波可以有效地滤除噪声, 同时保留图像边缘的细节信息更好. 在获取亚像素级边缘阶段, 本文提出了3种灰度过渡模型并自动选取灰度阈值, 同时利用Canny算子进行边缘的粗定位, 从而提高了算法的抗噪性和自适应性. 通过最小二乘圆拟合法进行实验分析, 可以明显地看出经过优化后的算法检测精度更高, 稳定性更强. 然而, 由于优化后的算法检测时间增加, 需要进一步优化算法以提高其时效性.
| 表 1 传统的Zernike矩的拟合数据 |
| 表 2 优化后Zernike矩的拟合数据 |
| [1] |
杨红娟, 张运楚, 曹建荣. 基于机器视觉的发动机连杆质量多参数检测. 计算机系统应用, 2022, 31(2): 129-136. DOI:10.15888/j.cnki.csa.008296 |
| [2] |
雷刚, 谭巍, 樊伟, 等. 气门油封结构参数设计及优化. 润滑与密封, 2021, 46(7): 121-127. DOI:10.3969/j.issn.0254-0150.2021.07.018 |
| [3] |
肖扬, 周军. 图像边缘检测综述. 计算机工程与应用, 2023, 59(5): 40-54. DOI:10.3778/j.issn.1002-8331.2209-0122 |
| [4] |
刘红涛, 陆安江, 彭熙舜, 等. 光照不均匀下的工件图像亚像素边缘检测. 国外电子测量技术, 2022, 41(10): 1-7. |
| [5] |
刘悦, 朱均超. 基于改进Zernike矩的光斑图像亚像素边缘检测算法. 激光杂志, 2021, 42(5): 32-35. DOI:10.14016/j.cnki.jgzz.2021.05.032 |
| [6] |
程敏杰, 王建文. 利用机器视觉的直齿轮在线测量方法研究. 机械设计, 2020, 37(3): 19-22. DOI:10.13841/j.cnki.jxsj.2020.03.003 |
| [7] |
董正通, 王涛, 赵侦钧, 等. 基于卷积神经网络的标识牌识别技术. 计算机系统应用, 2021, 30(10): 156-163. DOI:10.15888/j.cnki.csa.008158 |
| [8] |
Zhou JJ, Yu JB. Chisel edge wear measurement of high-speed steel twist drills based on machine vision. Computers in Industry, 2021, 128(6): 1034-1036. |
| [9] |
Sangeetha D, Deepa P. FPGA implementation of cost-effective robust Canny edge detection algorithm. Journal of Real-Time Image Processing, 2019, 16(4): 957-970. DOI:10.1007/s11554-016-0582-2 |
| [10] |
朱帅飞, 马伟, 杨芳. 改进Zernike矩的运动靶标高精度定位算法. 机械设计与制造, 2021, 366(8): 235-239, 245. DOI:10.3969/j.issn.1001-3997.2021.08.054 |
| [11] |
张鹏帆, 席剑辉, 朱琳琳. 基于梯度极值Otsu算法的Canny边缘检测改进. 沈阳航空航天大学学报, 2021, 38(5): 58-65. DOI:10.3969/j.issn.2095-1248.2021.05.009 |
 2023, Vol. 32
2023, Vol. 32


