深度强化学习解决了智能体如何将状态映射为动作的问题, 使得智能体能够在与复杂及不确定的环境交互时, 最大化累积获得的奖励, 从而使得深度强化学习能够广泛应用于游戏对抗, 机器人控制, 城市交通, 商业等领域^[1]. 该成功主要有以下几点原因, 首先是将强化学习与深度神经网络结合在一起, 利用深度神经网络强大的建模能力, 对高维状态模式的信息(图像, 声音等)进行建模, 使得智能体能够从中提取状态特征; 随后利用强化学习为提取出来的状态信息分配不同的价值, 赋予智能体连续决策的能力; 最后通过端到端的训练, 将特征提取和决策一起优化, 使得智能体能够如同人类一般处理高维状态模式的信息, 并进行判断与决策^[2]. 然而, 也正是因为这个原因, 为深度强化学习带来重大的挑战.

在深度强化学习中, 大多数环境状态都是复杂的高维状态模式, 而直接从高维环境状态进行观测学习是具有挑战性的. 智能体为了获取连续决策判断的能力, 需要从高维状态模式的环境中提取出低维的有效状态信息, 而这可能需要与环境进行百万次交互, 并收集大量的样本数据来进行训练^[3]. 尤其当面临复杂的任务或者充满随机性的环境时, 智能体所需的学习时间可能以指数倍的速度恶化. 其背后的一个瓶颈挑战是探索, 即在嘈杂未知环境的情况下, 智能体如何进行有效的探索, 并收集到有用的样本经验来最大限度地改善自身策略^[4].

针对这个效率低下的问题, 为了提高算法的探索效率, 近年来有专家学者提出过许多不同的探索策略. 根据这些策略的关键思想以及原理, 可将这些主流的探索策略归为两大类^[5].

第1类是基于不确定性导向的探索策略, 不确定性包含了环境不确定性和认知不确定性, 可通过值函数的贝叶斯后验或者值函数的分布对不确定性进行衡量. 该探索策略通常根据“乐观对待不确定性”的指导原则引导智能体对环境进行探索, 尤其是引导智能体更多地探索认知不确定性高的状态, 同时因为环境的随机性会对智能体产生干扰, 需要避免受到环境不确定性高的影响, 从而实现对环境的高效探索. 该类型的探索策略的典型工作有: Bootstrapped DQN算法^[6], 通过随机选择最有可能是最优的策略来进行探索; RLSVI算法^[7], 旨在通过线性参数化的价值函数进行有效的探索和归纳; OAC算法^[8], 通过最大化状态动作对的值函数的近似置信边界的方法进行探索; OB2I算法^[9], 通过非参数引导法构建了一个通用的UCB奖励, 并与线性设置的LSVI-UCB之间建立了理论联系, 利用偶发的后向更新, 提高了智能体的探索效率.

第2类是基于内在激励信号导向的探索策略, 该探索策略受到人类好奇心的启发, 通过产生内在激励奖励驱动智能体对环境进行探索. 根据设计内在激励信号所使用技术的不同, 可将该探索策略分为3类: 估计环境动力学误差的方法, 典型工作有: ICM算法^[10], 该算法提出了一个好奇心模块, 其用来估计一个状态的新奇程度, 并给予相应的内在奖励驱动探索. 状态新颖性估计方法, 典型工作有: RND算法^[11], 使用神经网络来作为状态新颖程度的估计, 促使智能体更多地探索新颖程度较高的状态. 基于信息增益的方法, 典型工作有: VIME算法^[12], 通过给予智能体一种基于信息增益的内在奖励, 弥补原本稀疏的奖励, 鼓励智能体更好地进行探索.

虽然目前有专家学者提出了许多的探索方法, 但对于这些探索方法之间是否能够进行互补, 并同时从不同的角度解决智能体探索效率低下的问题仍然不清楚.

本文将基于离散动作, 值函数算法的Bootstrapped探索方法^[6]引入基于连续动作, 策略梯度的CCLF算法^[13]中. 结合两种不同类型的探索策略, 提出了BCCLF(Bootstrapped CCLF)算法. 针对CCLF算法深度探索能力较弱, 稳定性差以及收敛速度慢的缺点, 通过将actor网络拓展为multi-head结构, 每个head根据自身的最优策略对环境进行深度探索, 同时多个head之间保持了对潜在最优动作的分布, 为神经网络引入不确定性, 并通过该不确定性引导智能体对环境进行深度探索. 最终通过实验结果证明, 在DMControl的多个连续控制任务上, 极大地提高了算法的探索效率及收敛速度, 超过近年来优秀的无模型算法.

1 相关工作

强化学习的目标是智能体如何在未知, 不确定的环境中进行决策, 最终最大化它所获得的奖励^[14]. 在强化学习中, 智能体不断与环境进行交互, 获取环境中的某个状态后, 进行决策选择最优动作并执行. 环境根据智能体所执行的动作, 输出下一个状态以及执行该动作所取得的奖励. 这个过程可以通过马尔可夫过程来建模.

在马尔可夫过程中, 通常使用元组 $ < S, A, P, R, \gamma > $ 来表示, 其中 $S$ 表示环境状态的有限集合, $A$ 表示智能体可采取动作的有限集合, $P$ 表示环境状态之间的转移概率, $R$ 表示智能体执行某一动作进入环境下一状态时所获得的奖励, $\gamma $ 表示折损因子. 智能体在与环境不断进行交互的过程中, 寻找出最优策略 ${\text{π}} ({{s}}, a)$ , 即在当前状态 $s$ 下执行动作 $a$ 的概率, 使得从当前状态 $s$ 开始执行策略 ${\text{π}}$ , 能够最大化如式(1)所示的值函数:

$ {\nu _{\text{π}} }(s) = {\mathbb{E}_{\text{π}} }\left(\sum\limits_{t = 0}^\infty {{\gamma ^t}{r_{t + 1}}} |{s_0} = s\right)s $

(1)

1.1 Bootstrapped DQN

在深度强化学习中的一个主要挑战是对环境进行有效探索, 而在常见的探索策略中, 其无法对环境进行时间上的深度探索, 而这可能导致样本效率的低下. Osband等人提出了Bootstrapped DQN算法^[6], 将深度探索与深度神经网络进行结合, 从而大大提高了算法的学习速度.

在该算法中, 受Thompson sampling算法的启发, 通过Bootstrapped修改DQN网络结构, 如图1所示, 使其能够更好地拟合Q值的分布.

在训练的每个回合开始之前, Bootstrapped DQN算法从其近似后验中采样单个的Q值函数, 然后, 智能体接下来会将这个Q值函数视为这个回合最优的策略, 并根据这个策略对环境进行探索, 由于每个Q值函数所生成的策略不尽相同, 从而实现对环境的深度探索. 其中每个单独的Q值函数所用于训练的样本 ${D_1}, {D_2}, \cdots, {D_N}$ 都是分别从一个来自未知分布F的数据样本 $D$ 中采用返回抽样的方法进行抽样的, 并利用这些样本训练Q值函数头对总体未知的分布F进行统计推断.

1.2 SAC算法

SAC (soft actor-critic)^[15]是由Haarnoja等人于2018年所提出的算法, 是一种区别于确定性策略的随机策略算法. SAC算法基于最大熵框架, 在最大化环境反馈的奖励基础上, 最大化每一时刻策略的熵, 从而使产生的策略尽可能随机, 进而能够采取更多潜在的最优动作. 该算法通过动作值函数 ${Q_\theta }$ , 温度系数 $\alpha $ 以及随机策略函数 ${{\text{π}} _\varphi }$ 来进行学习. 在训练的过程中, 智能体从经验回放池中采样一个批次的样本经验 $({s_t}, {a_t}, {r_t}, {s_{t + 1}})$ 进行学习, 并最小化贝尔曼误差:

$ {J_Q}(\theta ) = {\mathbb{E}_{({s_t}, {a_t})\sim D}}\left[\dfrac{1}{2}({Q_\theta }({s_t}, {a_t}) - {r_t} - \gamma {V_{\bar \theta }}({s_{t + 1}}))_{}^2\right] $

(2)

其中, 在SAC算法中目标值函数为:

$ V({s_{t + 1}}): = {\mathbb{E}_{{a_{t + 1}}\sim {\text{π}} }}[Q({s_{t + 1}}, {a_{t + 1}}) - \alpha \log ({\text{π}} ({a_{t + 1}}|{s_{t + 1}}))] $

(3)

其中, 温度系数 $\alpha $ 用于调节奖励与熵之间的相对重要程度. SAC算法中actor通过执行策略 ${{\text{π}} _\varphi }$ 选择动作以最小化损失:

$ {J_{\text{π}} }(\varphi ) = {\mathbb{E}_{{s_t}\sim D}}[{\mathbb{E}_{{a_t}\sim {{\text{π}} _\varphi }}}[\alpha \log ({{\text{π}} _\varphi }({a_t}|{s_t})) - {Q_\theta }({s_t}, {a_t})] $

(4)

SAC算法在标准最大化奖励的基础上增加了一个最大化熵的目标, 使其策略更加随机, 进而提高探索效率, 同时降低算法对估计误差的敏感性, 使算法更加稳定.

1.3 CURL算法

有大量的深度强化学习任务需要智能体直接从高维状态进行观测学习, 而这导致了深度强化学习的探索效率十分低效. 为了解决这个问题, Laskin等人在SAC算法基础上引入对比表征学习, 提出了CURL算法(contrastive unsupervised representation learning)^[16]. 该算法将对比表征学习与深度强化学习相结合, 通过学习表征函数, 将高维复杂的状态信息(诸如图像, 文本等)转化为低维的语义表征信息. 智能体基于这些语义表征进行学习训练, 能够使数据更加高效, 达到可以比肩向量化状态输入的数据利用率. 对比学习表征的生成方法如式(5)所示:

$ \left\{\begin{gathered} q = {f_q}({x_q}) \\ k = {f_k}({x_k}) \\ \end{gathered}\right.$

(5)

其中, x_q和x_k是对同一状态图像的两种不同增强, f_q和f_k是编码函数, q和k是最后的表征. 通过双线性内积去衡量q和k的相似度:

$ sim(q, k) = {q^{\rm{T}}}Wk $

(6)

其中, W为可学习参数矩阵. 整个对比学习的损失定义如式(7)所示:

$ {\mathcal{L}_q} = \log \frac{{\exp ({q^{\rm{T}}}W{k_ + })}}{{\exp ({q^{\rm{T}}}W{k_ + }) + \displaystyle\sum\limits_{i = 0}^{K - 1} {\exp ({q^{\rm{T}}}W{k_i})} }} $

(7)

1.4 CCLF算法

深度强化学习作为端到端的算法, 需要将高维的状态图像最终映射为一个动作, 而其中直接从状态图像进行观测, 并从中提取有用的信息进行学习是一项挑战. 最近有学者进行研究发现, 通过图像增强的方法对输入的状态图像进行增强, 利用编码原始像素的不变性能够有效提高特征提取的速度, 进而提升算法的效率. 但是如果仅简单地引入更多的图像增强方法, 没有对不同的经验进行加以区分, 这将可能导致Q学习的不稳定性.

Sun等人通过将对比好奇心引入CURL算法中, 提出了CCLF (contrastive-curiosity-driven learning framework)算法^[13], 系统地研究了这个问题. 该算法通过对比好奇心驱动智能体对环境进行探索, 并能够充分利用经验的重要性对重放经验池中的经验进行优先级排序, 使得智能体能够优先从最具有信息量的样本经验中进行学习, 以便可以专注于更多信息的经验, 进一步提高了探索效率. 同时使卷积网络更有效地学习表示不变性, 进而显著降低图像增强的影响.

对比好奇心通过CURL算法中的对比损失项来建模, 它可以在不引入任何额外神经网络体系结构和计算的情况下对好奇心水平进行衡量, 其中衡量对比好奇心大小如式(8)所示:

$ {c_{ij}} = 1 - IB({g_i}(o), {g_j}(o)) \in [0, 1] $

(8)

其中, $IB$ 表示智能体认为对同一状态图像通过两种不同的增强后是否具有相同的表征, 可通过式(7)计算, 并取反对数进行表示. 较高的对比好奇心则表明智能体不认为 $q$ 与 ${k^ + }$ 相似, 或者是错误地将 $q$ 与一些 ${k^ - }$ 匹配, 最终以这种自我监督的方式产生较高的对比好奇心, 而这一般意味着智能体尚未从该环境状态中学到新信息, 并且编码器目前仍不是从原始像素中提取有意义的状态表示的方案.

此外, 将基于对比好奇心生成内在奖励反馈给智能体, 从而驱动智能体对环境进行探索, 该内在奖励定义如式(9)所示:

$ r_t^i = \lambda \exp ( - \eta t)\frac{{r_{\max }^e}}{{r_{\max }^i}}\frac{{{c_{i*j*}} + c{'_{i*'j*'}}}}{2} $

(9)

其中, $\lambda $ 表示温度系数, $\eta $ 表示衰减权重, $t$ 表示环境步长, $r_{\max }^e$ 表示可获得的最大外部奖励, $r_{\max }^i$ 表示可获得的最大内部奖励. 有了上述公式所计算的对比好奇心大小后, 还能对经验重放池中的经验进行加权排序, 使智能体能够从中采样更多未被探索的经验进行学习, 同时选择信息最丰富的经验来提升卷积神经网络的编码不变性, 进而显著减少深度强化学习所需的经验量.

为了使智能体能够更频繁地学习相对较新状态, 通过对比好奇心来更新样本经验的权重:

$ {\omega _s} = \beta {\omega _{s - 1}} + \frac{1}{2}(1 - \beta )({c_{i*j*}} + c{'_{i*'j*'}}) $

(10)

其中, $\;\beta $ 表示动量系数. 动量更新的方式能够保持训练的稳定性, 这样对比好奇心较高的经验将逐渐降低采样的权重, 从而使智能体能够更频繁地抽样学习到较新且对比好奇心较高的经验.

2 Bootstrapped CCLF算法 2.1 问题分析

目前深度强化学习的探索效率仍然不够理想, 算法的探索能力还不足以在有限的资源与时间下尽快找到最优解, 距离实际落地仍有一段距离. 所以, 对于充分利用样本经验来尽可能地提高算法的探索效率是十分有必要的.

造成深度强化学习探索效率低下的一个重要原因是智能体在单一探索策略的引导下, 只能片面地解决探索问题. 例如, 当环境所能给予的外部奖励较为稀疏时, 智能体将难以根据奖励学习到较优的策略, 从而产生探索效率低下的问题, 基于内在激励信号导向的探索策略则能够很好地解决这类问题. 然而对于其他原因产生的探索难问题, 例如需要智能体执行一系列动作才能获取奖励, 则需要智能体拥有深度探索的能力, 基于内在激励信号导向的探索策略则难以发挥作用. 如果能够将不同的探索策略结合起来, 对各自的优缺点进行互补, 从不同的角度辅助智能体对环境进行探索, 那么将能大幅提升智能体的探索效率.

因此, 本文将基于内在激励信号导向的CCLF算法与基于不确定性导向的Bootstrapped DQN算法进行结合. 通过随机选择最有可能是最优策略的策略来进行探索, 将深度探索与深度神经网络相结合, 从而使算法能够更好地适应目标的分布, 进一步提高探索效率, 减少收敛时间, 同时提升算法的鲁棒性.

2.2 算法设计

为了将基于离散环境, 值函数的Bootstrapped DQN算法与基于连续环境, 策略梯度的CCLF算法相结合, 本文将CCLF算法中的actor-critic网络转换为一种全新结构, 如图2所示.

在Bootstrapped DQN算法中, 由于智能体选择的动作是根据值网络输出的目标值进行选择, 而CCLF算法为actor-critic结构, 动作的选择由actor网络给出, critic网络对actor网络所选择的动作进行评估, 所以如图1所示, critic网络由编码层及一个全连接层组成, actor网络由1个共享的编码层和K个不同head组成. 将actor网络的编码层设计为共享部分, 虽然会降低不同head之间的多样性, 但是能够使其学习到所有数据的联合特征表示, 并且有效地减少网络参数的数量和计算资源的消耗, 同时提升网络的鲁棒性. K个不同的head接收共享编码层的输出, 每个head都进行了随机且不同的初始化, 相互之间保持独立.

使用Bootstrapped方法修改了actor网络的结构, 通过Bootstrapped对动作的分布进行近似. 在每次训练开始前, 从actor网络的近似后验抽取一个head, 然后直至训练结束都认为该head所生成的策略是最优的策略, 使其保持对环境的乐观探索, 从而能够对环境进行时间上的深度探索.

在训练过程中, 为智能体收集的每一个样本经验生成一个长度为K的二进制数组, 数组中的每一位对应一个head. 从伯努利分布中以0.5的概率为对应的head生成一个掩码, 并储存在二进制数组中. 掩码值为1代表该样本经验能够被对应的head所学习, 为0则不用于学习. actor网络的随机梯度下降公式对应修改如式(11)所示:

$ g_t^k = m_t^k(y_t^Q - {Q_k}({s_t}, {a_t};\theta )){\nabla _\theta }{Q_k}({s_t}, {a_t};\theta ) $

(11)

其中, $m_t^k$ 代表每个样本经验对应head的掩码值. 从而使得每个head所学习到的样本经验子集之间互不相同, 进而每个head能够输出不同的策略, 充分反映潜在最优动作的分布, 并通过TD估计引入时间上的价值不确定性估计. 同时对式(3)也进行对应的修改:

$ \begin{split} & V({s_{t + 1}}): =\\ &\max \{ {\mathbb{E}_{a_{t + 1}^n\sim {{\text{π}} _n}}}[Q({s_{t + 1}}, a_{t + 1}^n) - {\alpha _n}\log ({\text{π}} (a_{t + 1}^n|{s_{t + 1}}))]\} _{n = 1}^K \end{split} $

(12)

通过使用掩码的方式, 使actor网络中的每个head所学习到的经验不尽相同, 从而接近动作概率的后验分布. 此外, 还通过对每个head网络进行随机初始化, 作为诱导神经网络产生动作多样性的先验, 并且在训练过程, 这些在初始化时产生的小差异将随着适应各自的TD误差逐渐变得更大. 一旦其中一个head探索到更优的状态, 便可以通过目标网络将这个信号传播回最初始的状态, 并被其他的head网络所学习到, 从而驱动智能体进行深度探索.

在该算法中, 并没有将critic网络做出与actor相同改动, 主要原因在于单一的critic网络能够学习到所有样本经验, 进而生成一个综合性的考量, 且能够更快更准确地评估动作所对应的Q值, 同时为actor网络提供一个更稳定的目标进行学习.

本文提出的Bootstrapped CCLF算法总结如算法1所示.

算法1. Bootstrapped CCLF

1. 初始encoder网络参数 $\scriptstyle \phi $ , critic网络参数 $\scriptstyle \theta $ 及actor网络参数 $\scriptstyle \left\{ {{\varphi _n}} \right\}_{n = 1}^k$ , 同时使用critic网络参数初始化target-critic网络 $\scriptstyle {\theta ^*}$ ; 初始化采样长度T, 回放经验池B.

2. for t=1 to T do:

3.　 $\scriptstyle n \sim Uniform\{ 1, 2, \cdots, K\}$ //选择一个head n

4. 　 $\scriptstyle {a_t} \sim {{\text{π}} _{{\varphi _n}}}(.|g({s_t}))$ //根据当前策略选择动作

5.　 $\scriptstyle {s_{t + 1}}, {r_t} \sim p({s_{t + 1}}, {r_t}|{s_t}, {a_t})$ //与环境交互

6.　 $\scriptstyle {m_t} \sim M$ //生成掩码

7.　 $\scriptstyle B \leftarrow B \cup ({s_t}, {a_t}, {r_t}, {d_t}, {m_t}, {s_{t + 1}})$ //存入样本经验

8.　 $\scriptstyle {\tau _t}\sim B$ //采样经验样本进行训练

9.　 $\scriptstyle \phi = \phi - {\eta _\phi }{\nabla _\phi }{\mathcal{L}_q}$ //更新encoder网络

10. $\scriptstyle \theta = \theta - {\eta _{_\theta }}\nabla {J_Q}(\theta )$ //更新critic网络

11. $\scriptstyle \varphi = \varphi - {\eta _\varphi }\nabla {J_\pi }(\varphi )$ //更新actor网络

12. $\scriptstyle {\omega _s} = \beta {\omega _{s - 1}} + \frac{1}{2}(1 - \beta )({c_{i*j*}} + c{'_{i*'j*'}})$ //更新经验权重

13. $\scriptstyle {\theta ^*} = \tau {\theta ^*}' + (1 - \tau ){\theta ^*}$ //更新target-critic网络

14. end for

3 实验分析

本文通过DMControl 100K基准对算法的性能及探索效率进行评价. 通过与DMControl的环境交互100k步, 比较BCCLF算法与基准算法的最高得分与平均得分来评价算法的性能和探索效率.

3.1 实验环境

为了验证算法的有效性, 将BCCLF算法和基准算法应用于DMControl环境的6个基准任务中, 如图3所示.

DMControl是由一系列连续控制任务基准环境所组成. 在不同的任务环境中, 智能体需要控制物理仿真机器人完成目标任务^[17]. 智能体获取的环境状态为3×84×84的RGB图像, 同时输入连续3帧状态图像能够为智能体提供仿真机器人的运动方向与速度等时间上的信息.

将本文提出的BCCLF算法与近年来在DMControl环境中性能表现较为优秀, 以SAC为基础的算法进行对比, 这些算法分别是:

(1) 以图像作为输入的SAC算法.

(2) 引入对比学习的CURL算法.

(3) 使用图像增强的DrQ算法^[18].

(4) 好奇心驱动探索的CCLF算法.

本文提出的算法以及进行对比的基准算法都是以SAC算法为基础, 因此大部分采用与原始算法CCLF相同的超参数, 具体超参数如表1所示.

3.2 对比实验

在6个不同的基准任务中, 将BCCLF算法在这些任务对应的环境均运行5次, 每次采用不用的随机种子进行初始化, 且都与环境进行100k步的交互, 计算所获取分数的平均值和标准差, 将其作为最终结果, 评价算法的最终性能. 在6个不同的连续控制任务中, BCCLF都取得了最高得分, 展现了其优秀的最终性能. 平均计算下来, BCCLF的性能相较于基准算法CCLF提升了12%. 评价数据如表2所示.

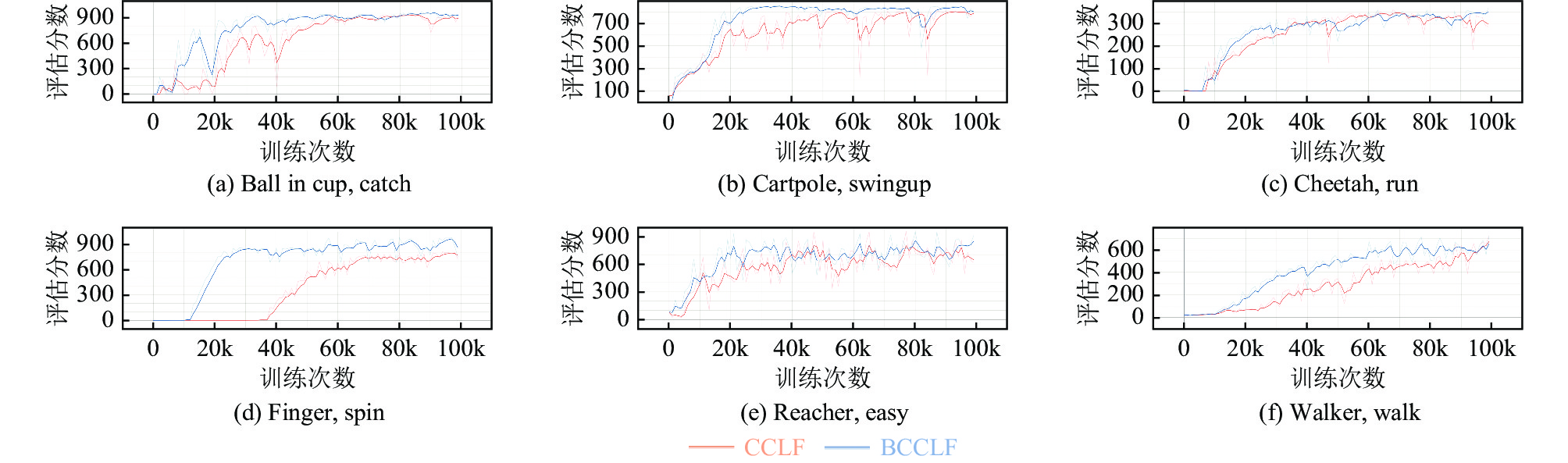
将BCCLF算法和CCLF算法运行于DMControl环境中的6个基准任务中当中, 其实验结果如图3所示, 横坐标表示训练的次数, 纵坐标表示算法所取得的平均分数. 从图4中可以看出, 在获取相同的分数时, BCCLF算法相较于原始CCLF只需更少的训练次数, 且收敛速度更快. 尤其是在finger-spin任务中, 由于该任务需要控制手指持续拨动铰链才能获取分数, 相对其他任务来说更需要智能体对环境进行一个深度的探索, 才能了解获取奖励的方式. 在该任务中, BCCLF算法大约学习了12k次后开始学会拨动铰链, 分数逐渐上升, 而原始的CCLF算法则需要学习37k次, 提升了约3倍探索效率. 同时, BCCLF算法从开始学会, 分数逐渐上升到分数收敛, 只需学习18k次; 而CCLF算法则需要学习23k次, 收敛速度提升了约1.3倍, 且BCCLF算法能够收敛到更高的分数.

3.3 消融实验

BCCLF算法与原始的CCLF算法之间最大的区别是在BCCLF算法中, actor网络为multi-head结构, CCLF算法可以视为只有单一head的BCCLF算法. 为了了解head数量对提升智能体探索效率的贡献. 本文分别将采用不同数量head的BCCLF算法运行于finger-spin的任务中. 该任务需要智能体对不断地对环境进行探索, 才能了解奖励获取的机制, 能够很好地体现出算法的探索效率. 由图5可知, 随着head数量的增加, 智能体的探索效率逐渐提升, 表明Bootstrapped探索方法能够有效地提升CCLF算法的探索性能.

4 结论与展望

本文针对CCLF算法存在探索效率低, 收敛速度慢的问题, 将Bootstrapped探索方法与其结合, 提出BCCLF算法. 该算法将actor网络拓展为multi-head结构, 使其能够在输出最优策略的同时引入动作值的不确定性, 进而提升算法的深度探索能力, 并且能够取得更高的性能. BCCLF算法能够输出多个潜在的最优动作, 虽然在离散动作环境下可通过投票法从中选择一个最优的动作, 但在连续动作环境下, 动作值是连续的, 如何从中选择一个最优的动作仍然是一个问题. 后续工作将针对这个问题进行展开更加全面与深入研究.