2. 复旦大学 信息科学与工程学院, 上海 201203
2. School of Information Science and Engineering, Fudan University, Shanghai 201203, China
去中心化计算是一种重要的分布式计算范式. 相对于中心化的分布式计算, 去中心化的特性使得训练集群没有一个特定的参数服务器. 在每个训练轮次, 计算节点与相邻节点交换数据并在本地进行模型更新. 本文研究以下两种去中心化计算方法: 分布式平均共识(distributed average consensus, 以下简称平均共识)和去中心机器学习(decentralized machine learning, DML). 平均共识通过节点间数据的交换和更新使得所有节点收敛于全局平均值. 它在分布式传感器网络和无人驾驶飞行器中具有广泛的应用[1]. DML允许计算节点与相邻节点协作训练机器学习模型, 是平均共识的重要扩展[2].
去中心化的特性使得以上两种方法可以很大程度上降低通信的复杂性, 但代价是计算的收敛率低于中心化的分布式训练[3]. 要高效地进行去中心化计算, 关键在于权衡好数据通信时间和收敛率的关系. 虽然收敛率降低使得训练需要更多轮次到达目标精度, 但更短的每轮通信时间使去中心化计算可以更快地完成训练任务[4]. 正因如此, DML逐渐被用于训练大规模机器学习模型中[5, 6].
节点的通信拓扑在权衡训练次数和通信时间的关系中起着至关重要的作用. 稀疏的拓扑意味着更少的数据传输, 降低每个轮次的通信时间. 另一方面, 具有高收敛率的拓扑意味着到达目标精度需要更少的训练轮次. 拓扑的谱间距, 定义为拓扑权重矩阵最大两个特征值的模之差, 可以准确刻画平均共识的收敛率[7]. 当节点间数据独立同分布时, 它也用来刻画DML收敛率的上界[4]. 设计一个通信高效且具有高谱间距的拓扑可以降低训练任务到达收敛的总时间.
然而现有的训练拓扑没有针对异构网络环境进行优化. 拓扑一般模式固定或基于节点带宽相同的假设设计获得[6, 8]. 但由于网络资源的竞争, 带宽异构在分布式计算中很常见. 一般来说, 享有更高上传带宽的节点在每个训练轮次应向更多节点发送数据, 因此应有更高的出度. 节点入度同理. Underlay网络是由连接每个节点的物理网络组成的图. 由于节点间线路故障或隐私考虑, 该图不一定是全连接的. 在Underlay网络之外的连接不可使用. 一个设计良好的拓扑结构应在满足上述两个约束的同时最大化谱间距.
本文研究在异构带宽和Underlay网络约束下最大化有向图谱间距的问题. 有向图的特性给本文带来了以下挑战: 一方面, 不对称的有向图使其权重矩阵特征值变为复值, 并且有向图的谱间距不再具有凸性; 另一方面, 拓扑设计问题本质上是一个整数规划问题, 任一条边存在与否由一个0-1变量表示. 随着节点数量增加, 该问题的搜索空间呈指数增长.
本文通过推导并计算谱间距针对加边或删边操作的梯度来解决以上拓扑设计问题. 通过该梯度值进行边的增删从而构建拓扑. 本文的主要工作如下.
1) 本文对异构网络环境下最大化谱间距的问题进行建模, 并推导出有向图的谱间距针对任一条边增删的梯度.
2) 本文设计了基于该梯度的算法来构建具有较大谱间距的稀疏有向拓扑. 该拓扑同时考虑了带宽异构性和底层Underlay网络的约束.
3) 本文通过实验验证了生成的拓扑在平均共识中具有更快的收敛率和更短的收敛时间, 且算法在不同程度的异构网络环境下能保持性能稳定. 本文将生成的拓扑应用于DML训练, 进一步验证了DML的收敛率对谱间距的弱相关性.
1 背景知识本节介绍了平均共识和DML的基本概念, 以及将两种机制应用在无向图和有向图上的不同算法.
1.1 平均共识考虑一个包含
| x(t+1)i=∑nj=1Pjix(t)j | (1) |
变量
在有向图上应用平均共识需要用到push-sum算法[10]. 该算法仅要求权重矩阵
| {x(t+1)=PT⋅x(t)y(t+1)=PT⋅y(t)z(t+1)=x(t+1)/y(t+1) | (2) |
其中,
权重矩阵的谱间距是描述平均共识收敛率的紧凑上界[9]. 谱间距表示为
去中心化机器学习是平均共识的重要的扩展, 它允许节点仅与邻居通信来协作训练模型. 在无向图上应用DML的基本算法是Decentralized SGD (D-SGD)[9]. 在每个训练轮次, 任一节点在本地进行梯度更新后, 将其模型与邻居节点模型进行加权求和.
| x(t+1)i=∑jPji(x(t)j−η⋅∇f(xj)(t)) | (3) |
变量
在有向图上进行DML训练需要使用Stochastic Gradient Push算法[11]. 它的核心思想是结合push-sum算法和随机梯度下降, 利用消除误差后的梯度更新模型参数. 本文在有向图上训练DML使用该算法.
由于DML与平均共识在训练过程的紧密联系, 谱间距也很自然地被多种文献用于推导并描述DML的收敛率上界[4, 6]. 然而谱间距对DML收敛率的影响在近期开始受到一些文献的质疑. 文献[12]发现在节点间数据独立同分布时, 谱间距对收敛率的影响虽然仍然存在但小于预期. 最新工作[13]则直接表明谱间距不能准确预测DML的性能. 本文工作可视为该文献的同时期工作. 本文提出了构建大谱间距拓扑的算法, 并在生成的有向图上进行DML实验, 进一步验证了谱间距和DML收敛率之间仅存在弱相关性.
2 问题动机 2.1 探索包含有向图的拓扑设计以往的拓扑设计研究主要讨论无向图和一些特殊类型的图. 无向图的权重矩阵具有实数特征值以及凸的谱间距[14]. 这些特性使得一些文献通过求凸优化模型的精确解来设计拓扑[15]. 尽管这些工作可以确保求得最优解, 但求解的时间复杂度使它们无法解决更大规模的问题. 因为随着节点数增加, 表示边存在的0-1变量使优化模型的搜索空间呈指数增长. 文献[14]采用松弛技术来求解更大规模的问题, 但所得拓扑仍然是无向的.
一些特殊类型的有向图, 如环状图, 正则图和指数图也受到了不同研究的关注[6, 12]. 尽管这些图是有的, 但它们的连接具有一定的模式, 使得它们的权重矩阵是双随机的. 这些特性有助于推导这些谱间距的表达式. 但这类拓扑不一定能够满足异构网络环境的约束.
只有一般的有向图才能满足不同程度带宽异构和 Underlay的约束, 因此需要新的算法在有向图上搜索和设计满足以上约束的高收敛率拓扑.
2.2 同时考虑带宽异构和Underlay网络约束带宽的异构性表明只追求更稀疏的拓扑并不是最优的. 为了避免出现掉队者(straggler)和增加吞吐量, 不同节点数据传输所消耗的时间应该相似. 具有更高上传带宽的节点应该向更多的邻居发送数据, 因此具有更高的出度. 同理, 下载带宽较低的节点应该有较少的入度. 这种针对每个节点的带宽约束相比于针对总通信次数的约束[16]更细粒度一些.
由于网络可能出现的中断和节点间的隐私要求, Underlay网络不能保证全连接, 某些连接可能不能使用. 文献[8]在设计拓扑时考虑了Underlay网络, 但假设不同节点带宽相同. 在Underlay网络约束下使用特定类型的图则必须对图进行删边, 此操作可能降低图的谱间距. 因此需要一种拓扑设计算法同时考虑这两个约束.
3 问题求解本节首先对拓扑设计问题进行建模, 之后将谱间距针对加边或删边的梯度进行推导和计算. 基于以上结果, 本文提出了一个基于梯度的拓扑构建算法.
3.1 问题建模给定一个包含
| A=∑l∈EAl=∑l∈MxlAl | (4) |
定义
| Pij=1douti,iflij∈E | (5) |
变量
| P=D−1out⋅A=diag(1dout1,⋯,1doutn)⋅∑lxlAl | (6) |
本文的目标是通过对每条边的变量
| maxxl,∀l∈M1−|λ2(P)| | (7) |
| s.t. dini=⌊dinmbinibinm⌋, 1⩽ | (8) |
| \begin{array}{*{20}{c}} {d_i^{{\rm{out}}} = \left\lfloor {d_m^{{\rm{out}}}\dfrac{{b_i^{{\rm{out}}}}}{{b_m^{{\rm{out}}}}}} \right\rfloor , {\text{ }}1 \leqslant i \leqslant n} \end{array} | (9) |
| {d}_{m}^{{\rm{out}}}=\left\lfloor {d}_{m}^{{\rm{out}}}\dfrac{{b}_{m}^{{\rm{out}}}}{{b}_{m}^{{\rm{out}}}}\right\rfloor | (10) |
| {x}_{l}= 0,\;\text{ if }\;l\in H | (11) |
| 图G是强连通图 | (12) |
约束(8)–(10)源于节点间的带宽异构性. 节点的出度和入度应与上传和下载带宽成正比, 使得数据传输消耗相似的时间. 这种方式可以避免straggler现象并增加吞吐量. 每个节点的带宽是一个已知的值, 可以通过节点主动探测或节点带宽分配获得. 常量
假设节点i的上传带宽为60%的
约束(11)源于给定Underlay网络的限制. 定义
与无向图不同, 有向图权重矩阵的谱间距关于
对以上模型进行直接求解并不可行. 首先, 0-1变量
为了能够推导出梯度的表达式, 本文首先引入矩阵微扰理论的相关概念. 矩阵微扰理论的目标是估计矩阵受到微扰时其对应矩阵函数的变化[18]. 在拓扑设计问题中, 微扰对应特定边的添加或删除, 特征值则是对应的矩阵函数. 通过微扰理论, 本文可以估计拓扑权重矩阵受到边的增删影响时特征值的变化.
将矩阵
| \frac{\partial \lambda }{\partial x} =\dfrac{{v}_{0}^{H}\dfrac{\partial P}{\partial x}{u}_{0}}{{v}_{0}^{H}{u}_{0} } | (13) |
其中,
因为简单特征值对
获得式(13)之后, 本文的目标则是推导出
| \frac{\partial A}{\partial {x}_{l}}=\frac{\partial {\displaystyle \sum}_{t\in M} {x}_{t}{A}_{t} }{\partial {x}_{l} }={A}_{l} | (14) |
梯度的另一部分涉及对角出度矩阵
| \frac{\partial {d}_{i}^{{\rm{out}}}}{\partial {x}_{l}}=\left\{\begin{array}{l}1,\; 如果{x}_{l}起点为i \\ 0,\; 其他情况\end{array}\right. | (15) |
注意到任意一条边的存在只能影响该边起点的出度. 因此, 出度矩阵针对某一条边
| \frac{\partial P}{\partial {x}_{l}}= {\rm{diag}}\left(0, \cdots , \frac{-1}{{d}_{i}^{2}}, \cdots , 0\right)\cdot A+{D}_{{\rm{out}}}^{-1}\cdot {A}_{l} | (16) |
本文的目标是计算特征值的模对特定边的梯度, 即
| \begin{split} \frac{\partial \text{ }\left|{\lambda}\right|}{\partial \text{ }{x}_{l}}&=\frac{\partial \sqrt{Re{\left(\lambda \right)}^{2}+Im{\left(\lambda \right)}^{2}}}{\partial \text{ }{x}_{l}}\\ &=\frac{Re\left(\lambda \right)}{\left|\lambda \right|}\frac{\partial Re\left(\lambda \right)}{\partial {x}_{l}}+\frac{Im\left(\lambda \right)}{\left|\lambda \right|}\frac{\partial Im\left(\lambda \right)}{\partial {x}_{l}}\\ &=\frac{Re\left(\lambda \right)}{\left|\lambda \right|}Re\left(\frac{\partial \lambda }{\partial {x}_{l}}\right)+\frac{Im\left(\lambda \right)}{\left|\lambda \right|}Im\left(\frac{\partial \lambda }{\partial {x}_{l}}\right)\end{split} | (17) |
将式(17)与式(13), 式(16)结合, 并定义
| \begin{split} \frac{\partial \text{ }\left|{\lambda}\right|}{\partial \text{ }{x}_{l}}=&\frac{Re\left(\lambda \right)}{\left|\lambda \right|}Re\left(\frac{{v}_{0}^{H}\dfrac{\partial P}{\partial {x}_{l}}{u}_{0}}{{v}_{0}^{H}{u}_{0}}\right)+\frac{Im\left(\lambda \right)}{\left|\lambda \right|}Im\left(\dfrac{{v}_{0}^{H}\dfrac{\partial P}{\partial {x}_{l}}{u}_{0}}{{v}_{0}^{H}{u}_{0}}\right)\\ =&\frac{Re\left(\lambda \right)}{\left|\lambda \right|}Re\left(\frac{{v}_{0}^{H}\left({D}_{i}^{-2}\cdot A+{D}^{-1}\cdot {A}_{l}\right){u}_{0}}{{v}_{0}^{H}{u}_{0}}\right)\\ &+\frac{Im\left(\lambda \right)}{\left|\lambda \right|}Im\left(\frac{{v}_{0}^{H}\left({D}_{i}^{-2}\cdot A+{D}^{-1}\cdot {A}_{l}\right){u}_{0}}{{v}_{0}^{H}{u}_{0}}\right) \end{split} | (18) |
式(18)表示了添加或删除某一条边对权重矩阵谱间距的影响. 可以基于该等式, 向一个基底图
式(18)的结构虽然看起来复杂, 但它的实际计算复杂度并不高. 其中计算特征值和特征向量的时间复杂度为
算法1. 基于梯度的拓扑构建算法
输入: 图
输出: 构建后的图
1. while
2. 计算图
3. for
4. 基于式(18)计算梯度
5. end for
6. 选择梯度值最小的边
7.
8. 基于新边
9. end while
算法1 还可加入进行删边的模块, 如经过固定轮次周期性的删边, 来帮助算法进一步避免局部最优值.
基础图
本节通过实验验证基于梯度的拓扑设计算法性能. 首先通过实验测试该算法在最大化谱间距上的效果. 然后将该算法生成的拓扑部署在平均共识和DML两种场景上, 来验证这些拓扑能否加快收敛率和训练时间. 为了更好地验证算法1 的有效性, 本文选择了3种基线对比方法.
• 指数图[6]: 其中每个节点仅与距离
• Havel-Hakim算法: 该算法是基于度数序列的图实现算法[17]. 只要该度数序列是可实现的, 该算法就可以给出一个有向图作为可行解.
• 基于贪心的启发式方法: 在每个轮次, 该算法向现有图中添加使谱间距最大化的边来构造拓扑.
4.1 具有对数度数的拓扑指数图在具有
不同算法生成拓扑的谱间距随节点数的变化如图1所示. 算法1 在绝大部分情况下具有更大的谱间距. 在节点数增大的情况下这种优势更为明显. 且该算法生成拓扑的谱间距在节点数量增加时可以保持稳定.

|
图 1 不同算法的谱间距随节点数变化图 |
Underlay约束产生的效果可在图1中明显观察到. 随着
本文接下来测试以上拓扑在平均共识上的性能, 采用设定如下: 各节点具有一个100维向量, 向量中每个元素的初始值从
在
本文接下来对基于梯度的算法在带宽异构的情景下进行性能测试, 并同时考虑Underlay网络对算法性能的影响. 实验中带宽异构的定义如下: 设上传和下载带宽相同,
在上述异构网络环境的约束下, 不同算法的性能如图3所示. 对于确定性的对比算法, 度数序列的约束则转化为节点的随机删边, 最后的结果是100次随机删边的最优结果. 由于有向图的谱间距对于增删边并不单调, 删边对于拓扑的影响是不确定的. 在异构带宽和Underlay网络的共同作用下, 对比方法的性能由于删边而出现了不稳定的波动. 随着

|
图 2 不同拓扑的平均共识收敛情况 |

|
图 3 异构网络环境下不同算法性能比较 |
在以上异构网络环境约束下, 本文测试30个节点的不同拓扑在平均共识下的收敛情况. 定义各节点在给定度数下的每轮通信时间为1单位时间. 由于30个节点的指数图度数均为5, 因此其带宽最少的一组节点传输数据时间为
在上述约束下, 不同拓扑的平均共识过程如图2(b)所示. 虽然指数图具有较小的谱间距, 但因其未考虑节点带宽异构性, 它随时间的收敛速度只能和谱间距小于它的图实现算法相似. 指数图同样可以通过随机删边的方法来应对异构网络环境的约束. 但经过删边的指数图在谱间距上没有太大变化. 而基于梯度的加边算法一方面考虑到带宽的异构性, 在传输时间上优于指数图这种固定模式的拓扑. 另一方面, 与其他可以适应度数序列的方法相比, 算法1 可产生具有更大谱间距的拓扑, 因此在随训练轮次的收敛率上也占优. 基于梯度的算法无论在所需传输时间还是传输轮次上都少于其他对比方法.
4.3 谱间距对DML的影响该部分研究谱间距对DML收敛率的影响. 机器学习实验的具体配置如下: 本文使用CIFAR-10数据集[20], ResNet-18残差神经网络[21], 并使用Stochastic Gradient Push算法进行训练[11]. 拓扑节点数为17, 节点间的数据是独立同分布的, batch size为128, 学习率为0.1, 使用不带动量的随机梯度下降算法. 本文通过程序仿真的方法来模拟集群DML训练的过程.
实验带宽异构配置如下: 17个节点的集群中各有6的节点具有4和5的出入度, 其余5个节点具有3的出入度, 参数
为了更加深入地探讨谱间距对DML收敛率的影响, 本文利用所有节点出入度
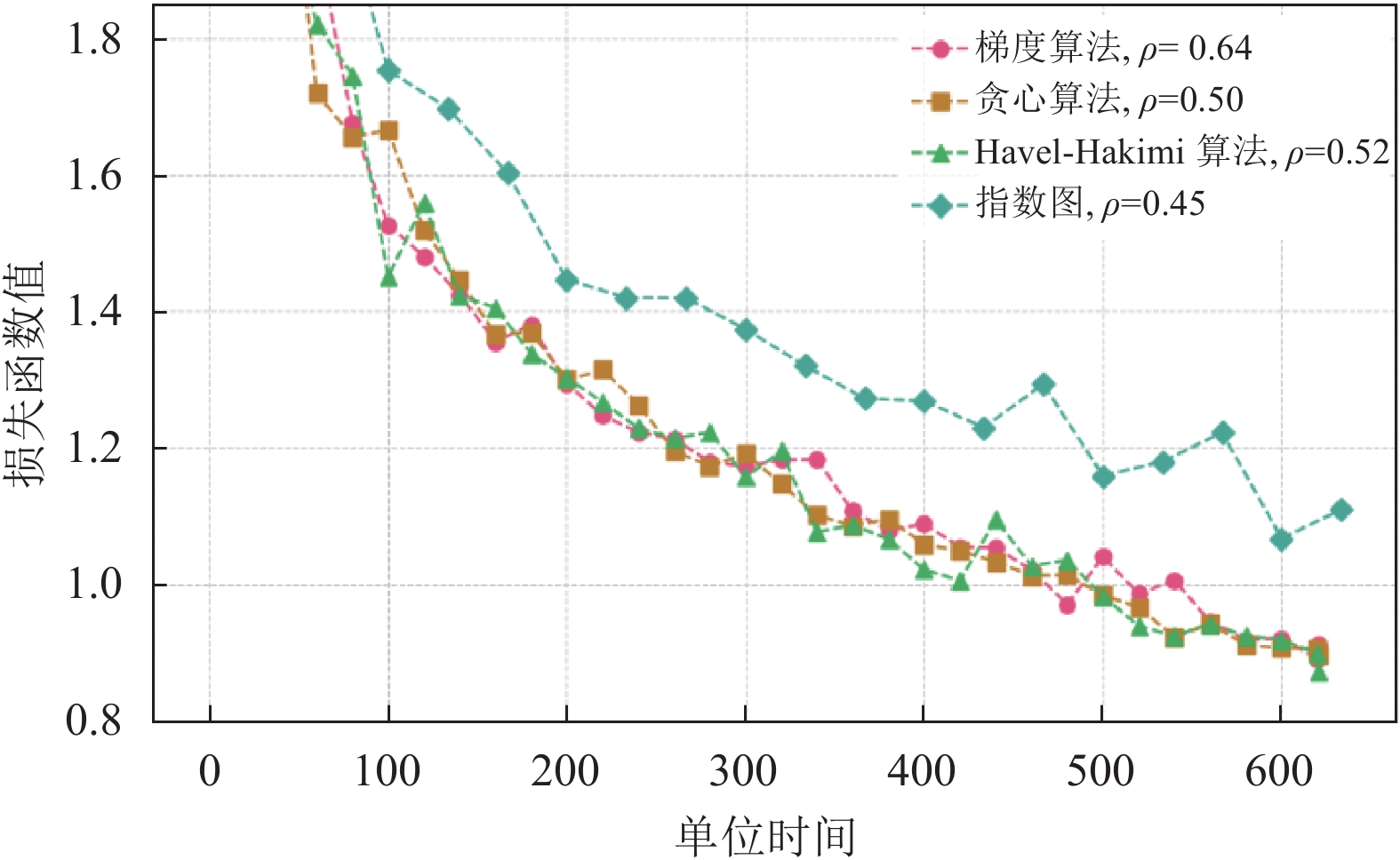
|
图 4 不同拓扑的 DML 训练损失随时间变化图 |

|
图 5 不同拓扑的谱间距与训练损失散点图 |
关于以上现象, 本文推测谱间距仅渐进地约束了DML的收敛率. 谱间距作为DML收敛率的上界并不是时刻紧凑的. 该上界的微小变化并不能准确反映真实收敛率的改变. 从DML的更新过程也可以理解该现象. 在DML的每个迭代轮次, 每个节点都会收到其他节点更新后的模型, 该更新版本的模型比前面轮次的模型对DML整体性能贡献更大. 但这个更新后的模型只经历了一步平均共识, 这种一次性平均共识的效果与谱间距不具有十分紧密的联系.
5 结语本文推导并计算了谱间距针对增删边的梯度, 基于该梯度提出拓扑构建算法解决了异构网络环境下最大化谱间距的拓扑设计问题. 该算法具有较低的时间复杂度, 能够生成谱间距更大的拓扑. 生成的拓扑在平均共识过程中的误差收敛速度显著快于其他拓扑. 该算法在不同程度的异构网络环境下性能保持稳定. 该算法在增删边数量极少的场景下可能不优于直接遍历, 由于搜索空间较小.
应用该算法, 本文生成大量拓扑来验证谱间距对DML收敛率的影响: 谱间距并不能准确预测DML收敛率的快慢. 虽然谱间距的大幅变化对收敛率的影响符合预期, 但小幅增加谱间距不能保证收敛率提升. 本文推测这是由于DML与平均共识的具体训练过程差异造成的.
| [1] |
Olfati-Saber R, Murray RM. Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. DOI:10.1109/TAC.2004.834113 |
| [2] |
Nedic A, Ozdaglar A. Distributed subgradient methods for multi-agent optimization. IEEE Transactions on Automatic Control, 2009, 54(1): 48-61. DOI:10.1109/TAC.2008.2009515 |
| [3] |
Li M, Andersen DG, Smola A, et al. Communication efficient distributed machine learning with the parameter server. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 19–27.
|
| [4] |
Lian XR, Zhang C, Zhang H, et al. Can decentralized algorithms outperform centralized algorithms? A case study for decentralized parallel stochastic gradient descent. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 5336–5346.
|
| [5] |
Yuan K, Chen YM, Huang XM, et al. DecentLaM: Decentralized momentum SGD for large-batch deep training. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV). Montreal: IEEE, 2021. 3009–3019.
|
| [6] |
Ying BC, Yuan K, Chen YM, et al. Exponential graph is provably efficient for decentralized deep training. Proceedings of the 32nd International Conference on Neural Information Processing Systems. NIPS, 2021. 13975–13987.
|
| [7] |
Gerencsér B, Gerencsér L. Tight bounds on the convergence rate of generalized ratio consensus algorithms. IEEE Transactions on Automatic Control, 2022, 67(4): 1669-1684. DOI:10.1109/TAC.2021.3067629 |
| [8] |
Marfoq O, Xu C, Neglia G, et al. Throughput-optimal topology design for cross-silo federated learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. NIPS, 2020. 19478–19487.
|
| [9] |
Koloskova A, Loizou N, Boreiri S, et al. A unified theory of decentralized sgd with changing topology and local updates. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 5381–5393.
|
| [10] |
Tsianos KI, Lawlor S, Rabbat MG. Push-sum distributed dual averaging for convex optimization. Proceedings of the 51st IEEE Conference on Decision and Control (CDC). Maui: IEEE, 2012. 5453–5458.
|
| [11] |
Assran M, Loizou N, Ballas N, et al. Stochastic gradient push for distributed deep learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 344–353.
|
| [12] |
Neglia G, Xu C, Towsley D, et al. Decentralized gradient methods: Does topology matter? Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics. PMLR, 2020. 2348–2358.
|
| [13] |
Vogels T, Hendrikx H, Jaggi M. Beyond spectral gap: The role of the topology in decentralized learning. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: NIPS, 2022.
|
| [14] |
Ghosh A, Boyd S. Growing well-connected graphs. Proceedings of the 45th IEEE Conference on Decision and Control. San Diego: IEEE, 2006. 6605–6611.
|
| [15] |
Dai R, Mesbahi M. Optimal topology design for dynamic networks. Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando: IEEE, 2011. 1280–1285.
|
| [16] |
Wang JY, Sahu AK, Yang ZY, et al. MATCHA: Speeding up decentralized SGD via matching decomposition sampling. Proceedings of the 6th Indian Control Conference (ICC). Hyderabad: IEEE, 2019. 299–300.
|
| [17] |
Havel V. A remark on the existence of finite graphs. Casopis Pest Mathematics, 1955, 80: 477-480. |
| [18] |
Stewart GW, Sun JG. Matrix Perturbation Theory. Boston: Academic Press, 1990.
|
| [19] |
Magnus JR. On differentiating eigenvalues and eigenvectors. Econometric Theory, 1985, 1(2): 179-191. DOI:10.1017/S0266466600011129 |
| [20] |
Krizhevsky A, Nair V, Hinton G. The CIFAR-10 dataset. http://www.cs.toronto.edu/~kriz/cifar.html. (2009-09-23)[2023-02-26].
|
| [21] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
 2023, Vol. 32
2023, Vol. 32



