2. 军事科学院, 北京 100071;
3. 四川大学 天府工程数值模拟与软件创新中心, 成都 610207;
4. 国防科技大学 空天科学学院, 长沙 410003
2. Academy of Military Science, Beijing 100071, China;
3. Tianfu Engineering-oriented Numerical Simulation & Software Innovation Center, Sichuan University, Chengdu 610207, China;
4. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410003, China
与普通的水下推进器相比, 鱼游具有推进效率高、机动性能好、隐蔽性能好等显著优点. 仿生机器鱼结合了鱼类推进机理和机器人技术, 为研制水下推进器提供了新思路, 具有重要的研究价值和应用前景[1]. 对于仿生鱼的控制, 首先要解决的是循迹问题, 即鱼体能够自主、准确地沿规定路线游动, 这需要引入合适的闭环控制算法.
比例积分微分(PID)算法被广泛应用于传统的机器人控制领域, 该算法通过减少目标与实际情况的偏差完成任务, 对于流程清晰的问题非常有效. 然而, 在复杂流动环境中, 仿生鱼不同时刻执行同一动作指令时, 所产生的位移并不相同, 导致PID算法无法进行稳定的控制, 因此, 需要使用更加智能的控制算法. 最近的研究成果表明, 强化学习算法在一定程度上具备解决复杂问题的通用智能, 已被用于解决多种复杂的机器控制问题, 这为仿生鱼控制提供了新的研究方向.
本文提出了一种基于强化学习的仿生鱼智能控制方法, 用以解决仿生鱼的循迹问题. 该方法有两个显著优势: 第一, 鱼体不需要对环境有任何先验知识, 而是通过试错对环境信息进行采样, 从而完成自主学习; 第二, 该方法能够解决鱼体游动中存在随机扰动的问题, 从而精准控制鱼体沿规定路线游动. 在多个场景中的实验结果表明, 本文提出的方法对探索鱼类在复杂环境中的游动机制与仿生鱼智能控制方面有着重要的指导意义.
1 相关工作仿生鱼的控制属于学科交叉问题, 包括计算流体动力学(CFD)和控制算法两部分. 其中, CFD用于计算鱼体的受力情况, 而控制算法用于闭环控制, 使鱼体可以根据设定好的目标自行选择自己的游动方式[2-5].
许多传统算法[6]都可以实现自动控制, 但在鱼游控制中表现不佳. Tian等人[7]通过反馈控制方式实现了鱼体的自主游动控制, 但生成的迹线波动较大, 不够平滑. Khan等人[8]使用PID算法控制机器鱼的下沉深度, 发现即使经过适当的增益调优, PID控制器仍存在一定的局限. 而在人工智能领域, Novati等人[9]使用深度强化学习(DRL)算法实现对水下2D椭圆型模型的控制, 他们发现使用DRL生成的迹线更加光滑, 并且比传统的控制优化算法更加稳定. Zhu等人[10]使用深度循环Q网络获取鱼游的序列信息, 控制鱼体完成了静水中捕猎、流动水中维持自身位置等任务. Yan等人[11, 12]使用DRL训练鱼体完成循迹任务, 在使用直线完成训练后, 鱼体可以沿着曲线游动, 同时能够完成简单的避障游动, 说明经过训练后的鱼体具有一定的泛化能力.
强化学习为解决仿生鱼游动的控制问题提供了智能方案, 但仍然存在一些问题. 在CFD中, 为了得到流体对鱼作用力的精确值, 需要进行鱼体模型离散化, 网格量达到数十万乃至百万, 导致完成一次数值解算非常耗时; 同时, 由于鱼体在流体中的游动是连续的, 鱼体在水中的每一时刻的运动状态都必须使用CFD的方式计算得到. 这两个因素叠加, 使得CFD模拟的时间成本巨大, 难以满足强化学习对大量训练数据的需求.
为了解决上述问题, 本文从两方面进行改进: 一是提高训练数据的产生效率, 用代理模型代替数值模拟产生训练数据, 提升训练效率; 二是提高训练数据的效用, 通过引入更加高效的强化学习算法PPO和训练策略, 加快策略模型的学习速度, 减少对训练数据的需求.
此外, 文献[11]中发现仿生鱼容易在急转弯区域偏移过度直至越界, 导致循迹任务的失败, 并通过增加转弯处的边界宽度以避免这一问题. 本文引入对速度参数的训练, 使鱼体学习在急转弯区域主动减速, 从而顺利通过该区域.
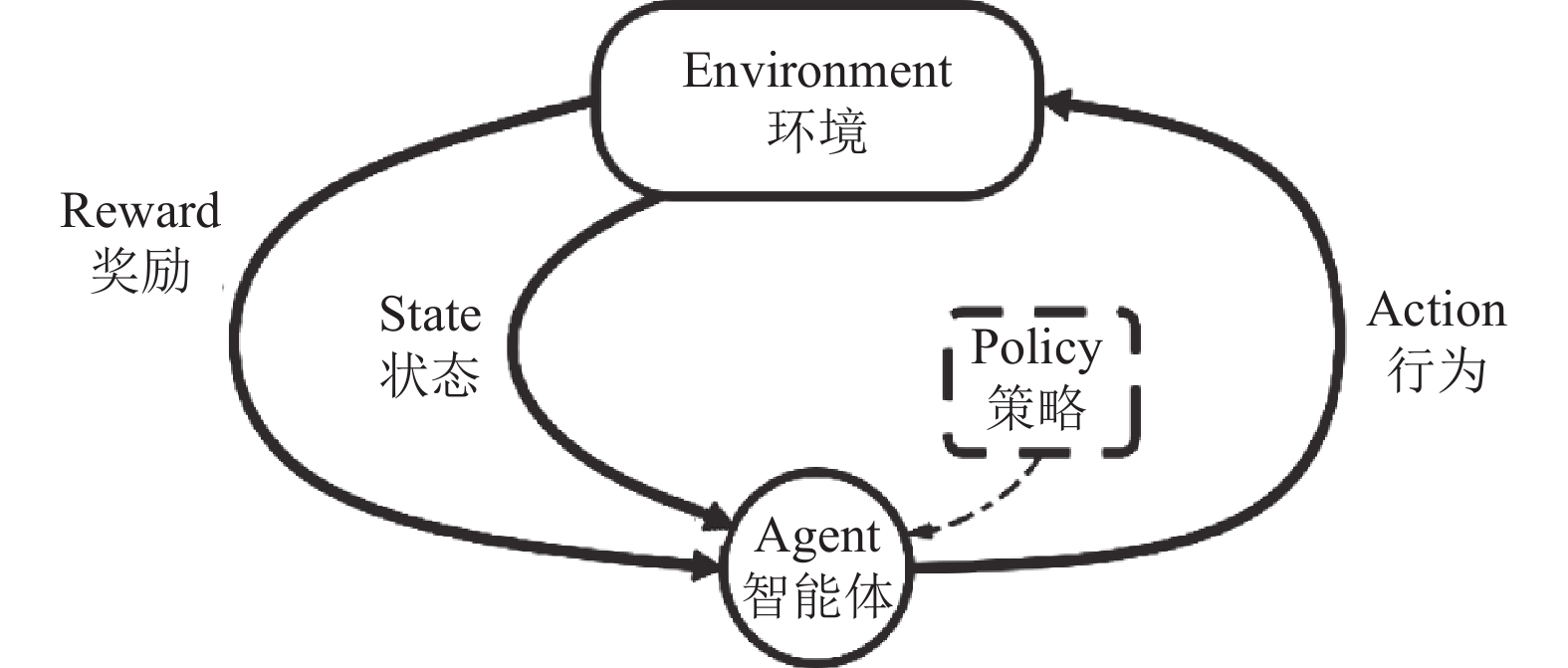
2 模型和算法如图1所示, 强化学习的基本结构由环境(Environment)、智能体(Agent)和策略(Policy)这3部分组成. 环境用于产生训练数据, 它根据当前状态(State)和智能体的动作(Action), 利用状态转移函数得到下一状态. 智能体利用大量的训练数据更新策略(Policy), 以获取更高的奖励值. 在鱼游问题中, 环境指的是鱼体所处的流体环境, 训练数据指的是鱼体的游动数据.
|
图 1 强化学习模型示意图 |
2.1 代理模型
过往的研究中大多采用CFD方法模拟流体环境, 得到的训练数据真实可靠, 与真实场景误差很小, 但时间成本十分高昂. 本文使用代理模型对鱼游环境进行建模, 提高数据的产生效率, 同时兼顾了数据精度. 代理模型包括鱼体动作数据库和雷达系统两部分.
2.1.1 鱼体动作数据库鱼体动作数据库储存了鱼体所有动作能够产生的位移效果, 用于描述环境的状态转移函数. 构建该数据库的步骤如下.
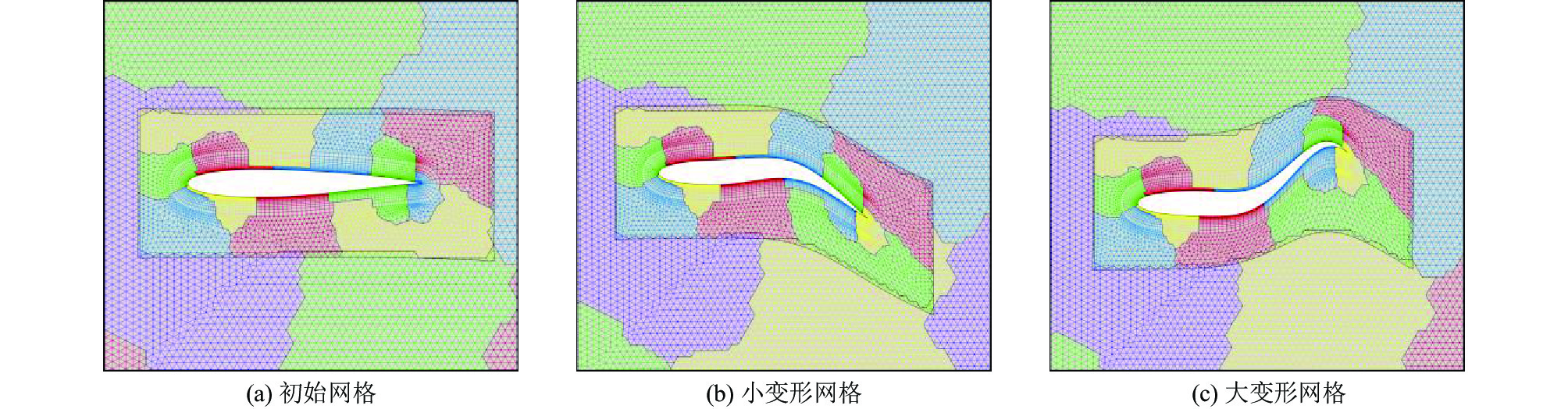
首先, 建立2D鱼体几何模型, 对模型生成计算域的初始重叠网格并分区, 图2中展示了鱼体不同动作下生成的网格及分区情况.
|
图 2 仿生鱼网格分区示意图 |
然后, 使用CFD软件在鱼体模型上完成对N-S方程[13, 14]的求解, 计算初始流场信息, 从而获取鱼体在流体中游动时所受到的压力和阻力信息.
最后, 结合动力学/运动学方程, 求得鱼体在某一状态下使用某动作能够得到的位移和转角, 并将对应结果存储在数据库中.
在本文中, 共计算了25个鱼体动作, 每个动作包括整周期和半周期两个状态. 实际训练中, 为了模拟流体环境的非定常特性, 要在数据库的数据上叠加一个随机值(噪声), 使得鱼体每一次的动作都会在一定范围内产生不确定的位移和转角.
代理模型通过上述方式, 仅在数据准备阶段进行一次CFD计算, 并在之后的训练中使用该结果, 从而在可接受的误差范围内, 大大降低了时间成本. 由于CFD的原理并不是本文的重点, 这里只简要叙述, 更详细的介绍可以查阅文献[11, 12].
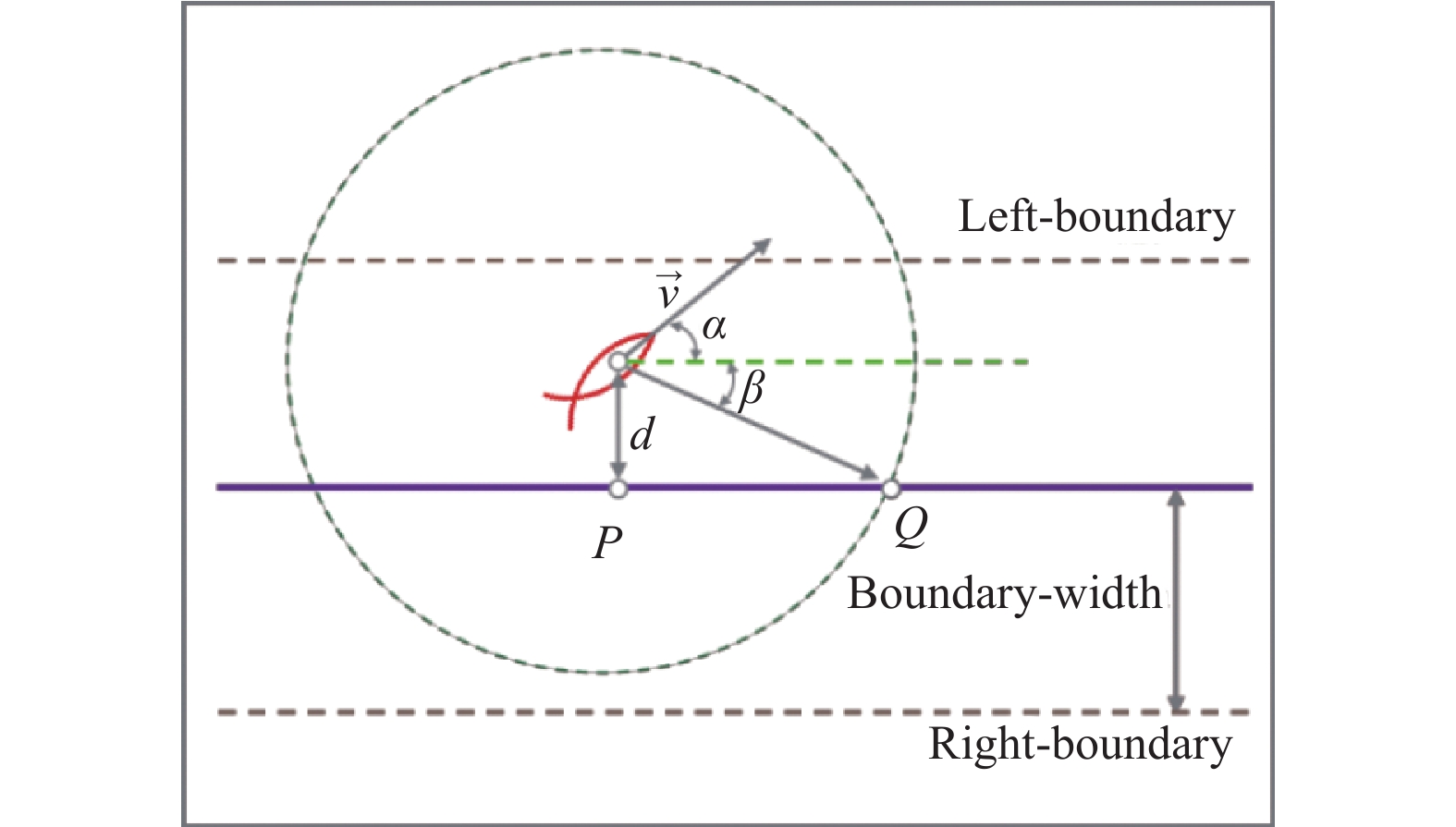
2.1.2 雷达系统鱼体使用雷达系统获取环境状态信息, 如图3所示, 中间的实线是轨迹, 鱼体将学习如何沿着该轨迹平滑游动. 点P表示鱼的质心在轨迹上的投影, 点Q表示雷达范围与轨迹的交点, 鱼体在游动时总是将此点视为目标点, d表示鱼体偏移轨迹的距离, v表示鱼体当前的速度.
|
图 3 雷达系统示意图 |
鱼体游动过程中, 使用雷达系统获取当前状态信息并传递给鱼体. 鱼体将获得的环境信息作为输入, 利用策略模型从数据库中选取动作, 每个动作都使鱼体完成一定的位移和转向, 并到达新的位置, 雷达系统再次获取新的状态信息. 重复以上步骤, 即可控制鱼体完成游动过程.
2.2 训练算法在鱼游问题中, 产生训练数据花费的时间占总训练时间的90%以上. 因此, 提高数据的效用, 加快策略模型的学习速度, 可以减少对训练数据的需求, 节省大量时间成本. 为了提高训练数据的效用, 本文使用近端策略优化(PPO)算法作为鱼体的训练算法.
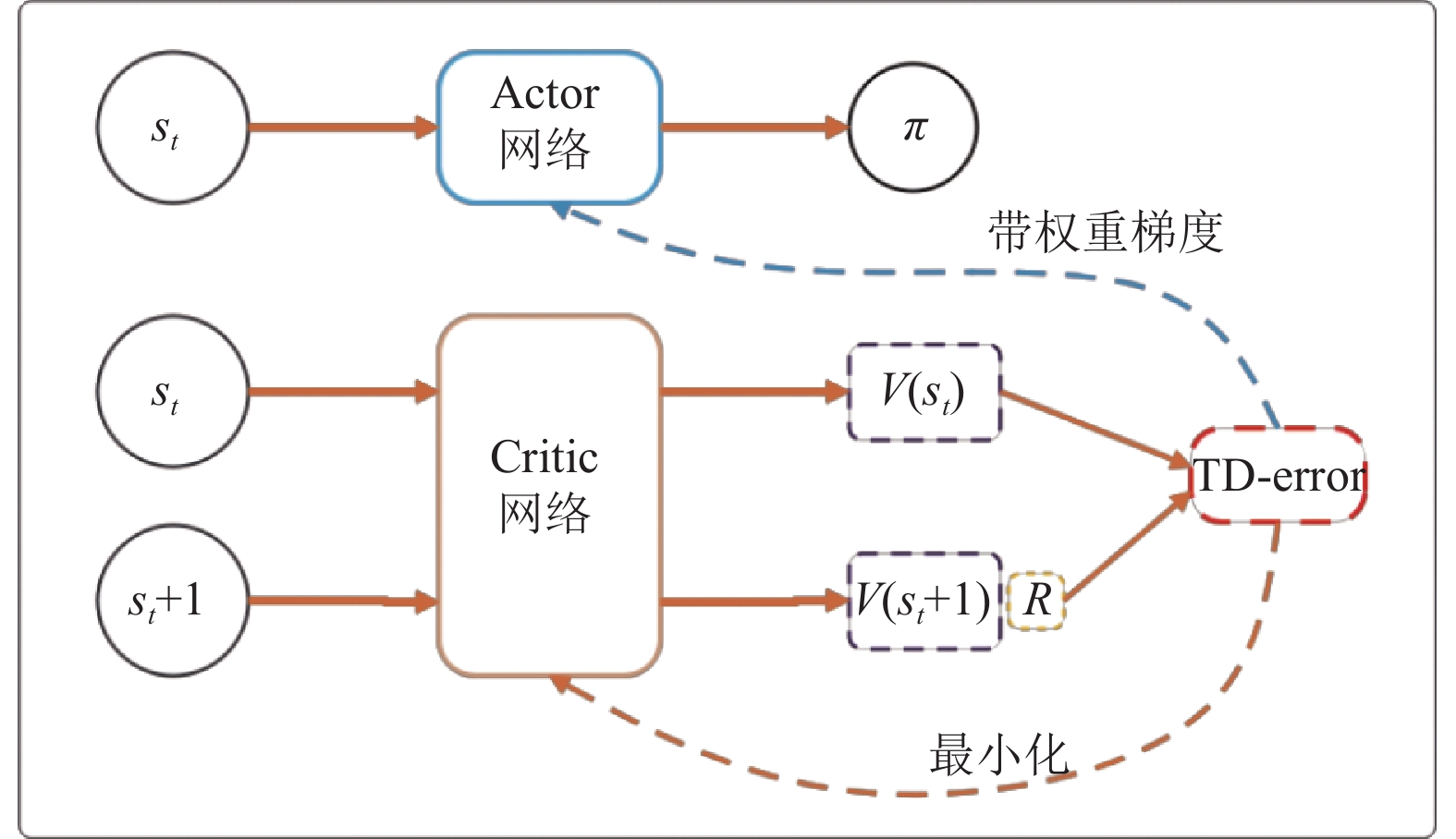
2.2.1 PPO算法PPO算法[15]是基于AC架构[16]的算法, 可以解决离散动作空间和连续动作空间的强化学习问题[17]. 如图4所示, AC架构的算法一般由两个神经网络组成: Actor网络和Critic网络. Actor网络的输入为状态, 输出为策略π; Critic网络的输入为状态, 输出为状态的价值. AC算法的训练中, Critic网络的学习目标是尽可能准确地评价当前状态的价值; 而Actor网络的学习目标是找到最优策略π*, 使得Critic网络的输出最大化.
|
图 4 AC算法的一般框架 |
相比AC算法, PPO算法有两个改进.
第一, 使用TD(n)算法取代TD(0)算法, 增强了算法的前向探索能力, 使得对动作的效果评估更加准确, 提高了算法泛化性. 具体做法是使鱼体按照当前策略运动n步, 得到n步后的价值, 再往回反推每一步的价值.
第二, 解决了AC算法的on-policy问题, 使算法可以重复利用训练数据, 从而提高了数据利用率, 加快算法收敛速度. 具体方法是使用重要性采样: 计算得到优势函数
| $ {r_t}(\theta ) = \frac{{{\pi _\theta }({a_t}|{s_t})}}{{{\pi _{{\theta _{{\rm{old}}}}}}({a_t}|{s_t})}} $ | (1) |
优势函数
| $ {\widehat A_t} = {G_t} - V({s_t}) $ | (2) |
| $ {G_t} = {r_{t + 1}} + \gamma {r_{t + 2}} + \cdots + {\gamma ^{n - 1}}V({s_n}) $ | (3) |
综上, 更新Actor网络的损失函数如式(4)所示, 其中clip函数用于将重要性权重的值限制在(
| $ {L^{clip}}(\theta ) = {\widehat E_t}[\min ({r_t}(\theta ){\widehat A_t}, clip({r_t}(\theta ), 1 - \varepsilon , 1 + \varepsilon ){\widehat A_t})] $ | (4) |
而Critic网络的更新方法是: 将折扣回报
状态空间中共有5个状态特征: 包括4个空间特征和1个时间特征. 空间特征变量的示意图如图3中的雷达系统所示, 各特征变量的含义如表1所示.
| 表 1 模型中状态变量含义 |
鱼体的动作空间包含25个离散值, 分别对应鱼体动作数据库中存储的25个动作的索引值.
算法的训练目标是使鱼体能够以平滑的路线沿着特定轨迹游动并到达终点, 游动过程中尽可能减少鱼体距离迹线的偏差和时间花费, 并规避越界情况的发生. 为达到这一目的, 奖励函数的设计包括距离奖励
| $ {R_1} = 1 - \frac{{|d|}}{{boundary\_width}} $ | (5) |
现有的模型条件下, 鱼体在急转弯处表现不佳, 很容易偏离轨迹并越界, 无法完成寻迹任务. 然而, 这种急转弯广泛存在于鱼类的真实运动轨迹中, 鱼类面对障碍、捕食或遇到天敌时, 都需要急速转弯机动. 若无法实现对急转弯曲线的循迹, 会极大限制仿生鱼的机动性能. 为解决这一问题, 需要在现有模型中加入对速度参数的训练.
2.3.1 速度参数对动作空间进行改进, 在鱼体25个动作的基础上, 增加一个减速标志, 并且使用另一个网络Actor2完成训练. 减速标志是一个布尔值, True表示执行减速动作, False表示不对速度进行干扰.
代理模型中不考虑减速时, 鱼体速度v的定义如式(6)所示, 其中
| $ v = {{{v}}_0} \cdot \left(1 - \frac{1}{{{{1.15}^n}}}\right) \cdot \theta $ | (6) |
考虑减速机制时, 为了简化问题, 当代理模型从Actor2网络中获取到的减速标志为True时, 将n重置为1, 使鱼体速度v恢复为初始状态, 并在之后的游动中根据式(6)逐渐增大.
为了防止出现Reward Hacking问题(鱼体为了获得更高的奖励而全程低速游动), 需要引入新的奖励函数R3. R3表示当鱼体执行减速动作时, 获得一个惩罚值(−5), 且训练不终止.
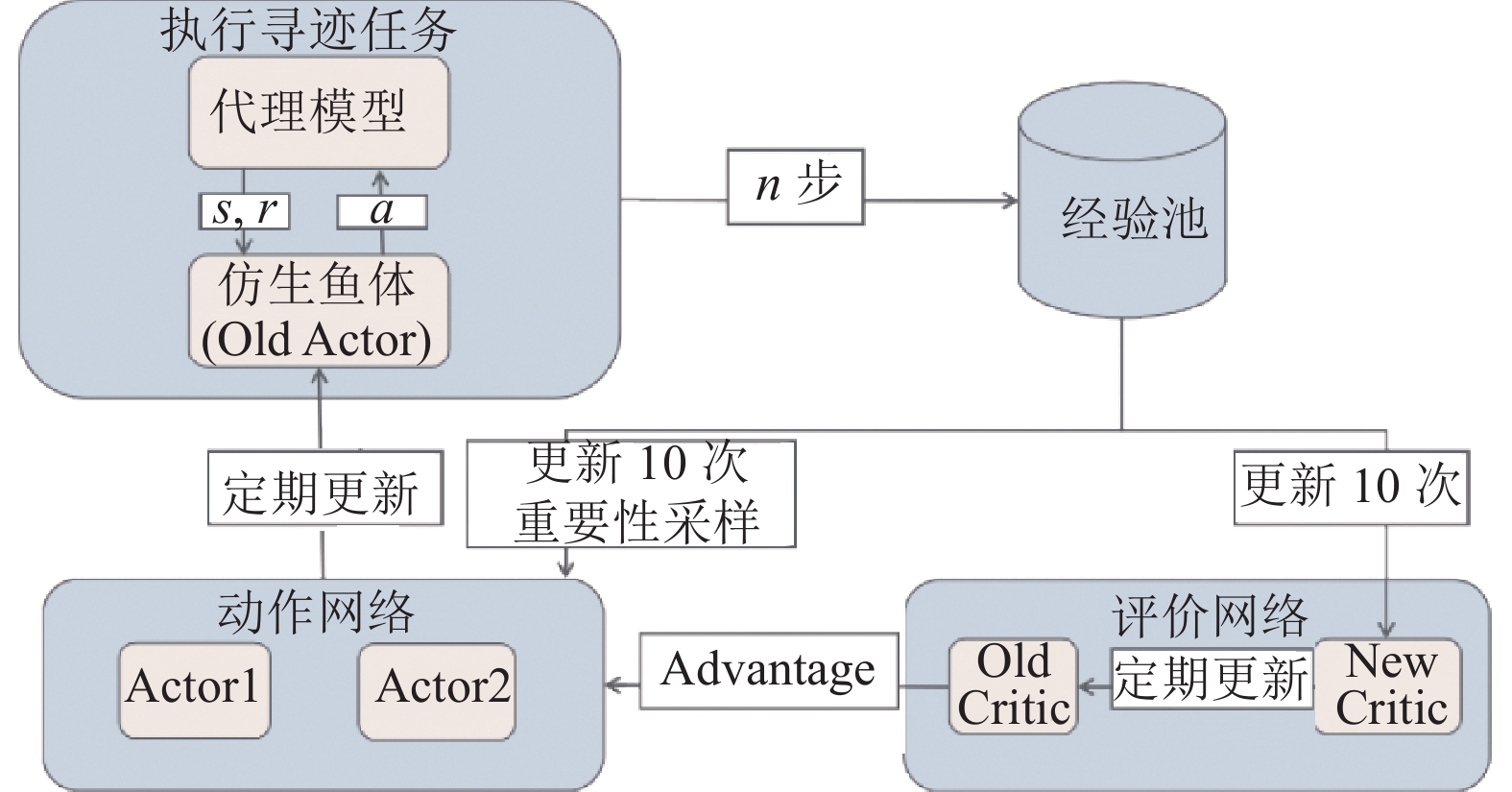
2.3.2 训练策略引入速度参数后的算法总体框架如图5所示. 其中Actor1网络输出动作, Actor2网络输出减速标志, Critic网络输出对鱼体所处环境状态的评价.
|
图 5 引入速度参数的鱼体循迹训练算法框架 |
训练策略如下, 首先在直线和曲线上训练Actor1网络和Critic网络, 使鱼体学习根据偏移情况选择正确的动作, 此时Actor2网络固定输出False, 不参与训练; 之后, 在包含急转弯区域的矩形中训练Actor2网络和Critic网络, 使鱼体学习在急转弯区域主动减速, 此时Actor1网络只利用, 不探索. 两个Actor网络分别训练完成后, 即可以控制鱼体完成在直线、曲线和急转弯区域上的循迹任务.
引入速度参数后, PPO算法的训练流程如算法1所示.
算法1. 鱼体循迹控制训练算法
输入: Actor网络和Critic网络使用同一组输入向量, 5个状态特征: α、β、d、v、
输出: 鱼体动作和减速标志.
训练过程:
1) for 迭代次数=1, 2, …, N do
2) 将代理模型重置为随机初始状态s0
3) while 鱼体未超出边界且未到达终点 do
4) 使用
5) if 经验池内数据达到容量 then
6) 利用重要性采样, 计算Loss值
7) 连续更新多次Actor1和Critic网络
8)
9) 清空经验池
10) end if
11) end while
12) end for
13) 对于Actor2网络的训练, 重复步骤1–12
3 直线与曲线实验分析强化学习中有两个评价算法性能的指标, 一是算法达到收敛所需的训练轮数, 用于衡量算法的收敛速度; 二是算法收敛后所能获取的Episode Reward值, 用于衡量智能体的学习效果. 本节实验的目标是使鱼体能够选取正确的动作以完成循迹任务, 同时使用评价指标评估所提算法模型的性能, 并与文献[11]中使用的AC算法进行对比.
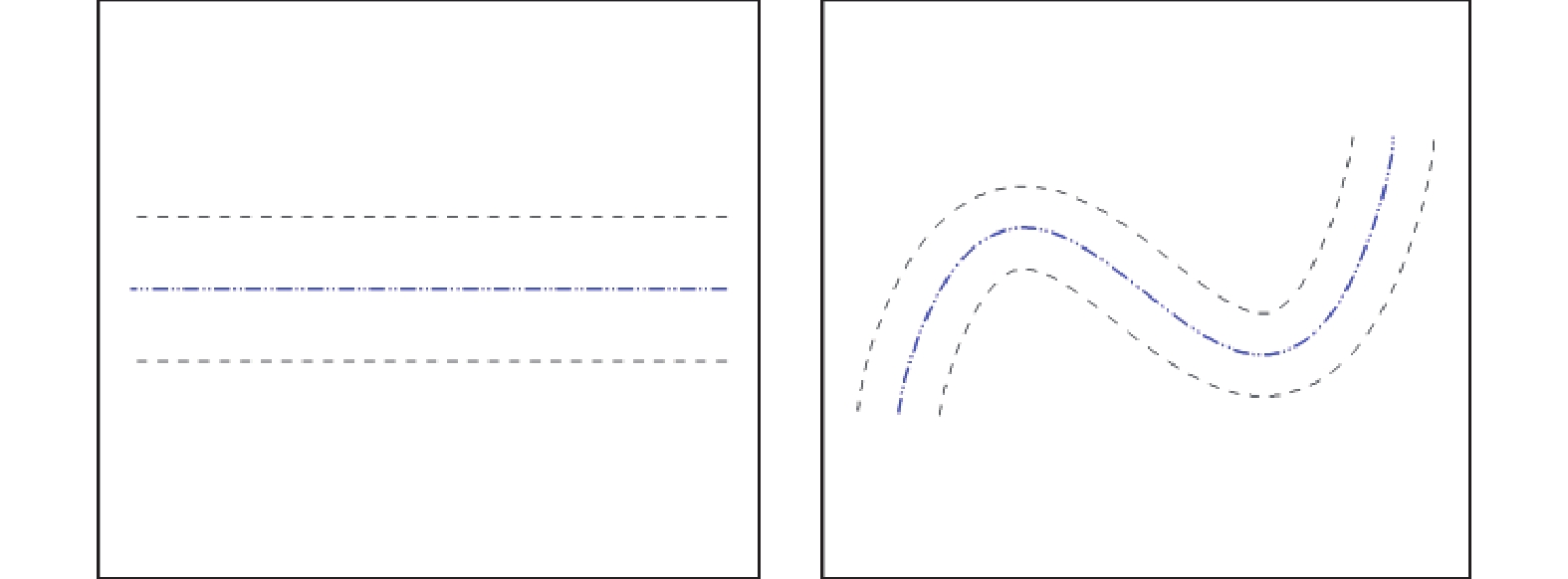
3.1 实验设置本节设置了直线和曲线两种循迹路线, 如图6所示, 中间虚线为鱼体跟随的轨迹, 两侧虚线表示边界, 当鱼体发生越界时, 循迹任务失败, 结束本轮训练并开始下一轮的训练.
由于本节不考虑急转弯区域的循迹控制, 因此只对Actor1网络和Critic网络进行训练, Actor2网络固定输出False. 实验参数配置如下: batch-size设置为32, Actor学习率为0.001, Critic学习率为0.01, 折扣率为0.9, PPO-clip参数为0.2, 鱼体的游动速度上限
|
图 6 实验场景示意图 |
3.2 直线训练
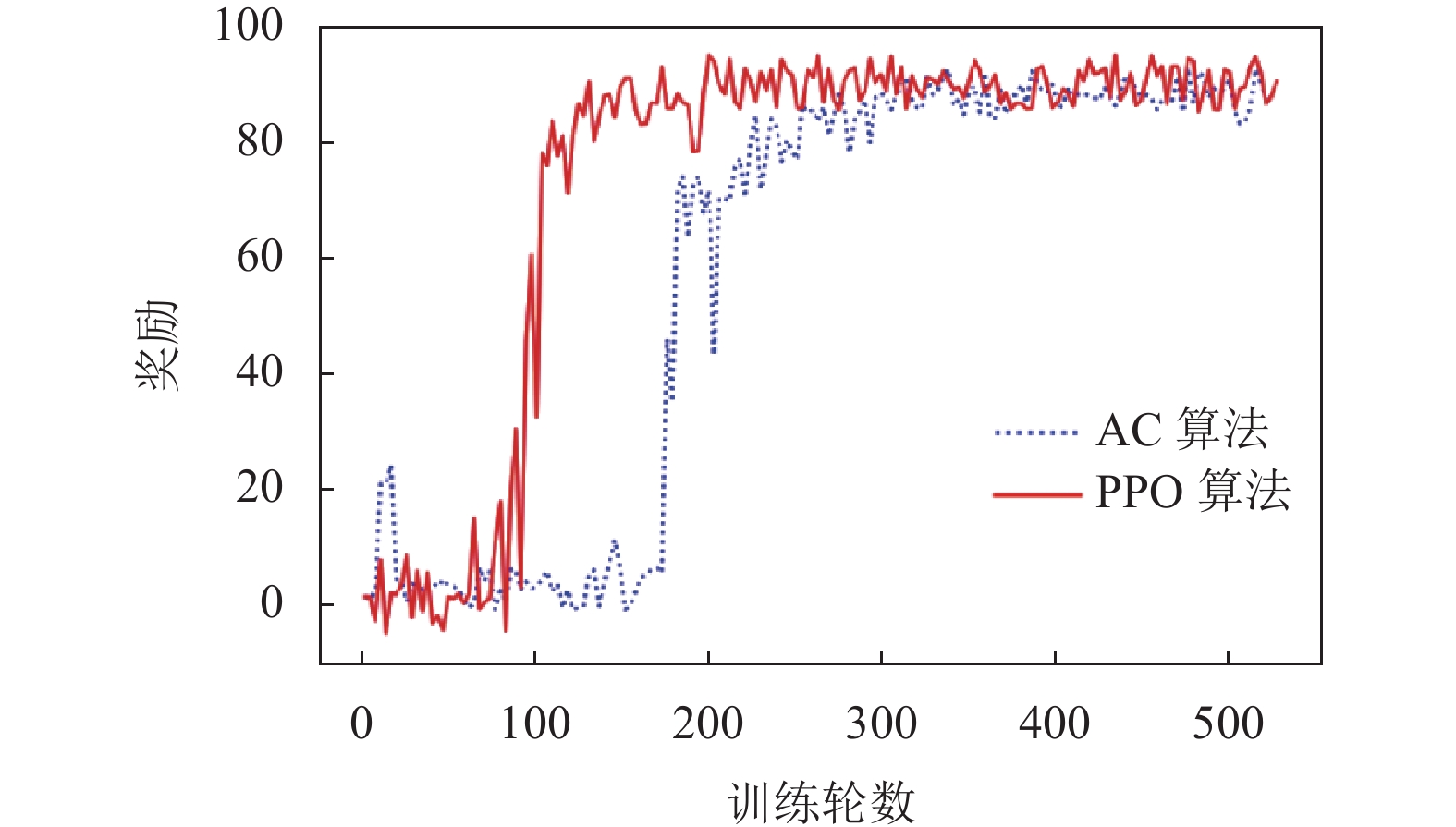
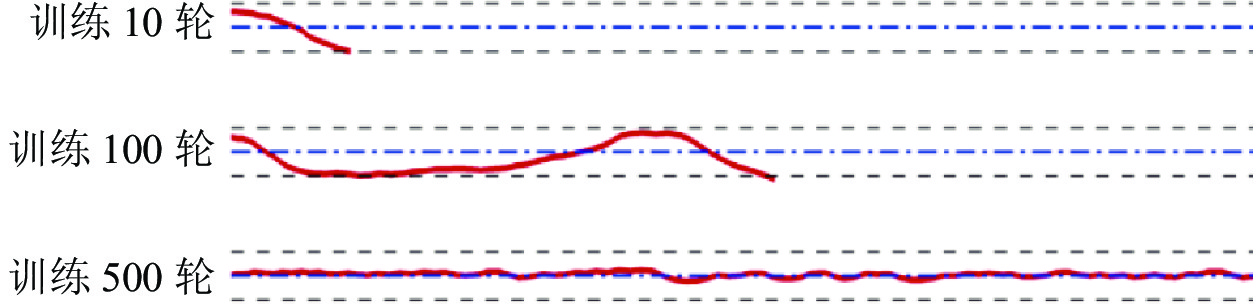
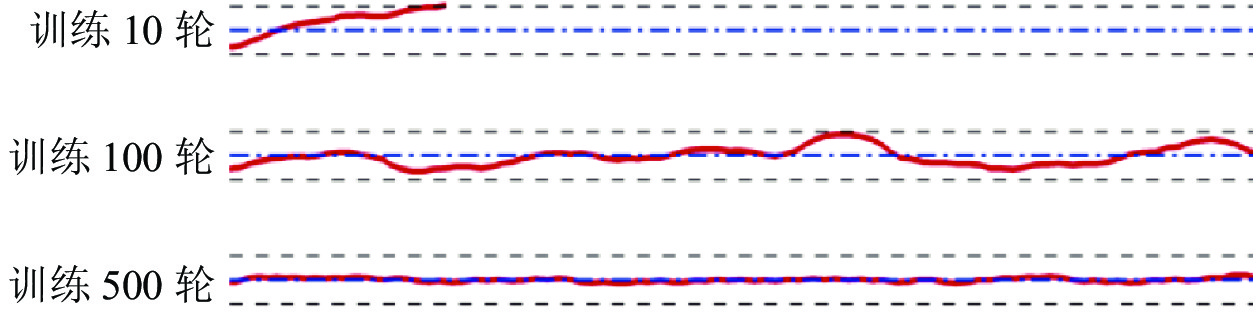
图7展示了两种算法在直线上的训练过程, 可以看出PPO算法在收敛速度上有明显的提升, 在Episode Reward方面也有轻微的提升, 并且算法的训练过程十分稳定. 从图8和图9中可以看到, 在训练到100轮时, PPO算法已经能够控制鱼体到达终点, 而使用AC算法控制的鱼体在中途就发生越界.
|
图 7 直线训练中奖励随训练轮数变化曲线 |
|
图 8 不同训练轮数下PPO算法轨迹展示 |
|
图 9 不同训练轮数下AC算法轨迹展示 |
3.3 曲线训练
在成功控制鱼体完成直线上的循迹任务后, 为了进一步验证算法的有效性, 我们使用直线训练后的DRL模型继续在曲线上进行训练.
如图10所示, 经过直线训练后的策略模型一开始在曲线上表现不佳, 获得的奖励不高, 而随着训练轮数的增加, 鱼体能够获取的奖励值也越来越高, 说明鱼体渐渐学会根据路径弯曲程度调整自身的动作. 从评价指标上看, PPO算法对Episode Reward值的提升并不明显, 但收敛速度非常快, 在100轮就基本收敛, 且后续训练非常稳定; 而AC算法在200轮才收敛, 且在之后有一定的震荡.

|
图 10 曲线训练中奖励随训练轮数变化曲线 |
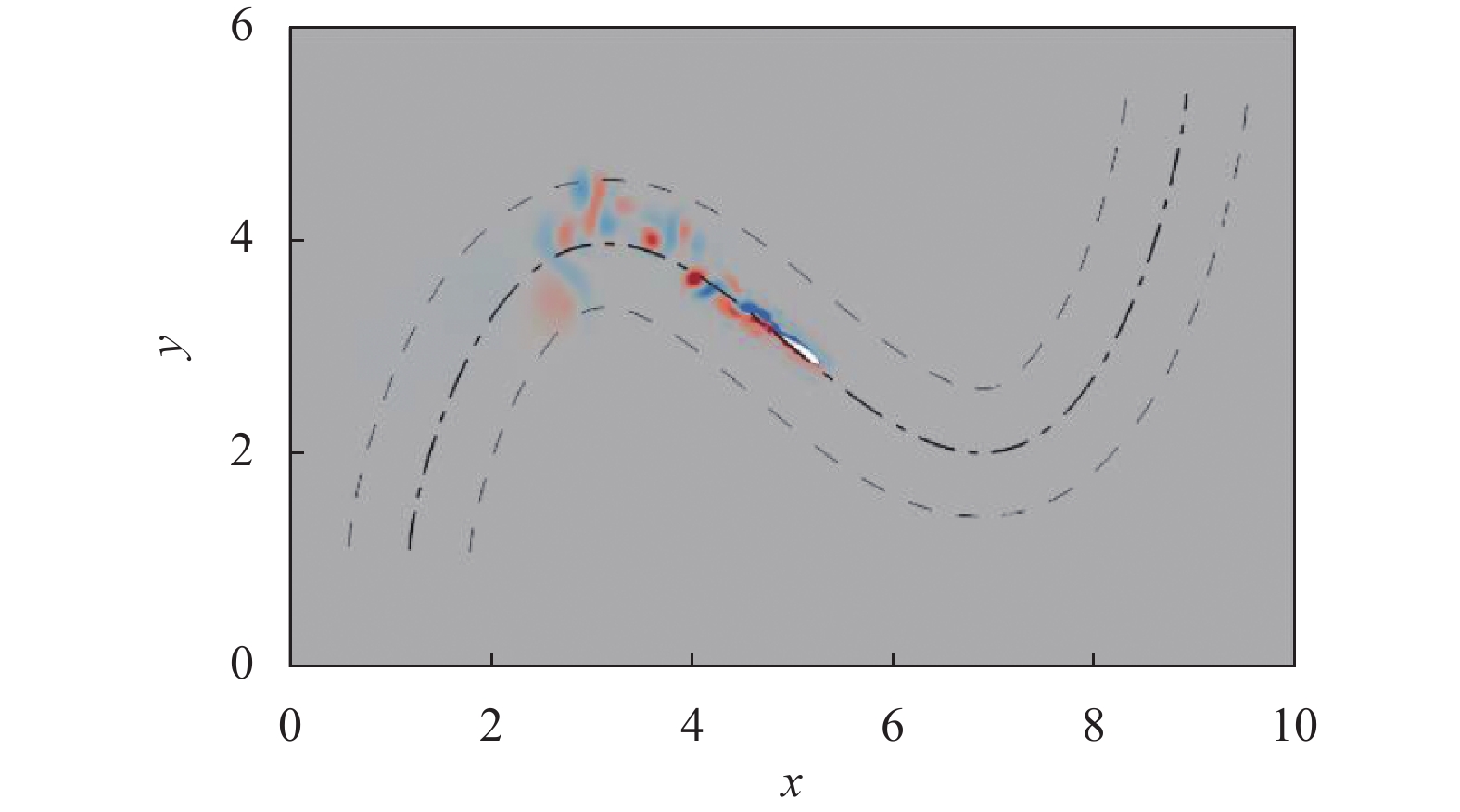
在成功控制鱼体完成曲线上的循迹任务后, 使用CFD环境替换代理模型以产生真实的游动数据, 对策略模型进行测试. 如图11所示, 经过代理模型训练后的鱼体在CFD环境下也能顺利完成循迹任务. 花费时间方面, 使用代理模型完成一次测试只需要30 s, 而使用CFD方式完成一次测试需要5.3 h. 综上可以得出结论, 使用代理模型可以在保证训练有效的前提下, 大大提升训练的效率.
|
图 11 鱼体在曲线中游动的涡度图 |
3.4 小结与讨论
在本节中, 我们对比了采用PPO算法与AC算法在直线和曲线上的循迹实验效果, 并最终在CFD环境中测试了策略模型. 实验结果表明, PPO算法在Episode Reward方面比AC算法表现略好, 且在收敛速度上有明显的提升, 能够有效提高数据的效用; 同时证明代理模型能够在保证训练有效的前提下, 大大提升训练数据的产生速度.
4 急转弯实验分析本节实验的目标是使鱼体能够在急转弯区域完成循迹任务, 因此需要对控制鱼体速度的Actor2网络进行训练, 并固定Actor1网络(不参与训练), 实验参数的设置与第3节一致.
4.1 矩形训练在矩形轨迹上对鱼体进行训练时, 鱼体需要在3个转角处完成90°的转向, 因此需要加入对速度的训练, 使鱼体在急转弯时能主动减速, 从而规避越界风险.
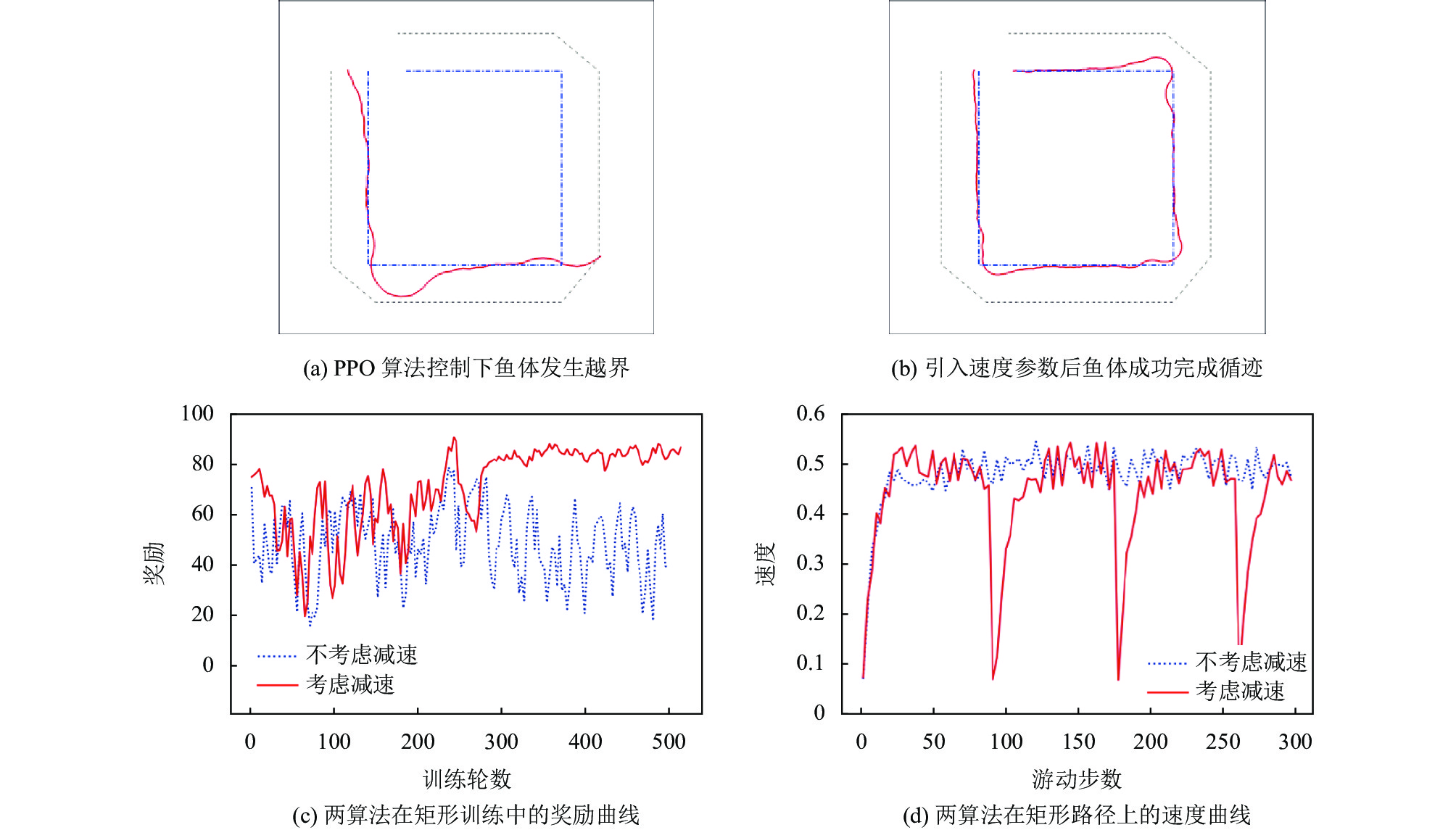
使用之前在直线和曲线上训练后的DRL模型继续在矩形上训练. 训练过程如图12(c)所示, 可以看到, 未引入减速机制的PPO算法在训练中不断震荡, 始终无法收敛, 而引入速度参数的PPO算法在经过300轮的训练后, 鱼体学会在急转弯处减速, 获取的Episode Reward值也稳定在80以上.
|
图 12 在折角曲线上训练 |
图12(a)和图12(b)分别为引入速度参数前后的PPO算法的循迹结果. PPO算法控制的鱼体在急转弯处发生越界, 无法完成循迹; 而引入速度参数后, 鱼体在转弯处主动减速, 从而顺利到达终点. 图12(d)是两个算法在训练500轮后鱼体从起点游到终点的速度, 可以看到, 引入速度参数后的PPO算法能够控制鱼体在矩形的3个转角处主动进行减速.
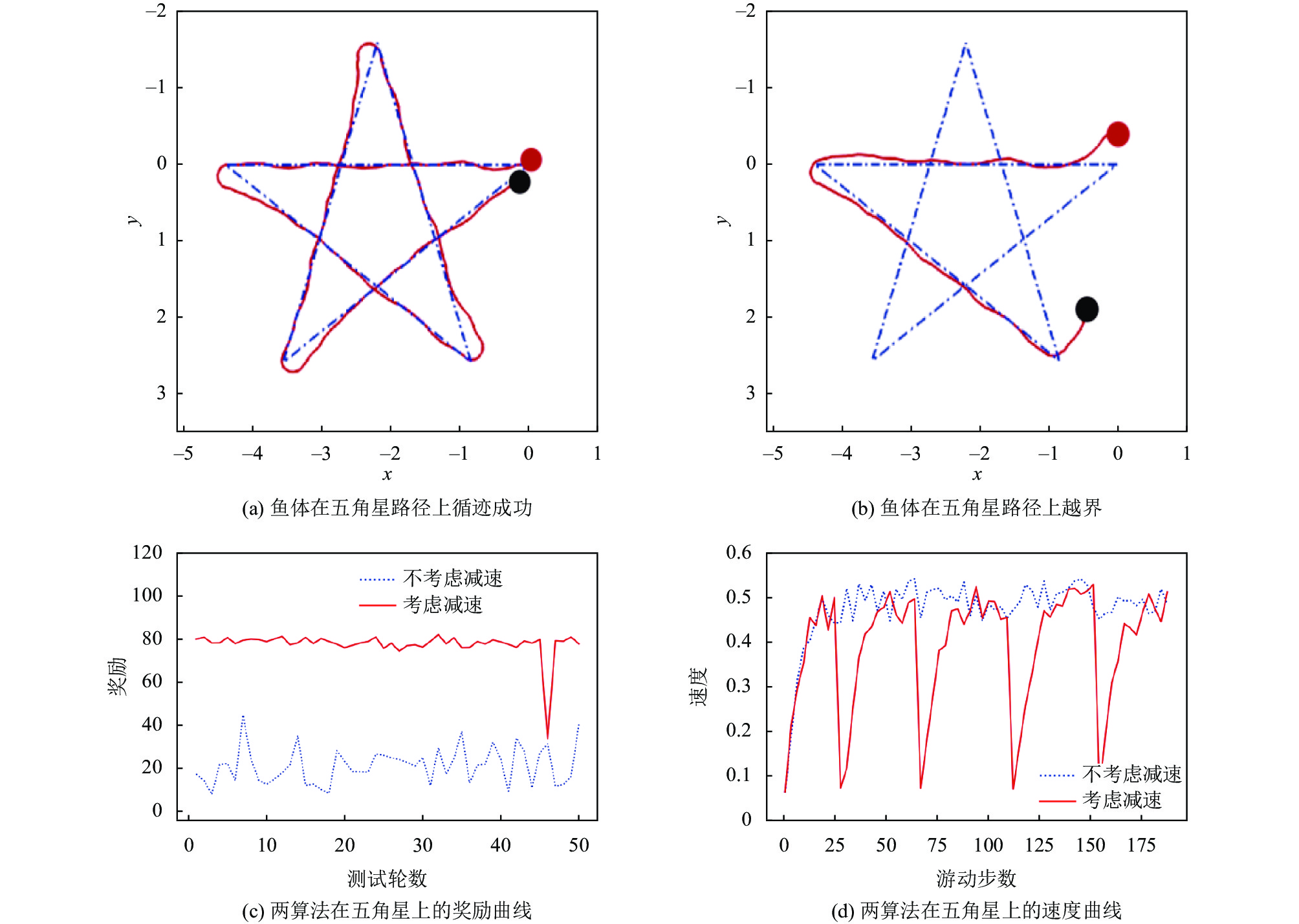
4.2 五角星路线测试更进一步, 为了评估控制算法的泛化能力, 需要测试鱼体在未见过的路径上的循迹能力. 本文使用正五角星作为测试路径, 如图13(a)所示, 红点为起点, 黑点为终点. 鱼体在每个转角需要完成144度的转向才能通过, 因此必须正确识别到转角并完成减速动作.
经过测试, 使用带减速机制的PPO算法训练得到的策略模型, 在测试集上的Episode Reward稳定在80左右(如图13(c)所示), 鱼体游完全程的成功率为98%, 且在4个转角处都完成了减速动作(如图13(d)所示). 使用不考虑减速的PPO算法时, 鱼体基本无法到达终点, 如图13(b)所示, 其奖励也一直在20附近震荡(如图13(c)所示).
|
图 13 鱼体在五角星上的测试结果 |
4.3 小结与讨论
在本节中, 我们使用引入速度参数的算法框架, 在矩形上对鱼体进行训练, 并在五角星路线上对模型进行测试. 实验结果表明, 与无速度参数的PPO算法相比, 引入速度参数的算法框架可以控制鱼体完成急转弯区域的循迹任务, 在矩形与五角星曲线上都达到接近100%的成功率.
表2是不同算法在不同轨迹上的成功率比较, 可以看出, 新的算法框架可以有效控制仿生鱼完成各种类型曲线上的循迹任务.
| 表 2 不同算法在不同轨迹上的成功率比较 |
5 结论与展望
本文中使用代理模型替代CFD环境产生训练数据, 大大节省了研究鱼游问题的时间成本, 并保证了训练的有效性; 同时引入新的训练算法, 提高了数据的效用, 在收敛速度和奖励获取上都表现出更好的性能; 最后, 引入速度参数, 使得仿生鱼在直线、曲线与急转弯区域上的循迹任务都获得了成功.
未来的工作中, 我们将进一步引入更加成熟的代理模型来进一步优化结果; 同时还可以使用原始感官输入(如图像、声呐等)代替雷达系统完成鱼体对环境的感知, 减少人工干预, 实现真实环境下的循迹、避障等智能行为.
| [1] |
林海. 仿生机器鱼机构设计及力学分析[硕士学位论文]. 西宁: 青海大学, 2015.
|
| [2] |
Gao A, Triantafyllou MS. Independent caudal fin actuation enables high energy extraction and control in two-dimensional fish-like group swimming. Journal of Fluid Mechanics, 2018, 850: 304-335. DOI:10.1017/jfm.2018.456 |
| [3] |
Gazzola M, Hejazialhosseini B, Koumoutsakos P. Reinforcement learning and wavelet adapted vortex methods for simulations of self-propelled swimmers. SIAM Journal on Scientific Computing, 2014, 36(3): B622-B639. DOI:10.1137/130943078 |
| [4] |
Novati G, Verma S, Alexeev D, et al. Synchronisation through learning for two self-propelled swimmers. Bioinspiration & Biomimetics, 2017, 12(3): 036001. DOI:10.1088/1748-3190/aa6311 |
| [5] |
Verma S, Novati G, Koumoutsakos P. Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proceedings of the National Academy of Sciences the United States of America, 2018, 115(23): 5849-5854. DOI:10.1073/pnas.1800923115 |
| [6] |
皮骏, 李想, 张志力, 等. 基于神经模糊PID控制的四旋翼飞行器算法. 计算机系统应用, 2021, 30(5): 228-233. DOI:10.15888/j.cnki.csa.007933 |
| [7] |
Tian RY, Li L, Wang W, et al. CFD based parameter tuning for motion control of robotic fish. Bioinspiration & Biomimetics, 2020, 15(2): 026008. DOI:10.1088/1748-3190/ab6b6c |
| [8] |
Khan S, Javed S, Naeem N, et al. Performance analysis of PID and state-feedback controller on the depth control of a robotic fish. Proceedings of the 2017 International Conference on Frontiers of Information Technology (FIT). Islamabad: IEEE, 2017. 7–11.
|
| [9] |
Novati G, Mahadevan L, Koumoutsakos P. Controlled gliding and perching through deep-reinforcement-learning. Physical Review Fluids, 2019, 4(9): 093902. DOI:10.1103/PhysRevFluids.4.093902 |
| [10] |
Zhu Y, Tian FB, Young J, et al. A numerical study of fish adaption behaviors in complex environments with a deep reinforcement learning and immersed boundary-lattice Boltzmann method. Scientific Reports, 2021, 11(1): 1691. DOI:10.1038/s41598-021-81124-8 |
| [11] |
Yan L, Chang XH, Tian RY, et al. A numerical simulation method for bionic fish self-propelled swimming under control based on deep reinforcement learning. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(17): 3397-3415. DOI:10.1177/0954406220915216 |
| [12] |
Yan L, Chang XH, Wang NH, et al. Learning how to avoid obstacles: A numerical investigation for maneuvering of self-propelled fish based on deep reinforcement learning. International Journal for Numerical Methods in Fluids, 2021, 93(10): 3073-3091. DOI:10.1002/fld.5025 |
| [13] |
Hirt CW, Amsden AA, Cook JL. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. Journal of Computational Physics, 1997, 135(2): 203-216. DOI:10.1006/jcph.1997.5702 |
| [14] |
Zhang LP, Wang ZJ. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes. Computers & Fluids, 2004, 33(7): 891-916. DOI:10.1016/j.compfluid.2003.10.004 |
| [15] |
Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms. arXiv:1707.06347, 2017.
|
| [16] |
Konda VR, Tsitsiklis JN. Actor-citic algorithms. Proceedings of the 12th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 1999. 1008–1014
|
| [17] |
李茹杨, 彭慧民, 李仁刚, 等. 强化学习算法与应用综述. 计算机系统应用, 2020, 29(12): 13-25. DOI:10.15888/j.cnki.csa.007701 |
 2023, Vol. 32
2023, Vol. 32


