2. 国家新能源汽车技术创新中心, 北京 102445
2. National New Energy Vehicle Technology Innovation, Beijing 102445, China
随着信息技术和网络服务的快速发展与应用, 线上采购成为我国民众不可或缺的一种生活方式. 国家邮政局数据显示, 我国每天约配送3亿件快递包裹. 当包裹到达收件人所在地区的物流配送中心后, 一般由快递员完成将包裹交付至消费者手中的最后一棒. 由于其路途通常远远小于包裹收寄点之间的距离, 故称之为最后一公里配送问题. 考虑到收件人在整个城市区域的分布分散性以及在局部地区的分布集中性, 物流公司通常需要设置庞大的快递点网络并雇佣大量快递员以提供更好的最后一公里配送服务, 使得人力成本的持续上涨成为快递企业面临的最大困境[1]. 以京东为例, 2019年的前8个月, 仅是为旗下员工缴纳五险一金的支出就超过10亿元[2]. 直营物流企业顺丰2019年人力成本支出占年度营业成本的1/3. 此外, 大量快递车辆上路, 给本就拥堵的城市交通造成更大压力[1], 降低配送时效, 还进一步加重环境污染, 不利于碳中和与碳达标政策.
针对传统最后一公里物流配送在时效、成本、环境等方面存在的问题, 亚马逊于2013年提出利用无人机配送包裹的概念[3], 引发国内外企业和学者的广泛关注. 谷歌在2014年宣布Wing项目, 研究使用小型无人机投递包裹[4]. 亚马逊于2015年启动名为Amazon Prime Air的无人机送货项目[5]. 同年, 阿里巴巴尝试用无人机向中国3个城市的400多名客户运送成箱的姜茶[6]. 2017年, 民航局批准京东在陕西省正式开展无人机物流配送的试点应用[7]. 2018年, 饿了么开通中国首批共17条无人机外卖航线, 开创了中国利用无人机配送外卖的先河[8]. 2020年亚马逊获得美国联邦航空管理局批准, 允许在美国地区运营Prime Air快递无人机, 最新版本的Prime Air有望实现30 min内将包裹交付给10英里范围内的客户[9]. 2021年, 中国四川省的无人机基地投入100多架无人机解决深山新鲜松茸的运输难题[10].
由上述案例可以看出, 无人机配送已经成为物流行业的重要发展趋势, 英国经济学人网站将无人机配送列为2022年值得关注的22项新兴技术之一[3]. 无人机配送作为一种新型的配送模式, 相较于传统纯快递员配送具有如下优势: (1)无人机在空中飞行, 不受地面交通影响, 配送时间短, 效率高. (2)无人机配送的单位公里配送成本远远低于车辆配送, 可以降低对快递员的数量需求, 进一步减少人工成本和运营成本. (3)无人机配送可以降低地面车辆配置数量和行驶里程, 减轻城市的交通拥堵和环境污染.
为深入了解当前国内外对无人机参与最后一公里配送的研究情况, 本文从无人机在最后一公里物流配送中的机遇与挑战、配送模式、配送路径规划算法、目前已公开的相关测试数据集等方面, 对国内外相关研究文献进行系统总结, 梳理已有研究现状, 并分析未来研究趋势.
1 无人机在最后一公里物流配送中的机遇与挑战无人机技术的逐渐成熟推动了其在物流、环境、农业、国防等领域的广泛应用[11]. 其中, 在民用领域, 无人机已经在航拍、农业、灾难救援、电力巡检等行业成熟应用. 在环境领域, 无人机在测绘、山地考察、空气质量和水监测、农作物监测等行业具有明显优势. 在国防领域, 无人机已应用于侦察监视、目标打击、应急配送等. 此外, 在应急医疗供应、情报搜集等方面也极具应用价值. 在物流领域, 中国的京东, 菜鸟, 顺丰, 圆通, 杭州迅蚁等, 美国的亚马逊, 谷歌和Matternet等, 都在进行无人机配送的技术储备和应用探索.
目前, 城镇地区的传统快递配送面临由交通堵塞导致的配送时间不确定, 客户分散性导致的配送效率低, 人力成本高等问题. 利用无人机进行快递配送可以有效改善上述缺陷, 因而比传统配送模式更具有吸引力. 然而, 无人机参与最后一公里配送仍存在一些关键制约因素: 技术, 政府法规和可熟练操作无人机的劳动力等[12]. 总之, 无人机在最后一公里物流配送中既有重要发展机遇, 又存在无可避免的挑战.
1.1 无人机在最后一公里物流配送中的机遇 1.1.1 成本优势Wang等[13]认为得益于无人机固有的灵活性、便捷性和低成本, 其在各种民用应用中具有巨大的潜力, 尤其是在物流行业的包裹配送方面, 传统的车辆配送包裹的方式容易受到路况和地理条件的限制, 例如交通拥堵的城市、地形复杂的偏远地区、环境动态变化的灾区等, 使得配送成本(车辆固定成本、人力成本等)居高不下. 相比于车辆配送包裹, 无人机在空中飞行, 可忽略路况和地理条件的限制, 飞行路线短, 且不会因为交通拥堵而增加额外等待时间. 同时, 无人机自重轻, 耗能少.
因此, 采用无人机进行物流配送, 可节省大量的成本.
另有许多学者通过实验模拟对无人机配送的成本节约效果进行验证. Chiang等[14]的实验结果表明使用无人机进行最后一公里物流配送, 可以减少使用传统运输车辆的固定成本和燃油消耗. Campbell等[15]通过多个案例研究认为车和无人机协同配送在节省成本方面具有巨大优势. 在为美国交通部提供的一份报告中指出: (1)车和无人机协同配送有可能大幅节省成本, 尤其是在郊区地区; (2)在单辆卡车上放置多架无人机可以带来极大的成本节省, 但边际效应的降低也可能是巨大的. Pugliese等[16]考虑真实场景的包裹配送, 分析了3种包裹配送方式: 卡车配送, 无人机配送, 车和无人机协同配送, 面向带时间窗约束的真实场景, 对比了3种配送方式在运输成本方面的优缺点. 结果表明车和无人机协同配送方式可以最大限度地节省对地面道路和基础设施进行维护的成本, 以及因交通拥堵而增加的成本.
1.1.2 环保优势传统运输车辆最大的缺点是尾气排放产生的二氧化碳等温室气体会对环境造成不可逆的影响. Campbell等[15]在为美国交通部提供的一份报告中指出使用无人机配送能减少温室气体的排放. Pugliese等[16]分析了卡车配送, 无人机配送, 车和无人机协同配送这3种配送方式在二氧化碳排放方面的优缺点. 结果表明车和无人机协同配送方式的环保收益高于另外两种方式. Chiang等[14]通过大量实验验证了用无人机进行包裹配送可以减少使用传统运输车辆的燃油消耗, 从而节省能源和减少二氧化碳的排放.
1.1.3 配送时效优势Chiang等[14]进行了大量实验, 验证了用无人机进行最后一公里配送相较于使用传统运输车辆, 可以减少配送时间. 另有一些文献研究配送时间的节省与哪些因素相关, Wang等[17]证明车和无人机协同配送相比于单独使用卡车运送包裹可以节省交付时间, 节省的时间取决于每辆卡车上无人机的数量和无人机相对于卡车的速度. Carlsson等[18]认为车和无人机协同配送的硬件系统虽然已经成熟, 但仍未取得大规模实际应用, 能在多大程度上显著提高服务质量还无法确定. 结合欧几里得平面理论分析和道路网的实时数值模拟, 证明了车和无人机协同配送效率的提升与卡车和无人机速度之比的平方根成正比. Pugliese等[16]考虑了带时间窗的真实场景, 分析了车和无人机协同配送相较于卡车配送和无人机配送, 在配送效率上具有显著优势.
1.1.4 无接触配送优势2020年1月, 美团首次提出无接触配送创新服务方式, 以应对新型冠状病毒肺炎传播[19], 减少交叉感染的风险. 2020年2月, 上海市奉贤区启用无人机送菜, 仅用5 min就可将活鱼鲜蔬等生活用品送到隔离居民家中[20]. 2020年4月, 湖北省武汉市的快递企业成功地使用无人机将医疗防疫物资送到武汉金银潭医院, 表明无人机物流运输具有独特的无接触配送优势[21].
综上, 无人机参与的最后一公里配送具有绿色低碳、不受地形和运输路线限制、降低配送固有成本和时间成本、减少人际接触等优势, 证明无人机在快递包裹、外卖、紧急医疗物资配送等方面具有较大的应用潜力.
1.2 无人机物流配送面临的挑战虽然无人机相较于传统车辆在物流配送领域有明显的优势, 但由于目前无人机应用技术尚未完全成熟, 在使用过程中仍存在一定风险, 故世界各国均暂未完全放开无人机的大规模应用.
1.2.1 空域管理政策限制无人机行业的快速发展, 滋生出许多安全问题. 例如, 无人机在未经许可的情况下飞入军事管制区、飞行过程因操作不当或突遇故障坠机引发伤人事故等. 因此, 政府必须制定完备的政策法规以引导无人机行业健康有序发展. 然而, 空域管理政策也会限制无人机的发展和大规模应用. Elsayed等[22]认为若民航局划定较多的严格空域管制区域, 则无人机需要频繁绕飞, 导致飞行路径大大增加, 反而会增加温室气体的排放. Baloch等[23]研究无人机包裹配送对电子零售商配送网络的影响. 结果表明政府法规, 无人机应用的社会阻力等因素都会对无人机配送效果产生一定影响.
2017年美国总统特朗普签署备忘录, 启动无人机系统整合试点项目(the unmanned aircraft systems integration pilot program). 该项目倾向于加速无人机融入国家空域系统, 减少政府过度监管, 激发市场活力. 我国在2019年也提出了无人机空域管理的政策, 重点在于无人机运行和空中飞行方面的管理. 随着无人机技术的逐渐成熟, 政策法规等的逐渐完善, 未来有可能逐渐放开对无人机的空域管制.
1.2.2 无人机自身技术限制无人机技术参数主要包括机重、续航能力、载重能力、飞行速度、飞行极限海拔、抗风性能、电池容量和重量、最大上升和下降速度等. 围绕这些技术参数, 相关文献分析了无人机技术限制对其配送服务的影响. Jeong等[24]对无人机遇到的多种问题因素进行了综合考虑, 并构建了考虑这些问题的车和无人机协同配送数学模型. Dukkanci等[25]认为将仓库作为无人机的出发点虽然不会产生运输工具(卡车)的成本, 但会导致无人机的航程增加. 无人机的电池容量可能无法满足大部分需求. 故需要重新设计无人机的出发点或者增加无人机的电池容量.
Song等[26], Lasla等[27], Jeong等[24]都提出无人机的续航能力和载重能力相对有限, 导致无人机的飞行时间受到限制, 配送能力相对传统交通工具更弱.
此外, 还有文献考虑到无人机的机载传感器技术所面临的挑战. Worden等[28]提出无人机在工作过程中, 极易受到机载传感器通信带宽受限的影响, 导致无人机工作状态的不稳定.
1.2.3 无人机面临的安全问题无人机比地面车辆面临更大的安全挑战. 一些文献[24, 29]考虑了天气因素对无人机配送包裹的影响. Adulyasak等[29]也认为天气因素是影响无人机任务执行效果的关键, 尤其是大风、雨雪等会降低无人机的飞行效率, 甚至危及飞行安全. 为此, 专门提出一种考虑天气因素的无人机配送方式, 即下午根据当天上午的天气做出预判, 对无人机配送的调度进行安排, 以减少不可控天气因素对无人机造成的影响和风险, 降低延迟交付的概率.
除天气因素外, Dayarian等[30]认为在无人机直接给客户配送包裹的场景下, 最大的限制因素是无人机在某些高密度高层住宅区飞行涉及的避障问题和安全问题. Eren等[31]提出了面向无人机运送包裹的风险评估方法, 考虑无人机飞跃高层住宅区的避障问题, 为决策者提供安全最佳的飞行路线, 降低事故率, 提高交付可靠性.
一些文献还考虑了无人机突遇故障等不确定性所引发的后续安全问题. Sawadsitang等[32]指出无人机属于精密器械, 任何部件的微小变动都会影响其飞行状态和使用寿命, 在物流配送过程中, 一旦发生各种各样的故障, 则会造成无法预料的危险. 其针对无人机可能发生的故障、事故、服务中断等不确定性问题, 提出一种地空联合配送服务优化和规划框架.
总的来看, 无人机在最后一公里配送中, 还面临载重能力和续航能力有限、安全因素容易受天气和高层建筑影响、空中交通安全与管理复杂等制约, 将无人机应用到现实的物流配送中还面临许多挑战. 这也是无人机至今未得到大范围推广的关键因素.
2 无人机最后一公里配送模式无人机参与最后一公里配送有多种模式, 本文通过对已有文献进行梳理和总结, 主要归类为如下4种配送模式: 无人机独立配送、无人机和地面车辆并行配送、无人机和地面车辆协同配送、无人机和地面车辆混合配送.
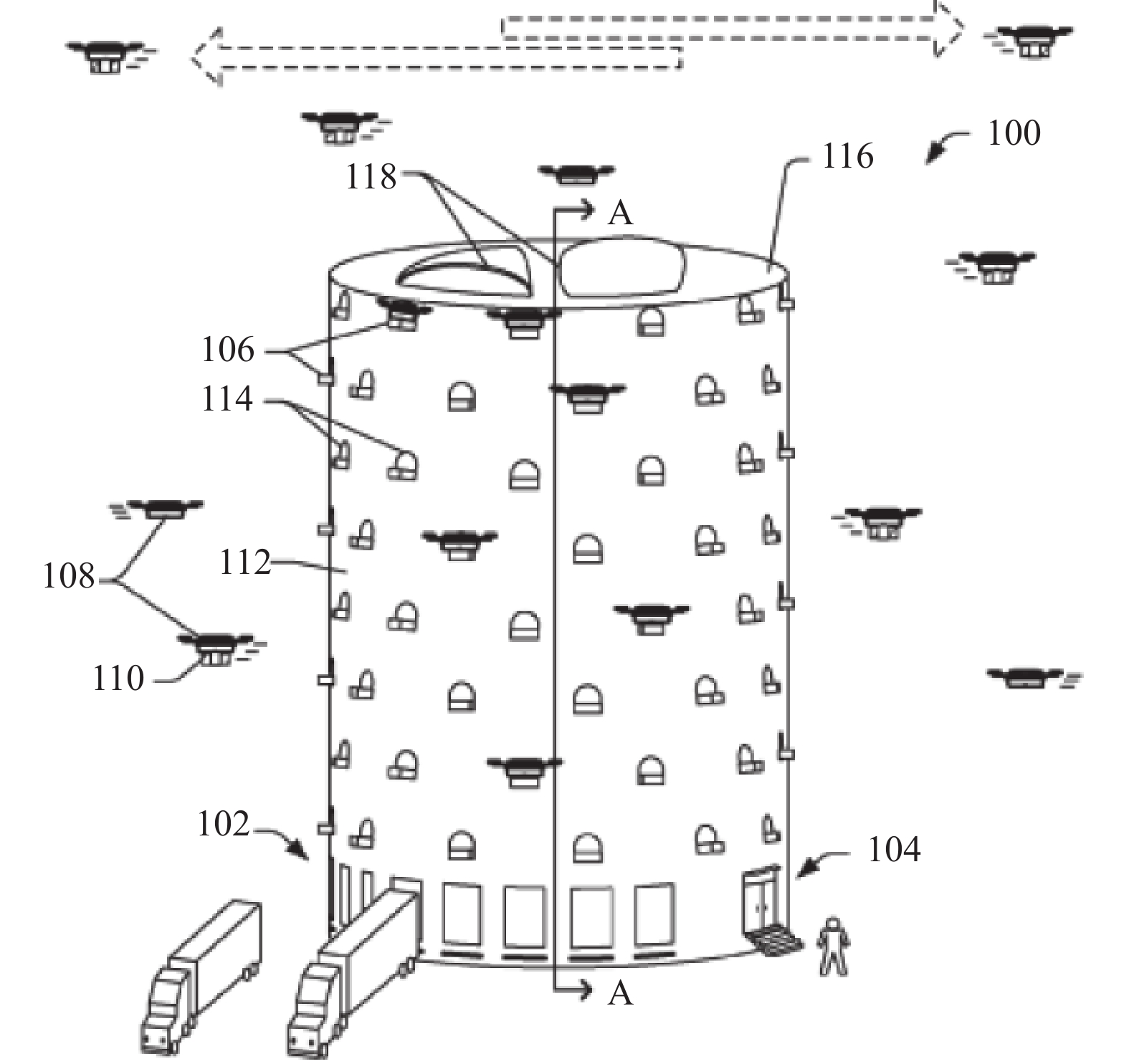
2.1 无人机独立配送针对客户点距离配送中心较近的情形, Curlander等[33]提出一种由无人机独立配送的模式, 设计了可以容纳无人机起飞和着陆的多层配送中心, 如图1所示.
该配送中心可以支持无人机的充电、检查、维修等操作, 还设置自助服务点支持客户自取包裹, 其中部分包裹可以由机器人进行分拣和装载.
Kuru等[34]针对无人机配送问题, 融合多维空间任务分配和三维路径规划方法(交叉熵蒙特卡罗), 提出一种面向应用的无人机配送技术框架, 如图2所示, 能够支持一架无人机配送多个包裹, 以及在动态环境中确定最优配送路径.
此外, 依托中继充电站的无人机配送模式可以为距离配送中心较远的客户点提供包裹配送服务. 固定中继充电站可为无人机提供充电保障, 提高无人机续航能力和配送效率. Song等[26]考虑无人机有限的续航能力和载重能力, 以及装载的货物重量对飞行能力的影响, 设计多个共享服务站点以补充无人机消耗品(充电电池, 交付货物等), 如图3所示, 以减少无人机配送过程中携带货物飞行的距离, 可在一定程度上缓解无人机装载能力和续航能力有限的劣势, 扩大无人机配送范围, 提高无人机配送服务的持续性.
|
图 1 多层级配送中心 |

|
图 2 一机多包配送模式 |

|
图 3 无人机中继停靠配送模式 |
依托中继充电站的无人机配送模式还可以应用于灾后应急物资的运送. Rabta等[35]面向受灾后偏远地区无法使用陆地运输车辆对灾民进行物品救济的情形, 考虑无人机的有效载重能力和能量约束下的总飞行距离, 提出设立临时充电站, 利用无人机配送救援物资的解决方案, 并通过分析验证了部署充电站能够大幅增加无人机配送应急物资的覆盖范围.
在无人机独立配送模式下, 考虑到旋翼无人机的载重能力和航程有限, 配送的对象往往较为特殊(食品、救援物资), 应用的场景也具有一定特殊性. 很少有研究能够应用于通用包裹最后一公里配送实践. 此外, 现有研究多将问题构建成一种理想的数学规划模型, 再采用一定算法进行问题求解, 而对无人机实际运行过程中与控制中心之间的通信限制、地形障碍、空中管制等实际环境要素考虑较少.
2.2 无人机和地面车辆并行配送Murray等[36]提出车和无人机并行配送问题(parallel drone scheduling traveling salesman problem, PDSTSP), 即无人机和卡车独立配送货物, 无人机从配送中心(仓库)起飞并返回, 与卡车不存在协同关系, 如图4所示.

|
图 4 无人机和卡车并行配送模式 |
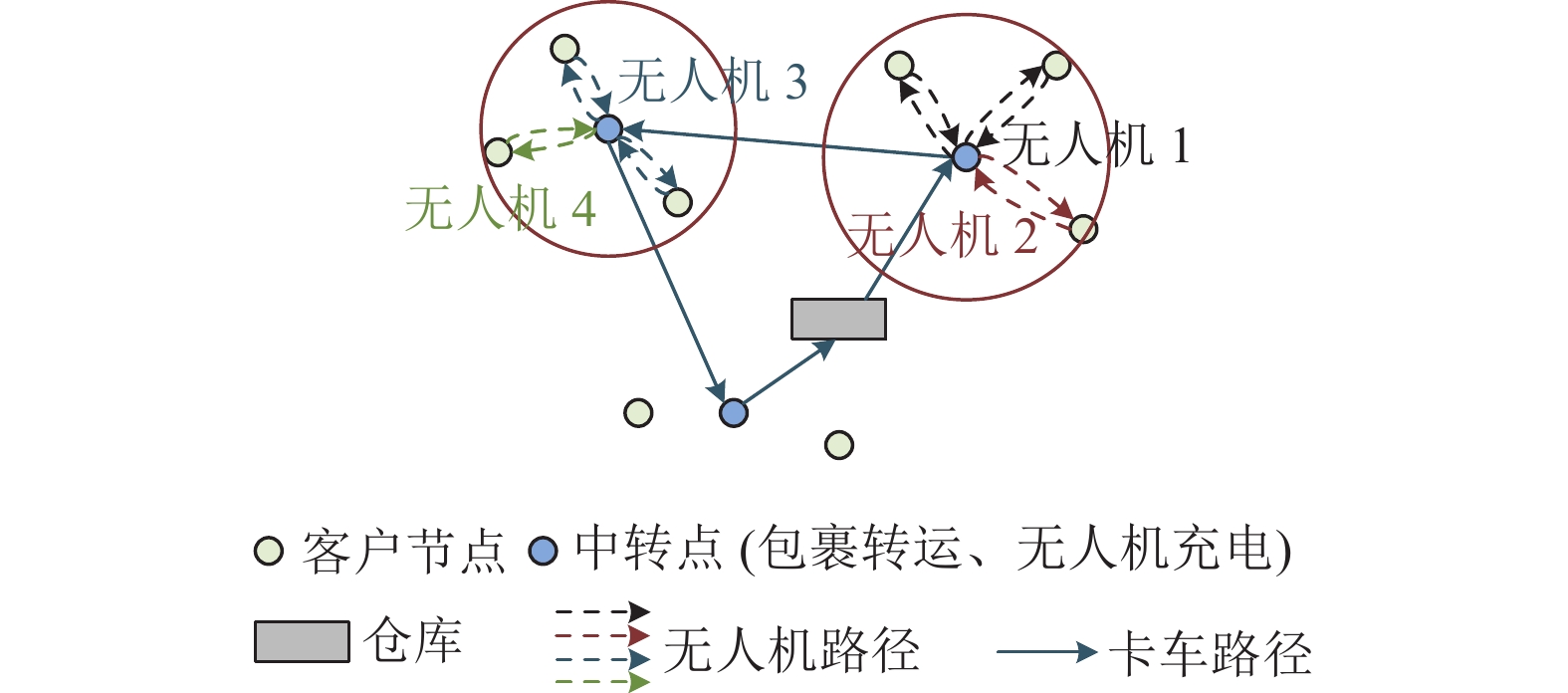
Li等[37]提出一种带中转点的无人机和卡车并行配送模式, 用卡车将包裹从配送中心运至中转点(中转点提供包裹转运以及无人机发射、回收和充电、维护功能), 然后由无人机将包裹从中转点运至客户点, 如图5所示. 其中, 红色圆圈表示无人机最大配送范围.
|
图 5 带中转点的无人机和卡车并行配送模式 |
2.3 无人机和地面车辆协同配送
目前, 有大量文献研究无人机和地面车辆协同配送问题, 主要分为以下5种配送模式, 分别为: 无人机同车起降配送模式、无人机异车起降配送模式、无人机-公共交通协同配送模式、无人机送货取货一体配送模式、无人机卡车途中起降配送模式, 如图6所示.

|
图 6 无人机和地面车辆协同配送模式 |
针对无人机和地面车辆协同配送的早期研究基本都立足于无人机同车起降配送模式. 如Murray等[36]提出的车和无人机协同配送问题(flying sidekick traveling salesman problem, FSTSP), 无人机必须在客户节点处从卡车起飞, 送货后返回卡车, 如图6(a)所示.
但是, 无人机同车起降配送模式存在车和无人机在会合时至少有一方需要等待的问题, 导致配送时间增加, 配送效率降低. 因此, 开始有文献研究无人机异车起降配送模式. Poikonen等[38]提出FSTSP问题的变体, 无人机可以从卡车A上起飞, 降落在卡车B上, 如图6(b)所示.
为促进能源可持续发展, 响应绿色低碳环保的政策. Lasla等[27]和Huang等[39]考虑利用公共交通网络作为无人机的起降平台以最大程度提高能源利用率, 即通过无人机搭载公交车增加无人机的配送距离, 而且可以在无人机电量用完之际, 通过公共交通扩展的充电设备进行充电, 如图6(c)所示. 这种模式除了可以扩大配送覆盖范围外, 还可以降低配送成本, 增加无人机的使用寿命.
在实际包裹配送场景中, 经常会有客户寄包裹的情况. 因此, 有些文献研究无人机取货-送货(pick-up and delivery)一体配送模式. Ham[40]提出两种无人机任务融合的配送方式, 即无人机完成包裹配送后, 可以根据需求返回卡车继续配送包裹, 或到客户处取货后返回卡车或仓库, 以减少任务完成时间, 如图6(d)所示.
上述配送模式中, 卡车只能在节点处, 即仓库或客户节点发射和回收无人机, 增加了卡车或无人机的额外等待时间. Marinelli等[41]针对现有方法的缺陷, 提出一种新的配送模式: 卡车不仅可以在节点处发射和回收无人机, 而且可以在路线途中发射和回收无人机, 如图6(e)所示. 通过这种方式, 无人机的路线与客户的位置不再严格关联, 可以服务于沿线更广阔的区域. 这种配送模式可以节省卡车和无人机的等待时间, 降低无人机的耗电量, 最大限度提升无人机配送包裹的效率.
车和无人机协同是一种车作为运输载体, 无人机在车上充电、发射和回收的新型配送模式. 这种配送模式既继承了传统运输车辆配送载重能力强、续航里程长的优势, 同时又能够改善传统运输车辆配送效率低、人力成本高等劣势. 因而有潜力成为物流公司一直致力于寻找的更便捷、更高效、更经济的最后一公里配送方式.
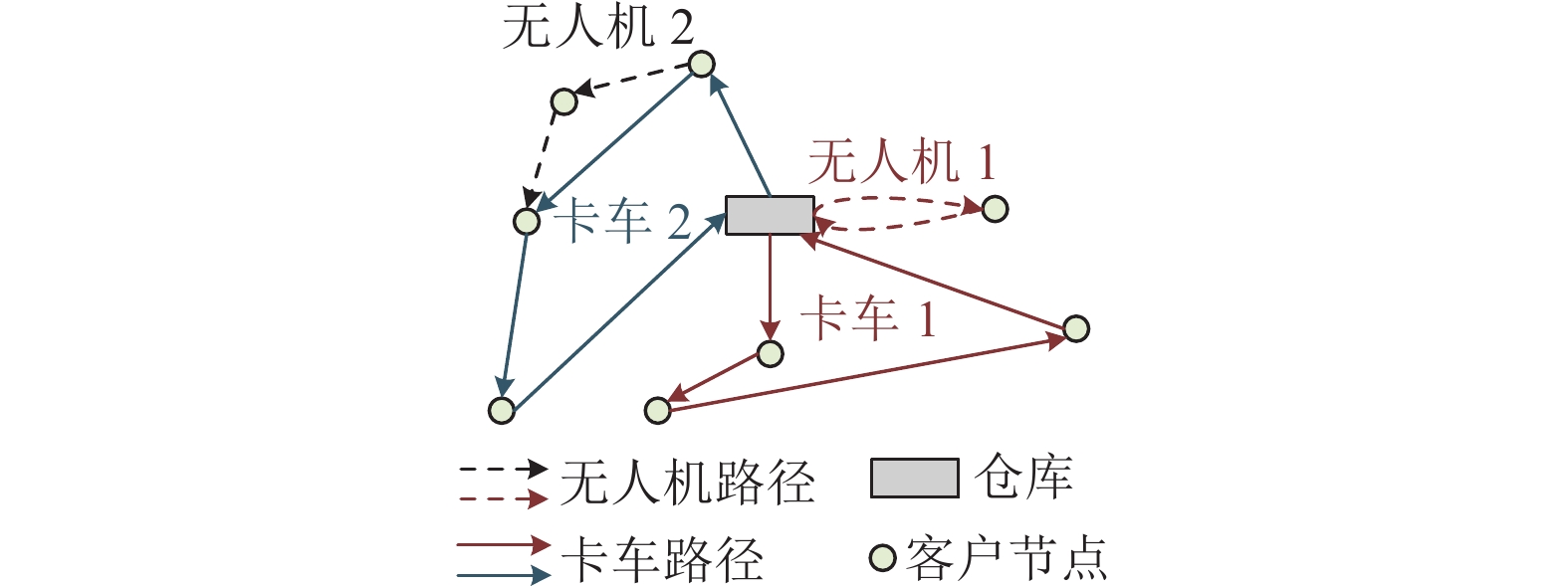
2.4 无人机和地面车辆混合配送相比于独立利用无人机或卡车携带无人机的方式, Wang等[13]提出同时使用卡车、卡车携带无人机和独立无人机的混合模式, 旨在构建一个更高效的卡车-无人机配送系统, 充分实现3种配送模式的优势互补, 如图7所示. 提出的模型允许无人机和卡车在会合之前访问多个客户, 即无人机可以访问多个客户点后再返回卡车.
|
图 7 无人机-卡车多模式融合配送模式 |
2.5 几种配送模式的对比总结
下面从配送时效性、配送重量、配送成本3个方面对无人机独立配送、无人机和地面车辆并行配送、无人机和地面车辆协同配送3种配送模式进行对比, 如表1所示.
当前的文献通常是针对几种配送模式中的一种, 结合具体问题背景, 在一定假设与简化的前提下, 从理论上开展针对性的问题建模与算法设计. 此外, 由于无人机配送的实际应用尚未推广, 基于实例开展具体应用验证研究的文献几乎没有, 由此也可以推断利用无人机配送距离规模化实际应用还有较远的距离. 依托地面车辆进行包裹配送可能仍是未来一段时间的主流配送模式.
| 表 1 3种配送模式的对比 |
3 无人机最后一公里配送路径规划算法
无人机最后一公里配送路径的规划有多种求解方法, 本文对已有文献进行总结, 主要归结为以下几种: 精确算法、启发式算法和混合算法. 其中, 精确算法可以找到最优解, 但是求解规模有限且求解时间长. 启发式算法虽然无法求得最优解, 但是可以保证找到近似最优解/满意解, 能够求解大规模问题且求解时间可控制在可接受范围内.
3.1 单目标问题 3.1.1 精确算法有些文献直接利用CPLEX或Gurobi等数学规划优化器对无人机最后一公里配送路径规划问题进行求解. 如Pugliese等[42]提出一种带时间窗的无人机配送(traveling salesman problem-drone, TSP-D)问题, 构建了相应的混合整数线性规划(mixed integer linear programming, MILP)模型, 并利用CPLEX进行求解, 其结论指出当无人机和卡车的使用成本相同时则没有使用无人机的必要, 当无人机的使用成本越低, 使用无人机的优势越大.
Yoon[43]针对一车多机问题, 即一辆卡车可以配备多架无人机进行包裹配送(traveling salesman problem with multiple drones, TSP-MD), 以最小化总配送成本(包含无人机的固定成本和可变成本, 卡车燃料成本, 人工成本)为目标, 构建了MILP模型, 通过Gurobi求解器进行求解. 由于问题的NP-hard属性, 设定求解时限为30 min. 案例研究对模型关键参数(无人机速度, 无人机续航里程, 可用无人机数量, 卡车速度, 配送区域)进行了灵敏度分析, 讨论了不同参数设置对各方面的影响, 发现与TSP相比, TSP-MD成本节约的中位数为30%.
Poikonen等[44]使用分支定界方法求解车和无人机协同配送问题, 针对不同问题的规模提出相应的算法变体, 能够在平均15 s内求解包含200个节点的问题.
Dell’Amico等[45]对Murray等[36]提出的FSTSP模型进行了改进, 提出了一组带3个下标和仅有2个下标的公式, 设计了新的目标函数, 可显著提高问题求解的 下界. 同时, 提出的多组不等式可分别用于分支和切割, 因此能以更快的速度获取更好的解. 案例证明所提方法能够针对大多数文献的案例找到最优解. 此外, 文章所提方法能够应用于两个变体问题: 一是允许无人机在客户处待机等待(大多数文献的假设), 二是只允许无人机在飞行模式下等待.
Othman等[46]把车和无人机协同路径规划问题转化为一种图论问题, 即在图上找到一种具有特殊结构路径的问题. 该问题被证明具有NP-hard属性. 作者定义了一种可多项式求解的特殊问题, 可以采用传统图论算法在多项式时间内精确求解. 此外, 作者并针对其他情形的图论问题, 提出了一种多项式近似算法, 并证明该算法可将近似解与最优解的差距限制在2%以内.
Torabbeigi等[47]假定无人机包裹配送的载重和电量消耗率存在线性关系, 设计了无人机包裹配送系统的区域规划模型, 以确定仓库的最佳位置. 然后考虑无人机的载重能力和续航能力, 以最小化无人机数量及其飞行路径为目标, 构建了一种MILP模型. 提出了一种变量预处理算法和原始界与对偶界(primal and dual bound generation)生成方法, 以提高求解模型的效率. 实验结果表明, 在无人机路线规划中必须考虑电池消耗率的影响, 才能保证实际应用的可行性.
Kim等[48]首次提出了带无人机站的车和无人机协同配送问题(the traveling salesman problem with a drone station, TSP-DS). 定义了无人机站的3个属性: 1)可以同时服务多个无人机. 2)远离配送中心. 3)载有包裹的卡车到达则激活服务. 在此基础上, 构建了一种MILP模型, 证明了该模型可分解为两个独立的子问题: 1)针对只能由卡车配送节点的最短卡车路径问题. 2)最小化无人机最终交货时间的无人机站调度问题. 通过问题分解降低了问题的复杂度, 从而可以进行精确求解. 案例分析表明所提方法适用于客户点距离配送中心较远的情形.
Liu[49]提出采用无人机进行送餐服务, 综合考虑业务场景的所有相关要素, 并构建了一个混合整数规划(mixed integer programming, MIP)模型. 针对问题模型设计了一种优化驱动的渐进式在线机群调度算法. 与典型的基于图的车辆路径问题不同, 作者提出的MIP模型是时间离散和空间连续的, 能够处理动态、实时环境下的订单交付和无人机调度问题.
对于需要设置无人机充电站的无人机独立最后一公里配送问题, Hassija等[50]认为频繁的充电和电池更换限制了无人机的使用. 因此, 构建了一种包含无人机和充电站的点对点分布式网络, 基于该网络支持, 设计了一种迭代拍卖的无人机调度算法. 首先考虑任务截止日期和任务临界度, 利用哈希图共识算法计算无人机充电请求的共识时间窗. 然后采用双边拍卖方法, 构建同时提高充电站和无人机利润的模型. 仿真结果表明, 所提算法能使无人机和充电站这两个网络节点的综合利润最大化. 虽然该文献并非专门针对最后一公里配送问题, 但具有较强的普适性, 能够应用于考虑充电站的无人机最后一公里配送问题中.
Yu等[51]提出基于广义TSP算法(generalized TSP, GTSP)为无人机寻找固定充电站或移动充电站进行充电. 该算法可以确定访问充电站点的顺序, 还可以确定充电时间和位置; 规划移动充电站的路线, 确定固定充电站的最佳位置; 找到移动充电站的最佳数量.
3.1.2 启发式算法由于利用精确求解算法解决无人机参与最后一公里物流配送问题的算法复杂度通常较高, 求解时间成本大, 算法设计难度大等原因, 有相当部分文献采用启发式算法对所提模型进行求解. 启发式算法是一种基于求解过程累积经验的启发而不断寻找更优解的近似优化算法, 能够应对大规模求解问题, 但只能得到满意解, 无法证明所求解的最优性. 启发式算法的分类较多, 下面对利用启发式算法求解无人机参与的最后一公里物流配送问题进行综述.
(1)贪婪算法
Ha等[52]没有采用其他文献常用的优化目标(车和无人机协同配送总时间), 而是将运营成本, 即运输成本和车辆等待无人机的时间成本作为优化目标. 针对提出的优化问题, 提出两种算法, 一种是对Murray等[36]所提算法的改进, 通过局部搜索将TSP最优解转换成TSP-D可行解; 第2种算法是贪婪随机自适应搜索算法, 基于一种新的分割算子, 将任意TSP路径最优地分割为TSP-D可行解, 再通过局部搜索算子对其进行改进. 其实验结果表明第2种算法的解质量优于第1种.
Crişan等[53]针对TSP-D问题提出一种新的贪婪启发式算法, 在原有卡车路径上, 如果将一个节点分配给无人机后的总运输时间减少, 则执行分配, 直到总运输时间无法再减少. 所提方法与其他类似方法相比, 在两个大规模TSP-D实例上显著节省算法耗时.
Oh等[54]针对单个无人机载重能力有限无法运送大型包裹的问题, 研究了一种多无人机协同配送问题, 将问题构建成一个整数规划模型, 并提出改进的序列贪婪算法对其进行求解. 通过数值模拟表明, 该算法具有更好的性能, 但耗时比传统方法更多.
Agatz等[55]将TSP-D问题转化为任务分配问题, 并提出一种基于局部搜索和动态规划的“快速路径优先, 聚类其次”的启发式算法, 首先构建包含所有客户节点的TSP路径, 然后再基于贪婪分区策略, 将该路径上的部分节点分配给无人机. 案例研究评估了车和无人机协同配送在不同客户密度、地理分布和无人机速度的性能, 证明了与传统的卡车送货相比, 无人机参与的模式可以节省大量的费用.
Yurek等[56]提出一种基于分解的迭代算法, 对提供配送服务的无人机和卡车行驶路径进行优化, 目标是最小化总配送时间. 第1阶段获取最短卡车路线, 第2阶段基于最短的卡车路线, 对无人机路径进迭代优化. 案例证明Yurek等所提算法的求解时间优于CPLEX工具.
Gonzalez-R等[57]将迭代算法和贪婪算法相结合, 提出一种基于分解和重构迭代过程的迭代贪婪启发式算法. 该算法提出一种创新的编码方式, 快速构造初始解, 并采用“破坏解-再构造”的机制对原始局部搜索方法进行改进, 大幅提高全局寻优能力.
Dell’Amico等[58]针对并行的车与无人机协同配送问题(parallel drone scheduling traveling salesman problem, PDSTSP), 以最小化配送总时间为目标函数, 构建了MILP模型, 提出一种随机重启局部搜索算法和快速启发式算法. 在基准测试集上的实验证明随机重启局部搜索算法的效果更好, 但效率不如快速启发式算法.
(2)邻域搜索算法
邻域搜索算法是针对车和无人机协同配送大规模求解问题的一种有效算法. Schermer等[59,60]针对可以在卡车行驶途中起降的车和无人机协同配送问题(vehicle routing problem with drones and en route operation, VRPDERO), 构建了一种MILP模型, 并提出一种可变邻域搜索的禁忌搜索算法, 求解大规模优化问题时取得良好性能.
Sacramento等[61]针对TSP-D问题提出一种自适应大邻域搜索(adaptive large neighborhood search, ALNS)元启发式算法, 根据搜索过程中的性能统计, 从大邻域搜索(large neighborhood search, LNS)算法中选择破坏(消除当前解的一部分)和修复(重建解决方案)当前解, 以权衡利用和探索两种策略.
(3) 遗传算法
Chiang等[14]针对TSP-D问题构建了一种混合整数无人机绿色路径模型, 并提出一种有效求解复杂模型的遗传算法, 可以减少使用传统运输车辆的固定成本, 燃油消耗, 配送时间以及二氧化碳的排放.
Ha等[62]提出一种混合遗传搜索算法, 嵌入了分裂算子、问题定制交叉算子和局部搜索算子, 能够实现种群动态管理和自适应多样性控制. 算法采用一种新的修复机制提高收敛性, 并采用自适应惩罚机制动态平衡可行与不可行解之间的搜索. 计算结果表明, 该算法在求解质量上优于现有方法, 并改进了文献中已知的最优解.
Peng等[63]针对TSP-MD问题设计了一种新的混合遗传算法, 用以求解考虑成本和时间的卡车和无人机协同配送路径规划问题. 算法包含3个主要模块: 1)种群初始化, 覆盖更多卡车停靠点以便有更高的概率获得更优解; 2)采用低访问成本交叉算法以避免过早收敛陷入局部最优; 3)设计基于卡车停靠点, 卡车路径, 客户节点的3层教育算法, 代替传统遗传算法的变异因子. 性能评价结果表明, 所提算法相比对比算法而言具有显著的效果提升.
针对无人机独立最后一公里配送问题, Sung等[64]采用遗传算法对配送区域进行优化分区, 即将服务区域划分为几个不相交的区域, 每个区域由一架无人机进行包裹的配送, 该方法可以减少控制无人机的工作量和无人机之间的潜在冲突, 提高无人机的利用率. 但文章没有考虑实际情况中无人机的载重和航程约束带来的一系列问题.
(4) 插入启发式算法
Ulmer等[65]考虑订单当天送达的场景, 研究了一种动态的车和无人机任务分配与路径规划问题. 构建了一种马尔可夫过程模型, 采用策略函数近似方法(policy function approximation)决策是否为一个订单需求分配车辆或无人机, 并利用一种有效插入启发式算法[66]进行路径规划. 通过案例分析得出以下结论: 有效地理分区可以增加当日预计送达数量, 无人机和车辆的组合可以显著减少所需的配送资源.
Kitjacharoenchai等[66]针对TSP-MD问题, 提出一种自适应插入启发式(adaptive insertion heuristic, ADI)算法. 算法包含两个步骤: (1)构建多车配送初始解; (2)通过移除卡车节点和插入无人机节点构建多车和多无人机协同配送方案. 案例结果表明: 在小规模案例中, CPLEX求解器和所提算法均能达到最优解, 但后者求解速度明显更快. 在大规模案例中: 与仅使用卡车, 多辆卡车和一车一机模式相比, 使用多车多机模型的配送完成时间更短.
(5) 模拟退火算法
Moshref-Javadi等[67]针对TSP-MD问题构建了混合整数规划模型, 提出一种基于模拟退火和禁忌搜索的混合元启发式算法以解决大规模求解问题. 案例分析表明TSP-MD模式与只使用卡车的配送系统相比, 客户等待时间大幅度减少.
Boysen等[68]根据卡车上无人机的数量和操作策略, 衍生出6个问题版本: DSP-A1 (每个卡车1个无人机, 无人机必须在同一个卡车上起飞降落, 无人机送货时卡车必须停靠); DSP-A2 (每个卡车2个无人机, 其他条件与DSP-A1相同); DSP-B1 (每个卡车1个无人机, 无人机可以在其起飞时的卡车停靠点降落, 也可以在卡车的下一个停靠点降落); DSP-B2 (每个卡车2个无人机, 其他条件与DSP-B1相同); DSP-C1 (每个卡车1个无人机, 无人机可以在其起飞后的卡车任意停靠点降落); DSP-C2 (每个卡车2个无人机, 其他条件与DSP-C1相同). 文章分析了6个问题的复杂度, 当无人机数量大于1时全部是NP-hard类问题, 当无人机数量为1时, DSP-A1和DSP-B1是多项式时间问题, DSP-C1是NP-hard类问题. 针对NP-hard类问题, 作者首先利用模拟退火算法解决卡车路径优化, 在此基础上, 再利用模拟退火算法解决给定卡车路径下的无人机路径规划子问题.
Dorling等[69]针对现有车辆路径问题(vehicle routing problem, VRP)模型无法规划无人机路径的缺陷(要么不允许多次前往仓库导致无人机数量过剩, 要么没有考虑电池重量和有效载重能力对能源消耗的影响导致方案不可行), 在考虑电池重量、有效载重能力和无人机重量的情况下, 提出成本或交付时间最小的无人机配送问题, 并将其转化为一种MILP模型. 提出一种基于模拟退火的启发式算法, 可以解决具有数百个配送地点的实际场景问题.
(6) 多阶段启发式算法
Saleu等[70]针对TSP-MD问题提出一种两步启发式算法: 1)将解决方案等价转换为对客户序列的编码; 2)将客户序列分解为车辆路径和无人机路径的解码. 解码过程利用双准则最短路模型, 通过动态规划实现.
Murray等[71]针对TSP-MD问题, 首先构建了一个MILP模型. 提出一种三阶段启发式算法(初始化卡车配送方案, 构建无人机的调度方案, 确定卡车和无人机的出发时间). 通过大量案例分析, 作者发现使用无人机的边际效益(减少平均配送时间)会随着无人机数量的增加而减少, 车和无人机配送在客户密度高的地区会带来更大的收益.
Schermer等[59]提出两种新的求解车和无人机协同路径规划问题的算法: 两阶段启发式算法(two-phase heuristic, TPH)和单阶段启发式算法(single-phase heuristic, SPH). TPH首先构建车辆路径, 然后通过插入无人机构建车和无人机协同配送路径. SPH则直接构建较好的车和无人机协同配送路径方案. 通过案例数值结果, 证明在大多数情况下, TPH的结果优于SPH.
Choudhury等[72]构建了一种大批无人机在城市地区同时配送包裹, 通过在公共交通工具上停靠实现充电以增加航程的新型TSP-MD问题. 设计了一种创新的综合算法框架, 上层框架采用近似最优任务分配算法为无人机分配包裹, 下层框架采用路径规划算法决定无人机停靠在哪个公共交通工具上. 以Washington D.C.包含8 000多个站点的大型公交网络为例, 针对200架无人机和5 000个包裹开展了大量实验, 证明该算法框架可以在几秒钟内给出解决方案.
Liu等[73]构建了无人机群配送问题的两阶段随机规划模型, 目标是使无人机配送的人工和运营的总成本最小. 第1阶段确定无人机群的数量, 类型和无人机连续两次起飞的时间段, 第2阶段确定无人机群的配送路径. 首先采用经典的样本平均近似(sample average approximation, SAA)方法, 可用于求解小规模问题. 此外, 进一步设计了一种混合遗传算法, 能够在可接受时间内获取中大规模问题的满意解.
Huang等[74]针对无人机配送提出两个阶段的无人机充电站布局方法, 在需求区域配置充电站以覆盖用户. 初始阶段以三角形布局完全覆盖需求区域, 该阶段采用全覆盖部署算法; 调整阶段移除不覆盖或需求小的充电站, 该阶段重复进行直至无法移除充电站为止.
随着无人机在震后人道主义应急行动中的作用越来越凸显, Macias等[75]首次同时考虑仓库选择, 电池管理, 轨道优化等要素, 提出一种双阶段运行规划方法, 该方法由考虑多个飞行阶段的轨迹优化算法和考虑电池管理的路径选择算法组成. 算法应用于1999年集集地震后的一个假设响应任务, 以任务持续时间和分配公平性为目标构建问题模型, 算法结果表明不超过90架无人机就可以在24 h内为2万人提供快速救援. 与其他启发式方法相比, 提出的方法显著减少了任务响应时间和电池库存需求.
3.1.3 机器学习算法除传统算法外, 由于人工智能的发展, 逐渐有学者将机器学习应用于车和无人机路径规划的组合优化问题中, 两者的结合可以大大缩短算法用时. Bengio等[76]认为机器学习用于组合优化存在3类范式: 一是基于端到端机器学习的组合优化, 即直接利用机器学习算法得出组合优化问题的最优解; 第2种是从优化问题中学习有价值的信息, 如利用机器学习算法从分支定界算法中挑选变量; 第3种是将机器学习算法嵌入到传统优化算法中, 如在邻域搜索类算法中, 可利用机器学习算法辅助挑选邻域结构.
Salama等[77]讨论了使用多架无人机与一辆卡车协同为一组客户节点配送订单的场景, 将停放在卡车上的无人机进行并行调度配送. 首先针对需要配送的地点进行集群划分, 以确定集群中心(卡车停放处), 然后针对无人机与车的路径规划构建了一种联合优化模型, 将无监督学习算法输出的解作为启发式算法的“热启动”解, 以加速求解效率.
Wu等[78]考虑到面对面接触配送会使新冠病毒传染风险更高的问题背景, 提出车和无人机协同交付系统, 将整个配送问题分解为3个子问题, 即客户聚类问题、卡车路径问题和无人机路径问题. 其中, 无人机负责配送隔离人员的日常必需品和医疗用品等, 卡车充当移动充电站和运输工具. 设计了一种与强化学习(reinforcement learning, RL)相结合的编码器-解码器框架以解决车和无人机的路径规划问题. 该方法无需设计启发式算法, 可以在1 s内获得高质量的解决方案, 且可以很好地应用于不同规模的问题, 求解效率非常高.
Xing等[79]提出一种低复杂度的混合强化学习方法, 以求解基于无人机的新冠肺炎检测盒交付系统中的路径优化问题. 算法由启发式算法和Q_learning算法组成: 首先, 使用启发式算法计算任意两个用户之间的最优路径, 然后, 应用Q_learning算法确定为用户交付新冠肺炎检测试剂盒的顺序. 仿真结果证明了与现有技术相比, 所提混合强化学习算法可以解决传统深度强化学习收敛速度慢和参数调整困难等问题.
3.1.4 混合算法有些文献中在求解无人机最后一公里配送问题时, 对精确算法和启发式算法进行了有机融合, 本节对采用混合算法的文献进行详细综述.
Bai等[80]将TSP-D问题转化为一种基于优先度排序的任务分配问题, 根据客户的紧急和重要程度进行排序, 优先为排序靠前的客户服务. 该问题具有NP-hard性质, 文章首先利用图论工具构造最优服务时间下界. 然后, 融合拓扑排序技术和启发式任务分配算法对问题进行求解. 数值仿真结果表明, 该算法与目前流行的遗传算法相比具有更好的性能.
还有部分文献将优化求解器和启发式算法结合起来进行问题求解, De Freitas等[81]针对车和无人机协同配送路径MIP问题, 考虑车和无人机协同路径规划问题的特殊约束: 无人机的飞行时间限制了单次访问客户的数量, 以及包裹不得超过无人机的有效载重能力等, 提出一种混合启发式算法, 初始解由Concorde求解器得到的最优TSP解生成, 再利用通用可变邻域搜索获取卡车和无人机的配送路线, 数值结果表明车与无人机配送模式能缩短原有配送时间的67.79%. De Freitas等[82]还研究了在Concorde求解TSP问题的基础上, 采用随机变量邻域下降启发式方法进行局部搜索. 在基于著名TSP基准集创建的11个实例中测试所提出方法, 使得配送包裹的总时间平均缩短近20%.
Poikonen等[83]提出一种k无人机-车路径规划问题(当k=1时等价于TSP-D问题), 每架无人机都能从卡车上起飞, 携带一个或多个包裹配送给客户, 然后返回卡车, 更换电池/充电, 再次执行配送任务. 构建了一种整数规划模型, 设计了包含3个阶段的启发式算法, 首先通过Gurobi求解卡车配送的TSP问题, 在TSP问题最优解的基础上利用一种启发式算子将某些客户点的配送任务分配给无人机, 然后再利用启发式算子对无人机的路径进行优化. 案例研究对无人机参数进行了灵敏度分析, 结果表明最优目标值对无人机的能耗, 速度和有效载荷容量都高度敏感.
Schermer等[84]针对TSP-MD, 提出一种无人机分配和调度问题, 给定一个现有卡车最优路线, 寻找无人机的最优分配和调度方案, 使最大配送时间最小化. 构建了相应的MILP模型. 为了提高利用Gurobi求解该模型的性能, 文章引入了几组有效不等式(时间限制, 对称性约束, Knapsack不等式). 此外, 由于Gurobi求解器在处理大规模实例时性能有限, 文章还提出一种有效利用问题结构的可精确求解启发式方法, 以应对大规模求解问题. 根据数值结果, 作者提出的算法效率很高, 并且能够在多种案例中提供最优解或近似最优解.
Wang等[85]针对TSP-MD问题, 提出一种基于弧的车和无人机协同配送的MILP模型, 设计了一种可以区分出不同类型路径和节点的特殊网络, 并采用分支定界算法求解. 文章提出了一种改进的脉冲算子(定制修剪和扩展策略), 同时, 为了解决列生成收敛缓慢的长尾效应问题, 通过计算拉格朗日下界提高了列生成速度. 算法与Gurobi求解器相比, 在效率上有所提升.
El-Adle等[86]针对TSP-D问题构建了0-1 MIP模型, 通过有效不等式、实例预处理和边界收缩策略, 采用分支定界算法对线性规划问题进行松弛, 并采用双贪婪算法(double greedy algorithm)确定车辆依次访问节点所需的时间, 以及无人机服务最近节点并飞往下一个最近节点与车辆会合所需的飞行时间. 以最小化无人机和卡车协同配送的总时间为目标函数, 提高了MIP模型的可用性.
Bouman等[87]提出一种基于3步动态规划的车和无人机协同配送路径规划问题和精确求解方法, 并在最后一步使用A*算法. 相比于已有精确算法能够求解更大规模的问题. 并证明了减少车的可访问节点数量可以在不影响最优解整体质量的情况下减少求解时间.
Ferrandez等[88]使用混合牛顿梯度下降法确定无人机从卡车发射的位置和最佳数量, 用遗传算法确定无人机两次发射之间车辆的路线. 通过在生成的案例上进行分析, 发现只有当无人机的速度超过车辆的3倍, 或者卡车配备2个以上的无人机时才能缩短包裹配送的时间.
Hong等[89]提出无人机配送充电选址模型以优化充电站的位置, 考虑了避障最短路径, 充电站定位, 最大覆盖, 区域定位等特点. 采用有效的启发式算法进行求解, 该算法结合了最小生成树, 贪婪算法, 空间交换和模拟退火算法.
3.1.5 几种算法的对比下面从最优性、时效性和通用性3个方面对无人机最后一公里配送的单目标求解算法进行对比, 如表2所示.
| 表 2 几种算法的对比 |
3.2 多目标问题
对于多目标的TSP-D问题(TSP-MD)中的车和无人机任务分配, Moshref-Javadi等[90]构建了一种以最小化客户等待时间为目标, 考虑客户与卡车和无人机的最优匹配, 卡车最优路径序列, 以及无人机沿卡车路径的最优发射和召回位置的MILP模型. 为解决实际问题, 对Ropke等[91]于2006年提出的ALNS算法进行了两处改进: 为了避免局部最优, 允许算法在初始解生成和改进过程中接受非改进解; 如果经过一定次数迭代后最优解没有得到改进, 则使用Shake启发式算法改变搜索邻域 . 结果分析表明, 当为每个卡车配备2架无人机时, 可减少客户46.8%的等待时间; 在高密度需求地区, 无人机的使用率和利用率明显增加.
有学者针对多目标的TSP-D问题, 采用遗传算法对车和无人机协同配送问题进行求解. Omagari等[92]提出一种“基于临时理想点”的方法, 通过定义一个“惩罚值”搜索可行解(对不满足约束的惩罚值进行求和, 总惩罚值为0的解即为可行解), 通过定义新的参考点(临时理想点), 搜索决策者的首选解决方案. 采用基本遗传算法(simple genetic algorithm, SGA)求解该问题. 该方法能够应用于约束条件较多的多目标优化问题, 并具有一定的可扩展性.
Wang等[93]构建了考虑运营成本和完成时间的TSP-D多目标优化问题, 并提出了一种改进的非支配排序遗传算法, 根据问题特征, 设计了基于标签的解码方法, 快速非支配排序方法, 拥挤距离计算和局部搜索算子, 计算结果验证了该算法改进相较于原有算法具有一定优势.
Shavarani等[94]提出一种无人机配送中心设施选址多目标优化问题. 每个设施都是一个配送中心, 可配备多个无人机. 其中, 第1个目标函数是考虑设施和无人机配送的总成本, 第2个目标函数是考虑无人机配送的续航能力. 采用NSGA-II和NSGA-III (non-dominated sorting genetic algorithm III)算法对其进行求解, 结论是NSGA-III在多样性, 平均理想距离和帕累托解数量上都优于NSGA-II.
考虑设置中继充电站的无人机配送问题, 结合无人机的充电需求和配送需求, Coelho等[95]构建了一种包含7个目标(距离, 时间, 无人机使用数量, 无人机群的最大速度, 所有包裹被揽收的最晚时间, 所有包裹被配送完的最晚时间, 总能源消耗)的无人机路径规划多目标优化问题. 考虑无人机路径规划过程中实时订单不断更新的实际情况, 作者首先从基于黑盒动态搜索算法形成的分支定界优化树中获取方案池, 再利用提出的多目标智能池搜索(multi-objective smart pool search)元启发式算法, 从中获取非支配解集. 研究案例表明所提多目标优化框架能够提供支持决策的高质量解方案.
Lu等[96]提出一个多目标的无人机人道主义配送路径优化问题, 将该问题分解为两个子问题: 协同配送子问题和救援物资分配子问题. 以最小化配送时间和最大化节点访问率为目标, 构建了一个多目标混合整数线性规划(MILP)模型. 提出两种元启发式算法以获得近似Pareto前沿, 分别是将特定局部搜索算子嵌入进化算法框架的混合多目标进化算法(HMOEAS)和一种混合多目标蚁群算法(HACO). 文章以武汉市为例, 研究卡车-无人机协同配送药物的问题, 通过对比HMOEAS, HACO以及传统的MOEA算法, 实验结果证明HMOEAS在超体积指标上比其他算法更优.
Luo等[97]针对带时间窗的车和无人机协同路径规划问题, 构建了一种使总配送成本最小, 同时使总体客户满意度最大的多目标优化问题, 提出一种基于种群的混合多目标优化算法(HMOA): 首先使用基于贪婪的启发式方法创建初始解, 然后引入面向该特定问题的解表征、遗传操作以及6种启发式邻域策略, 采用自适应邻域搜索策略进一步平衡算法的收敛性和多样性. 在基准案例上与MOEA/D, MOMA/D以及HMOA-noLS (不带邻域搜索的HMOA算法)展开对比研究, 结果表明所提出算法在超体积性能上最优.
Han等[98]针对带有时间窗和无人机运输约束的多目标车与无人机路径规划问题, 同时考虑最小化3个目标: 卡车总能耗, 无人机总能耗和卡车总数量. 文章将3个目标聚合为单目标, 并设计了一种改进的人工蜂群算法来求解该问题. 通过前推插入启发式算子获取有效初始解, 基于贪婪策略进行局部搜索, 同时, 提出了一种新的侦察蜂策略以提高全局搜索能力. 所提算法在与传统遗传算法, 禁忌搜索算法和自适应邻域搜索算法的对比中占优.
Omagari等[92]针对无人机配送问题, 构建了带约束的多目标优化问题. 为了解决无人机配送存在较多约束的情况, 提出一种基于临时理想点的优化方法. 首先定义惩罚值, 只有未受到惩罚的解才被视为可行解. 此外, 将每个目标维度上当前寻找到的最优解构成的向量定义为临时参考点, 距离临时参考点最近的点即为最优偏好解. 实验证明该方法计算复杂度较低, 在两种测试集上表现较好, 同时在无人机配送问题上可以有效求解问题.
4 相关测试集关于无人机最后一公里配送问题的测试集, 已知可公开获取的测试集数量较少. 因此, 许多文献都是采用随机生成的方式, 也有一些文献根据实际城市地理信息数据构建案例集, 下面对可公开获取的测试集进行归纳总结, 如表3所示.
| 表 3 无人机配送问题的公开测试集 |
5 结论和未来研究方向
本文综述了无人机在最后一公里物流配送问题的已有研究, 归纳总结了无人机参与的4类最后一公里配送模式. 详细阐述了无人机最后一公里配送路径规划算法. 整理了已公开的相关测试集.
目前, 在无人机参与的最后一公里物流配送问题研究中, 主要考虑的无人机参数有续航能力、载货能力、行驶里程等. 当前研究主要考虑的目标有各类成本、燃油消耗、配送时间、续航能力等. 随着研究的深入, 未来的相关研究将面向与现实应用的紧密结合, 力争实现无人机参与最后一公里配送的大规模应用. 根据现有文献研究, 总结未来需要深入研究的方向如下.
(1)在应用场景方面
1)考虑在线实时的动态请求. 目前, 大部分研究内容都是面向静态优化的无人机参与物流配送问题. 很少有研究面向实时订单任务, 研究无人机参与最后一公里物流配送的在线路径规划. 尤其是无人机参与配送应急物资, 同城急送, 外卖配送, 即时零售等问题会出现配送任务动态变化的情况, 比如客户点(需求点)变更, 包裹(物资)需求变更, 临时加急任务等. 因此, 针对随时出现的动态需求, 在满足所有客户点(需求点)的配送需求的前提下, 需要设计动态响应机制, 研究响应在线实时订单(需求)的规则和算法.
2)面向客户(需求)分布不确定的无人机参与配送路径规划研究. 在快递配送时, 配送的客户(需求)往往是已知的和固定的, 而战场物资配送, 同城急送, 外卖配送, 即时零售等需求是根据实时情况动态变化的, 没有办法直接给出包裹(物资)配送的明确任务. 所以, 在这些配送问题中的客户点(需求点)分布具有多变, 不确定, 分散等特点. 因此, 有必要开展面向客户(需求)分布不确定的无人机参与配送路径规划研究.
3)考虑无人机面临的各类威胁. 除了不确定的请求之外, 无人机在飞行过程中还容易受到恶劣环境的影响. 比如大风、雨雪、结冰、低温、湿度大、能见度低等. 此外, 各地区针对无人机飞行设置了相应的政策和法规, 比如, 一些地区设置无人机禁飞区域. 在无人机配送过程中, 还需考虑无人机的安全因素, 比如, 通信带宽受限导致无人机无法与控制中心联络、无人机最大允许飞行的高度等. 还有无论在民用或军事领域, 无人机在飞行过程中均会发生被击中, 突然故障等情况. 因此, 需要综合考虑以上限制和威胁因素, 对无人机参与配送的航路规划进行重新设计, 尽量避免无人机在配送包裹(物资)过程中的损失.
(2)在技术发展方面
1)考虑真实的无人机技术参数. 目前大多数针对无人机配送的研究都是使用非真实的技术参数. 只有少量学者采用真实的技术参数进行研究. 无人机的类型, 机重, 续航能力, 飞行速度, 飞行极限海拔, 抗风性能, 电池容量和重量, 最大上升和下降速度等技术参数都会影响配送时间, 配送里程和配送效率. 只有考虑这些真实的无人机技术参数, 在研究最后一公里的无人机物流配送问题时, 才能促进无人机参与配送的实际应用.
2)客户时间窗管理. 在无人机参与物流配送领域, 无人机必须在规定的时间窗内到达是对无人机的基本要求, 无人机早于最早时间或晚于最晚时间到达, 服务将被拒绝或给予一定的惩罚. 因此, 提高配送的及时性和配送效率尤为重要. 如何与客户商定合适的交付时间窗问题也是一个具有挑战性的研究领域.
3)采用真实数据集. 现有大部分研究的算法测试所用到的数据集均为随机生成的数据, 只有少部分研究采用真实数据集, 且真实数据集里的数据不全. 要全方面考虑无人机真实技术参数, 飞行限制区域, 无人机充电服务点, 确切的客户点位置, 楼层高度(无人机需避障), 道路网, 车辆各类成本等. 采用真实数据集将会使无人机参与最后一公里物流配送问题更有可信度, 为决策者有效分配研发资金, 敲定无人机配送的政策和法规提供真实数据支持.
(3)在核心算法方面
考虑将机器学习和启发式算法相结合进行研究. 现有研究几乎都是采用精确算法或者启发式算法对无人机最后一公里配送问题进行求解, 很少有文献采用机器学习算法应用在该问题中. 机器学习算法可以极大地减少算法用时, 提高无人机配送系统的效率. 因此, 机器学习和启发式算法相结合是一个值得深入研究的方向.
| [1] |
葛思诗. 电商物流最后一公里配送问题研究. 物流工程与管理, 2021, 43(2): 81-84. |
| [2] |
曾东. 电子商务物流成本控制问题探析——以京东商城为例. 商讯, 2020(1): 9, 11. |
| [3] |
Rose C. Amazon’s Jeff Bezos looks to the future. http://www.cbsnews.com/news/amazons-jeff-bezos-looks-to-the-future/. (2013-12-01).
|
| [4] |
Madrigal AC. Inside Google’s secret drone-delivery program. http://www.theatlantic.com/technology/archive/2014/08/inside-googles-secretdrone-delivery-program/379306/. (2014-08-01).
|
| [5] |
Welch A. A cost-benefit analysis of Amazon Prime Air. https://core.ac.uk/download/pdf/51197254.pdf. (2015-03-16).
|
| [6] |
Zhang JY. Alibaba tests drone delivery service to overcome domestic logistics obstacles. https://tech.huanqiu.com/article/9CaKrnJHvbo. (2015-02-05).
|
| [7] |
孟环. 京东获全球首个省域无人机物流经营许可证在7省进行常态化配送. https://baijiahao.baidu.com/s?id=1617256216118161349&wfr=spider&for=pc. (2018-11-16).
|
| [8] |
李知政. 外卖“飞”到家, 饿了么获批国内首条外卖无人机航线. https://baijiahao.baidu.com/s?id=1601797700690390268&wfr=spider&for=pc. (2018-05-29).
|
| [9] |
Xiao LJ. Amazon commercial UAV realizes 30 minute home delivery. When will the delivery in domestic unmanned cities be? https://new.qq.com/omn/20200904/20200904A0MGUP00.html. (2020-09-04).
|
| [10] |
Shao XW. To solve the first-mile transportation problem. The full coverage of drone distribution is not far from us! https://baijiahao.baidu.com/s?id=1694726507923302511&wfr=spider&for=pc. (2021-03-20).
|
| [11] |
Singhal G, Bansod B, Mathew L. Unmanned aerial vehicle classification, applications and challenges: A review. https://www.preprints.org/manuscript/201811.0601/v1. (2018-11-26).
|
| [12] |
Raj A, Sah B. Analyzing critical success factors for implementation of drones in the logistics sector using grey-DEMATEL based approach. Computers & Industrial Engineering, 2019, 138: 106118. |
| [13] |
Wang DS, Hu P, Du JX, et al. Routing and scheduling for hybrid truck-drone collaborative parcel delivery with independent and truck-carried drones. IEEE Internet of Things Journal, 2019, 6(6): 10483-10495. DOI:10.1109/JIOT.2019.2939397 |
| [14] |
Chiang WC, Li YY, Shang J, et al. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Applied Energy, 2019, 242: 1164-1175. DOI:10.1016/j.apenergy.2019.03.117 |
| [15] |
Campbell JF, Sweeney II DC, Zhang J, et al. Strategic design for delivery with linked transportation assets: Trucks and drones. https://rosap.ntl.bts.gov/view/dot/34894. (2018-01-01).
|
| [16] |
Pugliese LDP, Guerriero F, Macrina G. Using drones for parcels delivery process. Procedia Manufacturing, 2020, 42: 488-497. DOI:10.1016/j.promfg.2020.02.043 |
| [17] |
Wang XY, Poikonen S, Golden B. The vehicle routing problem with drones: Several worst-case results. Optimization Letters, 2017, 11(4): 679-697. DOI:10.1007/s11590-016-1035-3 |
| [18] |
Carlsson JG, Song SY. Coordinated logistics with a truck and a drone. Management Science, 2017, 64(9): 4052-4069. |
| [19] |
祝梅. 保护骑手保护自己, 美团外卖推“无接触配送”. https://zj.zjol.com.cn/news.html?id=1373275. (2020-01-28).
|
| [20] |
李一能. 上海奉贤区启用无人机送菜: 活鱼鲜蔬五分钟直送隔离户. https://baijiahao.baidu.com/s?id=1658847085908381943&wfr=spider&for=pc. (2020-02-18).
|
| [21] |
陈曦. 无接触配送或成未来发展趋势. http://www.igdzc.com/guonei/20200429/299568.html. (2020-04-29).
|
| [22] |
Elsayed M, Mohamed M. The impact of airspace regulations on unmanned aerial vehicles in last-mile operation. Transportation Research Part D: Transport and Environment, 2020, 87: 102480. DOI:10.1016/j.trd.2020.102480 |
| [23] |
Baloch G, Gzara F. Strategic network design for parcel delivery with drones under competition. Transportation Science, 2020, 54(1): 204-228. DOI:10.1287/trsc.2019.0928 |
| [24] |
Jeong HY, Song BD, Lee S. Truck-drone hybrid delivery routing: Payload-energy dependency and no-fly zones. International Journal of Production Economics, 2019, 214: 220-233. DOI:10.1016/j.ijpe.2019.01.010 |
| [25] |
Dukkanci O, Kara BY, Bektas T. The drone delivery problem. SSRN Electronic Journal, 2019, 10.
|
| [26] |
Song BD, Park K, Kim J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Computers & Industrial Engineering, 2018, 120: 418-428. |
| [27] |
Lasla N, Ghazzai H, Menouar H, et al. Exploiting land transport to improve the UAV’s performances for longer mission coverage in smart cities. Proceedings of the 89th IEEE Vehicular Technology Conference. Kuala Lumpur: IEEE, 2019. 1–7.
|
| [28] |
Worden MKR, Murray CC, Karwan MH, et al. Sensor tasking for unmanned aerial vehicles in disaster management missions with limited communications bandwidth. Computers & Industrial Engineering, 2020, 149: 106754. |
| [29] |
Adulyasak Y, Cheng C, Rousseau LM, et al. Robust drone delivery with weather information. https://hanalog.ca/wp-content/uploads/2020/07/7897.pdf. (2020-07-14).
|
| [30] |
Dayarian I, Savelsbergh M, Clarke JP. Same-day delivery with drone resupply. Transportation Science, 2020, 54(1): 229-249. DOI:10.1287/trsc.2019.0944 |
| [31] |
Eren H, Çelik Ü. Risk assessment for aerial package delivery. International Journal of Electrical and Computer Engineering, 2017, 11(10): 1074-1077. |
| [32] |
Sawadsitang S, Niyato D, Tan PS, et al. Joint ground and aerial package delivery services: A stochastic optimization approach. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6): 2241-2254. DOI:10.1109/TITS.2018.2865893 |
| [33] |
Curlander JC, Gilboa-Amir A, Kisser LM, et al. Multi-level fulfillment center for unmanned aerial vehicles: U.S., 9777502. 2017-10-03.
|
| [34] |
Kuru K, Ansell D, Khan W, et al. Analysis and optimization of unmanned aerial vehicle swarms in logistics: An intelligent delivery platform. IEEE Access, 2019, 7: 15804-15831. DOI:10.1109/ACCESS.2019.2892716 |
| [35] |
Rabta B, Wankmüller C, Reiner G. A drone fleet model for last-mile distribution in disaster relief operations. International Journal of Disaster Risk Reduction, 2018, 28: 107-112. DOI:10.1016/j.ijdrr.2018.02.020 |
| [36] |
Murray CC, Chu AG. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transportation Research Part C: Emerging Technologies, 2015, 54: 86-109. DOI:10.1016/j.trc.2015.03.005 |
| [37] |
Li YS, Zhang GZ, Pang ZB, et al. Continuum approximation models for joint delivery systems using trucks and drones. Enterprise Information Systems, 2020, 14(4): 406-435. DOI:10.1080/17517575.2018.1536928 |
| [38] |
Poikonen S, Wang XY, Golden B. The vehicle routing problem with drones: Extended models and connections. Networks, 2017, 70(1): 34-43. DOI:10.1002/net.21746 |
| [39] |
Huang HL, Savkin AV, Huang C. Reliable path planning for drone delivery using a stochastic time-dependent public transportation network. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(8): 4941-4950. DOI:10.1109/TITS.2020.2983491 |
| [40] |
Ham AM. Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming
. Transportation Research Part C: Emerging Technologies, 2018, 91: 1-14. DOI:10.1016/j.trc.2018.03.025 |
| [41] |
Marinelli M, Caggiani L, Ottomanelli M, et al. En route truck-drone parcel delivery for optimal vehicle routing strategies. IET Intelligent Transport Systems, 2018, 12(4): 253-261. DOI:10.1049/iet-its.2017.0227 |
| [42] |
Pugliese LDP, Guerriero F. Last-mile deliveries by using drones and classical vehicles. Proceedings of the 2017 International Conference on Optimization and Decision Science. Sorrento: Springer, 2017. 557–565.
|
| [43] |
Yoon JJ. The traveling salesman problem with multiple drones: An optimization model for last-mile delivery [Bachelor’s Thesis]. Boston: Massachusetts Institute of Tech-nology, 2018.
|
| [44] |
Poikonen S, Golden B, Wasil EA. A branch-and-bound approach to the traveling salesman problem with a drone. INFORMS Journal on Computing, 2019, 31(2): 335-346. DOI:10.1287/ijoc.2018.0826 |
| [45] |
Dell’Amico M, Montemanni R, Novellani S. Drone-assisted deliveries: New formulations for the flying sidekick traveling salesman problem. Optimization Letters, 2021, 15(5): 1617-1648. DOI:10.1007/s11590-019-01492-z |
| [46] |
Othman MSB, Shurbevski A, Karuno Y, et al. Routing of carrier-vehicle systems with dedicated last-stretch delivery vehicle and fixed carrier route. Journal of Information Processing, 2017, 25: 655-666. DOI:10.2197/ipsjjip.25.655 |
| [47] |
Torabbeigi M, Lim GJ, Kim SJ. Drone delivery scheduling optimization considering payload-induced battery consumption rates. Journal of Intelligent & Robotic Systems, 2020, 97(3): 471-487. |
| [48] |
Kim S, Moon I. Traveling salesman problem with a drone station. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(1): 42-52. DOI:10.1109/TSMC.2018.2867496 |
| [49] |
Liu YC. An optimization-driven dynamic vehicle routing algorithm for on-demand meal delivery using drones. Computers & Operations Research, 2019, 111: 1-20. |
| [50] |
Hassija V, Saxena V, Chamola V. Scheduling drone charging for multi-drone network based on consensus time-stamp and game theory. Computer Communications, 2020, 149: 51-61. DOI:10.1016/j.comcom.2019.09.021 |
| [51] |
Yu K, Budhiraja AK, Tokekar P. Algorithms for routing of unmanned aerial vehicles with mobile recharging stations. Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane: IEEE, 2018. 5720–5725.
|
| [52] |
Ha QM, Deville Y, Pham QD, et al. On the min-cost traveling salesman problem with drone. Transportation Research Part C: Emerging Technologies, 2018, 86: 597-621. DOI:10.1016/j.trc.2017.11.015 |
| [53] |
Crişan GC, Nechita E. On a cooperative truck-and-drone delivery system. Procedia Computer Science, 2019, 159: 38-47. DOI:10.1016/j.procs.2019.09.158 |
| [54] |
Oh G, Kim Y, Ahn J, et al. Task allocation of multiple UAVs for cooperative parcel delivery. In: Dołęga B, Głębocki R, Kordos D, et al., eds. Advances in Aerospace Guidance, Navigation and Control. Cham: Springer, 2018. 443–454.
|
| [55] |
Agatz N, Bouman P, Schmidt M. Optimization approaches for the traveling salesman problem with drone. Transportation Science, 2018, 52(4): 965-981. DOI:10.1287/trsc.2017.0791 |
| [56] |
Yurek EE, Ozmutlu HC. A decomposition-based iterative optimization algorithm for traveling salesman problem with drone. Transportation Research Part C: Emerging Technologies, 2018, 91: 249-262. DOI:10.1016/j.trc.2018.04.009 |
| [57] |
Gonzalez-R PL, Canca D, Andrade-Pineda JL, et al. Truck-drone team logistics: A heuristic approach to multi-drop route planning. Transportation Research Part C: Emerging Technologies, 2020, 114: 657-680. DOI:10.1016/j.trc.2020.02.030 |
| [58] |
Dell’Amico M, Montemanni R, Novellani S. Matheuristic algorithms for the parallel drone scheduling traveling salesman problem. Annals of Operations Research, 2020, 289(2): 211-226. DOI:10.1007/s10479-020-03562-3 |
| [59] |
Schermer D, Moeini M, Wendt O. Algorithms for solving the vehicle routing problem with drones. Proceedings of the 10th Asian Conference on Intelligent Information and Database Systems. Dong Hoi City: Springer, 2018. 352–361.
|
| [60] |
Schermer D, Moeini M, Wendt O. A hybrid VNS/Tabu search algorithm for solving the vehicle routing problem with drones and en route operations. Computers & Operations Research, 2019, 109: 134-158. |
| [61] |
Sacramento D, Pisinger D, Ropke S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transportation Research Part C: Emerging Technologies, 2019, 102: 289-315. DOI:10.1016/j.trc.2019.02.018 |
| [62] |
Ha QM, Deville Y, Pham QD, et al. A hybrid genetic algorithm for the traveling salesman problem with drone. Journal of Heuristics, 2020, 26(2): 219-247. DOI:10.1007/s10732-019-09431-y |
| [63] |
Peng K, Du JX, Lu F, et al. A hybrid genetic algorithm on routing and scheduling for vehicle-assisted multi-drone parcel delivery. IEEE Access, 2019, 7: 49191-49200. DOI:10.1109/ACCESS.2019.2910134 |
| [64] |
Sung I, Nielsen P. Zoning a service area of unmanned aerial vehicles for package delivery services. Journal of Intelligent & Robotic Systems, 2020, 97(3): 719-731. |
| [65] |
Ulmer MW, Thomas BW. Same-day delivery with heterogeneous fleets of drones and vehicles. Networks, 2018, 72(4): 475-505. DOI:10.1002/net.21855 |
| [66] |
Kitjacharoenchai P, Ventresca M, Moshref-Javadi M, et al. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Computers & Industrial Engineering, 2019, 129: 14-30. |
| [67] |
Moshref-Javadi M, Lee S, Winkenbach M. Design and evaluation of a multi-trip delivery model with truck and drones. Transportation Research Part E: Logistics and Transportation Review, 2020, 136: 101887. DOI:10.1016/j.tre.2020.101887 |
| [68] |
Boysen N, Briskorn D, Fedtke S, et al. Drone delivery from trucks: Drone scheduling for given truck routes. Networks, 2018, 72(4): 506-527. DOI:10.1002/net.21847 |
| [69] |
Dorling K, Heinrichs J, Messier GG, et al. Vehicle routing problems for drone delivery. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(1): 70-85. DOI:10.1109/TSMC.2016.2582745 |
| [70] |
Saleu RGM, Deroussi L, Feillet D, et al. An iterative two-step heuristic for the parallel drone scheduling traveling salesman problem. Networks, 2018, 72(4): 459-474. DOI:10.1002/net.21846 |
| [71] |
Murray CC, Raj R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transportation Research Part C: Emerging Technologies, 2020, 110: 368-398. DOI:10.1016/j.trc.2019.11.003 |
| [72] |
Choudhury S, Solovey K, Kochenderfer MJ, et al. Efficient large-scale multi-drone delivery using transit networks. Journal of Artificial Intelligence Research, 2021, 70: 757-788. DOI:10.1613/jair.1.12450 |
| [73] |
Liu M, Liu X, Zhu MR, et al. Stochastic drone fleet deployment and planning problem considering multiple-type delivery service. Sustainability, 2019, 11(14): 3871. DOI:10.3390/su11143871 |
| [74] |
Huang HL, Savkin AV. A method of optimized deployment of charging stations for drone delivery. IEEE Transactions on Transportation Electrification, 2020, 6(2): 510-518. DOI:10.1109/TTE.2020.2988149 |
| [75] |
Macias JE, Angeloudis P, Ochieng W. Optimal hub selection for rapid medical deliveries using unmanned aerial vehicles. Transportation Research Part C: Emerging Technologies, 2020, 110: 56-80. DOI:10.1016/j.trc.2019.11.002 |
| [76] |
Bengio Y, Lodi A, Prouvost A. Machine learning for combinatorial optimization: A methodological tour d’horizon. European Journal of Operational Research, 2021, 290(2): 405-421. DOI:10.1016/j.ejor.2020.07.063 |
| [77] |
Salama M, Srinivas S. Joint optimization of customer location clustering and drone-based routing for last-mile deliveries. Transportation Research Part C: Emerging Technologies, 2020, 114: 620-642. DOI:10.1016/j.trc.2020.01.019 |
| [78] |
Wu GH, Fan MF, Shi JM, et al. Reinforcement learning based truck-and-drone coordinated delivery. IEEE Transactions on Artificial Intelligence. https://ieeexplore.ieee.org/abstract/document/9471008?casa_token=TCQ8w5kVC3gAAAAA:VWHENUZAwpeUWuWLHJssCdEtlI-K41W8AMG-6g8ss3SvuNz1x5UhO8CC4e8mYdg6zWlB9ItcqafB. (2021-07-01).
|
| [79] |
Xing Y, Carlson C, Yuan H. Optimize path planning for UAV COVID-19 test kits delivery system by hybrid reinforcement learning. Proceedings of the 12th IEEE Annual Computing and Communication Workshop and Conference (CCWC). Las Vegas: IEEE, 2022. 177–183.
|
| [80] |
Bai XS, Cao M, Yan WS, et al. Efficient routing for precedence-constrained package delivery for heterogeneous vehicles. IEEE Transactions on Automation Science and Engineering, 2020, 17(1): 248-260. DOI:10.1109/TASE.2019.2914113 |
| [81] |
De Freitas JC, Penna PHV. A variable neighborhood search for flying sidekick traveling salesman problem. International Transactions in Operational Research, 2020, 27(1): 267-290. |
| [82] |
De Freitas JC, Penna PHV. A randomized variable neighborhood descent heuristic to solve the flying sidekick traveling salesman problem. Electronic Notes in Discrete Mathematics, 2018, 66: 95-102. DOI:10.1016/j.endm.2018.03.013 |
| [83] |
Poikonen S, Golden B. Multi-visit drone routing problem. Computers & Operations Research, 2020, 113: 104802. |
| [84] |
Schermer D, Moeini M, Wendt O. A matheuristic for the vehicle routing problem with drones and its variants. Transportation Research Part C: Emerging Technologies, 2019, 106: 166-204. DOI:10.1016/j.trc.2019.06.016 |
| [85] |
Wang Z, Sheu JB. Vehicle routing problem with drones. Transportation Research Part B: Methodological, 2019, 122: 350-364. DOI:10.1016/j.trb.2019.03.005 |
| [86] |
El-Adle AM, Ghoniem A, Haouari M. Parcel delivery by vehicle and drone. Journal of the Operational Research Society, 2021, 72(2): 398-416. DOI:10.1080/01605682.2019.1671156 |
| [87] |
Bouman P, Agatz N, Schmidt M. Dynamic programming approaches for the traveling salesman problem with drone. Networks, 2018, 72(4): 528-542. DOI:10.1002/net.21864 |
| [88] |
Ferrandez SM, Harbison T, Weber T, et al. Optimization of a truck-drone in tandem delivery network using K-means and genetic algorithm. Journal of Industrial Engineering and Management, 2016, 9(2): 374-388. DOI:10.3926/jiem.1929 |
| [89] |
Hong I, Kuby M, Murray AT. A range-restricted recharging station coverage model for drone delivery service planning. Transportation Research Part C: Emerging Technologies, 2018, 90: 198-212. DOI:10.1016/j.trc.2018.02.017 |
| [90] |
Moshref-Javadi M, Hemmati A, Winkenbach M. A truck and drones model for last-mile delivery: A mathematical model and heuristic approach. Applied Mathematical Modelling, 2020, 80: 290-318. DOI:10.1016/j.apm.2019.11.020 |
| [91] |
Ropke S, Pisinger D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transportation Science, 2006, 40(4): 455-472. DOI:10.1287/trsc.1050.0135 |
| [92] |
Omagari H, Higashino SI. Provisional-ideal-point-based multi-objective optimization method for drone delivery problem. International Journal of Aeronautical and Space Sciences, 2018, 19(1): 262-277. DOI:10.1007/s42405-018-0021-7 |
| [93] |
Wang KZ, Yuan B, Zhao MT, et al. Cooperative route planning for the drone and truck in delivery services: A bi-objective optimisation approach. Journal of the Operational Research Society, 2020, 71(10): 1657-1674. DOI:10.1080/01605682.2019.1621671 |
| [94] |
Shavarani SM, Golabi M, Izbirak G. A capacitated biobjective location problem with uniformly distributed demands in the UAV-supported delivery operation. International Transactions in Operational Research, 2021, 28(6): 3220-3243. DOI:10.1111/itor.12735 |
| [95] |
Coelho BN, Coelho VN, Coelho IM, et al. A multi-objective green UAV routing problem. Computers & Operations Research, 2017, 88: 306-315. |
| [96] |
Lu YC, Yang C, Yang J. A multi-objective humanitarian pickup and delivery vehicle routing problem with drones. Annals of Operations Research, 2022, 319(1): 291-353. DOI:10.1007/s10479-022-04816-y |
| [97] |
Luo QZ, Wu GH, Ji B, et al. Hybrid multi-objective optimization approach with Pareto local search for collaborative truck-drone routing problems considering flexible time windows. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(8): 13011-13025. DOI:10.1109/TITS.2021.3119080 |
| [98] |
Han YQ, Li JQ, Liu ZM, et al. Metaheuristic algorithm for solving the multi-objective vehicle routing problem with time window and drones. International Journal of Advanced Robotic Systems, 2020, 17(2): 172988142092003.
|
 2023, Vol. 32
2023, Vol. 32


