2. 中国气象局 兰州干旱气象研究所 甘肃省防灾减灾重点实验室, 兰州 730020;
3. 兰州理工大学 计算机与通信学院, 兰州 730050
2. Key Laboratory of Arid Climatic Change and Reducing Disaster of Gansu Province, Institute of Arid Meteorology, China Meterological Administration, Lanzhou 730020, China;
3. College of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China
天气现象与人们日常生活和各行各业息息相关, 气象变化极为不稳定, 容易受到各种气象因素的制约和相互影响, 这使得天气现象的演化成为一个复杂多变, 包含多种无法控制因素的过程, 因此能够准确地预测气象要素一直充满着挑战[1-3].
随着互联网技术、信息化技术以及气象观测技术的迅速发展, 气象地面观测站点不断增多, 观测频次从逐天逐时转变为逐分钟, 同时天气雷达和气象卫星的发射使得高空层面的数据越来越多, 气象数据的快速增长使得气象行业累积了海量的数据, 气象行业数据多种多样, 包括各类结构化、半结构化和非结构化数据, 数据量已达到PB以上, 具有典型的大数据特征[4].
传统的气象预报模型是在各种基本假设成立的条件下完成的, 基本假设决定了预报的准确率, 当大量的基本假设不成立时, 预测模型的效果将会很差, 同时传统预报模型的另外一个缺点就是运算量非常大[5]. 随着气象大数据的到来, 我们可以利用巨大的气象数据集, 分析不同气象要素之间的关联关系, 降低预测模型中的基本假设, 利用数据驱动模型进行天气现象的预测. 目前, 该模型已被广泛应用于各类气象要素的预测中[6, 7].
支持向量机(support vector machine, SVM)算法是一种通用的机器学习方法, 它在小样本数据情况下求解速度快, 预测精度高, 能够避免过拟合、高维度等问题, 由于该算法在非线性和高维度的复杂系统预测中表现出了许多特有的优势, 因此被广泛使用, 主要用途是分类和回归模型分析. 目前, 已被应用到人脸识别、邮件分类、故障诊断、各类预测等相关领域[8-10]. 支持向量机算法主要是通过核函数进行计算, 该算法对核函数和相关参数的初始化设置非常敏感, 参数的不同设置会对最终的预测结果产生极大的影响, 因此合适的参数选择一直是SVM研究的难点. 群体智能优化算法在参数寻优方面具有较强的并行处理能力, 能够平衡全局与局部搜索, 寻优速度快, 效果良好[11]. 朱晶晶等人[12]利用1970–2014年海南省全部市县的月平均资料, 构建了SVM回归预测模型, 实现了对气温的预测, 结果表明SVM算法在气温短期预测中具有很好的效果. 杨通晓等人[13]构建了SVM的雷达降水类型识别模型, 是SVM分类模型的一种应用. 在SVM中核函数采用径向基函数, 同时利用PSO对核函数参数进行寻优, 结果显示该方法有效地提高了雷达对流天气下降水类型的识别精度. 晋健等人[14]为提升中长期预报的预测精度, 以均方差作为目标函数构建了FA-SVM中长期径流预报模型, 结果验证了FA-SVM模型的预测效果优于基本的BP神经网络模型. 李纯斌等人[15]选取了甘肃省作为研究对象, 利用BP神经网络和SVM模型构建了降水量空间插值模型, 结果显示SVM的插值精度模型明显地高于BP神经网络模型. 史旭明等人[16]以桂林市13个站点24 h降水量为研究对象, 建立了改进的单站降水SVM回归集合预报模型, 与ECMWF模式降水预报相比, 该模型的预报精度显著提高. 目前, 利用群体智能算法对SVM相关参数进行寻优时, 由于群体智能算法自身的缺陷导致SVM出现过拟合、泛化能力差、容易陷入局部最优等问题.
针对上述问题, 本文从预测模型的参数优化方面进行了研究, 提出了一种改进PSO算法优化SVM的气温预测模型, SVM中两个参数的设置对预测模型影响很大, 由于粒子群算法在后期寻优的过程中种群的多样性降低, 容易陷入局部最优等问题, 需要对PSO算法进行改进, 本文采用了自适应的惯性权重, 提高了该算法的全局搜索能力和寻优效率, 利用改进后的IPSO算法对气温预测模型SVM进行寻优, 实现了模型的优化选择, 使得预测精度进一步提高.
1 IPSO-SVM算法 1.1 支持向量机回归支持向量机出现在20世纪90年代, 是一种优秀的机器学习方法[17], 其基本思想是支持向量回归(support vector regression, SVR)将原始输入数据的空间映射到高维的特征空间上, 实现了升维, 将原始空间中的非线性回归问题进一步线性化, 通过引入非线性的核函数来实现, 即定义一个最优线性超平面, 把寻找最优超平面的问题转化为一个求解最优解的问题, 使得期望值最小. 因此, 在特征空间中, 只需构造特征空间最优线性回归超平面. 如式(1)所示:
| f(x)=wTx+u | (1) |
其中, x表示样本集, w表示最优超平面的法向量.
为了使得间隔最大化, 通过最小化
| f(xnew)=u+∑ni(ai−a∗i)Φ(xnew,xi) | (2) |
| u=yi+ε−∑mnew=1(anew−a∗new)xTnewxi | (3) |
式(2)中,
粒子群算法是由Kennedy等人在1995年提出[20], 该算法来源于自然界对鸟群捕食行为的模拟, 在问题对应的解空间中有多个不同的食物源, 而最大的食物源只有一个, 最大的食物源可以类比为解空间的全局最优解, 剩余的食物源可以类比为解空间的局部最优解, 鸟群的任务就是找到全局最优解, 在整个群体寻优的过程中, 利用群体中的个体相互传递和共享位置信息实现整个种群向最大食物源不断靠拢, 从而找到全局最优解. 在PSO中, 解空间的每一个解向量称为粒子, 每个粒子都具有两个属性, 即位置向量和速度向量, 位置向量用来计算当前粒子所处位置的适应度值, 该适应度值表示当前粒子的位置到全局最优解的距离. 速度向量决定了粒子下次飞行的方向和速度. 在每次寻优的过程中, 种群中的粒子可以根据自身的经验和种群中最优的粒子不断变换自己的飞行方向和速度, 从而使得整个种群向全局最优解靠近.
PSO算法步骤如下.
(1)种群初始化. 包括种群的大小, 初始粒子的位置和速度, 并计算每个粒子的适应度值, 确定个体最优粒子和全局最优粒子.
假设在一个D维搜索空间中, 有N个粒子组成一个群落, 其中第i个粒子表示为一个D维向量. 如式(4)所示:
| Xi=(xi1,xi2,⋯,xiD,),i=1,2,⋯,N | (4) |
第i个粒子的速度如式(5)所示:
| Vi=(vi1,vi2,⋯,viD,),i=1,2,⋯,N | (5) |
同时记录每个粒子的最优解
(2)更新每个粒子自己的速度和位置, 并计算适应度值. 如果每个粒子的适应度值优于历史的适应度值, 更新粒子的位置和适应度值. 如果整个种群中最优适应度值优于当前全局最优适应度值, 更新全局最优粒子的位置和适应度值. 第i个粒子的速度和位置更新如式(6)和式(7)所示:
| v(i+1)d=wvid+c1r1(pid−xid)+c2r2(pgd−xid) | (6) |
| x(i+1)d=xid+v(i+1)d | (7) |
其中,
(3)判断算法收敛条件是否满足. 若满足, 则停止迭代, 输出结果; 否则跳转到第2步继续执行.
1.3 改进的粒子群优化算法在PSO算法中, 惯性权重因子代表的是粒子继承上一次迭代速度的能力, 惯性因子参数的设置会严重影响PSO算法的全局和局部搜索能力. 由于PSO算法中惯性因子是固定的, 则会导致其收敛速度慢且容易陷入局部最优. 搜索初期, 需要一个较大的惯性权重因子进行全局寻优. 搜索后期, 需要一个较小的惯性权重强化局部搜索能力, 为了更好地平衡算法的全局和局部搜索能力, 本文设置了自适应的惯性权重因子w, 如式(8)所示, 该参数可以随迭代次数的递增而变化, 改进后的算法称为IPSO.
| w(t)=(wmax−wmin)/(1+exp(15tT−8))+wmin | (8) |
其中,
在天气预报、气候评估及气象服务等领域, 温压湿风和能见度是最核心的观测要素, 是计算其他相关指标的基础要素, 也是社会大众最关注的天气信息; 地面自动气象站的观测任务不一, 这几个要素是普遍考核要素, 各种尺度的天气现象由热力和动力条件配合而发生的, 温压湿风可以定量地对热力和动力条件诊断分析, 因此本文选取了兰州地面自动站观测数据作为研究样本, 采集时间为2019年3月1日00时至2019年4月30日23时, 每隔1 h采集一次, 采集要素为能见度, 气压, 相对湿度, 风速, 风向和气温, 这些数据集来源于甘肃省气象局气象大数据云平台API接口, 其原始观测数据如表1所示, 表1选取了部分数据.
| 表 1 原始气象数据集 |
数据预处理主要包括两个方面, 即数据清洗和原始数据归一化处理.
(1)数据清洗. 原始数据质量可以很大程度决定模型的预测结果, 在保障数据质量的情况下研究预测模型才是有意义的, 为了提高数据的质量和可用性, 数据清洗是在数据被使用之前必不可少的环节. 具体包括重复数据、异常值、空值等. 本文编写了Java程序对重复数据进行删除, 对原始数据进行异常检测, 将检测到的异常值设置成空值, 对空值采用领域平均法进行填补, 清洗后的样本数据集共有1416条记录, 每一条记录包含6个要素特征.
(2)数据归一化. 不同的气象要素有不同的单位, 为了消除不同气象要素之间的量级对预测结果造成的影响, 使得输入的数据处于同一个区间. 本文采用最值归一化的方法对输入数据进行无量纲处理, 将数值归一化到区间[0, 1]之间, 在完成预测之后将预测值反归一化为原始值[21]. 数据归一化如式(9)所示:
| ^xi=xi−xminxmax−xmin,i=1,2,⋯,n | (9) |
其中,
本文选取了兰州地面自动站观测数据作为研究样本, 利用采集的数据对IPSO-SVM气温预测模型进行训练和测试. 本文选取样本的80%作为训练集, 20%作为测试集.
IPSO-SVM气温预测模型建立主要包括两个方面, 一是利用改进的IPSO算法优化SVM模型的惩罚因子c和核函数g, 从而提高SVM模型对历史气温的预测精度; 二是对IPSO-SVM气温预测模型预测性能进行评估, 利用气温预测值和真实值之间的误差检验该模型的性能. IPSO-SVM气温预测模型步骤如下.
(1)设定气温数据集并完成数据预处理. 将历史气温数据划分为训练集和测试集, 完成训练数据和测试数据归一化处理.
(2)构造气温预测模型适应度函数f (c, g). 使用气温真实值和预测值的均方误差(mean square error, MSE)作为气温适应度函数的返回值. 适应度值大小反映的是气温预测模型的性能, 值越小, 预测性能越好, 气温预测精度越高.
(3) IPSO-SVM算法种群初始化和参数设置. 设置种群大小、最大迭代次数、种群维度、学习因子、惯性权重的范围和优化参数的个数. 完成粒子位置和速度初始化.
(4)利用第2步构造的气温适应度函数f (c, g)计算种群中每个粒子的适应度值, 保存全局最优解的位置和适应度值, 以及个体最优解的位置和适应度值.
(5)更新粒子速度和位置. 粒子每次被更新之后, 都需要重新计算粒子的适应度值. 如果满足条件, 则更新粒子全局最优解和个体最优解.
(6)迭代优化. 如果当前的迭代次数未达到设置的最大迭代次数, 则继续执行步骤5, 反之, 则终止迭代, 算法停止.
(7)输出结果. 当算法终止之后, IPSO-SVM算法输出参数c和g的组合最优值.
本文将能见度, 气压, 相对湿度, 风速, 风向这5个要素特征作为输入变量, 利用最优组合(c,g)的SVM模型对气温进行预测, 将气温的预测值作为输出变量, 输出的气温值需要做反归一化处理. 通过气温真实值和预测值之间的误差分析等其他指标评估该预测模型的性能. IPSO-SVM气温预测模型流程如图1所示, 其伪代码如算法1.

|
图 1 IPSO-SVM气温预测模型流程图 |
算法1. IPSO-SVM气温预测模型伪代码
1. for t < T do
2. 根据公式更新惯性权重因子
3. for i属于[1:N] do
4. 计算粒子的速度Vi
5. 判断粒子速度是否越界
6. 更新粒子速度Vi
7. 计算粒子的位置Xi
8. 判断粒子的位置是否越界
9. 更新粒子的位置Xi
10. 计算粒子的适应度值fitness(i)=均方误差评价函数MSE
11. endfor
12. for i属于[1:N] do
13. if fitness (i) < fitness_pbest( i) then
14. pbest(i, :)=init_pop(i, :)
15. fitness_pbest(i)=fitness(i)
16. endif
17. if fitness (i) < fitness_gbest then
18. gbest=init_pop(i, :)
19. fitness_gbest=fitness(i)
20. endif
21. endfor
22. endfor
23. 打印最佳参数结果c=gbest(1), g=gbest(2)
24. 输入5个要素变量组成的样本数据集
25. 利用最优参数c和g进行SVM网络训练和预测分析
26. 输出气温预测值, 进行误差分析和评估预测模型性能
3 实验结果及分析 3.1 实验环境实验平台采用Windows 7操作系统, Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz , 8核CPU, 8 GB内存, 500 GB SSD. 编程环境为Matlab 2016, 开发工具采用 IntelliJ IDEA, IntelliJ IDEA主要用于Java代码开发.
3.2 参数设置实验中与 IPSO-SVM模型对比的算法包括BP、SVM、GRID-SVM、GWO-SVM, ABC-SVM, ACO-SVM. BP中输入层神经元个数为10, 隐含层神经元个数为8, 训练函数采用traingdx, 学习率为0.9, 训练次数为50 000次; SVM中核函数采用RBF, 损失函数P值为0.01; GRID-SVM中交叉验证的次数设置为5, 网格大小为10×10, 间隔为0.5, eps的值为0.001; 每个优化算法中种群大小PopSize设置为30, 最大迭代次数Max_iteration设置为100, 种群维度设置为2, 寻优区间为[0.01, 100], ABC-SVM中蜜源(解)数量设置为15; ACO-SVM中信息量权重设置为2, 启发量权重设置为2, 信息素挥发因子p=0.8, 区间缩小因子r=0.8; IPSO-SVM中惯性权重的最大值设置为wmax=0.9, 最小值wmin=0.4, 加速因子c1和c2均设置为1.5.
3.3 模型评价指标为了评估预测模型的性能和精度, 本文选择均方根误差RMSE、平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为预测结果的评价指标. 计算公式如式(10)–式(12)所示:
| RMSE=√1NN∑i=1(yi−^yi)2 | (10) |
| MAE=1NN∑i=1|yi−^yi| | (11) |
| MAPE=(1NN∑i=1|yi−^yiyi|)×100% | (12) |
其中, N为数据集的总个数,
为了验证改进IPSO算法的寻优性能, 本文采用标准PSO和改进IPSO同时对SVM参数进行寻优, 其结果如图2所示.
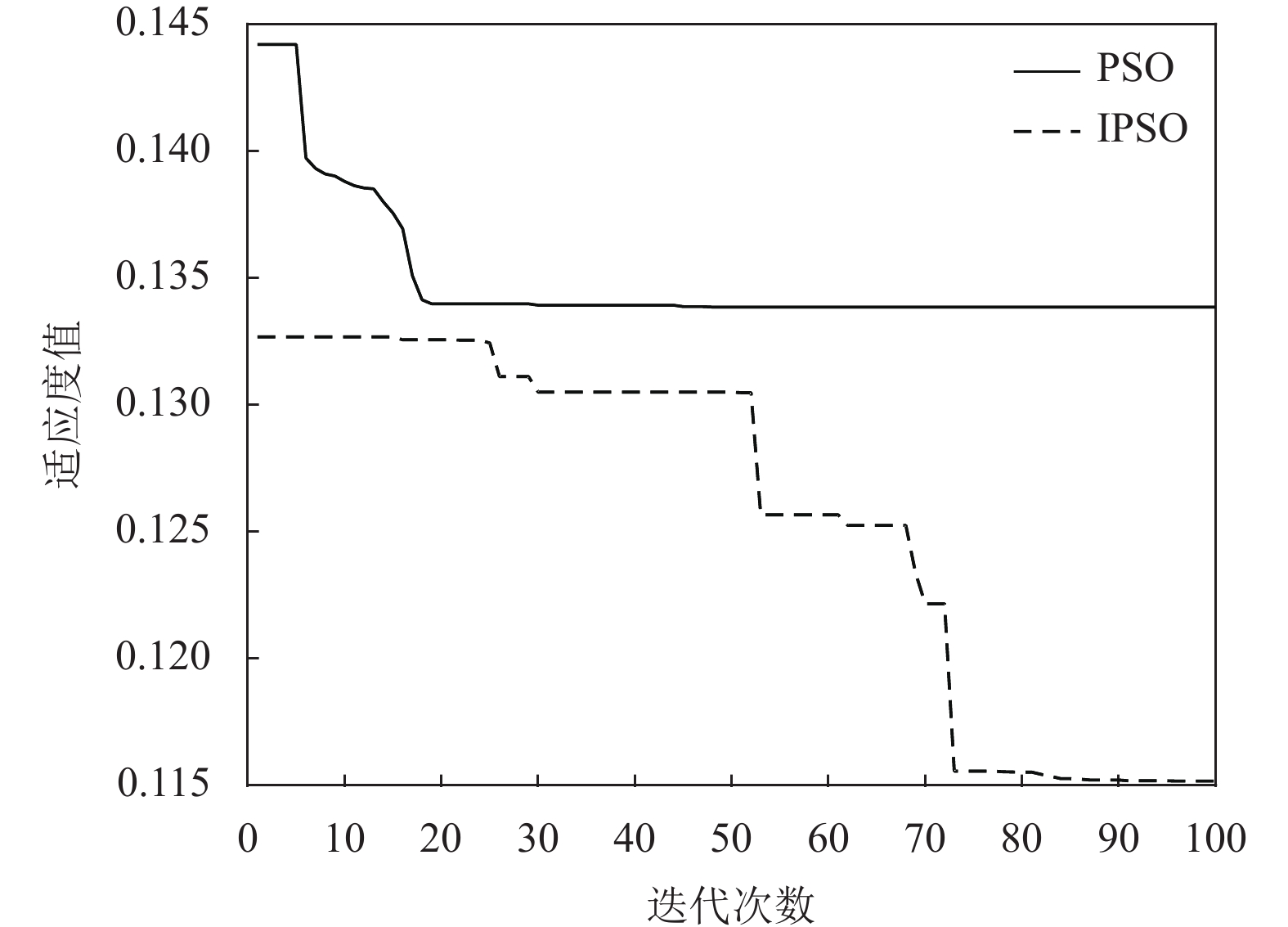
|
图 2 不同算法迭代曲线 |
从图2可知, PSO算法收敛速度较快, 在迭代的初期就开始收敛, 随着迭代次数的递增, 在第18次迭代左右时算法陷入了局部最优; 对于改进的IPSO算法, 随着迭代次数的增加, 在逐渐地向最优解靠近, 算法并没有出现早熟的现象, 这说明改进的IPSO具有更好局部探索和全局寻优能力, 并且收敛精度上要优于标准PSO算法.
3.5 IPSO-SVM模型实验结果及分析为了验证IPSO-SVM预测模型的有效性, 本文选取了168组连续样本数据作为模型的输入, 分别利用SVM和IPSO-SVM模型对预处理好的样本进行训练和测试, 得到如图3(a)和图3(b)的预测结果.
在图3(a)和图3(b)中, *代表实际气温值, 用黑色标记; □表示SVM算法预测的结果, 用蓝色标记; ○表示IPSO-SVM算法预测的结果, 用红色标记. 从图3(a)和图3(b)可知, 不论是在训练集还是在测试集上, 改进的IPSO-SVM模型的拟合效果明显优于SVM模型, IPSO-SVM曲线变化与实际值的曲线变化更加吻合.
为了能够从预测精度方面对比两个模型的性能, 表2列出了SVM和IPSO-SVM的RMSE, MAE, MAPE的性能指标, 同时为了能够分析每个算法的计算复杂度, 列出了每个算法的平均运行时长.
从表2可以看出, IPSO-SVM气温预测模型的RMSE, MAE, MAPE的预测指标值远优于SVM, 与SVM预测模型相比, RMSE值降低了4.5104, MAE值降低了3.9805, MAPE值降低了0.211 9. 由此可知改进的IPSO-SVM气温预测模型精度更高, 误差更小. 虽然IPSO-SVM气温预测模型较SVM模型的复杂度增加了很多, 但是针对气温预测这个问题, 多出的运行时间对整个预测模型的影响不大, 所以在合理的运行时间内IPSO-SVM气温预测模型的精度表现更佳.
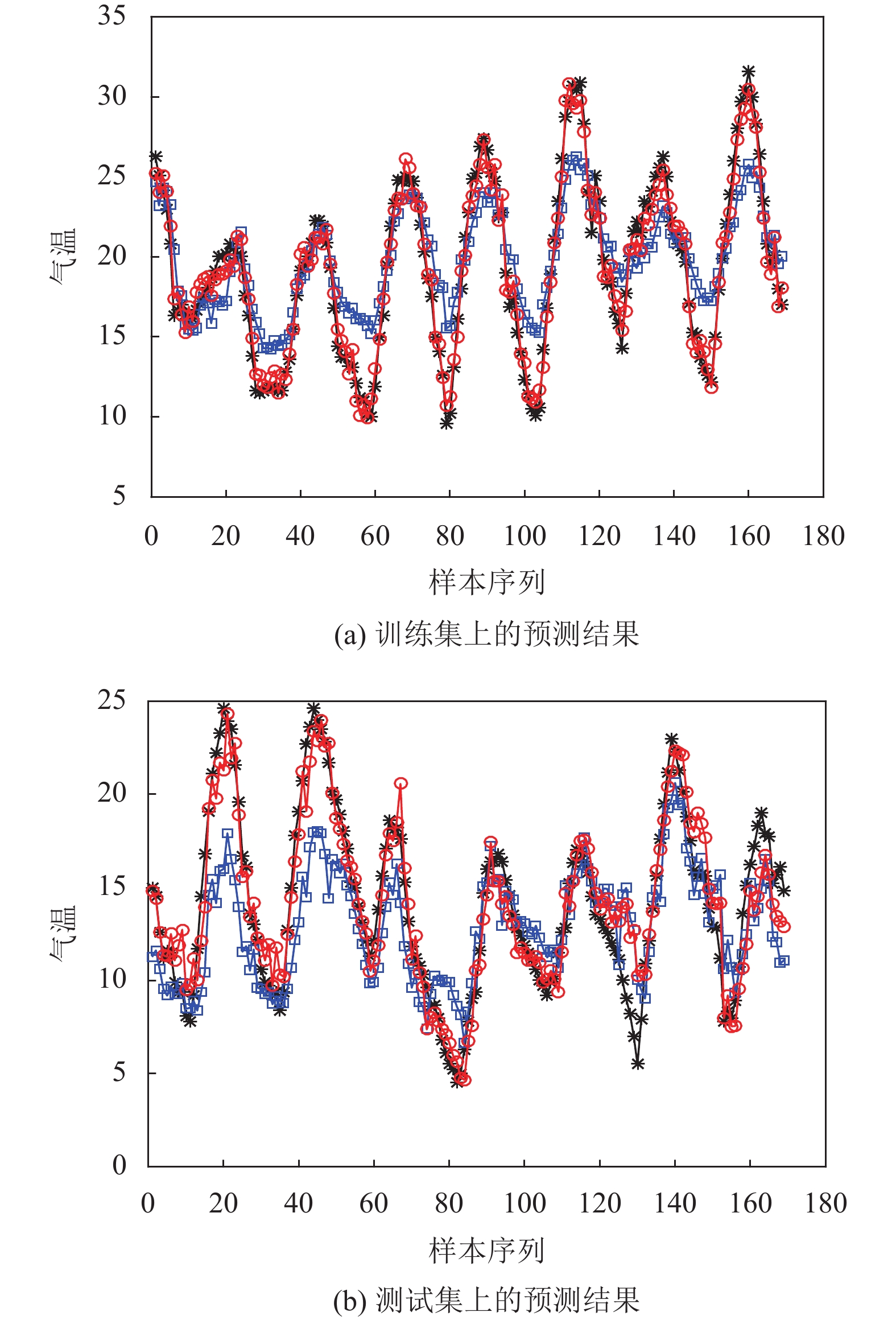
|
图 3 预测结果 |
| 表 2 SVM模型和IPSO-SVM模型的预测误差 |
3.6 IPSO-SVM模型与其他模型比较实验结果及分析
为了进一步验证IPSO-SVM模型在气温预测方面的有效性, 本文选取了BP神经网络[22]、GRID-SVM模型[23], GWO-SVM模型[24]进行了对比, 其训练集和测试集上的拟合曲线如图4(a)和图4(b)所示.

|
图 4 其他算法的预测结果 |
由图4(a)和图4(b)可知, 改进的IPSO-SVM模型在训练集和测试集上的拟合效果是最好的. BP模型在训练和测试的过程中波动比较大, 特别是在转折点的预测上, 预测值和真实值之间存在较大的误差. GRID-SVM模型在训练过程上的拟合效果要优于其在测试过程中的拟合效果. GWO-SVM模型的预测结果和真实之间的拟合程度与IPSO-SVM相对比较接近, 但是在整体的预测过程, IPSO-SVM模型的拟合效果优于GWO-SVM. 比如训练过程中, 在10–30个数据点时, GWO-SVM预测出的气温值和实际值偏差较大. 测试过程中, 在70–85个数据点时, GWO-SVM预测出的气温值和实际值偏差也是较大.
为了验证改进IPSO-SVM气温预测模型的精度, 将IPSO-SVM模型与其他气温预测模型进行对比, 表3列出了BP神经网络、GRID-SVM、GWO-SVM、ABC-SVM[25]、ACO-SVM[26]和IPSO-SVM的RMSE, MAE, MAPE的性能指标. 同时为了能够分析每个算法的计算复杂度, 列出了每个算法的平均运行时长.
| 表 3 IPSO-SVM气温预测模型和其他预测模型的预测误差 |
从表3可以看出, IPSO-SVM气温预测模型的RMSE, MAE, MAPE预测指标值都是最优的, 尤其是与BP和GRID-SVM相比, 改进的IPSO-SVM预测模型的值远小于这两个算法, RMSE分别降低了4.5500/4.4174, MAE值分别降低了3.7885/3.7095, MAPE分别降低了0.2093/0.1976; 同时与GWO-SVM预测模型和ACO-SVM相比, RMSE值降低了0.4965/0.4350, MAE值降低了0.3150/0.1367, MAPE值降低了0.018/0.0174. 在所有比对算法中, ABC-SVM预测模型性能仅次于IPSO-SVM模型, RMSE值相差0.0624, MAE值相差0.1367, MAPE值相差0.0077, 实验结果表明改进后的算法提高了模型的预测精度. 这是因为在IPSO-SVM模型中IPSO算法采用了自适应的惯性权重w, w值会随着算法的迭代次数递增而变化, 采用自适应的惯性权重使得PSO算法性能有了很大的提升. 算法进化初期, w值较大, 种群的多样性好, 有利于算法进行全局寻优, 随着进化的不断演变, 到进化的后期, w值逐渐减小, 有利于进行局部搜索, 并且防止算法陷入局部最优, 这种自适应的进化机制可以很好地平衡全局和局部寻优能力, 加快算法的收敛速度. 在算法的计算复杂度方面, 运行时间最长的是GRID-SVM模型, 这是因为该模型中含有交叉验证的过程, 这个比较耗时. IPSO-SVM相对于BP模型和GWO-SVM模型而言运行时间稍长, 但是对于气温预测这个问题, 本文预测的是每小时的气温, 则IPSO-SVM气温预测模型只要在一个小时内能运行出结果就不会影响在实际业务中的应用, 所以这个运行时长是在合理的范围内, 在合理的时间范围内IPSO-SVM预测模型的预测精度是最优的.
4 结束语为了解决支持向量机在气温预测方面误差大、参数选择灵敏等问题, 本文提出了一种改进的IPSO优化SVM回归模型, 并将该预测模型应用到气温预测研究中. 为了提高预测样本数据的质量, 首先对数据进行了预处理, 删除重复数据、填充缺测数据及数据的归一化和反归一化操作; 其次针对基本粒子群算法收敛速度慢, 后期容易陷入局部最优的问题, 对基本粒子群算法进行了改进并验证了其改进后的性能, 改进的算法有效地提高了全局寻优能力、加快了算法的收敛速度; 最后选取了兰州站点实际的观测数据, 以RMSE, MAE和MAPE为评价指标, 分别与BP模型、SVM模型、GRID-SVM模型、ABC-SVM模型、ACO-SVM模型、GWO-SVM模型的气温预测结果进行了对比分析, 实验结果表明, IPSO-SVM模型预测精度更高, 拟合度更好, 验证了该模型在气温预测方面的可行性、有效性及应用价值.
| [1] |
Maqsood I, Khan MR, Abraham A. An ensemble of neural networks for weather forecasting. Neural Computing & Applications, 2004, 13(2): 112-122. DOI:10.1007/s00521-004-0413-4 |
| [2] |
Haidar A, Verma B. Monthly rainfall forecasting using one-dimensional deep convolutional neural network. IEEE Access, 2018, 6: 69053-69063. DOI:10.1109/ACCESS.2018.2880044 |
| [3] |
程文聪, 史小康, 张文军, 等. 基于深度学习的数值模式降水产品降尺度方法. 热带气象学报, 2020, 36(3): 307-316. DOI:10.16032/j.issn.1004-4965.2020.029 |
| [4] |
中国气象局. 中国气象大数据(2018). 北京: 气象出版社, 2018. 3–29.
|
| [5] |
单大可. 基于深度学习的气温预测[硕士学位论文]. 福州: 福建师范大学, 2018.
|
| [6] |
Reichstein M, Camps-Valls G, Stevens B, et al. Deep learning and process understanding for data-driven Earth system science. Nature, 2019, 566(7743): 195-204. DOI:10.1038/s41586-019-0912-1 |
| [7] |
马景奕, 刘维成, 闫文君. 基于深度学习的气象要素预测方法. 热带气象学报, 2021, 37(2): 186-193. DOI:10.16032/j.issn.1004-4965.2021.018 |
| [8] |
郭飞, 谢立勇. 基于气象因素和改进支持向量机的空气质量指数预测. 环境工程, 2017, 35(10): 151-155. DOI:10.13205/j.hjgc.201710031 |
| [9] |
宋玉生, 刘光宇, 朱凌, 等. 改进的灰狼优化算法在SVM参数优化中的应用. 传感器与微系统, 2022, 41(9): 151-155. DOI:10.13873/J.1000-9787(2022)09-0151-05 |
| [10] |
张淑清, 张桂芬. 基于改进果蝇算法优化SVM的变速箱故障诊断. 组合机床与自动化加工技术, 2022(7): 71-74. DOI:10.13462/j.cnki.mmtamt.2022.07.017 |
| [11] |
李素, 袁志高, 王聪, 等. 群智能算法优化支持向量机参数综述. 智能系统学报, 2018, 13(1): 70-84. DOI:10.11992/tis.201707011 |
| [12] |
朱晶晶, 赵小平, 吴胜安, 等. 基于支持向量机的海南气温预测模型研究. 海南大学学报(自然科学版), 2016, 34(1): 40-44. DOI:10.15886/j.cnki.hdxbzkb.2016.0007 |
| [13] |
杨通晓, 岳彩军. 基于支持向量机的双偏振雷达对流降水类型识别方法研究. 暴雨灾害, 2019, 38(4): 297-302. DOI:10.3969/j.issn.1004-9045.2019.04.001 |
| [14] |
晋健, 刘育, 王琴慧, 等. 基于小波去噪和FA-SVM的中长期径流预报. 人民长江, 2020, 51(9): 67-72. DOI:10.16232/j.cnki.1001-4179.2020.09.013 |
| [15] |
李纯斌, 刘永峰, 吴静, 等. 基于BP神经网络和支持向量机的降水量空间插值对比研究——以甘肃省为例. 草原与草坪, 2018, 38(4): 12-19. DOI:10.13817/j.cnki.cyycp.2018.04.002 |
| [16] |
史旭明, 林汉燕, 金龙. 基于支持向量机的桂林短期定量降水预报方法研究. 桂林航天工业学院学报, 2017, 22(2): 171-175. DOI:10.3969/j.issn.1009-1033.2017.02.014 |
| [17] |
Vapnik VN. Statistical Learning Theory. New York: Wiley Press, 1999.
|
| [18] |
陈永义, 熊秋芬. 支持向量机方法应用教程. 北京: 气象出版社, 2011.
|
| [19] |
张梁. 基于ARIMA-SVR组合模型的北京市气温预测研究[硕士学位论文]. 大连: 大连理工大学, 2020.
|
| [20] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of the 1995 International Conference on Neural Networks. Perth: IEEE, 1995. 1942–1948.
|
| [21] |
朱昶胜, 李岁寒. 基于改进果蝇优化算法的随机森林回归模型及其在风速预测中的应用. 兰州理工大学学报, 2021, 47(4): 83-90. DOI:10.3969/j.issn.1673-5196.2021.04.013 |
| [22] |
陶晔, 杜景林. 基于随机森林的长短期记忆网络气温预测. 计算机工程与设计, 2019, 40(3): 737-743. DOI:10.16208/j.issn1000-7024.2019.03.024 |
| [23] |
张舒雅. 基于网格寻参优化SVM-KNN算法的老人跌倒检测研究[硕士学位论文]. 武汉: 华中师范大学, 2017.
|
| [24] |
何祖杰, 吴新烨, 刘中华. 基于改进灰狼算法优化支持向量机的短期交通流预测. 厦门大学学报(自然科学版), 2022, 61(2): 288-297. DOI:10.6043/j.issn.0438-0479.202104024 |
| [25] |
Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [26] |
Dorigo M, Stützle T. The ant colony optimization metaheuristic: Algorithms, applications, and advances. In: Glover F, Kochenberger GA, eds. Handbook of Metaheuristics. Boston: Springer, 2001. 250–285.
|
 2023, Vol. 32
2023, Vol. 32



