调度优化问题是一个组合优化问题, 可以将其界定为: 在一定的约束条件下, 将有限的资源及时的分配到几项任务中, 从而使一项或多项指标得到最优. 我国第1次对现代化工厂中生产的设备调度与系统问题等研究大约始于20世纪50年代. 这一理论问题研究具有极重要的理论价值和实际经济价值, 引起了当代国内外研究人员极大范围的广泛关注, 而车间调度是一种出现年代相对偏早、研究范畴较为广泛的生产调度问题. 柔性作业车间调度问题(flexible job shop scheduling problem, FJSP) 是生产调度问题的一个特例, 在每个工序中可以随机选择几台机器同时使用, 减少工序对资源的特殊需求. 随着车间系统内具有相同功能的机床逐渐增加, FJSP问题也随之越来越突出. 对于大规模和复杂的调度问题, 使用传统的运筹学方法很难保证在短时间内获得最优解. 目前有很多学者都研究了FJSP问题, 屈新怀等人[1]对柔性车间作业调度问题中高层启发式策略使用了遗传算法, 低层启发式策略设计了9个算子, 并提出了一个超启发式遗传算法. 最后, 使用标准实例测试了该算法的性能. 王玉芳等人[2]以最大完工时间为目标, 提出了一种改进的蛙跳算法, 弥补算法本身在局部搜索能力上存在的不足, 从而求解FJSP. 杜晓亮等人[3]以完工时间、机器的总负载量与机器总的生产成本比等为算法的优化的主要目标, 使用非支配排序的改进遗传算法, 建立多目标柔性作业车间调度模型, 选取前N×α个个体作为精英个体, 同时加入了邻域搜索, 通过实验验证了算法的有效性.
鲸鱼优化算法(whale optimization algorithm, WOA)是Mirjalilis 等人[4]在2016年提出的基于种群的智能优化算法. 由于提出的时间短, 适用领域相对较小. 徐伟民等人[5]将WOA应用于冷却器能效优化. 路雪刚等人[6]将WOA应用于畜禽废弃物运输路径优化. 李宏玉等人[7]将WOA应用于变压器诊断.
而在求解连续优化问题上, 许多学者也对WOA提出了各种各样的改进策略. 郝晓弘等人[8]引入两种非线性的策略, 当变异阈值根据种群的适配值的方差来设置时, 该算法也能发挥作用, 改善了算法的收敛准确性. 何庆等人[9]提出一种非线性收敛因子, 并结合阈值思想, 使算法够有效跳出局部最优. 王坚浩等人[10]利用混沌反向学习策略以及最优个体混沌搜索机制等策略进行改进, 结果表明算法的收敛速度以及鲁棒性上有较大提升. Kaur等人[11]在基本鲸鱼优化算法中引入混沌理论, 调整WOA最重要的参数. 考虑了各种混沌映射, 并对基准函数进行实验, 结果表明混沌映射(尤其帐篷映射)有助于提高WOA的算法.
目前, 鲸鱼优化算法在解决生产柔性流水线作业技术及调度管理问题中的应用较少. 本文尝试提出一种多策略鲸鱼优化算法用于求解柔性作业车间调度问题.
1 柔性作业车间调度问题FJSP描述如下: FJSP问题是一个在m台机器上
FJSP问题的约束条件:
(1)一台机器每次只能选择一个工序, 每个工序的顺序是针对每个工件确定的.
(2)一台机器只能同时加工一个工序.
(3)一个生产过程的加工不能中断.
(4)对于不同的工件, 加工优先级是相同的.
(5)确定同一工件的各个工序中的加工顺序.
(6)所有的工件都可以在零时加工, 所有的机器都可以在零时开始加工.
柔性作业车间调度可以划分为完全柔性车间调度和部分柔性车间调度. 完全柔性车间调度是指在每个工件的每道工序中, 可以在所有设备上加工, 而部分柔性车间调度则是至少有一道工序, 不能在所有设备上进行加工操作. 在实际的生产中, 部分柔性车间的调度更适合于企业的实际需要. 表1显示了3个零件在3台机器上的加工工序, 表1中的数值显示了该工序在该机床上的加工时间.
| 表 1 3×3的FJSP实例 |
(1)本文主要对部分柔性作业车间的调度安排情况进行了分析, 并将每个工件的完工时间最小化作为评价指标. 目标函数可以用式(1)表示.
| minCmax = min(max1⩽i⩽n(Ci)) | (1) |
其中, Ci表示工件
(2) 加工过程中的工序约束, 假设虚拟的第零道工序完工时间为零, 其数学模型用式(2)表示, 且同一个工件包含的工序必须按照先后顺序处理, 其数学模型用式(3)和式(4)表示.
| ci0=0 | (2) |
| sij+xijh×tijh⩽cij | (3) |
| ci(j−1)⩽sij | (4) |
其中,
(3) 加工过程中的工件完成时间约束, 任意工序的完工时间应小于或等于总的完工时间, 其数学模型用式(5)表示.
| cij⩽Cmax | (5) |
(4) 加工过程中的机器约束, 某一时刻的某一台机器上只允许加工一道工序, 其数学模型用式(6)和式(7)表示.
| sij+tijh⩽skl+K(1−yijhkl) | (6) |
| ci(j−1)⩽sij+K(1−yijhkl) | (7) |
其中,
(5) 加工过程中某一时刻的同一道工序只能在一台机器上处理, 其数学模型用式(8)表示.
| mij∑h=1xijh=1 | (8) |
(6) 加工过程中的任意工序的开始时间和完成时间都是非负的, 用式(9)所示.
| sij⩾0,cij⩾0 | (9) |
鲸鱼优化算法(WOA)是一种元启发式的优化算法, 它模仿座头鲸的狩猎行为, 在捕获猎物前包围目标区域. 根据座头鲸猎物捕食行为的特点, WOA主要包括3个阶段: 包围猎物, 气泡狩猎和随机搜索.
2.1 包围猎物在狩猎时, 鲸鱼需要识别目标猎物所处的位置, 并将其包围起来. 但是, 在搜索空间内, 其所处的位置常常是未知的. 假设通过猎物的位置或目标猎物的近似位置来分析当前种群中的最佳适应度值, WOA将更新当前候选组中其他搜索者的位置. 该过程可由式(10)表示.
| D=|CX∗(t)-X(t)|, X(t+1)=X∗(t)-A⋅D | (10) |
其中,
| A=2ar-a, C=2r | (11) |
其中,
根据座头鲸捕食时的行为, WOA以两种方式开发: 收缩更新和螺旋式更新. 收缩更新是通过降低式(11)中的收敛因子
| X(t + 1) = D′eblcos(2πl) + X∗(t) | (12) |
其中,
随着鲸鱼的螺旋式运动, 周围同时受到挤压, 因此WOA各有0.5的概率来模拟气泡狩猎同步过程, 以收缩包围并更新螺旋位置, 如式(13)所示.
| X(t+1)={X∗(t)-A⋅D, p<0.5D′eblcos(2πl)+X∗(t), p⩾0.5 | (13) |
在狩猎时, 若|A|>1, WOA不根据目标猎物更新其位置, 而是从种群中搜索随机目标来替代目标猎物. 实际的个体鲸鱼为了寻找目标猎物而被迫偏离原来的目标, 这可以提高算法的全局搜索能力. 随机搜索的数学模型如式(14)所示.
| D=|CXrand-X(t)|,X(t+1)=Xrand-A⋅D | (14) |
其中,
由于WOA通常用于解决连续优化问题, 柔性作业车间调度是组合优化问题, 所以在运用WOA求解优化问题时, 首先要考虑解的编码问题, 而FJSP编码要考虑两个问题, 即工序排列和机器选择. 在对编码规则设计时, 本文采用基于工序的两层编码, 如图1所示. 然后再根据机器和工序分别进行分类, 每个部分的长度都为所有工件的工序总和.

|
图 1 编码方式 |
每个位置的整数代表工件的序号. 整数出现的次数也代表了工件的工序号. 例如, 在图1中, 工序排列为[2 3 1 1 2 3], 其中第2整数位3代表第3工件的第1工序, 第6整数位3代表第3工件的第2工序, 以此类推.
与机器部分相对应的整数代码从左到右表示为代表某工序选择的机器, 每个整数代表在可用机器中为每个工序选择的第几台机器的编号, 而不是相应的机器编号. 以图1编码方式为例, 机器选择为[1 2 1 1 3 1], 第1个整数位1, 代表第1个工件的第1道工序
在迭代过程中工序向量按照WOA算法的个体更新策略更新本文采用 ROV 规则(ranked-order-value, ROV)[12], 将工序向量连续变量转化成工件序列. ROV 规则如表2所示.
根据 ROV 规则, 从最小分量值的位置开始, 依次赋予其 ROV 值, 然后可以得到解码后的工序向量 [2 3 1 1 2 3]. 通过ROV规则得到新的工序向量, 然后从每个工序的可用设备集中选择加工机器, 获得对应的机器向量.
| 表 2 工序解码 |
在每道工序机器的选择时, 选择式(15)将向量值转变为机器编号.
| u(i)=round(12ε(x(i)+ε)(s(i)−1)+1) | (15) |
其中,
WOA中的个体解为连续值向量, 无法实现工件排序的求解. 但是, 通过上面的转换机制就可以使得WOA从求解连续问题转换为求解柔性作业车间调度问题.
3.2 初始化在使用元启发式算法解决优化问题时, 初始种群的质量往往对全局的收敛速度和最终结果有很大的影响. 本文采取混合方式产生初始种群, 通过实验证明混沌初始化与随机初始化的个体数量比例为8:2.
混沌是一种具有随机并对初始值敏感的非线性动力学系统运动. 在混沌的帮助下, 初始解决方案的个体被分配到解决方案空间里, 从而增加了群体的多样性. 在各种混沌映射中, Logistic映射是最典型的混沌系统, Logistic混沌映射的系统方程如式(16)所示.
| X(k)=μ×X(k-1)×[1-X(k-1)] | (16) |
其中,
Logistic混沌映射与随机种群分布对比情况如图2所示, 图2(b)为随机种群生成方式的分布图, 搜索空间空隙大, 分布不均匀. 图2(a)为混沌映射方式的分布图, 此方式可以避免种群分布的不均匀, 增加解的多样性.
3.3 非线性收敛因子和惯性权重标准WOA中参数A是与算法局部优化能力有关的一个重要参数. 一方面, 在算法前期, 该算法具有较强的全局寻优功能, 可以在较大的范围内进行搜索, 以保证群体的多样性. 另一方面, 在算法后期, 具有强大的局部寻优能力, 可使该算法得到最佳的局部解. 鲸鱼优化算法主要通过控制系数向量A的值来实现全局搜索和局部优化迭代的转换, 原始的WOA的收敛因子a随着迭代次数的增加而线性减小. 这种线性变化不会帮助算法有效地调整全局搜索和局部搜索能力.

|
图 2 Logistic混沌映射与随机分布对比图 |
在此基础上, 采用一种新的优化方法, 该方法能够在初始阶段直接产生更大的参数A, 从而使其具有更好的全局寻优性能和更快的收敛速度; 通过在算法的后期阶段自动生成一个较小的A来帮助提高局部开发能力, 从而有助于提高算法全局的搜索能力. 收敛因子根据式(17)进行变化, 图3给出了式(17)所描述的非线性收敛因子变化过程. 文献[9]也是采用此种方式求解连续问题的.
| a=(2-2ttmax)(1-t3t3max) | (17) |
其中,
标准的WOA迭代过程中更新鲸鱼的位置时没有考虑到目标猎物不同而带来的差异. 在粒子群优化算法中结合惯性权重的思想来控制个体优化, 并在位置更新方程中引入适应性参数作为惯性权重, 提高优化算法的准确性. 具体改进如式(18)–式(21)所示.
| ω(t)=2πarcsin(ttmax) | (18) |
| X(t+1)=ωX∗(t)−A⋅D,p<0.5∧|A|⩽1 | (19) |
| X(t+1)=D′eblcos(2πl)+(1−ω)X∗(t),p⩾0.5 | (20) |
| X(t+1)=ωXrand (t)−A⋅D,p<0.5∧|A|>1 | (21) |
在式(19)与式(21)中, 非线性惯性权重会随着迭代次数的逐步增加而增大, 结果表明, 当前种群的最佳解决方案对鲸鱼更有吸引力, 能够更准确地确定目标, 并加快算法的收敛和准确性. 在式(20)中, 当个体鲸鱼以一定的概率更新其螺旋位置时, 它就会接近其猎物. 在这种情况下, 为了提高算法的局部能力, 应该使用较低的惯性权重, 以便鲸鱼在更新其位置时能够确定是否有更好的解.

|
图 3 非线性变化过程 |
3.4 差分进化策略
WOA位置的最终更新是通过贪婪的选择操作获得的, 这可能会导致算法的解落入局部最优. 由于差分进化算子(differential evolution, DE)具有很强的搜索能力, 所以可以通过差分进化算子改进了鲸鱼优化算法的搜索能力. 在WOA中嵌入DE算子, 在每次迭代中更新位置向量, 大大增加了个体向量解的信息共享.
为了提高搜索效率, 在WOA结束后通过比较随机数和交叉因子CR的大小, 当小于CR时进行基于DE算子的更新以交换种群信息, 从而引导个体到整体最优个体位置的转换. 保持群体活动的多样性. 本文引入差分进化算法的 DE/best/2变异策略[13]对种群进行寻优, 其计算过程如式(22)所示.
| Vi,g = Xbest,g + F(Xr1,g−Xr2,g) + F(Xr3,g−Xr4,g) | (22) |
其中,
在 WOA算法的循环后期, 由于种群中的个体都在最佳个体位置上, 种群中的多样性不足, 使得算法提前收敛到了非全局最优, 从而导致了早熟. 为降低 WOA算法早熟收敛的可能性, 采用混沌搜索方法对最优个体进行优化. 混沌搜索策略本质上是一种深度局部搜索方法, 其实现如式(23)所示.
| ytgbest,d=1−2(yt−1gbest,d)2 | (23) |
其中,
MWOA 算法实现步骤总流程如图4所示, 具体描述如下.
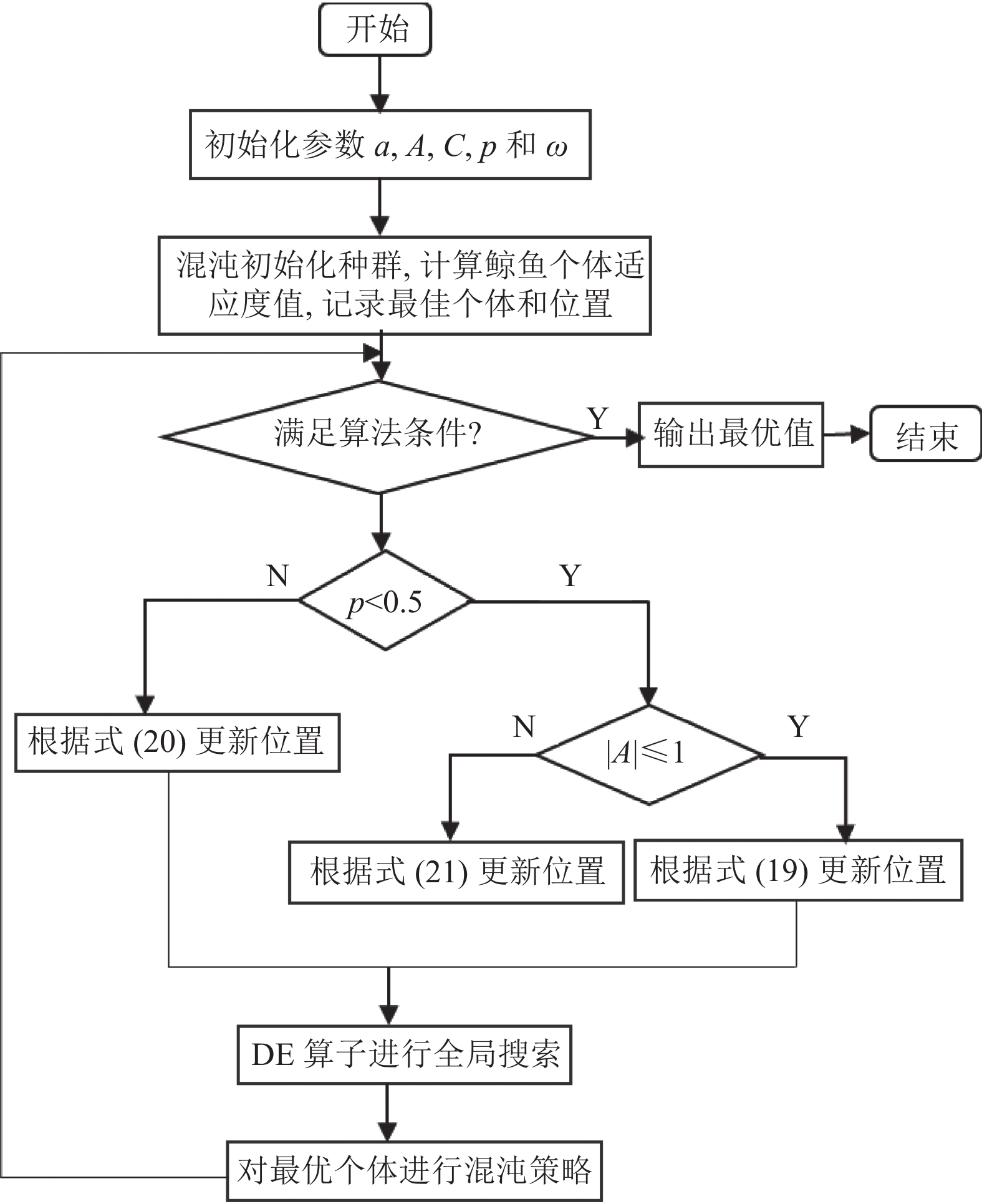
|
图 4 MWOA流程图 |
步骤1. 初始化算法参数.
步骤2. 根据混沌策略初始化种群, 计算种群的适应度值, 并搜索最佳个体和位置.
步骤3. 如果p<0.5, |A|≤1, 使用式(19)更新位置; 如果|A|>1, 使用式(21)更新位置.
步骤4. 如果p>0.5, 使用式(20)更新各个位置.
步骤5. DE策略对鲸鱼个体的每个维度的变量进行全局搜索.
步骤6. 对种群进行评估以找到全局最优个体, 并对全局最优个体采用最优混沌策略.
步骤7. 判断是否达到了周期结束的条件; 如果是, 终止算法并输出最优解的位置; 否则, 返回步骤3.
4 实验分析 4.1 求解基准问题为了客观验证本文所提出的MWOA算法是否有效, 本文选取Brandimarte标准测试系列[14]中的5个案例进行了实验. 把没有使用混沌初始化策略的MWOA算法称为NL-MWOA算法. 每个案例都独立运行20次, 并通过与粒子群优化算法、鲸鱼优化算法、NL-MWOA算法、贪婪算法 (Greedy)、SPT[14]以及文献[15]所得的结果进行比较, 对比结果如表3所示. SPT是一种基于最短加工时间规则的算法, 其思想与贪婪算法相似. 算法实现采用Matlab实现, 其中基于种群的算法的有关参数设置为: 种群规模为50, 迭代次数为100.
在表3中, Best是每个算法取得的最优适应度值, RPD是算法的准确性偏差, 它是用来衡量算法的求解精度的,
| RPD=100×(Best−Best∗)/Best∗ | (24) |
其中,
由表3数据可知, 本文改进算法求解的结果在所有基准测试上都优于贪婪算法与SPT所求解的结果. 结果表明MWOA能很好地跳出局部最优. NL-MWOA与MWOA分别在MK01、MK09、MK10这3个算例上进行对比, 最大完工时间从45降低到37、从385降低到375、从331降低到314. 在其他实例上, MWOA也取得了比NL-MWOA更好的结果, 说明混沌映射方式得到了很好的应用. MWOA算法在算例MK01、MK08、MK10都达到了最好的求解数据. MWOA算法在MK01算例中与基本鲸鱼算法进行对比最大完工时间从49降低到37, 说明本文算法的寻优能力得到了有效的提升. 另外本文算法在MK05和MK09算例中的求解精度得到了第2名, 优于WOA算法以及Henchir算法[15], 而在总体上来看MWOA算法的平均相对偏差达到了0.66比其他算法都要低.
| 表 3 基准算例对比结果 |
4.2 求解实际问题
实际案例的数据来源于文献[16], 实际案例中的家具公司主要生产家具的某个零件, 选取某阶段生产6种零件, 每个零件都有6道加工工序, 总共有10台机器. 现有的数控加工设备有两台冲床、两台铣床、两台线切割机、电火花机、钻床、电焊机和加工中心各一台. 实验参数设置与上述一致, 用改进的算法进行了求解, 得到案例中的最优解的甘特图如图5所示, 其中J5-1表示第5个工件的第1道工序, [0, 6]表示该工件的开始时间和结束时间, 所以该案例的最大完工时间为35 s, 远小于文献[16]中的最大完工时间48 s. 图6是算法求解该问题的收敛曲线. 由图6可知, 算法随着迭代次数不断收敛, 在迭代次数42代左右陷入局部最优解.
为了实验的完整性, 本文与基本鲸鱼算法进行对比, 最大完工时间从38 s降低到35 s, 平均值从44.9 s降低到40.4 s.

|
图 5 最优调度甘特图 |

|
图 6 MWOA在实例中的收敛曲线 |
5 结束语
柔性车间作业调度问题, 是目前国内外研究的热点之一. 针对柔性车间调度问题, 提出一种基于多策略的鲸鱼优化方法. 在传统鲸鱼优化算法上, 采用了各种策略, 以克服其精度低、收敛速度慢、易陷入局部最优的缺点. 以最大完工时间最小为目标, 将多个基准问题和一个家具制造问题作为研究对象, 与粒子群算法、贪婪算法等进行比较, 证明了该算法的有效性.
| [1] |
屈新怀, 纪飞, 孟冠军, 等. 超启发式遗传算法柔性作业车间绿色调度问题研究. 机电工程, 2022, 39(2): 255-261. DOI:10.3969/j.issn.1001-4551.2022.02.017 |
| [2] |
王玉芳, 缪昇, 葛嘉荣. 面向柔性作业车间调度的改进混合蛙跳算法. 组合机床与自动化加工技术, 2022, 579(5): 187-192. DOI:10.13462/j.cnki.mmtamt.2022.05.045. |
| [3] |
杜晓亮, 张楠, 孟凡云, 等. 改进NSGA2算法求解柔性作业车间调度问题. 组合机床与自动化加工技术, 2022, 579(5): 182-186. DOI:10.13462/j.cnki.mmtamt.2022.05.044 |
| [4] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [5] |
徐伟民, 邬剑升, 余数, 等. 交叉熵鲸鱼算法的制冷机组能效优化. 重庆理工大学学报(自然科学), 2022, 36(9): 137-145. DOI:10.3969/j.issn.1674-8425(z).2022.09.017 |
| [6] |
路雪刚, 张雪花, 张梦桃. 基于改进鲸鱼优化算法的畜禽废弃物运输路径优化问题. 科学技术与工程, 2022, 22(25): 11120-11129. DOI:10.3969/j.issn.1671-1815.2022.25.038 |
| [7] |
李宏玉, 毛泉, 祁忠伟, 等. 基于鲸鱼算法优化PNN的变压器故障诊断. 电气自动化, 2022, 44(4): 102-104. DOI:10.3969/j.issn.1000-3886.2022.04.030 |
| [8] |
郝晓弘, 宋吉祥, 周强, 等. 混合策略改进的鲸鱼优化算法. 计算机应用研究, 2020, 37(12): 3622-3626, 3655. DOI:10.19734/j.issn.1001-3695.2019.09.0528 |
| [9] |
何庆, 魏康园, 徐钦帅. 基于混合策略改进的鲸鱼优化算法. 计算机应用研究, 2019, 36(12): 3647-3651, 3665. DOI:10.19734/j.issn.1001-3695.2018.07.0382 |
| [10] |
王坚浩, 张亮, 史超, 等. 基于混沌搜索策略的鲸鱼优化算法. 控制与决策, 2019, 34(9): 1893-1900. DOI:10.13195/j.kzyjc.2018.0098 |
| [11] |
Kaur G, Arora S. Chaotic whale optimization algorithm. Journal of Computational Design and Engineering, 2018, 5(3): 275-284. DOI:10.1016/j.jcde.2017.12.006 |
| [12] |
姜天华. 混合灰狼优化算法求解柔性作业车间调度问题. 控制与决策, 2018, 33(3): 503-508. DOI:10.13195/j.kzyjc.2017.0124 |
| [13] |
Das S, Mullick SS, Suganthan PN. Recent advances in differential evolution—An updated survey. Swarm and Evolutionary Computation, 2016, 27: 1-30. DOI:10.1016/j.swevo.2016.01.004 |
| [14] |
Brandimarte P. Routing and scheduling in a flexible job shop by Tabu search. Annals of Operations Research, 1993, 41(3): 157-183. DOI:10.1007/BF02023073 |
| [15] |
Henchiri A, Ennigrou M. Particle swarm optimization combined with Tabu search in a multi-agent model for flexible job shop problem. Proceedings of the 4th International Conference on Advances in Swarm Intelligence. Harbin: Springer, 2013. 385–394.
|
| [16] |
刘婉莹. 蚁群优化算法在柔性作业车间调度中的应用[硕士学位论文]. 哈尔滨: 东北林业大学, 2018.
|
 2023, Vol. 32
2023, Vol. 32



