2. 无锡学院 自动化学院, 无锡 214105
2. School of Automation, Wuxi University, Wuxi 214105, China
在移动机器人的发展历史中有一个问题是逃避不了的, 那就是路径规划问题. 路径规划最早始于20世纪60年代, 早期的路径规划是在静态障碍物下进行的, 但是随着人们的需求和应用环境的变化, 人们不得不对路径规划进行“升级换代”. 路径规划在学术上可以定义为在存在障碍物的有界空间内寻找一条从起点到目标点的最优或次优且安全无碰撞路径[1-3], 通俗来说就是解决地洞机器人要去哪里的问题并且如何安全准确到达.
对于路径规划, 众多学者提出Dijkstra 算法[4]、A*算法[5]、蚁群算法[6]、人工势场法[7]、D*Lite 算法[8]、RRT 算法[9]等传统算法. 但是这些传统算法存在着很多的不足之处. 比如: 人工势场法中机器人容易陷入局部最小值, 局部最小值即在路径规划过中, 目标点对移动机器人的引力与障碍物对移动机器人的斥力大小相等, 方向相反, 无法继续向目标点移动. 同时人工势场法中还存在着目标不可达的问题, 即当障碍物出现在目标位置附近时, 因障碍物产生的斥力较大, 不能顺利到达目标点[10].
在局部路径规划中的算法有很多, 其中人工势场法因其算法本身较为简单, 易实现, 逻辑清晰, 因此被广大学者所喜爱. Abadlla等人提出了一种改进的人工势场法与模糊逻辑法相结合的新方法. 该方法克服了传统人工势场法局部极小点问题, 提高了复杂环境下的导航性能, 但未能完全克服机器人剧烈震荡问题[11]. Wang 等人引入虚拟目标点, 并改变斥力势场函数, 使得移动机器人可以跳出局部最小并可以解决目标不可达问题, 但同样会先陷入局部最小区域[12]. 徐小强等人对斥力的生成机制进行了调整, 在一定条件下对前进方向做出了改进, 通过设立虚拟的子目标点引导机器人运动, 但在复杂环境下, 移动机器人可能会陷入其中[13]. 郑来芳等人提出人工势场法对移动底盘和机械臂联合避障的局部行进路径规划, 使管道移动机械臂顺利避开支柱障碍到达目标位置. 该算法也易陷入局部极小值, 当障碍物靠近目标点时会导致目标点不可达[14].
针对人工势场法的缺陷, 本文通过加入系数项并结合模拟退火法进行改进. 首先针对目标不可达的情况, 设计一种新的斥力势场函数, 加入一个跟随目标点距离变化而变化的系数项, 使该算法在目标点靠近障碍物时不会因为斥力大于引力而无法到达目标点. 其次针对局部最优解, 采用人工势场法与模拟退火法相结合的算法, 模拟退火法对当前最优解增加扰动产生新解, 并以一定概率接受新解, 使其拥有跳出局部极小值的能力, 从而走出障碍物, 解决了人工势场法易陷入局部极小值的问题.
1 传统人工势场法人工势场法是由Khatib在1985年时所提出的一种虚拟力算法[15], 人工势场法原理是: 目标点会产生引力场, 障碍物会产生一个或者多个斥力场, 移动机器人受两种场的共同作用, 引力场对移动机器人产生一个指向目标点的引力, 斥力场由障碍物指向移动机器人的斥力, 二者的合力的方向最终决定它的移动方向并规划一条由起点指向终点的无碰路径. 本文中设机器人当前点为
在二维运动空间中, 机器人受到运动空间中所有障碍物的斥力. 由于斥力的影响, 会使得机器人远离障碍物, 避免发生碰撞. 当不在障碍物的影响范围内时, 斥力势场为零. 传统人工势场法中的斥力势场函数表达式为:
| $ {U_{{\rm{rep}}}}(X) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{K_{{\rm{rep}}}}{{\left( {\dfrac{1}{{\rho ({X_c}, {X_o})}} - \dfrac{1}{{{\rho _0}}}} \right)}^2}, \; {\text{0<}}\rho {\text{(}}{X_c}, {X_o}) \leqslant {\rho _0}} \\ {0 , \qquad\qquad\qquad\qquad\;\;\;\;\;\; \rho {\text{(}}{X_c}, {X_o}{\text{) > }}{\rho _0}{\text{ }}} \end{array}} \right. $ | (1) |
其中,
| $ {U_{{\rm{rep}}}}(X) = \left\{ {\begin{array}{*{20}{l}} {K_{{\rm{rep}}}}{{\left( {\dfrac{1}{{\rho ({X_c}, {X_o})}} - \dfrac{1}{{{\rho _0}}}} \right)}^2}{\text{ }}\dfrac{1}{{{\rho ^2}({X_c}, {X_o})}}\dfrac{{\partial \rho ({X_c}, {X_o})}}{{\partial X}}, \\ \quad {\text{ 0 < }}\rho {\text{(}}{X_c}, {X_o}{\text{) }} \leqslant {\rho _0} \\ {0, \; \rho {\text{(}}{X_c}, {X_o}{\text{) > }}{\rho _0}{\text{ }}} \end{array}} \right. $ | (2) |
移动机器人不仅会受到空间中障碍物所给的斥力, 还会受到目标点发出的引力. 在势场中机器人受到目标点的引力是随着本身与目标点的距离变化而产生变化的, 当机器人与目标点越近, 其所受到的引力越小, 当机器人与目标点越远, 其所受到的引力则越大. 在传统人工势场法中的引力势场函数表达式为:
| $ {U_{{\rm{att}}}}(X) = \frac{1}{2}{K_{{\rm{att}}}}{\rho ^2}({X_c}, {X_g}) $ | (3) |
其中,
| $ {F_{{\rm{att}}}}(X) = - {K_{{\rm{att}}}}\rho ({X_c}, {X_g}) $ | (4) |
由于移动机器人在路径规划过程中可能同时受多个障碍物作用, 因此根据式(1)和式(3)可得所受的合势场可表示为:
| $ U = {U_{{\rm{att}}}} + \sum\limits_{j = 1}^n {{U_{{\rm{rep}}}}(X)} $ | (5) |
受到的合力可以表示为:
| $ F = {F_{{\rm{att}}}}(X) + \sum\limits_{j = 1}^n {{F_{{\rm{rep}}}}(X)} $ | (6) |
其中, n为二维运动空间中的障碍物总数.
2 改进人工势场法 2.1 目标不可达问题目标不可达问题是指移动机器人到达目标点附近, 由于其周围存在的障碍物产生的斥力大于引力, 使得机器人在目标点附近徘徊, 不能到达目标点.
针对目标不可达问题, 本文在原斥力势场函数中添加关于目标点到当前点的影响函数. 函数具体为:
改进后斥力势场函数为:
| $ {U_{{\rm{rep}}}}(X) = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}{K_{{\rm{rep}}}}{{\left( {\dfrac{1}{{\rho ({X_c}, {X_o})}} - \dfrac{1}{{{\rho _0}}}} \right)}^2}{\text{(1 }}-{{\text{e}}^{( - (R/0.4))}}),\\ \quad {\text{ 0 < }}\rho {\text{(}}{X_c}, {X_o}{\text{) }} \leqslant {\rho _0} \\ {0, \; \rho {\text{(}}{X_c}, {X_o}{\text{) > }}{\rho _0}{\text{ }}} \end{array}} \right. $ | (7) |
改进后斥力函数为:
| $ {F_{{\rm{rep}}}}(X) = \left\{ {\begin{array}{*{20}{l}} {{F_{{\rm{rep}}1}} + {F_{{\rm{rep}}2}}, \; {\text{ 0 < }}\rho {\text{(}}{X_c}, {X_o}{\text{) }} \leqslant {\rho _0}} \\ {0, \qquad\qquad\quad \rho {\text{(}}{X_c}, {X_o}{\text{) > }}{\rho _0}} \end{array}} \right. $ | (8) |
其中,
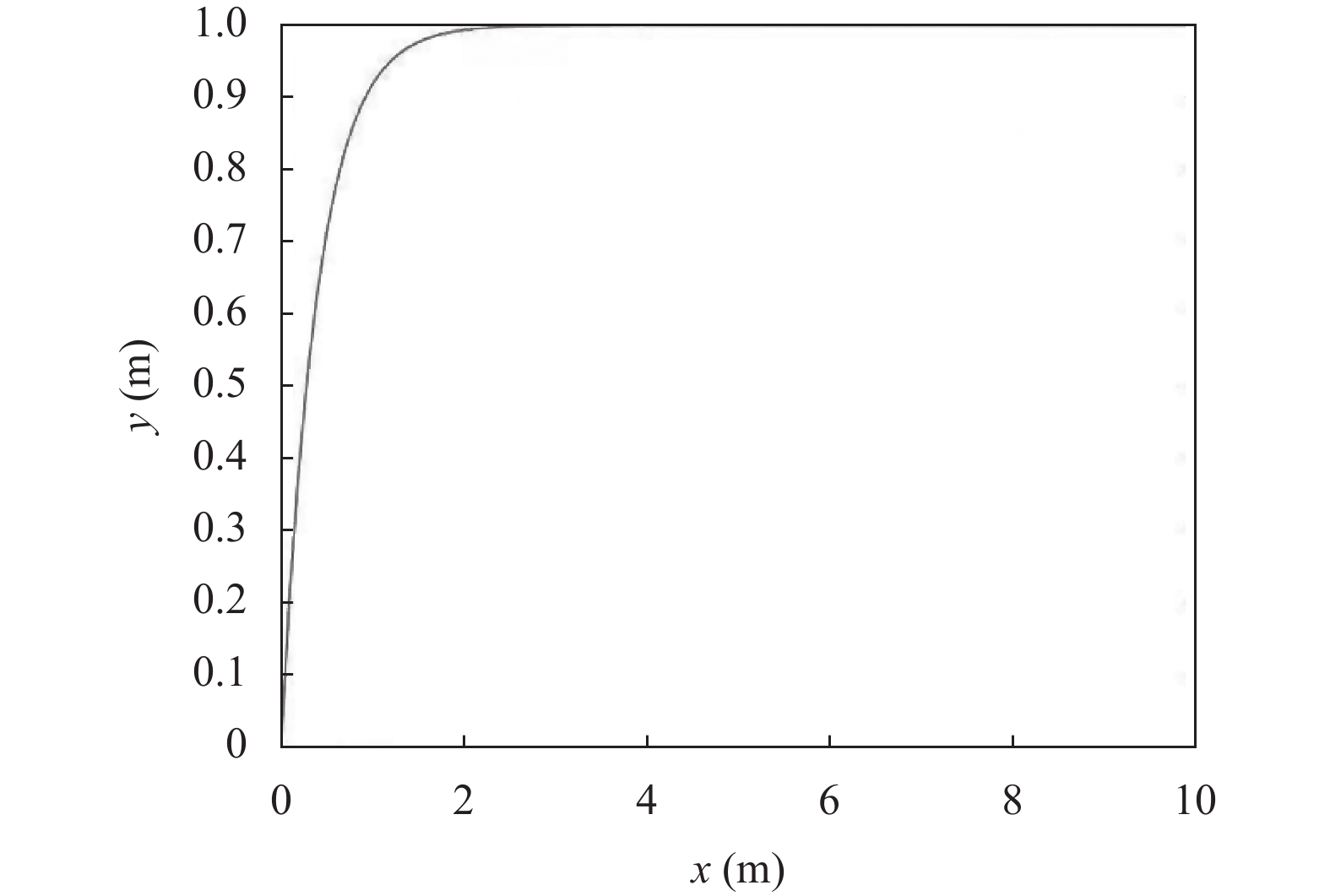
|
图 1 影响函数图 |
2.2 局部最优解问题
局部最优解问题指的是移动机器人在移动式, 在某个点出现合斥力与合引力大小相等, 方向相反的情况, 导致机器人停止在原地.
针对局部最优解问题, 本文采用传统人工势场法与模拟退火法相结合的方法进行解决. 由于移动机器人的两个力处在平衡状态, 这时通过模拟退火法在机器人周围随机产生一个虚拟目标点, 通过虚拟目标点给机器人增加新的引力, 从而打破机器人在移动过程中的平衡状态, 移动机器人能够顺利到达目标点. 如果当前点的合势场大于下一点的合势场, 则算法可以接受这一“真正”的点, 反之算法则需要根据Metropolis抽样准则进行选择. Metropolis抽样准则通常表示为:
| $ p = \left\{ {\begin{array}{*{20}{l}} {\exp \left( - \dfrac{{E({X_{n + 1}}) - E({X_n})}}{T}\right) , \; E({X_{n + 1}}) \geqslant E({X_n})} \\ {1, \qquad\qquad\qquad\qquad\quad\;\;\; E({X_{n + 1}}) \lt E({X_n})} \end{array}} \right. $ | (9) |
模拟退火算法[16]来源于固体退火的原理, 物体从高温到冷却, 接着慢慢达到一个稳定的状态. 高温时, 内部粒子内能大, 粒子可能在固体内部的任何地方活动; 当温度慢慢冷却, 粒子内能减少, 活跃度降低, 活动范围慢慢减小; 当固体冷却完毕或者达到平衡稳定, 粒子的位置就固定, 就可以获取最优解.
本文针对局部最优解算法流程如图2.
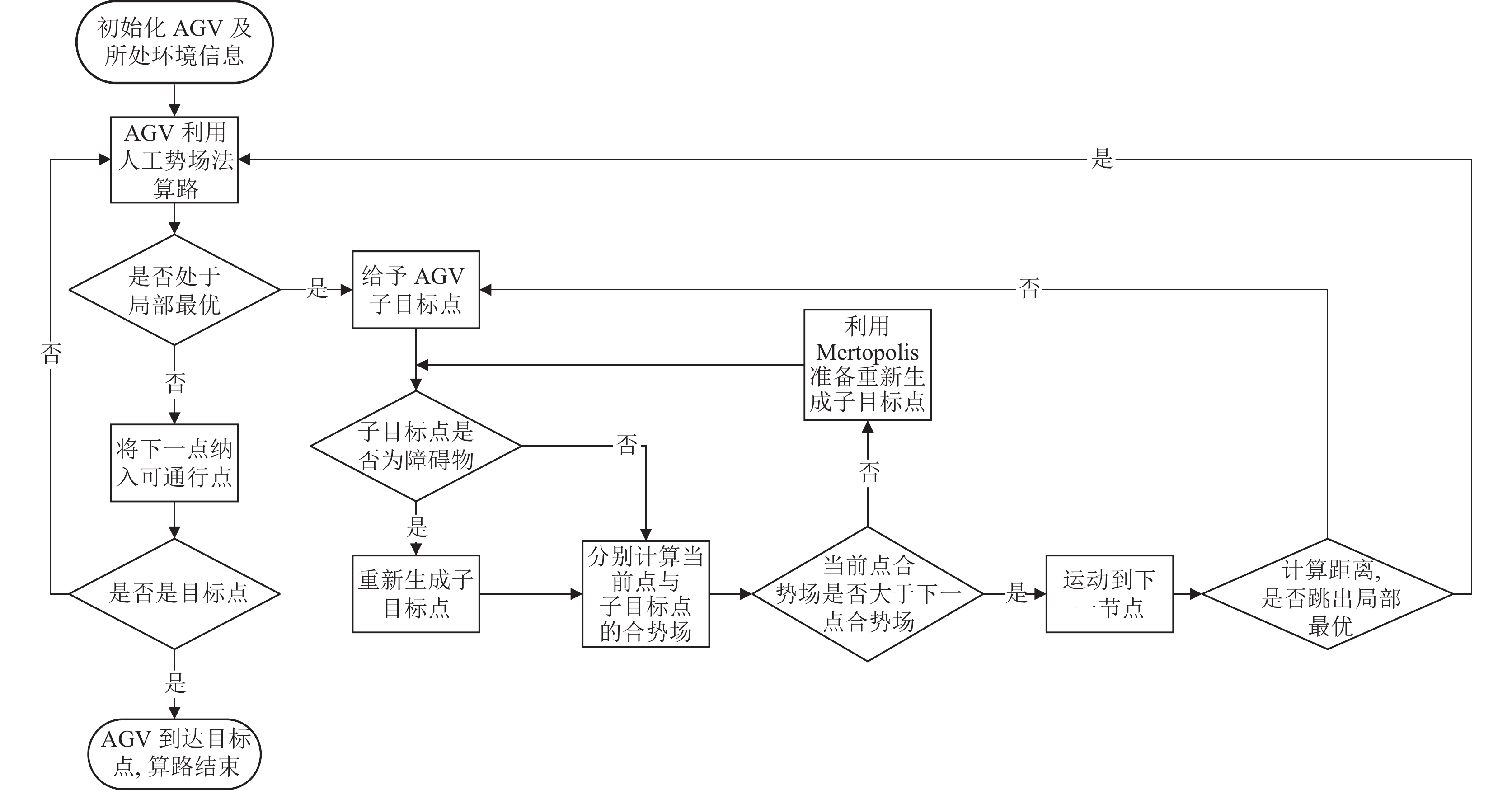
|
图 2 解决局部最优解算法流程图 |
3 仿真实验
表1为本文算法中的参数配置表.
| 表 1 改进算法的参数配置表 |
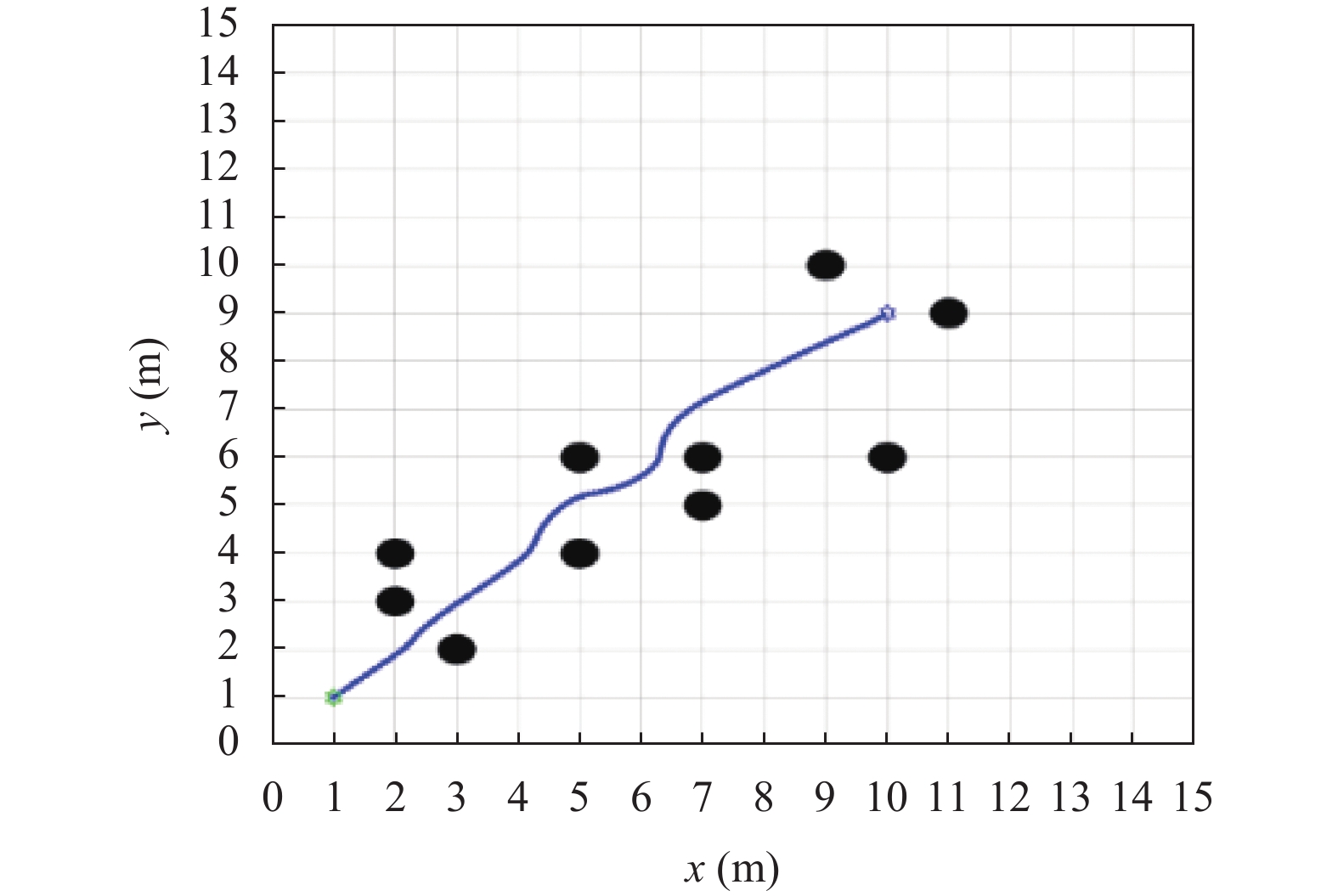
本文对传统人工势场法的目标不可达以及局部最优解进行仿真及实现, 机器人出发点和目标点分别在(1, 1)与(10, 9)处, 线条表示路径. 当障碍物位于目标点附近时, 目标点周围存在不可“翻越”的势场高点, 此时机器人会在目标周围产生多次航向震荡, 并且无法到达目标点, 即目标不可达问题(见图3). 本文针对障碍物斥力势场函数进行改进, 添加斥力势场函数影响因子, 当进入障碍物影响范围2 m内会出现斥力势场函数时, 以指数函数递减形式进行递减, 从而能够解决目标不可达问题(见图4). 当在行驶过程中, 机器人受到的引力和斥力大小相等方向相反, 此时即局部最优点(见图5). 针对传统人工势场法中的局部最优解问题, 本文将模拟退火法与人工势场法相结合, 当处在局部最优解的时候, 根据模拟退火法算法原理, 会在机器人附近增加虚拟点, 通过虚拟点给予机器人一个新的引力, 从而帮助其打破在局部最优解的平衡状态, 使其走出局部最优解(见图6).

|
图 3 传统人工势场法目标不可达 |
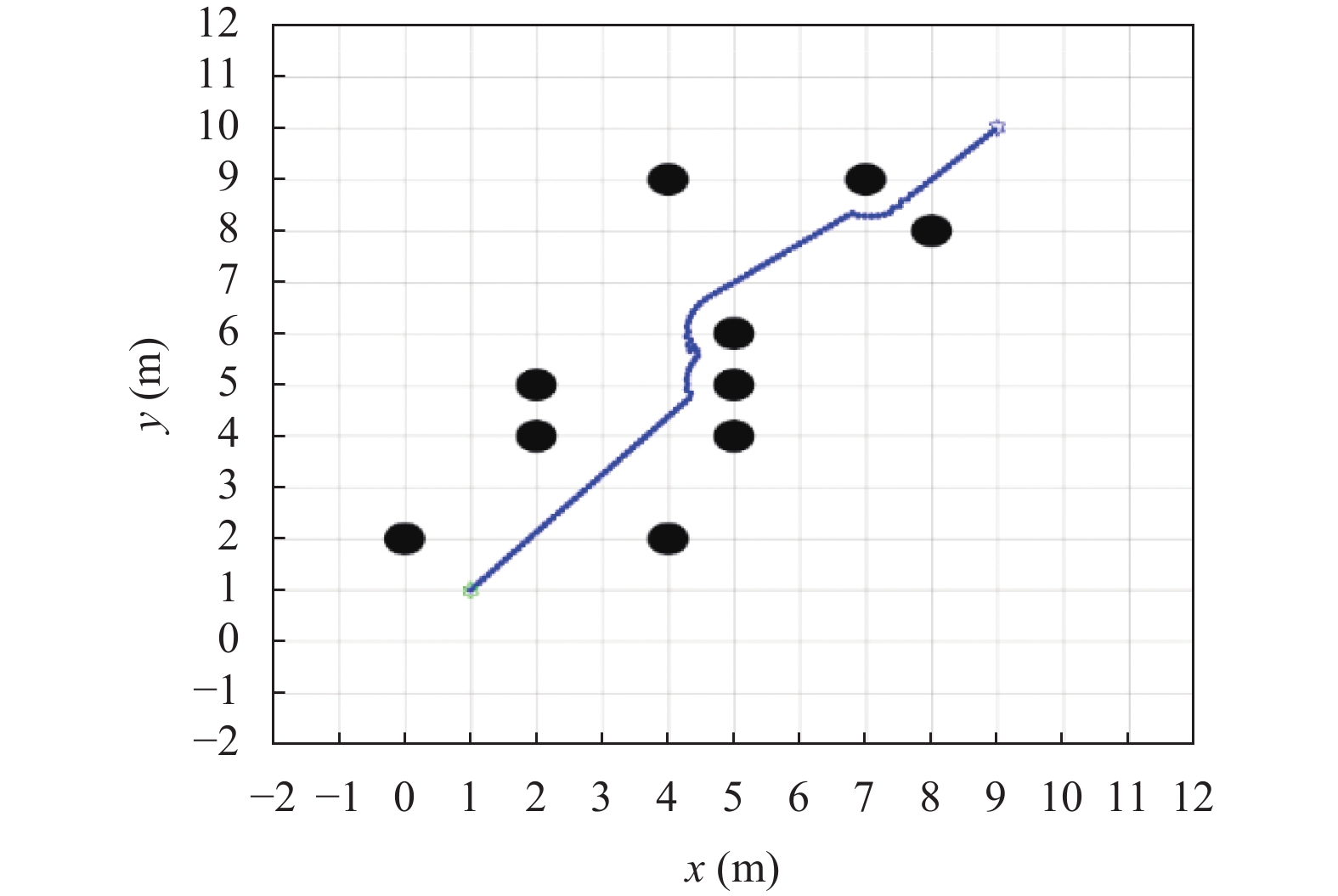
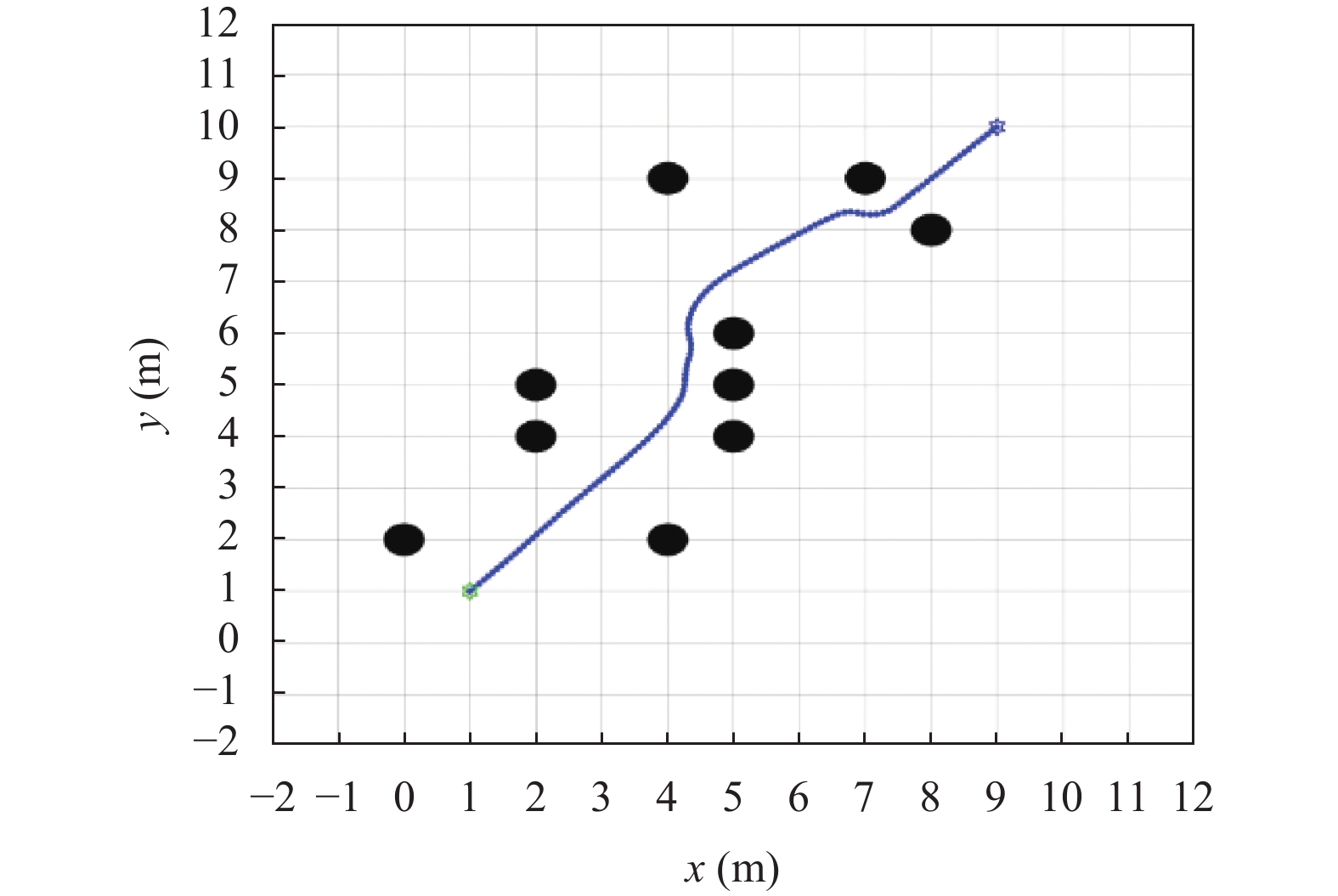
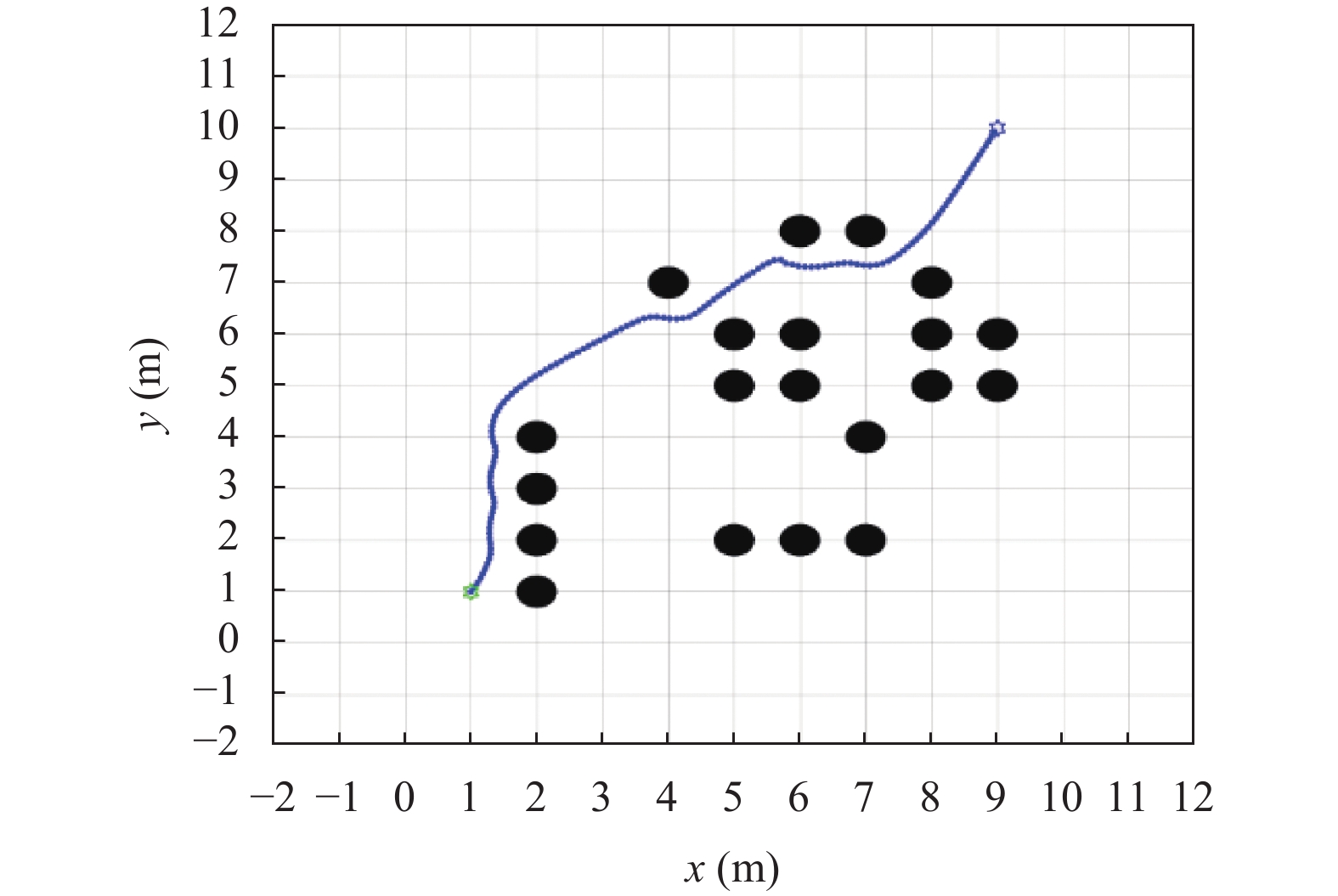
本文选取文献[17]与本文算法进行在10个障碍物与20个障碍物的地图中进行仿真, 在图7中, 可以看出机器人在行驶过程中在障碍物附近出现震荡, 整条运行轨迹不够平滑. 在对比图8中可以看出机器人在障碍物前方没有发生震荡, 并且行驶轨迹与障碍物还有一定安全距离. 在图9中, 可以看出机器人在行驶过程中多次在障碍物附近出现震荡, 即将触碰到障碍物, 增加了危险系数. 整条运行轨迹不够平滑. 在对比图10中可以看出机器人行驶路径相对平滑, 并且行驶轨迹与障碍物还有一定安全距离.
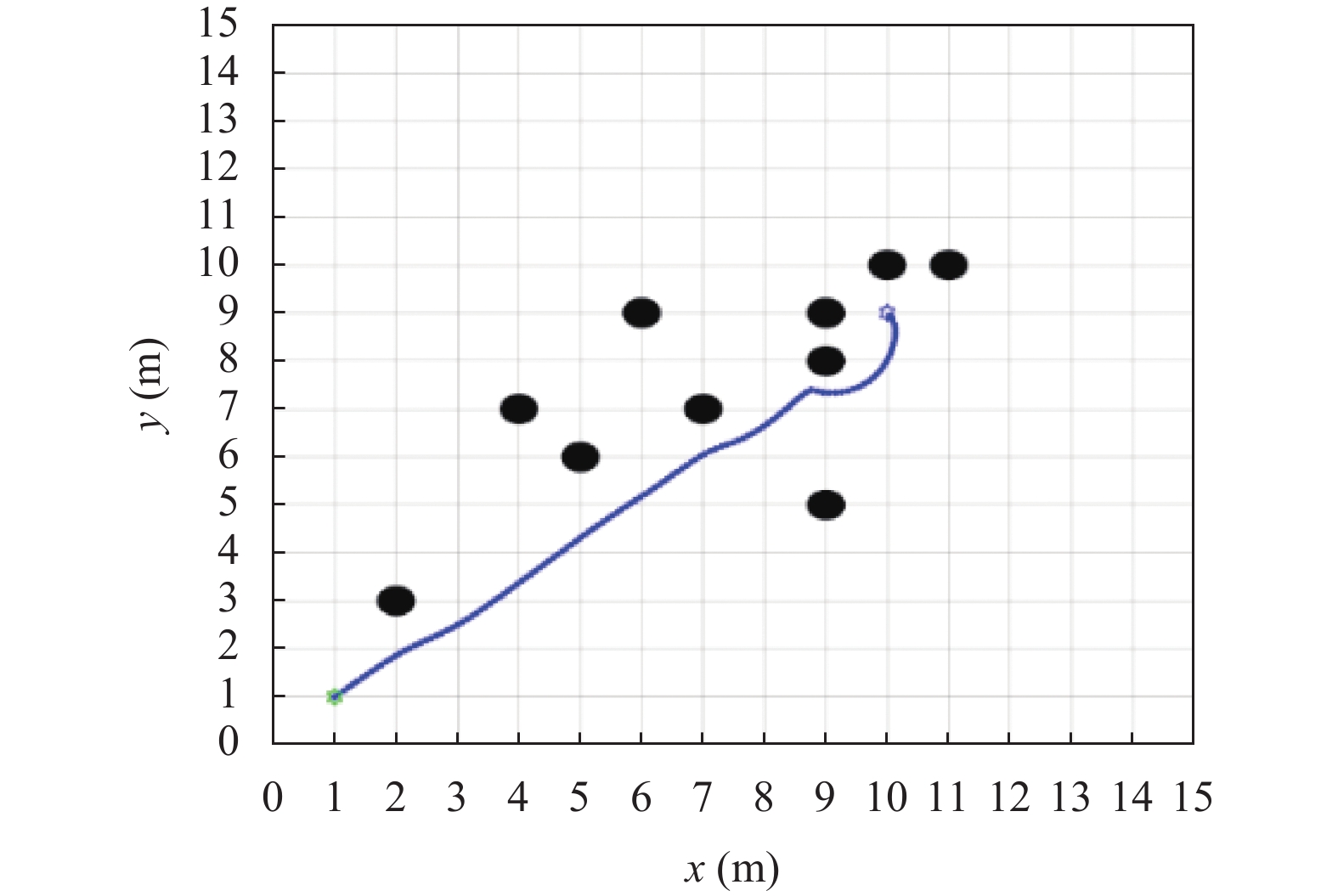
|
图 4 改进算法后的目标不可达 |
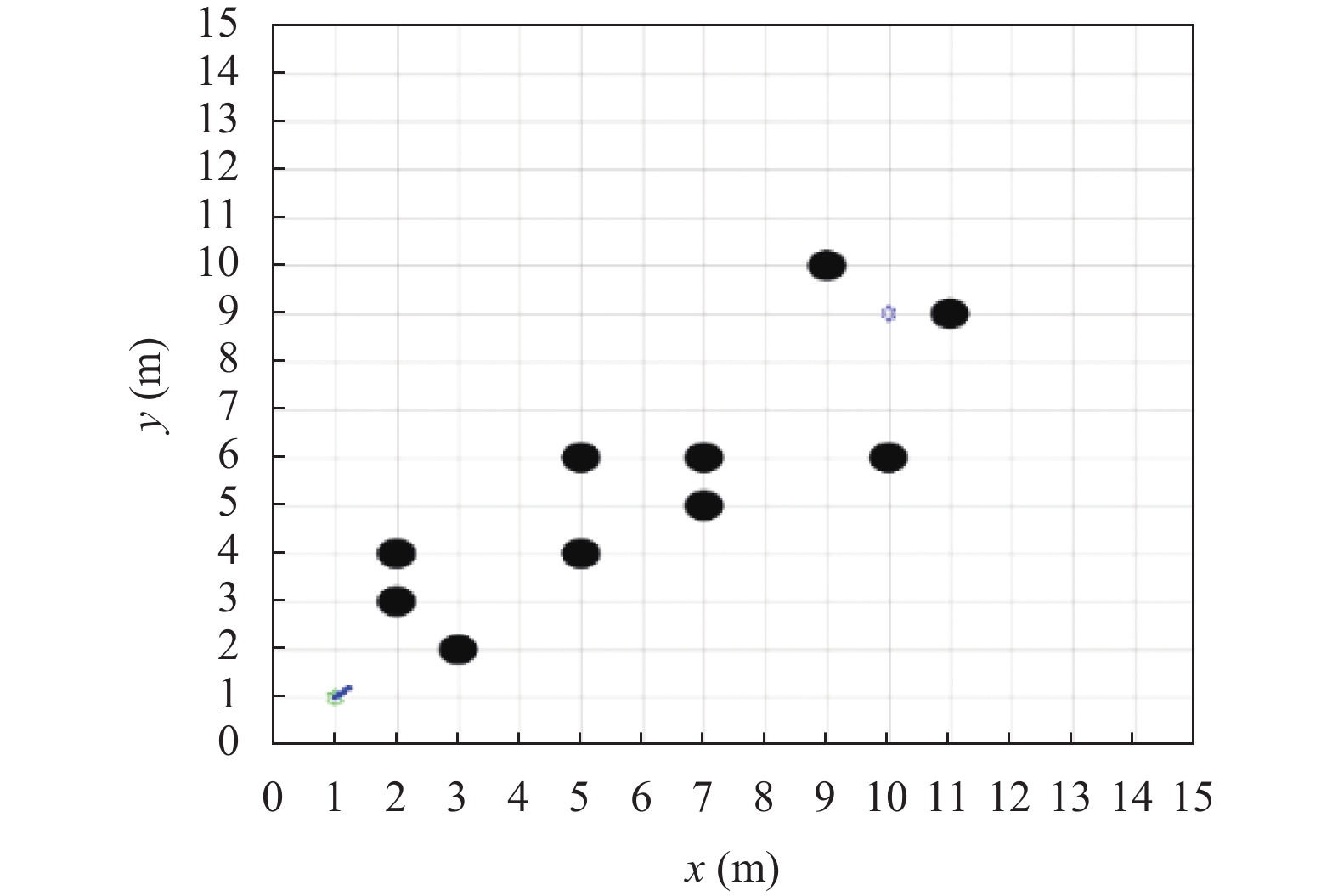
|
图 5 传统人工势场法局部最优解 |
|
图 6 改进算法后的局部最优解仿真图 |
|
图 7 10个障碍物地图文献[17]算法路径 |
|
图 8 10个障碍物地图本文改进算法路径 |

|
图 9 20个障碍物地图文献[17]算法路径 |
本文选取文献[17]中的改进人工势场法, 虽然该算法成功解决传统人工势场法中的目标不可达及局部最优值的问题, 但是在与本文算法比较时出现路径抖动、行驶时间较久和行驶路径距离较长等问题, 同时在设计斥力函数时, 本文充分考虑移动机器人的大小. 在4次实验后的算法对比图中显示, 如表2所示. 本文算法在10个障碍物中比文献[17]中算法的行驶时间提升6.70%, 路径长度减少9.20%. 本文算法在20个障碍物中比文献[17]中算法的行驶时间提升9.10%, 路径长度减少12.10%.
|
图 10 20个障碍物地图改进算法路径 |
| 表 2 算法对比 |
4 结论与展望
人工势场法作为移动机器人路径规划中的经典算法, 其本身非常适用于移动机器人的局部路径规划, 但由于其算法本身存在较多的局限性, 会导致移动机器人在路径规划中出现问题. 本文主要针对人工势场法在路径规划中的问题, 通过改进传统人工势场法中斥力势场函数并且结合模拟退火算法, 最终利用Matlab 仿真软件对改进优化后的算法进行验证. 可以看出本文算法相对于传统人工势场法在路径规划中具有良好效果.
| [1] |
Zhou JH, Zhou JQ, Zheng YS, et al. Research on path planning algorithm of intelligent mowing robot used in large airport lawn. Proceedings of the 2016 International Conference on Information System and Artificial Intelligence. Hong Kong: IEEE, 2016. 375–379.
|
| [2] |
金鑫. AGV小车的发展现状与应用趋势. 北京工业职业技术学院学报, 2021, 20(1): 10-13. DOI:10.3969/j.issn.1671-6558.2021.01.003 |
| [3] |
张雷. 移动机器人(AGV/AMR)行业: 繁荣发展, 融合创新. 物流技术与应用, 2022, 27(4): 63-65. DOI:10.3969/j.issn.1007-1059.2022.04.003 |
| [4] |
李全勇, 李波, 张瑞, 等. 基于改进Dijkstra算法的AGV路径规划研究. 机械工程与自动化, 2021(1): 23-25, 28. DOI:10.3969/j.issn.1672-6413.2021.01.008 |
| [5] |
孔慧芳, 盛阳. 基于改进A*算法的AGV路径规划研究
. 现代制造工程, 2021(10): 60-64. |
| [6] |
岳春擂, 黄俊, 邓乐乐. 改进蚁群算法在AGV路径规划上的研究. 计算机工程与设计, 2022, 43(9): 2533-2541. DOI:10.16208/j.issn1000-7024.2022.09.018 |
| [7] |
牛秦玉, 李美凡, 赵勇. 改进人工势场法的AGV路径规划算法研究. 机床与液压, 2022, 50(17): 19-24. |
| [8] |
朱蟋蟋, 孙兵, 朱大奇. 基于改进D*算法的AUV三维动态路径规划
. 控制工程, 2021, 28(4): 736-743. |
| [9] |
胡兵, 向凤红, 毛剑琳. 基于改进RRT算法的AGV路径规划研究. 软件导刊, 2018, 17(3): 28-31. |
| [10] |
翟丽, 张雪莹, 张闲, 等. 基于势场法的无人车局部动态避障路径规划算法. 北京理工大学学报, 2022, 42(7): 696-705. |
| [11] |
Abdalla TY, Abed AA, Ahmed AA. Mobile robot navigation using PSO-optimized fuzzy artificial potential field with fuzzy control. Journal of Intelligent & Fuzzy Systems, 2017, 32(6): 3893–3908.
|
| [12] |
Siming W, Tiantian Z, Weijie L. Mobile robot path planning based on improved artificial potential field method. Proceedings of the 2018 IEEE International Conference of Intelligent Robotic and Control Engineering (IRCE). Lanzhou: IEEE, 2018. 29–33.
|
| [13] |
徐小强, 王明勇, 冒燕. 基于改进人工势场法的移动机器人路径规划. 计算机应用, 2020, 40(12): 3508-3512. DOI:10.11772/j.issn.1001-9081.2020050640 |
| [14] |
郑来芳, 欧阳明华. 基于人工势场的风管机器人避障方法. 电子测量技术, 2018, 41(19): 18–21.
|
| [15] |
Khatib O. Real-time obstacle avoidance for manipulators and mobile robots. Autonomous Robot Vehicles. New York: Springer, 1986. 396–404.
|
| [16] |
杨士林. 基于改进人工势场法的移动机器人路径规划研究[硕士学位论文]. 佛山: 佛山科学技术学院, 2020.
|
| [17] |
何乃峰, 宿一凡, 刘子弘, 等. 基于改进人工势场法的移动机器人路径规划算法研究. 现代制造技术与装备, 2020, 56(12): 1-3. DOI:10.3969/j.issn.1673-5587.2020.12.003 |
 2023, Vol. 32
2023, Vol. 32


