基于自注意力机制的亲属关系识别

引用本文

李德财, 蒋行国, 何李, 李嘉莉. 基于自注意力机制的亲属关系识别. 计算机系统应用, 2023, 32(9): 89-96.http://www.c-s-a.org.cn/1003-3254/9205.html

Li DC, Jiang XG, He L, Li JL. Kinship Recognition Based on Self-attention Mechanism. Computer Systems and Applications, 2023, 32(9): 89-96(in Chinese).http://www.c-s-a.org.cn/1003-3254/9205.html

基于自注意力机制的亲属关系识别

李德财^1,2, 蒋行国^1,2, 何李^1,2, 李嘉莉^1,2

1. 四川轻化工大学自动化与信息工程学院, 宜宾 643002;
2. 人工智能四川省重点实验室, 宜宾 644002

收稿日期：2022-12-21; 修改日期：2023-01-09; 采用时间：2023-03-22; csa 在线出版时间：2023-07-14

基金项目：四川理工学院科研基金(2019RC12); 四川省人工智能重点实验室开放基金(2020RZJ03)

通讯作者：蒋行国, E-mail: tonny_jiang@suse.edu.cn.

摘要：目前, 基于局部注意力机制的卷积神经网络(CNNs)用于亲属关系识别特征提取获得了不错的效果, 但基于卷积神经网络的主干模型提升不明显, 同时鲜有研究者使用具有全局信息捕获能力的自注意机制. 因此, 提出使用基于一种无卷积主干特征提取网络的S-ViT模型, 即用具有自全局注意力机制的Vision Transformer作为基础主干特征提取网络, 通过构建孪生网络与具有局部注意力机制的CNN相结合, 扩大传统分类网络, 用于亲属关系识别相关问题的研究. 最终实验结果表明, 相比RFIW2020挑战赛领先的方法, 所提出的方法在亲属关系识别3个任务上获得了良好的效果, 第1个任务中获得了76.8%验证精度排名第二, 第2个和第3个任务中排名第三, 证明了该方法的可行性和有效性, 为亲属关系识别提出了一种新的解决方法.

关键词: 亲属关系识别自注意机制 Vision Transformer 卷积神经网络深度学习

Kinship Recognition Based on Self-attention Mechanism

LI De-Cai^1,2, JIANG Xing-Guo^1,2, HE Li^1,2, LI Jia-Li^1,2

1. School of Automation and Information Engineering, Sichuan University of Science & Engineering, Yibin 643002, China;
2. Sichuan Key Laboratory of Artificial Intelligence, Yibin 644002, China

Abstract: At present, convolutional neural networks (CNNs) based on local attention mechanism have yielded sound results in feature extraction of kinship recognition. However, the improvement of backbone models based on CNNs is not obvious, and few researchers employ self-attention mechanisms with global information capture ability. Therefore, an S-ViT model based on a convolution-free backbone feature extraction network is proposed, which is to adopt Vision Transformer with a self-global attention mechanism as the basic backbone feature extraction network. By constructing a twin network and a CNN with a local attention mechanism, the traditional classification network is expanded for research on related issues of kinship recognition. The final experimental results show that compared with the leading method of the RFIW2020 Challenge, the proposed method has performed well in the three kinship recognition tasks. The first task ranks second with verification accuracy of 76.8%, and the second and third tasks rank third. As a result, the feasibility and effectiveness of the method are improved to propose a new solution to kinship recognition.

Key words: kinship recognition self-attention mechanism Vision Transformer convolutional neural network (CNN) deep learning

1 引言

亲属关系识别是计算机视觉领域的一个新研究课题, 对于许多现实的应用(如亲属关系验证、自动照片管理、社交媒体应用等)至关重要. 目前, 亲属关系识别可以分为3个任务.

1) 亲属关系验证: 用于预测给定的两幅人脸图像之间是否具有亲属关系, 属于二分类问题.

2) 三主体验证: 用于确定一个孩子是否与一对父母有关.

3) 查询和检索: 目标是在图库中查找搜索对象的家庭成员, 该任务模拟了失踪人员的查找.

基于深度学习的方法^[1], 是当前研究亲属关系识别的热点, 通过自动从图像中学习、理解和构建深度特征, 并对深度特征进行分析, 从而得到亲属关系识别结果. 目前, 卷积神经网络(convolutional neural network, CNN)用于特征提取在计算机视觉领域取得了令人瞩目的成功^[2]. 基于深度学习的人脸亲属识别方法, 大多数使用具有局部注意力机制的CNN作为特征提取主干网络, 围绕着VGGFace-ResNet50架构和一些CNN网络来构建网络模型. 在亲属关系数据集FIW^[3]上, 亲属关系验证精度能达到80%^[4], 要在实际生活中使用亲属关系识别算法, 目前的验证精度还有待提高. 具有局部注意力机制的CNN虽然能很好地提取人脸图像高频分量(如边缘, 轮廓), 但对图像低频分量的全局语义信息关注较少. 在2020年, 有学者提出Vision Transformer (ViT)^[5]把自然语言处理领域大热的Transformer应用到计算机视觉领域. ViT主要特点是具有全局注意力机制, 能很好地捕获全局语义信息, 在图像分类任务上取得了很好的效果. 在亲属关系识别上, 卷积神经网络对亲属特征识别精度提升不太明显, 同时, 很少有研究者使用具有全局自注意力机制的ViT模型作为主干特征提取网络.

综上所述, 为拓宽用于亲属关系识别组合模型的基础分类网络, 本文提出一种基于无卷积ViT基础分类网络的S-ViT模型. 与传统使用的CNN模型相比, 结合自注意力机制作为特征提取主干网络预测结果的方式不同, S-ViT模型使用了具有自注意力机制的ViT网络, 使得模型可以并行化训练, 而且能够拥有捕获全局信息的能力, 更好的提取亲属人脸图像语义信息. 当与具有局部注意力机制的CNN组合成一个集成分类网络时, 能够更全面的提取亲属关系特征. 实验结果能够表明这种方法的可行性和有效性, 扩大了亲属关系识别传统基础分类网络的选择范围.

2 具有自注意力机制的PCPVT特征提取主干网络

Chu等人^[6]提出了两种新的ViT架构, PCPVT是其中的一种. PCPVT特征提取主干网络架构图如图1所示, PCPVT通过将CPVT^[7]中提出的条件位置编码(conditional positional encodings, CPE)取代PVT^[8]中的位置编码, CPE通过位置编码生成器(position encoding generator, PEG)得到, 把PEG模块放在每一个stage的第1个encoder.

在PVT中, stage i中的Transformer编码器有L_i个编码器层, 每个编码器层由注意力层和前馈网络层组成. 传统自注意机制详情如图2所示.

图 1 PCPVT网络架构图

PVT因其将传统的多头注意力层^[5]替换成了空间缩减注意力(spatial-reduce attention, SRA)层而更易于训练. 这个新设计的SRA层执行类似于多头注意力, 它接收一个查询 $ Q $ 、一个键 $ K $ 和一个值 $ V $ 作为输入, 并输出特性. 然而, SRA在注意力操作之前降低了 $ K $ 和 $ V $ 的空间尺度, 以减少计算开销.SRA的详细表述如下所示:

$ {Reduce} (x) = {Norm} \left( {{Reshape} \left( {x, {R_i}} \right){W^S}} \right) $

(1)

式(1)描述了如何对输入序列进行空间还原. 式中, $ x $ 表示一个输入序列, $ R $ 表示缩减比例, $ W $ 是对输入序列降维的线性投影, 将输入 $ x $ 调整大小为 $ \dfrac{{HW}}{{{R^2}}} \times \left( {{R^2}C} \right) $ .

$ {Attention} (Q, K, V) = {\textit{Softmax}} \left( {\frac{{Q{K^{\rm{T}}}}}{{\sqrt {{d_{{\text{head }}}}} }}} \right)V $

(2)

$ \begin{gathered} {{ head}_j} = {{ Attention (}}Q{W^Q}, {Reduce} (K){W^K}, {Reduce} (V){W^V}{\text{)}} \end{gathered} $

(3)

$ \begin{gathered} {\textit{SRA}} (Q, K, V) = {\text{ }} {{Concat }}\left( {{{ hea}}{{{d}}_0}, \cdots , {{ hea}}{{{d}}_{Ni}}} \right) \end{gathered} $

(4)

其余的计算与原始的多头注意力相同. 首先利用Attention计算序列的两个元素与其各自的 $ Q $ 和 $ K $ 之间的两两相似度. $ {W^Q} $ , ${W^K}$ , ${W^V}$ 分别是 $ Q $ , $ K $ 和 $ V $ 的线性投影参数. $ N $ 是第 $ i $ 阶段注意力层的头数. 然后, 计算出每个头部的注意力分数后串联起来用于最终的SRA输出. 因此, SRA是一种简单但有效的注意力层, 能够处理高分辨率的特征图, 同时降低计算和内存成本. PVT的最终输出是一个特征向量, 可以输入到Siamese网络中, 用于亲属关系验证的下游任务.

图 2 传统自注意机制详情

另外在最后一个stage用全局平均池化(GAP)代替一般Transformer使用的class token. 由于条件位置编码CPE支持输入可变长度, 使得PCPVT能够灵活处理来自不同空间尺度的特征. PCPVT所有层都利用具有全局信息捕获能力的自注意力机制, 同时依靠空间缩减降低处理整个序列的计算成本. 最终, PCPVT输出一个特征向量送入孪生神经网络, 用于亲属关系识别的后续任务.

3 基于自注意力机制的S-ViT亲属关系识别方法 3.1 S-ViT模型

如图3所示, 本文提出一个基于具有自注意力机制的PCPVT孪生结构网络模型, 为便于叙述, 简称为S-ViT. 本文提出使用孪生神经网络来构建模型. Bromley等人^[9]在1994年首次引入了孪生神经网络, 对于把特征比较应用于更复杂的数据样本, 并且特征具有不同的维度和类型, 可能需要在处理之前进行压缩, 那么这些度量是不合适的. 在这些情况下, 孪生神经网络可能是最好的选择: 它由两个相同的神经网络组成, 每个神经网络都能够学习输入向量的隐藏表示. 这两个神经网络都是前馈感知器, 在训练过程中采用误差反向传播; 它们并行串联工作, 并在最后比较它们的输出. 孪生神经网络执行生成的输出可以被认为是两个输入向量的投影表示之间的语义相似性. 在图3中, 首先使用PCPVT特征提取孪生主干网络为每张人脸图像提取特征, 图像被编码为固定长度的向量, PCPVT参数设置如表1所示. 然后, 将转换后的特征连接起来并将其送入全连接层.

在特征连接阶段, 需要对特征进行相应转换, 以提高辨别力.

1)使用特征融合提高网络的非线性能力. 特征融合的本质是对两个输入的人脸特征进行抽象编码, 有利于全连接网络学习更好的相似度指标. 设 $ x $ 和 $ y $ 表示提取的两个人脸的特征, 特征融合方式有 $ x+y\mathrm{、}x-y\mathrm{、} x\cdot y\mathrm{、}1/2(x+y) $ 这4种, 而S-ViT主干特征提取网络输入为224×224大小的一对人脸图像, 对输出两组特征向量通过feature fusion模块进行融合, 得到的4组融合特征.

2)将4组融合特征拼接成一个长向量送入全连接网络(full connection, FC), 该FC由3个全连接层、两个ReLU激活函数和一个Sigmoid激活层构成. 为了减少FC层计算量, S-ViT网络模型对第1层使用全局平局池化(global max pooling, GMP)得到第2层全连接网络, 然后再通过全连接得到32个神经元的第3层网络.

3)通过Sigmoid函数激活得到相似度评分, 以判断人脸图像对是否有亲属关系.

图 3 S-ViT模型架构

表 1 PCPVT特征提取主干网络配置细节

Stage	Output size	Layer name	PCPVT
Stage 1	$ \dfrac{H}{4}\times \dfrac{W}{4} $	Patch embedding	$ {P}_{1} $ =4; $ {C}_{1} $ =64
Stage 1	$ \dfrac{H}{4}\times \dfrac{W}{4} $	Transformer encoder with PEG	$ \left[ {\begin{array}{*{20}{l}} {{R_1} = 8} \\ {{N_1} = 1} \\ {{E_1} = 8} \end{array}} \right] \times 3 $
Stage 2	$ \dfrac{H}{8}\times \dfrac{W}{8} $	Patch embedding	$ {P}_{2} $ =2; $ {C}_{2} $ =128
Stage 2	$ \dfrac{H}{8}\times \dfrac{W}{8} $	Transformer encoder with PEG	$ \left[ {\begin{array}{*{20}{l}} {{R_{\text{2}}} = {\text{4}}} \\ {{N_{\text{2}}} = {\text{2}}} \\ {{E_{\text{2}}} = {\text{8}}} \end{array}} \right] \times 3 $
Stage 3	$ \dfrac{H}{16}\times \dfrac{W}{16} $	Patch embedding	$ {P}_{3} $ =2; $ {C}_{3} $ =320
Stage 3	$ \dfrac{H}{16}\times \dfrac{W}{16} $	Transformer encoder with PEG	$ \left[ {\begin{array}{*{20}{l}} {{R_{\text{3}}} = {\text{2}}} \\ {{N_{\text{3}}} = {\text{5}}} \\ {{E_{\text{3}}} = {\text{4}}} \end{array}} \right] \times {\text{6}} $
Stage 4	$ \dfrac{H}{32}\times \dfrac{W}{32} $	Patch embedding	$ {P}_{4} $ =2; $ {C}_{4} $ =512
Stage 4	$ \dfrac{H}{32}\times \dfrac{W}{32} $	Transformer encoder with PEG	$ \left[ {\begin{array}{*{20}{l}} {{R_{\text{4}}} = {\text{1}}} \\ {{N_{\text{4}}} = {\text{8}}} \\ {{E_{\text{4}}} = {\text{4}}} \end{array}} \right] \times 3 $

表 1 PCPVT特征提取主干网络配置细节

为使S-ViT网络模型获得更好的性能, 采用在ImageNet数据集^[10]上经过预训练的PCPVT特征提取主干网络来构建孪生网络, ImageNet数据集包含1000个类别, 14197122张图片. 数据依赖是深度学习中最严重的问题之一^[11], 因为它需要大量的数据来理解数据的潜在模式. 迁移学习(预训练模型)不需要训练数据和测试数据是独立同分布的, 目标域中的模型也不需要从头开始训练, 可以显著减少目标域对训练数据的需求和训练时间. 迁移学习旨在通过迁移不同但相关的源域中包含的知识来提高目标学习者在目标域上的表现, 这样可以减少构建目标学习器对大量目标域数据的依赖. 预训练模型能够获得人脸更多的语义信息, 更好地提取亲属人脸信息, 并且能够极大加快模型的训练速度.

3.2 损失函数

Softmax函数主要用于解决多分类问题, Softmax所获得的结果代表输入图像被分到每一类的概率. Softmax loss是Softmax和cross-entropy loss^[12]组合而成的损失函数, Softmax loss把正确类别对应的输出Softmax值最大化.

本文提出把Softmax损失与中心损失(center loss)^[13]进行联合监督学习, 这种方式能更好的收敛, 在增大类间距离的同时减小类内距离, 使网络模型获得的特征具有更强的鉴别能力. 联合Softmax损失与中心损失(center loss)函数如式(5)所示:

$ L = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\log } \frac{{{{\rm{e}}^{W_{y(i)}^{\rm{T}}x(i)}}}}{{\displaystyle\sum\limits_{l - 1}^k {{{\rm{e}}^{^{W_l^{\rm{T}}x(i)}}}} }}} \right] + \frac{\lambda }{2}\sum\limits_{i = 1}^m {\left\| {{x_i} - {c_{{y_i}}}} \right\|_2^2} $

(5)

其中, $ m $ 表示样本个数, $ w $ 为网络模型权重, $ {x_i} $ 表示第 $ i $ 张图片特征值, $ {y_i} $ 表示第 $ i $ 类, $ {c_{{y_i}}} $ 表示该第 $ i $ 张图片所属分类特征值的中心. $ \lambda $ 用来平衡2个损失函数, 合适的 $ \lambda $ 选择有助于增强网络的特征鉴别能力, 当 $ \lambda $ =0时, 训练网络时仅有Softmax损失监督学习.

4 实验与结果 4.1 实验设置与参数

实验环境为Windows 10、64位操作系统、内存16 GB、Python编程语言、TensorFlow深度学习框架、NVIDIA GeForce GTX 1650和Intel(R) Core(TM) i7-10700F CPU @ 2.90 GHz (16 CPUs). 对S-ViT特征提取主干网络预训练模型冻结全部权重, 仅训练全连接层参数. 然后, 使用学习率随着训练epoch线性下降的方法, 以防止学习率过大导致在收敛到接近全局最优点时来回震荡, 每迭代10个epoch后, 如果最大验证精度没有提升时, 学习率衰减一半. 实验参数设置如表2所示.

表 2 参数设置

4.2 实验数据集

采用目前最大、最全面的亲属识别人脸图像FIW数据集, 包含的共11种亲属关系可分为同代关系、第1代关系和第2代关系共3代. 同代关系包括兄弟(B-B)、姐妹(S-S)、兄妹(SIBS); 第1代关系包括父女(F-D)、父子(FS)、母女(M-D)、母子(MS); 第2代关系包括祖父孙女(GF-GD)、祖父孙子(GF-GS)、祖母孙女(GM-GD)、祖母孙子(GM-GS). 配偶之间不具有血缘关系, 不作为研究亲属关系的样本. 部分亲属关系人脸图片如图4所示.

4.3 结果与分析

用构建的S-ViT基线模型对FG2020挑战的3个任务进行全面的实验. 实验首先需要确定联合损失函数不同参数 $ \lambda $ 对S-ViT模型精度的影响, 结果如图5所示. 由图5可知, 一个合适的 $ \lambda $ 值有助于提高亲属关系验证精度, 参数 $ \lambda $ 的最佳结果为0.003. 同时, 从图4中也可以得到, 所提 Softmax损失和中心损失联合监督学习损失函数的亲属关系验证精度要高于仅 Softmax损失监督学习(当 $ \lambda $ =0时). $ \lambda $ =0.003时, 模型损失曲线和验证精度如图6所示, 迁移学习极大加快了模型训练速度, 模型最终获得了76.8%的验证精度.

图 4 FIW中部分亲属关系人脸图片

图 5 不同λ对应的S-ViT模型验证精度

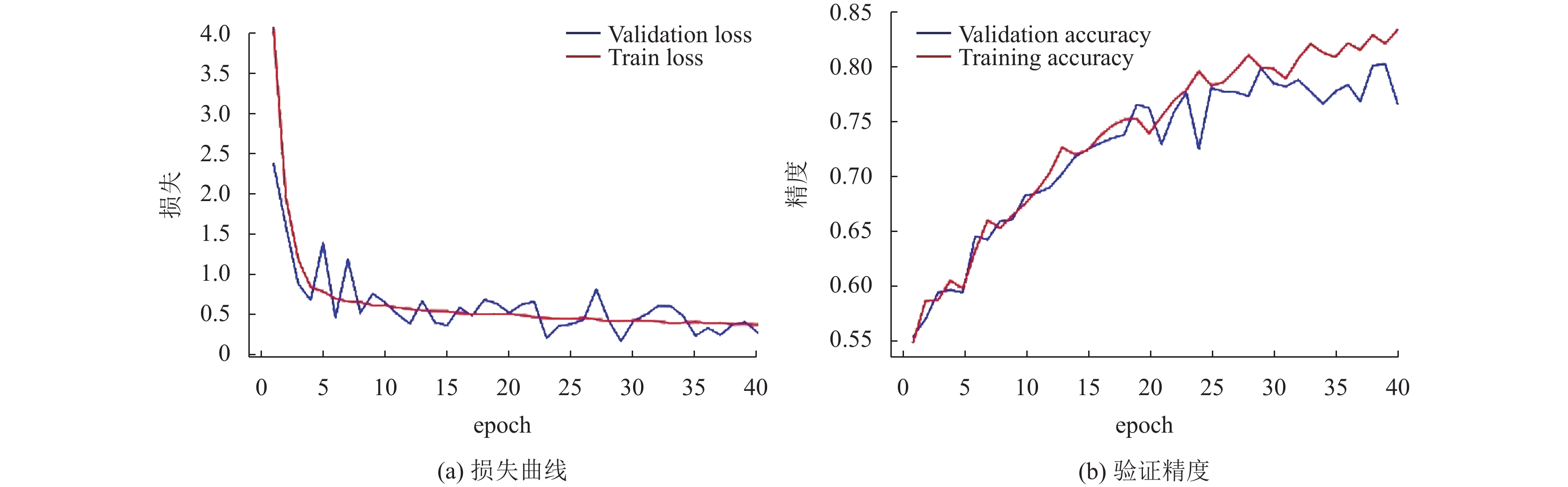
图 6 S-ViT模型损失曲线和验证精度

4.3.1 亲属关系验证和分析

为了验证S-ViT模型性能, 与FG2020挑战赛领先的方法进行对比, 结果如表3所示. 从实验结果可知, S-ViT验证精度比基线模型高14%, 并列排名第二, S-ViT方法获得不错的结果. 11种家庭关系对的验证精度折线图如图7所示, 由图7可以看出, 所提出的S-ViT方法在多数关系对验证上, 相比其他方法都能够取得较好的精度. 在GF-GS、GM-GS关系对上, 所列举的方法精度均较低, 这是因为关系对人脸图片数量较少以及年龄等因素导致的. 同时, 从实验结果可知, 所提出的基于具有全局自注意力机制的S-ViT模型获得了很好的基线精度. 另外, 在以上FG2020挑战赛领先方法中, 均采用基于卷积神经网络ResNet50或VGG作为主干特征网络来构建模型.

表 3 与FG2020挑战赛领先方法亲属关系验证精度对比

图 7 11种亲属关系对的验证精度折线图

为进一步证明所提出方法的性能, 用提出的S-ViT方法, 将常见的卷积神经网络VGG16、ResNet50和SENet50和分别作为S-ViT的主干特征提取模型, 替换PCPVT特征提取主干网络, 构建仅有CNN的网络模型. 且所有的卷积特征提取网络模型均在ImageNet上进行预训练, 构建的对比孪生网络其他参数设置与S-ViT一致. 获得的结果如表4所示. 作为基线方法, 所提出的基于自注意力机制S-ViT网络模型也获得了最好的精度, 这进一步证明了S-ViT网络的良好性能. 9种亲属关系验证方法对比如图8所示, 由此可知, 与FG2020挑战赛领先方法对比, 不同卷积主干模型所构建的孪生网络性能较差, 但所提出基于自注意力机制的S-ViT模型获得了较好的精度, 表明所提取的亲属人脸图像特征具有更强的语义信息.

表 4 不同主干特征提取网络验证精度对比(%)

图 8 9种亲属关系验证方法精度对比

4.3.2 三主体验证和分析

任务2的目标是预测一个孩子是否与一对父母有关系. 本质上, 它与任务1一样, 可以分为两个子问题, 即确定他们在“父-子”和“母-子”之间是否有亲属关系. 三主体(父母-孩子)通过S-ViT网络模型分别得到三主体特征表达, 对父亲-孩子和母亲-孩子的特征分别做余弦相似, 最后把得分求平均获得相似度得分. 如表5所示, 与FG2020挑战赛前三对比, 作为基于自注意力机制的基线方案, 所提S-ViT方法获得了令人鼓舞的评分, 获得了第3名. 其中, 在FG2020三主体验证领先方法中, 也都是采用基于卷积神经网络ResNet50或VGG作为主干特征网络来构建模型.

表 5 与FG2020三主体验证领先方法性能比较

4.3.3 亲属关系查询和检索

任务3的目标是在所有家庭人脸图片(图集)中找到搜索对象(即输入人脸图片)的家族成员, 这是一个多对多的排名问题. 通过比较全类平均正确率(mean average precision, mAP)和Rank@5正确率, 如表6所示, S-ViT网络模型获得了第3名, 这表明所提出S-ViT模型在亲属关系查询和检索任务上的可行性和有效性. 此处, 在FG2020查询和检索领先方法中, 构建网络模型采用的是卷积神经网络预训练模型.

表 6 与FG2020查询和检索领先方法性能比较

5 结论和未来的工作

本文把具有自注意力机制的Vision Transformer作为特征提取主干网络并与CNN结合起来, 为亲属关系识别挑战提出了新的集成解决方案. 实验表明, 通过自注意机制提取的特征与CNN不同, 通过与CNN结合可以更好地提取亲属关系人脸对的特征, 在亲属关系识别上获得良好的预测性能, 同时实验也验证了Vision Transformer和CNN可以产生不同的基础分类网络. 本文虽然没有对提出的S-ViT方法进行微调和消融实验验证, 但是提出的方法显示了巨大的潜力, 在FG2020挑战赛3个任务上也能排名前三.

尽管利用具有自注意力机制的PCPVT作为主干特征提取网络发挥了很好的作用, 但仍有一些特定的模块和优化在这项工作中没有考虑.

1)更多的具有自注意力机制的Vision Transformer也可以用作主干特征提取网络, 如Swin Transformer^[14]、PVT^[8]等, 同时也可以集成Vision Transformer和CNNs多种主干特征提取网络, 进一步提取更有鉴别能力的亲属关系特征.

2)除了S-ViT使用的联合损失函数外, 其他的损失函数, 如对比损失^[15]、三重损失^[16]也可能用到S-ViT中, 以便在训练中更有效地利用标签信息.

3)在特征融合阶段可以有更多选择, 如文献[17,18].

4)未对人脸图像集预处理, 如图像增强、人脸对齐等.

5) CNN的全连接层没有进行微调, 如层数、神经元个数、dropout, 优化器的选择等^[19,20].

总的来说, 具有全局信息捕获能力的自注意力机制用于亲属关系识别目前仍少. 相信未来还有许多潜在的变体需要探索, 希望提出的S-ViT模型可以作为一个参考.

参考文献

[1]	Dornaika F, Arganda-Carreras I, Serradilla O. Transfer learning and feature fusion for kinship verification. Neural Computing and Applications, 2020, 32(11): 7139-7151. DOI:10.1007/s00521-019-04201-0
[2]	Li ZW, Liu F, Yang WJ, et al. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(12): 6999-7019. DOI:10.1109/TNNLS.2021.3084827
[3]	Robinson JP, Shao M, Wu Y, et al. Visual kinship recognition of families in the wild. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(11): 2624-2637. DOI:10.1109/TPAMI.2018.2826549
[4]	Robinson JP, Qin C, Shao M, et al. The 5th recognizing families in the wild data challenge: Predicting kinship from faces. Proceedings of the 16th IEEE International Conference on Automatic Face and Gesture Recognition. Jodhpur: IEEE, 2021. 1–7.
[5]	Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16x16 words: Transformers for image recognition at scale. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
[6]	Chu XX, Tian Z, Wang YQ, et al. Twins: Revisiting the design of spatial attention in vision transformers. Proceedings of the 35th International Conference on Neural Information Processing Systems. 2021. 9355–9366.
[7]	Chu XX, Tian Z, Zhang B, et al. Conditional positional encodings for vision transformers. arXiv:2102.10882, 2021.
[8]	Wang WH, Xie EZ, Li X, et al. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 568–578.
[9]	Bromley J, Guyon I, LeCun Y, et al. Signature verification using a “Siamese” time delay neural network. Proceedings of the 6th International Conference on Neural Information Processing Systems. Denver: Morgan Kaufmann Publishers Inc., 1993. 737–744.
[10]	Deng J, Dong W, Socher R, et al. ImageNet: A large-scale hierarchical image database. Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009. 248–255.
[11]	Tan CQ, Sun FC, Kong T, et al. A survey on deep transfer learning. Proceedings of the 27th International Conference on Artificial Neural Networks. Rhodes: Springer, 2018. 270–279.
[12]	de Boer PT, Kroese DP, Mannor S, et al. A tutorial on the cross-entropy method. Annals of Operations Research, 2005, 134(1): 19-67. DOI:10.1007/s10479-005-5724-z
[13]	Wen YD, Zhang KP, Li ZF, et al. A discriminative feature learning approach for deep face recognition. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 499–515.
[14]	Liu Z, Lin YT, Cao Y, et al. Swin Transformer: Hierarchical vision transformer using shifted windows. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 10012–10022.
[15]	Khosla P, Teterwak P, Wang C, et al. Supervised contrastive learning. Proceedings of the 33rd International Conference on Neural Information Processing Systems. 2020. 18661–18673.
[16]	Hoffer E, Ailon N. Deep metric learning using triplet network. Proceedings of the 3rd International Workshop on Similarity-based Pattern Recognition. Copenhagen: Springer, 2015. 84–92.
[17]	Yu J, Li MY, Hao XL, et al. Deep fusion Siamese network for automatic kinship verification. Proceedings of the 15th IEEE International Conference on Automatic Face and Gesture Recognition. Buenos Aires: IEEE, 2020. 892–899.
[18]	Luo ZP, Zhang ZG, Xu ZY, et al. Challenge report recognizing families in the wild data challenge. Proceedings of the 15th IEEE International Conference on Automatic Face and Gesture Recognition. Buenos Aires: IEEE, 2020. 868–871.
[19]	Dahan E, Keller Y. A unified approach to kinship verification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(8): 2851-2857.
[20]	Huang JY, Strome MB, Jenkins I, et al. Solving the families in the wild kinship verification challenge by program synthesis. Proceedings of the 16th IEEE International Conference on Automatic Face and Gesture Recognition. Jodhpur: IEEE, 2021. 1–5.