1 引言

与煤炭、石油、天然气等传统能源相比, 风能具有污染低、成本少、可持续的特点, 目前已经成为新能源的主流, 并在世界范围内广泛应用. 根据全球风能理事会(GWEC)发布的最新报告^[1], 2020年全球风电装机容量达到743 GW, 新增装机同比增长53%. 然而, 对于包含风电场的电力系统来说, 风电场的随机性、波动性和间歇性, 对整个电力系统的运行控制提出了重大挑战^[2]. 风速的准确预测是电力系统运行控制的基础^[3]. 按照时间间隔, 风速预测可分为超短期(分钟)、短期(小时、天)、中期(周、月)和长期(年). 其中, 短期风速预测是制定日常调度计划必不可少的因素, 对电力系统的经济、可靠运行具有重要的影响^[4]. 目前, 风速预测技术可分为3类: 物理模型、统计模型和人工智能模型. 物理模型^[5]主要通过建立风速与气压、空气密度、空气湿度的关系完成风速预测. 该建模过程需要大量的计算, 通常用于特定区域的长期风速预测. 与物理模型相比, 统计模型简单易行, 在短期风速预测中广泛采用. 它利用历史风速数据, 建立系统输入和输出之间的线性映射关系, 进而预测风速, 如Kriging插值法^[6]和Von Mises分布^[7]等. 一些常用的统计模型方法有AR (自回归)^[8]、ARMA (自回归移动平均)^[9]等. 人工智能模型的基础是机器学习技术. 它基于大量风速时间数据, 描述系统输入和输出之间复杂的非线性关系. 例如, 文献[10]使用最小二乘支持向量机来预测风速. 最近, 随着深度学习技术的蓬勃发展, 它们也迅速应用于短期风速预测, 如CNN、循环神经网络(RNN)、门控循环单元(GRU)、LSTM等. 该类方法结合现有的风速预测技术以及混合神经网络模型取得了良好的预测结果^[11-13].

由于风速的波动性和随机性特征, 在实际应用中通常结合一定的处理方法, 获得相对平稳的子序列, 例如经验模态分解(empirical mode decomposition, EMD)^{[14, 15]}方法. 集合经验模态分解(ensemble empirical mode decomposition, EEMD)是在EMD方法上进行改进, 有效解决了EMD的混频现象^[16]. VMD方法于2014年提出^[17], 具有更好的噪声鲁棒性, 且通过收敛条件的合理控制, 其分量个数远小于EMD和EEMD, 在风速预测中取得了较好的结果^[18]. 因此, 本文采用VMD进行风速序列的分解.

目前的短期风速预测算法大多只关注时域数据, 但是目标风电场附近站点的风速数据也包含着丰富的信息, 即风速的空域数据. 基于时空相关性的数据分析已成为研究热点^{[13, 19]}, 这些算法同时考虑数据的时空特征来提高预测精度. 因此, 针对风速的时空特征, 文中提出一种基于VMD和混合时空深度学习模型的短期风速预测算法, 并取得了较好的实验结果.

本文的主要贡献如下.

1) 将VMD技术与混合时空深度学习模型CNN-LSTM-SAM相结合, 针对得到的相对稳定的子序列进行处理, 提高风速预测精度.

2) 提出的算法针对风速的时空特征进行处理, 有效利用风速的空域特征, 提高了预测精度.

本文第1节给出VMD的基本原理. 第 2 节从风速时空数据模型和CNN-LSTM-SAM混合深度学习框架两个方面叙述了文中提出的 VHSTN算法. 第3节是实验部分, 与相关算法进行比较并分析. 第4节对全文进行总结, 指出进一步的研究方向.

2 VMD原理

Dragomirestskiy等人提出的VMD是一种信号分解方法^[17], 整体框架是一个变分问题. 即假设每个“模态”是具有不同中心频率的有限带宽, 如何使每个模态的估计带宽之和最小. 为解决这一变分问题, 该方法采用了交替方向乘子法, 不断更新各模态及其中心频率, 逐步将各模态解调到相应的基频带, 最终将各个模态即相应的中心频率提取出来.

利用VMD, 可以把具有非线性和随机性的原始风速序列分解为一系列的稳定模态分量. 设预处理后的风速时空数据为 $x(i,j)_k^t$ , 这里t代表某个时刻, (i, j)代表某个站点. 具体过程如下.

1) 假定每个模式具有一个中心频率的有限带宽, 现在寻找模式, 使每个模式的估计带宽之和最小. 具体模型如下:

$ \left\{\begin{split} & \mathop {\min }\limits_{\left| {{u_k}} \right|,\left| {{\omega _k}} \right|} \sum\limits_{k = 1}^K {\left\| {{\partial _t}[\left(\delta (t) + \frac{j}{{\text{π} t}}\right)*{u_k}]{{\rm{e}}^{ - j{\omega _k}t}}} \right\|} _2^2 \\ & {\rm{s.t.}}\sum\limits_{k = 1}^K {{u_k} = \tilde X{{(t)}_l}} \end{split} \right.$

(1)

其中, $ K $ 为需要分解的模式个数(正整数), $ \{ {u_k}\} $ 、 $ \{ {\omega _k}\} $ 分别对应分解后第 $ k $ 个模式分量和中心频率, $ \delta (t) $ 为狄拉克函数, $ * $ 为卷积运算.

2) 为求解上述模型, 引入惩罚因子 $ \alpha $ (降低高斯噪声的影响)和拉格朗日乘法算子 $ \lambda $ , 将约束问题转化为非约束问题, 得到增广拉格朗日表达式:

$ \begin{split} L(\{ {u_k}\} , \{ {\omega _k}\} , \lambda ) &= \alpha \sum\limits_K {\left\| {{\partial _t}\left[\left(\delta (t) + \frac{j}{{\text{π} t}}\right)*{u_k}(t)\right] \cdot {{\rm{e}}^{ - j{\omega _k}t}}} \right\|} _2^2 \\ & + \left\| {f(t) - \sum\limits_K {{u_k}(t)} } \right\|_2^2 + \left\langle {\lambda (t)f(t) - \sum\limits_K {{u_k}(t)} } \right\rangle \end{split} $

(2)

3) 通过乘法器交替方向法迭代更新参数 $ {u_k} $ , $ {\omega _k} $ 和 $ \lambda $ . 公式如下:

$ \hat u_k^{n + 1} = \frac{{\hat f(\omega ) - \displaystyle\sum\limits_{i \ne k} {{{\hat u}_i}(\omega ) + \dfrac{{\hat \lambda (\omega )}}{2}} }}{{1 + 2\alpha {{(\omega - {\omega _k})}^2}}} $

(3)

$ \omega _k^{n + 1} = \frac{{\int_0^\infty \omega {{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}d\omega }}{{\int_0^\infty {{{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}d\omega } }} $

(4)

$ {\hat \lambda ^{n + 1}}(\omega ) = {\hat \lambda ^n}(\omega ) + \gamma (\hat f(\omega ) - \sum\limits_k {\hat u_k^{n + 1}} (\omega )) $

(5)

其中, $ \hat f(\omega ) $ 、 $ {\hat u_i}(\omega ) $ 、 $ \hat \lambda (\omega ) $ 和 $ \hat u_k^{n + 1}(\omega ) $ 表示 $ f(\omega ) $ 、 $ {u_i}(\omega ) $ 、 $ \lambda (\omega ) $ 和 $ u_k^{n + 1}(\omega ) $ 的傅立叶变换; n是迭代次数; $ \gamma $ 为噪声容忍度, 满足信号分解的保真度要求.

4) 对于给定的精度 $ e \gt 0 $ , 如果 ${\displaystyle\sum\limits_i {\left\| {\hat u_k^{n + 1} - \hat u_k^n} \right\|} _2^2} / \left\| {\hat u_k^n} \right\|_2^2 \lt e$ , 则停止迭代, 否则返回3). 最后, 可以得到 $ K $ 个分解的IMF分量, 记为 $ IMF_k^{t, l} $ .

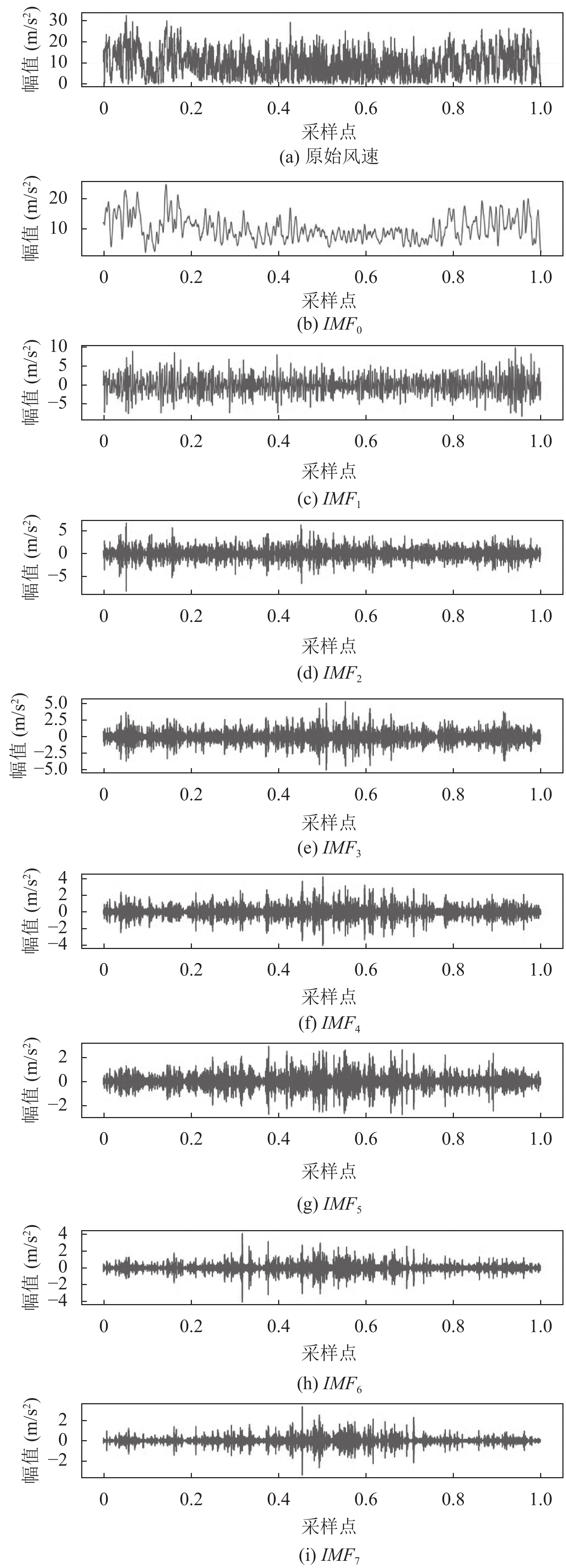
图1显示了不同频率的风速子序列 IMF分量. 主要参数设置如下: K = 8, α= 2000, γ= 0, e = 1E–7. 图1(a)是原始风速, 图1(b)–图1(i)依次为IMF₀到IMF₇, 共8个分量.

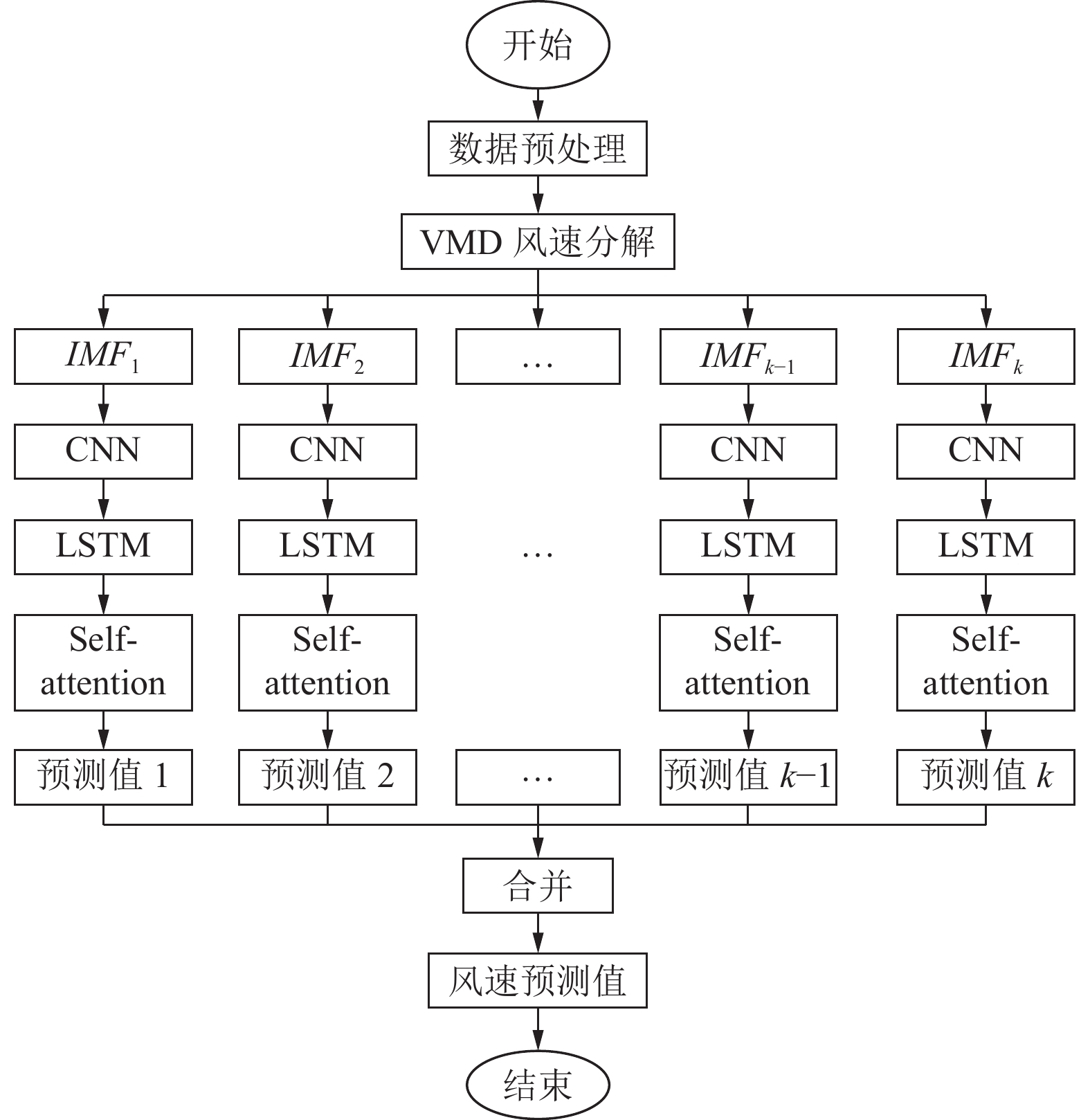
3 VHSTN算法描述

VHSTN算法首先对原始数据进行数据清洗的预处理, 即获取目标站点的原始时空风速序列. 对于缺失数据、重复数据和跳跃数据, 替换为值附近的平均风速. 然后应用VMD 对数据进行分解并得到各IMF分量; 针对IMF分量, 应用混合深度学习模型CNN-LSTM-SAM进行风速预测, 最后将各预测值叠加并得到最终值. 这里, 混合深度学习模型CNN-LSTM-SAM由两层构成, 下层为CNN模型, 处理风速的空域特征, 上层为LSTM和SAM的多级模型, 处理风速的时域特征. 算法的流程图可用图2表示.

3.1 风速时空数据模型

在VHSTN算法中, 处理的是时空数据. 风速数据除了一般的时序序列特征外, 空间数据存在大量有助于风速预测的信息. 对于风速的时空特征进行处理, 成为近年来的一个热点研究方向, 并取得了较好的预测成果. 文献[13]提出了一种深度架构PSTN, 联合学习时间和空间相关性进行短期风速预测. 该文献将风速的时空数据放到一个名为SWSM的二维矩阵中. SWSM中的项由 $ x{(i, j)_t} \in {R^{M \times N}} $ 定义, 其中 $ M \times N $ 是目标站点的邻接空间.

这里, 我们借鉴了该方法. 假设时间窗长度为T, 相邻站点数为 $ M \times N = L $ , IMF分量数为 $ K $ , 我们用 $ {F^T} = (IMF_k^{1, l}, IMF_k^{2, l}, \cdots, IMF_k^{T, l}) \in {R^T} $ 来表示风速的时域数据, $ {F^L} = (IMF_k^{t, 1}, IMF_k^{t, 2}, \cdots, IMF_k^{t, L}) \in {R^L} $ 描述风速的空域数据. 若假设在某个时刻 $ t $ , 对于某个 $ IM{F_k} $ 分量在站点 $ (i, j) $ 的值记为 $ x(i, j)_k^t $ , $ x(i, j)_k^t \in {R^{M \times N}} $ , 那么该 $ IMF $ 分量在时刻 $ t $ 的所有邻接站点的值可以表示如下:

$ x_k^t = \left[ {\begin{array}{*{20}{c}} {x(1, 1)_k^t}&{x(1, 2)_k^t}& \cdots &{x(1, N)_k^t} \\ {x(2, 1)_k^t}&{x(2, 2)_k^t}& \cdots &{x(2, N)_k^t} \\ \vdots & \vdots &{\ddots}& \vdots \\ {x(M, 1)_k^t}&{x(M, 2)_k^t}& \cdots &{x(M, N)_k^t} \end{array}} \right] $

(6)

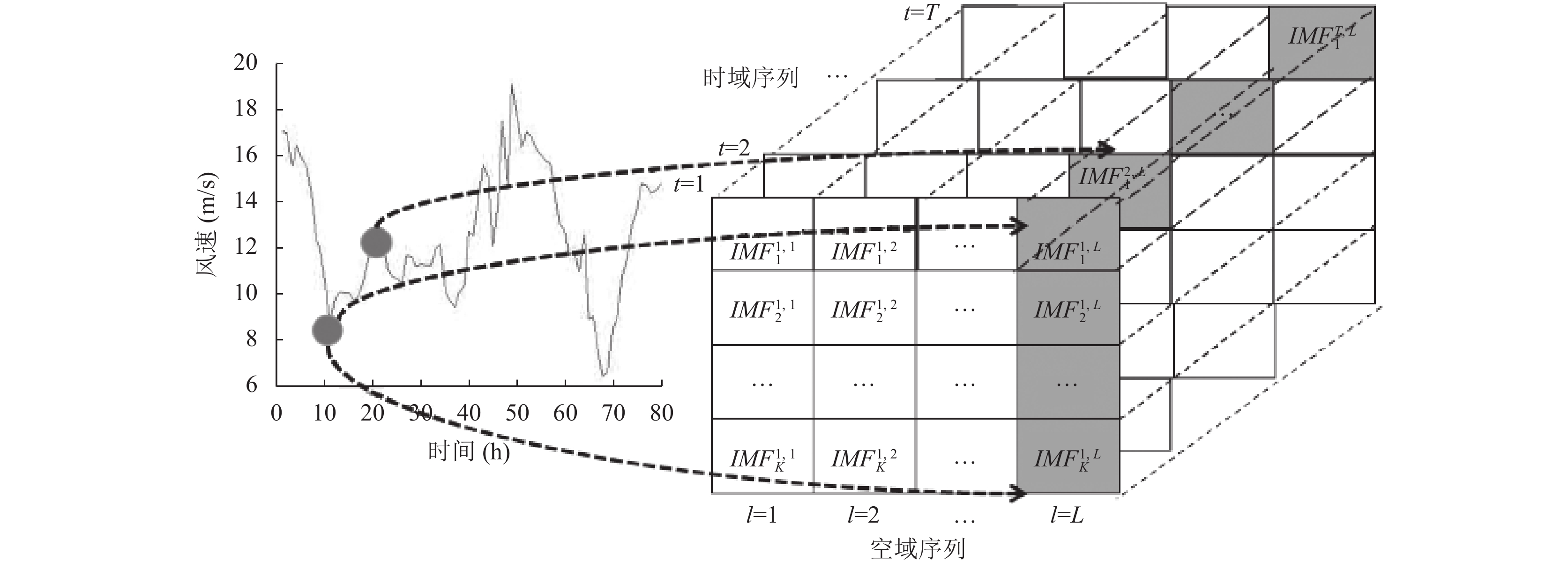
如图3 所示, 我们将原始风速分解为 $ K $ 个 $ IMF $ 分量, 用 $ IMF_k^{t, l} $ 表示. 图3的左侧是站点 $ L $ 经过预处理后的风速数据. 右侧沿 $ x $ 轴方向的数据是 $ IMF_k^{t, l} $ 的空域数据 $ {F^L} $ ; $ y $ 轴方向代表 $ K $ 个 $ IMF $ 分量; $ {\textit{z}} $ 方向表示风速的时域数据 $ {F^T} $ . 左侧图中的一个数据点可以分解为右图中 $ y $ 轴方向的 $ K $ 个分量, 如灰色部分. 沿着 $ {\textit{z}} $ 方向的灰色部分数据代表站点 $ L $ 在 $ T $ 时间窗内的所有第1个IMF分量.

3.2 CNN-LSTM-SAM混合深度学习框架

为了得到更好的预测结果, 我们采用了CNN-LSTM-SAM混合深度学习框架. CNN作为底层结构, 接收VMD分解得到的IMF分量的空间数据. 选用CNN模型的原因在于该模型可以很好地保留数据的原始拓扑结构^[20], 直接接收IMF的2D张量, 而没有进行元素的重新排列, 因此能够充分利用IMF分量的空间特性. 另外, 利用CNN特有的卷积层、池化层和全连接层, 可以分层提取空间特征. 因此, 该过程的特征学习可以合并较大的空间区域^[21].

在VHSTN算法中, 我们采用 LSTM和SAM作为混合深度学习框架的上层结构, 接收来自CNN提取的空间特征. 在LSTM层, 将对时域数据进行处理, 并最终得到各IMF分量的风速预测值. LSTM在时序数据的预测方面应用较广^{[22, 23]}. LSTM模型实质是一种时间循环神经网络, 主要用来解决循环神经网络(RNN)中存在的长期依赖问题, 具有捕捉长期和短期序列内的时间依赖性, 可以满足不同预测范围的需求. 同时, LSTM 可以将误差差异反向传播到其输入, 这使我们能够将空间模型和时间模型整合为一个统一的框架. 另外, LSTM还可以通过时间共享参数, 无论输入序列的长度如何, 都能保持恒定数量的参数, 方便模型的训练. 在SAM层, 通过对隐藏特征的自适应加权来加强关键信息并削弱无用信息的影响^[24]. 由于隐藏特征之间存在的内在相关性, 不同时间步长的隐藏特征对预测结果也有不同的影响^[25], 这是LSTM网络无法识别的, 因此在本文中引用SAM来协助LSTM层取关键特征.

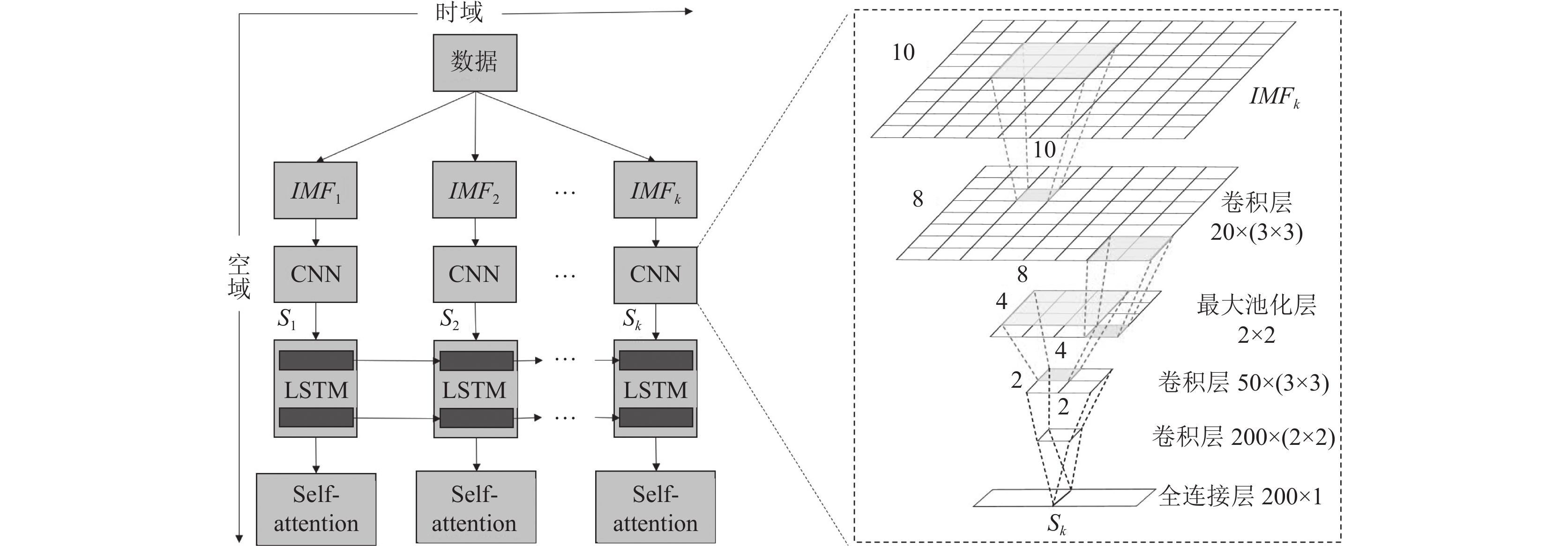
在混合深度学习模型中, CNN 采用5层结构, 即卷积层、最大池化层、两层卷积层和全连接层, 具体如图4所示. 图4的左半部分是混合模型的整体架构, 垂直方向处理空域数据, 由CNN完成. CNN的5层结构及主要配置在图4的右半部分给出, 详细数据可参见表1. 水平方向处理时域数据, 由LSTM和SAM联合完成. 这里, 假设CNN模型输入的变量为 ${S_k}, k = 1, 2, \cdots, K$ , $ K $ 为VMD分解的个数.

4 实验 4.1 设置

文中算法所用的实验数据选自美国国家可再生能源实验室(National Renewable Energy Laboratory)提供的风电一体化国家数据集(wind integration national dataset, WIND), 这是一个比较通用的风速数据集. WIND数据集包含2007–2013年美国大陆126000多个站点的风速数据, 时间间隔为5 min. 这里选用怀俄明州风电场内的10×10风力机阵列进行短期预测. 具体选取2012年的年度数据集, 将时间间隔设置为10 min, 数据集共有数据52560个, 其中最高风速35.48 m/s, 最低风速0.01 m/s. 实验中的GPU服务器配置为NVIDIA GeForce RTX 3070, 显存8 GB, CPU为E5-2689 16核16 GB, 200 GB SSD及2 TB硬盘. 开发环境为多框架组合环境, 即TensorFlow 2.4, Keras 2.4.2以及Python 3.7. 训练集共有 31536个风速, 5256和15768分别是验证集和测试集的风速个数, 这里根据时间间隔的不同, 各个集合会有个位数的差异. VMD的参数设置同第1节中的相关叙述. 混合深度学习框架的配置如图1所示.

这里, 风速预测的评估指标我们选用常用的均方根误差 (RMSE)和平均绝对百分比误差(MAPE), 具体由下列公式定义:

$ {E_{\textit{RMSE}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({Y_i} - {{\hat Y}_i})}^2}} } $

(7)

$ {E_{\textit{MAPE}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{Y_i} - {{\hat Y}_i}}}{{{Y_i}}}} \right|} \times 100{\text{%}} $

(8)

其中, $ N $ 是样本个数, $ {\hat Y_i} $ 为预测值, $ {Y_i} $ 为真实值. 针对时空数据, 我们可以很方便地将上述公式扩展成矩阵形式.

4.2 对比算法

我们将文中提出的VHSTN算法与类似处理时空数据的同类算法进行对比, 即上文提到的PSTN算法^[13]和PDCNN算法^[26], 以及VHSTN中去除VMD分解的算法, 记为CNN+LSTM+Attention. 同时进行时域数据和时空数据实验结果的对比. 在时域数据中, 我们选用常用的LSTM、MLP以及RNN算法. 为了进一步比较VMD分解的有效性, 我们在时域数据实验中增加VMD+LSTM算法以及VMD+CNN+LSTM算法. 这里, MLP和LSTM的激活函数为ReLU函数, RNN的激活函数为tanh; 时间间隔分别为20 min、30 min、60 min、120 min. 所有算法均运行于相同的实验环境. 对于每种算法, 实验测试不同的超参数, 以便找到每个超参数的最佳设置.

表2和表3显示不同算法预测误差的RMSE和MAPE对比. 从表2可以看出, 针对时空数据, PSTN的性能优于PDCNN, 文中提出的VHSTN算法优于PSTN. 对于20 min、30 min、60 min和120 min时间间隔, VHSTN的RMSE分别低于PDCNN为12%、12%、20%和9%, 平均降低13%; VHSTN分别低于PSTN为12%、11%、20%和9%, 平均降低13%. 同时, 文中所提算法VHSTN也比VMD+CNN+LSTM算法平均降低7.4%, 这部分性能的提升归功于ASM机制的引入, 比CNN+LSTM+Attention平均降低10%, 可见VMD分解有助于性能的提升; 相应在表3中, 对于预测误差MAPE, VHSTN在30 min间隔时与VMD+LSTM算法处理时域数据的性能相近, 同时优于其他算法. 在其他时间间隔, VHSTN依然是最优的, 例如, 20 min、60 min、120 min的时间间隔内, 比PDCNN平均降低21%, 比PSTN平均降低19%, 比VMD+CNN+LSTM平均降低16%, CNN+LSTM+Attention算法平均降低15%. 可以看出, 文中提出的VHSTN算法在总体性能上比较优异, 性能得到了很大提升, 从而得到较好的预测结果.

从表2和表3还可以看出, 时空数据比单纯的时域数据携带更多的预测信息, 除了表3中的30 min时间间隔, VMD+LSTM处理时域数据的性能与VHSTN处理时空数据的性能相近外, 其他是时空数据的预测性能占优. 对于处理时域数据的各个算法VMD+LSTM的性能较好, 预测结果都有很大提升. 这也说明, VMD分解对于短期风速预测具有良好的效果.

表4给出了不同模型训练和测试的时间对比, 可以看出时空数据的处理算法普遍时间较长, 特别增加了VMD分解之后, 训练时间和测试时间都大幅增长, 因此性能的提升是以时间开销增长为代价的.

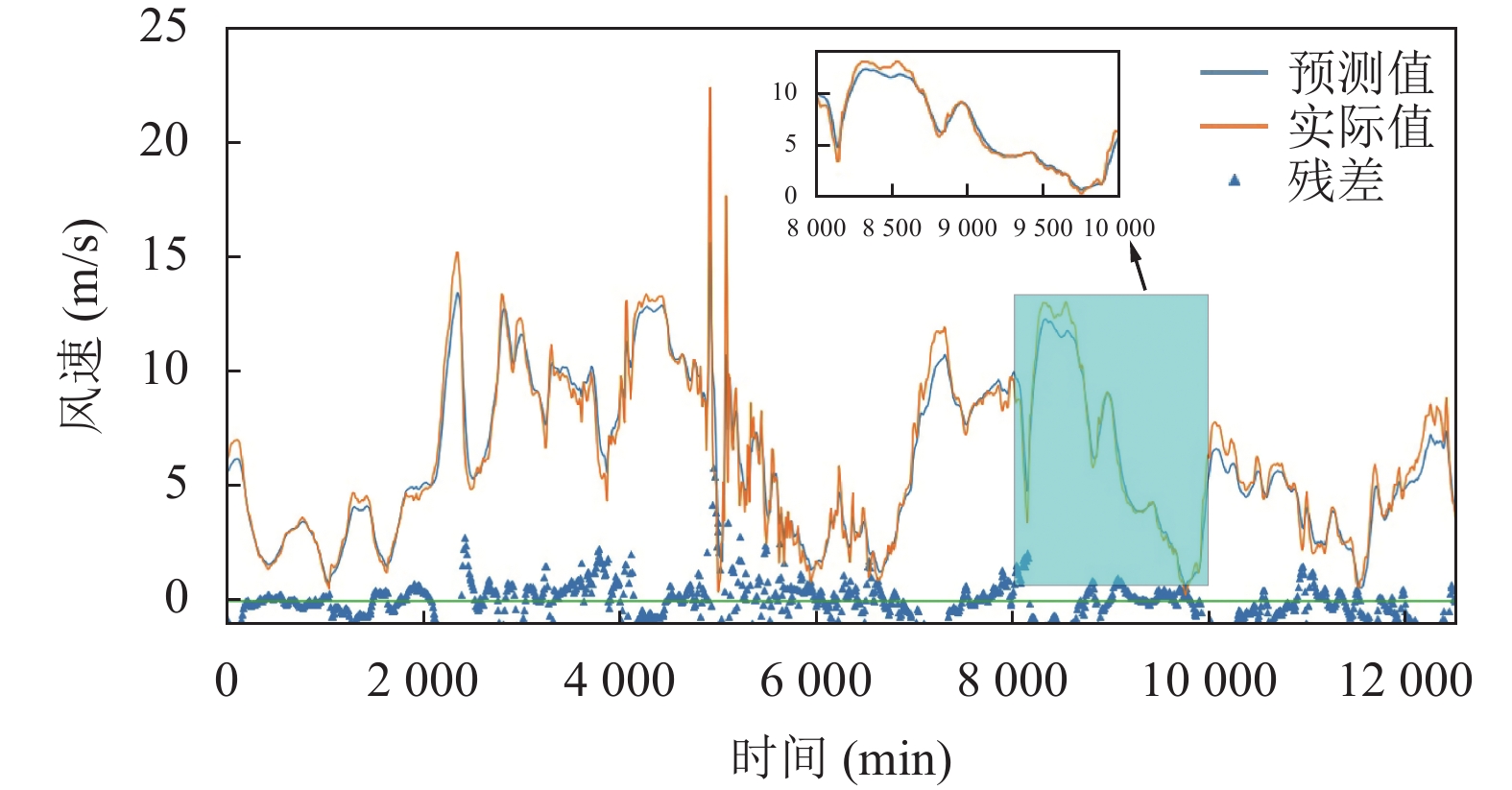
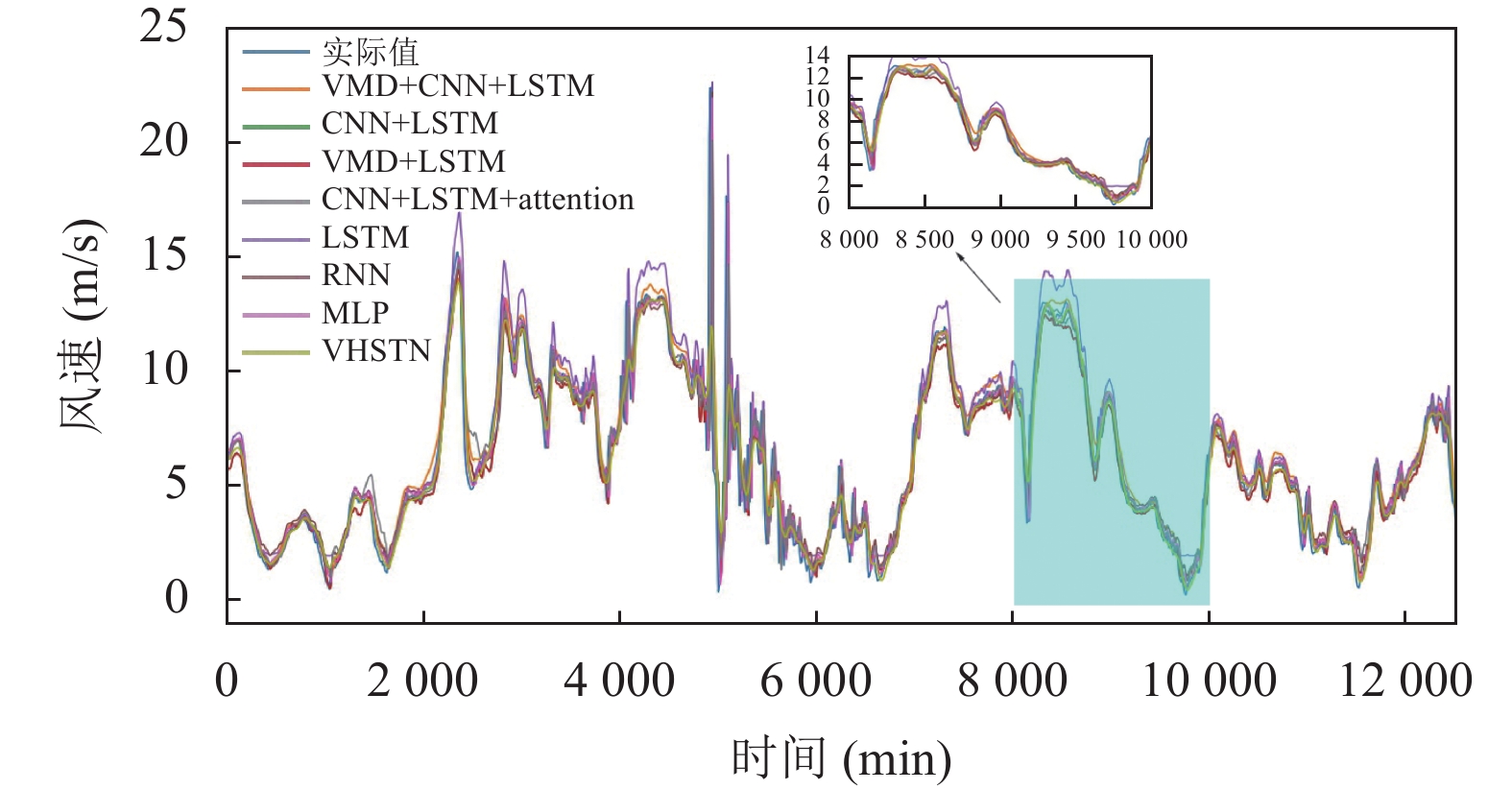
图5给出文中提出的VHSTN模型20 min间隔的预测结果. 可以看出, VHSTN模型的预测值与实际值吻合程度较高. 残差分析结果显示该模型的预测残差均匀且随机分布于零基准线的两侧, 说明建模过程中没有产生系统误差. 所以, 该模型用于短期风速预测是可行的. 不同模型的20 min风速预测结果如图6显示. 这些算法包括VMD+CNN+LSTM、CNN+LSTM、VMD+LSTM、LSTM、PSTN、MLP、CNN+LSTM+Attention和VHSTN. 图6同样显示了VHSTN模型的良好预测性能.

5 结束语

本文提出了一种用于短期风速预测的VHSTN算法, 它将时空特征集成到一个统一深度学习框架CNN-LSTM-SAM中. 在CNN层, 对经过VMD分解的IMF分量提取空间特征; 在LSTM-SAM层提取时域特征, 经过合并之后得到最终的风速预测值. 在WIND数据上的实验结果说明: 相对常用的风速时域数据, 时空数据携带更多的预测信息; VMD分解之后, 风速相对平稳, 预测精度提升; VHSTN算法总体优于同类算法, 但是会带来一些时间开销. 进一步地, 我们将考虑采用多层Attention机制, 提高算法的预测性能.