双目立体视觉一直是计算机视觉领域热门研究方向之一, 主要目标是根据双目立体相机拍摄的一对二维图像, 还原出三维场景的位置信息. 双目立体相机是模拟人眼的产物, 该相机由两个单目相机组成, 水平相隔一定距离, 同时各自成像, 形成一对图像. 双目立体匹配是双目立体视觉的关键一步, 目标是求解双目图像对应三维场景的深度信息, 用视差图表示. 有了视差图和这一对图像, 再联合双目立体相机参数就能够还原出真实的三维场景位置信息. 现实中, 像无人驾驶、移动机器人、虚拟现实、增强现实、星球探测、辅助视觉等^[1-3]都需要这种三维感知的能力, 因此双目立体匹配的应用十分广泛.

经过严格的数学推导, 求解双目立体匹配问题转化为求解一对双目图像之间像素点的匹配问题, 其深度可用该对匹配点坐标之差——视差表示. 双目立体匹配的难点在于双目图像中遮挡、弱纹理、高光、噪音、透射、重复图案等病态区域的存在, 导致求解过程中产生大量的多解. 为了解决这些难点, 大量的研究者提出了各种各样的双目立体匹配算法. 双目立体匹配算法大体上分为两种, 传统算法和深度学习算法. 传统算法是指无需通过数据集学习, 不使用神经网络, 直接计算出该对图像深度的算法. 深度学习算法指基于深层的神经网络, 一般是卷积神经网络, 在大量场景数据集下自主学习的算法.

传统算法一般由4个主要步骤^[4]——代价计算、代价聚集、视差选择、视差优化组成. 传统算法的输入是双目立体相机拍摄的, 经过对极几何校正后的双目图像对. 双目图像对经过对极几何校正后, 左右图像的匹配点均在同一行, 故可极大减少像素匹配搜索空间. 代价计算是计算同行任意两个左右像素的差异, 一般为亮度差异, 用这种差异衡量两个像素匹配的程度, 如绝对亮度差(absolute differences, AD^[4])、平方亮度差(squared differences, SD^[5])、加和绝对亮度差(sum of absolute differences, SAD^[6])、加和平方亮度差(sum of squared differences, SSD^[7])、归一化相关系数(normalized cross correlation, NCC^[8])、级别变换(rank transform, RT^[9])、统计变换(census transform, CT^[10])等. 代价聚集是使用一定的方法, 一般是基于窗口的方法, 将代价计算的像素代价聚集起来, 利用邻居信息, 以减少匹配的不确定性. 常用的聚集方法有固定窗口(fixed-size window, FW^[11])、多窗口(multiple windows, MW^[12])、自适应窗口(adaptive windows, AW^[13])、自适应支撑窗口(adaptive support weights, ASW^[14])等. 视差选择是根据代价聚集的结果选择聚集代价最小的视差, 即用“赢者通吃”的方法. 视差优化是为了补救视差选择步骤部分选择错误的视差, 方法通常有左右一致性校验、填充和插值、亚像素拟合、中值滤波、双边滤波等.

双目立体匹配的深度学习算法通常分为有监督的学习方法和无监督的学习方法. 有监督的学习方法需要视差真值图. 视差真值图一般通过如激光、雷达等其他物理手段直接测距获得. 有监督的深度学习方法需要在大量的标注数据集上长时间的训练, 消耗的计算资源大, 且标注数据集的获取较困难, 虽然在和训练集场景相似的场景下表现较好, 但在其他场景下表现较差, 即泛化能力差. 无监督的学习方法不需要视差真值图, 而是利用左右图像蕴涵关系指导训练. 与有监督的学习方法相比, 无监督学习方法的最大优点是无需昂贵的标注数据集, 缺点是收敛效果差些.

传统算法已经被无数学者探索了几十年, 最近几年进展缓慢, 而深度学习算法发展迅速, 然而, 深度学习算法的发展是以算力提升为基础的, 并不改变需要数据集训练的现象且泛化能力差. 考虑到左右像是同一场景经两次确定性投影生成的, 由左右像逆推可以找到至少一个关于深度场景位置信息的相容解, 故而左右像天然可以互为导师数据(由左像变换到右像, 由右像变换到左像). 基于此, 本文尝试从单个双目图像中学习其专有的匹配规则, 提出了一个以双目图像互为监督的深度场景相容解迭代优选算法. 该算法不同于传统算法和深度学习算法, 使用神经网络但不使用数据集训练, 用互监督损失函数通过梯度下降法指导网络收敛, 只在输入图像对上迭代学习, 优化相容解, 进而计算出双目图像的深度.

本文的主要贡献包括3个方面.

(1) 提出一个以双目图像互为监督的深度场景相容解迭代优选算法, 该算法不需要数据集训练, 只需在当前输入图像对上迭代学习, 故而摆脱了对数据集的依赖. 对比实验表明, 该算法有更低的误匹配率.

(2) 设计了场景位置猜测网络, 该网络避免了昂贵的3D卷积, 同时输出左右视差图, 进而能够使用视差优化技术, 提高匹配精度.

(3) 设计了互监督损失函数, 用于指导场景位置猜测网络的收敛, 该损失函数无需视差真值图.

1 相关工作

传统算法通常又可分为局部匹配算法和全局匹配算法^[4]. 局部匹配算法依据的是图像局部区域的特征, 具有计算复杂度低、运算速度快的特点, 典型的方法有SAD^[6]、SSD^[7]、CT^[10]等. SAD以窗口绝对亮度差之和计算代价量. SSD是以窗口平方亮度差之和计算代价量. CT是把窗口中心像素和邻居像素比较, 比较结果用二进制字符串表示, 以海明码距离计算代价量. 全局匹配算法依据的是图像全局的特征, 转化为求解能量函数最小化问题, 效果好, 但计算复杂度高, 典型方法有信任传播(belief propagation, BP^[15])、图割(graph cut, GC^[16])等. BP方法把立体匹配问题建模为3个成对的马尔科夫随机场. GC方法是用图割的方法转化为求解最小割问题. 还有个别方法不属于这两类, 如半全局匹配(semi-global matching, SGM^[17])、PatchMatch^[18]等. SGM使用扫描线的方法沿直线方向聚集匹配代价. PatchMatch把场景建模为由一个个三维平面拼接而成, 转化为求解三维标签问题. 总体上看, 传统算法的优点是无需数据集训练, 场景依赖性低, 占用的计算资源小, 缺点是求得的视差精度低.

在有监督的学习方法中, 除少数方法外, 如MC-CNN^[19], 其余都是端到端的学习方法, 即神经网络的输入是一对双目图像, 输出是目标视差图, 如GC-Net^[20]、PSMNet^[21]、GA-Net^[22]、HITNet^[23]、CREStereo^[24]、RAFT-Stereo^[25]、EAI-Stereo^[26]. MC-CNN方法是把传统算法4个主要步骤中的代价计算由孪生网络替代, 其余步骤不变, 首先学习左右图像块的相似度, 用相似度计算代价量, 其效果仍然受限于传统的代价聚集方法. GC-Net方法是把传统方式中的每个步骤都用神经网络替代, 是一个端到端的方法, 使用3D卷积对代价量进行视差回归. PSMNet方法采用多尺度的神经网络架构, 首先用沙漏模型提取图像多尺度特征, 计算不同尺度的代价量, 再用3D卷积在不同尺度上进行视差回归. GA-Net方法设计了两个特殊的网络层, 对代价量分别进行局部和全局的聚集, 不仅综合了全局和局部特征, 还避免了昂贵的3D卷积操作. HITNet以多清晰度和倾斜的平面块建模, 避免显式构建代价量, 达到实时预测的程度. CREStereo引入了级联的循环神经网络, 具有清晰的边缘且能够处理非理想校正的图片. RAFT-Stereo是在光流网络(RAFT^[27])的基础上进行多级卷积门控循环单元(gated recurrent unit, GRU)改造, 能够迭代细化视差. 有监督的深度学习方法之间的不同之处在于网络架构和损失函数, 相同之处是都需要在大量的标注数据集上长时间的训练, 消耗的计算资源大, 且标注数据集的获取较困难, 虽然在和训练集场景相似的场景下表现较好, 但在其他场景下表现较差, 即泛化能力差.

无监督的学习方法相对于有监督的学习方法要少得多. Zhou等人的方法^[28]使用无监督学习网络, 首先对网络参数初始化赋值, 通过左右一致性检测产生初始置信地图, 用迭代的方式更新置信地图, 指导网络训练. Wang等人的方法^[29]利用视差注意力机制计算特征相似度, 避免了视差范围过大的限制. 与有监督的学习方法相比, 无监督学习方法的最大优点是无需昂贵的标注数据集, 缺点是在有监督学习的训练场景下收敛效果不及有监督学习.

无论是有监督还是无监督的深度学习方法, 都需要大量数据集训练, 训练数据集的规模不足和获取难度限制了其预测效果和应用范围.

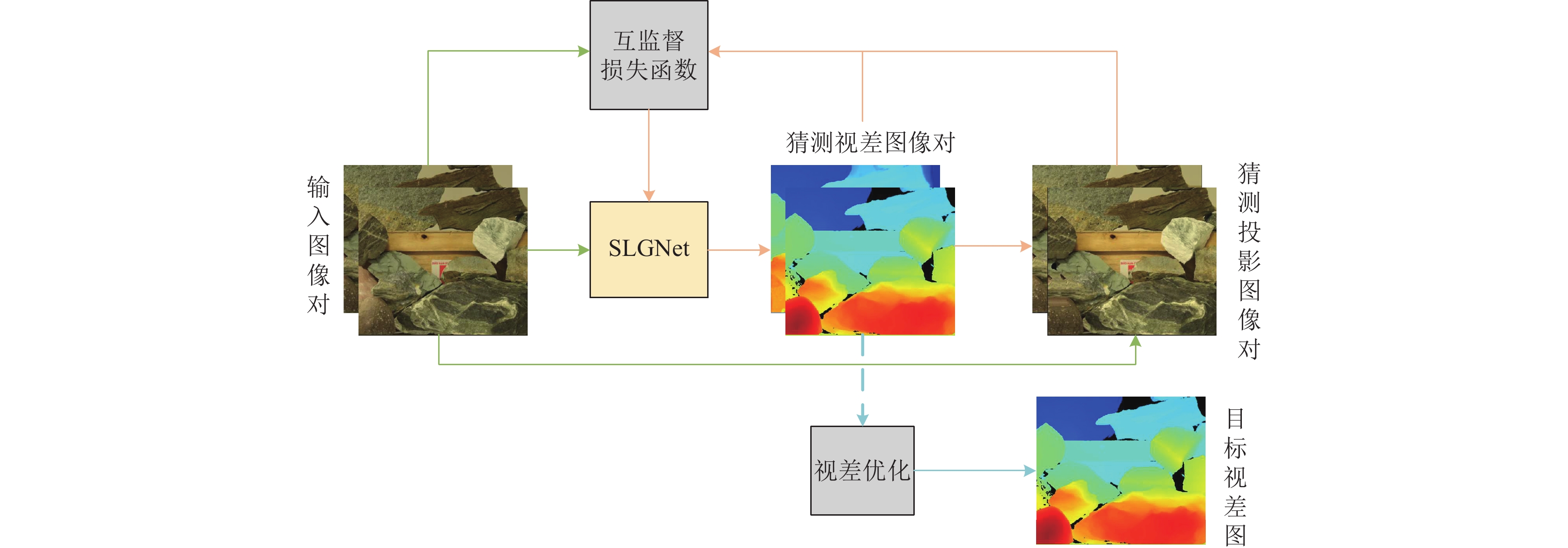
2 算法框架

算法框架如图1所示, 主要由场景位置猜测网络 (scene location guessing network, SLGNet)、互监督损失函数、视差优化等3个部分组成, 其输入是经过对极几何矫正后的双目图像对, 输出是视差图.

因为双目图像对是由同一场景经两次不同角度确定性投影生成的左右像, 故左右像天然可以互为导师数据. 假设已知场景深度, 则左像能够变换到右像, 右像能够变换到左像. 利用左右像互为导师数据的关系, 可以验证深度场景位置信息的合理性. 神经网络SLGNet, 就是模拟逆推的深度场景位置信息的相溶解空间, 网络输出是解空间中的一个解, 即猜测的一种深度场景位置, 用视差图表示. 有了猜测的深度场景位置信息, 可以得到深度场景按照输入图像对相同投影角度向左、向右的投影图像对, 即得到猜测投影图像对. 猜测投影图像对和输入图像对做比较, 可以验证这种猜测深度场景位置信息的相容性, 其差异用互监督损失函数表示, 当这种差异小到一定程度时, 即可认为这种猜测是其一相容解. 该算法用互监督损失函数指导SLGNet网络的学习, 迭代优化深度场景位置信息的相容解空间, 最终得到从左往右、从右往左都相容的优化解. 由于遮挡、弱纹理、高光、噪音、透射、重复图案等病态区域的存在, 导致相容解的多解性. 为了使猜测的视差图尽可能地接近真实解还需要视差优化技术, 综合左右视差图的信息, 最终得到以左视差图为参照的目标视差图.

具体的算法如算法1所示. SLGNet网络参数采用随机的方式初始化, 之后每一次迭代更新一次网络参数, 直到迭代达到一定次数为止, 再经过视差优化, 得到最终的视差图.

算法1. 以双目图像互为监督的相容解迭代优选算法

输入: 双目图像 $\scriptstyle {I^{\rm{L}}}$ 、 $\scriptstyle {I^{\rm{R}}}$ , 初始神经网络 $\scriptstyle {{\textit{SLGNet}}_0}$ ;

输出: 视差图 $\scriptstyle {D^{\rm{L}}}$ .

1. /* 上标 $\scriptstyle {\rm{L}}$ 、 $\scriptstyle {\rm{R}}$ 分别表示左、右. */

2. /*神经网络参数采用随机的方式初始化*/;

3. $\scriptstyle \text{FOR }i\text{ IN }RANGE\left(\text{0, }n\right) $ /* n为总迭代次数 */

4.　 $\scriptstyle D_i^{\rm{L}}, D_i^{\rm{R}} \leftarrow {{\textit{SLGNet}}_i}\left( {{I^{\rm{L}}}, \; {I^{\rm{R}}}} \right);$

5. 　 $\scriptstyle P_i^{\rm{L}} \leftarrow {\textit{project}}\left( {D_i^{\rm{L}}, \; {I^{\rm{R}}}} \right);$ /* project为投影函数 */

6.　 $\scriptstyle P_i^{\rm{R}} \leftarrow {\textit{project}}(D_i^{\rm{R}}, \; {I^{\rm{L}}});$

7.　 $\scriptstyle loss_i^{\rm{L}} \leftarrow supervise\left( {{I^{\rm{L}}}, \; P_i^{\rm{L}}, \; D_i^{\rm{L}}} \right);$ /* supervise为互监督损失函数 */

8.　 $\scriptstyle loss_i^{\rm{R}} \leftarrow supervise\left( {{I^{\rm{R}}}, \; P_i^{\rm{R}}, \; D_i^{\rm{R}}} \right);$

9. 　 $\scriptstyle loss \leftarrow loss_i^{\rm{L}} + loss_i^{\rm{R}};$ /* 总损失函数 */

10. $\scriptstyle {{\textit{SLGNet}}_{i + 1}} \leftarrow update\left( {{{\textit{SLGNet}}_i}, \; loss} \right);$ /* 梯度下降法更新网络参数 */

11. $\scriptstyle {\text{END FOR}}$

12. $\scriptstyle {D^{\rm{L}}} \leftarrow {\textit{refine}}\left( {D_n^{\rm{L}}, \; D_n^{\rm{R}}} \right);$ /* refine为视差优化函数 */

2.1 SLGNet网络架构

SLGNet网络整体架构如图2所示, 包括特征提取模块、特征联合、视差预测模块等3个部分. 输入是经过对极几何矫正后的双目图像对, 经过特征提取网络模块分别提取左右图像特征, 然后一起送入一个卷积层, 进行特征联合, 再分别送入两个结构相同但非共享权重的视差预测模块, 分别输出左右视差图.

SLGNet的每一个卷积层都是由卷积、归一化、非线性函数依次组成, 其中卷积核尺寸均是 $3 \times 3$ , 归一化方法为实例归一化(instance normalization^[30]), 非线性函数为ReLU^[31]. SLGNet网络无需批量数据集训练, 因此通常使用的批归一化(batch normalization^[32])并不适用SLGNet, 而实例归一化计算归一化统计量时只需要考虑单个样本的单层中的单个通道, 更能考虑到单个像素的特征, 适合SLGNet架构.

2.1.1 特征提取模块

特征提取模块的主要功能是从图像中自动提取联合所需要的特征. 特征提取模块结构如图3所示, 图3中卷积指步长为1的卷积; 下卷积指步长为2的卷积, 会使宽度和高度各减小1倍, 通道增加1倍; 上卷积指步长为2的转置卷积, 会使宽度和高度各增加一倍, 通道减小一倍; 上采样指用双线性插值的方式增大空间尺寸, 用于弥补上卷积过程中填充的零值; 箭头表示数据流向. 首先, 双目图像通过3次下卷积逐层收缩网络, 再通过两个残差块扩大感觉野, 然后通过3次上卷积逐层恢复原尺寸, 在上卷积过程中, 同时进行上采样以增加信息向后传递, 最终得到特征向量组. 出于特征联合应该使用相同特征提取原则的考虑, 对于输入的左右图, SLGNet使用同一个特征提取模块.

2.1.2 特征联合

特征联合是SLGNet中的关键一步, 让特征提取模块提取到的左右图像特征一起卷积, 形成视差预测所需要的综合特征. 该层只是简单的信息汇集, 故只有一个卷积层, 更深层的信息处理在视差预测模块. 只用一个卷积层的好处是既能够汇集信息, 又计算简单, 避免构造代价量、3D卷积等计算复杂的操作.

2.1.3 视差预测模块

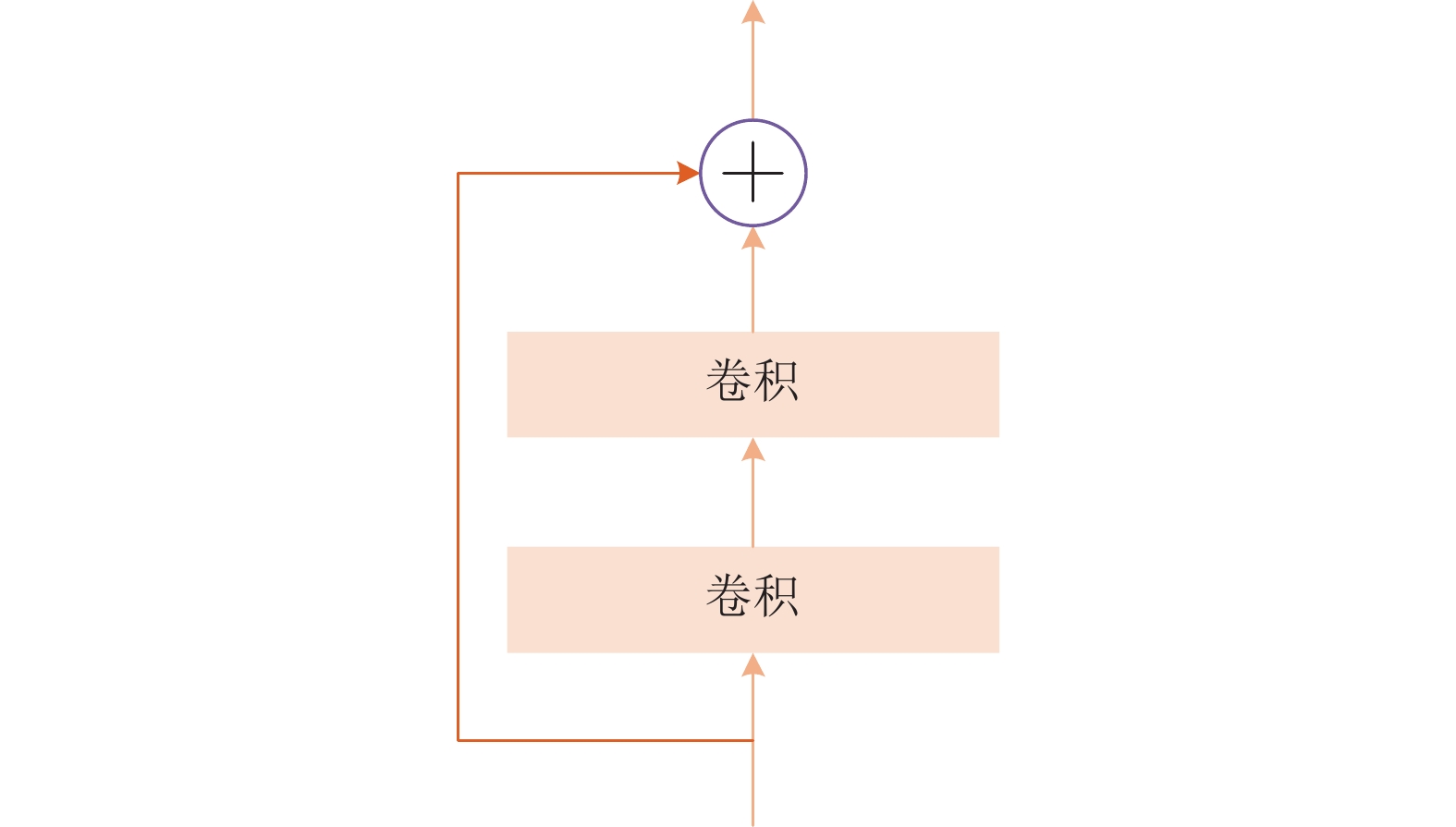
视差预测模块由若干个残差块(ResidualBlock^[33], 图4)后跟一个SoftArgmax组成, 主要功能是从联合特征中预测视差, 从而生成猜测视差图像对. 本文使用两个相同结构但非共享权重的视差预测模块分别预测左右视差. 两个视差预测模块之所以采用非共享权重的方式, 是因为左右图像对应视差的场景角度是不同的, 需要不同的预测方式. SoftArgmax是Argmax的可微变体, 公式如下:

$ {\textit{SoftArgmax}}\left({\textit{z}}\right)={\displaystyle \sum _{i}{\scriptstyle \dfrac{{{\rm{e}}}^{{{\textit{z}}}_{i}}}{{\displaystyle \sum _{j}{{\rm{e}}}^{{{\textit{z}}}_{j}}}}}}\cdot i $

(1)

其中, ${\textit{z}}$ 为一通道特征向量, ${{\textit{z}}_i}$ 为特征向量分量, $i$ , $j$ 为特征向量分量下标. SoftArgmax以可微的方式计算特征向量的最大分量的近似位置, 进而用该位置表示预测视差.

2.2 互监督损失函数

用 $d$ 表示视差, 上标 ${\rm{L}}$ 、 ${\rm{R}}$ 分别表示左图和右图, $x$ 、 $y$ 分别表示图像像素横坐标和纵坐标, 对于匹配像素点对, 根据视差定义, 则有关系式:

$ {d^{\rm{L}}} = {d^{\rm{R}}} = {x^{\rm{L}}} - {x^{\rm{R}}} $

(2)

故已知右图像和左视差图可以计算出左投影图像, 已知左图像和右视差图可以计算出右投影图像.

互监督损失函数由投影差异函数、梯度投影差异函数和视差平滑函数组成.

用 $I$ 表示图像亮度函数, $ \Vert \cdot\Vert $ 表示 ${L_1}$ 范式距离, 则以左图为基准的亮度差异函数为:

$ {B_1} = \sum\limits_x {\sum\limits_y {\left\| {{I^{\rm{L}}}(x, y) - {I^{\rm{R}}}(x - {d^{\rm{L}}}, y)} \right\|} } $

同理, 以右图为基准的亮度差异函数为:

$ {B_2} = \sum\limits_x {\sum\limits_y {\left\| {{I^{\rm{L}}}(x{\text{ + }}{d^{\rm{R}}}, y) - {I^{\rm{R}}}(x, y)} \right\|} } $

故, 总的投影差异函数为:

$ B = {B_1} + {B_2} $

(3)

用 $ {\nabla _x}I $ 表示图片 $x$ 方向的亮度梯度函数, 则以左图为基准的 $x$ 方向的亮度梯度差异函数为:

$ {G_1} = \sum\limits_x {\sum\limits_y {\left\| {{\nabla _x}{I^{\rm{L}}}\left( {x, y} \right) - {\nabla _x}{I^{\rm{R}}}(x - {d^{\rm{L}}}, y)} \right\|} } $

用 $ {\nabla _y}I $ 表示图片 $y$ 方向的亮度梯度函数, 则以左图为基准的 $y$ 方向的亮度梯度差异函数为:

$ {G_2} = \sum\limits_x {\sum\limits_y {\left\| {{\nabla _y}{I^{\rm{L}}}\left( {x, y} \right) - {\nabla _y}{I^{\rm{R}}}(x - {d^{\rm{L}}}, y)} \right\|} } $

同理, 以右图为基准的 $x$ 、 $y$ 方向的亮度梯度差异函数分别为:

$ {G_3} = \sum\limits_x {\sum\limits_y {\left\| {{\nabla _x}{I^{\rm{L}}}(x{\text{ + }}{d^{\rm{R}}}, y) - {\nabla _x}{I^{\rm{R}}}(x, y)} \right\|} } $

$ {G_4} = \sum\limits_x {\sum\limits_y {\left\| {{\nabla _y}{I^{\rm{L}}}(x{\text{ + }}{d^{\rm{R}}}, y) - {\nabla _y}{I^{\rm{R}}}(x, y)} \right\|} } $

故, 总的梯度投影差异函数为:

$ G = {G_1} + {G_2} + {G_3} + {G_4} $

(4)

亮度函数 $I$ 及其梯度 $\nabla I$ 都是离散的, 即对视差 $d$ 不可导, 因此投影差异函数对 $d$ 不可导. 为使投影差异函数对 $d$ 可导, 投影变换时, 采用Jaderberg等人的空间变换的可导化处理方法^[34].

对于弱纹理、遮挡、高光等病态区域, 投影差异函数和梯度投影差异函数均无能为力, 故还需要平滑约束函数. 用 $D$ 表示视差函数, $T$ 表示指示函数, $ \alpha $ 为用户定义的阈值, 则左视差图的 $x$ 方向平滑约束函数为:

$ \begin{split} {S}_{1}=&{\displaystyle \sum _{x}{\displaystyle \sum _{y}\left|{D}^{{\rm{L}}}\left(x, y\right)-{D}^{{\rm{L}}}\left(x-1, y\right)\right|}}\\ &\cdot T\left[\Vert {I}^{{\rm{L}}}\left(x, y\right)-{I}^{{\rm{L}}}\left(x-1, y\right)\Vert < \alpha \right]\end{split} $

左视差图的 $y$ 方向平滑约束函数为:

$ \begin{split} {S}_{2}=&{\displaystyle \sum _{x}{\displaystyle \sum _{y}\left|{D}^{{\rm{L}}}\left(x, y\right)-{D}^{{\rm{L}}}\left(x, y-1\right)\right|}}\\ &\cdot T\left[\Vert {I}^{{\rm{L}}}\left(x, y\right)-{I}^{{\rm{L}}}\left(x, y-1\right)\Vert < \alpha \right]\end{split} $

同理, 右视差图的 $x$ 、 $y$ 方向的平滑约束函数分别为:

$ \begin{split} {S}_{3}=&{\displaystyle \sum _{x}{\displaystyle \sum _{y}\left|{D}^{{\rm{R}}}\left(x, y\right)-{D}^{{\rm{R}}}\left(x-1, y\right)\right|}}\\ &\cdot T\left[\Vert {I}^{{\rm{R}}}\left(x, y\right)-{I}^{{\rm{R}}}\left(x-1, y\right)\Vert < \alpha \right]\end{split} $

$ \begin{split} {S}_{4}=&{\displaystyle \sum _{x}{\displaystyle \sum _{y}\left|{D}^{{\rm{R}}}\left(x, y\right)-{D}^{{\rm{R}}}\left(x, y-1\right)\right|}}\\ &\cdot T\left[\Vert {I}^{{\rm{R}}}\left(x, y\right)-{I}^{{\rm{R}}}\left(x, y-1\right)\Vert < \alpha \right]\end{split} $

上述平滑约束函数的加和就是平滑约束损失函数, 即:

$ S = {S_1} + {S_2} + {S_3} + {S_4} $

(5)

故总的互监督损失函数为:

$ loss = B + G + S $

(6)

2.3 视差优化

由于遮挡、弱纹理、高光等病态区域的存在, 匹配过程中难免存在误匹配、噪音的情况. 视差优化就是为了纠正这种误匹配和消除噪音. 本文算法仅使用3个视差优化步骤——左右一致性校验、填充、中值滤波.

2.3.1 左右一致性校验

已知左视差图和右视差图可以作左右一致性校验. 位置 $\left( {x, y} \right)$ 的校验规则为:

(1) 若 $d = {D^{\rm{L}}}\left( {x, y} \right)$ , 满足 $\left| {d - {D^{\rm{R}}}(x - d, y)} \right| \leqslant 1$ , 则为正确匹配.

(2) 若 $d \ne {D^{\rm{L}}}\left( {x, y} \right)$ , 满足 $\left| {d - {D^{\rm{R}}}(x - d, y)} \right| \leqslant 1$ , 则为错误匹配.

(3) 其他则为遮挡.

根据上述校验规则, 每个像素位置只可标记为3种情况——正确匹配、遮挡、错误匹配的一种.

2.3.2 填充

根据上述校验标记结果, 对于正确匹配, 不做处理; 对于遮挡, 用背景的视差值进行填充, 即从当前位置向左寻找第1个标记为正确匹配的视差值填充, 若找不到, 则视为错误匹配, 用错误匹配的填充方法进行填充; 对于错误匹配, 按以下步骤计算出的视差进行填充.

(1) 从16个不同方向分别寻找前 $m$ 个标记为正确匹配的视差值的位置, 得到16组位置集合.

(2) 对每一组位置集合, 累加集合中的位置与当前位置对应原图的绝对颜色差值.

(3) 取累加绝对颜色差值最小的位置集合为目标集合.

(4) 对目标集合中的 $m$ 个位置及对应视差值进行线性拟合, 进而推断出当前位置的视差.

2.3.3 中值滤波

填充之后再进行3次中值滤波, 以消除残留的离群点和噪声.

3 实验

本文使用Middlebury^[35]测评网站中的Aloe、Cloth4、Cone、Rocks1、Teddy等图像和SceneFlow^[36]数据集作为实验对象. Middlebury测评图像是在特定光照下拍摄的室内场景图像, 其真值视差图是用结构光的方式获得. SceneFlow是一个大规模的合成数据集, 用于光流、视差估计、场景流估计. 实验代码是用Python编程语言编写, 版本号为3.8.11, 使用PyTorch 1.9.0编程框架, CUDA 11.4, 其运行在硬件为Intel(R) Xeon(R) Silver 4210R CPU @ 2.40 GHz、NVIDIA GeForce RTX 3090, 操作系统为CentOS 7的环境下. 对比实验代码同样运行在该环境下. 除特别说明外, 以下实验的参数均是: 视差预测模块的残差网络块数量为15个; 平滑约束函数自定义阈值 $\alpha $ 为0.05; SLGNet使用Adam(0.9, 0.999)优化器, 共迭代3000次, 前2000次迭代的学习率为0.01, 后1000次为0.001; 视差优化步骤中的 $m$ 为6, 中值滤波大小为 $5 \times 5$ .

参照立体视觉行业惯例, 评估指标使用误匹配率指标和EPE (end-point error, 端点误差)指标. 误匹配率是指预测视差图和真值视差图相比误差大于 $\delta $ 个像素所占的比率, 公式如下:

$ {r_\delta } = \dfrac{1}{N}\sum\limits_x {\sum\limits_y {T\left[ {\left| {{D_p}\left( {x, y} \right) - {D_t}\left( {x, y} \right)} \right| > \delta } \right]} } $

(7)

其中, $ {D_p}\left( {x, y} \right) $ 表示预测的视差值, $ {D_t}\left( {x, y} \right) $ 表示真实的视差值, $N$ 为像素个数, $T$ 是表示指示函数, $\delta $ 为用户定义的阈值, 以下实验取 $\delta = 1$ . 误匹配率越小表示匹配错误的像素越少, 效果越好.

EPE指标公式如下:

$ EPE = \dfrac{1}{N}\sum\limits_x {\sum\limits_y {\left| {{D_p}\left( {x, y} \right) - {D_t}\left( {x, y} \right)} \right|} } $

(8)

EPE可以用来测量从立体匹配算法生成的视差图与基准视差图之间的差异. EPE越低, 意味着立体匹配算法具有更高的精度, 从而得到更准确的深度估计.

指标又分为所有区域和非遮挡区域两种情况. 所有区域指整张图片区域, 而非遮挡区域指双目图像对中像素在左右图均可见的区域.

4 收敛过程分析

以Teddy图像为例, 分析该算法的收敛过程. 图5展示了Teddy的不同迭代次数的收敛情况, 图中视差图均未经过视差优化处理. 先以随机的方式初始化网络SLGNet, 进而得到初始猜测视差左图, 再由初始猜测视差左图和输入右图经过投影变换得到初始猜测投影左图, 同理可得初始猜测视差右图和初始猜测投影右图. 由初始猜测视差图对、初始猜测投影图对和输入双目图对根据式(6)计算SLGNet网络的互监督损失函数, 再由梯度下降法更新SLGNet网络参数, 进而得到下一次迭代猜测视差图对、猜测投影图对, 如此循环迭代, 直至收敛. 从图5中可以看出, 初始时猜测视差图呈现出不连续的点, 迭代10次时视差已连成片, 迭代100次时视差图已有清晰的边界, 之后随着迭代次数的增加, 视差图越来越精细. 猜测投影图也和猜测视差图一样, 迭代次数越多, 和输入图的差异越小. 猜测视差左图最左边和猜测视差右图最右边没有匹配是因为这些区域对应的像素只在一张图片中出现, 即要么出现在左图, 要么出现在右图, 故没有匹配点.

5 对比实验

对比算法有CREStereo、LBPS^[37]、RAFT-Stereo、CDR-Fusion^[38]、CFNet^[39]、PSMNet、GA-Net、PCW-Net^[40], 均为近5年发表的算法, 其中CREStereo、CDR-Fusion、PCW-Net为2022年发表, RAFT-Stereo、CFNet为2021年发表. 对于深度学习算法, 其程序均是其作者公开的代码, 其中CREStereo、RAFT-Stereo使用其作者预训练好的ETH3D网络模型参数, PSMNet、GA-Net、CFNet、PCW-Net、LBPS使用其作者预训练好的kitti 2015网络模型参数. CDR-Fusion是无监督的方法, 使用其作者预训练好SceneFlow网络模型参数. 这里和深度学习算法作对比, 对比的是其泛化能力, 故使用的不是预训练好的和预测图像相同场景的模型参数. 所有算法均在同一台服务器下运行.

图6是Middlebury部分图像的对比效果. 算法得到的视差图和真值图均用相同方式着色, 故视差图与真值图相比, 越接近越好. 视差图下面是匹配错误分布图, 黑色的点表示匹配错误, 白色的点表示匹配正确, 从匹配错误分布图中可以清楚地看到, 匹配错误像素的位置. 从图6的匹配错误分布图可以看出, 匹配错误的像素集中在图像左边和纹理边缘处, 这些区域往往是遮挡区域. 遮挡区域的视差不能由匹配计算, 只能由周围像素推断填充, 而填充的结果并不可靠, 因此评价指标以非遮挡区域为主, 所有区域为辅. 从图6可以看出, 与LBPS算法相比, 本文算法的匹配错误区域要小, 与PCW-Net算法、CF-Net算法相比, 本文算法的匹配错误的像素左则部分(红色框框起区域)没有明显差别, 纹理边缘处(绿色框框起区域)要更少.

表1、表2是Middlebury对比实验的误匹配率数据. 表中黑体标注的数字表示该数字在各算法中排名第1. 从表1中可以看出, 在非遮挡区域, 9张图中, 本文算法有6张图的误匹配率排名第1, CFNet算法有2张, CREStereo算法有1张, 本文算法平均误匹配率为2.52%, 比表中其他算法都要低. 从表2中可以看出, 在所有区域, 9张图中, 本文算法有5张图的误匹配率排名第1, CFNet算法有2张, CREStereo算法和LBPS算法各有1张, 本文算法平均误匹配率为7.26%, 比表中其他算法都要低.

表3是Middlebury对比实验的平均EPE指标, 在非遮挡区域, 本文算法与CFNet算法的平均EPE均为0.30像素, 并列第1; 在所有区域, 本文算法的EPE为0.54像素, 次于CFNet、RAFT-Stereo算法, 优于LBPS、PCW-Net、PSMNet、GA-Net、CREStereo算法. 对于EPE指标, 误差大的像素比误差小的像素对指标的影响大, 而误差大的像素主要是由于遮挡区域的填充引起的. 在误匹配率对比中, 本文算法在非遮挡区域和所有区域均有优势, 在EPE对比中, 本文算法在非遮挡区域有优势, 在所有区域没有优势, 因此, 本文算法的优势主要在非遮挡区域.

表4、表5是30张SceneFlow图像的平均指标. 从表4中可以看出, 在非遮挡区域, 本文算法的平均误匹配率为3.01%, 小于其他算法, 效果最好; 在所有区域, 本文算法的平均误匹配率为6.39%, 小于其他算法, 效果最好; 从表5中可以看出, 在非遮挡区域, 本文算法的平均EPE为0.35像素, 低于其他算法, 效果最好; 在所有区域, 本文算法的平均EPE为0.76像素, 只次于PCW-Net的0.62像素. 在SceneFlow图像的对比实验和在Middlebury图像的对比实验一致, 均表明本文算法有更低的误匹配率, 优势主要在非遮挡区域.

6 视差优化实验

为了证明视差优化的有效性, 本文以Rocks1和Teddy图像为例, 对比了视差优化前和视差优化后的效果, 见图7. 图7中, 左右视差图是SLGNet生成的未经过视差优化的视差图; 校验图是视差优化步骤中左右一致性校验后形成的标记图, 其中白色为正确匹配区域, 灰色为遮挡区域, 黑色为误匹配区域; 目标视差图是以左视差图为基础经过视差优化生成的图, 即算法最终生成的视差图. 图中, 目标视差图与左视差图相比, 填充了校验图中的遮挡区域和误匹配区域.

表6是视差优化前后的误匹配率的变化, 优化前后的最小值用黑色字体标出. 从表中可以看出, 视差优化前, 非遮挡区域平均误匹配率为3.22%, 所有区域为14.29%, 视差优化后, 非遮挡区域平均误匹配率为2.52%, 所有区域为7.26%, 均有所下降, 但所有区域的下降幅度更大. 无论是在所有区域, 还是在非遮挡区域, 所有图片的误匹配率均下降.

7 结束语

本文提出一种既不同于传统算法又不同于深度学习算法的双目立体匹配算法, 该算法使用神经网络, 但不需要训练数据集训练, 以双目图像互为监督学习, 仅在一对当前图像上反复学习, 用迭代寻优过程不断精确视差图, 在Middlebury、SceneFlow数据集图像上的对比实验表明该算法比CREStereo、RAFT-Stereo、PCW-Net等算法有更低的误匹配率. 该算法使用SLGNet神经网络架构, 该网络产生一对视差图, 故可进行视差优化, 从而可以充分利用视差优化技术增强视差预测效果. 针对SLGNet网络的收敛, 本文还设计了互监督损失函数, 该损失函数的特点是无需视差真值图, 其可以应用于非监督学习的双目立体匹配算法.