心率、呼吸作为人体重要的生命体征, 对于家庭健康监护和人体健康状态分析有着重要作用^[1]. 在传统的检测方法中, 主要运用贴片电极、腕带、指夹、手环等接触式传感器, 被检测者无法自由活动, 对于皮肤敏感或皮肤损伤者容易造成二次伤害. 相比传统的监测方式, 非接触式检测具有显著优势^[2]: 无需佩戴传感器、无感检测, 无泄漏隐私风险. 目前非接触式心率呼吸检测主要通过视频、毫米波雷达实现, 其中采用调频连续波方式调制的毫米波雷达(FMCW)结构简单、集成度高、体积小, 可以检测毫米级微动, 对胸腔位移这类微小运动具有很高的灵敏度, 因此在检测生命体征领域具有广阔的应用前景^[3].

传统心率呼吸检测方法仅针对静态单目标个体, 而生物医学雷达系统仅针对理想条件下的生命体征监测, 即相对静止(例如, 坐着或躺着)的目标检测^[4]. Li等人^[5]使用连续波(CW)多普勒雷达实现单人心率呼吸检测, 提出一种基于小波变换的数据长度变化技术, 实现体征的快速检测. 目前已经实现了身体随机运动情况下的雷达心率检测, Muñoz-Ferreras等人^[6]通过两个雷达消除了与生命体征幅度相似的运动, 但限制条件是患者位置要精准的在两个雷达之间. 雷达对特定人体运动的跟踪也已被证明, 但仅适用于没有物体存在的室内环境^[7], 然而在居家或临床等真实场景中, 存在较强的静止杂波反射, 雷达难以正确跟踪运动目标.

目前雷达体征检测多为单人检测, 多目标体征检测少有研究, 但在实际应用场景中需要检测两人或更多目标的生命体征. 对于以上情况, Wang等人^[8]研究了高度集成的120 GHz MIMO雷达系统, 用于人体的3D定位和同步生命体征检测, 但该方法需要受试者与雷达距离不同, 对于距离相同角度不同的受试者无法检测; Ahmad等人^[9]使用FMCW波形和多个接收通道固有的距离门控功能来分隔空间内的受试者, 但在测量过程中, 要求两名受试者交替呼吸, 这在实际应用中很难实现; Wang等人^[10]提出Beamforming、微多普勒信号提取技术检测同距离不同角度的双人心率呼吸, 实验场景要求受试者与雷达的夹角为60°, 但是实际应用场景无法严格保证受试者与雷达的角度, 本文针对以上问题, 提出一种距离角度均可变的多人心率呼吸检测算法.

1 FMCW雷达检测心率呼吸原理 1.1 FMCW雷达信号调制与解调

FMCW雷达检测心率呼吸基本原理在于人体在进行心跳呼吸等生理活动时, 胸腔会发生毫米级或亚毫米级起伏微动, 微动引起FMCW雷达频率和相位变化, 通过提取目标相位获取胸腔位移变化, 实现检测心率呼吸的目的^[11]. 本文采用调频连续波雷达, 其发射信号为 $S(t)$ :

$S\left( t \right) = \alpha \cos \left( {2{\text π} \left( {{f_0} + \beta t} \right)t} \right)$

(1)

其中, $\alpha$ 为信号幅值、 $f_{0}$ 为初始频率、 $\; \beta$ 为调频连续波频率斜率.

雷达回波时延为 $\tau$ , 回波信号为 ${S_R}(t)$ :

${S_R}(t) = A\cos \left( {2{\text π} \left( {{f_0} + \beta \left( {t - \tau } \right)} \right)\left( {t - \tau } \right)} \right)$

(2)

回波信号与发射信号进行混频, 经过低通滤波器后得到中频信号 ${S_{IF}}\left( t \right)$ :

${S_{IF}}(t) = A\alpha {{\rm{e}}^{(j(2{\text π} \frac{B}{T}\tau t + 2{\text π} {f_0}\tau + {\text π} \frac{{\text{B}}}{T}{\tau ^{\text{2}}}))}}$

(3)

其中, A为回波幅值, $\tau$ 为时延.

中频信号频率为: ${f_{IF}} = \dfrac{{2BR}}{{cT}}$ .

中频信号相位为: ${\varphi _{IF}} = \dfrac{{4{\text π} R}}{\lambda }$ , 其中, ${\lambda }$ 为波长、c为光速、R为与雷达的距离, B为调频连续波的带宽、T为一个chirp的周期.

将chirp数据存入列数组中, 将chirp的AD采样频率称为快时间轴采样频率, 对于每个chirp按照时间顺序采样称为慢时间轴采样, 如图1所示.

1.2 生命体征信号提取

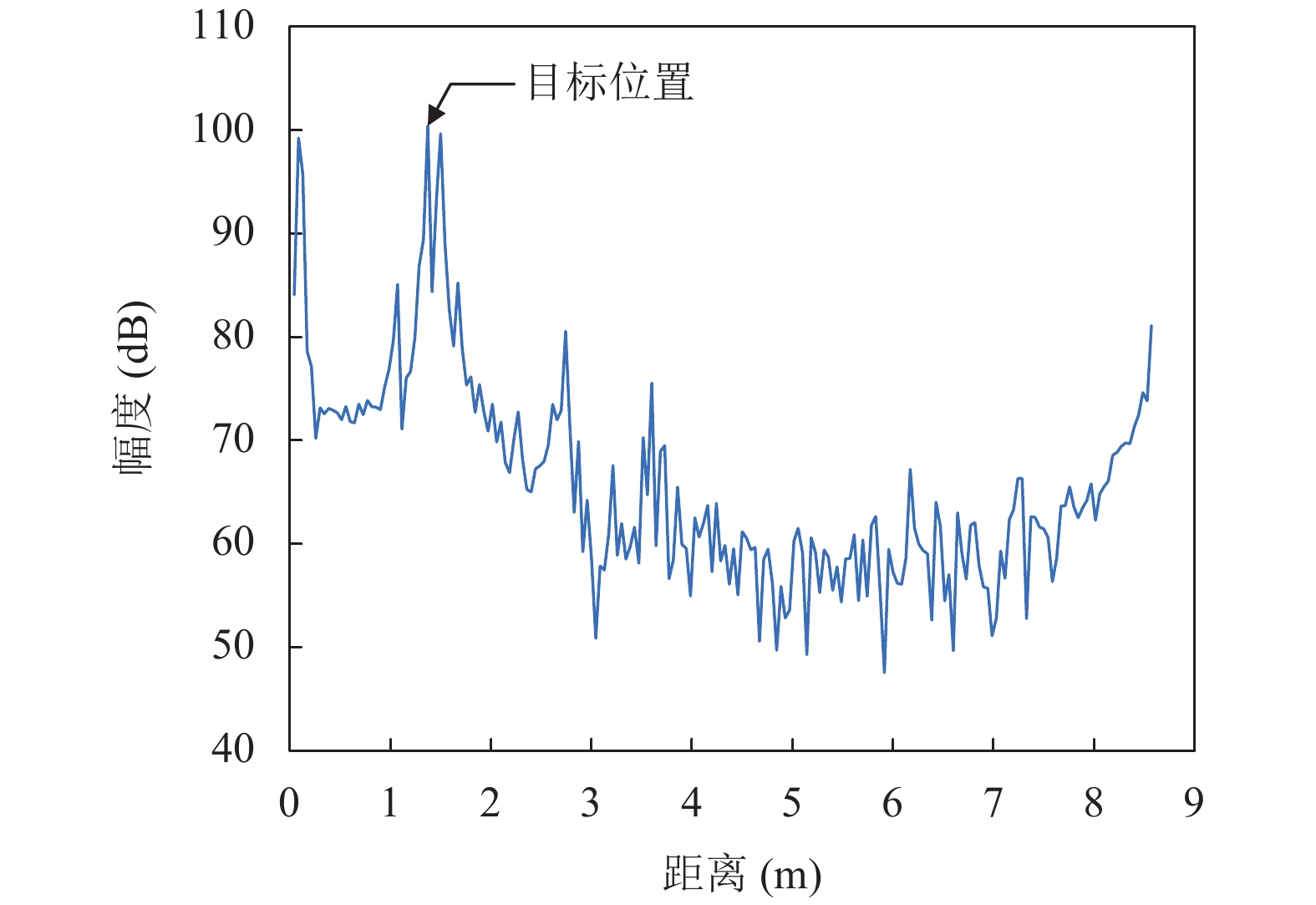
对所有chirp做一维FFT, 得到距离-幅度图, 如图2所示. 对所有chirp非相干累计, 能量最大的点即为目标位置, 由于数据采集模式为IQ正交采样^[12], 所以反正切后可获得相位如式(4):

$\varphi \left( n \right) = \arctan \left[ {\frac{{{x_I}\left( n \right)}}{{{x_Q}\left( n \right)}}} \right]$

(4)

其中, n为能量最大点的索引值, $x_{I}(n)$ 为I通道信号, $x_{Q}(n)$ 为Q通道信号.

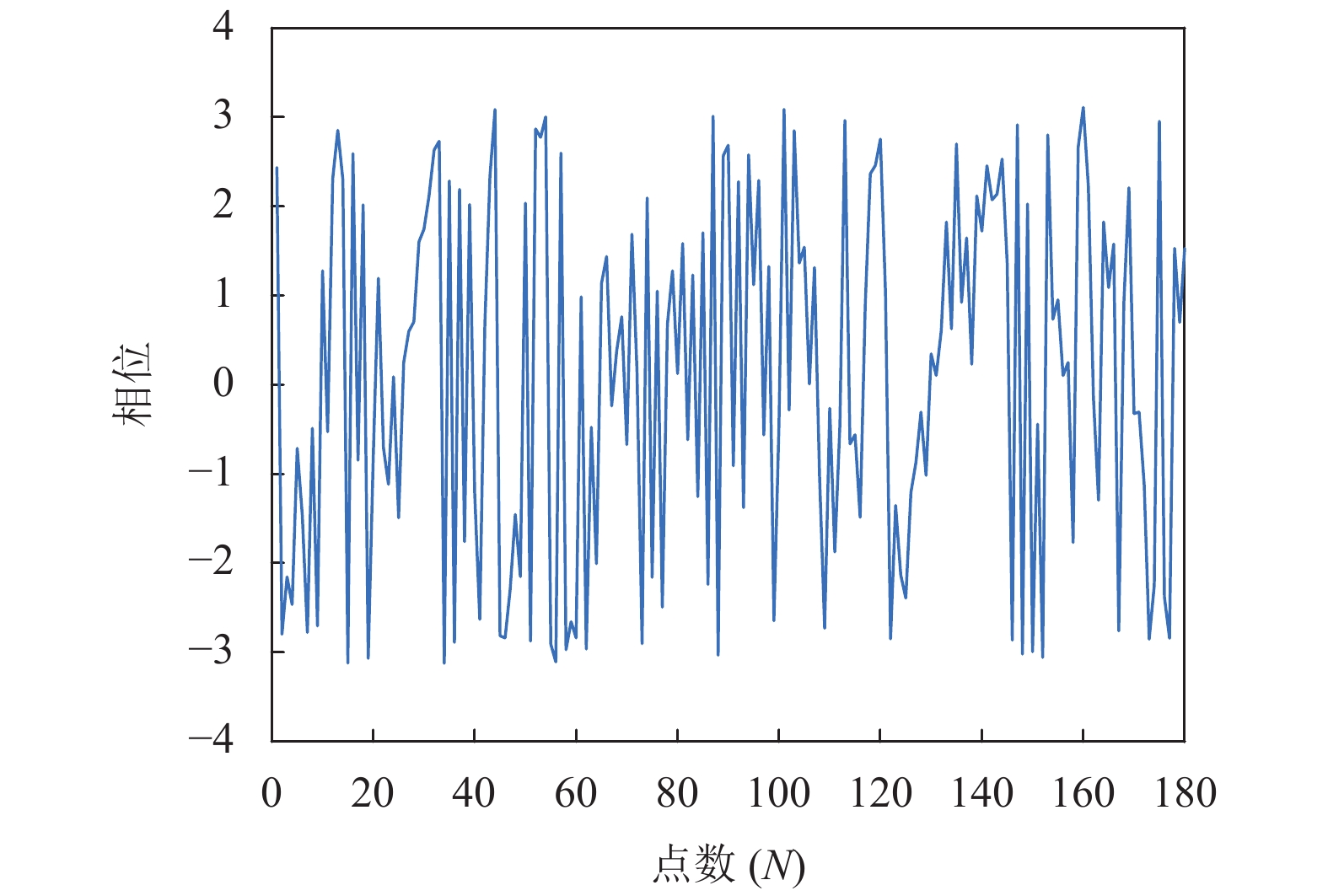
对反正切后的相位进行相位解缠绕. 得到最终相位时间序列. 解缠绕前和解缠绕后的相位时间序列如图3和图4所示.

1.3 基于Capon波束成形实现多目标分离

上述方案是直接从中频信号提取相位, 经过相位解缠之后得到相位时间序列. 若两目标处于同一距离, 此时两目标的胸腔振动相位无法分离, 因此通过上述直接提取相位的方法无法实现检测多人心率呼吸.

故本文使用由3个发射通道和4个接收通道组成的调频连续波雷达, 用于确定多个目标的角度, 从而在目标胸口聚焦形成单个波束, 将多个目标信号分离. 本文所提出的方案可以最大程度抑制其他角度的噪声及杂波.

雷达检测到多目标之后, 需要分别提取每个目标的相位变化, 若多目标与雷达径向距离相差较大, 距离FFT频谱峰值区分明显, 可分别提取目标相位信息; 若距离相同, 到达角不同, 由于人体胸腔波动差异性较小, 回波信号难以分离, 难以提取多目标相位信息, 此时必须抑制其他角度信号, 保持目标角度信号功率稳定. 常用的波达角检测算法, 如MUSIC算法, 但其限制是需要知道目标个数, 并需要保证天线数大于目标个数, 因此本文采用Capon波束成形算法对多目标分别提取信号.

若雷达有M阵元, 选用第1阵元为参考点, 则导向矢量为:

$\begin{split} a\left( \theta \right) =&{\text{ [1, }}{{\text{e}}^{ - j2{\text π} {f_0}\frac{{d\sin \left( \theta \right)}}{c}}}{\text{, }}{{\text{e}}^{ - j2{\text π} {f_0}\frac{{2d\sin \left( \theta \right)}}{c}}}, \cdots, {{\text{e}}^{ - j2{\text π} {f_0}\frac{{\left( {M - 1} \right)d\sin \left( \theta \right)}}{c}}}{\text{]}} \end{split}$

(5)

假设有N个目标, 回波信号分别为 $s_{1}(n), s_{2}(n), \cdots, s_{N}(n)$ , 分别以不同入射角 $\theta_{N}$ 到达天线阵列, 接收信号表示为:

$X\left( n \right) = a\left( {{\theta _N}} \right){S_N}\left( n \right)$

(6)

若存在权向量 $\omega$ 使得输出为 $\theta$ 角度的信号, 并且其他角度被最大程度抑制, 输出为:

$y\left( n \right) = {\omega ^{\rm{H}}}X\left( n \right)$

(7)

输出功率为:

$\begin{gathered} P = E\left[ {{{\left| {y\left( n \right)} \right|}^2}} \right] = E\left[ {{\omega ^{\rm{H}}}X\left[ n \right]{X^{\rm{H}}}\left[ n \right]\omega } \right] = {\omega ^{\rm{H}}}R\omega \end{gathered}$

(8)

其中, R为 $X(n)$ 的协方差.

假设角度 $\theta_{M}$ 为目标角度, 其他角度能量为 $N(n)$ , 接收信号分解如式(9)所示, 输出为式(10)所示:

$X\left( n \right) = a\left( {{\theta _M}} \right){S_M}(n) + N\left( n \right)$

(9)

$y\left( n \right) = {\omega ^{\rm{H}}}a\left( {{\theta _M}} \right){S_M}\left( n \right) + {\omega ^{\rm{H}}}N\left( n \right)$

(10)

由于需要提取 $\theta_{M}$ 角度信号, 其他角度最大程度抑制, 所以需满足条件:

${\omega ^{\rm{H}}}a\left( {{\theta _M}} \right) = 1$

(11)

${\omega ^{\rm{H}}}N\left( n \right) = 0$

(12)

虽然其他角度信号被抑制, 但输出噪声可能增大, 从提高信噪比的角度考虑, 所以加上约束条件式(13)使得输出功率最小.

$\mathop {\min }\limits_\omega p = \mathop {\min }\limits_\omega {\omega ^{\rm{H}}}R\omega$

(13)

采用拉格朗日乘数法求解, 构造:

$L = {\omega ^{\rm{H}}}R\omega - \lambda \left( {1 - {\omega ^{\rm{H}}}a\left( {{\theta _M}} \right)} \right)$

(14)

解得权向量 $\omega$ 为式(15)所示:

$\omega = \frac{{{R^{ - 1}}a\left( \theta \right)}}{{a{{\left( \theta \right)}^{\rm{H}}}{{\left( {{R^{ - 1}}} \right)}^{\rm{H}}}a\left( \theta \right)}}$

(15)

功率为式(16)所示:

$p = \frac{1}{{a{{\left( \theta \right)}^{\rm{H}}}{R^{ - 1}}a\left( \theta \right)}}$

(16)

首先针对无目标空间使用Capon算法, 对0– ${\text π}$ 角度按1°为步长计算功率P. 得到角度-功率谱, 作为搜索目标的背景模板.

若有目标出现, 当目标运动时, 不做检测; 若目标静止, 计算角度-功率谱, 与背景模板的角度-功率谱做差值处理得到目标所处角度.

将 $\omega$ 代入式(7)可得到目标信号:

$y\left( n \right) = \sum\limits_{\theta = {\theta _S}}^{{\theta _D}} {\omega _\theta ^{\rm{H}}X\left( n \right)}$

(17)

$y\left( n \right) = \sum\limits_{\theta = {\theta _S}}^{{\theta _D}} {\frac{{{R^{ - 1}}a\left( \theta \right)X\left( n \right)}}{{a{{\left( \theta \right)}^{\rm{H}}}{{\left( {{R^{ - 1}}} \right)}^{\rm{H}}}a\left( \theta \right)}}}$

(18)

其中, $\omega$ 为权向量, $a(\theta)$ 为导向矢量, $\theta$ 为波束聚集角度, $X(n)$ 为接收信号, R为接收信号自相关矩阵. $y(n)$ 即为波束成形之后的目标时域信号.

通过推导得出的式(18)可将 $\left[\theta_{S}, \theta_{D}\right]$ 角度信号分离, 使干扰角度的能量被最大程度抑制.

2 多目标心率呼吸检测策略

针对Capon波束成形的聚焦角度, 特别是零陷区域信噪比低的问题, 提出了一种基于自相关滤波的自适应谐波跟踪算法滤除噪声, 提高信噪比; 提出粒子群算法结合样本熵优化的VMD算法解决心率呼吸信号难以分离的问题.

2.1 改进的自相关滤波算法

由于心率呼吸有明显的周期性, 因此对心率、呼吸信号构建数学模型:

$S\left( t \right) = {A_B}\sin ({f_B}t + {\varphi _B}) + {A_H}\sin ({f_H}t + {\varphi _H})$

(19)

其中, $A_{B}$ 、 $A_{H}$ 为呼吸、心跳信号幅度, $f_{B}$ 、 $f_{H}$ 呼吸、心跳信号频率, $\varphi_{B}$ 、 $\varphi_{H}$ 为呼吸、心跳信号相位.

利用周期信号自相关时间范围宽的特点, 设计了一种基于自相关的自适应去噪算法, 其原理如图5所示.

由于心率呼吸信号为窄带信号, 其自相关时间 $T_{s}$ 范围较宽、干扰噪声为宽带信号, 其自相关时间 $T_{N}$ 范围较窄, 超出自相关时间后他们的自相关函数会迅速衰减, 因此延时时间 $\Delta$ 选取范围为 $T_{s}< \Delta < T_{N}$ .

由于延迟 $\Delta$ 比噪声自相关范围大, 因此经过延时之后的 $y_{n}(k-\Delta)$ 与 $y_{n}(k)$ 不相关, 自适应滤波过程中, 这个分量不能被响应, 窄带自相关范围窄, 所以利用自适应滤波器的相关抵消作用, 使得 $y_{s}(k)$ 被抵消掉, 抵消器输出的误差信号为 $e(k) \approx y_{n}(k)$ , FIR滤波器输出为相关的分量 $y_{s}(k)$ 的估计值, 从而将心率呼吸信号分离出来. 由于延迟 $\Delta$ 是由输出计算得到, 因此该反馈能够根据噪声和信号频率自适应调节延迟, 在一定范围内跟踪信号频率变化, 从而实现自调谐滤波.

2.2 改进的VMD算法分离呼吸心率信号

常用的心率呼吸提取方法有: 傅里叶变换、短时傅里叶变换、小波变换、经验模态分解^[13], 但是这些方法都有明显的缺陷: 傅里叶变换对于心率这种非平稳信号处理能力不足, 小波变换的小波基选取困难, 小波基无自适应性, 而经验模态分解虽然是自适应信号处理方法, 但是存在模态混叠、端点效应、模态数不可预测等缺陷, 所以不适用于心率呼吸信号的提取. 因此本文选用变分模态分解算法提取心率呼吸信号.

VMD虽然可以任意设定模态数k, 但是k值的选取是一个亟待解决的问题, 如果选取过小则会造成模态混叠, 选取过大则会产生一些虚假分量. 因此本文提出了粒子群算法(PSO)优化k值的自适应变分模态分解方法解决心率呼吸难以分解的问题.

2.2.1 VMD算法原理

VMD不同于EMD, 重新定义了约束条件更加严格的模态分量, 表达式为一个调幅-调频信号^[14]:

${\mu _k}(k) = {A_k}(t)\cos \left( {{\phi _k}\left( t \right)} \right)$

(20)

其中, $A_{k}$ 是包络函数, $\phi_{k}(t)$ 为相位, ${\phi}_{k}^{\prime}(t)$ 为瞬时相位, k为需要分解的模数. VMD算法通过在变分框架基础上搜寻约束模型的最优解, 根据信号的频域特性, 每个分量的中心频率和带宽不断地迭代更新, 直到满足迭代条件. 约束模型如式(21):

$\left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{\left\{ {{u_k}} \right\}, \left\{ {{\omega _k}} \right\}} \left\{ {\displaystyle\sum\limits_k {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \dfrac{j}{{{\text π} t}}} \right){u_k}\left( t \right)} \right]{{\rm{e}}^{ - j{\omega _k}t}}} \right\|_2^2} } \right\}} \\ {{\rm{s.t.}}\displaystyle\sum\limits_k {{u_k}} } \end{array}} \right.$

(21)

其中, $\left\{u_{k}\right\}$ 为分解得到的k个模态分量, $\left\{\omega_{k}\right\}$ 为各模态分量的中心频率.

求解该模型时还要引入增广Lagrange函数, 将约束变分问题转换为非约束变分问题:

$\begin{split} L(\left\{{u}_{k}\right\}, \left\{{\omega }_{k}\right\}, \lambda )=&\alpha {\displaystyle \sum _{k}{\Vert {\partial }_{t}[(\sigma (t)+\frac{j}{{\text π} t})\cdot{u}_{k}(t)]{{\rm{e}}}^{-j{\omega }_{k}t}\Vert _{2}^{2}}}\\ & + {\Vert f(t)- {\displaystyle \sum _{k}{u}_{k}(t)}\Vert_{2}^{2} } + \langle \lambda (t), f(t)- {\displaystyle \sum _{k}{u}_{k}(t)}\rangle \end{split}$

(22)

其中, $\alpha$ 为二次惩罚因子, $\lambda(t)$ 为拉格朗日算子.

2.2.2 PSO-SE-VMD算法

为解决VMD算法的k值选取问题, 本文提出了PSO-SE-VMD算法, 该算法引入粒子群算法(PSO), 并以最小样本熵(SE)^[15]为准则选取最优k值, 将信号分解为k个模态分量.

粒子群算法是一种模拟鸟群捕食而设计的智能寻优算法, 该算法定义了一种粒子, 粒子有速度和适应度函数值两个属性, 来不断调整飞行方向, 并将自身极值传递给种群其他粒子, 粒子可根据记录的自身最优位置和种群中最好的粒子位置不断学习, 不断逼近最优解.

引入样本熵作为粒子群的适应度函数. 样本熵^[16]是用来度量时间序列复杂性的方法, 常用于评价生命体征信号的复杂性. 熵越大说明包含的频率成分越杂, 熵越小说明包含频率成分越少.

PSO-SE-VMD求解的具体步骤如下.

(1)初始化PSO的所有参数, 设PSO的粒子位置为分解层数k, 迭代次数为m (m=0), 最大迭代次数为M.

(2)将所有的粒子位置作为参数, 进行VMD分解, 并计算所有模态分量的SE值; 最小SE为局部极小值.

(3)判断所有模态分量是否在呼吸 (0.2–0.4 Hz)和心率(0.8–2 Hz)范围内. 若不在则移除该极值点.

(4)将局部极小值和其他粒子的局部极小值进行对比, 得到全局极小值. 并根据全局最小值和粒子本身局部极小值更新粒子的位置和速度.

(5) $m=m+1$ ; 重复步骤(2)–(4), 当 $m=M$ 时, 停止迭代, 此时可得到PSO搜寻的最优k值.

VMD分解步骤如下. VMD分解效果如图6所示.

(a)初始化 $\left\{u_{k}\right\}$ 、 $\left\{\omega_{k}\right\}$ 、 $\lambda$ 、n为0; n为迭代次数.

(b)迭代次数自加1, 进入迭代循环.

(c)更新 ${u}_{k}$ , $\omega_{k}$ . 更新公式为:

${u_k}^{n + 1}\left( \omega \right) = \frac{{x\left( \omega \right) -\displaystyle \sum\limits_{i = 1, i \ne k}^K {{u_i} + \dfrac{{\lambda \left( \omega \right)}}{2}} }}{{1 + 2\alpha {{\left( {\omega - {\omega _k}} \right)}^2}}}$

(23)

${\omega _k}^{n + 1} = \frac{{\int_0^\infty {\omega {{\left| {{u_k}\left( \omega \right)} \right|}^2}d\omega } }}{{\int_0^\infty {{{\left| {{u_k}\left( \omega \right)} \right|}^2}d\omega } }}$

(24)

(d) $n=n+1$ , 判断 $n=K$ , 若不满足则重复步骤(3).

(e)更新 $\lambda$ , 更新公式为:

$\lambda^{n+1}=\lambda^{n}+\tau \left(x-\sum_{k} u_{k}^{n+1}\right)$

(25)

(f)代入迭代停止条件, 若满足则退出循环, 输出k个模态分量. 迭代停止条件为式(25):

$\sum\limits_k {\left( {\frac{{\left\| {u_k^{n + 1} - u_k^n} \right\|_2^2}}{{\left\| {u_k^n} \right\|_2^2}}} \right)} < \varepsilon$

(26)

2.3 短时自相关法检测心率呼吸

自相关函数如式(26)所示:

${R_{xx}}\left( m \right) = \sum\limits_{n = - \infty }^{ + \infty } {S{{\left( n \right)}_H}S{{\left( {n - m} \right)}_H}}$

(27)

由于心率呼吸是明显的周期信号, 利用周期信号自相关函数的性质和随机噪声自相关函数性质. 当m为0或者周期T时, $R_{x x}(m)$ 出现峰值, 且随着m增大, 峰值逐渐减小. 当m为0时, 自相关函数最大, 此时代表信号的平均功率; 当m>0, 且 $R_{x x}(m)$ 处于第1个极大值点时, 此时对应的m为周期函数的周期, 因此心率为:

${V_{{\rm{heart}}}} = 60\times \frac{1}{m}$

(28)

同理检测呼吸频率:

$\left\{ {\begin{array}{*{20}{l}} {m > 0} \\ {{R_{xx}}\left( m \right) = \displaystyle\sum\limits_{n = - \infty }^{ + \infty } {S{{\left( n \right)}_B}S{{\left( {n - m} \right)}_B}} } \\ {{V_{{\rm{breath}}}} = 60\times \dfrac{1}{m}} \end{array}} \right.$

(29)

较大的呼吸运动幅度可能会产生非常接近心率的高阶谐波, 并且具有与心跳信号相当的幅度. 这种干扰会导致心率测量误差, 无法过滤. 从心率自相关函数可以判断呼吸频率的二次谐波和三次谐波是否与心率信号混叠^[17], 若存在则去除此谐波, 重新计算心率.

3 实验结果与分析

为了验证本文提出算法的有效性和鲁棒性, 进行了相关验证性实验. 两位被检测者作为实验对象, 分别完成20组实验: (1)两位被检测者坐在雷达前方, 与雷达距离相同且与雷达呈30°夹角. (2)两位被检测者坐在雷达前方, 与雷达距离相同且与雷达呈60°夹角.

3.1 实验参数

本文使用的雷达是TI公司推出的IWR1843毫米波雷达, 是工业级调频连续波雷达, 工作频率在77–81 GHz, 天线部分是3发4收天线阵列, 实验场景如图7所示. 将实验所得数据与欧姆龙腕带式设备测得数据做对比实验. 本次实验雷达参数如表1所示.

实验时, 两位被检测者坐在雷达前方, 与雷达距离相同为1.5 m左右. 静坐并保持平稳呼吸状态, 通过DAC1000数据记录板卡采集雷达中频原始数据. 采集了两位检测者相同距离、不同角度的原始数据进行分析, 验证算法的可行性以及准确性. 心率呼吸的提取分别选择了30°和60°来验证本文普适性.

3.2 实验结果分析

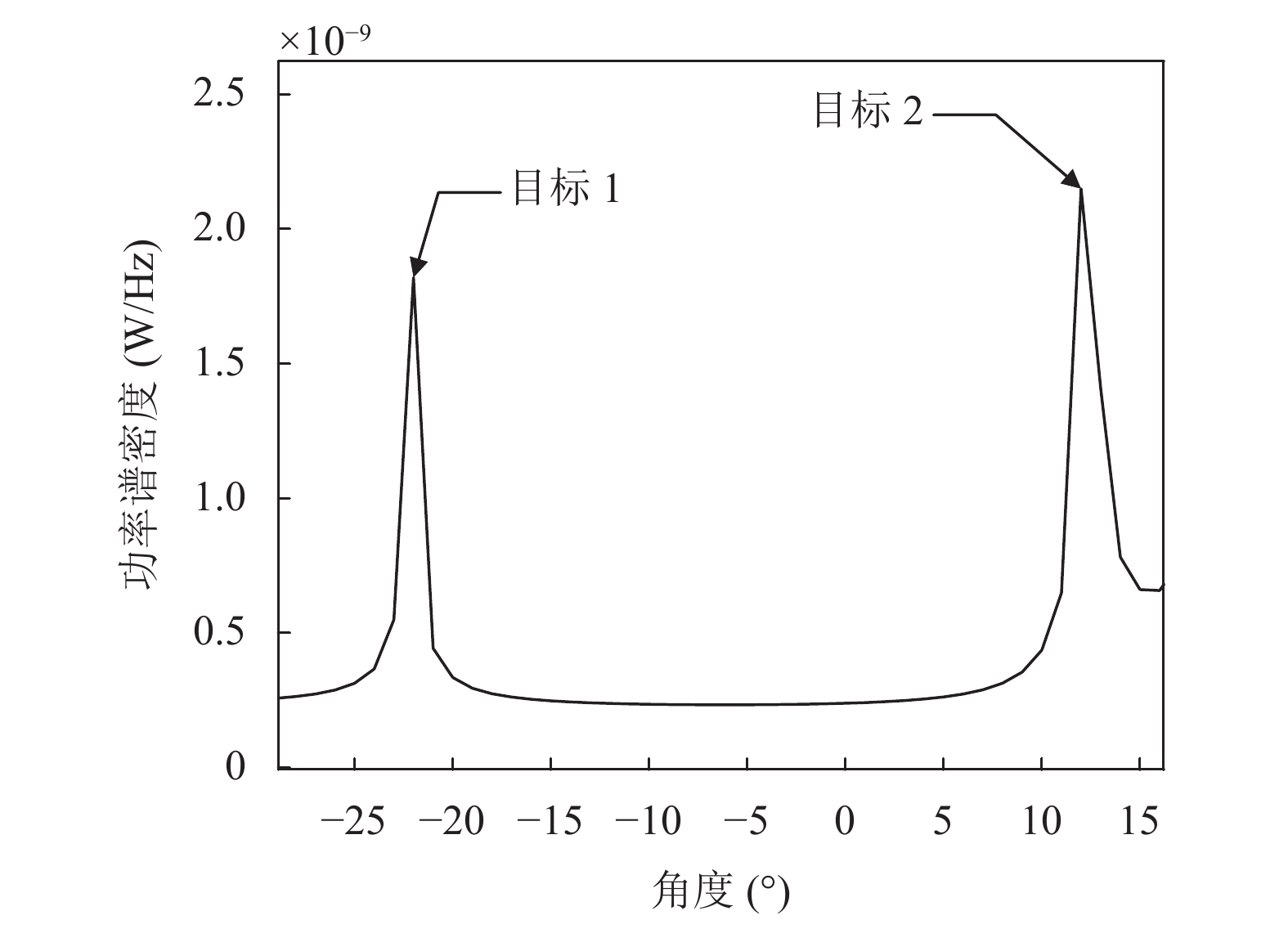
根据Capon波束成形算法获取的角度-功率谱与背景功率谱做差后, 可清晰分辨目标角度, 波束聚焦范围为针对目标角度左右5°, 这样可以最大程度抑制其他角度回波能量, 以达到划分目标检测仓的目的. 使用Capon算法的角度-功率谱和目标空间二维视图分别如图8和图9所示.

从图8可以看出实验人体目标在空间−20°和13°范围内存在, 夹角为33°, 与实验场景设置的30°相差3°. 分别对其使用Capon波束成形算法进行目标角度提取, 结果如图10所示, 由此可验证目标分离算法的可行性.

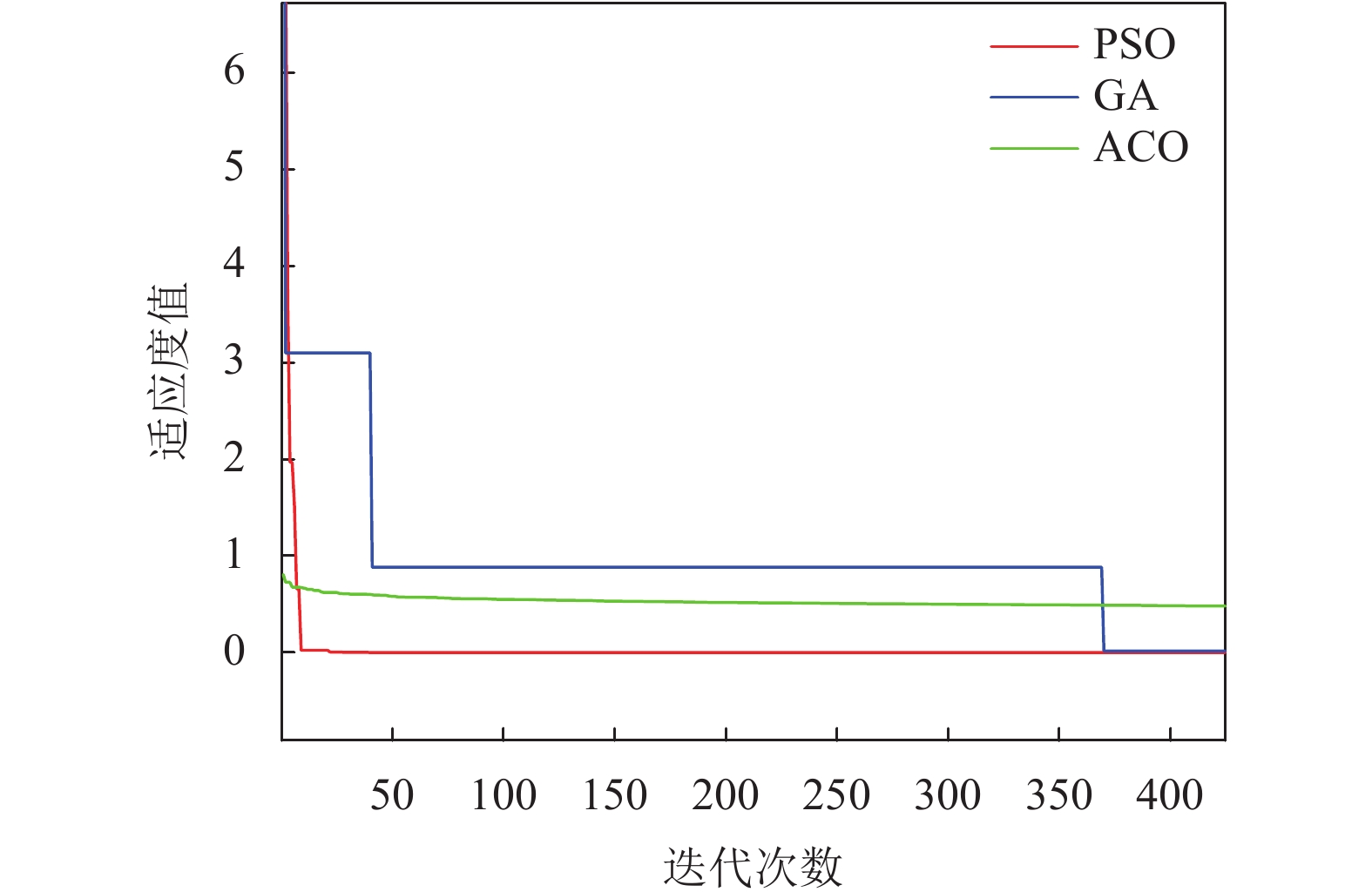
如图11所示的3种典型优化算法, 蚁群算法(ant colony optimization, ACO)、粒子群算法(particle swarm optimization, PSO)、基因遗传算法(genetic algorithm, GA). 蚁群算法和基因遗传算法在VMD分解上都有所研究以及应用, 为验证粒子群算法的优越性, 对3种算法进行对比, 并通过适应度进化曲线对3种算法进行性能比较. 从测试结果来看, 蚁群算法陷入局部最优解, 基因遗传算法虽然随着迭代次数增加不断接近最优解但是速度很慢, 而本文使用的粒子群算法不仅收敛速度快并且精度高, 具有最佳性能. 以上的实验结果验证了本文所使用的基于粒子群算法优化的VMD分解对于多人心率呼吸检测的优越性.

经过不同角度的心率检测数值对比, 验证本文方法检测心率的可行性. 本文设置5组心率检测对比实验. 随机选取两组绘制对比曲线. 图12表示相同距离、30°夹角的两目标的心率对比曲线, 图13表示相同距离、60°夹角的两目标心率对比曲线.

在图12和图13中, TURE折线表示欧姆龙腕带设备检测的心率折线图, VMD折线表示传统VMD算法得到的心率折线图, PSO-SE-VMD折线表示本文提出的PSO-SE-VMD算法得到的心率折线图. 图12和图13实验中的PSO参数如下: 种群规模为2, 最大速度为3, 惯性权重为0.6, 个体加速因子和社会加速因子分别为2.8和1.3.

本文选均方误差(mean square error, MSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为误差评估指标. 表达式如下:

${\textit{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}}$

(30)

$MAPE{\text{ = }}\frac{{\text{1}}}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} \times 100{\text{%}}$

(31)

其中, ${\hat y_i}$ 为预测值, ${y_i}$ 为真实值, $n$ 为样本数量.

从表2可以得知, PSO-SE-VMD算法在30°和60°时的预测均优于VMD算法, PSO-SE-VMD算法相较于VMD在30°和60°的MSE以及MAPE大幅度减小. 综上所述, 本文提出的PSO-SE-VMD算法优于传统VMD算法, 并且目标角度相差较大时, 目标分离效果更好, 同时侧面证明了PSO针对本问题的有效性.

心率呼吸信号是非平稳信号, VMD算法对非平稳、非线性信号具有良好处理效果, 因此选择VMD算法解决心率呼吸信号分解问题. 但是在实际场景k值(模态数)的选择只能依赖经验选取, 主观性较强, 所以无法较好适应不同场景的变化, 对于多人心率呼吸检测的复杂场景来说不具有较好鲁棒性, 而粒子群算法具有收敛速度快、参数少、算法简单易实现的优点, 可以选取最优k值以适应不同场景.

4 结论

本文通过理论分析及实验, 验证了基于毫米波雷达的多目标心率呼吸检测的有效性和鲁棒性. 采用Capon波束成形算法解决了多目标无法有效分离的问题, 并且提出了一种PSO-SE-VMD算法解决了心跳和呼吸信号分离不完全的问题. 多目标心率呼吸检测与腕带式检测的对比实验结果表明本文所提方法优于传统VMD算法, 有效提升了检测范围以及多角度自适应的能力. 为FMCW雷达检测心率呼吸提供了一种多人目标分离及信号提取的有效策略.

本文提出的多目标心率呼吸检测算法进一步在非接触式心率呼吸检测领域的多目标检测方向进行延伸. 但是由于数据样本的独特性和难以获取性, 因此在下一步工作中还要继续扩充数据库, 增加样本多样性.