调制识别是信号解调的关键, 准确的识别调制方式, 是信号进行下一步分析处理的前提. 无论在军用领域中的比低 情况下的调制方式的识别, 通过信息熵的方式去提取信号的特征, 在改进遗传算法后送到超限学习机中, 识电子对抗还是民用领域频谱管理, 准确、高效的通信信号调制方式识别都至关重要[1].
通信信号自动调制识别技术发展至今, 主要有3个技术方向: 判决理论、统计模式和深度学习为基础的识别方法[2-4]. 利用判决理论去识别的方法对信号的先验信息要求高, 需要人为设置判决门限使其性能受限. 使用统计模式的方法去识别主要依赖于特征提取和分类器的选择, 对先验信息的要求相对不高. 随着人工智能和通信的融合的发展, 应用深度学习的方法则充分利用通信系统中的大数据, 改善识别精度; 自动提取信号特征; 利用深度学习工具迅速迭代演进, 解决复杂通信场景下复杂调制识别的难题.
常见的信号预处理方式有时频图、星座图、高阶累积量、循环谱、眼图、熵以及特征融合等[5]. Shannon提出[6]信息熵理论, 最初用来描述信息的不确定度. 近几年, 国内学者将信息熵理论应用在基于深度学习的调制识别特征提取. 文献[7]研究的是在信噪别11种混合信号, 在2 dB信噪比下整体的识别精度可以达到92.5%. 文献[8]通过短时傅里叶变化, 实现时频信号转换, 利用图像处理方法, 使用卷积神经网络完成7种信号的调制识别. 文献[9]搭建了深度置信网络, 应用提取到的信号数据, 去完成数字调制方式和OFDM信号的调制方式识别. 上述的识别方法如卷积神经网络(CNN)、深度置信网络(DBN)等, 凭借强大的复杂拟合能力, 有效提升了通信信号调制方式识别的精度, 但其网络架构复杂, 运算量大, 对于设备过度依赖. 因此本文针对自动调制识别中的简单调制方式识别, 将MPSK、MQAM信号转换为星座图像, 对星座图像进行图像增强[10], 使用轻量型神经网络MobileNetV3作为分类网络, 解决调制识别中网络复杂的问题. 在保持识别精度的前提下, 网络的参数量有效减小, 降低训练时间, 在自动调制识别实际应用中具有重要意义.
1 信号模型和训练图像生成 1.1 信号模型通信信号接收器对接收到的信号进行下变频和同步处理, 处理后的信号为基带采样信号. 接收信号的候选集为{BPSK、QPSK、8PSK、16QAM、64QAM}之一. 离散信道下的信号模型如下:
| y(t)=∑nan(t)s(t−τn(t)) | (1) |
其中, s(t)表示带通输入信号,
| s(t)=Re{˜sej2πfct} | (2) |
那么信道的输出表示如下:
| y(t)=Re{[∑nan(t)e−j2πfcτn(t)˜s(t−τn(t))]ej2πfct} | (3) |
那么输出的复包络为:
| ˜y=∑nan(t)e−j2πfcτn(t)˜s(t−τn(t))=∑n~an(τn,t)˜s(t−τn(t)) | (4) |
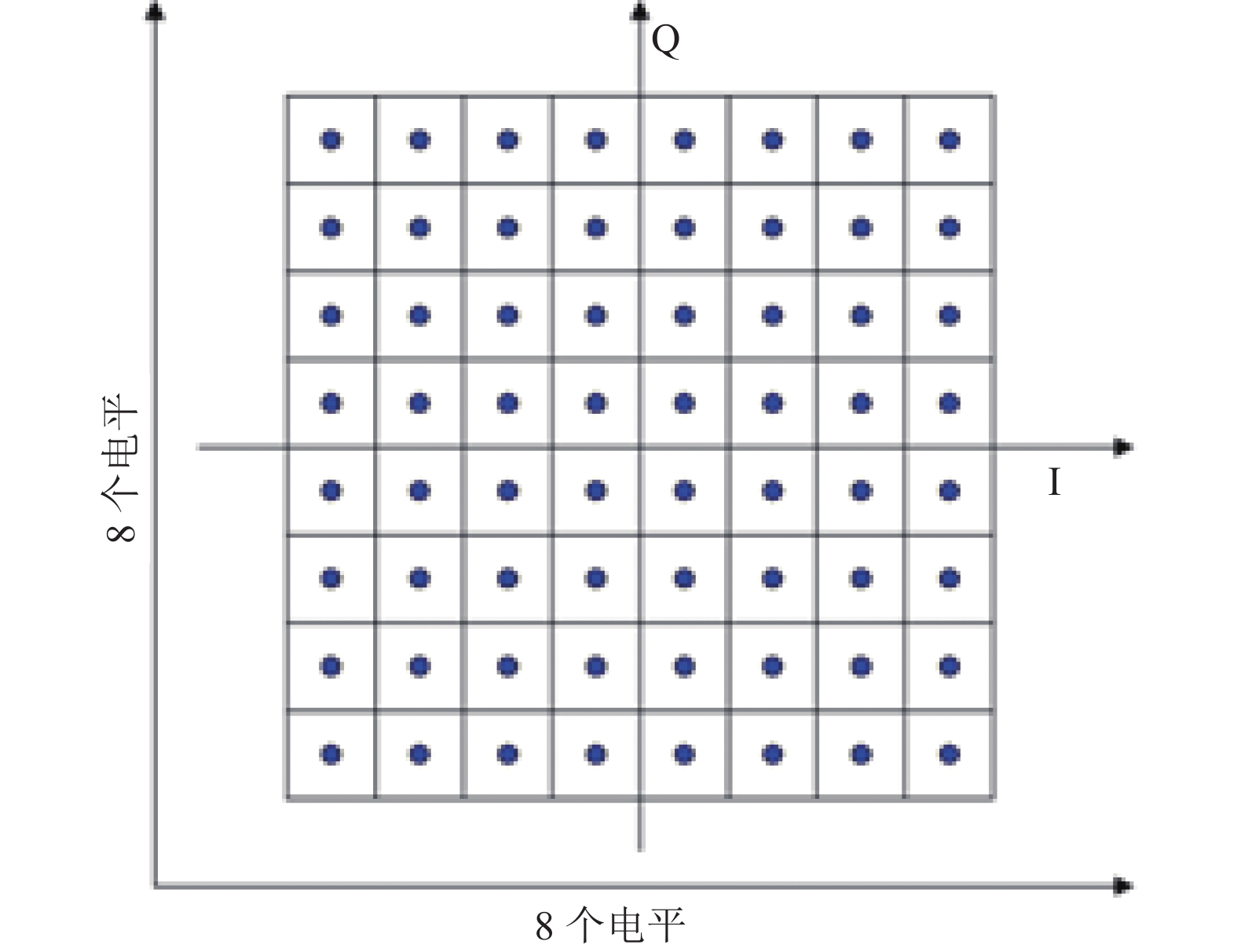
以QAM调制为例, 经过信道编码的二进制比特流进入QAM调制器, 信号被分为两路, 一路给I (同相分量), 另一路给Q (正交分量), 每一路一次给3比特数据, 这3比特的二进制数据一共有8种不同状态, 分别对应8种不同的电平幅度, I有8个不同幅度电平, Q有8个不同幅度电平, 且I、Q两路信号正交, 任意一个I的幅度与任意一个Q的幅度组合都会在极坐标图上映射一个相应的星座点, 每个星座点代表由6个比特的数据组成的一个映射, I和Q共有8×8共64中组合状态, 最后映射的星座图如图1所示.
1.2.1 星座图星座图已经广泛地应用于调制信号的二维表示将接收信号的样本映射到复平面的散射点, 但是复平面可以无限延伸, 而图像可以描绘的区域是有限的. 因此选取复平面的一部分来生成星座图图像, 如果选取的区域太小, 则一些信号样本可能由于噪声不在图像中, 反之, 选取的面积过大, 信号样本可能聚集在一个小区域内, 产生重叠. 图2(a)给出了星座图图像示例, 该星座图有1 000个8PSK调制信号样本产生, 信噪比为2 dB.
|
图 1 64QAM星座图 |

|
图 2 信噪比为2 dB的8PSK不同类型图像 |
1.2.2 灰度图像
假设像素的密度很大, 星座图像就可以等效为一个完整的信号样本. 在这种情况下每个样本可以由一个或多个像素表示. 然而, 由于像素密度有限, 一个像素内可能含有一个或多个样本, 如图2(b)所示. 星座图是一个二进制图像, 其中具有一个或多个采样点的像素被类似表示. 将像素强度值定义为像素内的采样数, 例如像素3、7、14的强度值可以表示为0、2、5. 这样就可以实现星座图与灰度图像的转换, 如图2(c)所示.
1.2.3 增强灰度图像灰度图像仍然有两个局限性, 不考虑每个样本在像素内的位置和默认忽视了像素里各个样本对旁边像素的干扰. 为解决这两种局限, 将图像处理中的增强灰度图像思想引入. 此外, 采用了衰减指数模型:
| Bi,j=P⋅e−λ⋅di,j | (5) |
其中, Bi,j表示采样点i对像素j的影响,P是每个采样点之间的功率, di,j为采样点i和像素j的质心之间的距离, 是指数衰减率. 生成增强的灰度图像如图2(d).
2 基于MobileNetV3改进的轻量型神经网络算法MobileNetV3是Google提出[11]的新一代基于互补搜索技术和新型架构的轻量级卷积神经网络. MobileNetV3是基于神经架构搜索(network architecture search, NAS)实现的MnasNet网络架构, 以MobileNetV1和MobileNetV2模型为基础, 使用SE模块(squeeze-and-excitation)和h-swish激活函数去达到提高网络模型性能的目的. 根据针对高低资源的目标, 可以将MobileNetV3定义为MobileNetV3-large和MobileNetV3-small的两种不同架构复杂性的模型. 它们的通用架构如图3所示.
2.1 深度可分离卷积为了提高计算效率, MobileNetV3引入了深度卷积可分离(depth separable convolution), 与传统的卷积相似. 它是由一层深度卷积和一层逐点卷积组合而成, 每层卷积后紧跟着批量规范化和ReLU激活函数. N×N的传统卷积是将卷积核和特征图像一一对应求乘积, 则传统卷积的计算量为

|
图 3 MobileNetV3网络架构图 |
深度可分离卷积实现了更小的空间代价和时间代价与标准卷积层一样的特征提取效果, 大大减少了参数量和计算量, 是MobileNetV3模型高效的关键.
2.2 改进前和改进后的MobileNetV3网络结构度可分离卷积MobileNetV3的网络结构主要由3个卷积层以及1个平均池化层组成, 如图4所示. 假定网络输入为X, 则网络输出可以表示为:
| F=ϕ(X;w) | (6) |
其中,

|
图 4 MobileNetV3的网络结构示意图 |
网络的损失函数采用交叉熵, 可表示为
| L=−N∑i=1y(i)×logˆy(i) | (7) |
其中,
| F=ϕ(X;w)+X | (8) |

|
图 5 引入ResNet的MobileNetV3的网络结构示图 |
2.3 基于MobileNetV3轻量级神经网络调制识别算法
基于MobileNetV3的轻量型网络调制识别方法主要分为数据预处理、输入MobileNetV3网络训练和分类器分类识别调制信号3部分. 在数据预处理阶段, 将接收到的二维数组形式的调制信号转换为星座图, 并进行灰度图像提取和灰度图像增强, 制作星座图像数据集, 将图像识别思想与调制识别相结合. 将星座图像数据集分为两部分, 分别是训练集和测试集, 训练改进的MobileNetV3网络模型, 然后利用训练好的网络模型对信号星座图像识别分类, 完成接收信号的调制方式识别.
3 实验仿真 3.1 数据集构建提取O’Shea等人[13]公开的RML2016.10a调制识别数据集中的BPSK, QPSK, 8PSK, 16QAM, 64QAM这5种调制方式信号的基带复样本, 每1 000个样本生成一个星座图, 根据样本的调制方式对每张星座图进行标记, 再用第2节介绍的图像增强方法, 构建星座图像数据集.
3.2 改进的MobileNetV3 网络仿真选取数据集中1 000张星座图图像为训练集, 100张为验证数据集, 100张作为测试数据集, 搭建MobileNetV3网络结构模型, 网络超参数值如表1所示, Max epoch设置为50次, batch size设置为64, leaning rate设置为0.001, 输入到网络中完成星座图像数据集的分类识别.
| 表 1 MobileNetV3网络的超参数 |
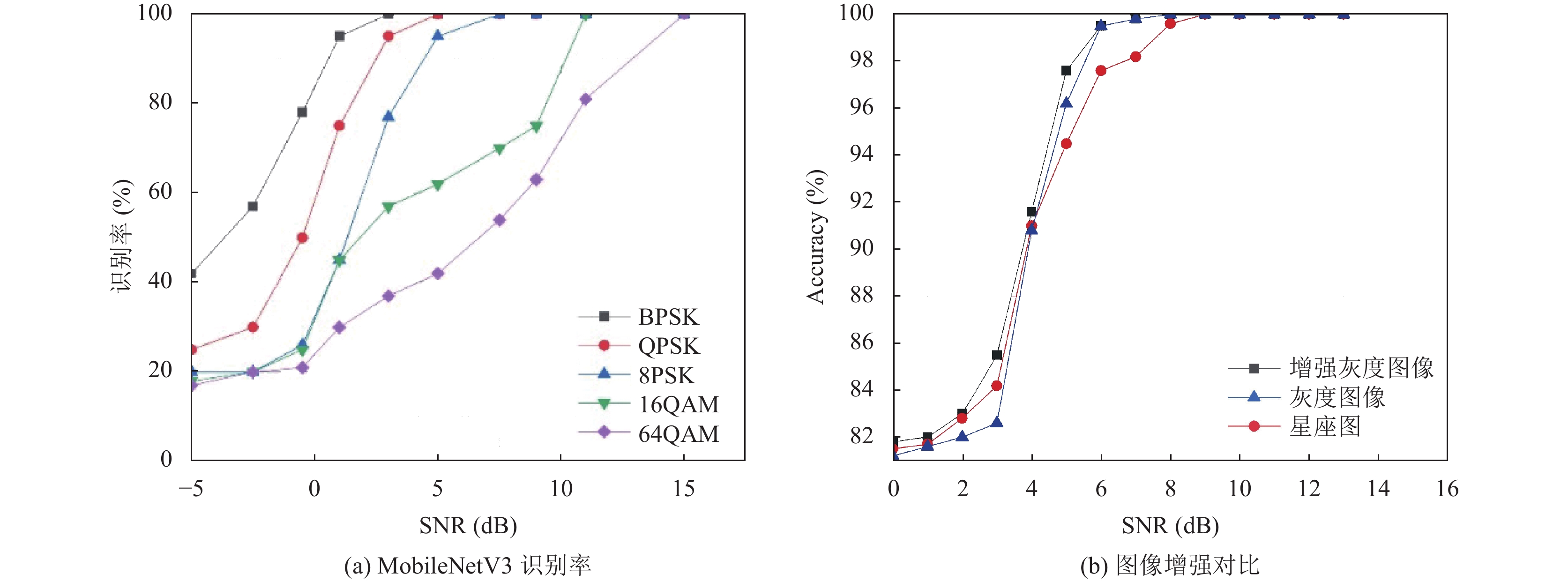
将本文中的用到的MobileNetV3的网络参数和计算量与传统调制识别深度学习网络对比. 如图6(c)和图6(d)所示, MobileNetV3网络的参数量和网络计算和ResNet18、ResNet50、Inception_V3、AlexNet和VGG16相比, MobileNetV3的参数量和计算量更少, VGG16的参数量和计算量相对更复杂. 如图7(a)所示, 在信噪比在[−5 dB, 15 dB]范围内, 信噪比大于5 dB时, BPSK, QPSK, 8PSK三种信号调制方式识别率达100%, 而16QAM和64QAM则是在信噪比12 dB以上才到达100%的识别率. 如图7(b)所示, 将原始信号的星座图直接输入到MobileNetV3网络中和灰度图像和图像增强后输入到网络进行对比, 可以得出在信噪比低于8 dB时, 增强灰度图像的星座图像信号识别率明显高于原始信号的识别率, 在信噪比较低的情况下, 由于噪声的干扰, 星座图中的星座点的数据样本难以在灰度图像中集中采集, 而增强灰度图像有效解决了数据样本的集中采集问题, 从而提高了低信噪比下的整体识别率. 通过仿真结果表明MobileNetV3网络整体识别率可以达到99.76%, 在不降低识别率的同时网络参数和计算量明显减少, 有效解决了在提高识别率时产生的网络结构复杂, 对硬件设备依赖高的问题.

|
图 6 MobileNetV3网络性能 |
4 结论
本文研究了将轻量化神经网络应用于无线通信中的调制识别, 解决了传统神经网络在提高识别率过程中不断提高网络复杂度, 过于依赖硬件设备的问题. 首先, 将接收信号转换为星座图像, 提取灰度图像, 并进行图像增强, 生成星座图像数据集, 并对MobileNetV3网络进行改进, 加入跃层结构, 有效解决了梯度消失现象; 然后将星座图像数据集输入到改进的MoblieNetV3网络中训练, 进行识别分类. 实验结果表明, MobileNetV3网络在不降低识别率的情况下, 网络参数和计算量明显减小, 性能有明显优势. 下一步, 将本文提出的改进的MobileNetV3网络算法应用到实际复杂信道环境下OFDM信号和其他类型单载波信号的调制模式识别中, 并对算法进行进一步优化.
|
图 7 MobileNetV3识别率 |
| [1] |
王飞扬. 基于深度学习的通信信号调制识别研究[硕士学位论文]. 成都: 电子科技大学, 2019.
|
| [2] |
Meng F, Chen P, Wu LN, et al. Automatic modulation classification: A deep learning enabled approach. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10760–10772.
|
| [3] |
Mihandoost S, Azimzadeh E. Introducing an efficient statistical model for automatic modulation classification. Journal of Signal Processing Systems, 2020, 92(1): 123-134. DOI:10.1007/s11265-019-01458-5 |
| [4] |
Fan CJ, Wang YF, Liu M. A hybrid approach for signal modulation recognition using deep learning methods. Journal of Physics: Conference Series, 2021, 1757: 012074. DOI:10.1088/1742-6596/1757/1/012074 |
| [5] |
林冲, 闫文君, 张立民, 等. 通信信号调制识别综述. 中国电子科学研究院学报, 2021, 16(11): 1074-1085. DOI:10.3969/j.issn.1673-5692.2021.11.002 |
| [6] |
Shannon CE. The lattice theory of informationIRE transactions information theory. Claude E. Shannon: Collected Papers. IEEE, 1993, 180–183.
|
| [7] |
李晨, 杨俊安, 刘辉. 基于信息熵和GA-ELM的调制识别算法. 系统工程与电子技术, 2020, 42(1): 223-229. DOI:10.3969/j.issn.1001-506X.2020.01.30 |
| [8] |
Jeong S, Lee U, Kim SC. Spectrogram-based automatic modulation recognition using convolutional neural network. Proceedings of the 10th International Conference on Ubiquitous and Future Networks (ICUFN). Prague: IEEE, 2018. 843–845.
|
| [9] |
Mendis GJ, Wei J, Madanayake A. Deep learning-based automated modulation classification for cognitive radio. Proceedings of the 2016 IEEE International Conference on Communication Systems (ICCS). Shenzhen: IEEE, 2016. 1–6.
|
| [10] |
Peng SL, Jiang HY, Wang HX, et al. Modulation classification based on signal constellation diagrams and deep learning. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(3): 718-727. DOI:10.1109/TNNLS.2018.2850703 |
| [11] |
Howard A, Sandler M, Chen B, et al. Searching for MobileNetV3. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 1314–1324.
|
| [12] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [13] |
O’Shea TJ, West N. Radio machine learning dataset genera-tion with GNU radio. https://pubs.gnuradio.org/index.php/grcon/article/view/11. (2016-09-06).
|
 2023, Vol. 32
2023, Vol. 32



