负荷监测是一种节能技术, 可以给消费者和电网公司提供住宅内每个电器的详细用电信息. 该技术按照实现方式被分为侵入式和非侵入式. 1992年, Hart以稳态有功功率和无功功率为特征, 提出了最初的NILM框架[1], 相对于侵入式负荷监测, NILM采用家庭的总功率水平作为输入来估计每个设备对总能耗的贡献程度[2], 大大降低了对用户生活的影响以及装设成本.
为提高能源利用效率和智能电网的发展[3], 响应科学、合理用电的需求, 越来越多的研究者致力于提高NILM的准确性和适用性, 由此衍生出诸多模型与算法. 通过使用NILM技术, 电力部门可以为用户提供详细的电力使用情况和个性化的节能建议, 保证电网的合理运行. 因此, NILM是一种高效且经济的能源消耗技术框架, 对电力用户、电网和整个社会都具有重要意义[4, 5]. 负荷分解算法可以分为数学优化方法[6, 7]和机器学习方法[8]. 前者尝试将观察到的功率测量值与 (设备特征库中) 设备功率信号的可能组合进行匹配, 以减少匹配误差作为优化策略[7], 达到分解目的, 但效果并不理想. 后者则先处理电器的电气信息, 然后通过机器学习算法从数据中学习设备的特征模式, 从而实现对负荷的辨识与分解, 本文的落脚点在于机器学习方法. 根据学习过程是否使用标签信息, 可以进一步划分为监督学习[8-13]和无监督学习[14-17]两种. 通常, 监督学习需要已知负载的标签数据, 适用于负载类型较少的情况. 如文献[8, 9]采用支持向量机对负荷功率进行分解, 但其训练时间较长, 且对噪声敏感. 文献[10]通过深度稀疏编码实现负荷分解, 文献[11]通过基于簇的稀疏编码以提取多事件场景下所涉及的潜在单个事件, 但它们无法被用于实时分解. 文献[12]提出了利用域间知识转移的负荷分解方法. 文献[13]将随机森林作为负荷分解的学习算法; 无监督学习并不需要已知负载的标签数据, 只需从数据中挖掘特征的相似性. 隐马尔可夫模型 (HMM) 是一种常用的无监督学习方法, 在时间序列数据的分析方面具有很大优势, 被广泛应用于电器的能耗序列模拟, 其扩展形式, 因子隐马尔可夫模型(FHMM)常被应用于NILM领域. 文献[15]提出了一种基于分段整数二次约束规划的FHMM负荷分解模型. 文献[16]提出加性因子隐马尔可夫模型, 具有较高的分解精度. 文献[17]利用迭代模糊C均值算法以自适应的方式确定HMM的隐状态数. 文献[18]对处于启状态的设备建立FHMM进行负荷分解. 上述文献从不同的角度对基于FHMM的负荷模型进行改进, 但HMM的模型训练通常采用的是Baum-Welch算法[19]. 这种方法虽然经典且容易实现, 但由于其初值选取的随机性, 模型参数估计时容易受到局部最优的限制, 影响分解结果的精确性.
为克服上述缺点, 一些学者将粒子群优化算法[20]同HMM相结合, 提升学习的效率. 文献[21]将粒子群算法(PSO)引入HMM的参数训练过程, 并用于识别和预测报警信息, 文献[22]将自适应粒子群算法融入HMM中, 并用于识别地面装备的退化情况. 本文提出一种基于改进粒子群算法优化FHMM的非侵入式负荷分解方法, 通过线性递减策略动态控制惯性权重, 提升PSO算法的全局搜索能力, 并利用改进的PSO算法对因子隐马尔可夫模型的参数学习过程进行优化, 使之跳出局部极值点, 有效地提升了FHMM在负荷分解任务中的表现.
1 负荷分解模型的建立 1.1 单电力负载模型在不同的运行条件下, 电力负载的电流幅值、有功功率和无功功率等电气参数是不同的, 但在相同的运行条件下总是表现出固有的特性. 通常, 电力负荷的运行过程可以看作是一系列的状态转移, 这与隐马尔可夫模型是一致的[23].
根据负载稳态特征的不同, 负荷类型可分为 ON/OFF型负荷、FSM型负荷、CVD型负荷. 其中, ON/OFF型负荷与FSM型负荷并无本质区别, 都具有相对稳定的有限工作状态, 以上负荷类型可以涵盖大多数家用电器的情况[1]. 单个电器的HMM模型示例如图1所示.

|
图 1 单个电器的HMM模型示例 |
电力负载的工作状态通常采用有限状态集:
A代表状态转移概率矩阵, 即
B指的是观测概率矩阵, 即
FHMM[24]可用于建立具有多电力负载的负荷分解模型并进行分析[25]. 在这里, 每个设备都可基于HMM建立负荷模型: 对于负荷
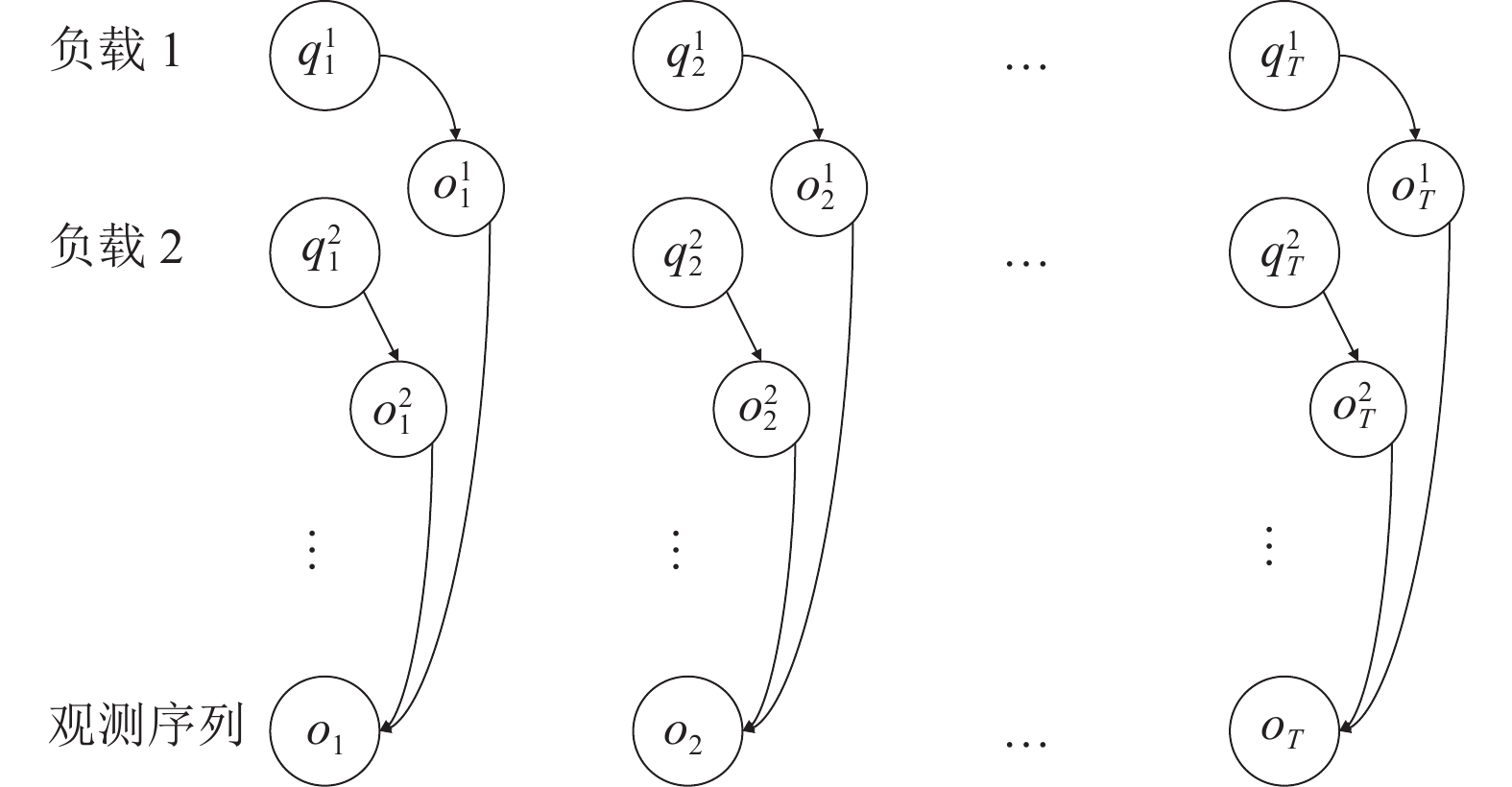
|
图 2 总负荷的FHMM模型 |
2 模型求解 2.1 基于GMM的负荷状态聚类
电器每个工作状态的功率可认为服从均值为
| p(x)=M∑m=1ωmp(x|m)=M∑m=1ωmN(xm|μm,Σm) | (1) |
其中, M为模型个数,
通常采用EM算法估计GMM的参数. 先假定数据的类别, 然后根据迭代估计出GMM的权值
(1) E步: 计算后验概率:
| γ(znm)=πmN(xn|μn,Σn)M∑i=1ωiN(xn|μi,Σi) | (2) |
(2) M 步: 根据 E 步计算的后验概率
(3) 计算对数似然函数:
| L(p(x))=M∑m=1log{M∑m=1ωmN(xn|μm,Σm)} | (3) |
(4) 重复迭代直到似然函数的值收敛.
2.2 负荷模型的参数估计基于FHMM的负荷分解可以描述为: 在时段T内, 对于包含N个负载的负荷对象, 在已知模型参数
模型参数的估计方法可分为无监督和有监督两种. 无监督方法直接利用总负荷功率数据训练模型, 而非利用单个设备的功率数据. 本文中单个设备的工作状态为隐变量, 故采用无监督方法对模型参数进行估计. Baum-Welch算法作为一种典型方法常被用于解决这类问题, 根据初始参数
根据HMM的前/后向算法可知:
| γt(i)=p(qt=si,O|Σ)p(O|Σ)=αt(i)βt(i)T∑j=1αt(i)βt(j) | (4) |
| ζt(i,j)=p(qt=si,qt+1=sj,O|Σ)p(O|Σ)=αt(i)aijbjot+1βt(j)T∑j=1αt(i)βt(j) | (5) |
其中,
参数估计的过程如下.
(1) 设定初始值:
(2) 按以下公式进行迭代:
| Πn+1i=γ1(i) | (6) |
| an+1ij=T−1∑t=1ζt(i,j)T−1∑t=1ζt(i) | (7) |
| bn+1i(k)=T−1∑t=1Iot=nkγt(i)T−1∑t=1γt(i) | (8) |
设置迭代条件:
由于Baum-Welch算法容易陷入局部最优, 本文考虑将粒子群算法与Baum-Welch算法相结合, 对上文中参数的训练过程进行优化.
PSO算法是Kennedy等人[20]提出的一种进化优化算法. 它通过对鸟类的社会行为进行模拟来寻找优化问题的全局最优值, 并已应用于诸多科学领域[29-31]. 在PSO中, 每个粒子就是一个解, 代表着该粒子目前的位置, 种群的解由一个群体组成. 为寻到最优解, 也即粒子的最佳位置, PSO以迭代的方式不断更新群体中所有具有速度向量的粒子的位置, 直到满足终止条件. 假设粒子i的位置由一个K维向量
| vi(t)=ωvi(t−1)+c1r1(pbest−xi(t−1))+c2r2(gbest−xi(t−1)) | (9) |
| xi(t)=xi(t−1)+vi(t) | (10) |
其中,
用标准的粒子群算法求解优化问题时, 如果开始时
| ω=ωmax−T(ωmax−ωmin)Tm | (11) |
其中,
方便起见, 将粒子i的位置坐标
算法1. IPSO-FHMM
1) 初始化: 依据训练规模, 随机生成N组模型参数
2) 依据Baum-Welch算法, 基于初始参数
3) 将这N组参数作为粒子, 根据式 (9)与式(10), 通过比较每次更新后的适应度值的大小来调整粒子的位置和速度.
4) 根据式 (11), 调整惯性权重
5) 确定最大训练次数
在确定了FHMM的最优参数
| ρt(q)=max[p(q1,q2,⋯,qT,o1,o2,⋯,oT|Σ)] | (12) |
递推可知:
| ρt+1(q)=max[ρt(p)apqbq(ot+1)] | (13) |
其中,
本文选用公开数据集AMPds2[32]进行非侵入式负荷分解, 这是一个低频数据集, 采样周期为1 min, 监测持续时间为2年. 从2个负荷中选择5种负荷作为研究对象, 分别为洗衣机、洗碗机、热力泵、壁挂炉、烘干机, 包含了FSM型负荷、CVD型负荷, 如此选取的研究对象使得研究更加贴合现实生活中的负荷使用状况. AMPds2中包含了11种电力测量参数, 本文选择有功功率作为负荷特征进行研究, 选用F1-score和归一化分解误差(NDE)指标评估负载分解算法的性能. F1-score是准确率和召回率的调和平均值, 其计算方法如下:
| P=TPTP+FP | (14) |
| R=TPTP+FN | (15) |
| F1-score=2PRP+R | (16) |
其中, TP表示预测为正类实际也为正类的样本数, FP表示预测为正类实际为负类的样本数, FN表示预测为负类实际为正类的样本数, 对于ON/OFF设备, 开状态是正例, 关状态是反例; 对于多状态设备, 指定的工作状态为正例, 其余为负例. NDE则描述了实际功率和分解功率之间的重合程度[9], 其定义如下:
| NDE=√(yit−ˆyit)2(yit)2 | (17) |
其中,
采用GMM对负荷数据进行聚类, 所选5台设备的聚类结果如表1所示. 洗衣机属于CVM负载, 基于分解精度和计算速度的考量, 将该设备的聚类数设置为 4.
选取8周的采样数据进行负荷分解. 其中前3/4的数据设置为训练样本集, 用以获取设备的工作状态, 并估计出模型参数. 剩余1/4的数据作为测试集, 对算法的性能进行测试. 负荷分解的结果如图3 所示.
| 表 1 电器状态聚类结果 |

|
图 3 负荷分解的算法对比 |
F1-score越趋于1, NDE越趋于0则代表算法的性能越理想, 为了验证本文所述方法的准确性, 进行了计算机仿真, 并将结果与Hart方法、Hart w/ MAP方法以及AFAMAP算法[16]、IFCM 算法[17]的结果进行对比, 仿真研究过程分为4组, 即有2–5个设备同时工作的情况.
从图3可以看出, 本文提出的模型在两种指标上明显优于Hart及其改进后的模型. 也优于AFAMAP模型的表现. 在与IFCM模型进行比较时, 可以发现当2–4台电器同时工作的状态下, 本文模型表现最佳. 当分解电器数量较多时, 比如5台电器同时工作时, 本文的模型精度略低于IFCM模型. 由此可同样得出, 负荷数增多, F1-score逐渐减小, NDE逐渐增大, 即分解精度逐渐下降, 显然负荷数对分解结果有较大影响.
所提出方法对于各个电器的分解效果如图4所示. 随着同时工作的设备数量的增加, 对于每个电器而言, F1-score降低, NDE值上升. 可见对于单个电器, 分解精度也随电器数目的增加而降低. 烘干机、热力泵、壁挂炉这3种电器都属于典型的FSM型负荷, 工作状态为有限个, 且能按照一定顺序切换状态, 各个工作状态的功率水平相差较大, 分解结果在各个电器数目的情况下都较为理想. 洗碗机的分解结果随电器数目增加而呈现显著下降的趋势. 洗衣机的分解结果始终低于其他设备, 可见连续状态型负荷通过FHMM建模的准确性并不够理想, 进而影响了分解的效果.

|
图 4 模型对各个电器的分解效果 |
4 结论与展望
本文针对目前关于负荷分解研究中存在的问题, 提出了基于改进粒子群优化因子隐马尔可夫模型的非侵入式负荷分解方法. 通过对负荷基于FHMM建立总负荷模型, 将负荷分解问题转变为求解最优状态组合的问题. 根据电器工作状态的功率服从高斯分布的特性, 采用GMM进行电器状态聚类, 避免了K-means聚类中心不稳定问题. 同时, 本文对FHMM的训练算法, 即Baum-Welch算法进行了改进, 引入了粒子群优化算法对模型参数估计过程进行优化, 避免了陷入局部最优问题. 同时考虑到粒子群算法的惯性权重对搜索能力的影响, 采用线性递减的方式来选取惯性权重. 最后通过Viterbi算法求得了最优的状态序列, 实现了对总负荷功率的分解. 最后将本文提出的方法分别与Hart方法、Hart w/ MAP方法、AFAMAP方法IFCM方法在不同设备同时工作的情况下进行性能比较. 结果表明本文的方法在性能上优于上述其他方法. 值得注意的是, 本文所提出的负荷分解方法, 计算成本相对较高, 同时随着负荷数增多, 分解精度会呈现一定程度的下降. 在下一步的研究中需要针对这些问题, 考虑结合深度学习方法[33-35], 对负荷分解问题进行更深入的讨论.
| [1] |
Hart GW. Nonintrusive appliance load monitoring. Proceedings of the IEEE, 1992, 80(12): 1870-1891. DOI:10.1109/5.192069 |
| [2] |
邓晓平, 张桂青, 魏庆来, 等. 非侵入式负荷监测综述. 自动化学报, 2022, 48(3): 644-663. DOI:10.16383/j.aas.c200270 |
| [3] |
Xia M, Wang ZW, Lu M, et al. MFAGCN: A new framework for identifying power grid branch parameters. Electric Power Systems Research, 2022, 207: 107855. DOI:10.1016/j.jpgr.2022.107855 |
| [4] |
Najafi B, Moaveninejad S, Rinaldi F. Data analytics for energy disaggregation: Methods and applications. In: Arghandeh R, Zhou YX, eds. Big Data Application in Power Systems. Amsterdam: Elsevier, 2018. 377–408.
|
| [5] |
刘恒勇, 史帅彬, 徐旭辉, 等. 一种关联RNN模型的非侵入式负荷辨识方法. 电力系统保护与控制, 2019, 47(13): 162-170. DOI:10.19783/j.cnki.pspc.180785 |
| [6] |
杨立余, 陈昊, 黎明, 等. 非侵入式电力负荷多目标分解框架. 电力系统保护与控制, 2020, 48(6): 100-107. DOI:10.19783/j.cnki.pspc.190559 |
| [7] |
Du Y, Du L, Lu B, et al. A review of identification and monitoring methods for electric loads in commercial and residential buildings. Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition. Atlanta: IEEE, 2010. 4527–4533.
|
| [8] |
Hernandez AS, Ballado AH, Heredia APD. Development of a non-intrusive load monitoring (NILM) with unknown loads using support vector machine. Proceedings of the 2021 IEEE International Conference on Automatic Control & Intelligent Systems. Shah Alam: IEEE, 2021. 203–207.
|
| [9] |
武昕, 严萌, 郭一凡, 等. 基于结构化特征图谱的组合支持向量机非侵入式负荷辨识. 电力系统自动化, 2022, 46(12): 210-219. DOI:10.7500/AEPS20210924004 |
| [10] |
Singh A, Majumdar A. Deep sparse coding for non-intrusive load monitoring. IEEE Transactions on Smart Grid, 2018, 9(5): 4669-4678. DOI:10.1109/TSG.2017.2666220 |
| [11] |
Song Y, Wang W, Zhang ZF, et al. Multiple event detection and recognition for large-scale power systems through cluster-based sparse coding. IEEE Transactions on Power Systems, 2017, 32(6): 4199-4210. DOI:10.1109/TPWRS.2017.2656146 |
| [12] |
Lin J, Ma J, Zhu JG, et al. Deep domain adaptation for non-intrusive load monitoring based on a knowledge transfer learning network. IEEE Transactions on Smart Grid, 2022, 13(1): 280-292. DOI:10.1109/TSG.2021.3115910 |
| [13] |
Wu X, Gao YC, Jiao D. Multi-label classification based on random forest algorithm for non-intrusive load monitoring system. Processes, 2019, 7(6): 337. DOI:10.3390/pr7060337 |
| [14] |
de Baets L, Develder C, Dhaene T, et al. Detection of unidentified appliances in non-intrusive load monitoring using Siamese neural networks. International Journal of Electrical Power & Energy Systems, 2019, 104: 645-653. DOI:10.1016/j.ijepes.2018.07.026 |
| [15] |
Kong WC, Dong ZY, Ma J, et al. An extensible approach for non-intrusive load disaggregation with smart meter data. IEEE Transactions on Smart Grid, 2018, 9(4): 3362-3372. DOI:10.1109/TSG.2016.2631238 |
| [16] |
Bonfigli R, Principi E, Fagiani M, et al. Non-intrusive load monitoring by using active and reactive power in additive factorial hidden Markov models. Applied Energy, 2017, 208: 1590-1607. DOI:10.1016/j.apenergy.2017.08.203 |
| [17] |
Ji TY, Liu L, Wang TS, et al. Non-intrusive load monitoring using additive factorial approximate maximum a posteriori based on iterative fuzzy C-means. IEEE Transactions on Smart Grid, 2019, 10(6): 6667-6677. DOI:10.1109/TSG.2019.2909931 |
| [18] |
于超, 覃智君, 阳育德. 基于启停状态识别改进因子隐马尔可夫模型的非侵入式负荷分解. 电网技术, 2021, 45(11): 4540-4550. DOI:10.13335/j.1000-3673.pst.2020.1893 |
| [19] |
Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, 1989, 77(2): 257-286. DOI:10.1109/5.18626 |
| [20] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of the 1995 International Conference on Neural Networks. Perth: IEEE, 1995. 1942–1948.
|
| [21] |
耿宁. 基于粒子群优化的隐马尔科夫模型的复合攻击预测方法. 通信电源技术, 2015, 32(3): 69-71. DOI:10.19399/j.cnki.tpt.2015.03.022 |
| [22] |
郭森, 王大为, 张绍伟, 等. 改进隐马尔科夫模型的地面装备退化状态识别. 西北工业大学学报, 2021, 39(S1): 32-40. |
| [23] |
Wu Z, Wang C, Peng WX, et al. Non-intrusive load monitoring using factorial hidden Markov model based on adaptive density peak clustering. Energy and Buildings, 2021, 244: 111025. DOI:10.1016/j.enbuild.2021.111025 |
| [24] |
Ghahramani Z, Jordan MI. Factorial hidden Markov models. Machine Learning, 1997, 29(2): 245-273. DOI:10.1023/A:1007425814087 |
| [25] |
Parson O. Unsupervised training methods for non-intrusive appliance load monitoring from smart meter data [Ph.D. Thesis]. Southampton: University of Southampton, 2014.
|
| [26] |
燕续峰, 翟少鹏, 王治华, 等. 深度神经网络在非侵入式负荷分解中的应用. 电力系统自动化, 2019, 43(1): 126-132, 167. |
| [27] |
Kanungo T, Mount D M, Netanyahu N S, et al. An efficient K-means clustering algorithm: Analysis and implementation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 881-892. DOI:10.1109/TPAMI.2002.1017616 |
| [28] |
Viterbi A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory, 1967, 13(2): 260-269. DOI:10.1109/TIT.1967.1054010 |
| [29] |
AlRashidi MR, El-Hawary ME. A survey of particle swarm optimization applications in electric power systems. IEEE Transactions on Evolutionary Computation, 2009, 13(4): 913-918. DOI:10.1109/TEVC.2006.880326 |
| [30] |
Abido MA. Multiobjective particle swarm optimization for environmental/economic dispatch problem. Electric Power Systems Research, 2009, 79(7): 1105-1113. DOI:10.1016/j.jpgr.2009.02.005 |
| [31] |
Yeung CW, Leung FHF, Chan KY, et al. An integrated approach of particle swarm optimization and support vector machine for gene signature selection and cancer prediction. Proceedings of the 2009 International Joint Conference on Neural Networks. Atlanta: IEEE, 2009. 3450–3456.
|
| [32] |
Makonin S, Ellert B, Bajić IV, et al. Electricity, water, and natural gas consumption of a residential house in Canada from 2012 to 2014. Scientific Data, 2016, 3: 160037. DOI:10.1038/sdata.2016.37 |
| [33] |
Wu ZH, Pan SR, Chen FW, et al. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4-24. DOI:10.1109/TNNLS.2020.2978386 |
| [34] |
Singhal V, Maggu J, Majumdar A. Simultaneous detection of multiple appliances from smart-meter measurements via multi-label consistent deep dictionary learning and deep transform learning. IEEE Transactions on Smart Grid, 2019, 10(3): 2969-2978. DOI:10.1109/TSG.2018.2815763 |
| [35] |
杨秀, 李安, 孙改平, 等. 基于改进GMM-CNN-GRU混合的非侵入式负荷监测方法研究. 电力系统保护与控制, 2022, 50(14): 65-75. DOI:10.19783/j.cnki.pspc.211238 |
 2023, Vol. 32
2023, Vol. 32



