1 引言

随着互联网的迅速发展, 信息的访问和交流变得便利, 但是信息安全需要克服的困难也变得艰巨. 例如我们非常关注的版权问题^[1], 在网络中的版权被称作网络版权^[2], 其面临最普遍的问题就是: 原创作品在未经允许的情况下被下载、篡改、拷贝等; 以及在通信交流的场景中被第三方截取的问题. 为能够有效保护信息的安全, 提出的主流方案有密码学、信息隐藏^[3-5]等. 密码学是将秘密信息加密成无法理解的密文; 而信息隐藏技术是将信息的隐藏方式从“看不懂”转为“看不见”或者“听不见”, 并且信息隐藏技术在2020年由中国商务部、科技部调整发布的《中国禁止出口限制出口技术目录》(商务部科技部公告2020年第38号)的公告中, “信息隐藏与发现技术”作为新增技术被列入其中, 这直接证明了信息隐藏技术在信息安全领域的重要性.

可逆信息隐藏技术对载体图像的改变可以做到无损恢复, 满足了对载体图像精确度要求高的领域, 例如: 医学、军事、司法等. 在图像信息隐藏技术中若以载体形式分类, 可分为单图像和双图像, 其中基于双图像的可逆信息隐藏技术由Chang等人^[6]在2007年首次提出, 将秘密信息嵌入到载体图像之后得到两幅画面相同的载密图像, 接收方需要同时拥有两幅载密图像才能恢复载体图像和提取秘密信息, 如果只获得其中任意一幅载密图像将毫无意义, 双图像的可逆信息隐藏技术一般框架如图1所示. 因为双图像相对于单图像, 一方面可极大提高信息的安全性, 以及可用于一对二的交流场景中, 例如医疗保健行业和一些在线内容分发系统等; 另一方面双图像可以解决一些基于单图像的信息隐藏技术无法做到载体图像无损恢复的问题^[7], 所以近些年来双图像可逆信息隐藏成为了信息隐藏领域中的研究热点.

可逆信息隐藏技术保证了载体图像的无失真, 而载体图像被嵌入秘密信息之后得到的载密图像的失真程度决定了信息隐藏方案的载密图像质量和安全性. 为提高载密图像质量, 在2011年, Lou等人^[8]使用PVD和模函数结合的方案, 将秘密信息的嵌入分为两部分嵌入, 第1部分主要利用了Wu等人^[9]的基于PVD隐写方案, 第2部分则主要利用了Thien等人^[10]的基于模函数的隐写方案来增加嵌入容量和提高载密图像质量, 同时解决了两种方案的兼容性问题, 但是未解决原方案中的溢出问题. 在2015年, Lu等人^[11]提出中心折叠策略, 通过2^k–1与k位二进制流的值进行相减得到折叠数, 缩小载体像素值的修改量, 以此来提高载密图像质量, 但载密图像质量还是有待提高. 在2018年, Maniriho等人^[12]利用每个像素块的基点不变以及减少像素对之间的差值展开来改进信息隐藏方案, 此方案为了提高载密图像质量对缩减差分展开的计算表达式进行了改进和对每个像素块选择不同的新的恒定基点, 但实验表明此方法对不同的载体图像嵌入容量波动太大且当嵌入量达到最大时有些载密图像PSNR值不到40 dB. 在2019年, Sahu等人^[13]将图像划分为大小为1×2的子块, 通过对像素值进行最低有效位(least significant bit, LSB)匹配修改, 最后像素对再进行调整来达到可逆性和得到高质量载密图像, 但溢出问题未提出解决方案. 在2019年, Shastri等人^[14]通过将3位二进制数进行中心折叠和分奇偶操作构建了查找表以此来降低嵌入信息时像素值的修改量从而提高载密图像质量, 但由于需要记录每次嵌入秘密信息时的奇偶, 所以需要额外信息跟踪表. 在2019年, Sahu等人^[15]使用模函数和PVD提出了两种方案, 两种方案通过不同的PVD范围表来变换不同的嵌入信息位数, 其中一种方案具有更高的峰值信噪比(peak signal-to-noise ratio, PSNR), 但是在嵌入秘密信息之后像素对之间的差值发生变化导致新的差值可能和之前的落入的范围不一致, 所以恢复秘密信息时可能会出现信息嵌入位数误判的情况. 在2019年, PMTA^[16]提出在PVD满足规定条件之后, 使用正负差值来嵌入信息, 再利用模2运算提取信息, 从而提高载密图像质量, 但载密图像质量还是有待提高. 在2020年, Kim等人^[17]提出了一种基于块的PVD方法, 先将原始图像分成大小相同的非重叠块, 使用块内的最大像素值差进行秘密信息嵌入和提取, 保持载密图像视觉质量的同时进一步提高了嵌入容量, 但是溢出问题未提出解决方案. 在2020年, Wang等人^[18]通过将载体图像转换成一维阵列, 将相邻像素之间的差分向两个方向扩展, 为提高载密图像质量给出了差分阈值并同时解决溢出问题, 但是实验表明在嵌入4万比特之后PSNR值低于30 dB失真严重. 在2021年, Meikap等人^[19]通过将Lu等人^[11]的中心折叠策略和Peng等人^[20]定向像素值排序(directional pixel value ordering, DPVO)方案进行有效结合, 所以比Lu等人^[11]的方案具有更高的载密图像质量, 但是此方案在排序时需要经过多次for循环, 所以导致计算复杂度较高. 在2022年, Kong等人^[21]提出利用不同通道之间变化趋势的相关性和不同颜色通道的相邻像素之间的差异进行排序并, 结合优化后的预测误差来选择嵌入信息的位置, 以此来提高载密图像的质量, 但是只适用于彩色图像. 在2022年, Sahu等人^[22]提出PVD结合改进的LSB匹配来提高载密图像质量, 但是溢出问题未提出解决方案. 在2022年, Chen等人^[23]提出利用修正方向(exploiting modification direction, EMD)矩阵的双图像可逆信息隐藏算法, 该算法在一个载体图像像素值中同时隐藏一个秘密比特和一个5进制数字, 但是在载密图像和原载体图像的PDH折线图还是有较大区别.

为解决上述中为提高载密图像质量而提出的可逆隐写方案中存在的载密图像质量、溢出问题、误差问题、适用性、产生额外信息表, 抗分析能力等问题, 本文将Wu等人^[9]和Jung^[24]分别提出的不同基于PVD隐写方案的部分进行改进与结合并加入模函数提出了一种基于模函数与像素值差值的可逆信息隐藏方案.

2 相关工作

本节分别在第2.1节和第2.2节介绍了Wu等人^[9]和Jung^[24]提出的基于PVD的隐写方案. 其中Wu等人^[9]的算法是通过改变相邻像素对的差值来嵌入秘密信息, Jung^[24]的算法是通过改变双图像中相同位置像素的差值来嵌入秘密信息. 为了便于叙述, 在此说明一下, 从此处开始以及到论文其余部分, 我们把秘密信息看作一个比特流s, 载体图像被设定为灰度图像Z大小为 $M \times N$ (其中 $M$ 为载体图像的宽, $N$ 为在载体图像的高).

2.1 基于像素值差值的隐写方案

Wu等人^[9]的基于像素值差值的隐写方案, 将载体图像Z中连续的像素值划分为 $ {{\left( {M \times N} \right)} \mathord{\left/ {\vphantom {{\left( {M \times N} \right)} 2}} \right. } 2} $ 组互不重叠的像素对之后计算像素对差值, 将秘密信息隐藏在差值中. 具体信息嵌入步骤如下.

首先将像素值的范围[0, 255]划为v个连续的子区间 $ {R_k} $ :

$ {R}_{k}=\left[{l}_{k} , {u}_{k}\right] \; \left(k=1, 2, \cdots , v\right) $

(1)

其中, ${l_k}$ 与 $ {u_k} $ 分别表示 ${R_k}$ 的下限和上限, 即可得到PVD范围表. 计算像素对 $\left({x}_{i} , {y}_{i}\right) \; \left(0\leqslant i < \left(M\times N/2\right)\right)$ 之间的差值 $ {d_i} $ :

$ {d_i} = {y_i} - {x_i} $

(2)

判断差值 ${d_i}$ 落入的区间 ${R_k}$ , 利用式(3)计算得到信息嵌入位数 ${n_i}$ :

$ {n}_{i}= {\mathrm{log}}_{2}\left({u}_{k}-{l}_{k}+1\right) $

(3)

取 ${n_i}$ 位二进制比特流转换成十进制数 ${b_i}$ 后, 得到新差值 $ {D_i} = \left| {{l_k} + {b_i}} \right| $ . 再计算差值 ${d_i}$ 和新差值 ${D_i}$ 之间的最终差值 ${m_i} = {D_i} - {d_i}$ , 最后将最终差值 ${m_i}$ 代入式(4), 得到嵌入秘密信息之后的新像素对 $\left({x}'_{i}, {y}'_{i}\right)$ :

$ \left({x}'_{i}, {y}'_{i}\right)=\left\{\begin{array}{c}\left({x}_{i}-\dfrac{{m}_{i}}{2}, {y}_{i}+\dfrac{{m}_{i}}{2}\right)\text{, } \; {d}_{i}为奇数\\ \left({x}_{i}-\dfrac{{m}_{i}}{2}, {y}_{i}+\dfrac{{m}_{i}}{2}\right)\text{, } \; {d}_{i}为偶数\end{array}\right. $

(4)

到这里信息嵌入步骤就已经完成了.

通过上述信息嵌入过程可知, 此方法利用相邻像素之间相关性将图像划分为平滑区和边缘区, 对图像不同的区域嵌入不同的信息位数n, 从而提高了嵌入容量, 但是随着范围表子区间的取值越大, 嵌入秘密信息时像素值的修改量可能会是2的幂次方倍增加, 从而导致载密图像质量降低.

2.2 基于像素值差值的双图像可逆隐写方案

Jung^[24]提出的基于像素值差值的双图像可逆隐写方案, 将载体图像Z划分为m个非重叠 $B \times B$ 大小的子块, 通过计算子块中相邻像素之间的平均值来确定嵌入的信息位数, 最后利用平均法将秘密信息嵌入到双载体图像中. 具体信息嵌入步骤如下.

首先计算子块中像素 $ {p_i} $ 的相邻像素的平均值并通过式(5)得差值 ${w_i}\; \left( {0 \leqslant i, j < \left( {B \times B} \right)} \right)$ :

$ {w_i} = \left| {{p_i} - \left| {\frac{{\displaystyle\sum\nolimits_{j = 0}^{i - 1} {{p_j}} }}{{\left( {B \times B} \right) - 1}}} \right|}\; \right|, \; i \ne j $

(5)

通过对数函数计算得到嵌入信息的比特位数 ${n_i} = \log _2 {{w_i}}$ , 将 ${n_i}$ 位比特流转换为十进制数 ${b_i}$ 最后通过式(6)将秘密信息嵌入双载体图像中:

$ \left( {p_i^1, p_i^2} \right) = \left( {{p_i} + \left\lfloor {\frac{{{b_i}}}{2}} \right\rfloor , {p_i} - \left\lceil {\frac{{{b_i}}}{2}} \right\rceil } \right) $

(6)

到这里信息嵌入步骤就完成了. 通过上述信息嵌入过程可知, 此方法相比Wu等人^[9]利用相邻像素之间相关性要更加充分并且将原本不可逆的像素值差值方法赋予了可逆性, 但是此方法溢出问题未得到很好的解决, 并且随着差值 ${w_i}$ 增大, 像素值的修改量也可能会是2的幂次方倍增加, 从而导致载密图像质量降低.

3 像素值差值结合模函数的可逆信息隐藏方案

在空间域中可逆信息隐藏方法主要可分为4大主流技术^[3]: 基于压缩技术、基于直方图修改技术、基于量化技术、基于扩展的技术. 其中基于扩展技术的与前面技术相比较, 它实现了高嵌入容量和低计算复杂度. 而基于PVD技术是基于扩展技术中之一, 因为其具有的优点再通过结合合适的方法可以在保持高嵌入容量和低计算复杂度的同时提高载密图像质量, 所以本文选择了基于PVD技术的可逆信息隐藏方法, 其中使用了Wu等人^[9]方案中利用相邻像素值之间的相关性方法并将PVD范围表进行重新构建和Jung^[24]方案中赋予基于PVD技术可逆性的方法. 为便于叙述, 在此说明一下, 从此处开始以及到论文其余部分, 两幅载密图像分别设为 ${Z^1}, {Z^2}$ , $Z$ 的像素对表示为 $\left( {{x_i}, {y_i}} \right)$ , ${Z^1}$ 的像素对表示为 $ \left( {x}_{i}^{1} , {y}_{i}^{1}\right) $ , ${Z^2}$ 的像素对表示为 $ \left( {x}_{i}^{2} , {y}_{i}^{2}\right)(0 < i < m, m=\left(M\times N\right)/2) $ .

3.1 确定PVD范围表

本文算法中将PVD划分为 $j \; \left( {0 \leqslant j \leqslant 4} \right)$ 个不同的子区间, 与Wu等人^[9]提出的基于PVD的隐写方案中划分的方法不同, 本文通过将模函数的模代入对数函数计算得到每个子区间的上限和下限, 以及得到每个子区间像素值的修改量范围和对应的信息嵌入位数. 首先模函数^[25] $ f(x, y) $ 如式(7), 通过此公式可知像素值 $x, y$ 的最大允许修改范围由模a决定为 $ \left\lceil { - \left( {a - 1} \right)/2, \left( {a - 1} \right)/2} \right\rceil $ .

$ f(x, y)=(x+ay) \; \mathrm{mod} \; {a}^{2}, \; a\geqslant 3且a是奇数 $

(7)

再通过式(8)可得到 ${a_j}$ , 利用式(7)可以计算出假如模 $a = 3$ , 那么x和y最大修改量为1就可以表达9种不同信息即: 0–8, 那么最多表示3位二进制数.

$ {a_j} = \left\{ {\begin{array}{*{20}{c}} {2\left( {j + 2} \right) - 1, \; 0 \leqslant j < 4} \\ {2\left( {j + 3} \right) - 1, \; 4 \leqslant j < 5} \end{array}} \right. $

(8)

为获得不同模函数最多可以表达的二进制信息位数(即嵌入的信息位数 ${b_j}$ )可通过式(9)计算得到.

$ {b_j} = \left\lfloor {\log_2 {{a_j^2}}} \right\rfloor $

(9)

最后利用式(10)得各个差值范围 ${R_j}$ .

$ {R_j} = \left\{ {\begin{array}{*{20}{l}} {\left[ {0, {2^{{b_{j + 1}}}} - 1} \right], \;\;\;\quad j = 0} \\ {\left[ {{2^{{b_{j - 1}}}}, {2^{{b_{j + 1}}}} - 1} \right], \; 0 < j < 4} \\ {\left[ {{2^{{b_{j - 1}}}}, 255} \right], \qquad \; j = 4} \end{array}} \right. $

(10)

通过以上步骤就可以得到PVD范围表1.

3.2 信息嵌入算法

本文提出的信息嵌入算法, 利用了在单位面积上像素对的差值, 通过表1可知信息嵌入位数为7位时, x和y的修改量为[−6, 6], 但是在嵌入信息时通过模函数和平均法运算之后, x和y的修改量折半为[−3, 3], 所以本方案在像素对差值越大的图像中越占有优势. 因为像素值的范围为[0, 255], 所以存在嵌入信息之后像素值出现溢出的情况, 对于溢出的处理方法将在第3.4节详细阐述. 首先将 $Z$ 划分成 $m$ 个大小为1×2的非重叠子块. 通过式(11)计算得到像素对的差值 ${d_i}$ :

$ {d}_{i}=\left|{x}_{i}- {y}_{i}\right| $

(11)

再将差值 ${d_i}$ 代入表1查询确定其属于的 $ {R_j} $ 范围以及模函数的模 ${a_j}$ . 利用式(9)计算得到嵌入信息的比特位数 ${b_j}$ , 并将 ${b_j}$ 比特流转换成十进制数B. 改变 $ \left({x}_{i} , {y}_{i}\right) $ 得到新像素对 $\left({x}'_{i}, {y}'_{i}\right)$ , 使其新像素对 $\left({x}'_{i}, {y}'_{i}\right)$ 满足式(7): $f\left({x}'_{i}, {y}'_{i}\right) = B$ . 通过式(12)求得像素对 $ \left({x}_{i} , {y}_{i}\right) $ 的修改量 $ ({c}_{x }, {c}_{y}) $ :

$ \left\{\begin{array}{c}{c}_{x}= {x}_{i}- {x}'_{i}\\ {c}_{y}= {y}_{i}- {y}'_{i}\end{array} \right.$

(12)

使用式(13)得到改变原像素值的修改量 $k_x^1, \; k_x^2, \; k_y^1, \; k_y^2$ :

$ \begin{array}{*{20}{c}} {k_x^1 = \left\lfloor {\dfrac{{{c_x}}}{2}} \right\rfloor } \end{array}, k_x^2 = \left\lceil {\dfrac{{{c_x}}}{2}} \right\rceil , \begin{array}{*{20}{c}} {k_y^1 = \left\lfloor {\dfrac{{{c_y}}}{2}} \right\rfloor } \end{array}, k_y^2 = \left\lceil {\dfrac{{{c_y}}}{2}} \right\rceil $

(13)

最后利用式(14)计算得已经嵌入秘密信息的新像素对 $ \left( {x_i^1, y_i^1} \right) $ ; $ \left( {x_i^2, y_i^2} \right) $ :

$\left\{ \begin{gathered} \begin{array}{*{20}{l}} {x_i^1 = {x_i} - k_x^1} \end{array}, \begin{array}{*{20}{c}} {x_i^2 = {x_i} + k_x^2} \end{array} \\ \begin{array}{*{20}{c}} {{{y}}_i^1 = {{{y}}_i} - k_{{y}}^1} \end{array}, \begin{array}{*{20}{c}} {{{y}}_i^2 = {{{y}}_i} + k_{{y}}^2} \end{array} \\ \end{gathered} \right.$

(14)

重复上述操作步骤, 直到所有秘密信息嵌入完毕.

3.3 信息提取算法

本节描述了针对上述中的信息嵌入算法的信息提取与恢复算法. 通过简单的平均法来无损恢复原载体图像, 而秘密信息提取主要是得到代入模函数的像素对, 从而得到隐藏信息的值. 首先将 ${Z^1}, {Z^2}$ 均划分成 $m$ 个大小为1×2的非重叠子块. 将 $\left( {x_i^1, y_i^1} \right)$ $\left( {x_i^2, y_i^2} \right)$ 代入式(15)得到像素对的修改量 $ \left({c}_{x }, {c}_{y}\right) $ :

$\left\{ \begin{array}{l}\begin{array}{c}{c}_{x }= {x}_{i}^{2}-{x}_{i}^{1}\end{array}\\ \begin{array}{c}{c}_{y }= {y}_{i}^{2}-{y}_{i}^{1}\end{array}\end{array}\right. $

(15)

将 $\left( {x_i^1, y_i^1} \right)$ 与 $\left( {x_i^2, y_i^2} \right)$ 代入式(16)得到原像素值 $\left( {{x_i}, {y_i}} \right)$ :

$\left\{ \begin{array}{l}{x}_{i}=\left\lfloor \dfrac{{x}_{i}^{1}+ {x}_{i}^{2}}{2}\right\rfloor \\ {y}_{i}=\left\lfloor \dfrac{{y}_{i}^{1}+ {y}_{i}^{2}}{2}\right\rfloor \end{array} \right.$

(16)

将得到的原像素值 $\left( {{x_i}, {y_i}} \right)$ 代入式(11)得到像素对的差值 ${d_i}$ 后查表1, 确定差值 ${d_i}$ 属于的 ${R_j}$ 范围以及模函数的模 ${a_j}$ , 代入式(9)得到嵌入信息的比特位数 $ {b_j} $ . 再将原像素值和像素修改量相加如式(17)得到被嵌入秘密信息的像素值 $\left({x}'_{i}, {y}'_{i}\right)$ :

$\left\{ \begin{array}{l}\begin{array}{c}{x}'_{i}={x}_{i}+{c}_{x }\end{array}\\ \begin{array}{c}{y}'_{i}={y}_{i}+{c}_{y }\end{array}\end{array}\right. $

(17)

将 $\left({x}'_{i}, {y}'_{i}\right)$ 带函数式(7)得到隐藏信息的十进制数: $f\left({x}'_{i}, {y}'_{i}\right)=B$ 后将B转化为 ${b_j}$ 位的二进制流, 即得到嵌入的秘密信息流. 重复上述操作步骤, 直到提取出所有嵌入的秘密信息.

3.4 溢出处理

为解决嵌入秘密信息时, 对像素值进行修改之后产生的溢出问题, 本文提出的解决办法为不予可能导致溢出的像素值对进行信息嵌入. 在信息嵌入算法中, 我们知道嵌入信息之后的像素对 $ \left( {x_i^1, y_i^1} \right) $ ; $ \left( {x_i^2, y_i^2} \right) $ 是和 ${a_i}$ 值有关, 可以推测出在嵌入时可能造成溢出的范围:

$ \begin{array}{*{20}{c}} {x - \left( {\dfrac{{a - 1}}{2}} \right) \times \dfrac{1}{2} < 0} \end{array} $

(18)

$ x + \left( {\frac{{a - 1}}{2}} \right) \times \frac{1}{2} > 255 $

(19)

在信息嵌入算法中得到模函数的模 $a$ 之后, 判断是否满足式(18)或式(19), 若满足则跳过此像素对不予嵌入信息, 否则按照算法继续嵌入信息.

在信息提取与恢复算法中得到原像素值对之后, 首先判断是否两幅载体图像的像素值相同, 且是否满足式(20), 若均满足则未嵌入信息, 直接跳过不予提取信息, 否则按照提取算法继续提取信息.

$\left\{ \begin{gathered} x \in \left[ {0, \left\lceil {\frac{{a - 1}}{4}} \right\rceil } \right) \\ x \in \left( {255 - \left\lceil {\frac{{a - 1}}{4}} \right\rceil , 255} \right] \\ \end{gathered} \right.$

(20)

3.5 举例说明本文的信息隐藏方案

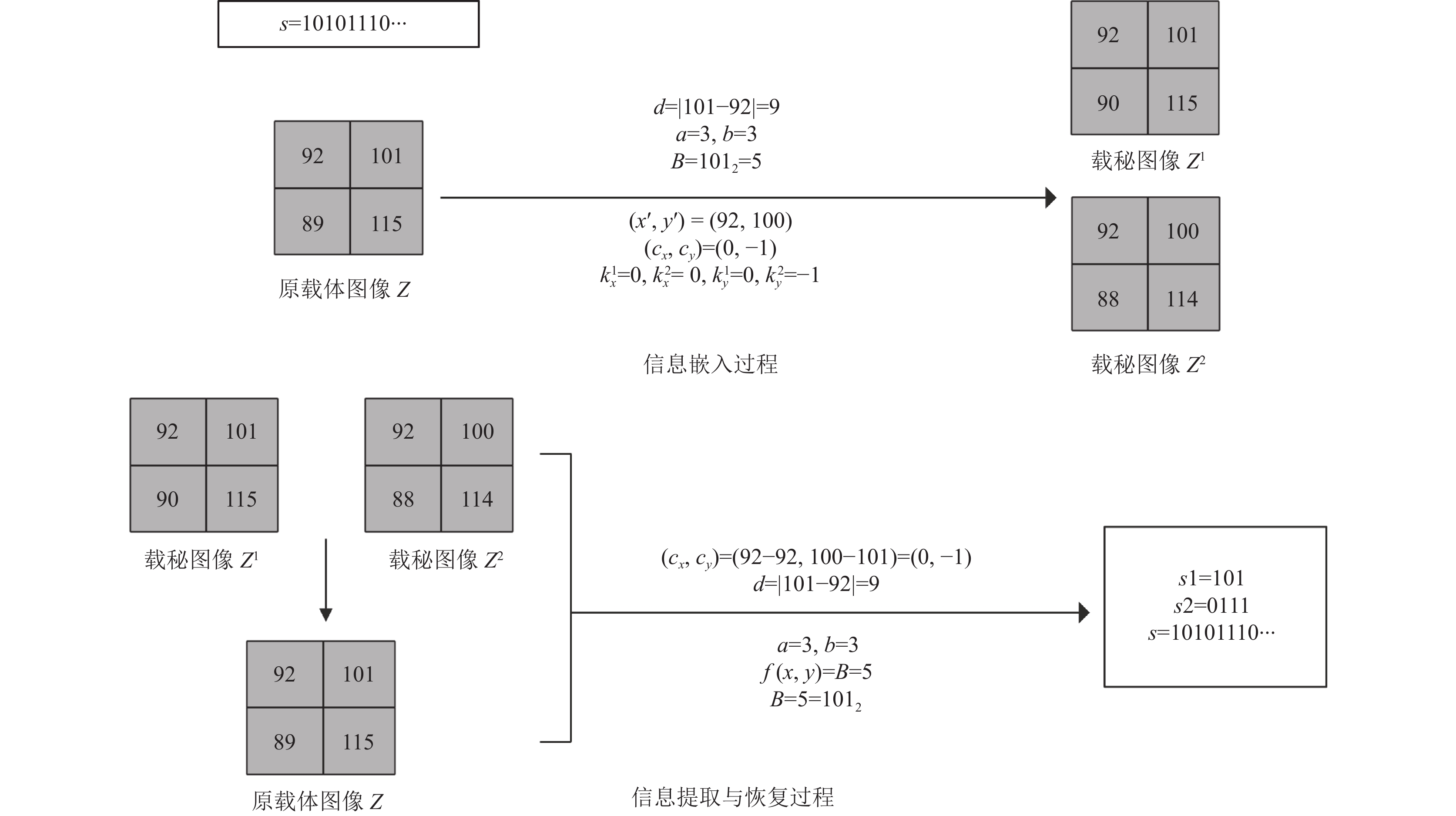
本文信息隐藏流程如图2. 假设载体图像中两个连续的像素值对为(92, 101)嵌入的秘密信息比特流s=10101110₂. 通过式(11)得到差值 $d = \left| {92 - 101} \right| = 9$ , 查询表1, 确定 $d$ 属于 ${R_1}$ , 模函数的模 $a = 3$ 和嵌入信息的比特位数 $b = 3$ , 将 $b$ 位比特流转换为十进制数 $B = 5$ . 通过式(7)计算修改 $ \left(x , y\right) $ 后, 得到的 $\left( {x', y'} \right) = \left( {92, 100} \right)$ 可知修改量 $ \left({c}_{x }, {c}_{y}\right)=\left(0, -1\right) $ , 用式(13)得最终像素修改量 $k_x^1 = 0, \; k_x^2 = 0, \; k_y^1 = 0, \; k_y^2 = - 1$ , 最后通过式(14)得到嵌入信息之后的像素对为 $\left( {92, 101} \right), \left( {92, 100} \right)$ .

提取信息过程为: 首先将 $\left( {92, 101} \right), \left( {92, 100} \right)$ 代入式(15)得到像素的修改量 $ \left({c}_{x }, {c}_{y}\right)=\left(0, -1\right) $ , 然后通过平均法得到原载体图像的像素对 $ \left(x , y\right)=\left(92, 101\right) $ , 并通过式(11)计算确定 $d$ 属于 ${R_1}$ , 模函数的模 $a = 3$ 和嵌入信息的比特位数 $b = 3$ , 通过式(17)得到像素值 $\left( {x', y'} \right) = ( 92, 100 )$ , 最后通过式(7)得到嵌入的十进制数B=5并将其转换为b位的比特流.

4 实验结果与数据分析

为测量本文所提出的可逆信息隐藏方案的各项性能^[26]. 通过在Windows 10操作系统上, 使用IntelliJ IDEA软件, 基于JavaFX框架开发了一个信息隐藏系统. 实验中进行的性能评估包括: PSNR、结构相似性(structural similarity, SSIM)、溢出问题、HC (hiding capacity)、嵌入率(bits per pixel, BPP)和RS隐写分析、PDH隐写分析. 并在此说明一下, 除特别声明以外, 从此处开始以及到论文其余部分, 实验数据中双图像信息隐藏方案的PSNR、SSIM均取平均值来进行比较.

灰色图像每个像素由一个分量组成, 彩色图像则将每个像素扩展为由3个不同的分量(即3个不同颜色通道)组成. 本文所提出的方案通过利用相邻像素的相同分量之间的差值, 所以本文提出的方案可用于彩色和灰色图像实现. 由于彩色图像比灰色图像多两条通道, 且对每条通道操作相同, 所以本文从USC-SIPI图像数据库^[27]中选取如图3所示的8幅大小为512×512的常见且具有代表性的标准灰色测试图像其中包括了纹理相对简单的人像和纹理相对复杂的自然环境、建筑物等.

4.1 嵌入容量与视觉不可感知性的分析

在本文的实验中, 用PSNR^[28]来衡量载密图像的质量, PSNR值越高表示载密图像质量越高, 而当PSNR值达到50 dB之后图像质量极好(即非常接近原图像), 所以也致使每提高一点都非常艰难. 如式(21)定义了PSNR (表示原载体图像和载密图像之间的失真度), 式(22)定义了MSE (表示原载体图像和载密图像之间的均方误差), 其单位为分贝(dB). MSE中, h表示载体图像的高, w表示载体图像的宽, C和S分别为载体图像和载密图像的在坐标 $\left( {i, j} \right)(0 \leqslant i < w, 0 \leqslant j < h)$ 上的像素值.

$ \begin{array}{*{20}{c}} {{\textit{PSNR}} = 10 \times {{\rm{log}}_{10}}\dfrac{{{{255}^2}}}{{{\textit{MSE}}}} \; \left( {{\text{dB}}} \right)} \end{array} $

(21)

$ \begin{array}{c}{\textit{MSE}}=\dfrac{1}{h \times w} \times {\displaystyle \sum }_{i=1}^{h}{\displaystyle \sum }_{j=1}^{w} {\left({C}_{\left(i, j\right)}- {S}_{\left(i, j\right)}\right)}^{2}\end{array} $

(22)

SSIM是一种对图像进行评估指标算法, 其通过计算原载体图像和载密图像的相似评估值, 而相似评估值的取值在[0, 1], 数值越靠近1两张图像之间相似性越高, 则隐藏效果更好. 式(23)定义了SSIM (用于表示两张图像之间的结构相似性大小), 其中 $x, y$ 分别代表载体图像和载密图像, $\;{\mu _x}$ 与 $\;{\mu _{{y}}}$ 分别代表 $x, y$ 均值, $ {\sigma _x} $ 和 $ {\sigma _y} $ 代表 $x, y$ 准差, ${\sigma _{xy}}$ 代表 $x, y$ 协方差. $ {C}_{1}=\text{ }{\left({K}_{1}\times L\right)}^{2} $ , $ {C}_{2}= {\left({K}_{2}\times L\right)}^{2} $ , 其中 ${K_1} = 0.01$ , ${K_2} = 0.03$ , $L = 255$ .

$ {\textit{SSIM}}= \frac{\left(2\times {\mu }_{x}{\mu }_{y}+{C}_{1}\right)\left(2\times {\sigma }_{xy}+{C}_{2}\right)}{\left({\mu }_{x}^{2}+ {\mu }_{y}^{2}+ {C}_{1}\right)\left({\sigma }_{x}^{2}+{\sigma }_{y}^{2}+{C}_{2}\right)} $

(23)

HC为原载体图像所能嵌入秘密信息的最大容量, BPP是载体图像像素的平均容量, 其定义为如式(24), 其中C代表有效载荷, S代表载体图像中字节总数量.

$ \begin{array}{c}BPP= \dfrac{C}{S}\end{array} $

(24)

溢出现象为当秘密信息被嵌入隐写像素中之后, 像素值超出允许范围. 溢出会直接导致无法正确写入图像中, 如果选择经过强制处理成[0, 255]范围内, 则可能会导致无法正确提取秘密信息, 或者选择直接简单粗暴的跳过该像素, 将秘密信息嵌入下一个像素中而没有任何依据, 则会在提取秘密信息时无法正确判断该像素是否嵌入秘密信息, 又或者增加额外信息跟踪表用于提取时判断是否在此像素嵌入信息, 但是会增加存储难度, 所以能正确有效且不增加额外信息的处理溢出问题非常重要.

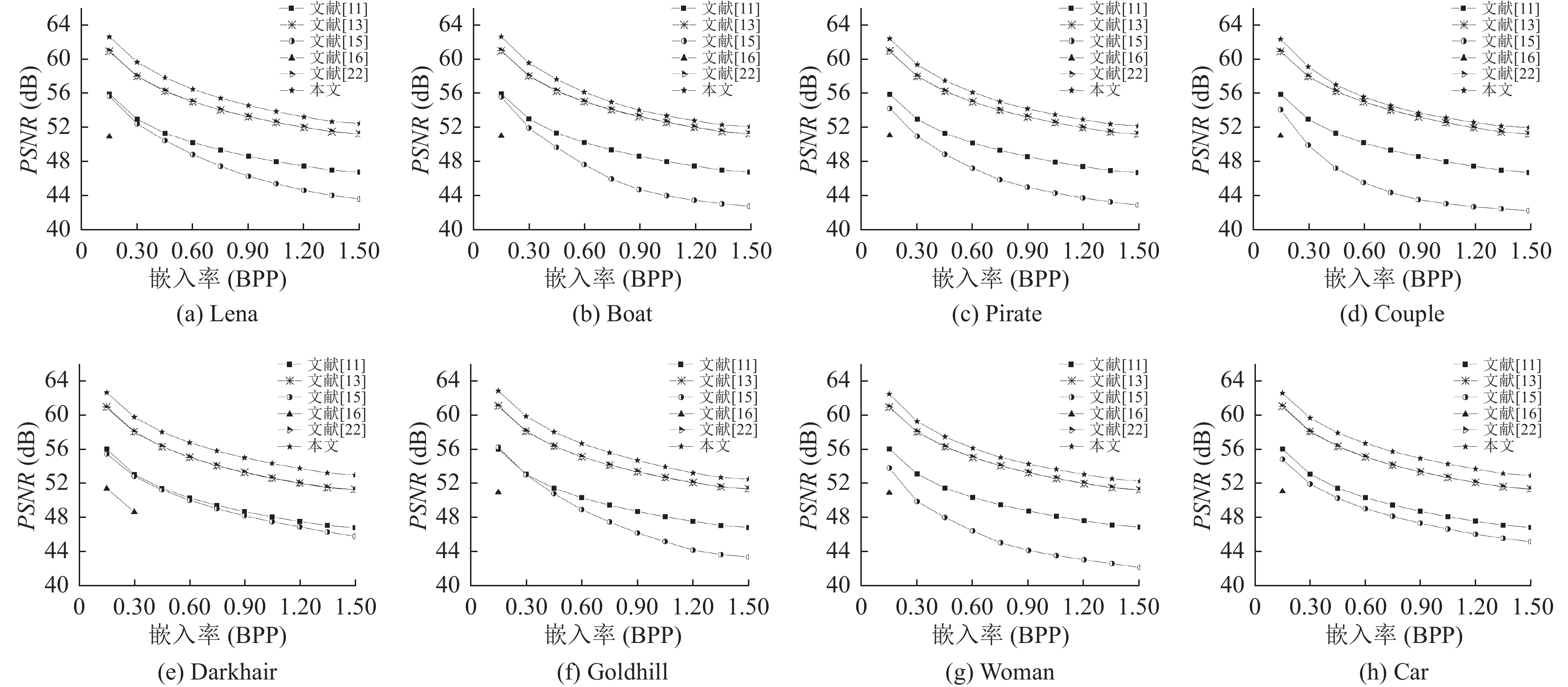
为便于观察在相同载体图像中, 6种方案在嵌入相同信息时, 随着嵌入量的增加, 载密图像的PSNR值的变化过程, 绘制如图4中8幅折线图所示, 通过观察可以发现在所有的图中本算法的PSNR值均高于其他5种方案, 所以实验结果表明本文所提出的算法产生的载密图像具有更好视觉不可感知性.

在表2中展示了获取USC-SIPI图像数据库中大小为: 256×256、512×512、1024×1024的所有灰色图像并进行相关的各项性能测试. 其中用不同的方案对所有灰色图像嵌入8万比特值, 计算得到的不同方案不同图像大小的所有载密图像的PSNR、SSIM的值的平均值(其中文献[16]在大多数图像中无法满足嵌入相同容量的要求), 最后用本方案的平均值作为参考值, 得到如表2中所示各个方案与本方案的PSNR、SSIM平均值偏差, 可观察到均为负值(即均小于本方案的PSNR、SSIM平均值差值). 所以实验结果表明本文所提出的算法具有更好嵌入效率.

表3统计了对USC-SIPI图像数据库中所有灰色图像使用各个信息隐藏方案的BPP的平均值, 以及可能出现不可预测或不可处理的溢出数据的平均值, 通过观察本方案在嵌入容量方面, 虽并不都优越于其他所有方案, 但通过表1和表4可知本方案在像素差值越大(即图像纹理差距越大)的图像中的嵌入信息容量越高, 最优BPP可高达3.5而嵌入容量高达90万+比特, 并且本方案未出现不可预测或不可处理的情况, 在未增加额外的信息跟踪表情况下, 成功解决了溢出问题, 所有本方案相对于其他方案更具有灵活性和相对于某些方案具有更完整的信息隐藏过程.

4.2 RS隐写分析与PDH隐写分析

RS隐写分析和PDH隐写分析都是用于评估信息隐藏方案安全级别的分析算法, 两者从不同的方面来测试隐写方案具有的安全程度. 后文第4.2.1节和第4.2.2节分别介绍了RS隐写分析和PDH隐写分析以及展示了实验分析结果图.

4.2.1 RS隐写分析

RS隐写分析通过翻转函数和平滑度函数来计算分析, 其中翻转函数的掩码算子M, 本次实验取 $ M = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right] $ , 通过计算之后像素被分为3组: 正则组 $\left( {{R_m}, {R_{ - m}}} \right)$ 、奇异组 $ \left({S}_{m} \approx {S}_{-m}\right) $ 、不可用组.

$\left\{ \begin{array}{l} {R}_{m}+ {S}_{m}\leqslant 1, \; {R}_{-m}+{S}_{-m}\leqslant 1\\ {R}_{m} \approx {R}_{-m}, \; {S}_{m} \approx {S}_{-m}\\ {R}_{m} > {S}_{m} , \; {R}_{-m} > {S}_{-m}\end{array} \right.$

(25)

如果正则组和奇异组满足式(25)中所有的关系式, 则该隐写信息方案可抵抗RS隐写分析, 否则不能抵抗.

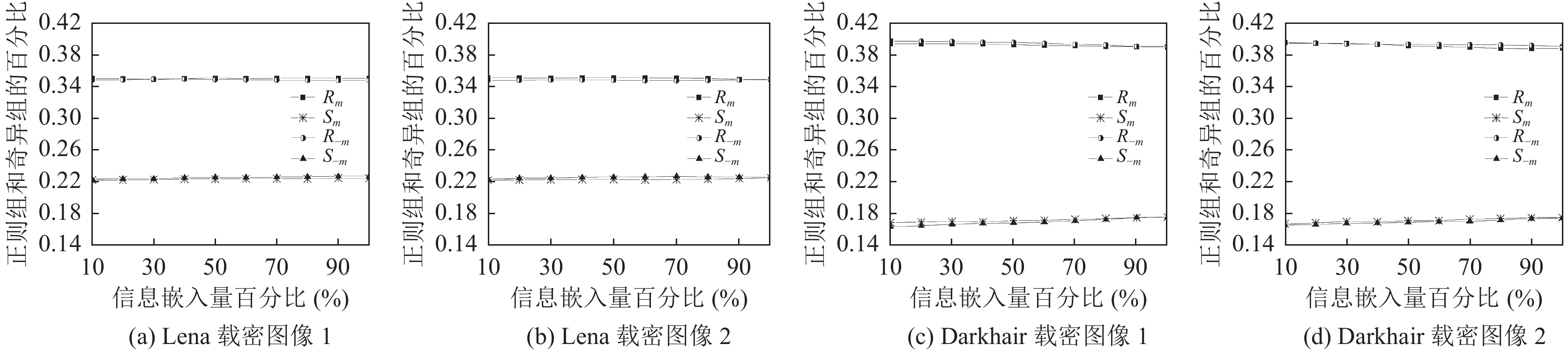
因篇幅限制只展示对Lena、Darkhair灰色图像嵌入信息之后产生的双图像的RS分析测试图(以10%的嵌入率递增到100%, x轴表示信息嵌入量的百分比, y轴表示规则组或奇异组的百分比). 如图5中4幅RS分析图所示正则组和奇异组均满足式(25)中所有的关系式, 所以本文提出的方案可抵抗RS隐写分析.

4.2.2 PDH隐写分析

PDH隐写分析通过计算图像中相邻像素值的差值并统计分析差值的频率, 差值均在[−255, 255]范围内, 这里截取差值频率最高的范围[−40, 40]. PDH隐写分析的原理: 由于相邻像素值之间的具有高度相关性, 在载体图像中PDH曲线通常是平滑, 频率值集中在零值附近, 而在嵌入秘密信息之后, PDH曲线通常会产生锯齿状、阶梯效应或产生扁平化, 导致嵌入秘密信息的载密图像的PDH值分布与原载体图像有所区别.

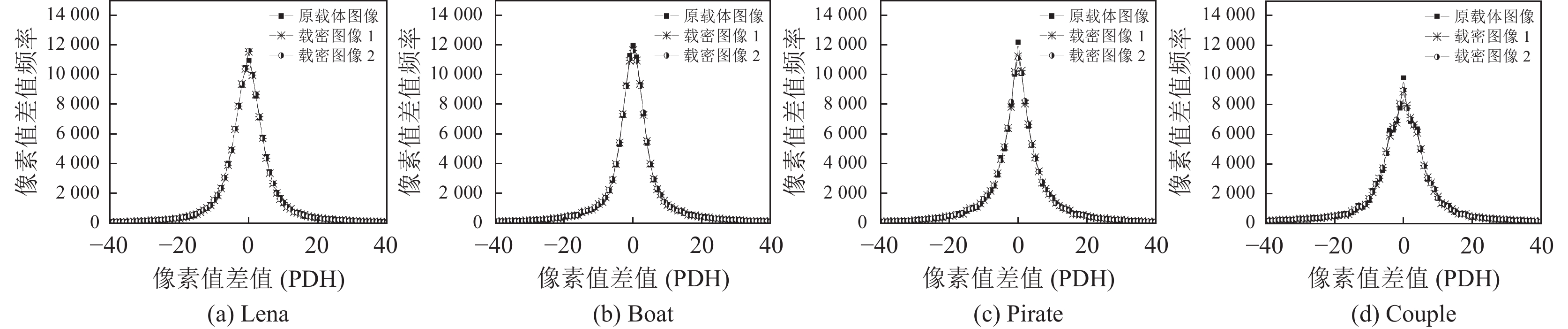
通过本文提出的方案在嵌入信息率为100%产生的双载密图像, 绘制了Lena、Boat、Pirate、Couple这4幅如图6所示(x轴表示PVD, y轴表示PVD频率)的PDH分析图, 双载密图像的PDH曲线均没有产生锯齿状或是阶梯效应, 与原载体图像的PDH曲线也非常的接近未出现扁平化, 几乎很难与原载体图像区分开来. 所以本文所提出的方案可以抵抗PDH隐写分析.

5 结束语

本文针对传统的基于像素值差值的隐写方案像素值修改量大的问题, 本文提出了一种基于模函数与像素值差值的高质量双图像可逆信息隐藏算法, 优先将PVD范围表划分方法调整为根据模函数和对数函数, 再根据差值和查表确定每组像素对信息的嵌入位数, 最后利用模函数和平均法嵌入信息. 实验结果表明本文设计的隐写方案可以做到无损恢复原载体图像和无差错提取秘密信息, 在载密图像的视觉质量上优于目前学界中的其他同类型方法, 并且安全性上可抵抗RS和PDH隐写分析, 下一步可以考虑探究基于模函数和PVD的算法在保障不降低载密图像视觉质量的基础上提高, 例如嵌入容量等性能问题.