近年来, 人工智能和机器人技术的应用场景不断发展, 如消毒机器人、室外巡检机器人、救援机器人等. 现实问题的逐渐复杂, 对机器人数量的需求也逐渐增多. 相比于单机器人导航, 多机器人协作导航可以更好地利用机器人共享的信息完成多目标导航任务, 提升对环境的适应性与容错性. 多机器人协作导航问题(multi-robot cooperative navigation problem, MCNP)是移动机器人领域的热点问题之一, MCNP在实际场景中有协作搜救、编队控制、智能仓储和物流等应用.

在MCNP的研究中, 根据目标点是否提前分配主要分为两个方向: 目标点预先分配问题和目标点动态分配问题. 在目标点预先分配问题中, 每个机器人要前往的目标点是固定的, 在运行过程中不会改变^[1-5]. Chen等^[1] 提出了一种基于地图的DPPO (distributed proximal policy optimization) 方法, 在分布式和无通信环境中无碰撞的到达各自预先分配的目标点, 并利用课程学习的方法提升整体训练的效果. Ma等^[2] 研究了已知地形中的智能体团队的目标分配和路径查找问题, 提出了CBM (conflict-based min-cost flow) 分层算法, 为所有智能体分配目标点, 然后规划出一条无碰撞的路径. Boldrer等^[3] 采用分层体系结构, 通过将全局路径规划, 预测性路径规划和反应性方法相结合, 获得安全且具有社会意识的多智能体导航策略. 但是预先分配目标策略通常适用于已知环境, 无法很好扩展到未知或动态的环境. 在目标点动态分配问题中, 每个机器人在运行过程中可以动态改变要前往的目标点, 动态目标分配策略可以更好地与环境相适应^[6-11]. 在简单环境下, 常采用启发式方法, 为所有机器人集中分配目标点. Han等^[6] 将启发式目标分配策略与基于强化的目标导航策略相结合, 解决了动态环境中多机器人的导航问题, 并设计了从模拟环境到真实环境的迁移机制, 将训练好的策略更好地应用在真实环境中. Panagou等^[7]应用启发式的方法, 将动态多智能体系统的分配问题和安全问题转换为交换系统的稳定性问题, 只有在通信范围内的两个智能体才可以决定是否更换目标点, 从而确保互换目标位置的安全性和全局稳定性.

然而, 未知复杂环境下的不确定性因素众多, 需要增加对环境的感知, 而启发式的方法需设计更为复杂的规则来实现目标的分配. 因此, 常采用基于多智能体深度强化学习(multi-agent deep reinforcement learning, MARL)的分布式目标点分配方法, 来为每个机器人独立分配目标点. Marchesini等^[9] 提出了一种基于集中训练分散执行体系结构的GDQ (multi-agent global dueling Q-learning)算法, 解决了多机器人无地图导航问题. Jin等^[10] 提出了一种新的分层稳定的分布式框架解决未分配目标的多智能体导航问题. 相较于集中式目标点分配方法, 分布式目标点分配方法的主要难点是重复选点问题(多个机器人前往同一目标点)和局部最优解问题. 目前通过MARL实现目标点动态分配策略的研究相对较少, 且大多是在简单的仿真环境中进行测试, 不利于模拟环境到真实环境的迁移.

因此, 针对未知环境下目标点的动态分配问题, 本文提出了一种基于课程学习和优先经验回放的多智能体深度强化学习算法, 在机器人操作系统(robot operating system, ROS)^[12] 环境下完成算法训练和测试. 在未知环境下, 只有目标点位置已知, 每个机器人可以前往任意目标点, 以最短时间无冲突地到达所有目标点. 具体来说, 机器人利用激光雷达对周围环境进行感知, 获取其他智能体和目标点的相对距离, 通过目标决策层给每个机器人独立分配目标点, 通过目标导航层引导每个机器人到达相应目标点.

本文的贡献主要包括3个方面.

(1)设计了分层控制协作导航策略(hierarchical control cooperative navigation, HCCN), 高层为目标决策层, 低层为目标导航层.

(2)提出基于课程学习和优先经验回放的多智能体深度强化学习算法, 解决协作导航中稀疏奖励问题, 加速训练.

(3)选用基于ROS的物理仿真平台, 便于实现仿真环境到真实环境的迁移.

1 背景知识 1.1 多智能体强化学习

强化学习(reinforcement learning, RL)^[13] 是一种常用的机器学习方法, 智能体在与环境交互中通过奖励信号改进策略, 目标是最大化累计奖励. 单智能体强化学习任务可以通过马尔可夫决策过程(Markov decision process, MDP)来描述. 多智能体深度强化学习^[14]将强化学习、博弈论等应用到多智能体系统, 从而使多个智能体在交互和决策中完成更复杂的任务. 多智能体在不确定环境中的决策过程, 通常利用分布式部分可观测马尔可夫决策过程(decentralized partially observable Markov decision process, Dec-POMDP)来描述.

Dec-POMDP由多元组 $ (I, S, {A}_{i}, {\Omega }_{i}, P, O, R) $ 表示, 其中 $ I $ 是有限的智能体集合; $ S $ 是系统的状态空间; $ {A_i} $ 是智能体 $ i $ 的动作空间; $ {\Omega _i} $ 是智能体 $ i $ 可获得的观测空间; $ P:S \times A \times S \to [0, 1] $ 是系统的状态转移函数; $ A $ 是所有智能体的联合动作空间; $ P(s'\left| {s, a)} \right. $ 是在状态 $ s \in S $ 中采取联合动作a转移到新的状态 $ s' \in S $ 的概率; $ O:S \times A \times \Omega \to [0, 1] $ 是系统的观测函数; $O(o\left| {s' , a)} \right.$ 是采取联合动作 $ a $ . 转移到新状态 $s'$ 得到联合观测 $ o $ 的概率; $ R:S \times $ $A \to R $ 是系统的奖励函数; $ R(s, a) $ 是在状态s下采取联合动作a后整个团队获得的奖励.

在多智能体强化学习中, 每个智能体 $ i $ 的自身策略 $ {\pi _{{i}}}:S \times {A_i} \to [0, 1] $ , 多智能体根据联合策略π不断与环境进行交互, 获得经验样本来优化联合策略. 联合策略的优化目标是最大化期望累积奖励:

$ E(R) = \sum\limits_i^N \left(\sum\limits_{t = 0}^T {{\gamma ^t}} {R_i}(s_i^t, a_i^t\sim\pi (s_i^t))\right) $

(1)

其中, $ {R_i} $ 是智能体 $ i $ 的奖励函数, 当智能体之间为完全合作关系时, 所有智能体共享同一奖励函数; $ s_i^t $ 是智能体 $ i $ 在 $ t $ 时刻的状态; $ a_i^t $ 是智能体自身策略 $ {\pi _i} $ 所决策的动作; $ \gamma \in [0, 1] $ 是折扣因子, 用于衡量未来奖励的重要性.

多智能体强化学习易受非平稳性问题的影响^[15], 即在训练过程中, 策略随时间不断变化, 状态转移函数和奖励函数受智能体动作的影响也不断变化, 智能体有时无法判断某一时刻获得的奖励是受自身动作还是其他智能体动作的影响. 为了解决非平稳性问题, Lowe等^[16] 采用集中式训练分布式执行框架对演员-评论家算法进行扩展. Foerster等^[17] 利用通信机制来稳定训练过程, 不同智能体之间能够交换其观测与动作信息. Finn等^[18] 通过元学习对环境变化进行预测, 为解决环境非平稳性问题提供了新的思路.

1.2 优先经验回放

在强化学习中, 智能体每与环境进行一次交互, 就会产生一次状态转移(transition): $ ({s_t}, {a_t}, {r_t}, {s_{t + 1}}) $ . 在传统的时序差分学习中transition使用一次就会被舍弃, 而经验回放机制^[19] 可依次将这些transition存储在一定容量的回放缓存中, 每次训练时随机均匀地从经验中进行抽样. 通过经验回放机制重复利用过去的经验, 能够提高样本的利用率, 随机采样打破了序列的相关性, 使神经网络的学习更符合传统监督学习.

在稀疏奖励场景中, 增大重要样本被采样的概率非常重要, 通常使用优先经验回放机制(prioritized experience replay, PER)^[20] 来解决这一问题. 优先经验回放利用时序差分误差进行采样, 一个transition的时序差分误差越大, 说明它越重要, 被抽取的概率就越大. 时序差分误差 $ {\delta _t} $ 计算公式为:

$ {\delta _t} = {r_t} + \gamma V({s_{t + 1}}) - V({s_t}) $

(2)

其中, $ r $ 是即时奖励; $ \gamma $ 是折扣因子; $ V(s) $ 是状态价值. 如果只根据 $ \left| \delta \right| $ 的大小选择更新的样本, 神经网络只会基于一小部分样本进行更新, 很容易陷入局部最优, 因此通常选用更具随机性的方法, 对每个transition都计算出一个抽样概率, 根据这个抽样概率来采样. 抽样概率 $ P(t) $ 公式为:

$ P(t) = \frac{{p_t^\alpha }}{{\displaystyle\sum\nolimits_k {p_k^a} }} $

(3)

其中, $ \alpha \in [0, 1] $ 是权衡因子, 用于控制采样在均匀采样和贪婪采样的偏好; $ P(t) $ 是抽样权重, 目前常用的方式是让 $ {p_t} $ 正比于 $ \left| \delta \right| $ , 即 $ {p_t} = \left| \delta \right| + \varepsilon $ , $ \varepsilon $ 是一个很小的数, 避免 $ {p_t} $ 等于零.

由于优先经验回放的抽样是非均匀的, 不同的transition有不同的抽样概率, 这样会导致强化学习算法预测有偏差. 本文通过引入重要性采样、退火因子 $ \;\beta $ , 设置较小的重要性采样权重 $ {\omega _t} $ , 计算每条transition的抽样概率, 调整学习率来减小不同抽样概率造成的预测偏差. 采样权重( $ {\omega _t} $ )计算公式为:

$ {\omega _t} = \frac{{{{(M \times P(t))}^{ - \beta }}}}{{{{\max }_k}({\omega _k})}} $

(4)

其中, $ M $ 是经验缓存区中样本数; $ P(t) $ 是抽样概率; $\;\beta \in [0, 1] $ 是一个超参数, 用于控制优先经验回放对收敛结果的影响; $ {\max _k}({\omega _k}) $ 是所有transition中的最大采样权重.

1.3 全局路径规划算法

全局路径规划是在已有地图信息的基础上, 根据当前位置与目标位置, 规划一条可行的全局路径. $ {{\text{A}}^*} $ 算法^[21] 是一种简单有效的基于图搜索的方法, 可以很好地解决最短路径问题. 它在Dijkstra算法的基础上加入了启发估算函数来引导搜索路径向目标点扩展, 进而减少搜索空间, 加速规划过程. 计算公式为:

$ f(n) = g(n) + h(n) $

(5)

其中, $ g(n) $ 是从起始状态到 $ n $ 状态的最短路径代价; $ h(n) $ 是从 $ n $ 状态到目标状态的启发式路径代价估计值, 通常采用欧氏距离或曼哈顿距离计算. 若每个状态到目标状态的最优启发式代价估计值 $ {h^*}(n) $ 已知, 就可得到机器人从当前状态到目标状态的最短路径.

2 协作导航策略

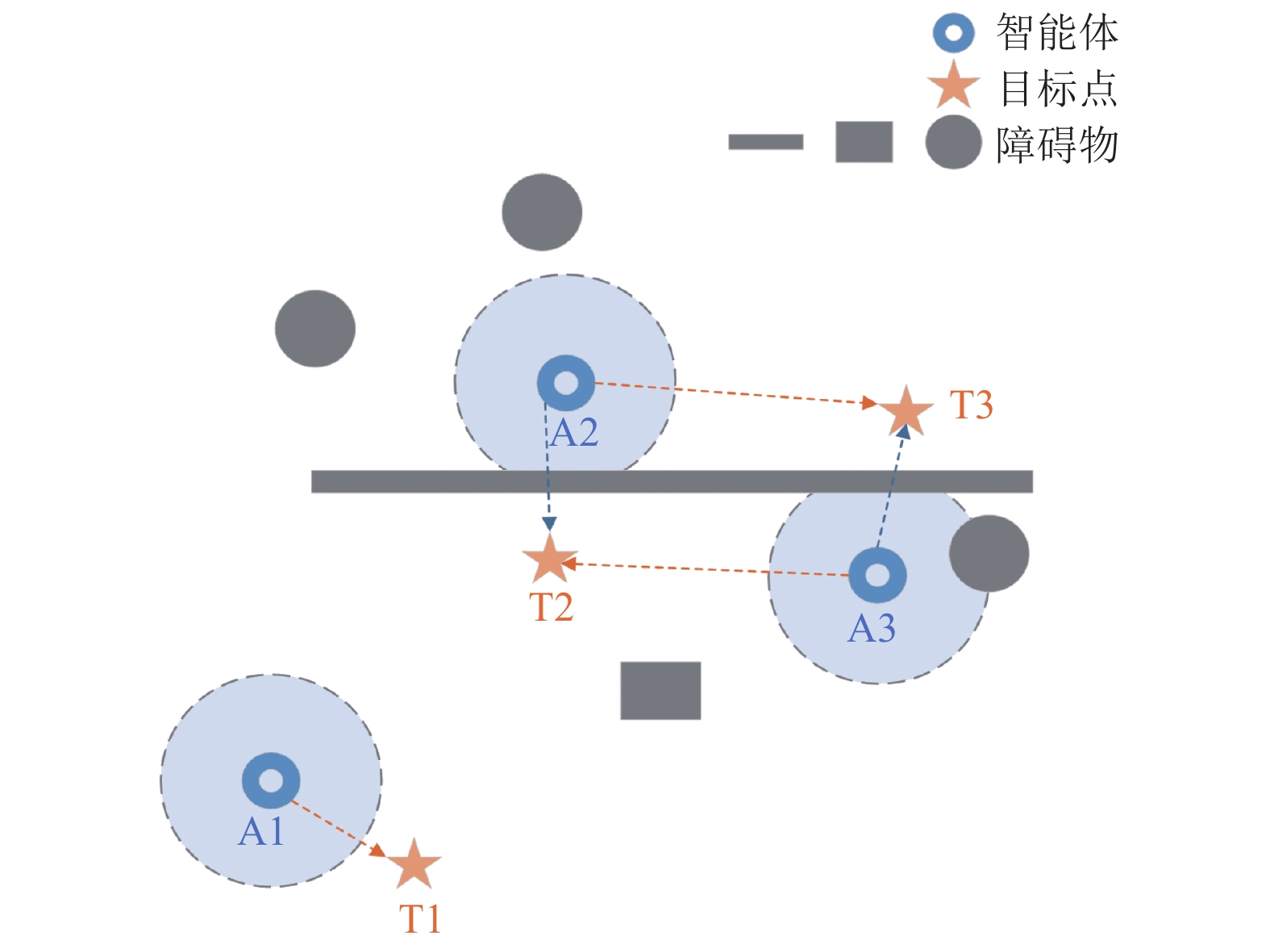
通过分层控制结构来实现协作导航策略, 使 $ N $ 个机器人花费最短的时间无冲突、无碰撞的到达 $ N $ 个目标点, 如图1所示, 蓝色区域表示智能体激光雷达的感知信息, 黄色虚线表示智能体要前往的目标点.

2.1 分层控制结构

本文提出了一种分层控制结构, 高层为目标决策层, 为智能体动态分配目标点; 低层为目标导航层, 用于引导智能体无碰撞的到达所选目标点, 分层控制结构如图2所示. 每个时间步中, 目标决策层中的每个智能体根据环境的观测信息, 通过MARL算法决策自身要前往的目标点, 将目标点输入目标导航层, 再依据全局路径规划算法和局部路径规划算法, 向目标点移动一段距离(运行时间为9 s), 更新自身状态. 若未完成整体任务要求, 则继续迭代, 由目标决策层重新分配目标点, 目标导航层进行路径规划, 直至所有智能体无冲突地到达所有目标点.

2.2 目标决策

目标决策层基于MATD3 (multi-agent twin delayed deep deterministic policy gradient)^[22] 算法, 引入课程学习和优先经验回放, 使智能体更快地学会动态目标分配策略.

2.2.1 问题建模

多机器人协作导航问题可看作完全协作问题, 所有智能体共用一个奖励函数最大化团队的总收益. 本文将多智能体的目标决策建模为Dec-POMDP, 每个智能体基于对环境的局部感知以及相互之间的部分信息共享, 独立进行目标点决策.

(1)观测空间

在 $ t $ 时刻, 每个智能体 $ i $ 的观测信息 $o_i^t = [o_{i, r}^t, o_{i, {\rm{tar}}}^t, o_{i, {\rm{ag}}}^t, o_{i, {\rm{his}}}^t]$ 主要由4部分组成: 智能体装载的激光雷达对周围环境的距离感知 $ o_{i, r}^t $ 、智能体到所有目标点的相对位置 $o_{i, {\rm{tar}}}^t$ 、智能体到其他智能体的相对位置 $o_{i, {\rm{ag}}}^t$ 以及上一时刻各个智能体所选目标点 $o_{i, {\rm{his}}}^t$ . 在未知环境中, 如果未对周围环境进行感知, 仅根据相对位置信息进行决策, 智能体最终学出的策略可能会贪婪的选择距离自己最近的目标点, 如图3所示, 智能体2、3可能会选择距离自己最近的目标点2、3 (如图中蓝色虚线所示). 这种决策方式在某些场景中是不合理的, 正确的决策应该如图中橙色线所示. 因此, 需要增加对周围环境感知, 综合环境信息进行目标决策.

(2) 动作空间

本文将每个智能体 $ i $ 的动作 $ {a_i} \in [0, 1] $ 作为连续值进行输出, 通过建立于目标点的映射 $ta{r_i} = {a_i} \times nu{m_{{\rm{tar}}}}$ 得到智能体所选的目标点, 其中 $nu{m_{{\rm{tar}}}}$ 是所有目标点的数量.

(3) 奖励空间

协作导航任务的目标是以最小的代价无冲突的到达所有目标点, 基于此将奖励函数 $ r $ 分为以下3部分:

$ r = {r_{{\rm{done}}}} + {r_{{\rm{repeat}}}} + {r_{{\rm{step}}}} $

(6)

其中, ${r_{{\rm{done}}}}$ 是任务完成奖励, 当智能体无冲突的到达所有目标点, 将会获得一个较大正奖励; ${r_{{\rm{step}}}}$ 为时间步惩罚, 每个时间步都会给予一个较小负奖励, 鼓励智能体尽快完成任务要求; ${r_{{\rm{repeat}}}}$ 为重复选点惩罚, 如果任意两个智能体选择同一目标点, 两者会给予一个负奖励, 由于每个智能体是分布式执行的, 不确定其他智能体此时的选点情况, 所以需要利用重复选点惩罚来帮助智能体尽快完成任务. 在训练过程中, 一个回合的终止条件为所有智能体无冲突的到达所有目标点, 当智能体到达决策目标点但未满足终止条件时, 会对所有智能体进行重新决策.

尽管设置了主线奖励和辅助奖励对智能体进行引导, 但是整体的奖励信号是稀疏的, 需通过课程学习和优先经验回放进行改进.

2.2.2 课程学习

课程学习是一种训练策略^[23], 模仿了人类课程中的学习顺序, 先在简单的样本中训练智能体, 然后逐步增加难度进行训练, 从而提高模型的泛化能力和收敛率. 课程学习策略通常分为学习简单的示例集和学习目标训练集两步. 本文中智能体先在简单目标任务中学习无冲突的到达所有目标点, 即先让智能体学会如何完成最终目标任务; 然后设置更具挑战性的目标点, 使智能体在第1阶段的基础上完成更复杂的任务要求, 更有效地到达所有目标点.

2.2.3 基于优先经验回放的MATD3算法

将MATD3算法与优先经验回放相结合来解决目标决策过程中稀疏奖励的问题. 各分布式智能体共用同一POMDP结构, 进而共用同一Actor-Critic网络, 具体如图4所示.

在训练过程中, 首先采用随机策略让智能体与环境进行交互, 增强智能体对环境的探索能力, 然后采用PER-MATD3算法进行智能决策. 具体来说, 根据式(3)计算每个transition的抽样概率, 并将其存入经验缓存区; 网络更新时根据采样概率从经验缓存区中取出一批数据, 利用Critic目标网计算目标值(式(8)) , 与预测值进行对比, 计算均方误差(式(7)), 通过误差更新Critic网络; 基于Critic网络的评价进行梯度计算(式(9))更新Actor网络.

Critic网络的目标是尽可能准确的预测Q值, 因此, 将损失函数 $ L({\phi _{i, c}}) $ 定义为预测值与目标值的均方误差:

$ L({\phi _{i, c}}) = \frac{1}{B}\sum\limits_j {{\omega _j}({y^j}} - Q_c^\mu ({s^j}, a_{1:N}^j){)^2} $

(7)

其中, $ {\omega _j} $ 是样本 $ j $ 重要性采样权重, 可通过式(4)计算; N是智能体数量; $ Q_{}^\mu $ 是Critic网络的预测值; $ B $ 是批量大小; $ {y^i} $ 是样本 $ j $ 实际目标 $ Q $ 值, 通过最小化预测值与目标值差距, 引导网络得到更加准确的预测值. $ {y^j} $ 计算公式为:

$ {y^j} = r_i^j + \gamma \mathop {\min }\limits_{c = 1, 2} Q_c^{\mu ' }({s'^{ j}}, a'_{1:N} )\left| {_{a'_k = \mu' (o_k^j) + \mathcal{N}}} \right. $

(8)

其中, $\;\mu '$ 是目标Actor网络; $Q_{}^{\mu' }$ 是目标Critic网络, 为避免智能体在学习过程中出现Q值过高估计的情况, 同时学习两个Critic网络, 然后使用其中较小的Q值来计算 $ {y^j} $ .

Actor网络的目标是选出最优action, 因此Actor网络将最大化Q值作为更新方向, 其梯度计算为:

$ {\nabla _{{\theta _i}}}J \approx \frac{1}{B}\sum\limits_j {{\omega _j}} {\nabla _{{\theta _i}}}{\mu _i}(o_i^j){\nabla _{{a_i}}}Q_1^\mu (s{}^j, a_1^j,\cdots, \mu (o_i^j), \cdots, a_N^j) $

(9)

具体PER-MATD3如算法1所示.

算法1. PER-MATD3

1. 初始化Actor网络 $\scriptstyle \mu $ 及其参数 $\scriptstyle \theta $ 、Critic网络 $\scriptstyle Q $ 及其参数 $\scriptstyle \phi $ , 及其对应的目标网络 $\scriptstyle \theta ' \leftarrow \theta$ , $\scriptstyle \phi ' \leftarrow \phi$

2. 初始化经验缓存区 $ \scriptstyle D $

3. 对于训练回合 $\scriptstyle episode = 1 $ 到M:

4. 　初始化高斯随机过程 $\scriptstyle \mathcal{N} $ 用于动作探索

5. 　初始化环境、智能体状态, 获取每个智能体观测信息 $\scriptstyle o $

6.　 对于回合步数 $\scriptstyle t = 1 $ 到 $\scriptstyle max\_episode\_length $ :

7.　　 对每个智能体 $\scriptstyle i $ , 根据当前策略和动作噪声获得动作 $ \scriptstyle {a_{i, t}} = \scriptstyle \;{\mu _\theta }({o_{i, t}}) + \mathcal{N} $

8.　　 执行动作 $ \scriptstyle{a_{i, t}} $ , 计算奖励 $\scriptstyle {r_t} $ , 得到新的观测信息 $ \scriptstyle{o_{i, t + 1}} $

9.　　 根据式(3)计算每个transition的采样优先级 $　\scriptstyle P(j)$

10.　　将 $\scriptstyle ({s_t}, {o_t}, {a_t}, {r_t}, o_t', s_t') $ 存储到经验缓存区 $\scriptstyle D $

11.　　 $\scriptstyle o \leftarrow {o_{t + 1}}$

12.　　对于每个智能体 $\scriptstyle i $ 到 $\scriptstyle N $ :

13.　　　 根据采样概率 $\scriptstyle {P_j} $ 在缓存区采样 $\scriptstyle D $ 个样本

14.　　　 根据式(8)计算目标值

15.　　　 根据式(4)计算采样权重

16.　　　 通过最小化损失(式(7))更新Critic网络

17.　　　 如果 $\scriptstyle episode\% policy\_delay = 0 $ :

18.　　　　　 根据式(9)计算梯度更新Actor网络

19.　　　　　 更新目标网络参数:

　　　　　　　 $\scriptstyle \theta _{i, c}' \leftarrow \tau {\theta _{i, c}} $ + $\scriptstyle (1 - \tau )\theta _{i, c}' $

　　　　　　　 $\scriptstyle \phi _{i, c}' \leftarrow \tau {\phi _{i, c}} + (1 - \tau )\phi _{i, c}'{\text{ }}{\rm{for}}{\text{ }}c{\text{ }} =$ 1, 2

2.3 目标导航

在目标导航层, 智能体根据当前所在位置与被分配的目标点位置, 规划一条无碰撞、能安全到达目标点的有效路径. 路径规划是智能体导航和控制的基础, 根据环境的状态可分为全局路径规划和局部路径规划, 前者基于已知环境的信息, 按性能指标规划一条全局路径; 后者侧重于智能体当前的局部环境信息, 让智能体具有良好的避障能力. 利用全局路径规划和局部路径规划相结合的方法, 可以在避障的基础上规划一条从起始点到目标点的最短可行路径, 以便更好地适应不同复杂场景.

本文选用A^*算法作为全局路径规划算法, 动态窗口法(dynamic window approach, DWA)^[24]作为局部路径规划算法. 由于环境未知, 全局规划生成的路径只是智能体当前位置到目标点的大致可行路径, 未考虑环境中未知障碍物的信息. 为矫正全局规划结果, 还需要结合局部路径规划. DWA算法可以根据当前机器人状态计算速度空间, 采样多组线速度、角速度的组合, 生成一段时间运动轨迹, 通过评价函数对轨迹进行评价, 选取最优的速度组合发送给机器人下层运动控制模块, 使其按照目标轨迹进行运动. 分层控制协作导航策略如算法2所示.

算法2. 分层控制协作导航

1. 对于训练回合 $\scriptstyle episode = 1 $ 到M:

2. 　基于课程学习的思想, 根据当前训练回合, 由易到难设置训练环境 env(episode)

3. 　对于回合步数 $ 　\scriptstyle t = 1 $ 到 $　\scriptstyle max\_episode\_length $ :

4.　 　通过MATD3算法生成每个智能体的动作 $　\scriptstyle a $

5.　 　建立动作 $\scriptstyle a $ 与目标点 $\scriptstyle g $ 的映射 $\scriptstyle a \to g $

6.　 　每个智能体 $\scriptstyle i $ 根据目标点, 通过全局路径规划 $ \scriptstyle {{\text{A}}^*} $ 算法规划一条到目标点的大致可行路线

7.　 　局部路径规划DWA算法在全局路线基础上, 基于当前局部环境感知生成一条避免碰撞的运动轨迹, 引导智能体向所选目标点移动

8.　 　每个智能体根据分配目标点执行一段时间后, 计算奖励 $\scriptstyle r $ , 得到下一时刻状态 $\scriptstyle {s_{t + 1}} $ , 并将 $\scriptstyle ({s_t}, {o_t}, {a_t}, {r_t}, {o_{t + 1}}, {s_{t + 1}}) $ 存储到经验缓存区

9.　 　当经验缓冲区达到一定数量样本时, 基于优先经验回放进行采样并对MATD3网络进行更新

3 实验结果及分析 3.1 实验设置

ROS作为机器人软件开发和控制的平台, 广泛应用于真实机器人和仿真环境中. Gazebo与ROS紧密集成, 内置多种物理引擎, 支持多种机器人模型和传感器(如激光雷达、相机、惯性测量单元等)的导入, 可以很好地模拟真实机器人的行为(如机器人的动力学、运动控制和传感器数据等). 相较于其他强化学习算法使用的小型格点环境^[8-11] , Gazebo环境具有可定制性和真实性, 能够灵活搭建各种场景, 降低算法到真实环境的迁移难度. 因此, 本文选用Gazebo物理仿真平台创建了训练和测试的仿真环境, 选用Turtlebot3 Burger作为仿真移动机器人, 每个机器人装载一个2D 360度激光雷达, 发射24条激光用于感知机器人周围的距离信息, 每个机器人最大运行速度为0.1 m/s.

基于课程学习思想, 创建了如图5所示的训练环境, 整体环境大小为12 m×13 m, 包含3个智能体、3个目标点以及不同类型的障碍物. 智能体在训练过程中, 从易到难依次学习不同的目标任务, 网络训练参数如表1所示. 目标任务相对简单的场景中, 智能体需学会如何完成最终的目标任务(图5(a)), 在此基础上, 不断增加任务难度(图5(b)和图5(c)), 通过协作以最小的代价完成目标任务.

3.2 训练结果分析

为验证课程学习及优先经验回放对目标决策的影响, 将本文提出的结合课程学习和优先经验回放的C-PER-MATD3算法与仅使用优先经验回放的MATD3算法(PER-MATD3)、仅使用课程学习的MATD3算法(C-MATD3)以及基线MADDPG^[16]、MATD3算法在仿真环境下进行对比, 回报结果如图6所示.

MATD3和MADDPG都是目前主流的多智能体强化学习算法. 由于稀疏奖励的问题, 这两种基线算法自始至终未学会智能行为, 在加入课程学习和优先经验回放后, 智能体更好地利用已有的历史经验, 学会了智能协作策略. 本文提出的 C-PER-MATD3 算法在简单场景(图5(a))的学习中表现出较好的协作效果: 在第1次训练任务切换时(任务目标从图5(a) →图5(b)), 1000步有一段较长时间回报降低的阶段, 从1500步开始智能体逐渐适应该任务目标, 回报不断增加; 在第2次训练任务切换时(任务目标从图5(b) →图5(c)), 仅出现一小段时间回报降低, 随后快速学习, 在6000步达到收敛. PER-MATD3算法与C-MATD3算法均在4000步左右才开始表现出智能协作行为, 在7000步左右开始收敛. 与单独使用课程学习或优先经验回放相比, 本文提出的算法在收敛速度上至少提高了16.6%. 因此, 将课程学习与优先经验回放相结合可以很好地解决协作导航问题, 提高训练速率.

3.3 测试结果分析

为验证算法在不同场景下的适应性, 设计了几种不同的测试环境. 对本文提出的算法在不同测试场景下进行可视化展示(图7所示), 每个智能体移动轨迹的颜色与所选目标点的颜色相同. 在图7(a)场景中, 环境相对简单, 每个智能体分别前往距离自己最近的目标点; 在图7(b)场景中, 每个智能体通过对周围环境的感知以及共享的位置信息, 协作分配要前往的目标点; 在图7(c) 中, 每个智能根据当前感知信息动态选择目标点, 在初始阶段会向同一目标点进行移动, 随着不断运动, 智能体会分散前往不同目标点.

选择任务目标完成的平均运行时间及成功率作为评价算法性能的指标, 前者为所有智能体从起始点出发, 无冲突的到达所有目标点平均所花的时间; 后者为在有限时间内, 完成任务目标的次数与测试总数的比例. 文中每个算法在每个测试环境下均运行30次, 每次运行最大时长为120 s, 具体测试结果如表2所示. 本文提出的算法在不同的测试场景下均表现良好, 进一步说明课程学习和优先经验回放的结合可以提升算法对不同场景的适应性.

4 结论与展望

(1)本文提出了一种新的分层控制结构来解决未知环境下多机器人协作导航问题, 使机器人以最小的代价无冲突的到达所有目标点. 在高层利用MARL算法完成目标点的决策; 在低层利用路径规划算法引导机器人到达相应目标点. 经对比实验验证, 课程学习和优先经验回放可以很好地解决协作导航过程稀疏奖励问题, 增强协作导航策略的适应性, 加速MARL算法的学习效率.

(2)本文提出的方法默认各个机器人都可以共享自己的位置信息, 在实际工作环境中, 可能会出现通信中断的情况, 未来将考虑通信受限环境下的多机器人协作导航问题; 且当前训练和测试的环境均为仿真环境, 未来将在实体机器人中进行迁移测试.