21世纪以来危险天气一直是影响航班正点率的首要原因, 当计划航路发生危险天气时, 航空公司常采用原地等待的方式, 导致大量乘客滞留机场. 频繁发生航班延误乃至取消事件, 将严重影响民航高效、准时的口碑, 同时严重制约空管系统的服务水平和效率. 确保安全的前提下, 合理进行危险天气下的改航路径规划是提高空域容量, 保障航空器飞行安全, 减少航班延误以及提升民航经济效益的有效途径^[1]. 路径规划算法作为改航路径的求解方法, 其准确性以及高效性是影响改航结果的关键^[2].

目前, 国内外已有不少学者对危险天气下的改航路径规划算法进行研究. 李善梅等人^[3]开发了一种基于蒙特卡罗模拟和改进遗传算法的考虑飞行时间可靠性的规划算法, 有效提高了航班改航的效率和安全性; Bojorquez等人^[4]提出了一种基于图形处理单元的并行计算框架, 基于A*算法在风险承受能力下生成飞行器重新路由计划, 并可以从其中找到最小的时间和距离轨迹; Wang等人^[5]利用改进的自适应蚁群算法研究改航路径的相互联系, 对航空器飞行时的空域容量和流量进行匹配, 降低了规划误差; Tolstaya等人^[6]提出结合反向强化学习和基于搜索的运动规划算法, 融合人工势场创建了自主空中交通管制, 从而确保航空器处于安全状态; 向征等人^[7]提出了引入人工势场法改进传统蚁群算法中的启发因子信息从而提高路径规划模型中搜索的有效性; 赵元棣等人^[1]利用A*算法分别对栅格法构建的静态和动态空域环境进行快速改航规划建模, 减少了计算复杂度的同时实现了快速合理规划路径; 陈可嘉等人^[8]同时考虑等待策略和改航策略, 设计了两阶段求解算法, 使用遗传算法优化等待时长和改航路径后使用“化曲为直”和“二分法”思想调整改航路径; 王莉莉等人^[9]将栅格法与动态规划法相结合, 针对平行航路提出通过改航优先权分配机制解决飞行经济和安全冲突问题的改航路径规划方法; 朱承元等人^[10]利用几何算法预先规划可选改航路径后, 使用改进的离散粒子群优化算法探索最优改航路径; 陈万通等人^[11]通过几何法处理危险区域凸多边形, 并提出一种面向空管的亚轨道碎片危险区预测与路径规划方法, 更利于飞机平稳、高效、安全改航. 上述文献多对人工势场法、经典规划算法以及智能优化算法3大类改航路径规划求解算法改进.

本文的主要贡献可以概括为3个方面: 1)将分块和并行概念引入到Graham扫描凹形片状分布的危险天气边界, 使得划设的结果更贴近实际, 初始环境构建的合理性将直接提升路径规划算法的效率. 2)对蚁群算法的信息素更新策略进行改进, 采取实时更新获取信息素初始值代入后续全局性更新策略, 加快收敛的同时保持了探索新路径的能力, 避免陷入局部最优. 3)考虑危险天气的突发性, 提出在D*Lite全局规划路径基础上智能分割, 融合改进蚁群局部搜索的复合结构动态改航路径规划算法D*Lite-ACO (ant colony optimization), 充分结合两类算法优势, 扬长避短.

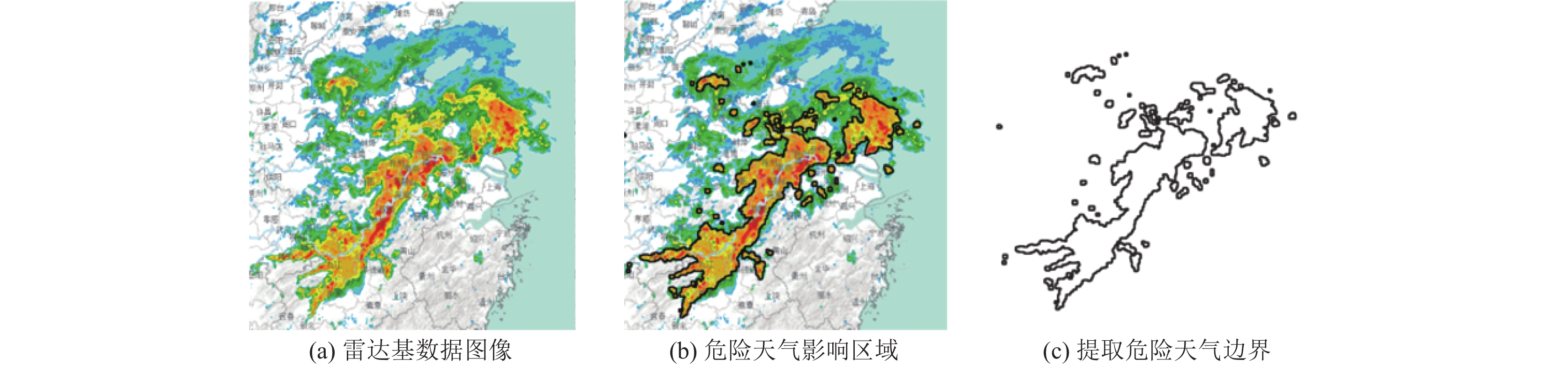
1 改进初始环境建模

飞行受限区的划设是试验改航路径规划算法的前提和基础, 通常为受雷暴、冰雹、强雨雪等恶劣天气影响的区域, 指在危险天气下的飞行限制区(flight forbidden area, FFA). 民航空管部门通常采用雷达探测数据来分析恶劣天气的分布情况, 当雷达回波反射率大于40 dBZ时, 为了确保飞行安全问题, 航空器将被禁止穿越该区域. 改航还需要对未来的飞行受限区位置进行预测. 以实时的天气雷达探测图像数据为基础, 对雷达回波图进行外推, 划设飞行受限区预测位置. 对雷达回波图中反射率大于40 dBZ的危险天气影响区域边界进行提取如图1所示.

Graham扫描划设飞行受限区的原理是以边界点位置为基础, 通过不断的循环、迭代获取一个凸多边形的区域边界^[12]. 经研究发现, 当其处理凹形片状分布或散点状分布的危险天气时, 划设的结果与实际受限区偏差较大. 因此, 本文提出分块并行Graham扫描划设飞行受限区的方法.

根据民航有关航空器绕飞的规定, 在两个雷暴体边界之间的距离小于20公里的情况下, 航空器必须禁止从两者之间穿越. 因此, 首先需要对提取的危险天气影响区域边界间距小于20公里的部分进行合并. 接着, 将合并后的飞行受限区视为一个整体, 判断提取区域的顶点坐标 ${G_1}, {G_2}, \cdots , {G_n}$ 所形成的多边形是否存在凹形带状分布区域, 倘若存在, 为了提高划设精度, 则需要对其分块的关键点进行确定; 倘若不存在, 可直接利用Graham算法对合并的危险天气影响区域扫描划设.

确定分块关键点的步骤如下: 将提取区域的顶点坐标 ${G_1}, {G_2}, \cdots , {G_n}$ 中形成凹形的位置坐标 ${G_p}$ 和 ${G_q}$ 连接并对线段 ${G_p}{G_q}$ 作中线并与危险天气影响区域边界相交于点 ${O_{\left( {p, q} \right)}}$ , 以 ${O_{\left( {p, q} \right)}}$ 为中心向 $x$ 轴垂直方向绘制直线, 直线与危险天气影响区域的边界相交于点 $G_t^\sim$ 和 $G_k^\sim$ . 此时, 贯穿 ${O_{\left( {p, q} \right)}}$ 的直线实现了对合并的危险天气影响区域的分块.

对危险天气影响区域进行分块后再并行扫描划设的方法不仅使得划设的结果更精细, 减小无效区域面积, 而且并行一定程度上也减少了Graham扫描划设的时间, 提高了效率. 分块并行Graham扫描划设的处理流程如图2所示.

2 复合结构动态改航路径规划算法 2.1 改进信息素更新策略

蚁群算法是从自然界蚂蚁觅食行为获得的灵感, 是一种启发式群体智能优化算法. 研究发现, 蚂蚁初始的运动方向是随机的, 其经过的路径上会释放出一种物质, 称之为信息素, 蚂蚁间通过该物质相互交流.

蚂蚁将根据信息素浓度来决定来选择下一步的运动方向, 信息素浓度越大的路径被选择的机率也就越大, 最终能得到一条出发点到目的点最短路径. 路径上释放的信息素会逐渐消失, 信息素的更新计算如式(1)、式(2)^[13]所示:

$ {\tau _{ij}}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}}\left( {{t}} \right) $

(1)

$ \Delta {\tau _{ij}} = \mathop \sum \nolimits_{k = 1}^m \Delta {\tau _{ij}^k} $

(2)

其中, 挥发系数 $ \;\rho\; (0 < \rho < 1) $ 表示路径上信息素的挥发程度, ${\tau _{ij}}$ 表示栅格 $i$ 与栅格 $j$ 路径上的信息素浓度.

常用的蚁群算法多采用全局性更新策略, 蚂蚁搜索的收敛速度较快, 能尽早找出一条拟最优路径. 然而, 由于全局过早收敛, 蚂蚁将会更快地集中在当前循环信息素浓度最高的一条路径上, 从而阻碍发现更优解, 导致最终搜索结果陷入局部最优. 局部实时性信息素更新策略却恰恰与之相反. 蚂蚁每进行一次栅格选择, 都将根据距离长度进行局部信息素更新, 虽然导致收敛速度较慢, 但却更易发现最优解. 针对上述两种信息素更新策略的特点和局限性, 本文将提出一种将实时性与全局性融合的信息素更新策略对蚁群算法进行改进.

首先采用局部实时性信息素更新策略对初始点放置的蚂蚁由栅格 $i$ 到栅格 $j$ 的每段路径均进行信息素更新. 经过M次循环后, 每次迭代过程中选择当前循环的蚂蚁进行信息素的更新, 此时的信息素增量计算如式(3)所示:

$ \Delta {\tau _{ij}^{{k_{{\rm{best}}}}}} = {{Q}}/{d_{ij}} $

(3)

其中, ${{Q}}$ 表示当前迭代路径上的总信息素浓度, ${d_{ij}}$ 表示栅格 $i$ 和栅格 $j$ 的路径, ${k_{{\rm{best}}}}$ 表示当次循环中表现最好的蚂蚁, $\Delta {\tau _{ij}^{{k_{{\rm{best}}}}}}$ 表示当前迭代最优蚂蚁的信息素增量值.

接着为了尽可能减少信息素浓度受外界因素影响而造成的误差, 采用M次循环中蚂蚁信息素增量的均值作为栅格 $i$ 到栅格 $j$ 路径上的信息素初始值, 其计算如式(4)所示:

$ \Delta {\tau _{ij}^{{\text{init}}}} = \mathop \sum \nolimits_{n = 1}^M \Delta {\tau _{ij}^{{k_{{\rm{best}}}}}\left( {{n}} \right)}/M $

(4)

使用信息素局部实时更新策略使得蚂蚁不会过早收敛于一条不是最优解的路径上, 而是持续探索新的路径, 避免蚂蚁陷入局部最优. 最后, 采用信息素全局性更新策略, 融合前M次循环获得的信息素初始值, 对蚂蚁经过路线的信息素全局更新. 这种融合信息素初始值的更新规则如式(5)所示:

$ {\tau _{ij}}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}^{{\text{init}}}} $

(5)

这种先对蚂蚁进行信息素局部实时更新, 获取栅格两点间路径的初始信息素值后, 再使用全局性信息素更新策略融合初始信息素值, 对蚂蚁进行后续信息素更新的蚁群算法很好地结合了两种信息素更新策略的优势. 蚂蚁在迭代过程中既保持了局部信息素更新策略持续探索新路径的能力, 以便找到更多可行解, 又保持了全局信息素更新策略较快收敛的优势. 搜索过程中的蚂蚁根据路径上的信息素浓度和启发式信息计算下个栅格选择概率如式(6)所示:

$ p_{i j}^k(t)=\left\{\begin{array}{l} \dfrac{\tau_{i j}^\alpha(t) \eta_{i j}^\beta(t)}{\displaystyle\sum_{u \in { allowed }} \tau_{i u}^\alpha(t) n_{i j}^\beta(t)},\quad\; j \in { allowed }_k \\ 0, \qquad\qquad\qquad\qquad\text { 其他 } \end{array}\right. $

(6)

其中, $p_{ij}^k\left( t \right)$ 表示蚂蚁k在时刻 $ t $ 由栅格 $i$ 选择栅格 $j$ 的概率; $\alpha $ 表示信息素重要程度因子; $\;\beta $ 表示启发函数的重要程度因子; ${\tau _{ij}}$ 表示栅格 $i$ 与栅格 $j$ 路径上的信息素浓度; ${\eta _{ij}}$ 表示栅格 ${{i}}$ 与栅格 $j$ 间的启发函数.

2.2 改进信息素更新策略

改进信息素更新策略的蚁群算法伪代码如算法1.

算法1. 改进信息素更新策略的蚁群算法

Initialize number of ants m, number of iterations M, pheromone volatilization coefficient $\scriptstyle \rho $ , information elicitation factor $\scriptstyle \alpha $ , expected elicitation factor $\scriptstyle \beta $ .

Repeat

　For Current iteration number n in M do

　　For current number of ants k=1, 2, …, m do

　　　 If the next grid $\scriptstyle j\in allowe{d}_{k} $ Then

　　　　　　 $\scriptstyle {p}_{ij}^{k}\left(t\right)\leftarrow {\tau }_{ij}^{\alpha }\left(t\right){\eta }_{ij}^{\beta }\left(t\right)/{ \sum }_{u\in allowe{d}_{k}}{\tau }_{iu}^{\alpha }\left(t\right){n}_{ij}^{\beta }\left(t\right) $

　　　Else

　　　　　　 $ \scriptstyle {p}_{ij}^{k}\left(t\right)\leftarrow 0 $ ; /*栅格 $\scriptstyle j $ 不被允许访问*/

　　　　　　Update pheromones in real time $\scriptstyle \Delta {\tau _{ij}}^{{k_{{\rm{best}}}}} \leftarrow {{Q}}/{d_{ij}}$ ;

　　End for

　End for

　 $ \scriptstyle \Delta {\tau }_{ij}{}^{\text{init}}\leftarrow {{ \sum }}_{n=1}^{M}\Delta {\tau }_{ij}{}^{{k}_{{\rm{best}}}\left({n}\right)}/M$ ; /*信息素初始值赋值用于全局迭代*/

Repeat

　For Current iteration number n≤M do

　　For current number of ants k=1, 2, …, m do

　　　　Update pheromones $\scriptstyle {\tau _{ij}}\left( {t + 1} \right) \leftarrow \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}}^{{\text{init}}}$ ;

　　End for

　End for

Untilall ants finish the iteration.

Until the maximum iteration is reached or the optimal solution is obtained.

算法1首先对蚁群算法的参数初始化, 随机将m只蚂蚁放置在栅格初始点, 根据状态转移方程计算蚂蚁选择下一个栅格的概率, 依据 $p_{ij}^k$ 对蚂蚁进行移动, 前 $M$ 轮遍历每次移动都将实时更新栅格 $i$ 到栅格 $j$ 间的信息素. 当所有蚂蚁都搜索出一条到达目的点的路径, 选择表现最好的蚂蚁搜索路径作为当前最优解, 并将M次最优的信息素局部更新值的均值作为初始信息素值 $\Delta {\tau _{ij}^{{\text{init}}}}$ 代入后续全局信息素更新策略的迭代过程, 直至达到最大迭代次数或得到最优解.

2.3 D*Lite-ACO

针对危险天气的随机性与突发性, 本文先采用具有动态避障重规划能力的D*Lite算法对改航路径进行全局规划. 采用反向搜索模式, 以减少搜索节点数. 当初始规划路径上检测到突发危险物时, 将重规划的范围控制在目标点与当前航空器之间, 避免对已规划的有效路径的无效计算. 针对全局规划在密度较高环境下, 效率低下、数据量大、规划路径不平滑等缺陷, 在全局规划路径的基础上分割局部区域使用改进的蚁群算法进行搜索.

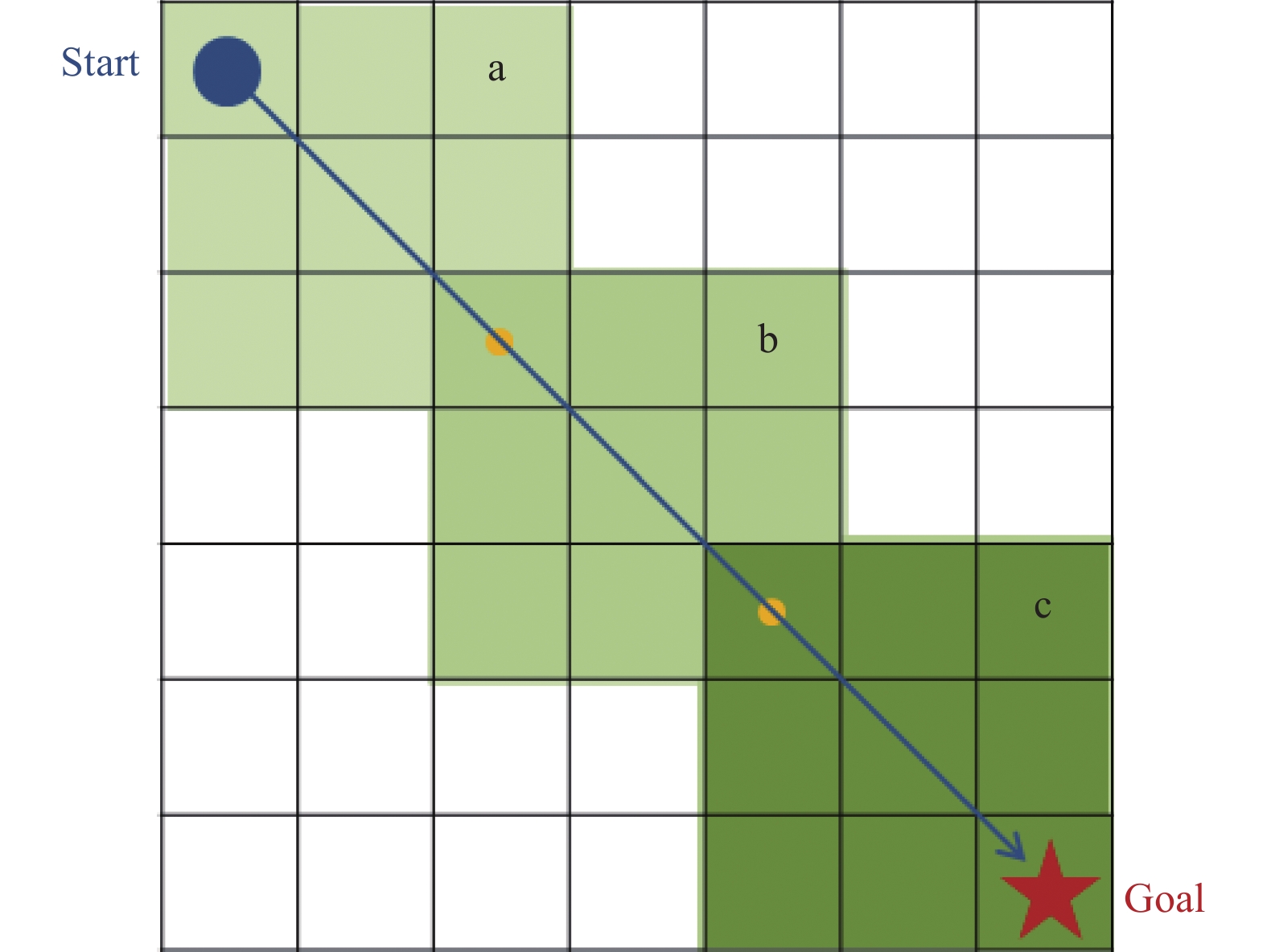
为了减小蚂蚁局部搜索的范围, 从而减少迭代时间, 局部区域的分割将建立在全局规划路径的基础上. 仅对全局规划路径的周边区域范围采用改进的蚁群算法进行搜索, 很大程度上避免对无效区域的迭代计算. 目前, 民航的管制工作规定当计划航线上出现危险天气时, 绝对禁止航空器从危险天气影响区域的上、下方垂直改航或从当中穿越, 因此本文研究的改航环境是二维的, 以从飞行受限区的安全边界绕飞为出发点, 提出相关策略. 以7×7的栅格图为例说明, 箭头表示由起始点到目标点全局规划的路径, 基于全局规划路径分割局部区域如图3所示.

圆点表示起始点, 五角星表示目标点, 小圆点表示对全局初始路径的分割点, 路径上的方块区域分别代表了分割出的不同局部搜索的范围. 其分割的依据是根据全局规划结果自定义局部初始横向 ${X_{{\rm{def}}}}$ , 分割局部的个数如式(7)所示:

$ {N_{{\rm{local}}}} = ({W_o} - 1)/{X_{{\rm{def}}}} - 1 $

(7)

分别对 ${N_{{\rm{local}}}}$ 局部区域遍历获取分割局部区域的关键值 ${\tilde x}_H$ 与 ${\tilde y}_H$ , 它们分别对应着局部区域分割的最大 $x$ 轴与 $y$ 轴范围. 计算 ${\tilde x}_H$ 和 ${\tilde y}_H$ 如式(8)所示:

$ \left\{ \begin{array}{l} {x}_{H}={x}_{o}^{i}, {\rm{abs}}\left({x}_{H}-{x}_{H-1}\right) < {\rm{abs}}\left({x}_{o}^{i}-{x}_{H-1}\right) 且i\in \left[1, {\textit{Step}}_{H}\right)\\ {y}_{H}={y}_{o}^{i}, {\rm{abs}}\left({y}_{H}-{y}_{H-1}\right) < {\rm{abs}}\left({y}_{o}^{i}-{y}_{H-1}\right) 且i\in \left[1, {\textit{Step}}_{H}\right)\\ {\tilde x}_{H}={x}_{H}, {\tilde y}_{H}={y}_{H}, i= {\textit{Step}}_{H}\end{array}\right. $

(8)

其中, $H$ 表示当前遍历的局部区域, $H \in \left[ {1, {N_{{\rm{local}}}}} \right]$ . $i$ 表示从上个关键点 ${\omega _{H - 1}}\left( {{x_{H - 1}}, {y_{H - 1}}} \right)$ 到当前关键点 ${\omega _H}\left( {{x_H}, {y_H}} \right)$ 的全局路径迭代, ${\textit Step}_{H}$ 表示这段范围全局规划路径的遍历格点数. ${x_{H - 1}}$ 表示上一个局部区域的关键点, 当 $H$ 为1时, ${x_0} = {x_{{\rm{start}}}}$ ; ${y_{H - 1}}$ 表示上一个局部区域的关键点, ${y_0} = {y_{{\rm{start}}}}$ . $x_o^i$ 表示全局规划路径上点的横坐标, $y_o^i$ 表示全局规划路径上点的纵坐标.

分割的局部区域 ${P_{H1}}{P_{H2}}{P_{H3}}{P_{H4}}$ 的坐标点分别对应 ${P_{H1}}\left( {{\tilde x}_{H - 1} - 1, {\tilde y}_{H - 1} + 1} \right)$ , ${P_{H2}}\left( {{\tilde x}_H + 1, {\tilde y}_{H - 1} + 1} \right)$ , ${P_{H3}}\left( {\tilde x}_H + \right. \left. 1, {\tilde y}_H - 1 \right)$ , ${P_{H4}}\left( {{\tilde x}_{H - 1} - 1, {\tilde y}_H - 1} \right)$ . 由图3可知, 在全局路径基础上分割确定局部范围后, 再进行改进的蚁群算法搜索的方法, 使得局部搜索的范围总和明显降低, 更有利于效率的提升.

将栅格初始化后的全部未知区域视为自由空间, 采用D*Lite算法从目标点开始向初始点反向增量式地搜索最优路径. 增量式的思想可以理解为在学得模型之后, 当再接收到新的障碍样本时, 算法能够重复利用之前搜索过程中的获得的信息, 来规划出新的可以避开危险天气障碍的路径, 规划算法无需完全重新规划, 有效地减少了重规划关联的节点数以及降低重规划的次数. 引入权值 $rhs$ (right-hand side)作为父节点到当前点的最小代价值, $rhs$ 的计算如式(9)所示:

$ rhs\left( s \right) = \left\{ {\begin{array}{*{20}{l}} {\min_{s \in {\textit{Succ}}\left( s \right)}(c\left( {s', s} \right) + g\left( {s'} \right),\;\;\; s \ne {s_{{\rm{start}}}}} \\ {0,\qquad\qquad\qquad\qquad\qquad\quad {\rm{otherwise}}} \end{array}} \right. $

(9)

对于未知环境的全局规划D*Lite算法具有良好的性能, 然而在精细规划问题上却无法应对局部复杂环境. 蚁群算法是一种融入人类智能的通用型随机优化算法, 改进的蚁群算法在高密度环境中可以很好地实现避障和规划最优路径, 分布式的特征以及较强的鲁棒性使其模型只需稍加修改便可与其他启发式算法结合使用. 复合结构D*Lite-ACO的整体流程如图4所示.

3 实验结果分析 3.1 改航环境构建

由中国气象数据网可知, 2022年4月25日我国华东地区多地持续具有恶劣天气, 本文将采用当日上午10点36分的华东地区雷达拼图作为改航环境, 采用分块并行Graham算法对提取的危险天气影响区域划设凸包, 进而对飞行受限区栅格化处理构建改航路径规划的初始环境. 试验资料来源于国家气象数据中心( http://data.cma.cn/). 本文涉及的面积、路径长度等计算均在地形图比例尺为1:100000下进行.

首先根据民航规定的安全飞行间距, 对危险天气影响区域边界间距较小的模块进行合并, 选取合并后的最大区域作为危险天气下划设飞行受限区域的对象进行试验. 然后对最大区域边界的坐标定点进行提取, 对整个区域进行分块, 尤其以凹陷处作为关键位置. 分割线与区域的交点必须重复引入相邻分块是后续零散凸包组合的关键. 为了验证本文所提出的对飞行受限区分块后采用Graham算法并行扫描划设静态飞行受限区方法的有效性, 将本文所提方法划设和Graham算法直接划设凹形带状分布危险天气影响区域的结果进行比较. 基于Graham扫描法的凸包划设实验对比结果如表1所示.

观察表1可知, 本文所提方法划设的危险天气凸包面积仅占Graham算法直接划设凸包面积的48.14%, 这也印证了分块后采用Graham算法并行划设的方法能够有效剔除由Graham算法划设原理导致的凹形区域的无效面积. 本文所提方法在划设精确度上提升了0.475, 划设的结果更接近危险天气影响区域的实际形状. 改航环境的合理性是进行路径规划求解算法研究的基础, 飞行受限区域面积的减小也将直接提高路径规划阶段的选择性, 所以使用本文所提方法划设的静态飞行受限区可以取得更好的结果.

3.2 改航算法的对比和验证

为了验证改进的信息素更新策略对蚁群算法搜索结果的影响, 构建初始栅格环境进行实验. 设置每次迭代的蚂蚁数量 $M = 50$ , 表示信息素重要程度的参数 $\alpha $ = 1, 启发函数的重要程度因子 $\;\beta = 7$ , 信息素的蒸发系数 $\;\rho = 0.3$ , 将蚁群算法采用本文改进的信息素更新策略与全局更新、局部更新策略下搜索路径的结果进行对比.

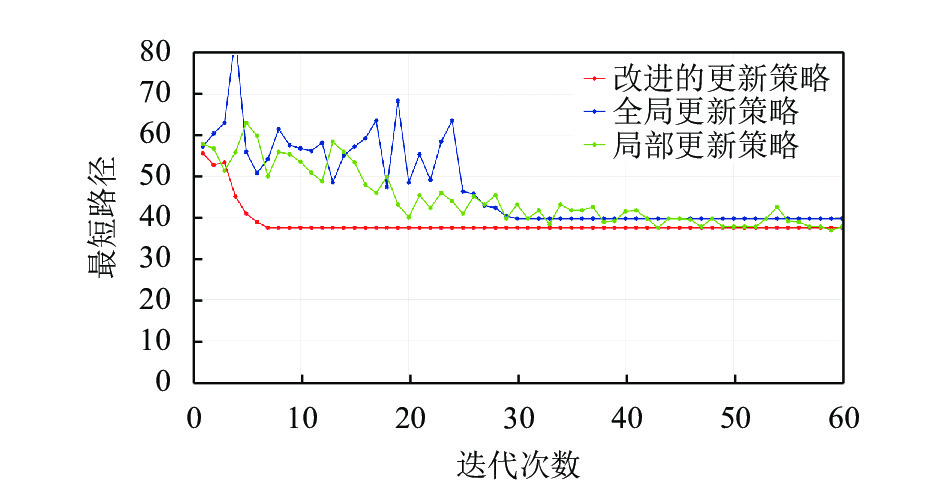
分别采用全局性更新策略、局部性更新策略以及本文所提改进的信息素更新策略进行对比实验. 观察不同信息素更新策略下蚁群算法搜索的最小路径长度和迭代过程中收敛曲线的变化趋势. 任取试验中某次蚁群搜索结果为例, 采用不同信息素更新策略的蚁群算法对相同环境进行搜索的收敛曲线变化趋势对比如图5所示.

全局性更新策略下的蚁群算法相比局部实时性更新, 其收敛曲线能较快趋向平稳. 局部实时性更新策略下的蚁群算法由于需要不断更新, 收敛曲线趋向平稳所需时间相对较长. 但是, 由于其一直保持着搜索新路径的能力, 该策略下的蚁群算法搜索的最小路径长度明显低于全局更新策略下的搜索结果. 采用本文所提方法的蚁群算法在迭代次数为10时便已趋向平缓, 这是由于引入信息素初始值 $\Delta {\tau _{ij}}^{{\text{init}}}$ 使得后续路径信息素浓度的更新无限接近最优值, 从而显著加快了蚁群算法的收敛速度, 甚至比全局性更新策略下收敛趋向平稳所需迭代时间更短. 同时, 改进的信息素更新策略下搜索出的最小路径长度也明显优于全局性更新策略, 基本趋向局部更新策略下搜索路径的最优解. 由此可见, 本文所提改进的信息素更新策略将保持新路径搜索的能力和收敛速度快的优势完美结合, 无论是在最小路径长度还和迭代收敛速度方面, 都取得了最好的效果.

为了进一步验证本文提出的全局规划基础上融合改进蚁群算法局部搜索的复合结构动态路径规划算法的可行性与有效性, 构建50×50且障碍物设置相对复杂的栅格环境, 采用当前应用最为广泛的全局规划算法A*、Bidirectional A*、Anytime Repairing A* (ARA*)、Lifelong Planning A* (LPA*)、D*、Anytime D*、D*Lite等分别进行初始的全局规划, 比较融合蚁群算法进行局部搜索前各类全局规划算法性能的差异. 全局路径规划算法进行初始规划以及重规划的对比测试结果如表2所示.

由表2可知, 各类算法起初对静态环境中规划的全局路径长度相等, 这是由于静态环境下D*Lite类动态规划算法与A*算法一样, 都是利用启发式搜索提高效率, 规划路径的方式与A*算法一致. 为了验证几类动态规划算法的重规划能力, 在初始规划路径的相同位置添加突发障碍物对重规划的结果进行比较. 实验发现D*Lite-ACO全局重规划在路径长度上效果较差, 其他动态规划算法重规划路径长度也基本一致.

为了验证上述方法在动态环境下的重规划性能, 本文对几种方法规划的初始路径进行分析研究, 选择在全部初始路径都经过的相同位置添加突发障碍物, 对几种方法的重规划结果进行比较分析. 实验结果如表2所示, A*-ACO、Bidirectional A*-ACO和ARA*-ACO不能适用于动态环境, 其余几种方法具有动态重规划性, 除了 D*-ACO动态重规划的性能较差, 其余几种方法动态重规划的路径长度也相同. 下面将这几种方法作具体对比分析:

Anytime D*-ACO在全局规划过程中引入了Anytime的概念, 但本文全局规划的目的在于较快获取全局初始路径用于对局部区域进行分割搜索, 因此Anytime类算法反复求精的过程是非必要的, 反而影响了路径规划效率.

LPA*-ACO与D*Lite-ACO都采用了增量式的模式进行路径规划, 可以充分利用之前搜索过程中的存储信息, 因此这两种方法在对动态环境进行重规划时, 具有良好的性能. 不过, LPA*-ACO重规划的路径考虑的范围始终为固定的起始点与目标点之间, 假设航空器位置已经发生了变动, 则其根据环境信息变动重新规划的由起始点到目标点的路径对于航空器所在位置而言很有可能并非最优路径. 而本文提出的D*Lite-ACO复合结构动态改航路径规划方法则采用反向搜索的方式, 能够将重规划的区域范围设定在航空器当前所在位置与目标点之间, 重规划的起始点可以随航空器位置的变化而不断更新, 在确保路径为当前航空器最优解的同时, 也减少了对已规划路径的无效搜索.

在初始规划路径上添加相同障碍物后, LPA*-ACO、D*-ACO、D*Lite-ACO的动态全局重规划路径对比结果如图6所示. 由图6和表2可知, D*Lite-ACO全局重规划路径相对平滑且长度较短, 且反向搜索的特征也使其规划全局路径时, 大大减少了访问节点的数量.

为了进一步验证对全局规划路径分割后采用改进的蚁群算法对复杂环境进行局部搜索的路径规划效果更佳, 将改进的蚁群算法PDG-ACO^[14]与本文所提D*Lite-ACO复合结构动态改航路径规划方法在相同环境信息下进行路径规划对比实验, 详细结果如表3所示.

观察表3发现, 基于全局初始路径智能分割局部区域的策略将改进的蚁群算法的遍历范围缩小了66.7%, 显著提高了搜索效率. 与改进的蚁群PDG-ACO相比, 本文所提方法在规划的路径长度上减少了1.2%, 总耗时上降低了40.7%. 另外, 比D*Lite算法直接规划的结果在路径长度方面也有所提升, 可以发现复杂环境下的最优解. D*Lite-ACO算法相比直接采用改进的蚁群算法处理复杂环境的改航路径规划问题, 无论是在规划路径长度、处理时间, 还是在迭代范围方面都有明显优势. 最为重要的是, 这种复合结构改航路径规划在动态环境中具备迅速重规划性.

4 总结

为了实现危险天气下高效、安全的改航路径规划, 对实时以及外推提取的危险天气区域分块, Graham算法并行扫描后, 对外扩的飞行受限区进行栅格化处理. 为了加快蚁群算法的收敛速度、避免陷入局部最优, 对其信息素更新策略进行改进, 采用实时信息素更新算得初始信息素 $\Delta {\tau _{ij}^{{\text{init}}}}$ 带入后续的全局更新策略. 考虑危险天气的突发性特征, 同时尽可能提高改航路径规划效率, 提出D*Lite算法规划全局路径, 在此基础上智能分割局部区域采用改进的蚁群算法进行局部搜索的复合结构动态改航路径规划算法D*Lite-ACO. 实验结果表明, D*Lite-ACO赋予蚁群算法动态重规划的性能, 且大大降低了蚁群局部搜索的遍历范围, 有效提高了路径规划效率, 确保了航空器的飞行安全.