随着云计算、无线传感器技术等新一代信息技术的快速发展, 基于物联网支持的大数据应用遍及工业、医学、军事、教育及城市管理等各个领域^[1]. 例如, 无人驾驶技术通过传感器融合技术、人工智能、定位系统、自动控制系统等的协同工作, 实现汽车的自动驾驶. 当无人驾驶汽车行驶时, 需要在高速动态下对周围环境做出迅速反应, 所以动态任务的响应时间是一个极其重要的指标^[2]. 由于传统的云计算难以满足地理上分散分布的物联网设备对数据处理低时延、高带宽和实时决策的高需求, 雾计算应运而生, 通过将计算和存储能力配置在网络边缘对时延敏感型任务进行及时的处理, 从而减少网络数据传输量并降低时延, 云雾层的协同计算为超高密度的信息接入提供了便捷^[3]. 作为雾计算核心基础设施, 近年来我国数据中心规模随着海量数据的产生而不断扩大, 2019年全国数据中心行业耗电总量约为600亿–700亿千瓦时, 预计2030年总能源消耗量将在2019年基础上翻一番^[4], 数据中心成为能源消耗和碳排放大户.

而数据中心的资源利用率低是造成数据中心高能耗的主要原因之一, 据统计数据显示处于空闲状态的主机要消耗其能耗峰值的70%, 大多数活动主机的平均CPU利用率仅为10%–50%^[5]. 因此, 通过合理的资源调度提高数据中心的资源利用率并满足用户的低时延需求对于数据中心节能、推进可持续发展有着重要意义.

应用任务可以通过容器技术和容器自动编排工具实现资源虚拟化和服务自动化部署^[6]. 容器和虚拟机都是虚拟化技术, 与虚拟机相比, 容器更加轻量便于在不同操作平台上快速部署. 我们将应用任务实例化为Docker容器, 部署到云雾计算节点上, 利用检查点/恢复技术^[7]实时迁移容器来调整容器与物理主机之间的映射关系. 如何合理地调度容器, 充分利用雾计算资源, 本质是一个资源分配调度问题. 针对此问题目前已有一些相关研究. Beloglazov等^[8]将虚拟机整合问题分解为主机过载检测、主机欠载检测、虚拟机选择和虚拟机放置4个子问题, 并提出了多种自适应启发式虚拟机整合算法, 验证了其在数据中心节能和保证用户服务质量方面的优越性. 这类启发式算法简单高效, 但是相对静态, 不适用于任务负载动态波动的环境. 为解决这个问题, Han等^[9]将虚拟机的动态资源管理问题转化为求解大规模Markov决策过程, 以最小化数据中心能耗为目标, 促进了虚拟机迁移决策的准确性. 然而, 这类基于状态模型的调度决策方法很难对实际的云计算系统建立精确的状态模型, 并且随着云计算系统规模的扩大, 将导致状态空间爆炸. Liu等^[10]针对任务到达、环境状态及奖励的不确定性, 提出了悲观-乐观在线调度方法(pessimistic-optimistic online dispatch, POND), 利用上限置信区间算法来最大化估计累计奖励, 基于虚拟机队列悲观地跟踪约束违反, 应用最大权重方法进行虚拟机调度, 使系统达到最大化奖励和避免违反约束之间的平衡. 在雾计算框架基础上, 戴志明等^[11]为提高智能工厂的数据处理效率和资源使用率, 提出改进的遗传算法(GA)对智能工厂中容器应用进行调度分配, 将资源分配问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程, 进而寻求最优解. 韩奎奎等^[12]针对雾环境下用户的高服务质量需求, 使用神经网络模型来近似目标值, 并利用改进的遗传算法进行最优任务调度决策, 为资源调度方法提供了新的借鉴. 但遗传算法等进化方法属于无梯度优化方法^[13], 通常需要更长的时间来收敛. 此外还有一些研究针对雾计算网络的其他性能进行优化, 如任务完成率、公平性和信息安全等^[14-16]. 因此, 目前仍缺少一种在不稳定环境中快速适应, 同时兼顾低能耗和低响应时间的资源调度方法.

基于以上研究, 为了对雾计算资源调度进行准确、可扩展的建模, 同时加快模型的收敛速度, 本文在雾计算基础架构上, 提出了一种基于深度强化学习的容器整合方法(container consolidation based on deep reinforcement learning, DR-CI). 该方法利用神经网络近似器以数据中心基础设施能耗和平均响应时间最小化为目标进行精确建模, 基于A2C算法构建了从系统资源状态到容器迁移策略的端到端决策模型, 提出自适应多目标奖励函数, 智能体通过与环境的实时交互、学习产生最优的调度策略, 利用基于梯度的反向传播算法加快决策模型的收敛速度, 从而获得能耗和响应时间的最优性能. 得益于强化学习本身的自主学习能力, DR-CI还能支持不同场景下的目标优化.

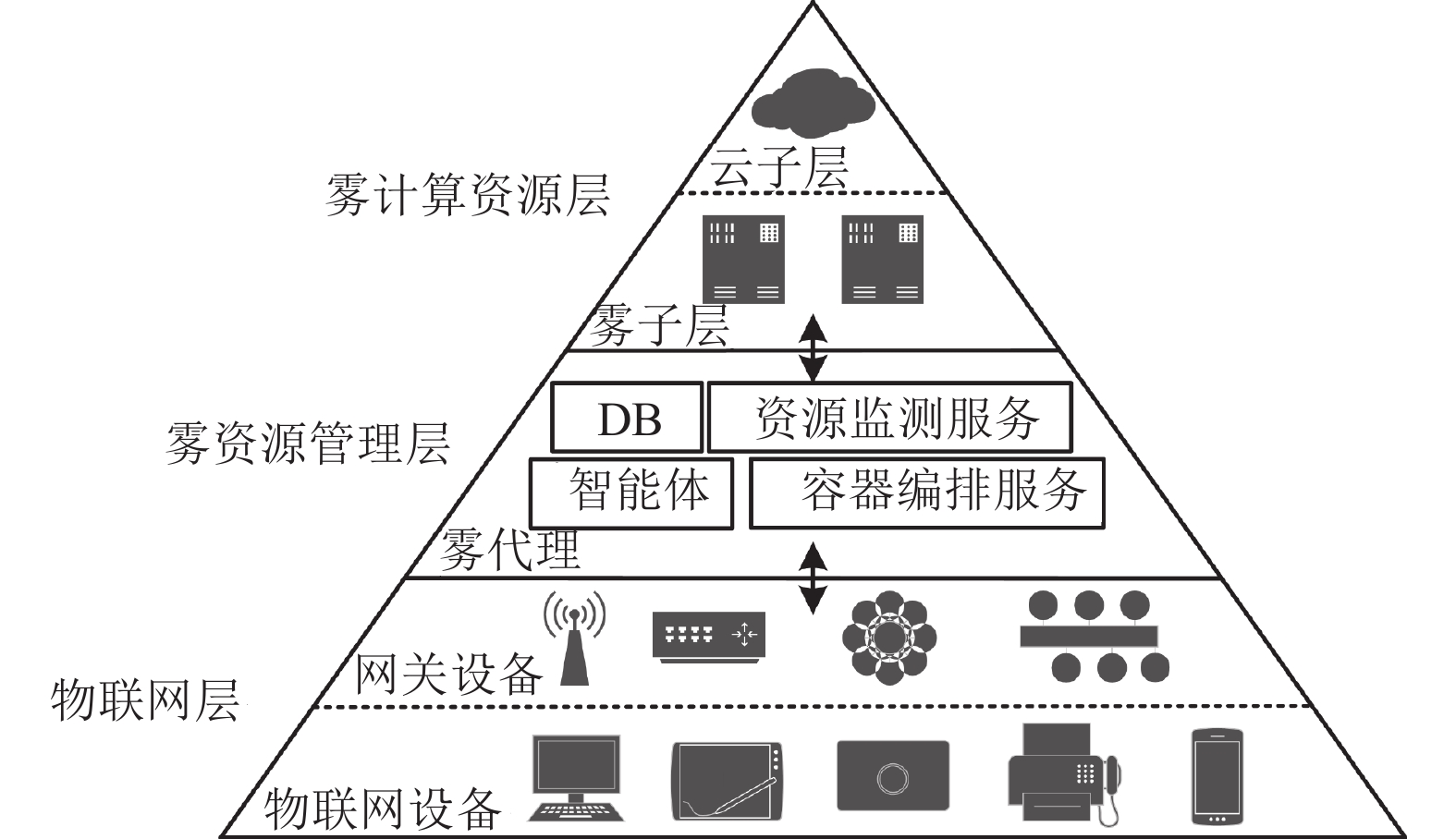
1 问题描述与建模 1.1 雾系统架构

本文考虑一个标准的分布式异构的雾计算环境, 如图1所示, 它主要由雾计算资源层、雾资源管理层和物联网层组成. 雾计算资源层由云子层和雾子层的计算节点组成, 云子层具有丰富的计算资源能够处理和存储大量数据, 但距离终端用户远, 通信延迟较高; 雾子层的主机更接近终端用户, 与雾代理和网关设备的通信延迟低, 但计算资源较少, 本文考虑不同层之间的主机通信延迟, 忽略同一层的主机之间的通信延迟. 雾计算资源层由雾资源管理层控制, 雾资源管理层由数据库、智能体、资源监测服务和容器编排服务等模块组成. 智能体接受来自物联网层网关设备的任务请求, 根据优化目标周期性地做出容器整合决策, 将时延敏感、计算量小的任务根据调度决策分配到雾层进行处理, 将时延不敏感、计算量大的任务根据调度决策分配到云层进行处理.

1.2 动态任务负载模型

用户在任意时刻产生任务请求, 且任务对CPU、RAM、网络带宽和时延的需求随着终端设备的移动性而不断发生变化. 将一天24 h以 $\Delta = 300\;{\rm{s}}$ 为一个调度间隔划分为288个连续调度间隔, 第t个调度间隔用 ${I_t}$ 表示. 动态任务负载模型如图2所示, 在调度间隔 ${I_{t - 1}}$ 结束时, 完成的任务集记为 ${L_t}$ , 等待队列的任务记为 ${W_{t - 1}}$ . 在调度间隔 ${I_t}$ , 生成的新任务记为 ${N_t}$ , 活动任务集(主机上执行的任务)记为 ${A_t}$ , 由新任务, 前一调度间隔的等待任务和剩余活动任务组成, 表示为 ${A_t} = {N_t} \cup {W_{t - 1}} \cup {A_{t - 1}}\backslash{L_t}$ .

1.3 问题描述

在数据中心, 任务运行在容器实例上, 所有容器部署在主机上. 任务执行后, 销毁它所对应的容器实例, 释放资源. 数据中心的主机是异构的, 假设在基础设施层共有N台主机, 主机集合表示为 $H = \{ {h_0}, {h_1}, \cdots, {h_{N - 1}}\} $ , 主机的计算资源特征由主机的类型决定, 包括CPU、RAM、磁盘和网络带宽等. 在任意调度间隔 ${I_t}$ , 主机 ${h_i}$ 的资源利用表示为 $U(h_i^t)$ , 最大容量记为 $C(h_i^t)$ ; 假设活动任务数量的上限为M, 活动任务集合表示为 ${A_t} = \{ a_0^t, a_1^t, \cdots, a_j^t\} $ . 活动任务 $a_j^t$ 的资源利用表示为 $U(a_j^t)$ .

调度器定义为系统状态到调度决策之间的映射模型: $stat{e_t} \to actio{n_t}$ . 调度决策 $actio{n_t}$ 包含新任务的主机分配和活动任务的迁移决策. 在第一个调度区间, 由于没有等待任务、剩余活动任务和完成任务, 所以模型只对新任务进行分配决策. 同时, 调度决策需满足约束条件, 即当目标主机最大容量可以容纳预定的任务时, $U(a_j^t) + U(h_i^t) \leqslant C({h_i})$ , 才执行调度决策, 将已执行的调度决策记为 $\widehat {actio{n_t}}$ . 调度器的性能通过奖励函数 $rewar{d_t}$ 来量化, 因此寻找最优调度决策的过程即最大化奖励函数过程, 如式(1)所示:

$ stat{e_t}\xrightarrow{{\max \sum\limits_t {rewar{d_t}} }}actio{n_t} $

(1)

1.4 能耗模型

研究表明, 主机的电能消耗主要集中在CPU上, 且主机的功率与其CPU利用率呈线性关系^[17]. 在任意调度间隔 ${I_t}$ , 主机 ${h_i}$ 的CPU利用率可表示为资源利用与资源最大容量的比值, 如式(2)所示:

$ UR(h_i^t) = U(h_i^t)/C({h_i}) $

(2)

主机的实时功率情况可根据其CPU利用率进行线性表示, 如式(3)所示:

$ P(h_i^t) = P_{{h_i}}^{{\rm{idle}}} + (P_{{h_i}}^{\max } - P_{{h_i}}^{{\rm{idle}}}) \times UR(h_i^t) $

(3)

其中, $P_{{h_i}}^{{\rm{idle}}}$ 和 $P_{{h_i}}^{\max }$ 分别为主机在CPU利用率为0和100%时的功率. 因此在调度间隔 ${I_t}$ , 数据中心基础设施层的总能耗可表示为所有活动主机的能耗之和, 如式(4)所示. 由于雾节点和云节点能源供应源的异构性, 给主机 ${h_i} \in H$ 乘以一个系数 ${\alpha _{{h_i}}} \in [0, 1]$ , 表示雾节点和云节点的能源消耗.

$ {\textit{TEC}}_t^H = \sum\nolimits_{{h_i} \in H} {{\alpha _{{h_i}}}\int_t^{t + \Delta } {{P_{{h_i}}}} } (t)dt $

(4)

1.5 时延模型

在执行某个任务的过程中使用到的所有容器应用定义为集合 $C = \{ {c_0}, {c_1}, \cdots, {c_i}\} $ , 完成任务的时延包括任务对应容器的总执行时间和总迁移时间(容器被放置在目标主机上)两部分. 容器的属性包括创建时间startTime、销毁时间destroyTime、IPS、RAM、磁盘带宽和所在主机 ${h_{{c_i}}}$ 等. 在调度间隔 ${I_t}$ , 所有完成任务 ${L_{t + 1}}$ 的总执行时间表示为所对应容器的执行时间之和, 如式(5)所示:

$ {\textit{TET}}_t^{{L_{t + 1}}} = \sum\nolimits_{{a_j} \in {L_{t + 1}}} {\sum\nolimits_{{c_i} \in C} {(destroyTime - startTime)} } $

(5)

若容器分配到不同的节点, 则要进行迁移, 迁移时间包括云雾节点间的通信延迟和传输容器的时间两部分. 忽略同一层(云子层或雾子层)上主机之间的通信延迟, 只考虑不同层之间主机的通信延迟. 容器传输的时间基于网络带宽和容器RAM大小. 在调度间隔 ${I_t}$ , 所有完成任务的总迁移时间表示为所对应容器的迁移时间之和, 如式(6)所示. 其中 $y(i)$ 为0或1的变量, 如果容器 ${c_i}$ 进行迁移, 则 $y(i) = 1$ , 否则为0; $B{W_{{h_{{c_i}}}}}$ 指容器所在主机的带宽, $ latenc{y_{{{\hat h}_{{c_i}}}}} $ 和 $ latenc{y_{{h_{{c_i}}}}} $ 分别指容器 ${c_i}$ 迁移前后所在主机的通信延迟.

$ \begin{split} &{\textit{TMT}}_t^{{L_{t + 1}}} =\\ &\sum\nolimits_{{a_j} \in {L_{t + 1}}} {\sum\nolimits_{{c_i} \in C} {y(i)} } \left( {\frac{{B{W_{{h_{{c_i}}}}}}}{{RA{M_{{c_i}}}}} + |latenc{y_{{{\hat h}_{{c_i}}}}} - latenc{y_{{h_{{c_i}}}}}|} \right) \end{split} $

(6)

因此在调度间隔 ${I_t}$ , 完成任务的总时延为总执行时间与总迁移时间之和, 如式(7)所示:

$ {\textit{TRT}}_t^{{L_{t + 1}}} = {\textit{TET}}_t^{{L_{t + 1}}} + {\textit{TMT}}_t^{{L_{t + 1}}} $

(7)

2 基于A2C算法的容器整合决策模型 2.1 模型整体架构

DR-CI方法中容器整合决策模型的基本架构如图3所示. 该方法基于A2C算法进行模型优化, 智能体包括演员(actor)和评论家(critic)这2部分. 演员根据数据中心资源状态和动态负载需求产生动作策略, 评论家根据当前环境状态计算状态价值, 容器编排服务模块执行演员做出的动作策略后, 数据中心计算此次容器迁移所导致的服务质量等性能变化所对应的奖励, 评论家根据状态价值和奖励估算出动作状态价值, 若动作状态价值大于状态价值, 则说明该动作策略是积极的; 若动作状态价值小于状态价值, 则说明该动作策略是消极的. 其中, 状态价值指从当前状态开始到结束的期望奖赏; 动作状态价值指在当前状态容器编排服务模块执行演员给出的容器整合动作后, 能耗和响应时间等指标变化所对应的期望累积折扣奖赏; 我们将动作状态价值与状态价值的差称为优势(advantage). 评论家通过计算优势评估演员决策的良好程度, 随着演员与评论家两个模型的不断交互, 他们各自的角色变得越来越好, 决策模型更加准确

离线训练阶段, 假定当前时刻为t. 资源检测服务检测到环境状态 $stat{e_t}$ , 演员策略网络根据当前环境状态产生容器迁移决策 $actio{n_t}$ , 评论家计算当前状态价值 $V({s_t})$ , 容器编排服务完成容器迁移后, 系统计算此次容器迁移所导致的服务质量等性能变化所对应的奖赏值 $ { reward_t } $ , 并转换为下一时刻状态 $stat{e_{t + 1}}$ . 评论家中值网络根据 $stat{e_{t + 1}}$ 和 $rewar{d_t}$ 计算出 $stat{e_t}$ 在迁移策略 $actio{n_t}$ 下的动作状态价值 $Q({s_t}, {a_t})$ . 若优势函数 $A({s_t}, {a_t}) = Q({s_t}, {a_t}) - V({s_t}) > 0$ , 则说明该动作是积极的, 若优势函数 $A({s_t}, {a_t}) < 0$ , 则说明该动作是消极, 进而优化调整策略网络.

2.2 模型输入

在各调度间隔 ${I_t}$ , 容器整合决策模型的输入是雾计算环境的系统状态 $stat{e_t}$ , 它包括数据中心主机的资源利用情况 $\phi ({H_t})$ 、容器的资源需求情况 $\phi ({A_t})$ 以及在前一间隔 ${I_{t - 1}}$ 容器所在主机的分布情况 $\phi (\widehat {actio{n_{t - 1}}})$ , 表示为一个二维的特征矩阵 $stat{e_t} = [\phi ({H_t}), \phi ({A_t}), \phi (\widehat {actio{n_{t - 1}}})]$ . 其中, 主机的资源利用情况 $\phi ({H_t})$ 为一个N×F的特征矩阵 $\{ U(h_i^t)|\forall i, h_i^t \in {H_t}\} $ , 包括主机CPU利用率、RAM、带宽和磁盘读写速率等特征, F指主机特征数量; 容器的资源需求情况 $\phi ({A_t})$ 为一个M×F'的特征矩阵 $\{ U(a_j^t)|\forall j, a_j^t \in {A_t}\} $ , 包括任务对CPU、RAM、带宽等的需求, F'指容器特征数量; 在前一间隔 ${I_{t - 1}}$ 容器所在主机分布情况 $\phi (\widehat {actio{n_{t - 1}}})$ 表示为一个M×N的分布矩阵. 综上, 系统状态表示为一个N×F+M×F'+M×N二维的特征矩阵 $stat{e_t} = [\phi ({H_t}), \phi ({A_t}), \phi (\widehat {actio{n_{t - 1}}})]$ .

2.3 模型输出

在各调度间隔 ${I_t}$ , 容器整合决策模型根据系统环境状态 $stat{e_t}$ 为活动任务 ${A_t}$ 做出调度决策, 任务对应的主机优先级列表如式(8)所示:

$ actio{n_t} = \begin{array}{*{20}{c}} \begin{array}{*{20}{c}} \;\;\;\;\;&{h_0}&{h_1}&\cdots &{h_i} \end{array}\\ \begin{array}{*{20}{c}} {a_0^{}} \\ {a_1^{}} \\ \vdots \\ {a_j^{}} \end{array} \left[ {\begin{array}{*{20}{c}} {h_0^0}&{h_0^1}&\cdots &{h_0^i} \\ {h_1^0}&{h_1^1}&\cdots &{h_1^i} \\ \vdots &\vdots &\ddots &\vdots \\ {h_j^0}&{h_j^1}&\cdots &{h_j^i} \end{array}} \right]\end{array}, \;{a_j} \in {A_t}, {h_i} \in H $

(8)

其中, $h_j^i$ 表示活动任务 ${a_j}$ 对应主机 ${h_i}$ 的优先级, 令优先级最高的主机为该任务对应的目标主机. 若容器在前一调度间隔 ${I_{t - 1}}$ 所在主机的编号与调度策略所给出的编号相同, 则无需迁移; 否则, 要进行迁移.

2.4 奖励函数

为降低雾数据中心的能耗并满足用户的低时延要求, 在学习模型中, 奖励函数 $ rewar{d_t} $ 主要从能耗和响应时间2个方面来量化, 便于定义 $ rewar{d_t} $ , 将各项指标规范化为[0, 1].

1)平均能源消耗(average energy consumption, AEC). 在任意调度间隔 $ {I_t} $ , 基础设施层所有工作状态的雾节点和云节点的平均能源消耗(容器任务完成后, 每个节点会立即进入休眠状态), 根据能耗模型可表示为式(9):

$ AEC_t^H = \dfrac{{\displaystyle\sum\nolimits_{{h_i} \in H} {{\alpha _{{h_i}}}\int_t^{t + \Delta } {{P_{{h_i}}}(t)dt} } }}{{\displaystyle\sum\nolimits_{{h_i} \in H} {{\alpha _{{h_i}}}P_{{h_i}}^{\max }(\Delta )} }} $

(9)

其中, 由于雾节点和云节点能源供应源的异构性, 系数 $ {\alpha _{{h_i}}} \in [0, 1] $ 用来区分表示雾节点和云节点, $ P_{{h_i}}^{\max } $ 为主机 $ {h_i} $ 在调度间隔 $ {I_t} $ 的最大功率 $ P_{{h_i}}^{\max } $ , 以最大功率 $ P_{{h_i}}^{\max } $ 为标准对总能耗进行归一化.

2)平均响应时间(average response time, ART). 在任意调度间隔 $ {I_t} $ 所有完成任务 $ {L_{t + 1}} $ 的平均响应时间, 根据时延模型可得平均响应时间式(10), 按最大响应时间对其进行归一化.

$ ART_t^{{L_{t + 1}}} = \dfrac{{\displaystyle\sum\nolimits_{{a_j} \in {L_{t + 1}}} {{\textit{ResponseTime}}({a_j})} }}{{\left| {{L_{t + 1}}} \right|{{\max }_t}{{\max }_{{a_j} \in {L_{t + 1}}}}{\textit{ResponseTime}}({a_j})}} $

(10)

在任意调度间隔 $ {I_t} $ , 奖励函数 $ rewar{d_t} $ 为平均能源消耗和平均响应时间指标的加权函数, 如式(11)所示, 平均能源消耗和平均响应时间越小, 则奖励越多.

$ \begin{split} rewar{d}_{t}= & -(\alpha \cdot AE{C}_{t-1}+\beta \cdot AR{T}_{t-1})\text{, }\\ & \alpha , \beta \geqslant 0\wedge \alpha +\beta =1 \end{split} $

(11)

3 基于策略梯度学习的随机动态调度 3.1 神经网络结构

利用神经网络的优势对目标函数进行精确建模, 并使用基于梯度的方法使其快速收敛. 神经网络分为公共网络、策略网络 $\pi (a|s;\theta )$ (演员)和价值网络 $v(s;\omega )$ (评论家)这3部分, 均由标准的前馈神经网络组成, 如图4所示. 网络的输入为一个大小为N×F+M×F'+M×N的二维状态特征向量(见第2.2节), 输入首先被平整化, 经过公共网络2个全连接层fc1、fc2充分提取特征后, 传给演员和评论家网络. 演员策略网络为2层全连接神经网络, 用于进一步增强演员策略网络的表达能力. 由于容器和主机的上限均为50, fc4层的输出被重塑为一个二维的50×50向量, 以此保证模型产生的调度决策能使容器映射到有效主机上. 便于计算, 在第2维度上对其应用Softmax函数进行归一化, 让所有值都在[0, 1], 且每一行中所有值的和为1. 评论家价值网络通过2层全连接层, 输出是一个常数, 表示价值函数. 神经网络训练过程中, 折扣因子γ=1, 学习率γ₁=γ₂=0.0001, 优化器选择AdamW. 神经网络结构及参数如表1所示.

3.2 学习策略

特征向量从输入层到演员、评论家的输出, 属于一个神经网络的前向传播; 然后通过基于梯度的反向传播来更新网络参数, 演员、评论家网络的参数训练过程如下.

1)价值网络 $v(s;\omega )$ 通过最小化损失函数 $Loss(\omega ) \triangleq {[V({s_t};\omega ) - V({s_{t + 1}};\omega )]^2}/2$ 来更新网络参数, 其中, 定义 ${\delta _t} \triangleq V({s_t};\omega ) - V({s_{t + 1}};\omega )$ 为时序差分误差. $V({s_t};\omega )$ 为价值网络 $v({s_t};\omega )$ 在 $t$ 时刻对状态价值函数的估计; 给定当前状态 ${s_t}$ , 智能体执行动作 ${a_t}$ 后, 环境会给出奖励 ${r_t}$ 并转换为新的状态 ${s_{t + 1}}$ , 利用蒙特卡洛近似得到 $t + 1$ 时刻状态价值函数的时序差分目标函数为 $V({s_{t + 1}};\omega ) \triangleq {r_t} + \gamma \cdot v({s_{t + 1}};\omega )$ . 通过最小化损失函数来优化价值网络 $v(s;\omega )$ , 如式(12)所示:

$ \left\{\begin{split} & {\nabla _\omega }Loss(\omega ) = {\delta _t} \cdot {\nabla _\omega }v({s_t};\omega ) \\ & \omega \leftarrow \omega - {\gamma _1} \cdot {\delta _t} \cdot {\nabla _\omega }v({s_t};\omega ) \end{split} \right.$

(12)

2) 策略网络 $\pi (a|s;\theta )$ 通过优势函数 ${A_\pi }({s_t}, {a_t}) = {Q_\pi }({s_t}, {a_t}) - {V_\pi }({s_t})$ 来评判其策略的优劣, ${Q_\pi }({s_t}, {a_t})$ 为动作价值函数. 其策略梯度表示为 ${\nabla _\theta }J(\theta ) = [{Q_\pi }({s_t}, {a_t}) - {V_\pi }({s_t})] \cdot {\nabla _\theta }\ln \pi ({a_t}|{s_t};\theta )$ . 当智能体执行动作 ${a_t}$ 之后, 环境给出新的状态的 ${s_{t + 1}}$ 的奖励 ${r_t}$ ; 利用 ${s_{t + 1}}$ 和 ${r_t}$ 对状态动作价值函数做蒙特卡洛近似可得式(13):

$ \begin{split} {\nabla _\theta }J(\theta )& \triangleq [{r_t} + \gamma \cdot v({s_{t + 1}};\omega ) - V({s_t};\omega ] \cdot {\nabla _\theta }\ln \pi ({a_t}|{s_t};\theta ) \\ & = - {\delta _t} \cdot {\nabla _\theta }\ln \pi ({a_t}|{s_t};\theta ) \end{split} $

(13)

因此, 策略网络参数 $ \theta $ 更新过程如式(14)所示:

$ \theta \leftarrow \theta - {\gamma _2} \cdot {\delta _t} \cdot {\nabla _\theta }\ln \pi ({a_t}|{s_t};\theta ) $

(14)

3.3 离线训练算法伪代码

本文通过A2C算法来完成容器整合决策模型的训练. 训练算法的伪代码如算法1所示.

算法开始阶段, 初始化演员和评论家网络; 初始化一个缓冲池, 用于存放当前状态、动作、下一时刻状态及奖赏; 初始化累计折扣因子(steps 1–3).

本文采用时序差分的学习方法来训练决策模型. 每个回合(steps 4–20), 首先随机产生容器负载和分配决策, 得到环境初始状态 $s$ . 每个回合都包含T步处理, 表示环境从状态 $s$ 出发, 每个回合历经T次与智能体的交互(steps 6–19). 每个阶段, 首先根据数据中心主机的资源利用情况 $\phi ({H_t})$ 、容器的资源需求情况 $\phi ({A_t})$ 以及在前一间隔 ${I_{t - 1}}$ 容器所在主机的分布情况 $\phi ({\widehat {action}_{t - 1}})$ 得到环境的当前状态 ${s_t}$ . 演员的策略网络g根据状态 ${s_t}$ 产生动作 $actio{n_t}$ (step 9). 执行动作后, 产生环境下一调度间隔的状态 ${s_{t + 1}}$ (steps 10, 11). 计算单步奖赏, 并将相关结果存储到缓冲池中(steps 12, 13). 然后, 每次从缓冲池中随机抽取K条记录, 利用时序差分方法计算下一时刻的状态价值, 通过最小化损失函数训练评论家网络(steps 14–17). 演员网络通过最大化优势函数更新参数(step 18). 网络参数更新后继续执行下一回合.

算法1. DR-CI容器调度决策模型训练算法

step 1. 随机初始化策略网络 $\scriptstyle \pi (a|s;\theta )$ 和价值网络 $\scriptstyle v(s;\omega )$ ;

step 2. 初始化一个重放缓冲池R, 用于存放 $\scriptstyle {s_t}$ 、 $\scriptstyle {a_t}$ 、 $\scriptstyle {r_t}$ 和 $\scriptstyle {s_{t + 1}}$ ;

step 3. 初始化累计折扣因子 $\scriptstyle \lambda $ 、 $\scriptstyle {\lambda _1}$ 和 $\scriptstyle {\lambda _2}$ ;

step 4. for episode=1 toK do

step 5.　 随机产生任务负载和容器到主机的分配决策 $\scriptstyle { action } $ ;

step 6. 　 for t=1 to T do

step 7. 　 　 $\scriptstyle {s_t} \leftarrow [\phi ({A_t}), \phi ({H_t}), \phi ({\widehat {action}_{t - 1}})] $ ;

step 8. 　　 策略网络产生调度决策 $\scriptstyle actio{n_t} \leftarrow \pi ({s_t}|\theta )$ ;

step 9. 　　 价值网络产生状态价值 $\scriptstyle V({s_t};\omega ) \leftarrow v({s_t};\omega )$ ;

step 10. 　 　按高斯分布产生 $\scriptstyle t + 1$ 时刻的任务负载;

step 11. 　　 $\scriptstyle {s_{t + 1}} \leftarrow [\phi ({A_{t + 1}}), \phi ({H_{t + 1}}), \phi ({\widehat {action}_t})] $ ;

step 12. 　　 计算奖励 $\scriptstyle {r_t} \leftarrow - (\alpha TE{C_t} + \beta AR{T_t})$ ;

step 13. 　　在R中存储 $\scriptstyle ({s_t}, {a_t}, {r_t}, {s_{t + 1}})$ ;

step 14. 　　 从R中随机采样K个样本;

step 15. 　　 计算 $\scriptstyle V({s_{t + 1}};\omega ) \triangleq {r_t} + \gamma \cdot v({s_{t + 1}};\omega )$ ;

step 16. 　　 计算 $\scriptstyle Loss(\omega ) \triangleq \frac{1}{2}{[V({s_t};\omega ) - V({s_{t + 1}};\omega )]^2}$ ;

step 17. 　　 $\scriptstyle \omega \leftarrow \omega - {\gamma _1} \cdot {\delta _t} \cdot {\nabla _\omega }v({s_t};\omega )$ ;

step 18. 　　 $\scriptstyle \theta \leftarrow \theta - {\gamma _2} \cdot {\delta _t} \cdot {\nabla _\theta }\ln \pi ({a_t}|{s_t};\theta )$ ;

step 19.　　 end for

step 20. end for

4 性能评估 4.1 实验参数

通过在PyCharm平台上进行仿真实验与基线方法进行比较. 设定雾计算基础设施层共有50台主机, 云、雾节点数量比为8:2, 基于以往的一些研究经验设定雾节点的延迟时间为3 ms, 云节点的响应时间为76 ms. 此外, 由于云雾环境是异质的, 雾主机和云主机的计算能力有很大的差异, 主机CPU、RAM以及SPEC基准下的平均耗电量参数如表2所示. 模型离线训练过程中, 设定奖励函数中权重 $\alpha = \beta = 0.5$ , 折扣率 $\gamma = 1$ , 自适应学习率从0.000 1开始, 使用AdamW优化器, 防止优化循环卡在局部优化区.

4.2 数据集

工作负载数据集由运行在BitBrain分布式数据中心的1 750台虚拟机的资源利用指标的真实痕迹组成. 该数据集由每个时间戳(相隔5 min)的工作负载信息组成, 包括请求的CPU内核数量、CPU利用率、请求的RAM与网络(接收/传输)带宽等特征. 基于用户需求的随机性和物联网设备的移动性, 任务的计算量和带宽需求随时间变化. 本文考虑一个动态任务生成模型, 在每个区间 $ {I_t} $ 开始, 新任务集 $ {N_t} $ 的大小遵循高斯分布 $ N({\mu _n}, \sigma _n^2) $ , $ ({\mu _n}, \sigma _n^2) = (5, 1.5) $ , 每个任务的需求长度为 $ N({\mu _t}, \sigma _t^2) $ , $ ({\mu _t}, \sigma _t^2) = (20, 3) $ .

4.3 评估指标

评估指标除前文提出的总能源消耗TEC、平均能源消耗AEC和平均响应时间ART(见第2.4节)外还包括服务水平目标违反率(fraction of service level object violation, SLOV).

服务水平目标违反率SLOV定义如式(15)所示. 其中 $ \psi (T) $ 是以DR-CI方法为基线的第95百分位响应时间.

$ SLO{V_t} = \frac{{\displaystyle\sum\nolimits_{T \in {L_{t + 1}}} {({\textit{ResponseTime}}(T) - \psi (T))} }}{{\displaystyle\sum\nolimits_{T \in {L_{t + 1}}} {\psi (T)} \times \displaystyle\sum\nolimits_t {|{L_{t + 1}}|} }} $

(15)

4.4 实验分析

为验证本文提出的基于深度强化学习的DR-CI方法的有效性, 将其与局部回归-最小迁移时间方法(local regression-minimum migration time, LR-MMT)、中位数绝对偏差-最大关联方法(median absolute deviation-maximum correlation, MAD-MC)、悲观-乐观在线整合方法POND和基于遗传算法的整合方法GA进行比较研究.

从图5可以看出, 在容器整合决策模型离线训练过程中, 平均损失函数不断下降, 并且在第800次迭代开始稳定收敛, 趋近于0, 意味着雾计算中心的性能在不断提高.

图6和图7分别为100个时间间隔内在50个物理节点的总能源消耗和平均能源消耗情况. 如图6所示, DR-CI方法的总能耗最小, 约为0.64 kW·h, POND算法次之, 约为0.68 kW·h. 从图7可以看出, 基线方法中POND方法的平均间隔能耗最少, 约为0.1829 kW·h, LR-MMT方法的平均间隔能耗最好, 约为0.1981 kW·h; DR-CI方法平均间隔能耗约0.1597 kW·h, 比POND低12.7%, 比LR-MMT低19.4%. 这是因为DR-CI方法整体调度更能充分利用计算资源且更稳定.

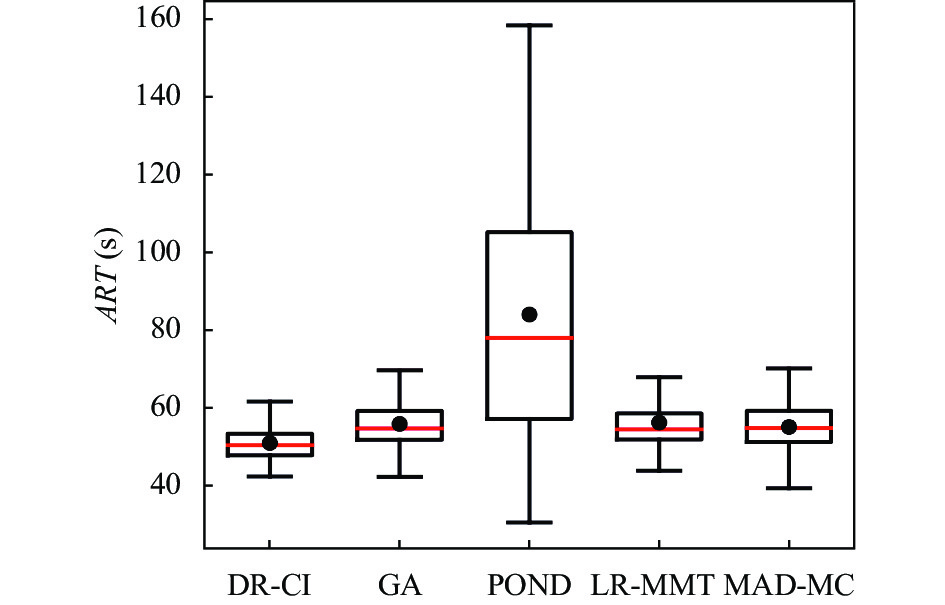
图8和图9分别为100个时间间隔内在50个物理节点的平均响应时间和服务水平目标违反率情况. 这里响应时间是指从物联网传感器创建任务到网关接收响应的时间, 从图8可以看出, 在基线方法中, MAD-MC方法的平均响应时间最低, 为54.88 s, POND的平均响应时间最高, 达到83.82 s, DR-CI方法平均响应时间为50.76 s, 比MAD-MC方法低7.5%, 比POND方法低39.44%. 又因为响应时间是服务质量的关键指标, 所以如图9所示, 在基线算法中, MAD-MC方法的平均响应时间最低, 其服务水平目标违反率也是基线中最低的为6%, DR-CI的SLOV为4.7%, 要优于其他基线算法.

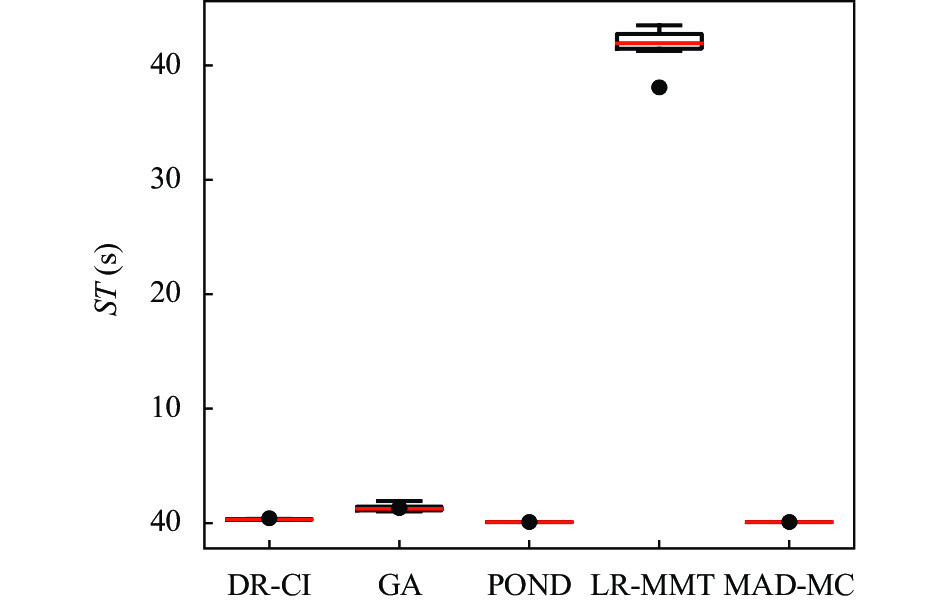
图10和图11分别为100个时间间隔内完成任务数和各种容器整合方法的决策时长. 如图10所示, DR-CI方法和MAD-MC在特定时间内完成任务数最多. 从图11可以看出, 基线方法中LR-MMT方法由于要进行大量数据拟合的原因, 其决策时间相比其他方法约高出一个数量级, POND和LR-MMT方法决策时间最短, 分别为0.29 s、0.44 s; DR-CI方法次之, 决策时间约为33 s. 这是因为DR-CI方法的决策模型网络结构产生了更多的计算开销.

5 结论

本文针对雾环境任务负载不稳定性、数据中心高能耗以及用户低时延需求等问题提出了一种基于深度强化学习的容器整合方法DR-CI, 构建了直接从系统状态到容器整合的决策模型, 避免了容器整合复杂的中间过程, 增强了使用的灵活性. 基于真实负载数据进行仿真实验, 实验结果表明DR-CI方法能够在降低能耗的同时保证系统服务质量. 未来工作中, 本文计划在真实的雾环境中实现这个模型, 结合实际的任务负载特征来优化容器调度决策模型.